Gradient Estimator-Based Amplitude Estimation for Dynamic Mode Atomic Force Microscopy: Small-Signal Modeling and Tuning
Abstract
1. Introduction
2. Gradient Estimator: Small-Signal Modeling and Tuning
2.1. Brief Overview of the Gradient Estimator
2.2. Small-Signal Modeling
2.3. Parameter Tuning
2.4. Extension to Harmonic Deflection Signal
3. Results and Discussions
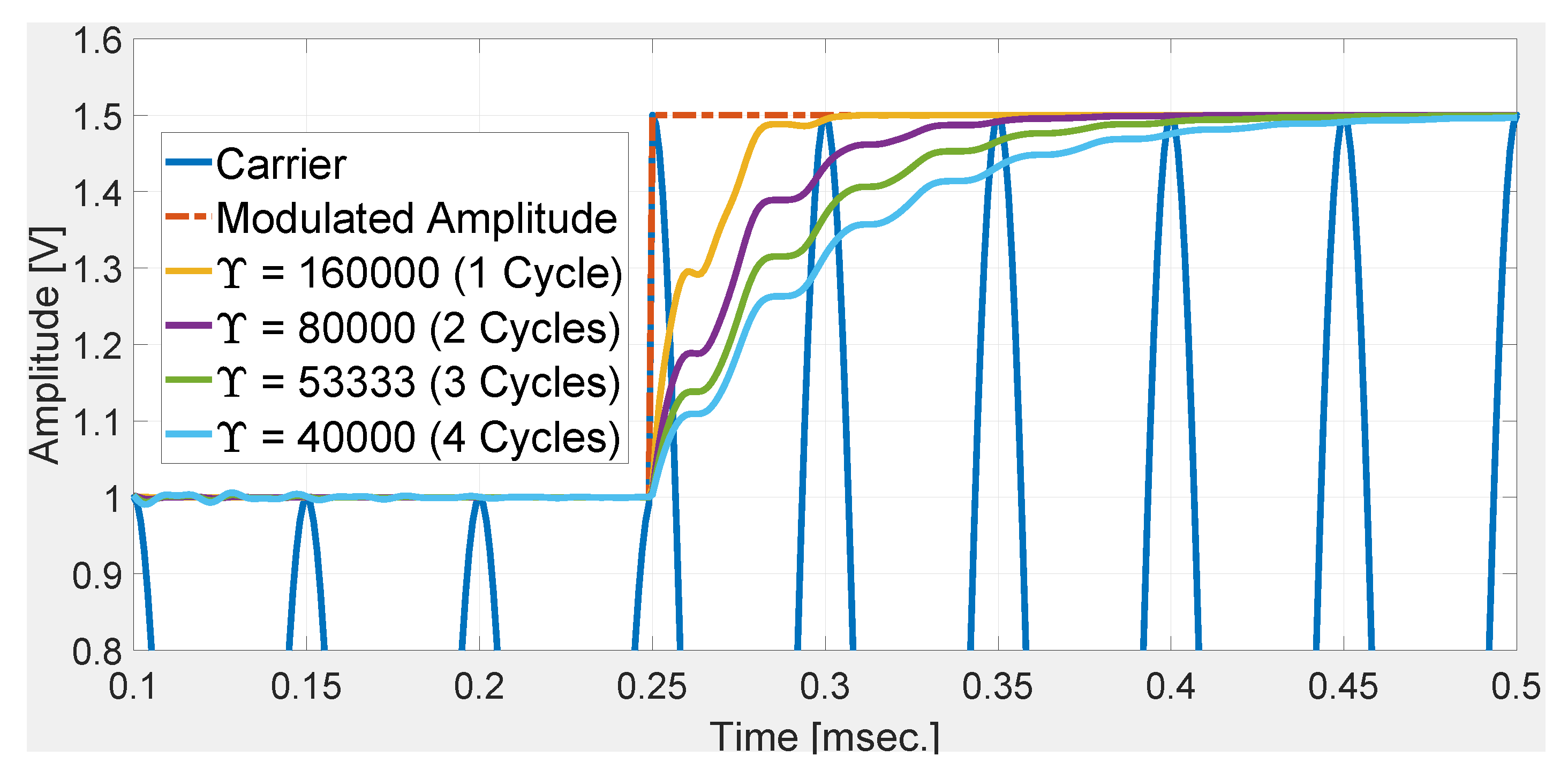
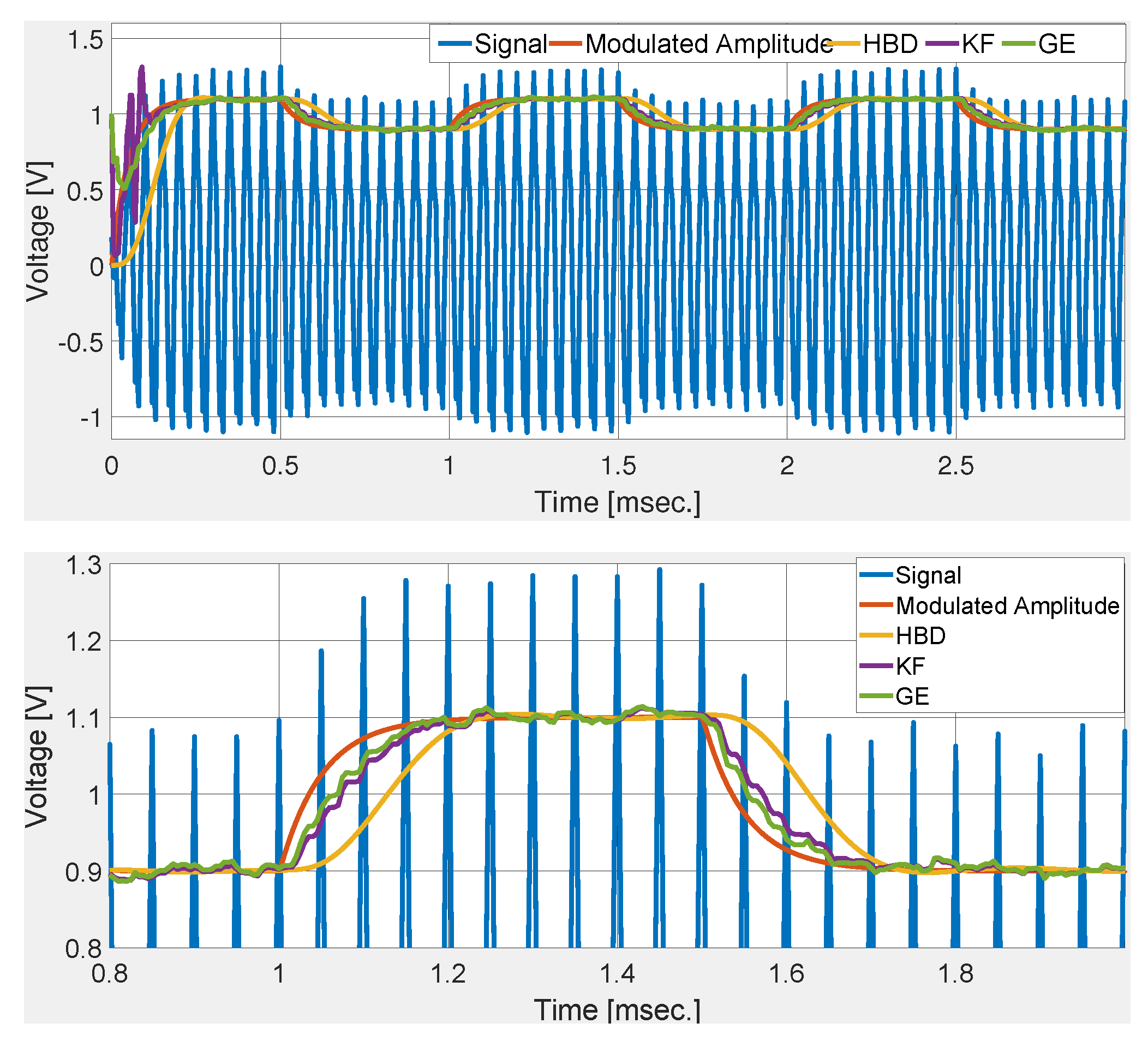
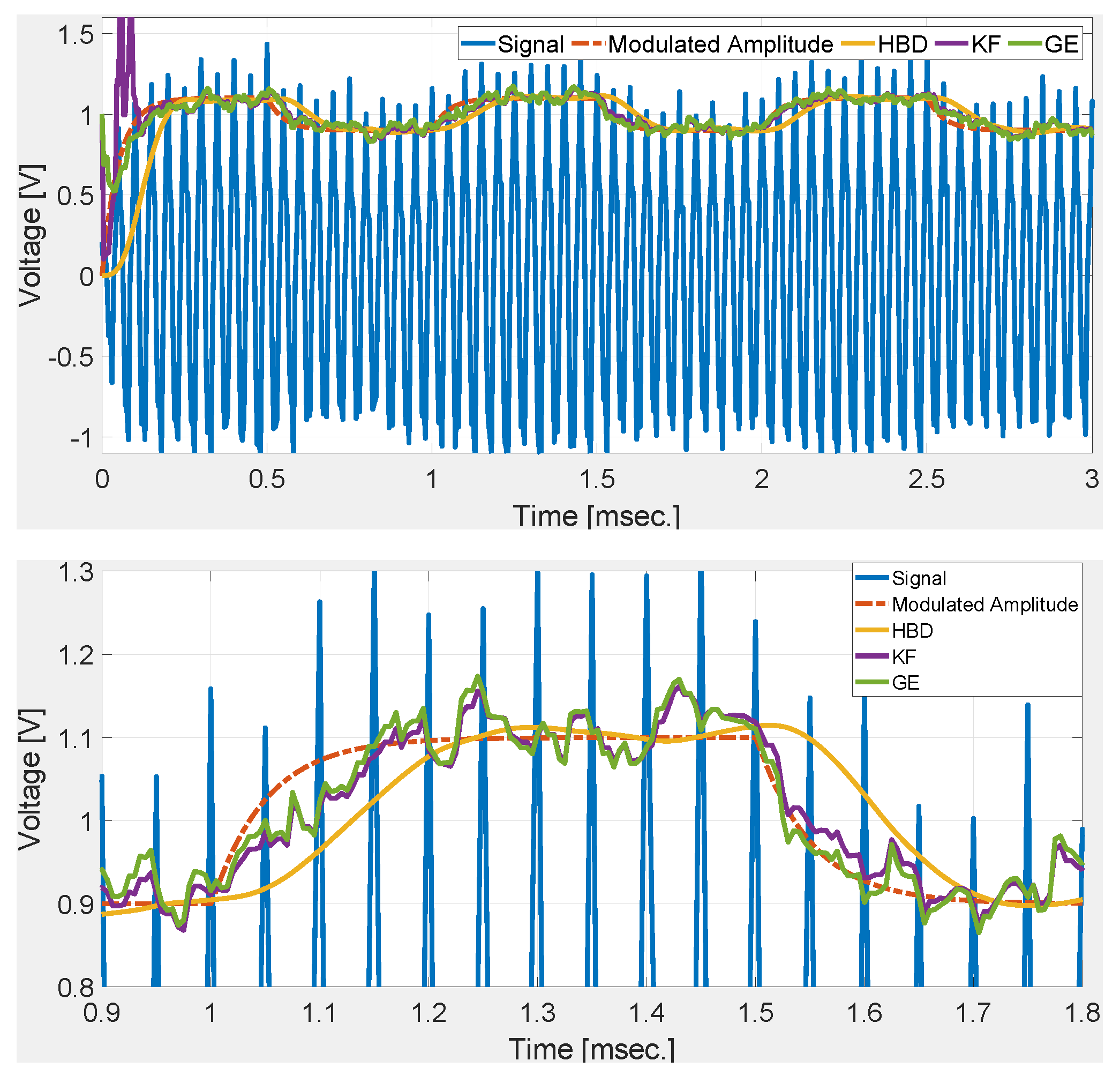
3.1. Simulation Study
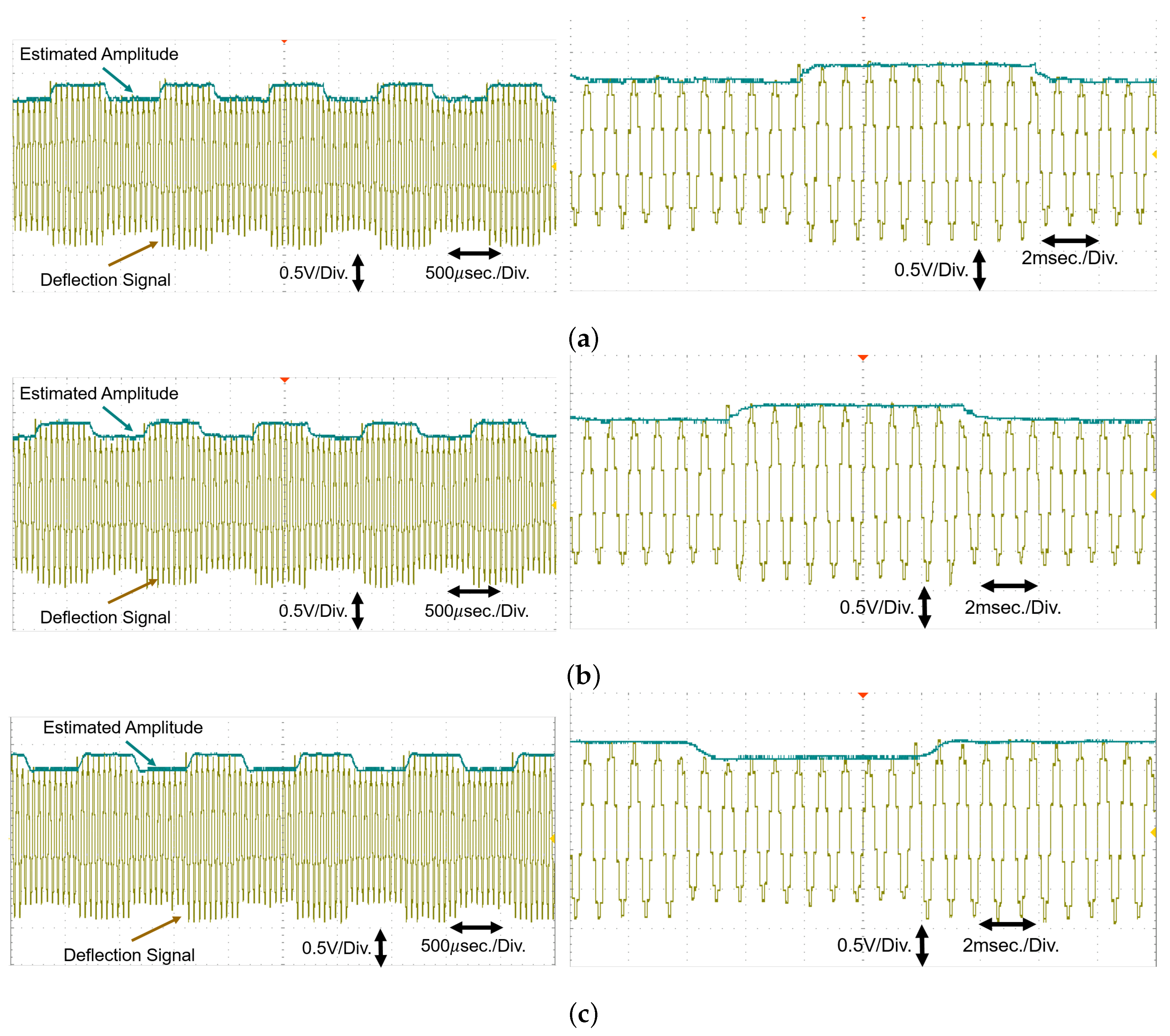
3.2. Experimental Study
4. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Shen, T.; Shirinzadeh, B.; Zhong, Y.; Smith, J.; Pinskier, J.; Ghafarian, M. Sensing and Modelling Mechanical Response in Large Deformation Indentation of Adherent Cell Using Atomic Force Microscopy. Sensors 2020, 20, 1764. [Google Scholar] [CrossRef]
- Abramovitch, D.Y.; Andersson, S.B.; Pao, L.Y.; Schitter, G. A tutorial on the mechanisms, dynamics, and control of atomic force microscopes. In Proceedings of the IEEE American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 3488–3502. [Google Scholar]
- Hölscher, H.; Schwarz, U.D. Theory of amplitude modulation atomic force microscopy with and without Q-control. Int. J. Non-Linear Mech. 2007, 42, 608–625. [Google Scholar] [CrossRef]
- Schlecker, B.; Nievergelt, A.; Ortmanns, M.; Fantner, G.; Anders, J. An analog high-speed single-cycle lock-in amplifier for next generation AFM experiments. In Proceedings of the IEEE Sensors, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar]
- Belikov, S.; Alexander, J.; Surtchev, M.; Magonov, S. Digital Q-Control and Automatic Probe Landing in Amplitude Modulation Phase Imaging AFM Mode. IFAC-PapersOnLine 2017, 50, 10882–10888. [Google Scholar] [CrossRef]
- Nievergelt, A.P.; Andany, S.H.; Adams, J.D.; Hannebelle, M.T.; Fantner, G.E. Components for high-speed atomic force microscopy optimized for low phase-lag. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 731–736. [Google Scholar]
- Pérez-Bailón, J.; Calvo, B.; Medrano, N. A CMOS Low Pass Filter for SoC Lock-in-Based Measurement Devices. Sensors 2019, 19, 5173. [Google Scholar] [CrossRef]
- Wang, G.; Reboul, S.; Choquel, J.B.; Fertein, E.; Chen, W. Circular regression in a dual-phase lock-in amplifier for coherent detection of weak signal. Sensors 2017, 17, 2615. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, Y.; Qi, N.; Dong, X. AM-AFM system analysis and output feedback control design with sensor saturation. IEEE Trans. Nanotechnol. 2013, 12, 190–202. [Google Scholar] [CrossRef]
- Karvinen, K.; Moheimani, S.R. A high-bandwidth amplitude estimation technique for dynamic mode atomic force microscopy. Rev. Sci. Instruments 2014, 85, 023707. [Google Scholar] [CrossRef] [PubMed]
- Ayat, M.; Karami, M.A.; Mirzakuchaki, S.; Beheshti-Shirazi, A. Design of multiple modulated frequency lock-in amplifier for tapping-mode atomic force microscopy systems. IEEE Trans. Instrum. Meas. 2016, 65, 2284–2292. [Google Scholar] [CrossRef]
- Ruppert, M.G.; Karvinen, K.S.; Wiggins, S.L.; Moheimani, S.R. A Kalman filter for amplitude estimation in high-speed dynamic mode atomic force microscopy. IEEE Trans. Control. Syst. Technol. 2016, 24, 276–284. [Google Scholar] [CrossRef]
- Ruppert, M.G.; Harcombe, D.M.; Moheimani, S.R. High-bandwidth demodulation in MF-AFM: A Kalman filtering approach. IEEE/ASME Trans. Mechatronics 2016, 21, 2705–2715. [Google Scholar] [CrossRef]
- Haghighi, M.S.; Sajjadi, M.; Pishkenari, H.N. Model-based topography estimation in trolling mode atomic force microscopy. Appl. Math. Model. 2020, 77, 1025–1040. [Google Scholar] [CrossRef]
- Huang, P.; Andersson, S.B. On detection and estimation in atomic force microscopy at different scan speeds. In Proceedings of the IFAC Symposium on Mechatronics, Hangzhou, China, 10–12 April 2013; pp. 153–160. [Google Scholar]
- Harcombe, D.M.; Ruppert, M.G.; Fleming, A.J. A review of demodulation techniques for multifrequency atomic force microscopy. Beilstein J. Nanotechnol. 2020, 11, 76–91. [Google Scholar] [CrossRef] [PubMed]
- Ruppert, M.G.; Harcombe, D.M.; Ragazzon, M.R.; Moheimani, S.R.; Fleming, A.J. A review of demodulation techniques for amplitude-modulation atomic force microscopy. Beilstein J. Nanotechnol. 2017, 8, 1407–1426. [Google Scholar] [CrossRef] [PubMed]
- Ragazzon, M.R.; Ruppert, M.G.; Harcombe, D.M.; Fleming, A.J.; Gravdahl, J.T. Lyapunov estimator for high-speed demodulation in dynamic mode atomic force microscopy. IEEE Trans. Control. Syst. Technol. 2018, 26, 765–772. [Google Scholar] [CrossRef]
- Harcombe, D.M.; Ruppert, M.G.; Ragazzon, M.R.; Fleming, A.J. Lyapunov estimation for high-speed demodulation in multifrequency atomic force microscopy. Beilstein J. Nanotechnol. 2018, 9, 490–498. [Google Scholar] [CrossRef]
- Ahmed, H.; Benbouzid, M. Demodulation type single-phase PLL with DC offset rejection. Electron. Lett. 2020, 56, 344–347. [Google Scholar] [CrossRef]
- Achlerkar, P.D.; Panigrahi, B.K. Recursive Least Squares based Adaptive Parameter Estimation Scheme for Signal Transformation and Grid Synchronization. IEEE J. Emerg. Sel. Top. Power Electron. 2020. [Google Scholar] [CrossRef]
- Pay, M.L.; Ahmed, H. Modeling and Tuning of Circular Limit Cycle Oscillator FLL With Preloop Filter. IEEE Trans. Ind. Electron. 2019, 66, 9632–9635. [Google Scholar] [CrossRef]
- Ahmed, H.; Benbouzid, M. Simplified Second-Order Generalized Integrator-Frequency-Locked Loop. Adv. Electr. Electron. Eng. 2019, 17, 405–412. [Google Scholar] [CrossRef]
- Ahmed, H.; Pay, M.L.; Benbouzid, M.; Amirat, Y.; Elbouchikhi, E. Hybrid estimator-based harmonic robust grid synchronization technique. Electr. Power Syst. Res. 2019, 177, 106013. [Google Scholar] [CrossRef]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Ahmed, H.; Bierhoff, M.; Benbouzid, M. Multiple Nonlinear Harmonic Oscillator-Based Frequency Estimation for Distorted Grid Voltage. IEEE Trans. Instrum. Meas. 2019, 1. [Google Scholar] [CrossRef]
- Shewale, M.; Razban, A.; Deshmukh, S.; Mulik, S. Design, Development and Implementation of the Position Estimator Algorithm for Harmonic Motion on the XY Flexural Mechanism for High Precision Positioning. Sensors 2020, 20, 662. [Google Scholar] [CrossRef] [PubMed]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, H.; Benbouzid, M. Gradient Estimator-Based Amplitude Estimation for Dynamic Mode Atomic Force Microscopy: Small-Signal Modeling and Tuning. Sensors 2020, 20, 2703. https://doi.org/10.3390/s20092703
Ahmed H, Benbouzid M. Gradient Estimator-Based Amplitude Estimation for Dynamic Mode Atomic Force Microscopy: Small-Signal Modeling and Tuning. Sensors. 2020; 20(9):2703. https://doi.org/10.3390/s20092703
Chicago/Turabian StyleAhmed, Hafiz, and Mohamed Benbouzid. 2020. "Gradient Estimator-Based Amplitude Estimation for Dynamic Mode Atomic Force Microscopy: Small-Signal Modeling and Tuning" Sensors 20, no. 9: 2703. https://doi.org/10.3390/s20092703
APA StyleAhmed, H., & Benbouzid, M. (2020). Gradient Estimator-Based Amplitude Estimation for Dynamic Mode Atomic Force Microscopy: Small-Signal Modeling and Tuning. Sensors, 20(9), 2703. https://doi.org/10.3390/s20092703





