Image Motion Measurement and Image Restoration System Based on an Inertial Reference Laser
Abstract
:1. Introduction
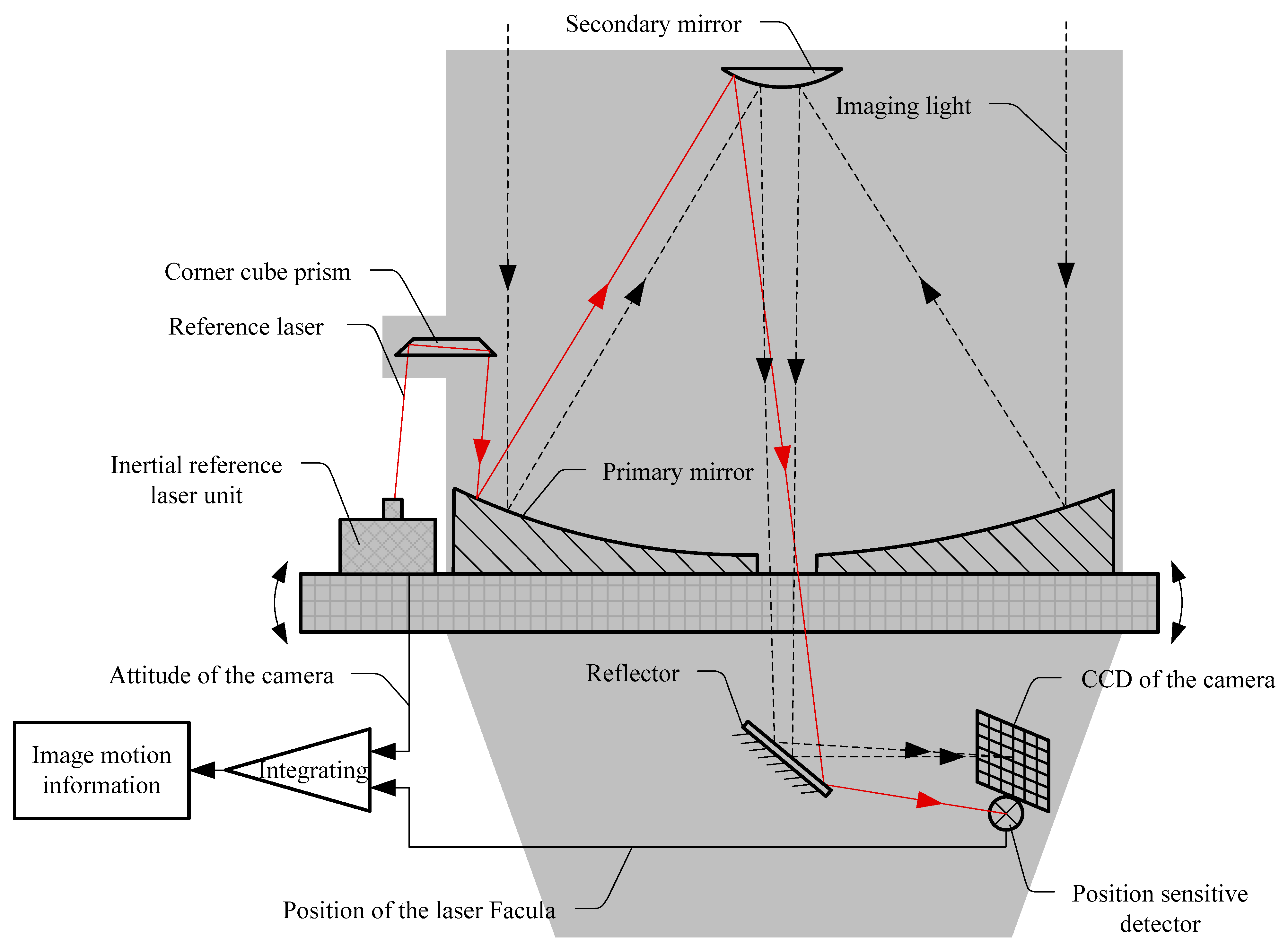
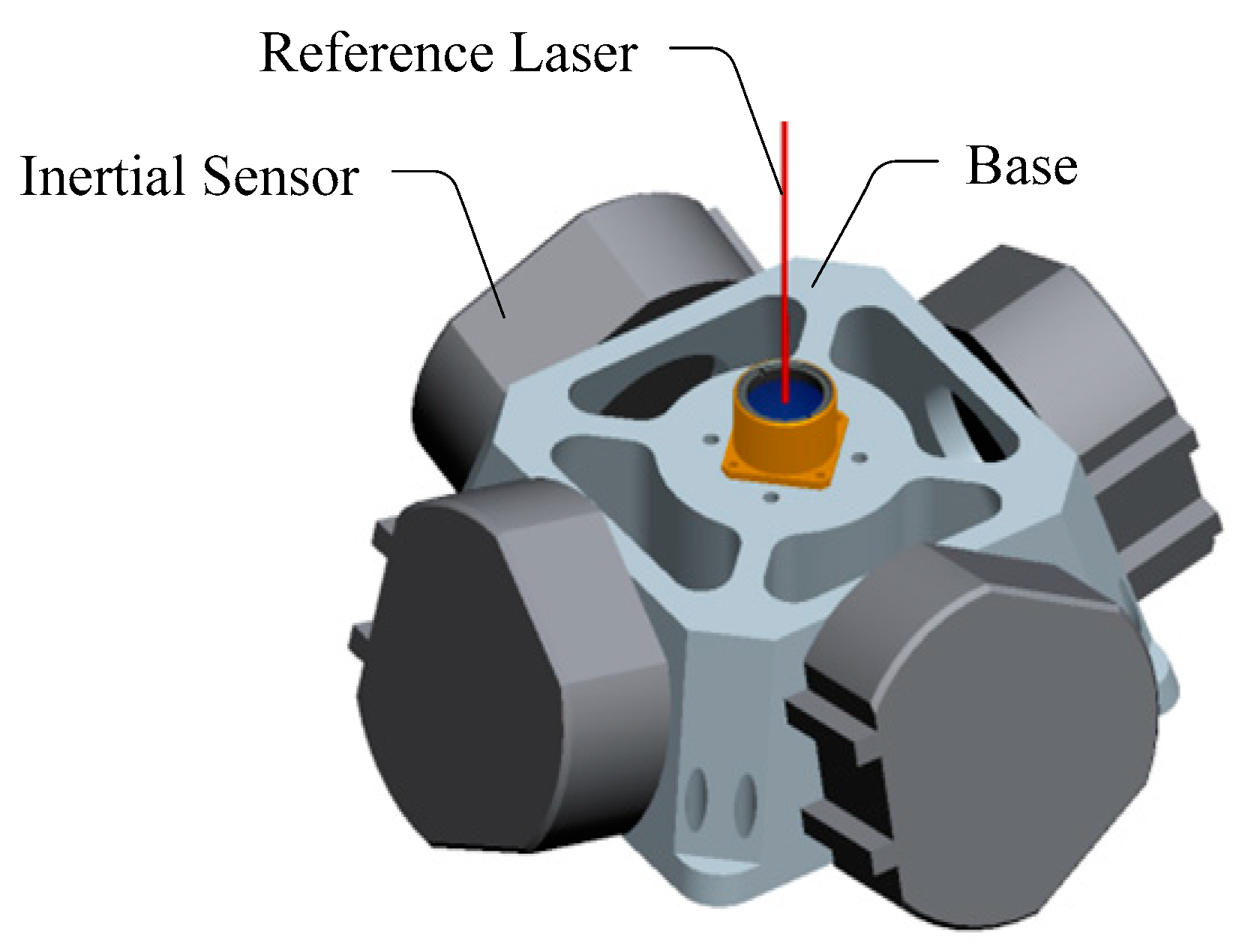
2. Principle of Image Motion Measurement Based on Inertial Reference Laser
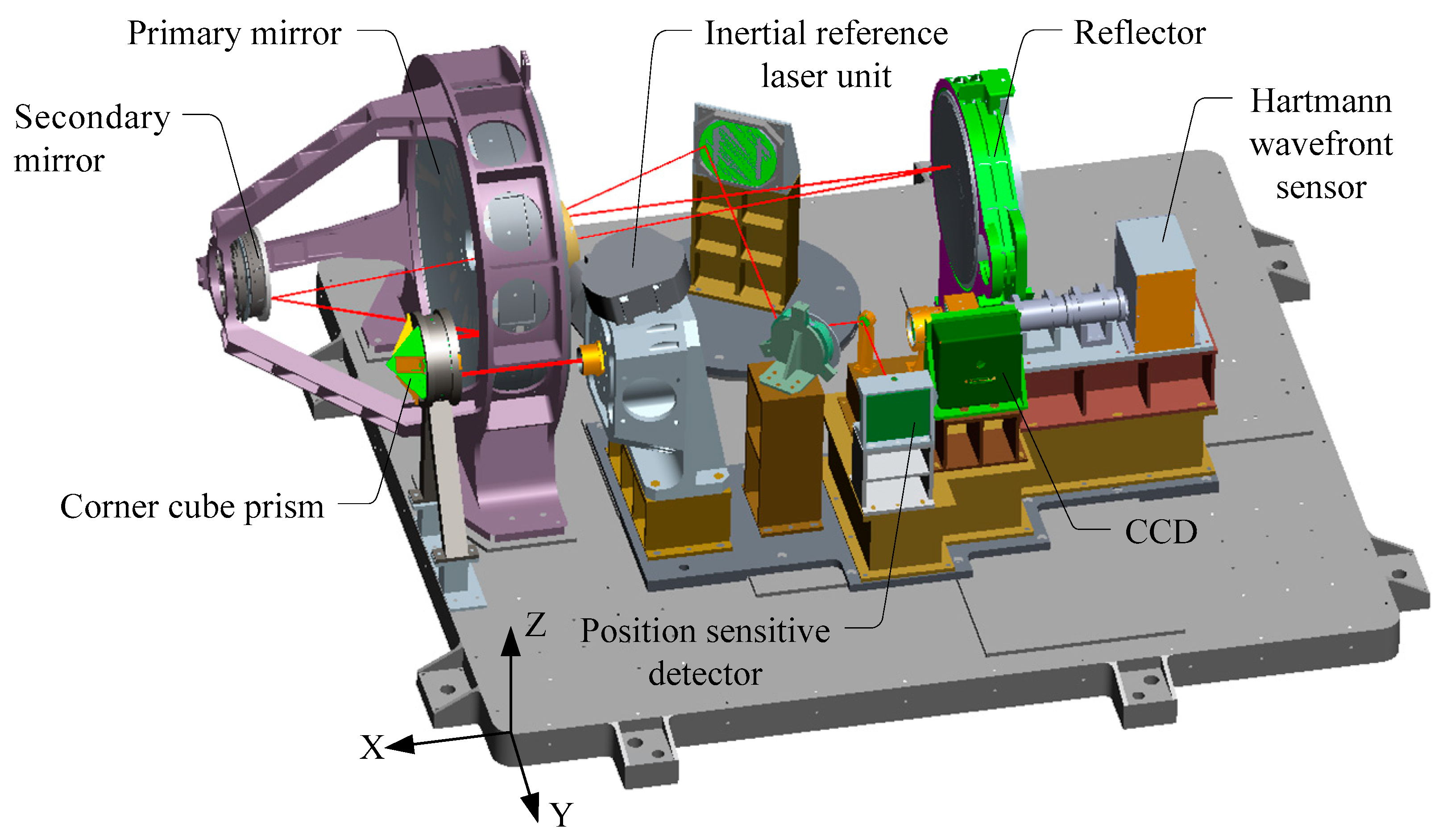
3. Image Motion Measurement System and Experimental Environment
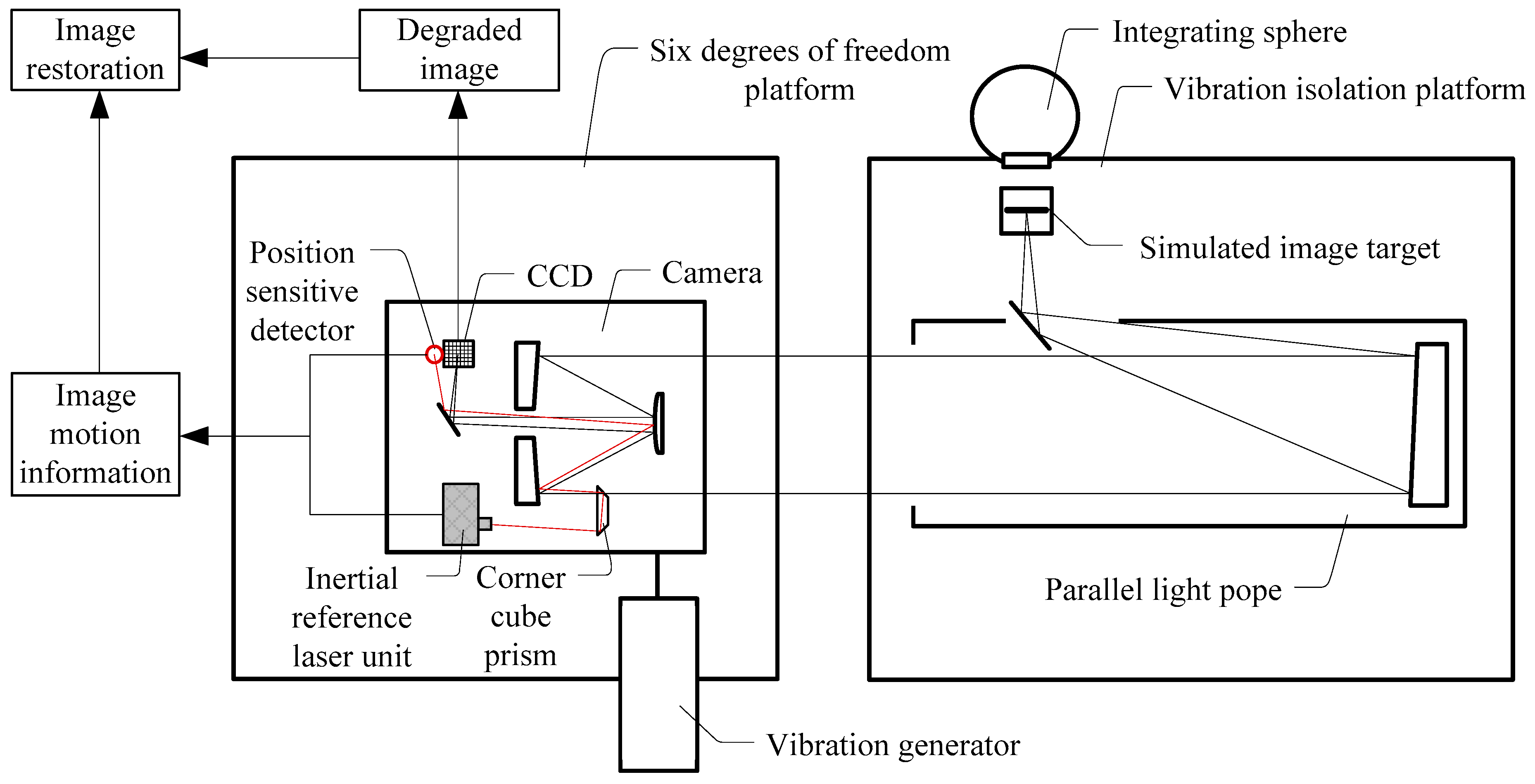
3.1. Image Motion Measurement Experimental System
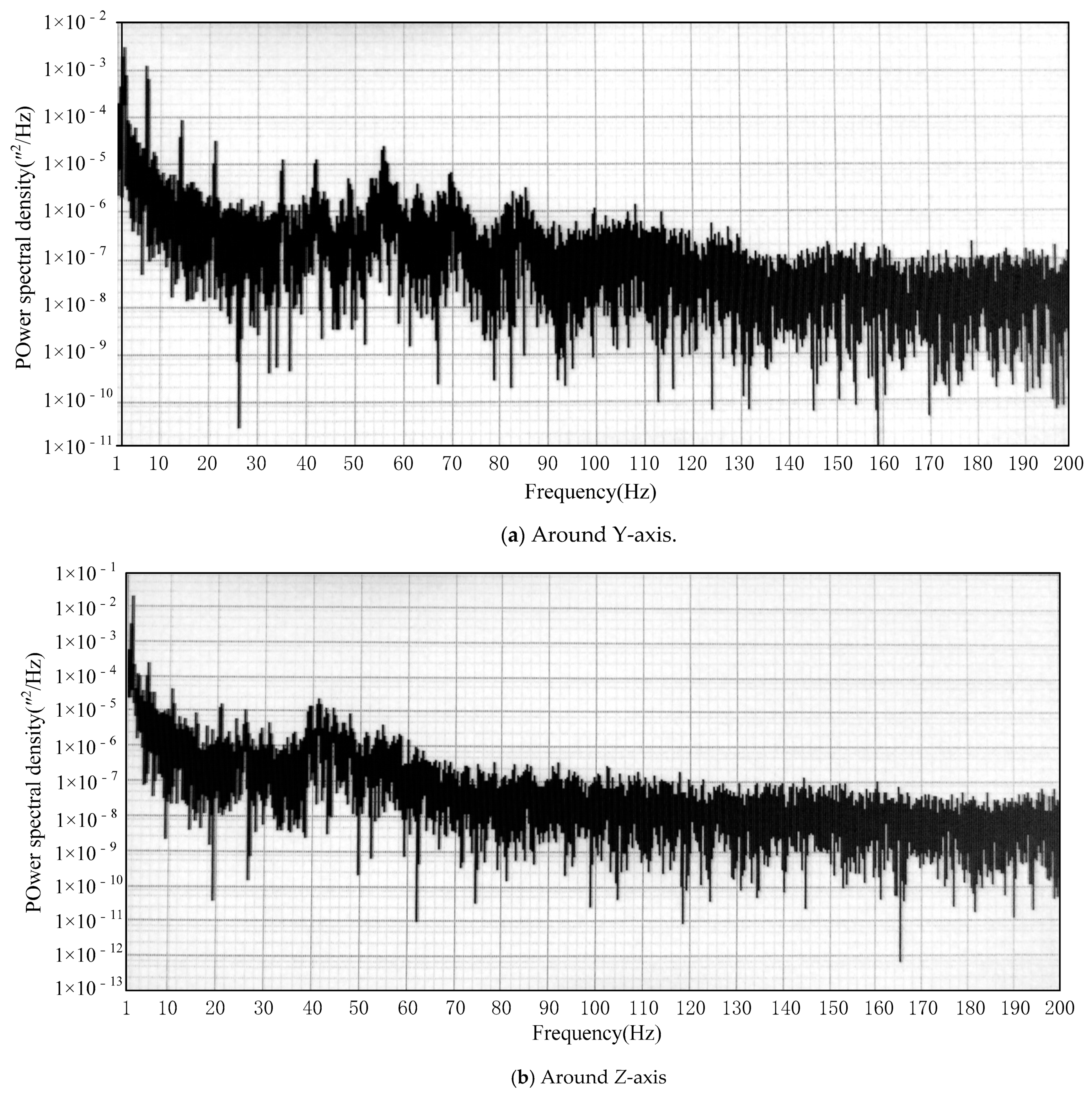
3.2. Measurement of Background Noise in the Experiment Environment
4. Principles of Image Restoration
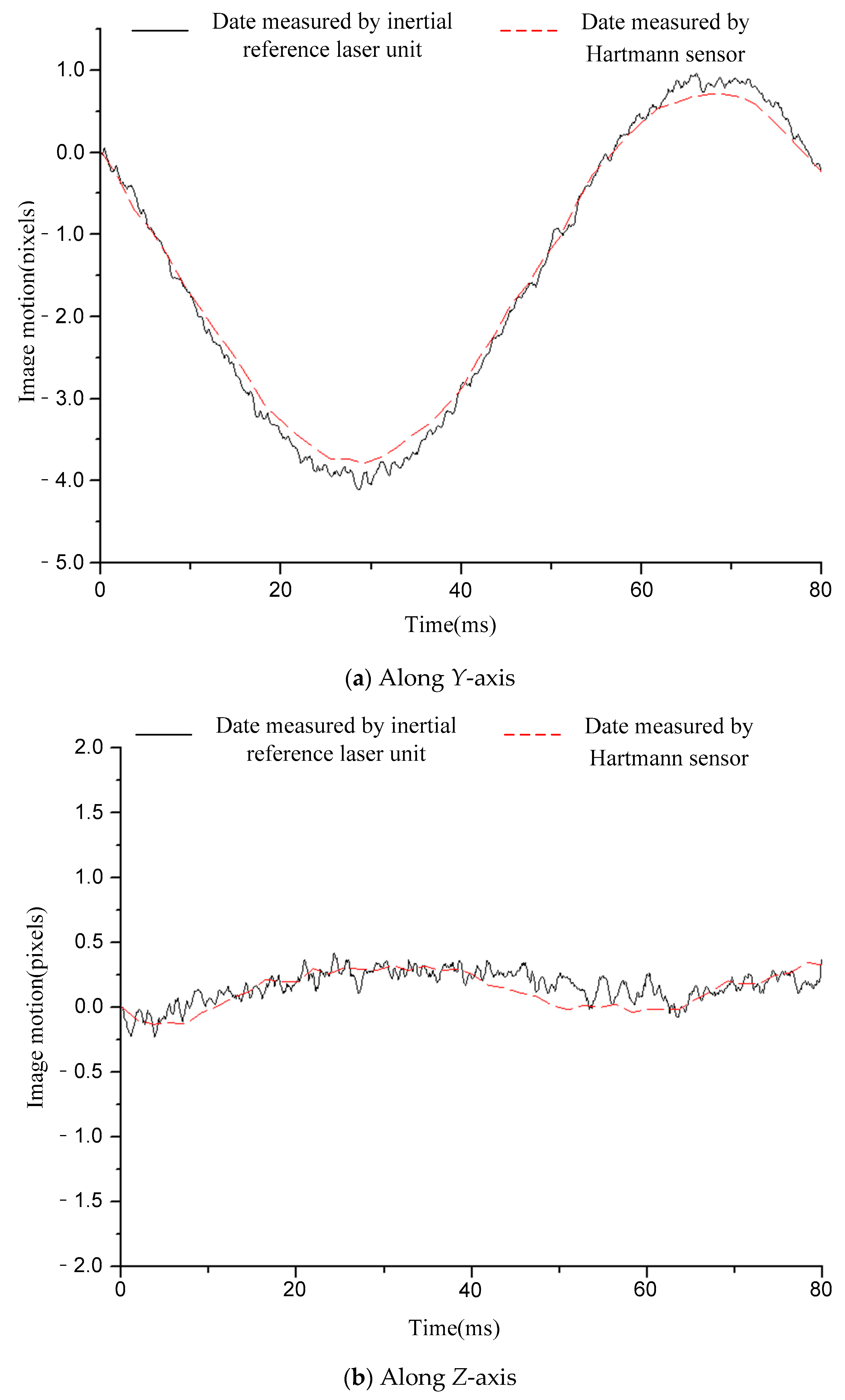
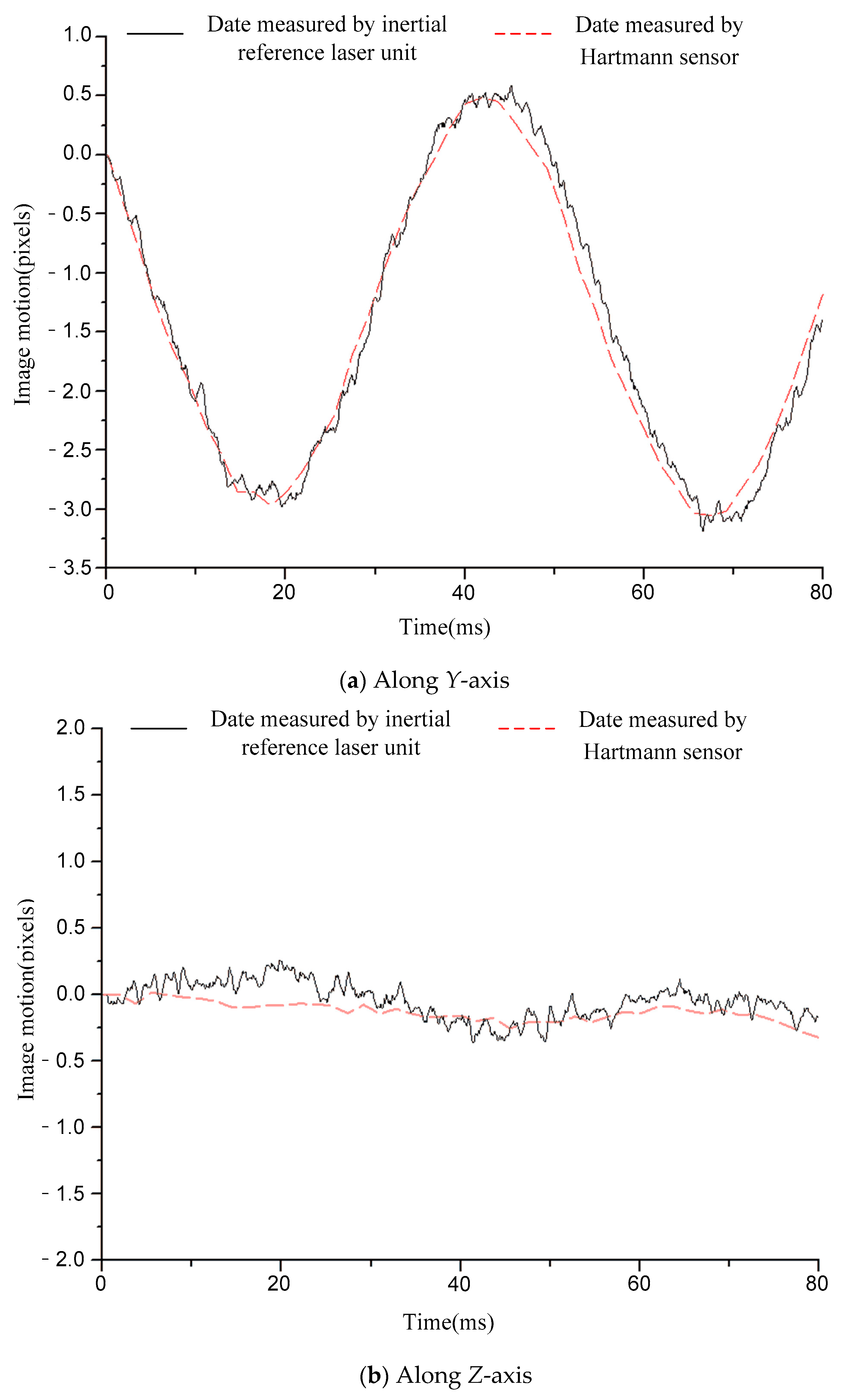
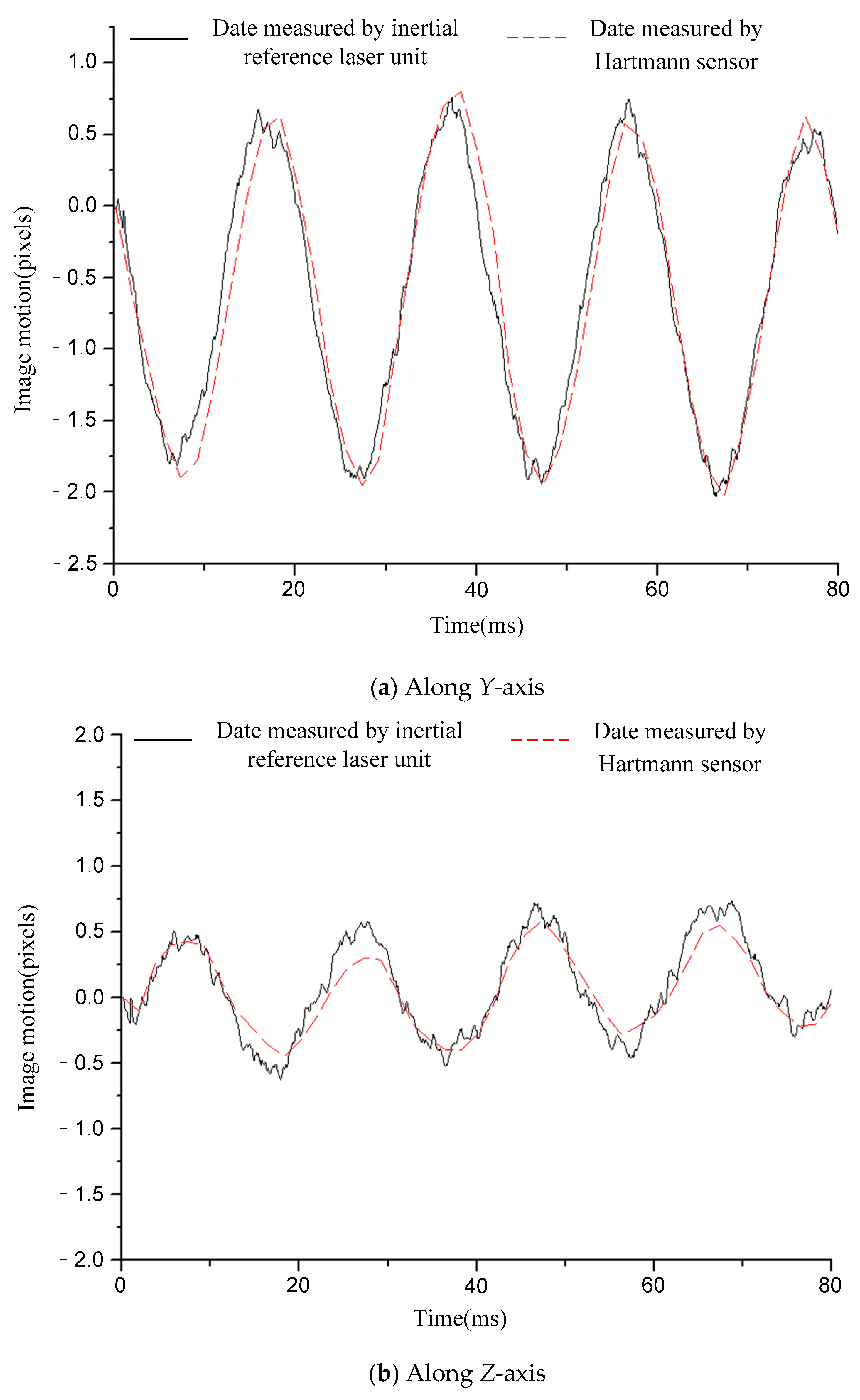
5. Accuracy Verification for Image Motion measurement
6. Image Quality Improvement Experiment Based on Inertial Reference Laser
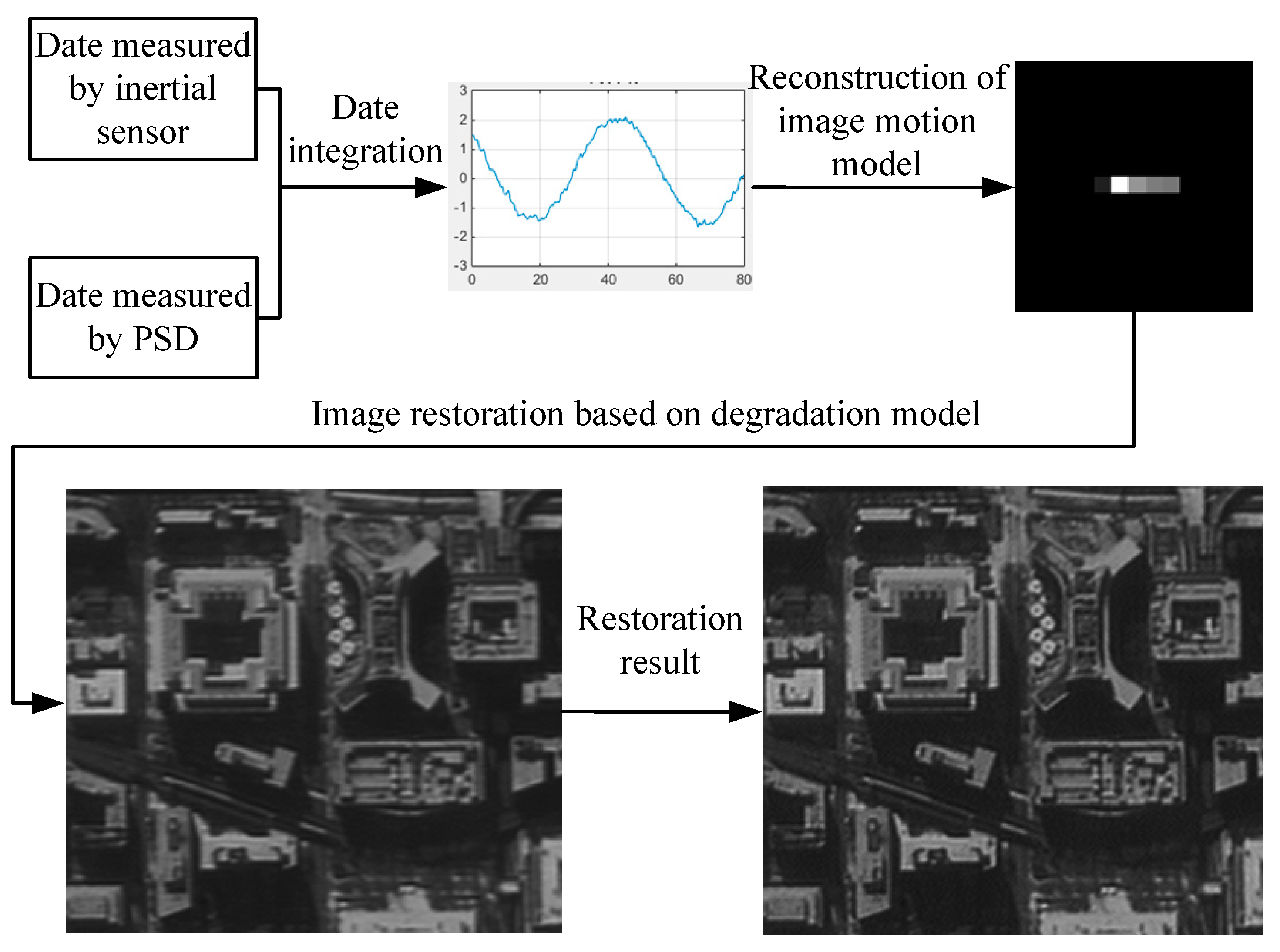
6.1. Experimental Method and Process
- (1)
- A degraded image was taken using the camera, and the inertial reference laser system was used to measure the image motion information of the optical system.
- (2)
- The image motion model was reconstructed based on the image motion information, and the image motion degradation model in the integral time was obtained.
- (3)
- Based on the comprehensive degradation model, the degraded image was restored using image restoration software to obtain a clear image.
- (4)
- The MTF values of the degraded and restored images at a Nyquist frequency were calculated for a quantitative evaluation.
6.2. Image Quality Improvement Based on Inertial Reference Laser
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wikipedia.GeoEye-1[EB/OL]. Available online: https://en.wikipedia.org/wiki/GeoEye-1 (accessed on 17 September 2018).
- Wikipedia.WorldView-4[EB/OL]. Available online: https://en.wikipedia.org/wiki/WorldView-4 (accessed on 17 September 2018).
- Wang, D.; He, H. Observation Capability and Application Prospect of GF-4 Satellite. Spacecr. Recovery Remote Sens. 2017, 38, 98–106. (In Chinese) [Google Scholar]
- Li, X.; Hu, Y. Vibration suppression in optical inter-satellite communications. J. Astronaut. 2002, 23, 77–80. (In Chinese) [Google Scholar]
- Park, G.; Lee, D.O.; Han, J.H. Development of multi-degree-of-freedom microvibration emulator for efficient jitter test of spacecraft. J. Intell. Mater. Syst. Struct. 2014, 25, 1069–1081. [Google Scholar] [CrossRef]
- Toyoshima, M.; Takayama, Y.; Kunimori, H.; Jono, T.; Yamakawa, S. In-orbit measurements of spacecraft microvibrations for satellite laser communication links. Opt. Eng. 2010, 49, 083604. [Google Scholar] [CrossRef]
- He, S.; Xu, Z.; Wang, X.; Li, A.; Huo, Q. Design and testing of a parallel manipulator for space micro-vibration simulation. In Conference towards Autonomous Robotic Systems; Springer: Cham, Switzerland, 2017; pp. 86–100. [Google Scholar]
- Prashant, A.R.; Madheswaran, M.; Kartik, V.; Naidu, V.R.; Govindan, P.; Aravindakshan, P. System development for micro vibration measurements on spacecrafts. In Proceedings of the International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Kumaracoil, India, 16–17 December 2016; IEEE: New York, NY, USA, 2016; pp. 98–103. [Google Scholar]
- Ge, R.; Wu, Q.; Wang, Y. The Study of Image Motion Measurement based on Joint Transform Correlator. Comput. Simul. 2010, 27, 215–219. (In Chinese) [Google Scholar]
- Liu, H.; Xu, S.; Wang, D. Space camera image motion measurement based on images from time delayed integration sensors overlapped area. Acta Opt. Sin. 2014, 34, 0212001. [Google Scholar]
- Wang, Z.; Zhuang, X.; Zhang, L. Effect of image motion and vibration on image quality of TDICCD camera. Appl. Mech. Mater. 2012, 128, 584–588. [Google Scholar] [CrossRef]
- Wang, C.; You, Z.; Xing, F.; Zhang, G. Image motion velocity field for wide view remote sensing camera and detectors exposure integration control. Acta Opt. Sin. 2013, 33, 0511002. [Google Scholar] [CrossRef]
- Hayden, W.L.; McCullough, T.; Reth, A. Wideband Precision Two-axis Beam Steer Tracking Servo Design and Test Results. SPIE 1993, 1866, 271–279. [Google Scholar]
- Li, J.; Liu, Z.; Liu, S. Suppressing the image smear of the vibration modulation transfer function for remote-sensing optical cameras. Opt. Soc. Am. 2017, 56, 1616–1624. [Google Scholar] [CrossRef]
- Janscher, K.; Tchernykh, V. Optical Correlator for Image Motion Compensation in the Focal Plane of a Satellite Camera. Space Technol. 2001, 21, 127–132. [Google Scholar]
- Valerij, T.; Sergei, D.; Klaus, J.; Wolgang, G.; Bernd, H. SmartScan--Hardware Test Results for Smart Optoelectronic Image Correction for Push broom cameras. SPIE 2002, 4814, 264–272. [Google Scholar]
- Tchernykh, V.; Beck, M.; Janschek, K. Optical correlator based optical flow processor for real time visual navigation. In Obinata G, Dutta A Vision Systems: Application; Tech Education and Publishing: Rijeka, Croatia, 2007. [Google Scholar]
- Yi, H.; Zhao, H.; Li, Y.; Wen, D. Improved Digital Processing Method Used for Image Motion Measurement Based on Hybrid Opto-digital Joint Transform Correlator. Chin. Opt. Lett. 2010, 8, 989–992. [Google Scholar]
- Nayar, S.K.; Ben-Ezra, M. Motion-based Motion Deblurring. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 689–698. [Google Scholar] [CrossRef]
- Fan, C.; Li, Y.C.; Yi, H.W. Research on Measurement Method of Image Motion of Space Camera Based on Optical Correlator. Acta Opt. Sin. 2011, 3, 1–5. (In Chinese) [Google Scholar]
- Barrera, J.F.; Vargas, C.; Tebaldi, M. Known-plain text attack on a joint transform correlator encrypting system. Opt. Lett. 2010, 35, 3553–3555. [Google Scholar] [CrossRef]
- Nishchal, N.K.; Goyal, S.; Aran, A.; Beri, V.K.; Gupta, A.K. Binary differential joint transform correlator based on a ferroelectric liquid crystal electrically addressed spatial light modulator. Opt. Eng. 2006, 45, 026401. [Google Scholar] [CrossRef]
- Qian, Y.; Li, Y.; Shao, J. Real-time image stabilization for arbitrary motion blurred image based on opto-electronic hybrid joint transform correlator. Opt. Express 2011, 19, 10762–10768. [Google Scholar] [CrossRef]
- Qian, Y.; Hu, F.; Cheng, X.; Jin, W. Real-time image deblurring by optoelectronic hybrid processing. Appl. Opt. 2011, 50, 6184–6188. [Google Scholar] [CrossRef]
- McEwen, A.S.; Banks, M.E.; Baugh, N.; Becker, K.; Boyd, A.; Bergstrom, J.W.; Beyer, R.A.; Bortolini, E.; Bridges, N.T.; Byrne, S.; et al. The high resolution imaging science experiment (HiRISE) during MRO′s primary science phase (PSP). Icarus 2010, 205, 2–37. [Google Scholar] [CrossRef]
- Bely, P.Y.; Lupie, O.L.; Hershey, J.L. Line-of-sight jitter of the Hubble space telescope. Proc. SPIE 1993, 1945, 55–61. [Google Scholar]
- Mattson, S.; Boyd, A.; Kirk, R.L. HiJACK: Correcting spacecraft jitter in HiRISE images of Mars. Health Manag. Technol. 2009, 33, A162. [Google Scholar]
- Wang, M.; Fan, C.; Pan, J.; Jin, S.; Chang, X. Image jitter detection and compensation using a high-frequency angular displacement method for Yaogan-26 remote sensing satellite. ISPRS J. Photogramm. Remote Sens. 2017, 130, 32–43. [Google Scholar] [CrossRef]
- Tong, X.; Xu, Y.; Ye, Z.; Liu, S.; Tang, X.; Li, L.; Xie, H.; Xie, J. Attitude oscillation detection of the ZY-3 satellite by using multispectral parallax images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3522–3534. [Google Scholar] [CrossRef]
- Zhou, P.; Jin, S.; Dong, C.; Li, N. Development of a blurred spectral images restoration technology for CTIS imaging spectrometer. Opt. Soc. Am. 2016, 24, 4881–4889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, H.; Ma, H.; Yan, D.; Jiang, Z. Image Motion Detection for Space Camera. Laser Optoelectr. Prog. 2019, 56, 080006. (In Chinese) [Google Scholar]
- Olivas, S.J.; Šorel, M.; Ford, J.E. Platform motion blur image restoration system. Appl. Opt. 2012, 51, 8246–8256. [Google Scholar] [CrossRef]
- Joshi, N.; Kang, S.B.; Zitnick, C.L.; Szeliski, R. Image deblurring using inertial measurement sensors. ACM Trans. 2010, 29, 30:1–30:9. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 2nd ed.; Publishing House of Electronics Industry: Beijing, China, 2002; pp. 144–211. [Google Scholar]
- Yang, Z.; Yang, Z.; Gui, G. A convex constraint variational method for restoring blurred images in the presence of alpha-stable noises. Sensors 2018, 18, 1175. [Google Scholar] [CrossRef] [Green Version]
- Xiang, J.; Ye, P.; Wang, L.; He, M. A novel image-restoration method based on high-order total variation regularization term. Electronics 2019, 8, 867. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, P.; Wohlberg, B. Efficient Minimization Method for a Generalized Total Variation Functional. IEEE Trans. Image Process 2009, 18, 322–332. [Google Scholar] [CrossRef] [PubMed]
- Takeyama, S.; Ono, S.; Kumazawa, I. A constrained convex optimization approach to hyperspectral image restoration with hybrid spatio-spectral regularization. Remote Sens. 2020, 12, 3541. [Google Scholar] [CrossRef]
- Levin, A.; Fergus, R.; Durand, F.; Freeman, W.T. Image and depth from a conventional camera with a coded aperture. ACM Trans. Graph. 2007, 26. [Google Scholar]
- Krishnan, D.; Fergus, R. Fast image deconvolution using hyper-laplacian priors. Adv. Neural Inf. Process. Syst. 2009, 22, 1–9. [Google Scholar]
- Dong, W. Research on Image Restoration Based on Vibration Detection Using Fiber Optic Gyroscope; Zhejiang University: Hangzhou, China, 2013. (In Chinese) [Google Scholar]
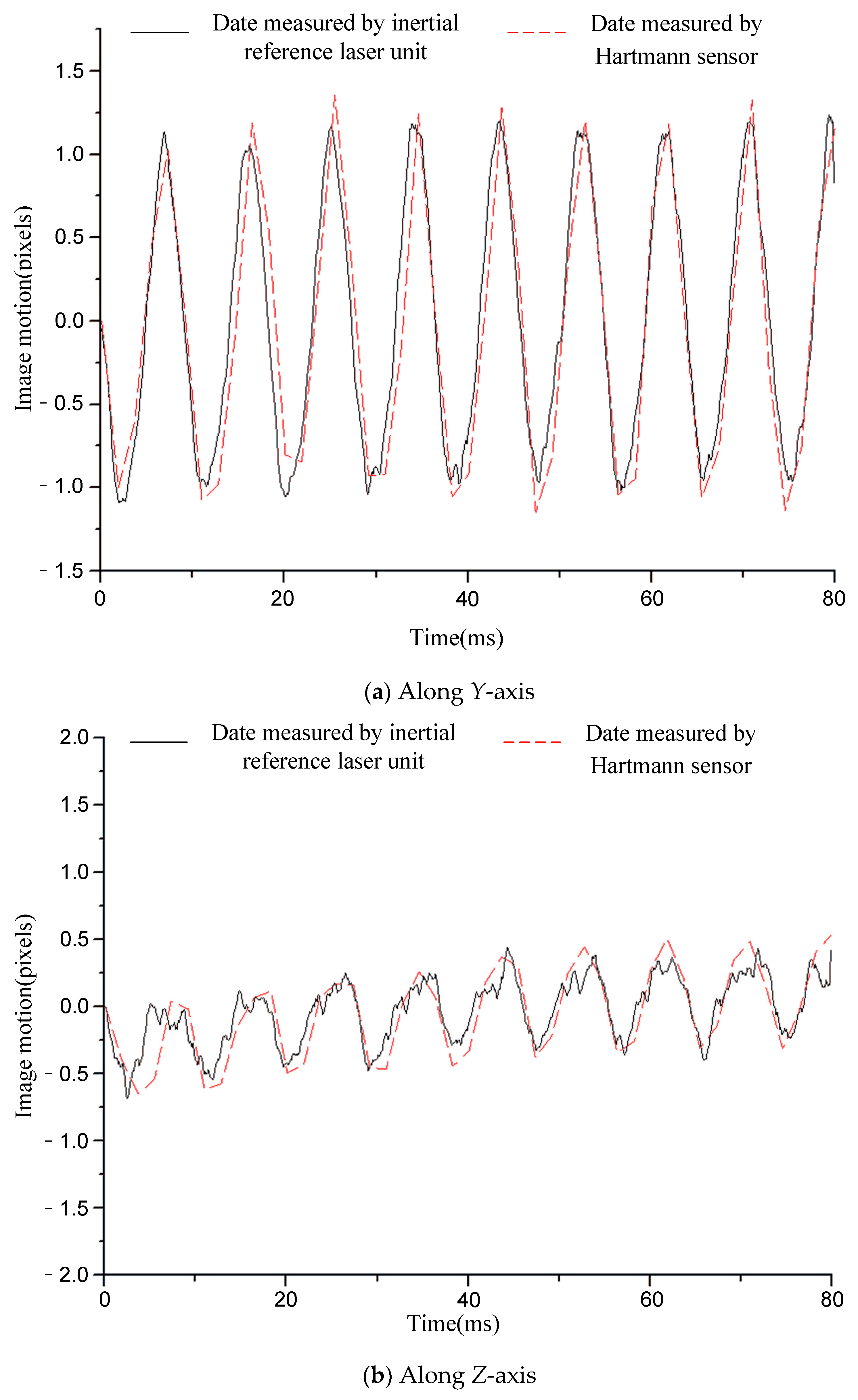
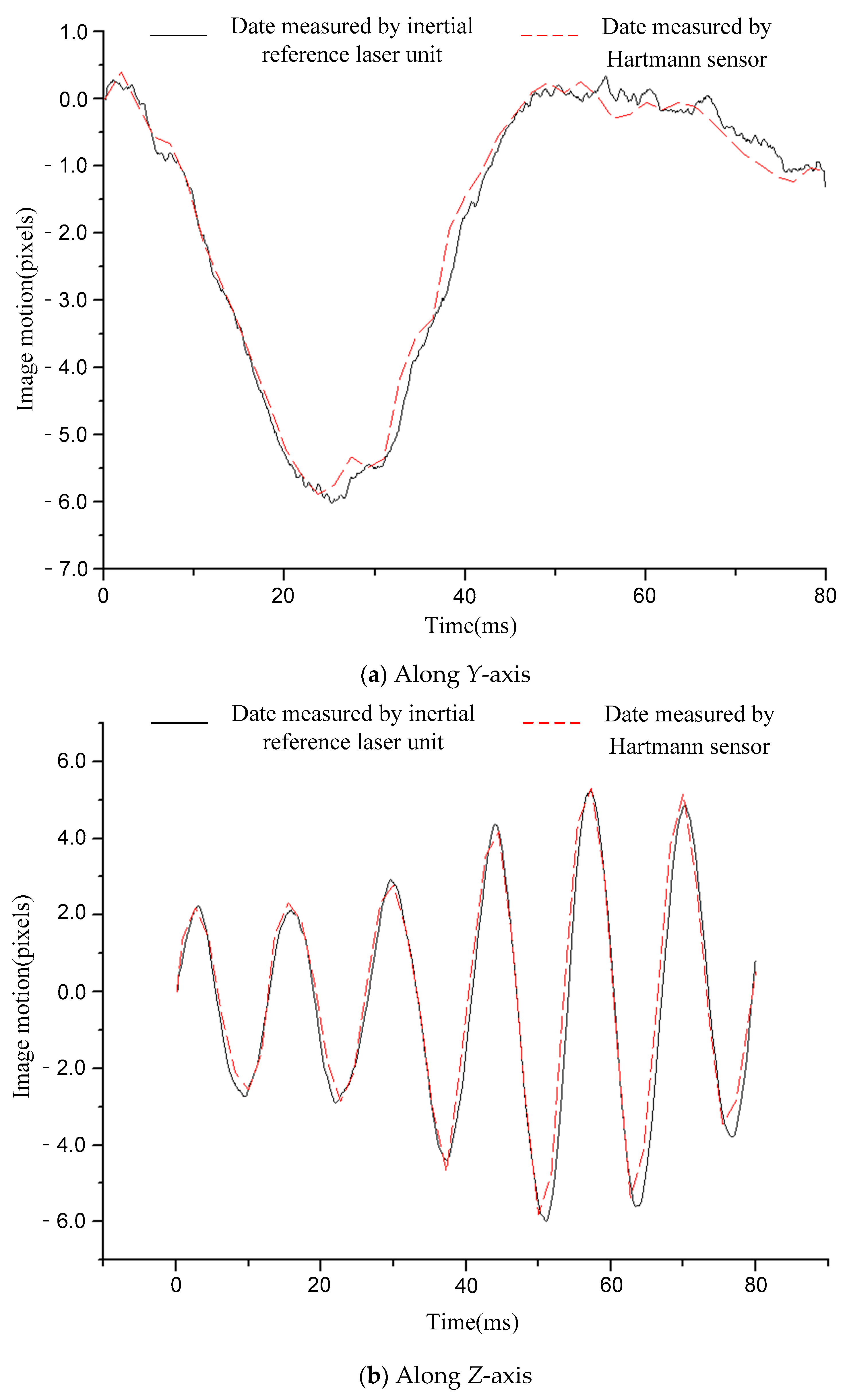





| Around Y-Axis (″) | Around Z-Axis (″) | |
|---|---|---|
| Background noise (1–200 Hz, RMS) | 0.029 | 0.037 |
| Background noise (3–200 Hz, RMS) | 0.014 | 0.012 |
| Condition | 12.5 Hz Sinusoidal | 20 Hz Sinusoidal | 50 Hz Sinusoidal | 110 Hz Sinusoidal | Random Vibration | |
|---|---|---|---|---|---|---|
| Difference | Y-axis | 0.07 pixel | 0.07 pixel | 0.12 pixel | 0.09 pixel | 0.08 pixel |
| Z-axis | 0.06 pixel | 0.12 pixel | 0.11 pixel | 0.07 pixel | 0.06 pixel | |
| Excitation | 20 Hz Sinusoidal | 50 Hz Sinusoidal | 110 Hz Sinusoidal | Random Vibration | |
|---|---|---|---|---|---|
| Jitter (P-V) | 3.5 pixels | 2.5 pixels | 2.5 pixels | 3 pixels (Y) and 2 pixels (Z) | |
| Integration time | 80 ms | 80 ms | 80 ms | 40 ms | |
| MTF | Original | 0.037 | 0.045 | 0.044 | 0.048 |
| Increased | 0.067 | 0.080 | 0.071 | 0.090 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, R.; Wang, H.; Jin, T.; Gao, Y.; Sun, X.; Yan, T.; Zang, J.; Yin, K.; Wang, S. Image Motion Measurement and Image Restoration System Based on an Inertial Reference Laser. Sensors 2021, 21, 3309. https://doi.org/10.3390/s21103309
Yue R, Wang H, Jin T, Gao Y, Sun X, Yan T, Zang J, Yin K, Wang S. Image Motion Measurement and Image Restoration System Based on an Inertial Reference Laser. Sensors. 2021; 21(10):3309. https://doi.org/10.3390/s21103309
Chicago/Turabian StyleYue, Ronggang, Humei Wang, Ting Jin, Yuting Gao, Xiaofeng Sun, Tingfei Yan, Jie Zang, Ke Yin, and Shitao Wang. 2021. "Image Motion Measurement and Image Restoration System Based on an Inertial Reference Laser" Sensors 21, no. 10: 3309. https://doi.org/10.3390/s21103309





