Nanomechanical Molecular Mass Sensing Using Suspended Microchannel Resonators
Abstract
:1. Introduction
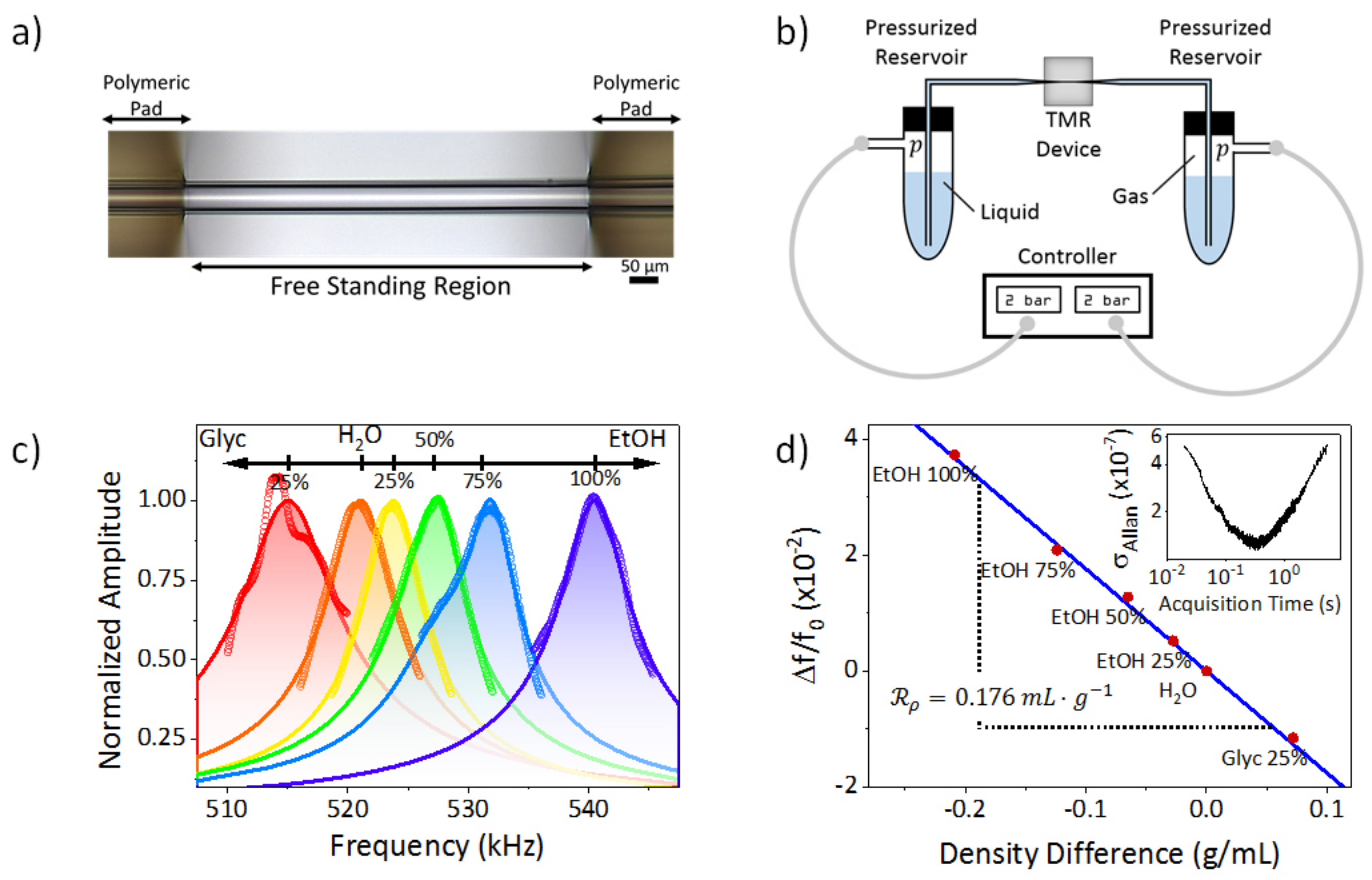
2. Experimental Setup
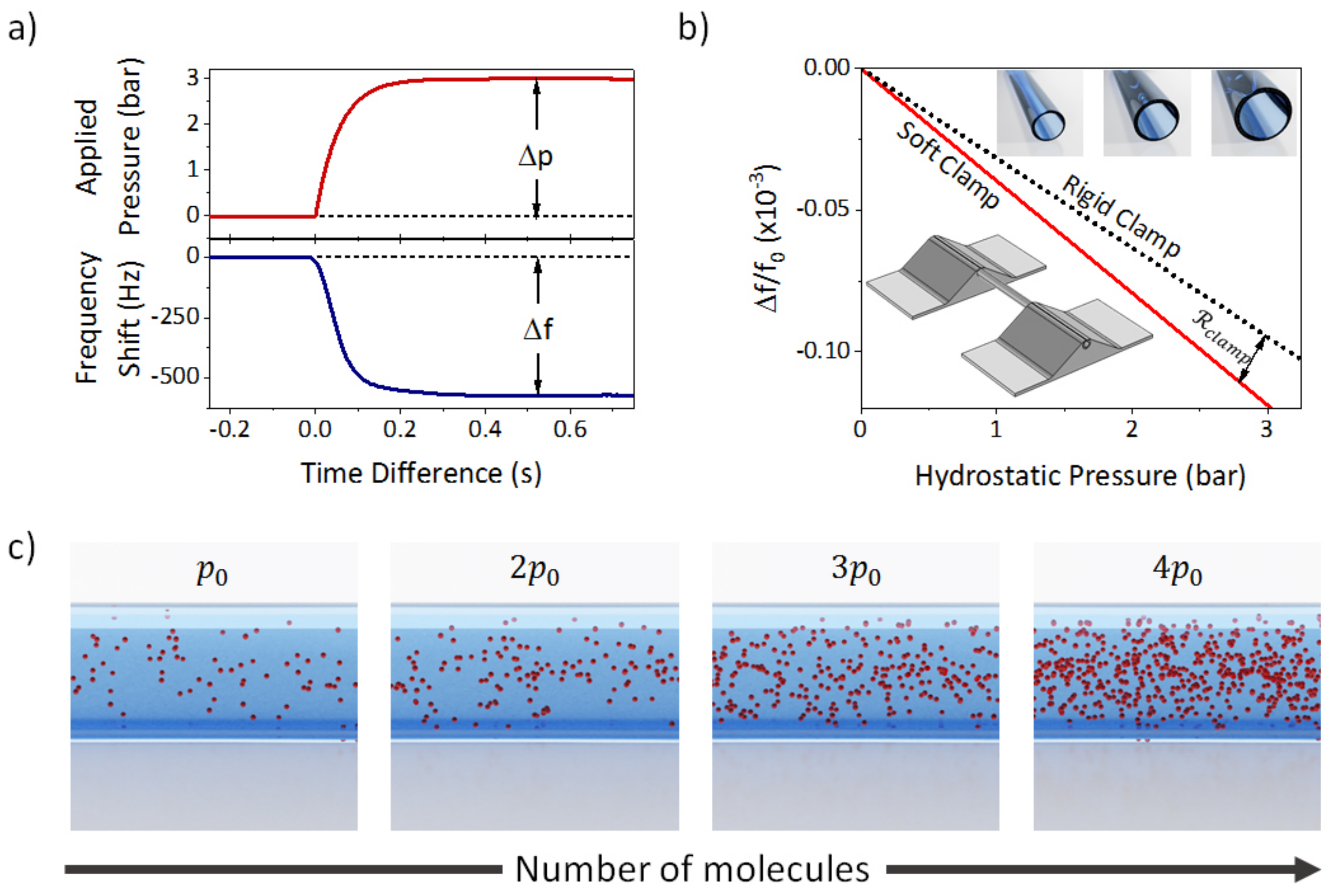
3. Analytical Model
4. Experimental Measurements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Van Cauwenberghe, L.; Vanreusel, A.; Mees, J.; Janssen, C.R. Microplastic pollution in deep-sea sediments. Environ. Pollut. 2013, 182, 495–499. [Google Scholar] [CrossRef]
- Galloway, T.S.; Cole, M.; Lewis, C. Interactions of microplastic debris throughout the marine ecosystem. Nat. Ecol. Evol. 2017, 1, 0116. [Google Scholar] [CrossRef]
- Danopoulos, E.; Twiddy, M.; Rotchell, J.M. Microplastic contamination of drinking water: A systematic review. PLoS ONE 2020, 15, e0236838. [Google Scholar] [CrossRef]
- Bhakta, H.C.; Choday, V.K.; Grover, W.H. Musical Instruments As Sensors. ACS Omega 2018, 3, 11026–11032. [Google Scholar] [CrossRef] [PubMed]
- Bryan, A.K.; Hecht, V.C.; Shen, W.; Payer, K.; Grover, W.H.; Manalis, S.R. Measuring single cell mass, volume, and density with dual suspended microchannel resonators. Lab Chip 2014, 14, 569–576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, X.J.; Liu, A.Q.; Lim, C.S.; Ayi, T.C.; Yap, P.H. Determining refractive index of single living cell using an integrated microchip. Sens. Actuators A Phys. 2007, 133, 349–354. [Google Scholar] [CrossRef]
- Martín-Pérez, A.; Ramos, D.; Gil-Santos, E.; García-López, S.; Yubero, M.L.; Kosaka, P.M.; San Paulo, Á.; Tamayo, J.; Calleja, M. Mechano-Optical Analysis of Single Cells with Transparent Microcapillary Resonators. ACS Sens. 2019, 4, 3325–3332. [Google Scholar] [CrossRef] [PubMed]
- Han, K.; Suh, J.; Bahl, G. Optomechanical non-contact measurement of microparticle compressibility in liquids. Opt. Express 2018, 26, 31908–31916. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.H.; Miettinen, T.P.; Chen, L.; Olcum, S.; Katsikis, G.; Doyle, P.S.; Manalis, S.R. Noninvasive monitoring of single-cell mechanics by acoustic scattering. Nat. Methods 2019, 16, 263–269. [Google Scholar] [CrossRef]
- Herráez, J.V.; Belda, R. Refractive Indices, Densities and Excess Molar Volumes of Monoalcohols + Water. J. Solut. Chem. 2006, 35, 1315–1328. [Google Scholar] [CrossRef]
- Volk, A.; Kähler, C.J. Density model for aqueous glycerol solutions. Exp. Fluids 2018, 59, 75. [Google Scholar] [CrossRef] [Green Version]
- Onori, G. Adiabatic compressibility and structure of aqueous solutions of ethyl alcohol. J. Chem. Phys. 1988, 89, 4325–4332. [Google Scholar] [CrossRef]
- Ramos, D.; Mertens, J.; Calleja, M.; Tamayo, J. Phototermal self-excitation of nanomechanical resonators in liquids. Appl. Phys. Lett. 2008, 92. [Google Scholar] [CrossRef]
- Burg, T.P.; Godin, M.; Knudsen, S.M.; Shen, W.; Carlson, G.; Foster, J.S.; Babcock, K.; Manalis, S.R. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 2007, 446, 1066–1069. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chaudhari, S.; Chaudhari, K.; Kim, S.; Khan, F.; Lee, J.; Thundat, T. Electrophoresis assisted time-of-flow mass spectrometry using hollow nanomechanical resonators. Sci. Rep. 2017, 7, 3535–3541. [Google Scholar] [CrossRef] [Green Version]
- De Pastina, A.; Villanueva, L.G. Suspended micro/nano channel resonators: A review. J. Micromech. Microeng. 2020, 30, 043001. [Google Scholar] [CrossRef]
- Etayash, H.; Khan, M.F.; Kaur, K.; Thundat, T. Microfluidic cantilever detects bacteria and measures their susceptibility to antibiotics in small confined volumes. Nat. Commun. 2016, 7, 12947. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.F.; Schmid, S.; Larsen, P.E.; Davis, Z.J.; Yan, W.; Stenby, E.H.; Boisen, A. Online measurement of mass density and viscosity of pL fluid samples with suspended microchannel resonator. Sens. Actuators B Chem. 2013, 185, 456–461. [Google Scholar] [CrossRef]
- Pastina, A.D.; Maillard, D.; Villanueva, L.G. Fabrication of suspended microchannel resonators with integrated piezoelectric transduction. Microelectron. Eng. 2018, 192, 83–87. [Google Scholar] [CrossRef]
- Lee, J.; Khan, F.; Thundat, T.; Lee, B.J. Microfluidic resonators with two parallel channels for independent sample loading and effective density tuning. Micro Nano Syst. Lett. 2020, 8, 16. [Google Scholar] [CrossRef]
- Burg, T.P.; Manalis, S.R. Suspended microchannel resonators for biomolecular detection. Appl. Phys. Lett. 2003, 83, 2698–2700. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.F.; Miriyala, N.; Lee, J.; Hassanpourfard, M.; Kumar, A.; Thundat, T. Heat capacity measurements of sub-nanoliter volumes of liquids using bimaterial microchannel cantilevers. Appl. Phys. Lett. 2016, 108, 211906. [Google Scholar] [CrossRef]
- Lee, J.; Shen, W.; Payer, K.; Burg, T.P.; Manalis, S.R. Toward Attogram Mass Measurements in Solution with Suspended Nanochannel Resonators. Nano Lett. 2010, 10, 2537–2542. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Son, S.; Grover, W.H.; Burg, T.P.; Manalis, S.R. Suspended Microchannel Resonators for Ultralow Volume Universal Detection. Anal. Chem. 2008, 80, 4757–4760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malvar, O.; Ramos, D.; Martínez, C.; Kosaka, P.; Tamayo, J.; Calleja, M. Highly sensitive measurement of liquid density in air using suspended microcapillary resonators. Sensors (Basel) 2015, 15, 7650–7657. [Google Scholar] [CrossRef]
- Lee, D.; Kim, J.; Cho, N.-J.; Kang, T.; Kauh, S.; Lee, J. Pulled microcapillary tube resonators with electrical readout for mass sensing applications. Sci. Rep. 2016, 6, 33799–33807. [Google Scholar] [CrossRef] [Green Version]
- Calmo, R.; Lovera, A.; Stassi, S.; Chiadò, A.; Scaiola, D.; Bosco, F.; Ricciardi, C. Monolithic glass suspended microchannel resonators for enhanced mass sensing of liquids. Sens. Actuators B Chem. 2019, 283, 298–303. [Google Scholar] [CrossRef]
- Ko, J.; Lee, D.; Lee, B.J.; Kauh, S.K.; Lee, J. Micropipette Resonator Enabling Targeted Aspiration and Mass Measurement of Single Particles and Cells. ACS Sens. 2019, 4, 3275–3282. [Google Scholar] [CrossRef] [PubMed]
- Martín-Pérez, A.; Ramos, D.; Tamayo, J.; Calleja, M. Coherent Optical Transduction of Suspended Microcapillary Resonators for Multi-Parameter Sensing Applications. Sensors 2019, 19, 5069. [Google Scholar] [CrossRef] [Green Version]
- Martín-Pérez, A.; Ramos, D.; Yubero, M.L.; García-López, S.; Kosaka, P.M.; Tamayo, J.; Calleja, M. Hydrodynamic assisted multiparametric particle spectrometry. Sci. Rep. 2021, 11, 3535. [Google Scholar] [CrossRef]
- Martín-Pérez, A.; Ramos, D.; Tamayo, J.; Calleja, M. Real-Time Particle Spectrometry in Liquid Environment Using Microfluidic-Nanomechanical Resonators. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 2146–2149. [Google Scholar]
- Tamayo, J.; Kosaka, P.M.; Ruz, J.J.; San Paulo, Á.; Calleja, M. Biosensors based on nanomechanical systems. Chem. Soc. Rev. 2013, 42, 1287–1311. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, M.F.; Knowles, B.; Dennison, C.R.; Ghoraishi, M.S.; Thundat, T. Pressure modulated changes in resonance frequency of microchannel string resonators. Appl. Phys. Lett. 2014, 105, 013507. [Google Scholar] [CrossRef]
- Landau, L.D. Theory of Elasticity, 3rd ed.; Elsevier: Oxford, UK, 1986. [Google Scholar]
- Kumar, S.; Sarkar, S.; Bagchi, B. Microscopic origin of breakdown of Stokes–Einstein relation in binary mixtures: Inherent structure analysis. J. Chem. Phys. 2020, 152, 164507. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín-Pérez, A.; Ramos, D.; Tamayo, J.; Calleja, M. Nanomechanical Molecular Mass Sensing Using Suspended Microchannel Resonators. Sensors 2021, 21, 3337. https://doi.org/10.3390/s21103337
Martín-Pérez A, Ramos D, Tamayo J, Calleja M. Nanomechanical Molecular Mass Sensing Using Suspended Microchannel Resonators. Sensors. 2021; 21(10):3337. https://doi.org/10.3390/s21103337
Chicago/Turabian StyleMartín-Pérez, Alberto, Daniel Ramos, Javier Tamayo, and Montserrat Calleja. 2021. "Nanomechanical Molecular Mass Sensing Using Suspended Microchannel Resonators" Sensors 21, no. 10: 3337. https://doi.org/10.3390/s21103337
APA StyleMartín-Pérez, A., Ramos, D., Tamayo, J., & Calleja, M. (2021). Nanomechanical Molecular Mass Sensing Using Suspended Microchannel Resonators. Sensors, 21(10), 3337. https://doi.org/10.3390/s21103337








