Toward an Estimation of the Optical Feedback Factor C on the Fly for Displacement Sensing
Abstract
:1. Introduction
2. Proposed Method
2.1. OFI Overview
2.2. OFI as a Non-Uniform Sampling System
2.3. Proposed C Estimation Method
- , estimation of C based on the direct amplitude of the 3rd harmonics and on (3).
- , minimization of the amplitude of the 3rd harmonics by tuning the parameter that is added (subtracted) to all the samples corresponding to the rising (decreasing) phase.
- , minimization of the amplitude of all the harmonics, the frequency of which exceeds twice the frequency of the highest significant peak (>) by tuning the parameter that is added (subtracted) to all the samples corresponding to the rising (decreasing) phase.
2.4. Analysis of the Impact of Variations of C on the Reconstructed Displacement
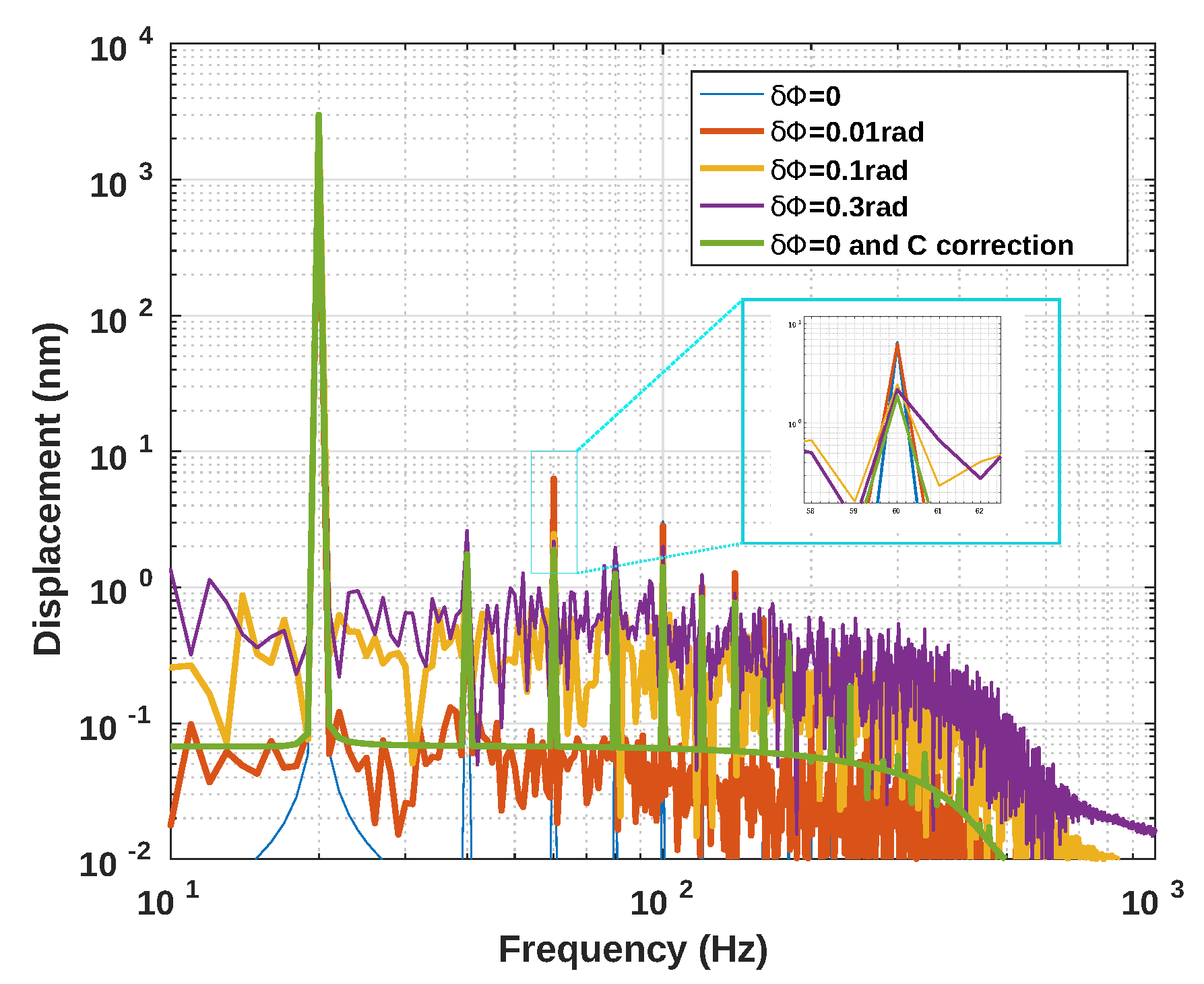
2.5. Phase Noise Effect
3. Simulation Results and Analysis
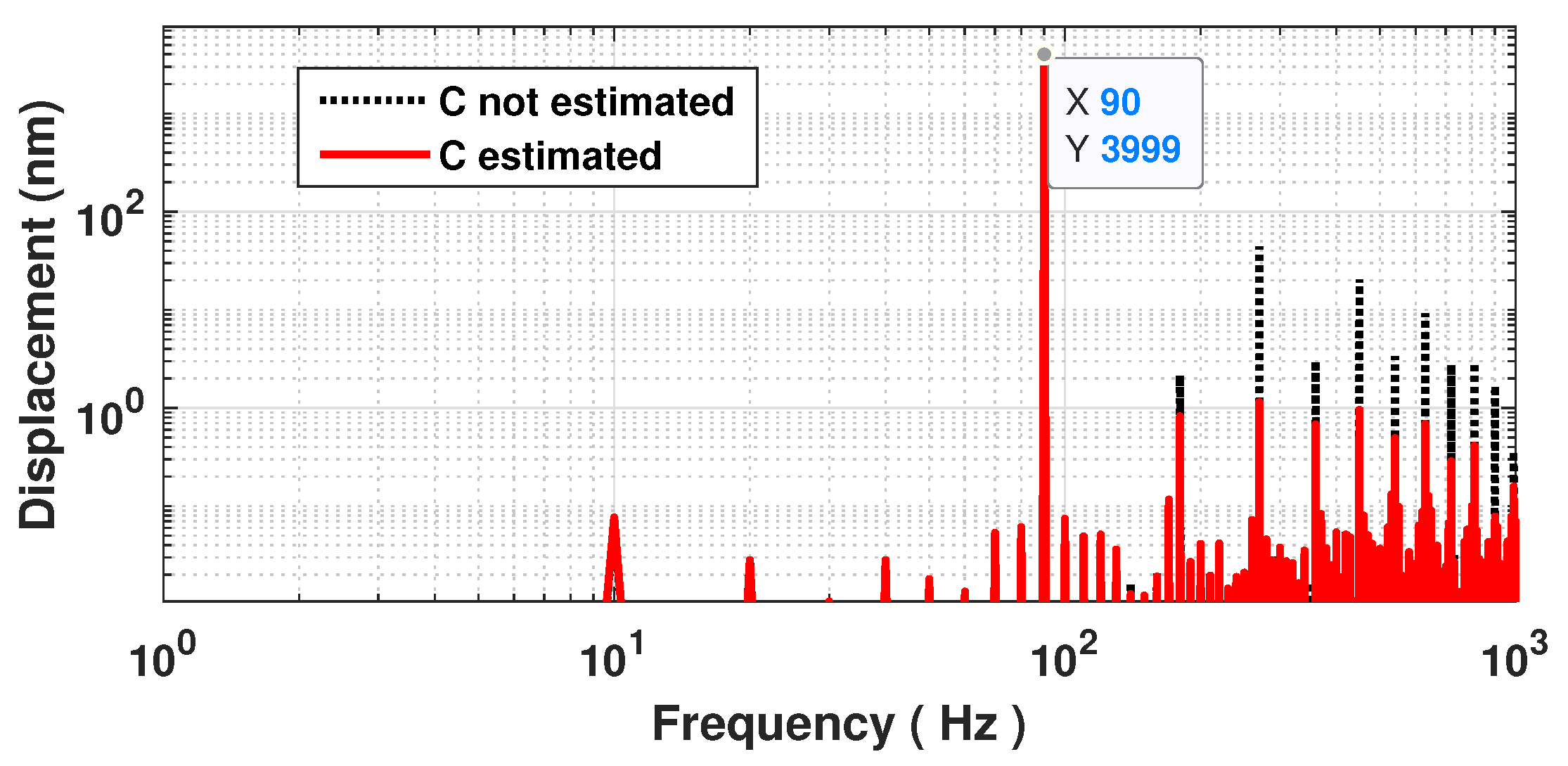
3.1. Influence of the Sampling Frequency and Displacement Amplitude
3.2. Influence of Phase Noise
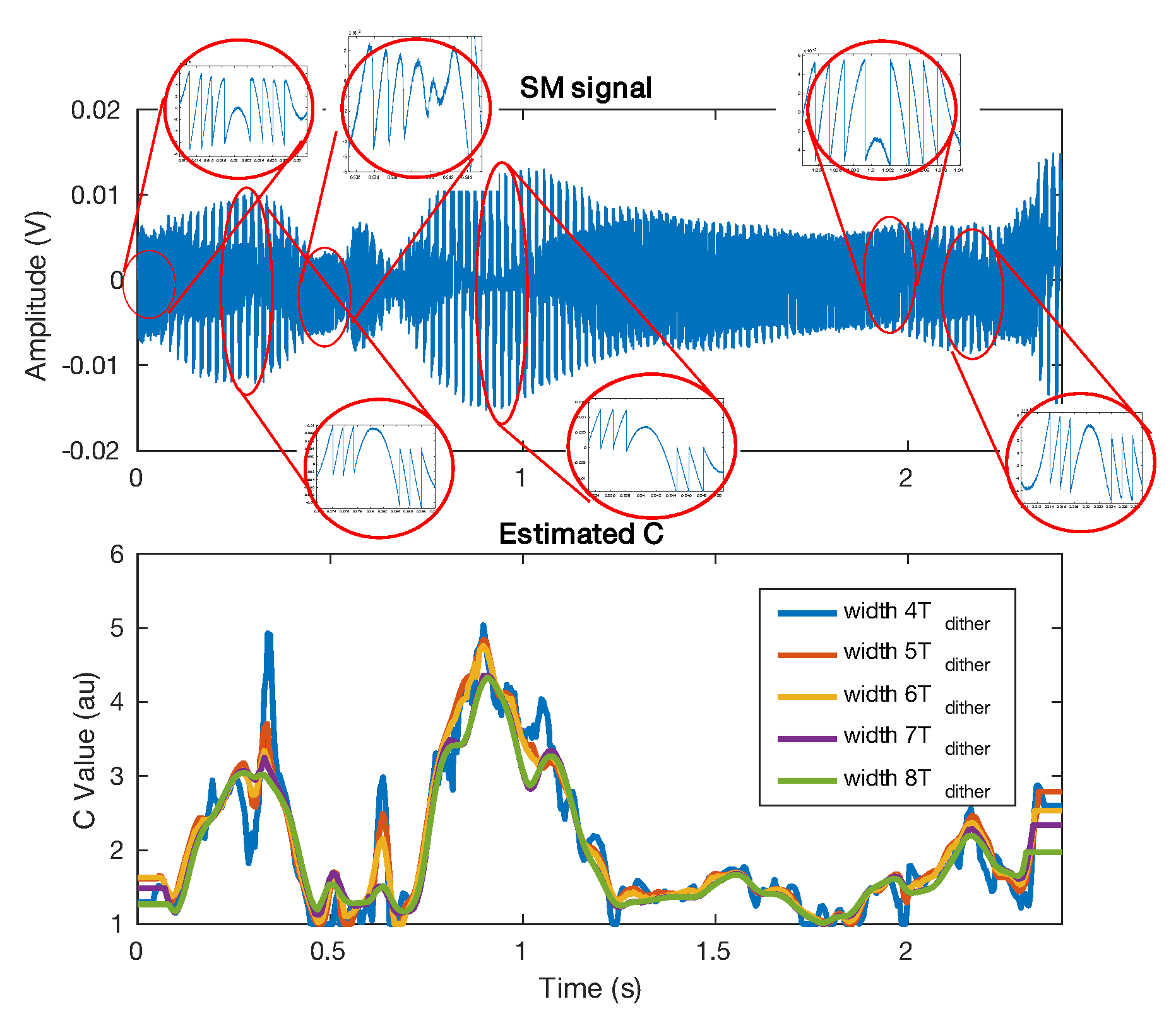
3.3. Arbitrary Displacement
3.4. Speckle Affected SM Signals
4. Experimental Results
4.1. Experimental Setups
4.2. C Constant without Dithering (TB1)
4.3. C Constant with Dithering (TB2)
4.4. C Varying
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| OFI | Optical Feedback Interferometry |
| SM | Self Mixing |
| LD | Laser Diode |
| NUS | Non Uniform Smapling |
| OOP | Optical Output Power |
| TB | Test Bench |
| TB1 | Test Bench 1 |
| TB2 | Test Bench 2 |
| PZT | Piezoelectric Transducer |
| NI | National Instruments |
References
- Donati, S. Developing self-mixing interferometry for instrumentation and measurements. Laser Photonics Rev. 2012, 6, 393–417. [Google Scholar] [CrossRef]
- Taimre, T.; Nikolić, M.; Bertling, K.; Lim, Y.L.; Bosch, T.; Rakić, A.D. Laser feedback interferometry: A tutorial on the self-mixing effect for coherent sensing. Adv. Opt. Photonics 2015, 7, 570–631. [Google Scholar] [CrossRef]
- Mezzapesa, F.P.; Ancona, A.; Sibillano, T.; Lucia, F.D.; Dabbicco, M.; Lugarà, P.M.; Scamarcio, G. High-resolution monitoring of the hole depth during ultrafast laser ablation drilling by diode laser self-mixing interferometry. Opt. Lett. 2011, 36, 822–824. [Google Scholar] [CrossRef]
- Giuliani, G.; Bozzi-Pietra, S.; Donati, S. Self-mixing laser diode vibrometer. Meas. Sci. Technol. 2002, 14, 24–32. [Google Scholar] [CrossRef]
- Wei, Z.; Huang, W.; Zhang, J.; Wang, X.; Zhu, H.; An, T.; Yu, X. Obtaining Scalable Fringe Precision in Self-Mixing Interference Using an Even-Power Fast Algorithm. IEEE Photonics J. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Jiang, C.; Li, C.; Yin, S.; Huang, Z. Multiple self-mixing interferometry algorithm based on phase modulation for vibration measurement. Opt. Quantum Electron. 2017, 49, 111. [Google Scholar] [CrossRef]
- Bes, C.; Plantier, G.; Bosch, T. Displacement measurements using a self-mixing laser diode under moderate feedback. IEEE Trans. Instrum. Meas. 2006, 55, 1101–1105. [Google Scholar] [CrossRef]
- Bernal, O.D.; Zabit, U.; Bosch, T. Study of Laser Feedback Phase Under Self-Mixing Leading to Improved Phase Unwrapping for Vibration Sensing. IEEE Sens. J. 2013, 13, 4962–4971. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Yu, Y.; Xi, J.; Chicharo, J.F. Improving the measurement performance for a self-mixing interferometry-based displacement sensing system. Appl. Opt. 2011, 50, 5064–5072. [Google Scholar] [CrossRef]
- Arriaga, A.L.; Bony, F.; Bosch, T. Real-Time Algorithm for Versatile Displacement Sensors Based on Self-Mixing Interferometry. IEEE Sens. J. 2016, 16, 195–202. [Google Scholar] [CrossRef] [Green Version]
- Merlo, S.; Donati, S. Reconstruction of displacement waveforms with a single-channel laser-diode feedback interferometer. IEEE J. Quantum Electron. 1997, 33, 527–531. [Google Scholar] [CrossRef]
- Ehtesham, A.; Zabit, U.; Bernal, O.D.; Raja, G.; Bosch, T. Analysis and Implementation of a Direct Phase Unwrapping Method for Displacement Measurement Using Self-Mixing Interferometry. IEEE Sens. J. 2017, 17, 7425–7432. [Google Scholar] [CrossRef] [Green Version]
- Zabit, U.; Bernal, O.D.; Amin, S.; Qureshi, M.F.; Khawaja, A.H.; Bosch, T. Spectral Processing of Self-Mixing Interferometric Signal Phase for Improved Vibration Sensing under Weak-and Moderate-Feedback Regime. IEEE Sens. J. 2019, 19, 11151–11158. [Google Scholar] [CrossRef] [Green Version]
- Melchionni, D.; Magnani, A.; Pesatori, A.; Norgia, M. Development of a design tool for closed-loop digital vibrometer. Appl. Opt. 2015, 54, 9637–9643. [Google Scholar] [CrossRef]
- Magnani, A.; Melchionni, D.; Pesatori, A.; Norgia, M. Self-mixing digital closed-loop vibrometer for high accuracy vibration measurements. Opt. Commun. 2016, 365, 133–139. [Google Scholar] [CrossRef]
- Barland, S.; Gustave, F. Convolutional neural network for self-mixing interferometric displacement sensing. Opt. Express 2021, 29, 11433–11444. [Google Scholar] [CrossRef]
- Taimre, T.; Rakić, A.D. On the nature of Acket’s characteristic parameter C in semiconductor lasers. Appl. Opt. 2014, 53, 1001–1006. [Google Scholar] [CrossRef] [Green Version]
- Bernal, O.D.; Zabit, U.; Bosch, T.M. Robust Method of Stabilization of Optical Feedback Regime by Using Adaptive Optics for a Self-Mixing Micro-Interferometer Laser Displacement Sensor. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 336–343. [Google Scholar] [CrossRef] [Green Version]
- Yanguang, Y.; Giuliani, G.; Donati, S. Measurement of the linewidth enhancement factor of semiconductor lasers based on the optical feedback self-mixing effect. IEEE Photonics Technol. Lett. 2004, 16, 990–992. [Google Scholar] [CrossRef]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Yu, Y.; Xi, J.; Chicharo, J.F. Measuring the feedback parameter of a semiconductor laser with external optical feedback. Opt. Express 2011, 19, 9582–9593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernal, O.D.; Zabit, U.; Jayat, F.; Bosch, T. Sub-λ/2 Displacement Sensor with Nanometric Precision based on Optical Feedback Interferometry used as a Non-Uniform Event-Based Sampling System. IEEE Sens. J. 2020, 20, 5195–5203. [Google Scholar] [CrossRef]
- Giordano, M.C.; Mastel, S.; Liewald, C.; Columbo, L.L.; Brambilla, M.; Viti, L.; Politano, A.; Zhang, K.; Li, L.; Davies, A.G.; et al. Phase-resolved terahertz self-detection near-field microscopy. Opt. Express 2018, 26, 18423–18435. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xia, W.; Liu, Q.; Hao, H.; Guo, D.; Wang, M.; Chen, X. Sinusoidal phase-modulating self-mixing interferometer with nanometer resolution and improved measurement velocity range. Appl. Opt. 2015, 54, 7820–7827. [Google Scholar] [CrossRef] [PubMed]
- Bernal, O.D.; Zabit, U.; Bosch, T. Classification of laser self-mixing interferometric signal under moderate feedback. Appl. Opt. 2014, 53, 702–708. [Google Scholar] [CrossRef] [Green Version]
- Magnani, A.; Pesatori, A.; Norgia, M. Self-mixing vibrometer with real-time digital signal elaboration. Appl. Opt. 2012, 51, 5318–5325. [Google Scholar] [CrossRef]
- Plantier, G.; Bes, C.; Bosch, T. Behavioral model of a self-mixing laser diode sensor. IEEE J. Quantum Electron. 2005, 41, 1157–1167. [Google Scholar] [CrossRef]
- Marvasti, F. Nonuniform Sampling: Theory and Practice; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Donati, S.; Martini, G.; Tambosso, T. Speckle pattern errors in self-mixing interferometry. IEEE J. Quantum Electron. 2013, 49, 798–806. [Google Scholar] [CrossRef]
- Siddiqui, A.A.; Zabit, U.; Bernal, O.D.; Raja, G.; Bosch, T. All analog processing of speckle affected self-mixing interferometric signals. IEEE Sens. J. 2017, 17, 5892–5899. [Google Scholar] [CrossRef]
- Servagent, N.; Bosch, T.; Lescure, M. Design of a phase-shifting optical feedback interferometer using an electrooptic modulator. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 798–802. [Google Scholar] [CrossRef]
- Vezyrtzis, C.; Tsividis, Y. Processing of signals using level-crossing sampling. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 2293–2296. [Google Scholar] [CrossRef]
- Wang, T.; Wang, D.; Hurst, P.J.; Levy, B.C.; Lewis, S.H. A Level-Crossing Analog-to-Digital Converter With Triangular Dither. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 2089–2099. [Google Scholar] [CrossRef]
- Bernal, O.D.; Seat, H.C.; Zabit, U.; Surre, F.; Bosch, T. Robust Detection of Non-Regular Interferometric Fringes From a Self-Mixing Displacement Sensor Using Bi-Wavelet Transform. IEEE Sens. J. 2016, 16, 7903–7910. [Google Scholar] [CrossRef] [Green Version]
- Giuliani, G.; Norgia, M. Laser diode linewidth measurement by means of self-mixing interferometry. IEEE Photonics Technol. Lett. 2000, 12, 1028–1030. [Google Scholar] [CrossRef]






















| C | Our Work | [19] | [21] | [8] | ||
|---|---|---|---|---|---|---|
| F1 | F2 | F3 | ||||
| 0.5 | N/A | N/A | N/A | N/A | 0.613 | 0.488 |
| 1 | 1.184 | 1.046 | 1.003 | 1.01 | 0.991 | 0.999 |
| 1.5 | 1.458 | 1.511 | 1.501 | 1.46 | 1.506 | 1.499 |
| 2 | 1.887 | 2.01 | 2.001 | 1.98 | 2.015 | 1.999 |
| 2.5 | 2.323 | 2.506 | 2.501 | 2.47 | 2.518 | 2.499 |
| 3 | 2.771 | 3.004 | 3.000 | 2.98 | 3.009 | 2.999 |
| 3.5 | 3.256 | 3.507 | 3.505 | N/A | 3.494 | 3.499 |
| 4 | 3.286 | 4.056 | 3.999 | N/A | 4.043 | 3.991 |
| 4.5 | 3.663 | 4.476 | 4.497 | N/A | 4.553 | 4.493 |
| 5 | 4.05 | 5.08 | 4.965 | N/A | 5.016 | 4.989 |
| 6 | 4.85 | 6.13 | 6.060 | N/A | 6.096 | 5.98 |
| 7 | 5.75 | 7.19 | 7.069 | N/A | 7.135 | 6.974 |
| C | ||
|---|---|---|
| No Dither | Dither | |
| 1 | 1.422 | 1.003 |
| 1.5 | 1.529 | 1.491 |
| 2 | 1.743 | 1.998 |
| 2.5 | 1.605 | 2.503 |
| 3 | 1.976 | 3.005 |
| 3.5 | 2.649 | 3.521 |
| 4 | 1.997 | 4.013 |
| 4.5 | 2.582 | 4.526 |
| N | Our Work | [19] | [21] | [8] | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1.01 | 0.03 | 1.01 * | 0 * | 1.75 | 0.7 | 0.94 | 0.07 |
| 2 | 1.03 | 0.06 | 1.01 * | 0 * | 1.84 | 0.4 | 1.17 | 0.04 |
| 3 | 1.71 | 0.05 | 1.9 | 0.06 | 2.87 | 0.25 | 2.49 | 0.03 |
| 4 | 2.15 | 0.10 | 2.3 | 0.08 | 2.95 | 0.2 | 2.84 | 0.05 |
| 5 | 3.42 | 0.10 | 3.5 | 0.1 | 3.57 | 0.21 | 3.96 | 0.12 |
| 6 | 4.05 | 0.10 | – | – | 3.97 | 0.33 | 4.53 | 0.17 |
| N | (a) | (b) | (c) | [19] | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1.21 | 0.13 | 1.23 | 0.3 | 1.32 | 0.45 | 1.18 | 0.09 |
| 2 | 1.57 | 0.02 | 1.54 | 0.09 | 1.49 | 0.24 | 1.48 | 0.04 |
| 3 | 1.87 | 0.09 | 1.78 | 0.06 | 2.21 | 0.17 | 1.86 | 0.05 |
| 4 | 2.08 | 0.04 | 2.21 | 0.07 | 2.38 | 0.13 | 2.07 | 0.05 |
| 5 | 2.30 | 0.07 | 2.32 | 0.03 | 2.51 | 0.18 | 2.342 | 0.04 |
| 6 | 2.79 | 0.07 | 2.75 | 0.05 | 3.01 | 0.31 | 2.70 | 0.07 |
| 7 | 3.31 | 0.10 | 3.30 | 0.12 | 3.48 | 0.39 | 3.23 | 0.08 |
| 8 | 4.65 | 0.14 | 4.19 | 0.05 | 4.27 | 0.35 | 4.24 * | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernal, O.D.; Zabit, U.; Jayat, F.; Bosch, T. Toward an Estimation of the Optical Feedback Factor C on the Fly for Displacement Sensing. Sensors 2021, 21, 3528. https://doi.org/10.3390/s21103528
Bernal OD, Zabit U, Jayat F, Bosch T. Toward an Estimation of the Optical Feedback Factor C on the Fly for Displacement Sensing. Sensors. 2021; 21(10):3528. https://doi.org/10.3390/s21103528
Chicago/Turabian StyleBernal, Olivier D., Usman Zabit, Francis Jayat, and Thierry Bosch. 2021. "Toward an Estimation of the Optical Feedback Factor C on the Fly for Displacement Sensing" Sensors 21, no. 10: 3528. https://doi.org/10.3390/s21103528
APA StyleBernal, O. D., Zabit, U., Jayat, F., & Bosch, T. (2021). Toward an Estimation of the Optical Feedback Factor C on the Fly for Displacement Sensing. Sensors, 21(10), 3528. https://doi.org/10.3390/s21103528







