SEED-G: Simulated EEG Data Generator for Testing Connectivity Algorithms
Abstract
:1. Introduction
2. Toolbox Description
- The generation of a predefined ground-truth connectivity model with:
- a selected size (number of signals to be generated);
- a selected density;
- parameters randomly assigned within a given range;
- stationary or time-resolved connectivity values.
- The generation of pseudo-EEG time series with:
- spectral similarity to reference EEG scalp- or source-level data;
- given length in terms of number of samples;
- number of trials;
- predefined SNR;
- inter-trial variability;
- presence of ocular artifacts.
2.1. Simulated Data Generation
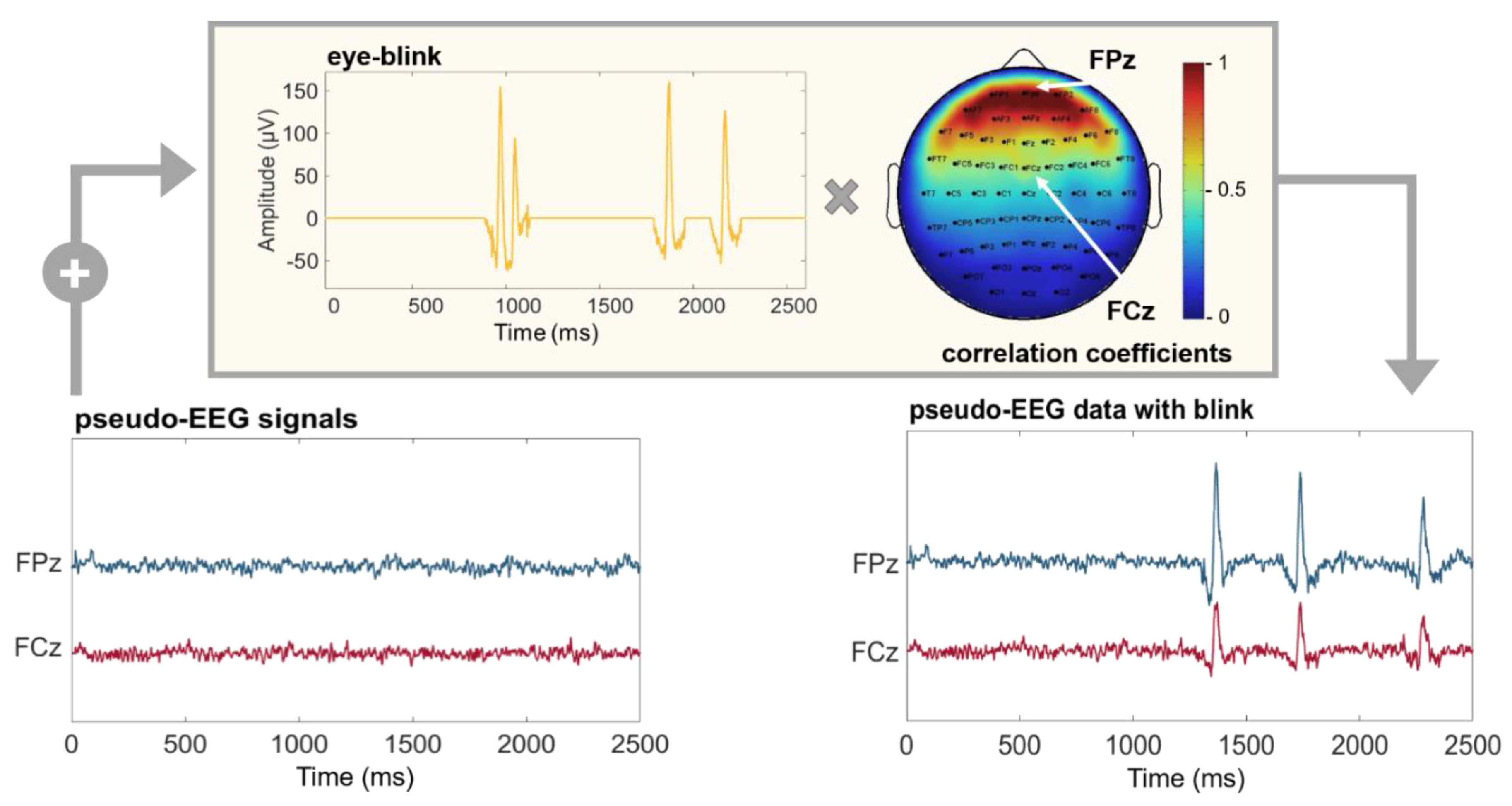
2.2. Realistic Features Modeling
3. Evaluation of SEED-G Toolbox Performances
3.1. Methods
3.1.1. Pseudo-EEG Time Series Generation
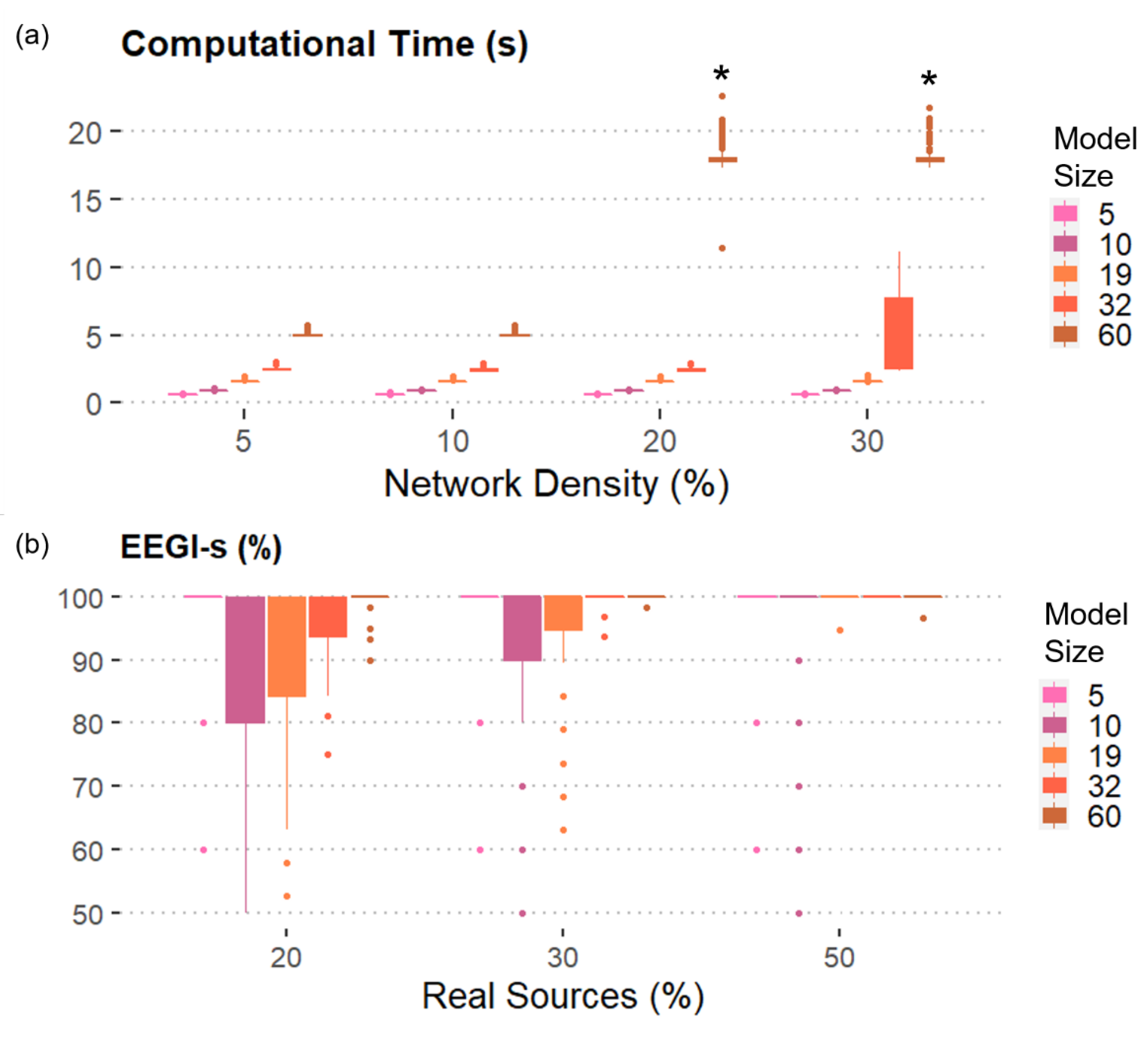
- “Model size” is the number of time series composing the dataset. Levels: (5, 10, 19, 32, 60) nodes, simulating a range between few electrodes and the most commonly used extended 10–20 scalp EEG montage.
- “Network density” is the percentage of non-null coefficients. Levels: (5%, 10%, 20%, 30%) of the possible connections.
- “Real sources” are the percentage of real sources included as sources in the model with respect to all generated signals. Levels: (20%, 30%, 50%) of the number of the generated time series.
3.1.2. Performance Parameters
3.2. Results
4. SEED-G Toolbox Application: Evaluation of the Inter-Trial Variability Effect on PDC Estimates
- by increasing/decreasing the value of some existing connections in the ground-truth network (Study I);
- by modifying the ground-truth network density by adding some spurious connections to the existing ones (Study II).
4.1. Methods
4.1.1. Study I: The Effect of Unstable Connectivity Values
- Model size: 5, 10, 20 nodes;
- Network density: 20% of the possible connections;
- Connections’ intensity: randomly selected in the range [−0.5:0.5];
- Percentage of modified trials: 1, 10, 30, 50% of the total number of the generated trials;
- Percentage of modified links across-trials: 10, 20, 50% of existing connections;
- Amplitude of the variation: 20, 50, 70% of the original value of the connection;
- Type of variation: positive (increase), negative (decrease).
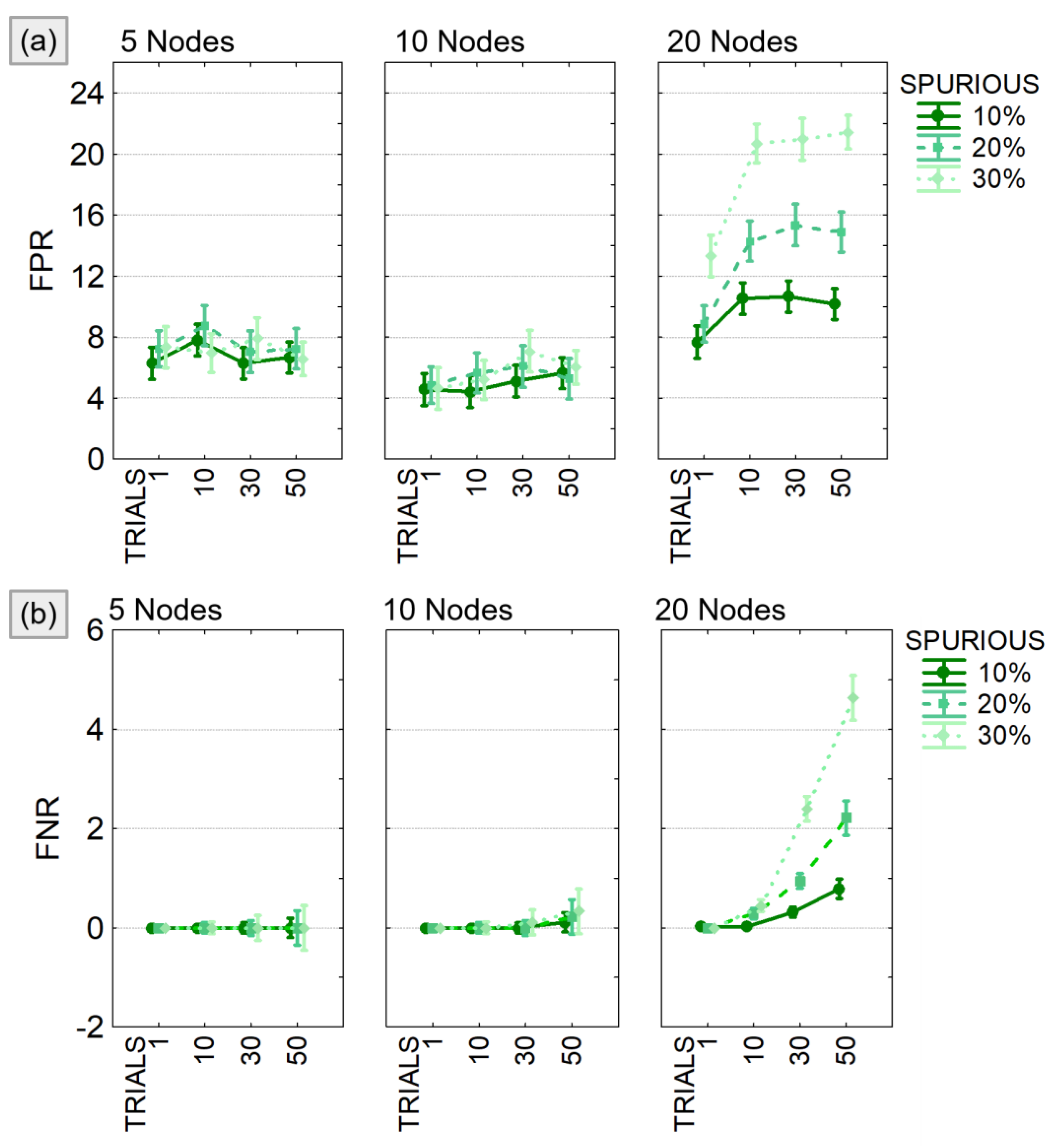
4.1.2. Study II: The Effect of Spurious Connections
- Model size: 5, 10, 20 nodes;
- Network density: 20% of the possible connections;
- Connections’ intensity: randomly selected in the range [−0.5:0.5];
- Percentage of modified trials: 1, 10, 30, 50% of the total number of trials generated;
- Percentage of added spurious links: 10, 20, 30% of all existing connections.
4.2. Results
4.2.1. Study I: The Effect of Unstable Connectivity Values
4.2.2. Study II: The Effect of Spurious Connections
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- main: it is the core of the toolbox and contains all the functions for the generation of EEG data according to a predefined ground-truth network.
- dependencies: containing parts of other toolboxes required to successfully run SEED-G functions. The links to the full packages can be found in the documentation on the GitHub page. The additional packages are Brain Connectivity Toolbox (BCT) [40], FieldTrip [41], Multivariate Granger Causality Toolbox (MVGC) [24], and AsympPDC Package (PDC_AsympSt) [42,43]. Additionally, the implemented forward model is solved according to the New York Head (NYH) model, whose parameters are contained in the structure available on the ICBM-NY platform [28].
- real data: containing real EEG data acquired from one healthy subject during resting state at scalp level (‘EEG_real_sources.mat’) and its reconstructed version in source domain (‘sLOR_cortical_sources.mat’). These signals can be employed to extract the AR components to be included in the model to generate data with the same spectral properties of the real ones.
- demo: containing examples of MATLAB scripts to be used to learn the different functionalities of the toolbox. For example, the code ‘run_generation.m’ allows to specify the directory containing the real sources and each specific input of the function ‘simulatedData_generation.m’.
- auxiliary functions: containing either original MATLAB functions or modified version of free available functions.
References
- Lee, L.; Harrison, L.M.; Mechelli, A. The Functional Brain Connectivity Workshop: Report and commentary. Netw. Comput. Neural Syst. 2003, 14, 1–15. [Google Scholar] [CrossRef]
- Kuś, R.; Kamiński, M.; Blinowska, K.J. Determination of EEG Activity Propagation: Pair-Wise Versus Multichannel Estimate. IEEE Trans. Biomed. Eng. 2004, 51, 1501–1510. [Google Scholar] [CrossRef]
- Brovelli, A.; Ding, M.; Ledberg, A.; Chen, Y.; Nakamura, R.; Bressler, S.L. Beta oscillations in a large-scale sensorimotor cortical network: Directional influences revealed by Granger causality. Proc. Natl. Acad. Sci. USA 2004, 101, 9849–9854. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brovelli, A.; Lachaux, J.-P.; Kahane, P.; Boussaoud, D. High gamma frequency oscillatory activity dissociates attention from intention in the human premotor cortex. NeuroImage 2005, 28, 154–164. [Google Scholar] [CrossRef] [Green Version]
- Astolfi, L.; Cincotti, F.; Mattia, D.; Marciani, M.G.; Baccala, L.A.; Fallani, F.D.V.; Salinari, S.; Ursino, M.; Zavaglia, M.; Ding, L.; et al. Comparison of different cortical connectivity estimators for high-resolution EEG recordings. Hum. Brain Mapp. 2007, 28, 143–157. [Google Scholar] [CrossRef] [Green Version]
- Greenblatt, R.; Pflieger, M.; Ossadtchi, A. Connectivity measures applied to human brain electrophysiological data. J. Neurosci. Methods 2012, 207, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bowyer, S.M. Coherence a measure of the brain networks: Past and present. Neuropsychiatr. Electrophysiol. 2016, 2, 1. [Google Scholar] [CrossRef]
- Anzolin, A.; Presti, P.; Van De Steen, F.; Astolfi, L.; Haufe, S.; Marinazzo, D. Quantifying the Effect of Demixing Approaches on Directed Connectivity Estimated Between Reconstructed EEG Sources. Brain Topogr. 2019, 32, 655–674. [Google Scholar] [CrossRef] [PubMed]
- Toppi, J.; Petti, M.; Vecchiato, G.; Cincotti, F.; Salinari, S.; Mattia, D.; Babiloni, F.; Astolfi, L. The Effect of Normalization of Partial Directed Coherence on the Statistical Assessment of Connectivity Patterns: A Simulation Study. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 4346–4349. [Google Scholar] [CrossRef]
- Petti, M.; Caschera, S.; Anzolin, A.; Toppi, J.; Pichiorri, F.; Babiloni, F.; Cincotti, F.; Mattia, D.; Astolfi, L. Effect of Inter-Trials Variability on the Estimation of Cortical Connectivity by Partial Directed Coherence. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milano, Italy, 25–29 August 2015; pp. 3791–3794. [Google Scholar] [CrossRef]
- Wang, H.E.; Bénar, C.G.; Quilichini, P.P.; Friston, K.J.; Jirsa, V.K.; Ebernard, C. A systematic framework for functional connectivity measures. Front. Neurosci. 2014, 8, 405. [Google Scholar] [CrossRef] [PubMed]
- Silfverhuth, M.J.; Hintsala, H.; Kortelainen, J.; Seppänen, T. Experimental Comparison of Connectivity Measures with Simulated EEG Signals. Med. Biol. Eng. Comput. 2012, 50, 683–688. [Google Scholar] [CrossRef]
- Ghumare, E.; Schrooten, M.; Vandenberghe, R.; Dupont, P. Comparison of Different Kalman Filter Approaches in Deriving Time Varying Connectivity from EEG Data. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milano, Italy, 25–29 August 2015; pp. 2199–2202. [Google Scholar]
- Plomp, G.; Quairiaux, C.; Michel, C.M.; Astolfi, L. The physiological plausibility of time-varying Granger-causal modeling: Normalization and weighting by spectral power. NeuroImage 2014, 97, 206–216. [Google Scholar] [CrossRef] [PubMed]
- Mill, R.D.; Bagic, A.; Bostan, A.; Schneider, W.; Cole, M.W. Empirical validation of directed functional connectivity. NeuroImage 2017, 146, 275–287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baccalá, L.A.; Sameshima, K. Chapter 3 Overcoming the limitations of correlation analysis for many simultaneously processed neural structures. Prog. Brain Res. 2001, 130, 33–47. [Google Scholar] [CrossRef]
- Sameshima, K.; Takahashi, D.Y.; Baccalá, L.A. Partial Directed Coherence Statistical Performance Characteristics in Frequency Domain. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milano, Italy, 25–29 August 2015; pp. 5388–5391. [Google Scholar] [CrossRef]
- Schelter, B.; Winterhalder, M.; Hellwig, B.; Guschlbauer, B.; Lücking, C.H.; Timmer, J. Direct or indirect? Graphical models for neural oscillators. J. Physiol. 2006, 99, 37–46. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, L.F.A.G. Multivariate Frequency Domain Analysis of Causal Interactions in Physiological Time Series. Biomed. Eng. Trends Electron. Commun. Softw. 2011, 8, 403–428. [Google Scholar]
- Astolfi, L.; Cincotti, F.; Mattia, D.; Fallani, F.D.V.; Tocci, A.; Colosimo, A.; Salinari, S.; Marciani, M.G.; Hesse, W.; Witte, H.; et al. Tracking the Time-Varying Cortical Connectivity Patterns by Adaptive Multivariate Estimators. IEEE Trans. Biomed. Eng. 2008, 55, 902–913. [Google Scholar] [CrossRef] [PubMed]
- Ghumare, E.G.; Schrooten, M.; Vandenberghe, R.; Dupont, P. A Time-Varying Connectivity Analysis from Distributed EEG Sources: A Simulation Study. Brain Topogr. 2018, 31, 721–737. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moran, R.J.; Pinotsis, D.A.; Friston, K.J. Neural masses and fields in dynamic causal modeling. Front. Comput. Neurosci. 2013, 7, 57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seth, A.K. A MATLAB toolbox for Granger causal connectivity analysis. J. Neurosci. Methods 2010, 186, 262–273. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Seth, A.K. The MVGC multivariate Granger causality toolbox: A new approach to Granger-causal inference. J. Neurosci. Methods 2014, 223, 50–68. [Google Scholar] [CrossRef] [Green Version]
- Haufe, S.; Ewald, A. A Simulation Framework for Benchmarking EEG-Based Brain Connectivity Estimation Methodologies. Brain Topogr. 2019, 32, 625–642. [Google Scholar] [CrossRef] [PubMed]
- Corbetta, M.; Patel, G.; Shulman, G.L. The Reorienting System of the Human Brain: From Environment to Theory of Mind. Neuron 2008, 58, 306–324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pascual-Marqui, R.D. Standardized low-resolution brain electromagnetic tomography (sLORETA): Technical details. Methods Find. Exp. Clin. Pharmacol. 2002, 24 (Suppl. D), 5–12. [Google Scholar]
- Huang, Y.; Parra, L.C.; Haufe, S. The New York Head—A precise standardized volume conductor model for EEG source localization and tES targeting. NeuroImage 2016, 140, 150–162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Takahashi, D.Y.; Baccal, L.A.; Sameshima, K. Connectivity Inference between Neural Structures via Partial Directed Coherence. J. Appl. Stat. 2007, 34, 1259–1273. [Google Scholar] [CrossRef]
- Toppi, J.; Mattia, D.; Risetti, M.; Formisano, R.; Babiloni, F.; Astolfi, L. Testing the Significance of Connectivity Networks: Comparison of Different Assessing Procedures. IEEE Trans. Biomed. Eng. 2016, 63, 2461–2473. [Google Scholar] [CrossRef]
- Hutchison, R.M.; Womelsdorf, T.; Allen, E.A.; Bandettini, P.A.; Calhoun, V.D.; Corbetta, M.; Della Penna, S.; Duyn, J.H.; Glover, G.H.; Gonzalez-Castillo, J.; et al. Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage 2013, 80, 360–378. [Google Scholar] [CrossRef] [Green Version]
- Islam, K.; Rastegarnia, A.; Yang, Z. Methods for artifact detection and removal from scalp EEG: A review. Neurophysiol. Clin. Neurophysiol. 2016, 46, 287–305. [Google Scholar] [CrossRef]
- Robbins, K.A.; Touryan, J.; Mullen, T.; Kothe, C.; Bigdely-Shamlo, N. How Sensitive Are EEG Results to Preprocessing Methods: A Benchmarking Study. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1081–1090. [Google Scholar] [CrossRef]
- Grech, R.; Cassar, T.; Muscat, J.; Camilleri, K.P.; Fabri, S.G.; Zervakis, M.; Xanthopoulos, P.; Sakkalis, V.; Vanrumste, B. Review on solving the inverse problem in EEG source analysis. J. Neuroeng. Rehabil. 2008, 5, 25. [Google Scholar] [CrossRef] [Green Version]
- Mahjoory, K.; Nikulin, V.V.; Botrel, L.; Linkenkaer-Hansen, K.; Fato, M.M.; Haufe, S. Consistency of EEG source localization and connectivity estimates. Neuroimage 2017, 152, 590–601. [Google Scholar] [CrossRef] [PubMed]
- Hedrich, T.; Pellegrino, G.; Kobayashi, E.; Lina, J.; Grova, C. Comparison of the spatial resolution of source imaging techniques in high-density EEG and MEG. Neuroimage 2017, 157, 531–544. [Google Scholar] [CrossRef] [PubMed]
- Daniel, E.; Meindertsma, T.; Arazi, A.; Donner, T.H.; Dinstein, I. The Relationship between Trial-by-Trial Variability and Oscillations of Cortical Population Activity. Sci. Rep. 2019, 9, 16901. [Google Scholar] [CrossRef]
- Latinus, M.; Mofid, Y.; Kovarski, K.; Charpentier, J.; Batty, M.; Bonnet-Brilhault, F. Atypical Sound Perception in ASD Explained by Inter-Trial (In)consistency in EEG. Front. Psychol. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Oostenveld, R.; Fries, P.; Maris, E.; Schoffelen, J.-M. FieldTrip: Open Source Software for Advanced Analysis of MEG, EEG, and Invasive Electrophysiological Data. Comput. Intell. Neurosci. 2010, 2011, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Sameshima, K.; Baccala, L.A. Methods in Brain Connectivity Inference through Multivariate Time Series Analysis, 1st ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Sameshima, K.; Takahashi, D.Y.; Baccala, L.A. On the statistical performance of Granger-causal connectivity estimators. Brain Inform. 2015, 2, 119–133. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| 5 Nodes | 10 Nodes | 20 Nodes | |
|---|---|---|---|
| VAR_DIR | 98 | 162 | 15 |
| VAR | 995 | 2992 | 7275 |
| MOD_CON | 1237 | 4290 | 10176 |
| TRIALS | 1415 | 2860 | 6190 |
| VAR × VAR_DIR | 5 | 33 | 904 |
| MOD_CON × VAR_DIR | 2.91(NS) | 22 | 558 |
| MOD_CON × VAR | 340 | 1806 | 5205 |
| TRIALS × VAR_DIR | 37 | 87 | 45 |
| TRIALS × VAR | 756 | 1676 | 4061 |
| TRIALS × MOD_CON | 690 | 1994 | 6458 |
| MOD_CON × VAR × VAR_DIR | 13 | 167 | 1361 |
| TRIALS × VAR × VAR_DIR | 8 | 28 | 539 |
| TRIALS × MOD_CON × VAR_DIR | 4 | 24 | 376 |
| MOD_CON × VAR × TRIALS | 132 | 405 | 1345 |
| MOD_CON × VAR × TRIALS × VAR_DIR | 4 | 39 | 322 |
| FPR * | FNR * | |
|---|---|---|
| MOD_SIZE | 740.7 | 251.1 |
| SPURIOUS | 237.3 | 118.7 |
| TRIALS | 77.3 | 189.4 |
| SPURIOUS × MOD_SIZE | 186.8 | 88.0 |
| TRIALS × MOD_SIZE | 39.6 | 149.3 |
| SPURIOUS × TRIALS | 4.2 | 50.7 |
| SPURIOUS × TRIALS × MOD_SIZE | 6.8 | 33.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anzolin, A.; Toppi, J.; Petti, M.; Cincotti, F.; Astolfi, L. SEED-G: Simulated EEG Data Generator for Testing Connectivity Algorithms. Sensors 2021, 21, 3632. https://doi.org/10.3390/s21113632
Anzolin A, Toppi J, Petti M, Cincotti F, Astolfi L. SEED-G: Simulated EEG Data Generator for Testing Connectivity Algorithms. Sensors. 2021; 21(11):3632. https://doi.org/10.3390/s21113632
Chicago/Turabian StyleAnzolin, Alessandra, Jlenia Toppi, Manuela Petti, Febo Cincotti, and Laura Astolfi. 2021. "SEED-G: Simulated EEG Data Generator for Testing Connectivity Algorithms" Sensors 21, no. 11: 3632. https://doi.org/10.3390/s21113632
APA StyleAnzolin, A., Toppi, J., Petti, M., Cincotti, F., & Astolfi, L. (2021). SEED-G: Simulated EEG Data Generator for Testing Connectivity Algorithms. Sensors, 21(11), 3632. https://doi.org/10.3390/s21113632







