Extraction of the Structural Properties of Skin Tissue via Diffuse Reflectance Spectroscopy: An Inverse Methodology
Abstract
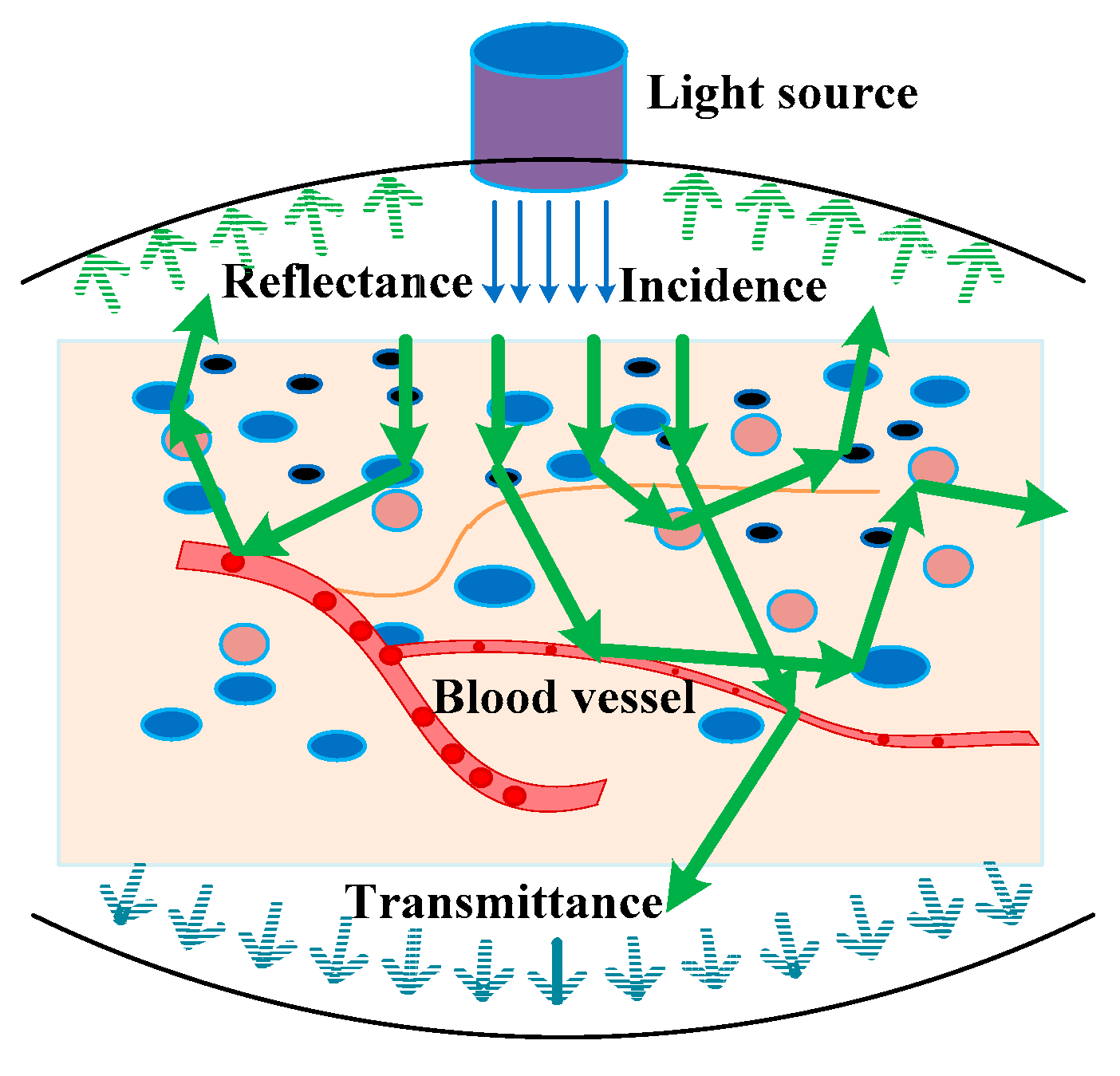
1. Introduction
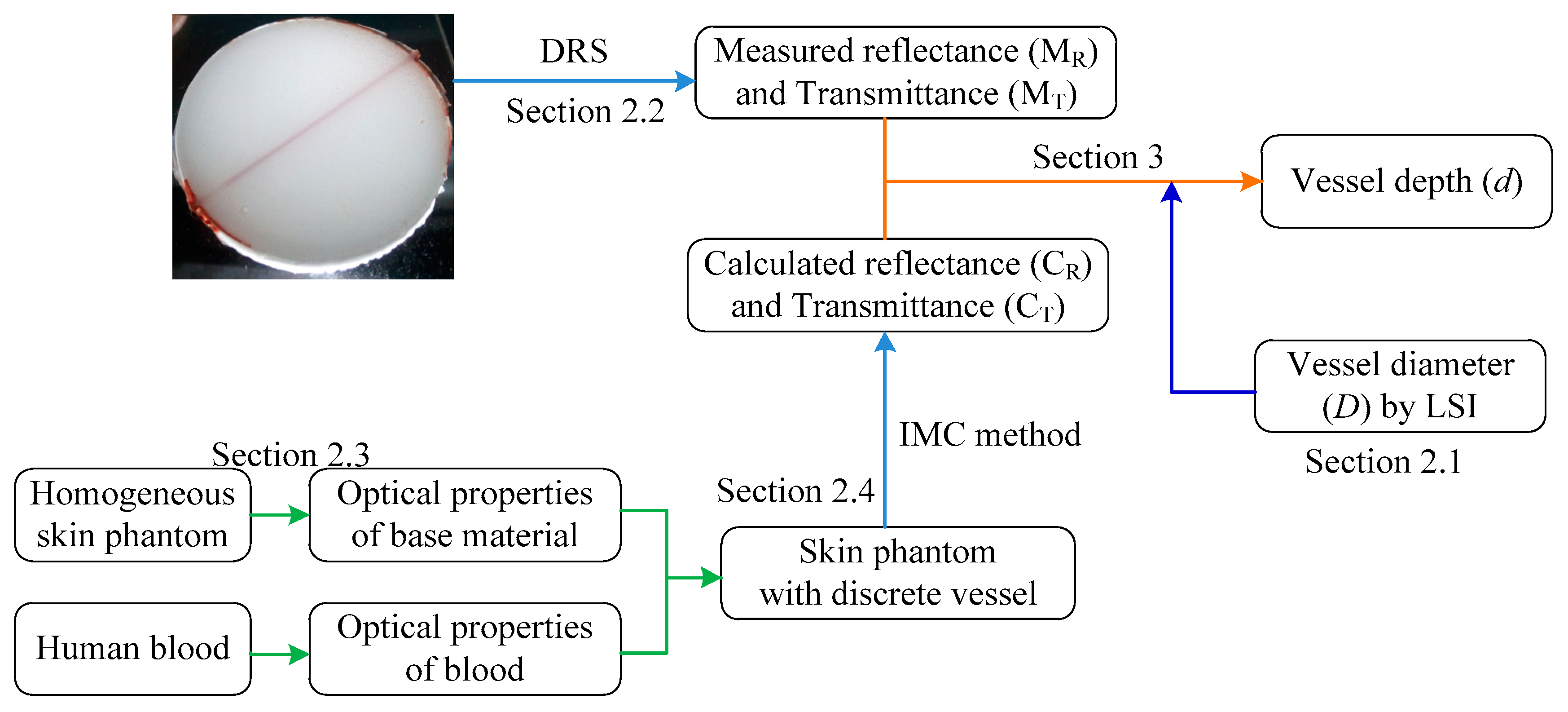
2. Method and Materials
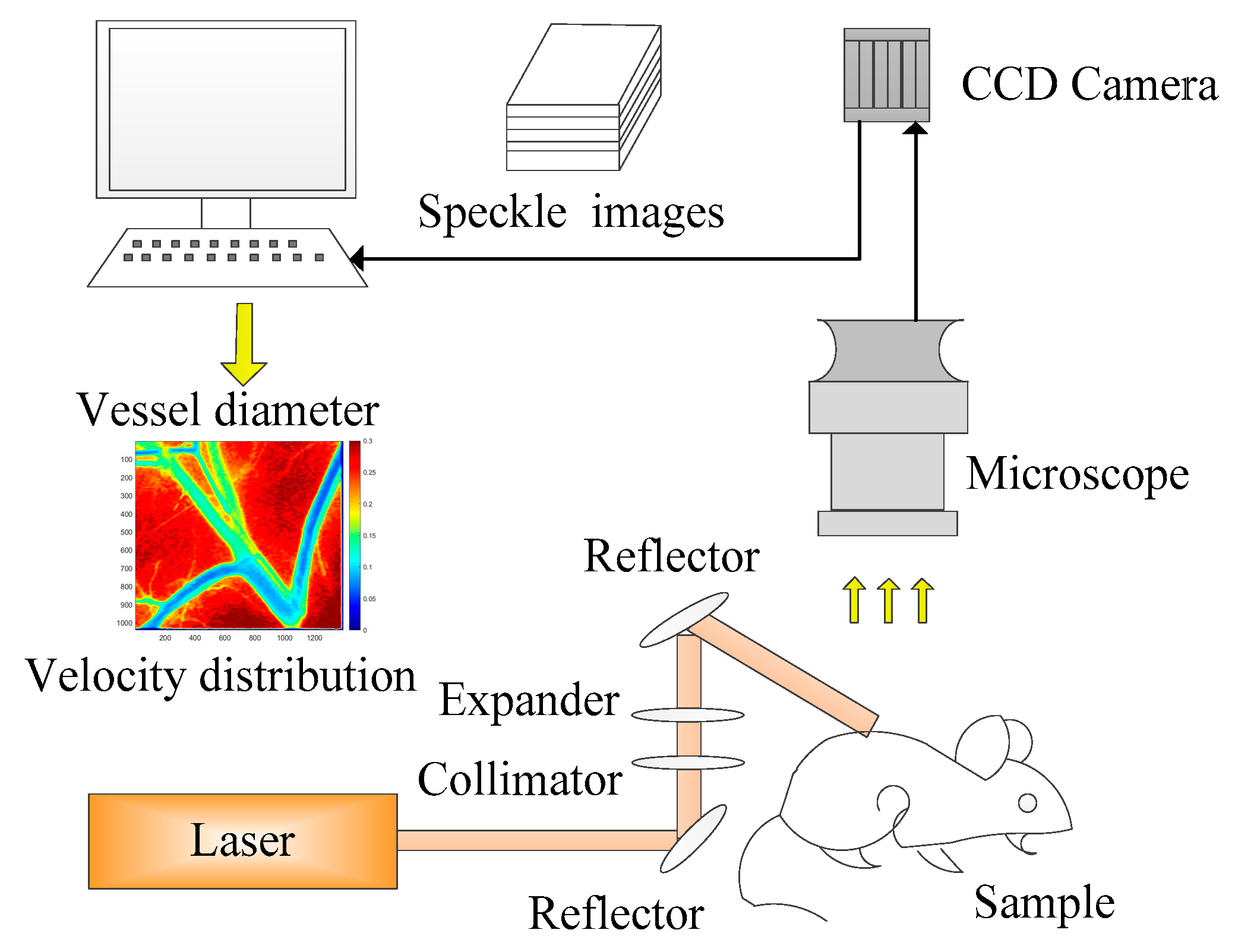
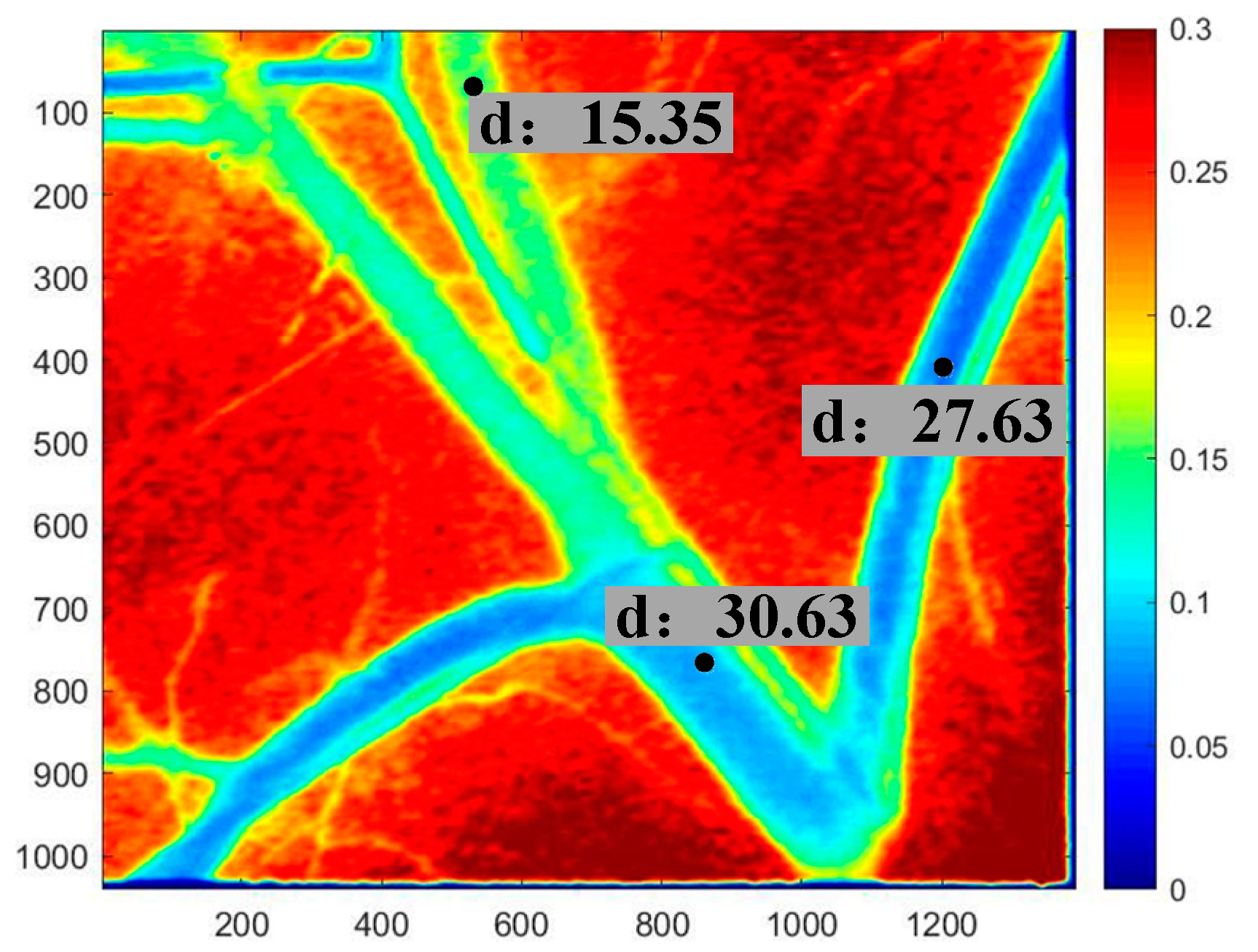
2.1. Estimation of Blood Vessel Diameter Via LSCI
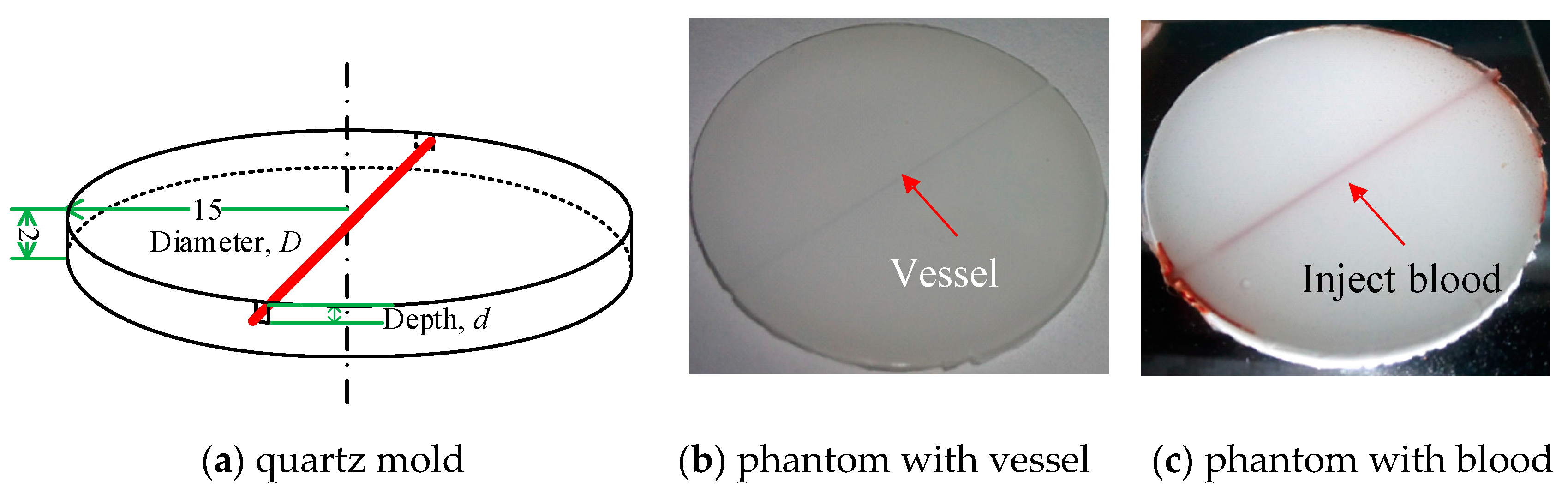
2.2. Skin Phantom Preparation and Spectral Measurement
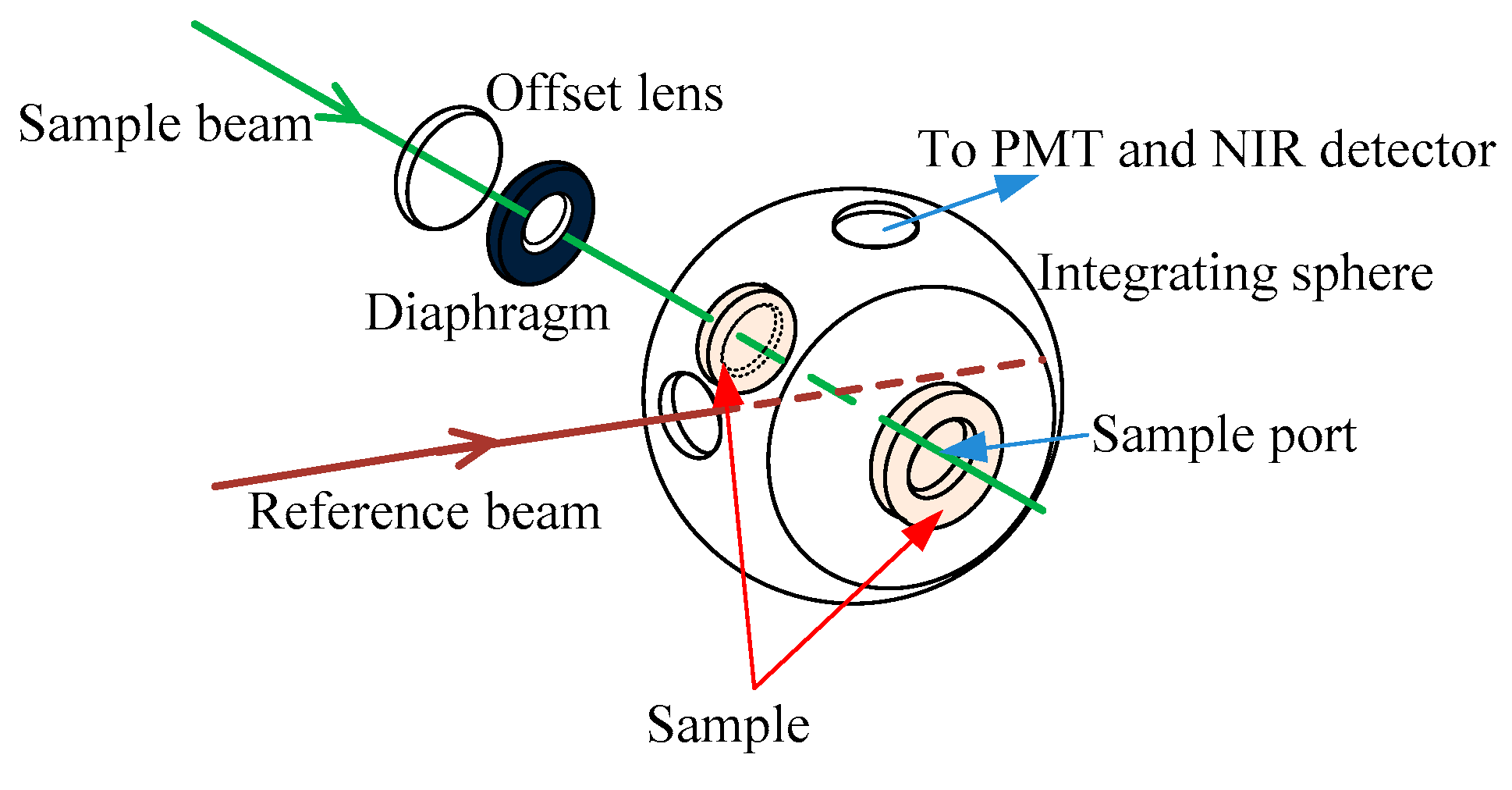
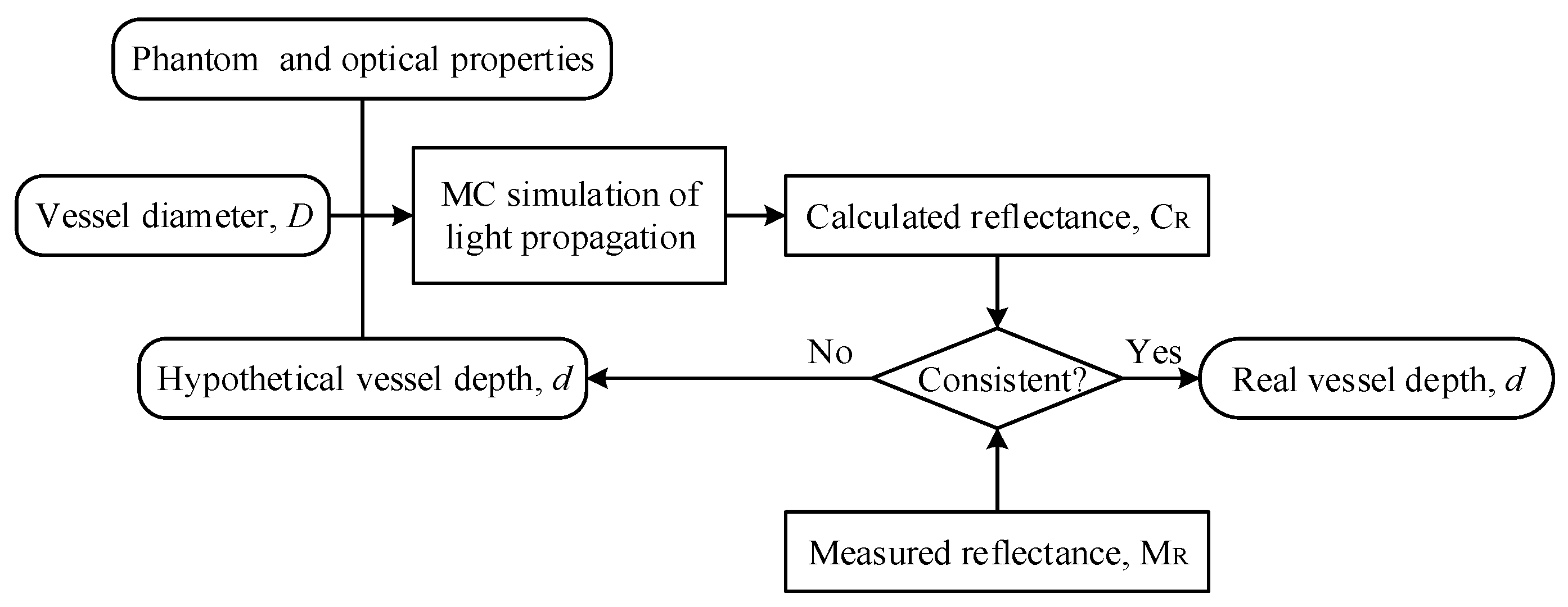
2.3. Overview of the DRS-Based Inverse Method
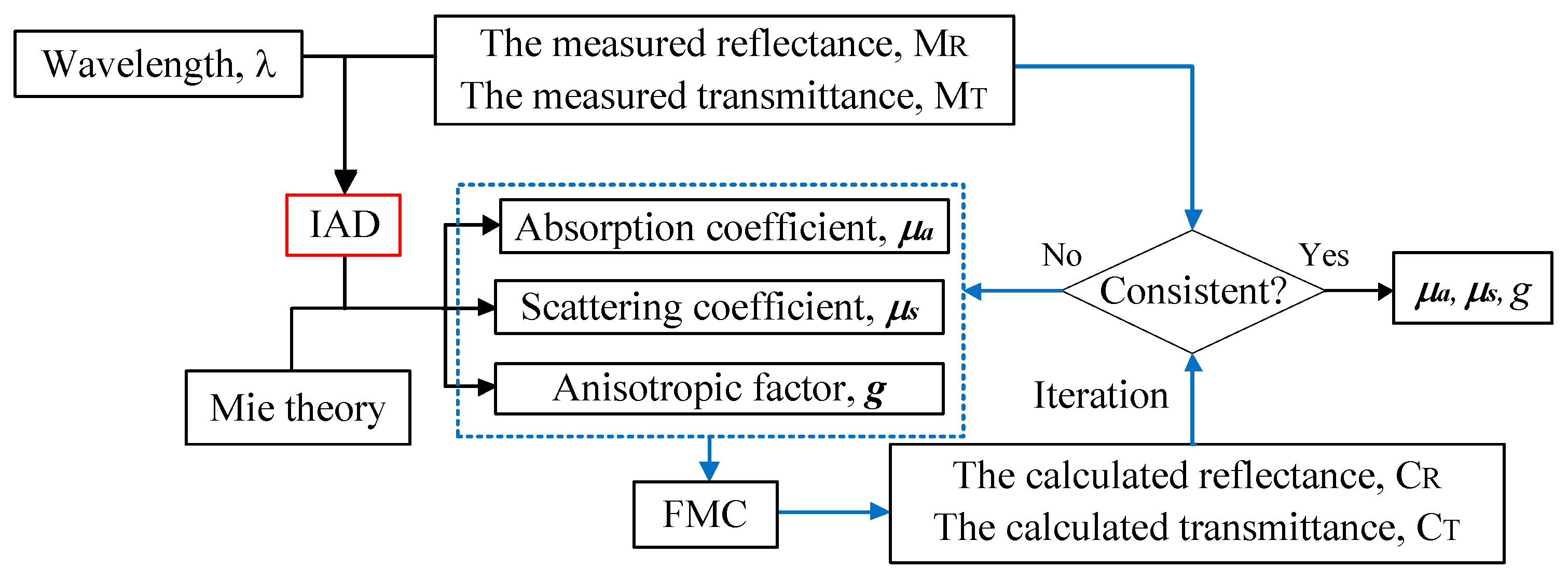
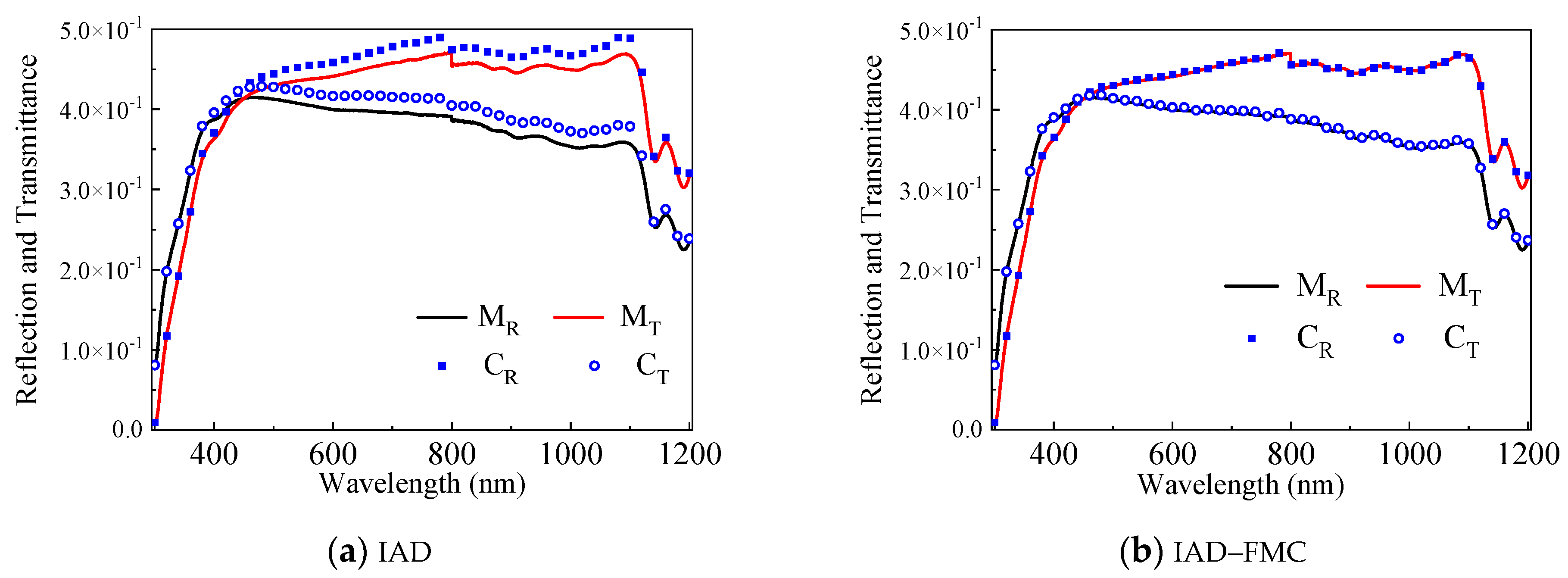
2.4. Integrated IAD–FMC Method
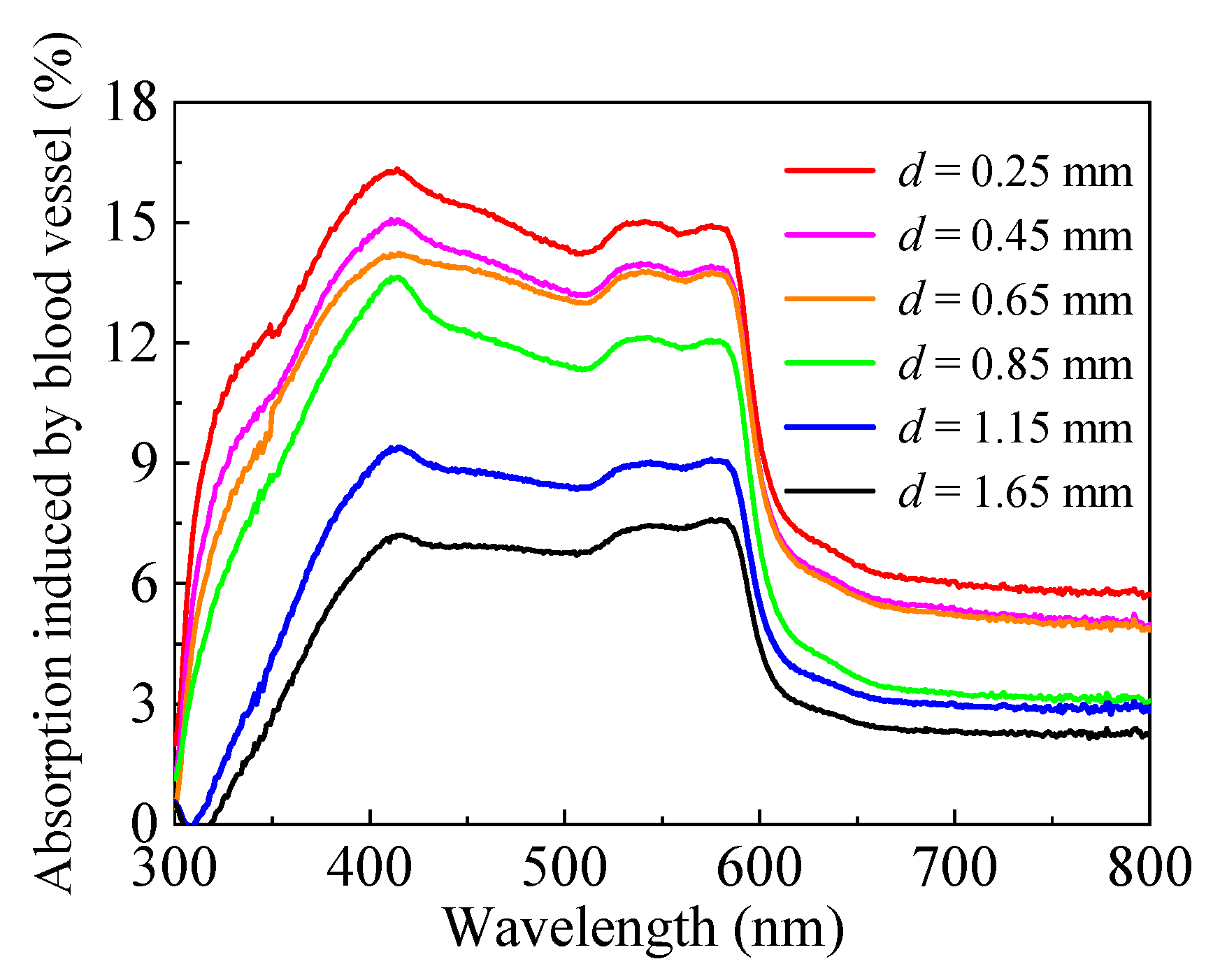
3. Extraction of Vessel Depth
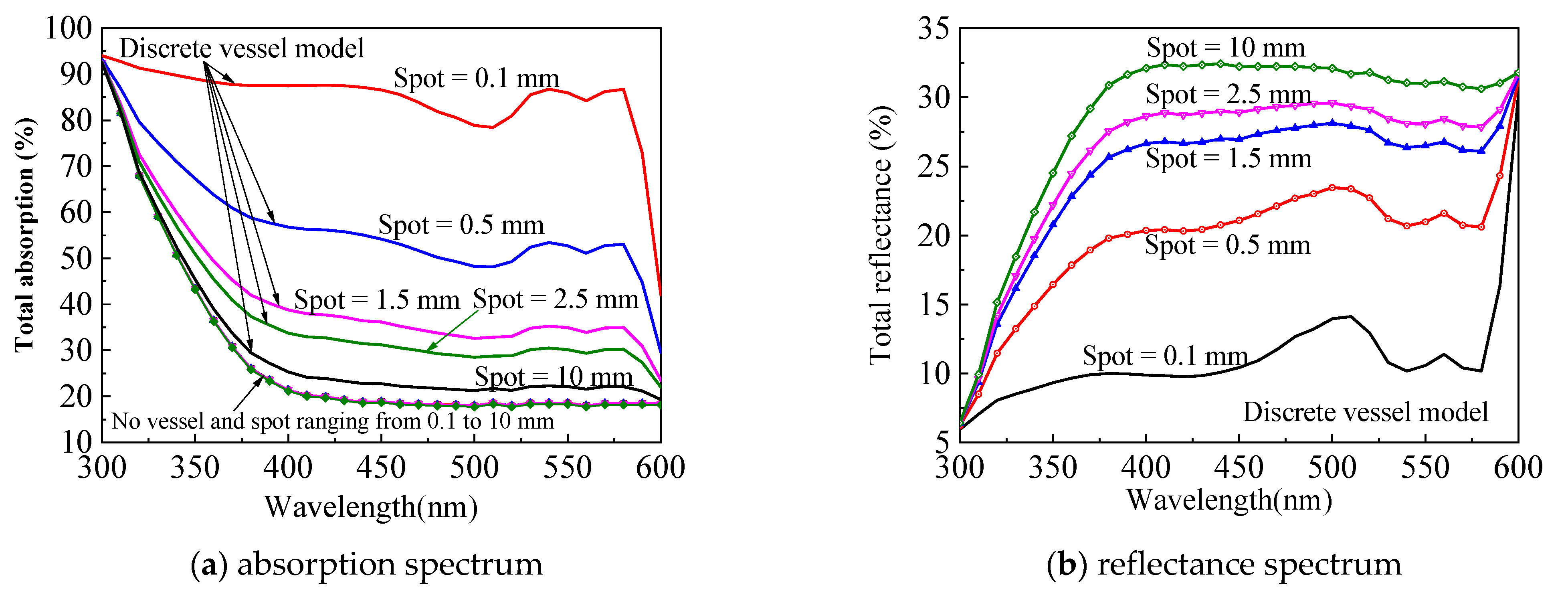
3.1. Depth-Related Spectral Signal and Error Propagation
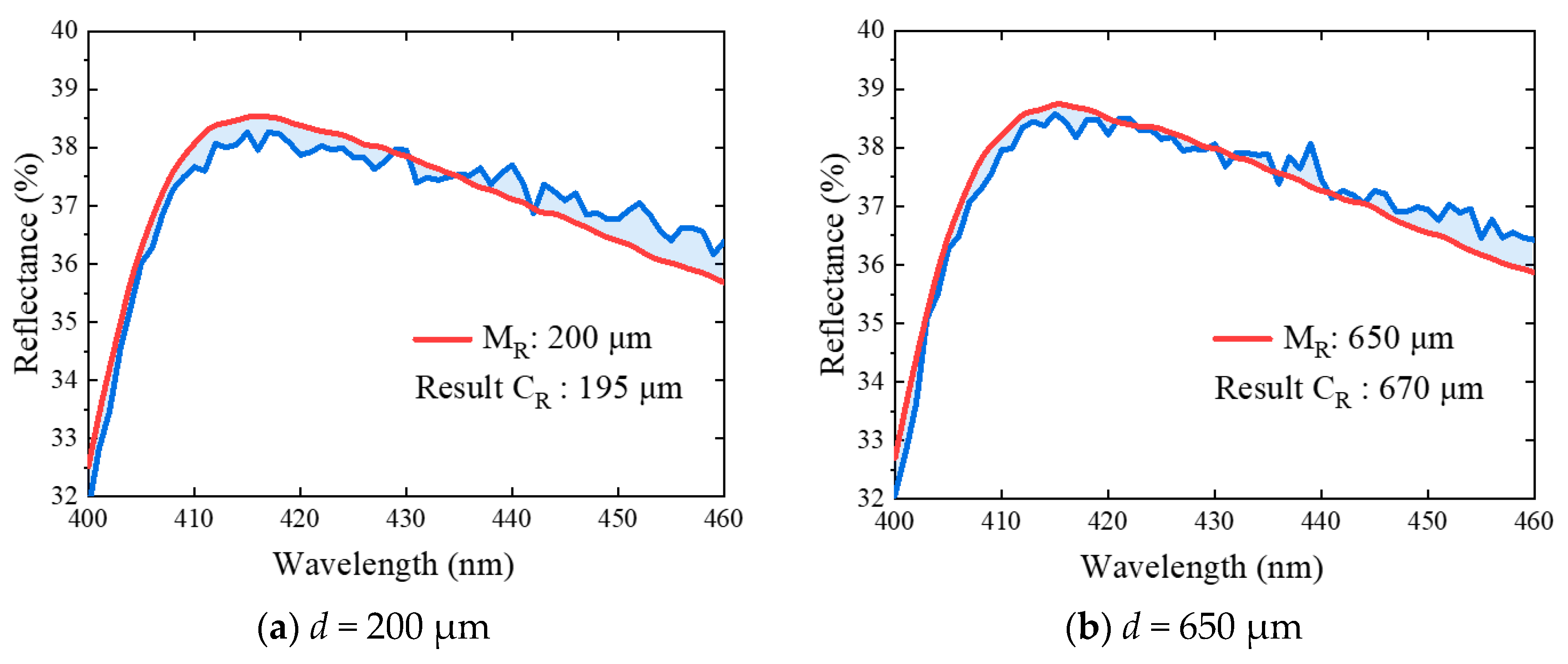
3.2. Reconstruction of the Spectral Signal
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lister, T.; Wright, P.; Chappell, P. Spectrophotometers for the clinical assessment of port-wine stain skin lesions: A review. Lasers Med. Sci. 2010, 25, 449–457. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.; Parrish, J. Selective photothermolysis: Precise microsurgery by selective absorption of pulsed radiation. Science 1983, 220, 524–527. [Google Scholar] [CrossRef]
- Bernstein, E.F. Treatment of a resistant port-wine stain with a new variable pulse-duration pulsed-dye laser. J. Cosmet. Dermatol. 2008, 7, 139–142. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.K.; Ghasri, P.; Aguilar, G.; van Drooge, A.M.; Wolkerstorfer, A.; Kelly, K.; Heger, M. An overview of clinical and experimental treatment modalities for port wine stains. J. Am. Acad. Dermatol. 2012, 67, 289–304.e29. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, R.; Jia, H.; Chen, B.; Wu, W.; Ying, Z. Experimental and numerical investigation on the transient vascular thermal response to multi-pulse Nd:YAG laser. Lasers Surg. Med. 2017, 49, 852–865. [Google Scholar] [CrossRef]
- Widdowson, D.C.; Shakespeare, P.G.; Moore, J.C.; Wright, P.A. Construction of a novel port wine stain phantom and measurement of colour by digital imaging and reflectance spectrophotometry. Lasers Med. Sci. 2007, 23, 369–374. [Google Scholar] [CrossRef]
- Le, K.-V.T.; Shahidullah, H.; Frieden, I.J. Review of Modern Techniques in Detecting Port-wine Stain Response to Laser Therapy. Dermatol. Surg. 1999, 25, 127–132. [Google Scholar] [CrossRef]
- Choi, B.; Tan, W.; Jia, W.; White, S.M.; Moy, W.J.; Yang, B.Y.; Zhu, J.; Chen, Z.; Kelly, K.M.; Nelson, J.S. The Role of Laser Speckle Imaging in Port-Wine Stain Research: Recent Advances and Opportunities. IEEE J. Sel. Top. Quantum Electron. 2015, 22, 307–318. [Google Scholar] [CrossRef]
- Bazant-Hegemark, F.; Meglinski, I.; Kandamany, N. Optical coherence tomography: A potential tool for unsupervised prediction of treatment response for Port-Wine Stains. Photodiagnosis Photodyn. Ther. 2008, 5, 191–197. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Z.; Saxer, C.E. Monitoring laser treatment of port wine stains using phase-resolved optical Doppler tomography. In Proceedings of the SPIE—The International Society for Optical Engineering, San Jose, CA, USA, 22 January 2000; Volume 3915. [Google Scholar]
- Li, B.; Majaron, B.; Viator, J.A.; Milner, T.E.; Chen, Z.; Zhao, Y.; Ren, H.; Nelson, J.S. Accurate measurement of blood vessel depth in port wine stained human skin in vivo using pulsed photothermal radiometry. J. Biomed. Opt. 2004, 9, 961–966. [Google Scholar] [CrossRef]
- Zhang, E.Z.; Laufer, J.G.; Pedley, R.B. In vivo high-resolution 3D photoacoustic imaging of superficial vascular anatomy. Phys. Med. Biol. 2009, 54, 1035–1046. [Google Scholar] [CrossRef] [PubMed]
- Jia, H.; Chen, B.; Li, D. Dynamic optical absorption characteristics of blood after slow and fast heating. Lasers Med. Sci. 2017, 32, 513–525. [Google Scholar] [CrossRef] [PubMed]
- Goldman, M.P. Cutaneous and Cosmetic Laser Surgery; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Gemert, M.; Smithies, D.J.; Verkruysse, W.; Milner, T.E.; Nelson, J.S. Wavelengths for port wine stain laser treatment: Influence of vessel radius and skin anatomy. Phys. Med. Biol. 1997, 42, 41–50. [Google Scholar] [CrossRef][Green Version]
- Xiang, H.; Chen, B.; Wu, W.; Zhang, Y.; Jia, H. An integral MPS model of blood coagulation by laser irradiation: Application to the optimization of multi-pulse Nd:YAG laser treatment of port-wine stains. Int. J. Heat Mass Transf. 2017, 114, 1220–1233. [Google Scholar] [CrossRef]
- Schuh, S.; Holmes, J.; Ulrich, M.; Themstrup, L.; Jemec, G.; Carvalho, N.D. Imaging blood vessel morphology in skin: Dynamic optical coherence tomography as a novel potential diagnostic tool in dermatology. Dermatol. Ther. 2017, 7, 187–202. [Google Scholar] [CrossRef] [PubMed]
- Nagaoka, T.; Nakamura, A.; Aizawa, K.; Ohtsubo, S.; Mochizuki, T.; Kiyohara, Y.; Sota, T. Development of blood vessel viewer using multi spectral imaging technology. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Montréal, QC, Canada, 17 June 2008; Volume 2008, pp. 1234–1237. [Google Scholar]
- Cuper, N.J.; Verdaasdonk, R.M.; De Roode, R. Validation of the performance of a practical blood vessel imaging system to facilitate vessel punctures. SPIE BiOS Biomed. Opt. 2009, 7169, 716918. [Google Scholar] [CrossRef]
- Prince, J.L. Medical imaging signals and systems. Signal 2014, 48, 69–76. [Google Scholar]
- Selim, M.M.; Kelly, K.M.; Nelson, J.S.; Wendelschafer-Crabb, G.; Kennedy, W.R.; Zelickson, B.D. Confocal Microscopy Study of Nerves and Blood Vessels in Untreated and Treated Port Wine Stains: Preliminary Observations. Dermatol. Surg. 2004, 30, 892–897. [Google Scholar]
- Welzel, J. Optical coherence tomography in dermatology: A review. Skin Res. Technol. 2001, 7, 1–9. [Google Scholar] [CrossRef]
- Bjorgan, A.; Milanic, M.; Randeberg, L. Estimation of skin optical parameters for real-time hyperspectral imaging applications. J. Biomed. Opt. 2014, 19, 066003. [Google Scholar] [CrossRef]
- Rajaram, N.; Reichenberg, J.S.; Migden, M.R.; Nguyen, T.H.; Tunnell, J.W. Pilot clinical study for quantitative spectral diagnosis of non-melanoma skin cancer. Lasers Surg. Med. 2011, 42, 716–727. [Google Scholar]
- George, R.; Chandrasekaran, A.; Brewer, M.A.; Hatch, K.D.; Utzinger, U. Clinical research device for ovarian cancer detection by optical spectroscopy in the ultraviolet C-visible. J. Biomed. Opt. 2010, 15, 410–417. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zhu, C.; Palmer, G.M.; Breslin, T.M.; Harter, J.M.; Ramanujam, N. Diagnosis of breast cancer using fluorescence and diffuse reflectance spectroscopy: A Monte-Carlo-model-based approach. J. Biomed. Opt. 2008, 13, 034015. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Prahl, S. The Inverse Adding-Doubling (IAD) Program. 2011. Available online: http://omlc.org/software/iad/index.html (accessed on 26 May 2020).
- Prahl, S.A.; Gemert, M.; Welch, A.J. Determining the optical properties of turbid media by using the adding-doubling method. Appl. Opt. 1993, 32, 559–568. [Google Scholar] [CrossRef] [PubMed]
- Honda, N.; Ishii, K.; Kimura, A.; Sakai, M.; Awazu, K. Determination of optical property changes by laser treatments using inverse adding-doubling method. SPIE BiOS Biomed. Opt. 2009, 7175, 71750. [Google Scholar] [CrossRef]
- Martinelli, M.; Gardner, A.; Cuccia, D.; Hayakawa, C.; Venugopalan, V. Analysis of single Monte Carlo methods for prediction of reflectance from turbid media. Opt. Express 2011, 19, 19627–19642. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Li, D.; Wang, G.-X. Efficient and Accurate Simulation of Light Propagation in Bio-Tissues Using the Three-Dimensional Geometric Monte Carlo Method. Numer. Heat Transf. Part A Appl. 2015, 68, 827–846. [Google Scholar] [CrossRef]
- Barsky, S.H.; Rosen, S.; Geer, D.E.; Noe, J.M. The Nature and Evolution of Port Wine Stains: A Computer-assisted Study. J. Investig. Dermatol. 1980, 74, 154–157. [Google Scholar] [CrossRef]
- Svaasand, L.; Fiskerstrand, E.; Kopstad, G. Therapeutic response during pulsed laser treatment of port-wine stains: Dependence on vessel diameter and depth in dermis. Lasers Med. Sci. 1995, 10, 235–243. [Google Scholar] [CrossRef]
- Hohmann, M.; Hecht, D.; Lengenfelder, B.; Späth, M.; Klämpfl, F.; Schmidt, M. Proof of Principle for Direct Reconstruction of Qualitative Depth Information from Turbid Media by a Single Hyper Spectral Image. Sensors 2021, 21, 2860. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Zhang, Y.; Gao, S.; Li, D. Extraction of the Structural Properties of Skin Tissue via Diffuse Reflectance Spectroscopy: An Inverse Methodology. Sensors 2021, 21, 3745. https://doi.org/10.3390/s21113745
Chen B, Zhang Y, Gao S, Li D. Extraction of the Structural Properties of Skin Tissue via Diffuse Reflectance Spectroscopy: An Inverse Methodology. Sensors. 2021; 21(11):3745. https://doi.org/10.3390/s21113745
Chicago/Turabian StyleChen, Bin, Yong Zhang, Shang Gao, and Dong Li. 2021. "Extraction of the Structural Properties of Skin Tissue via Diffuse Reflectance Spectroscopy: An Inverse Methodology" Sensors 21, no. 11: 3745. https://doi.org/10.3390/s21113745
APA StyleChen, B., Zhang, Y., Gao, S., & Li, D. (2021). Extraction of the Structural Properties of Skin Tissue via Diffuse Reflectance Spectroscopy: An Inverse Methodology. Sensors, 21(11), 3745. https://doi.org/10.3390/s21113745





