A High-Resolution Reflective Microwave Planar Sensor for Sensing of Vanadium Electrolyte
Abstract
:1. Introduction
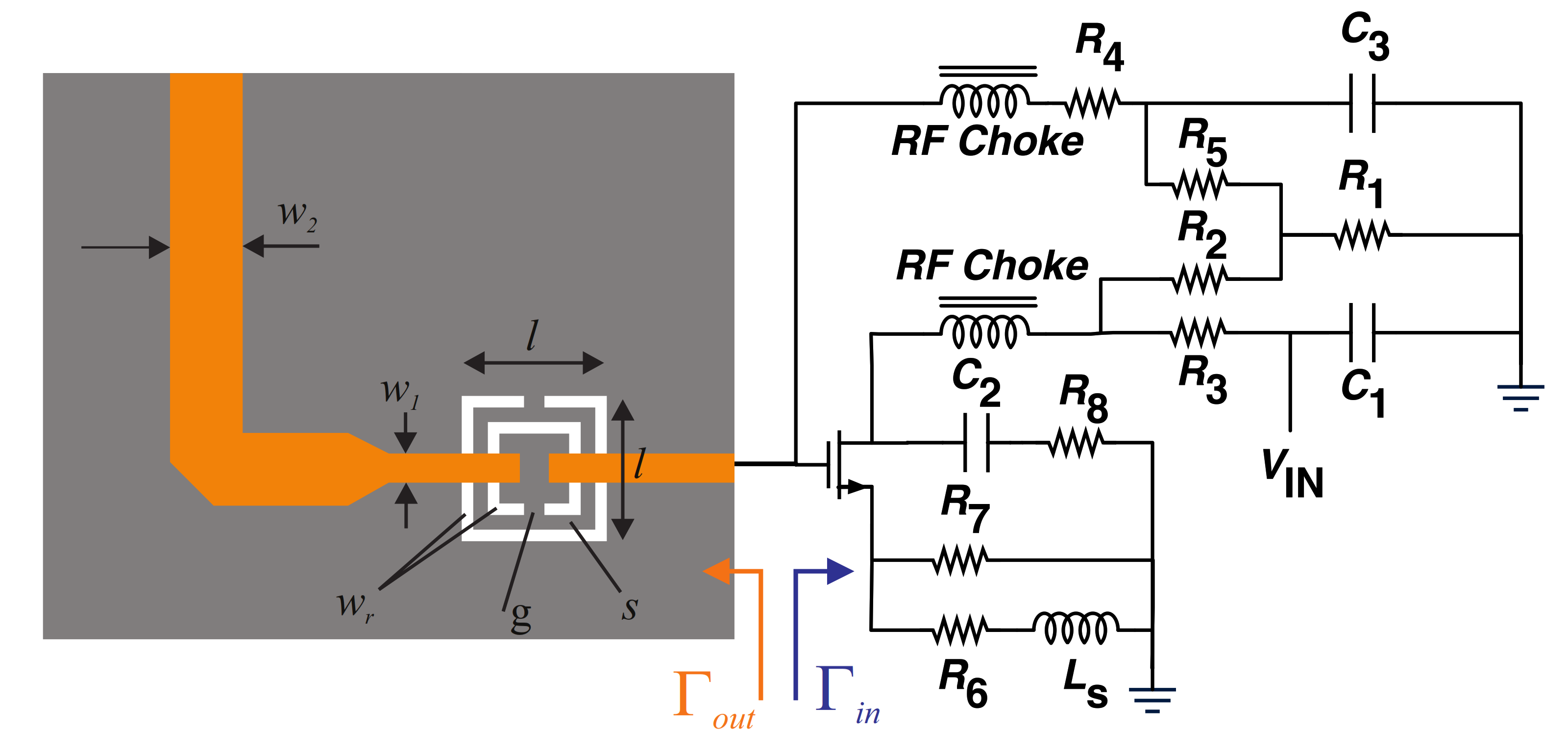
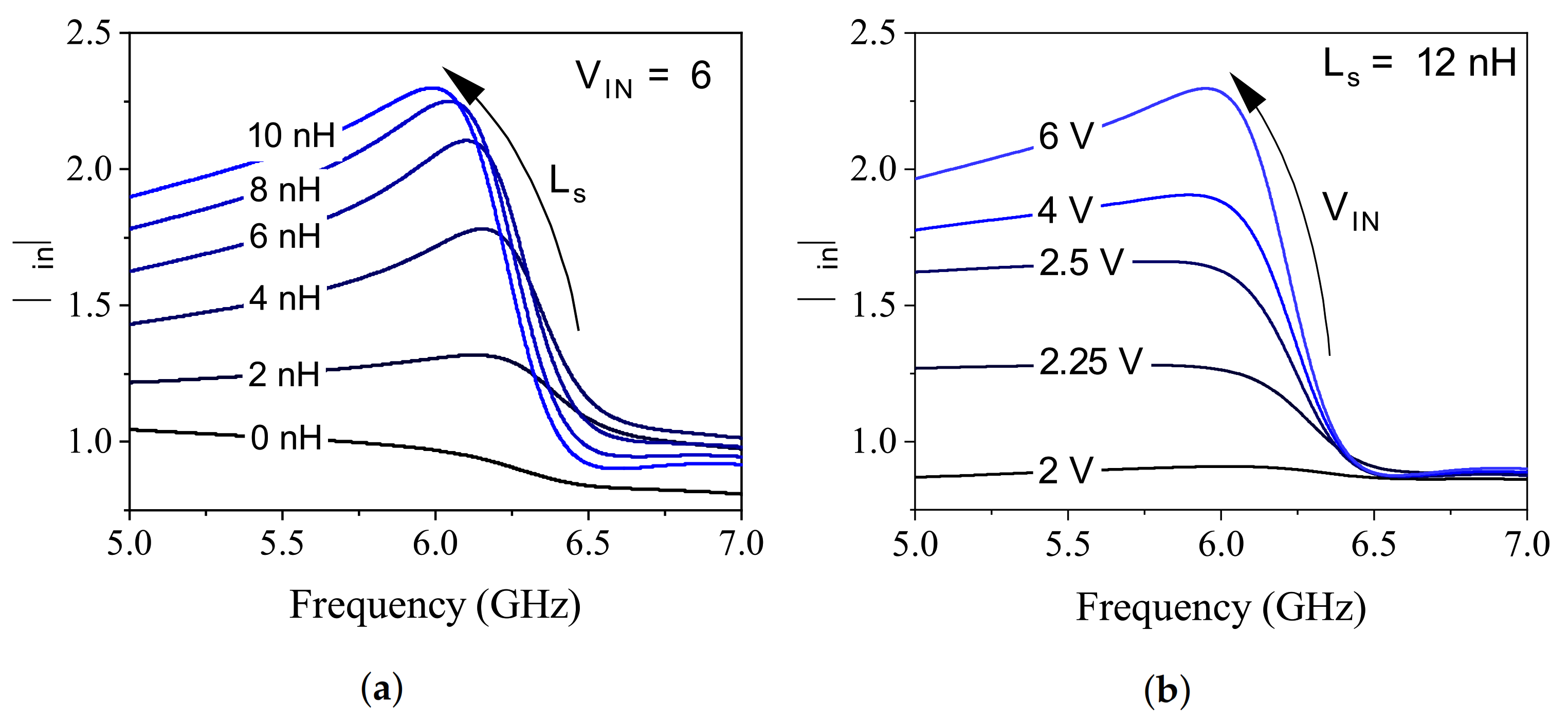
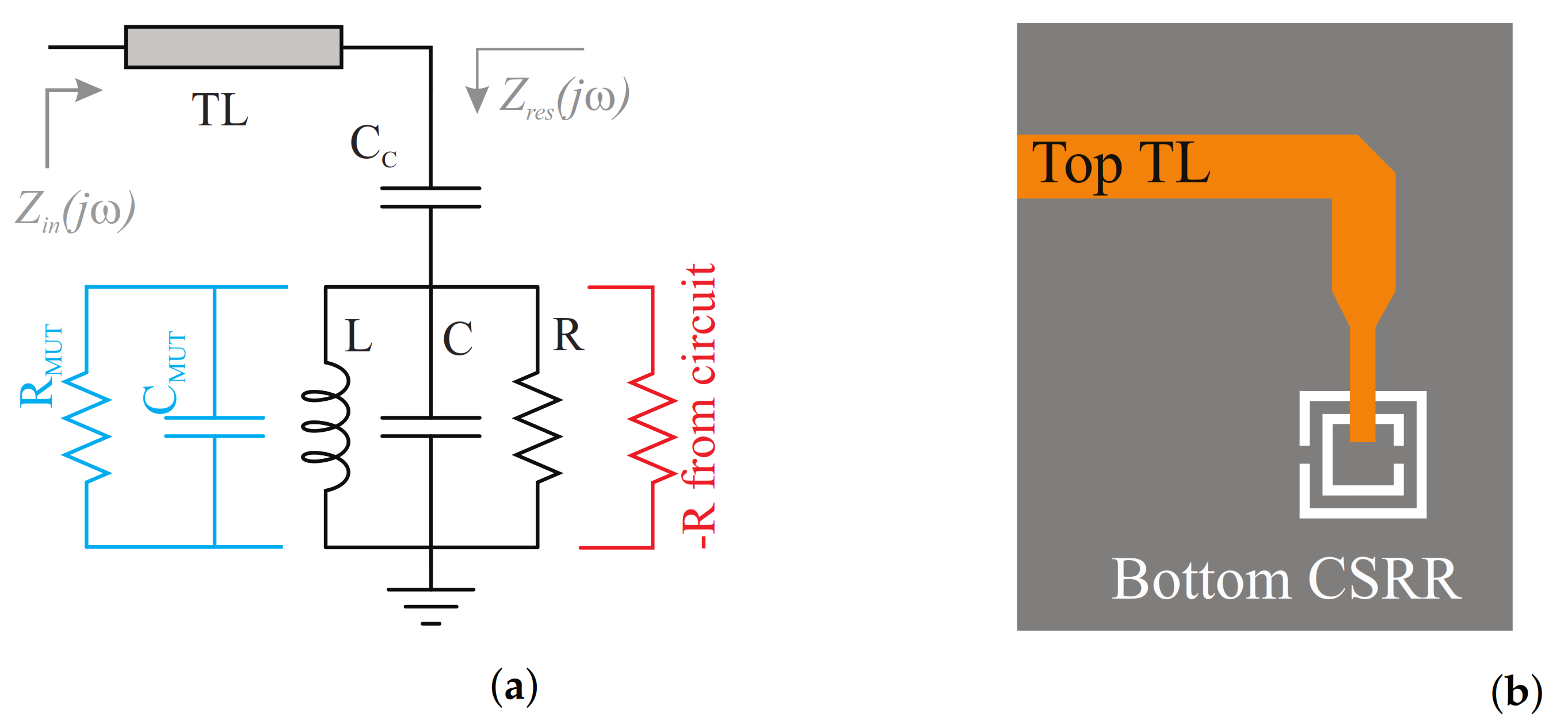
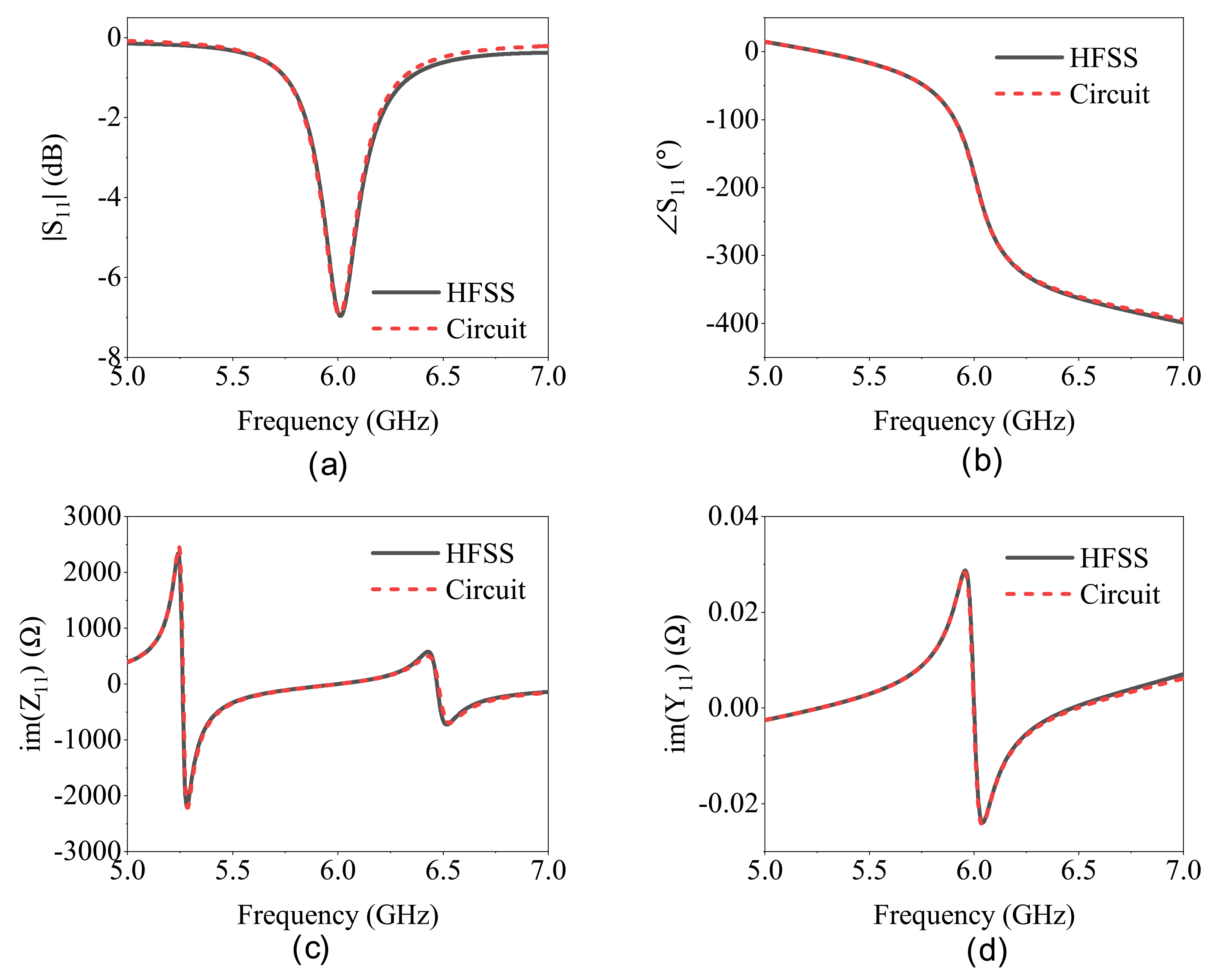
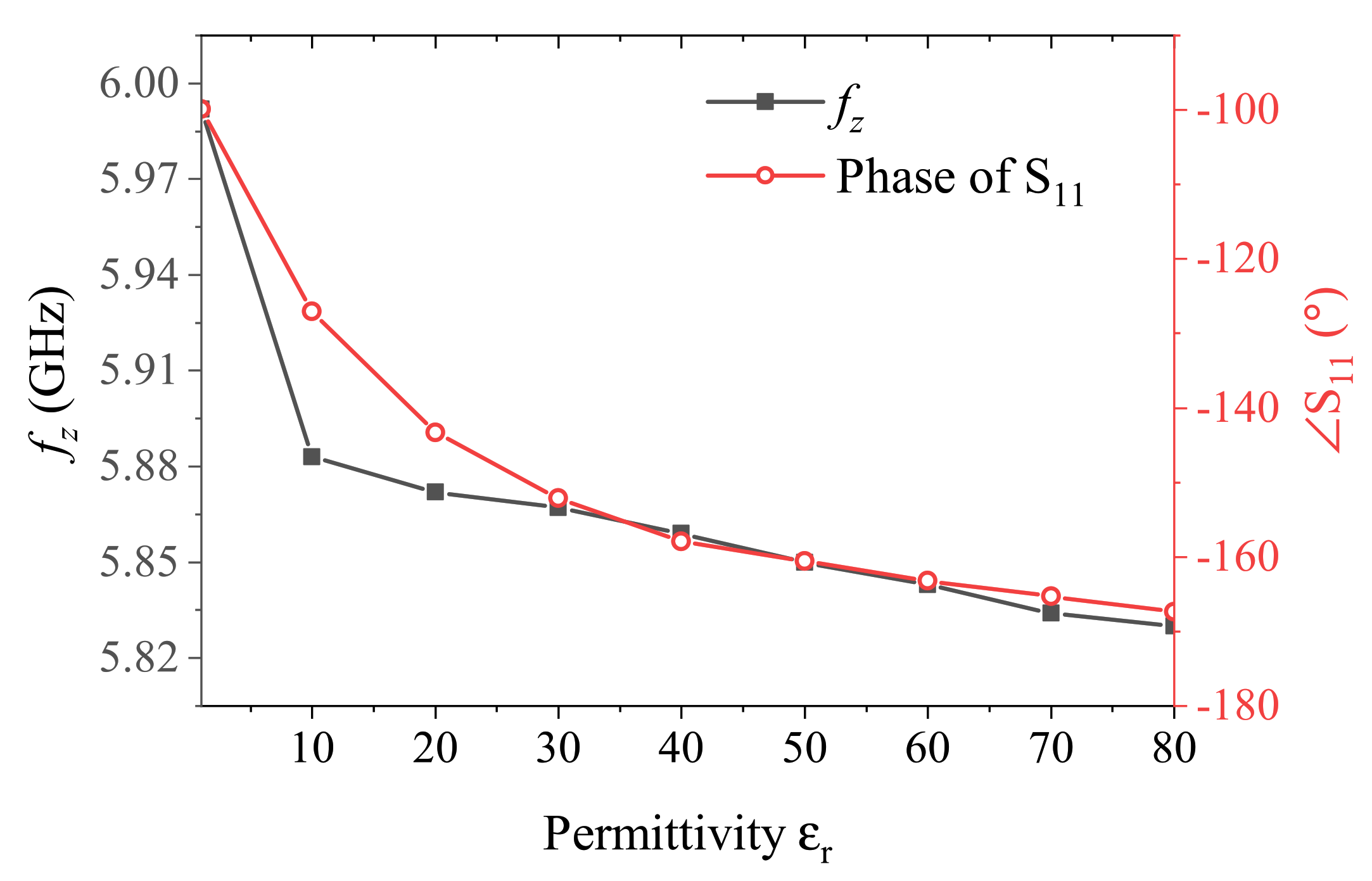
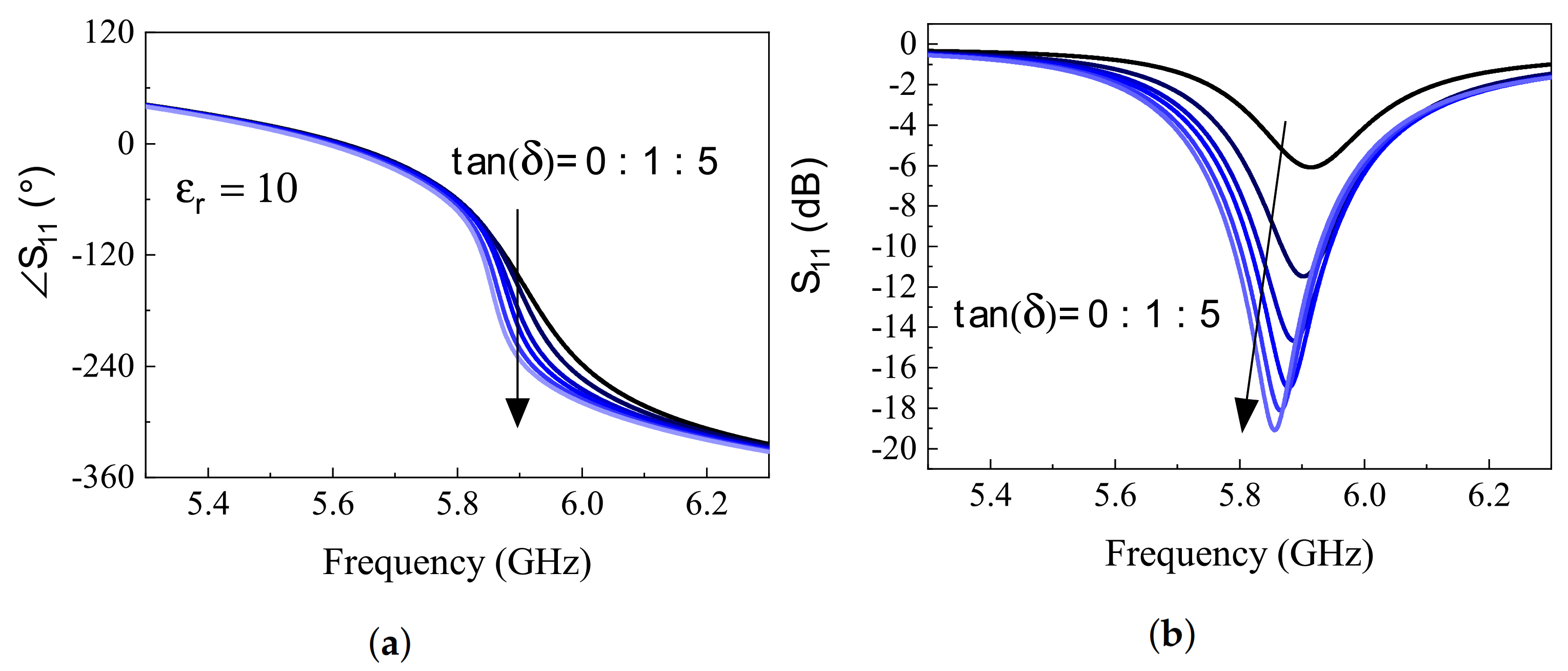
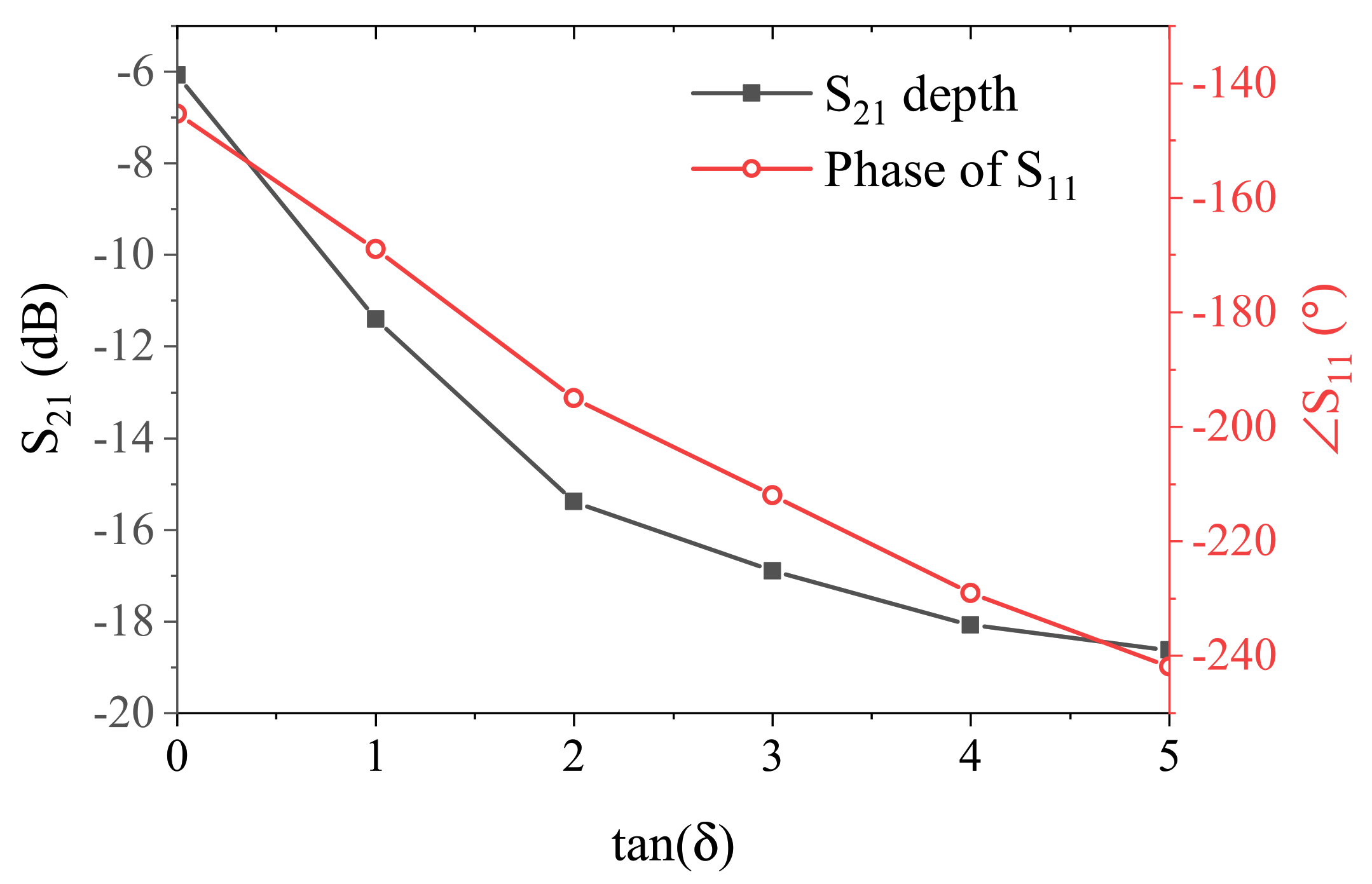
2. Sensor Design and Analysis
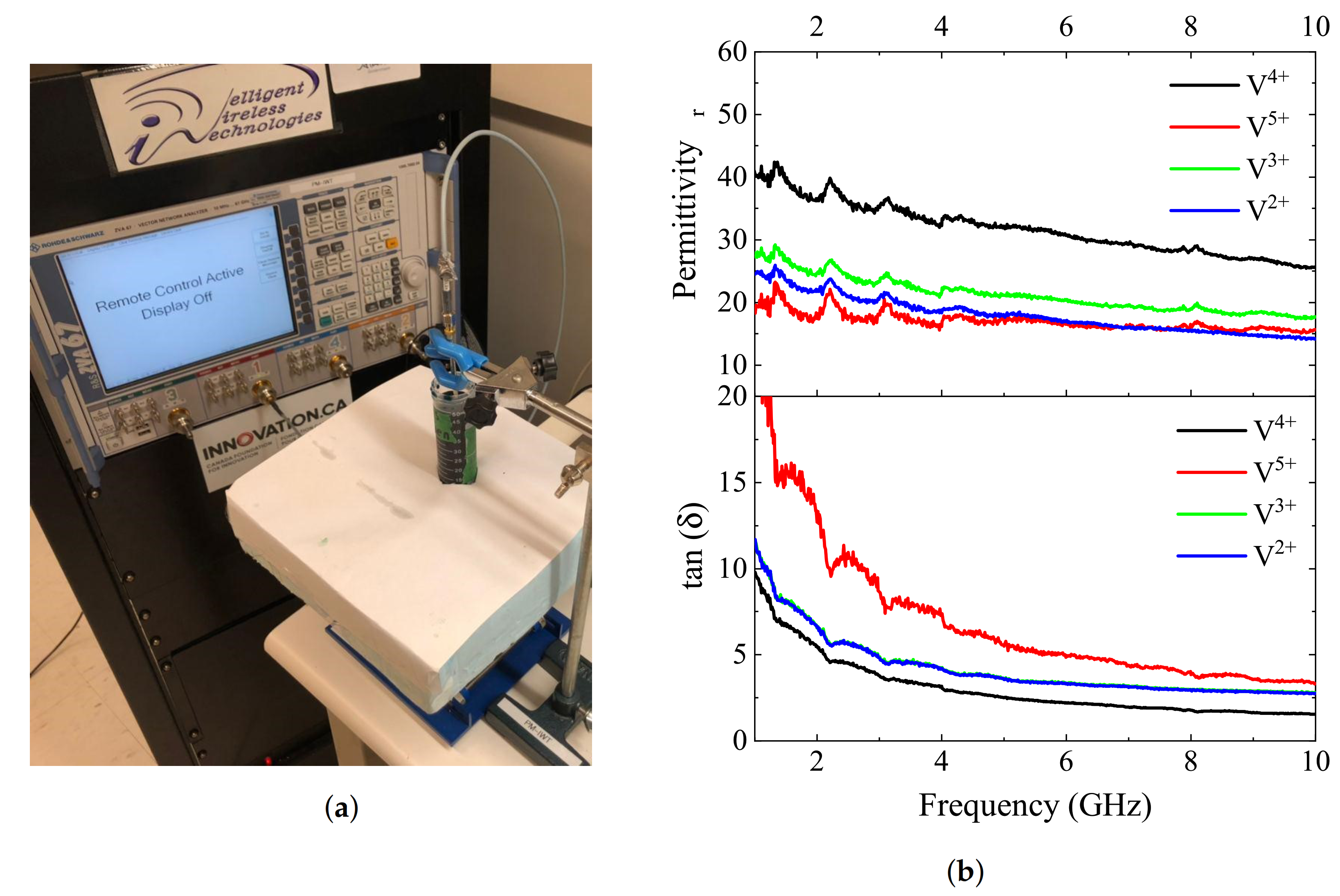
3. Vanadium Electrolyte (MUT)
4. Measurement Results and Discussion
4.1. Common Liquid Measurement
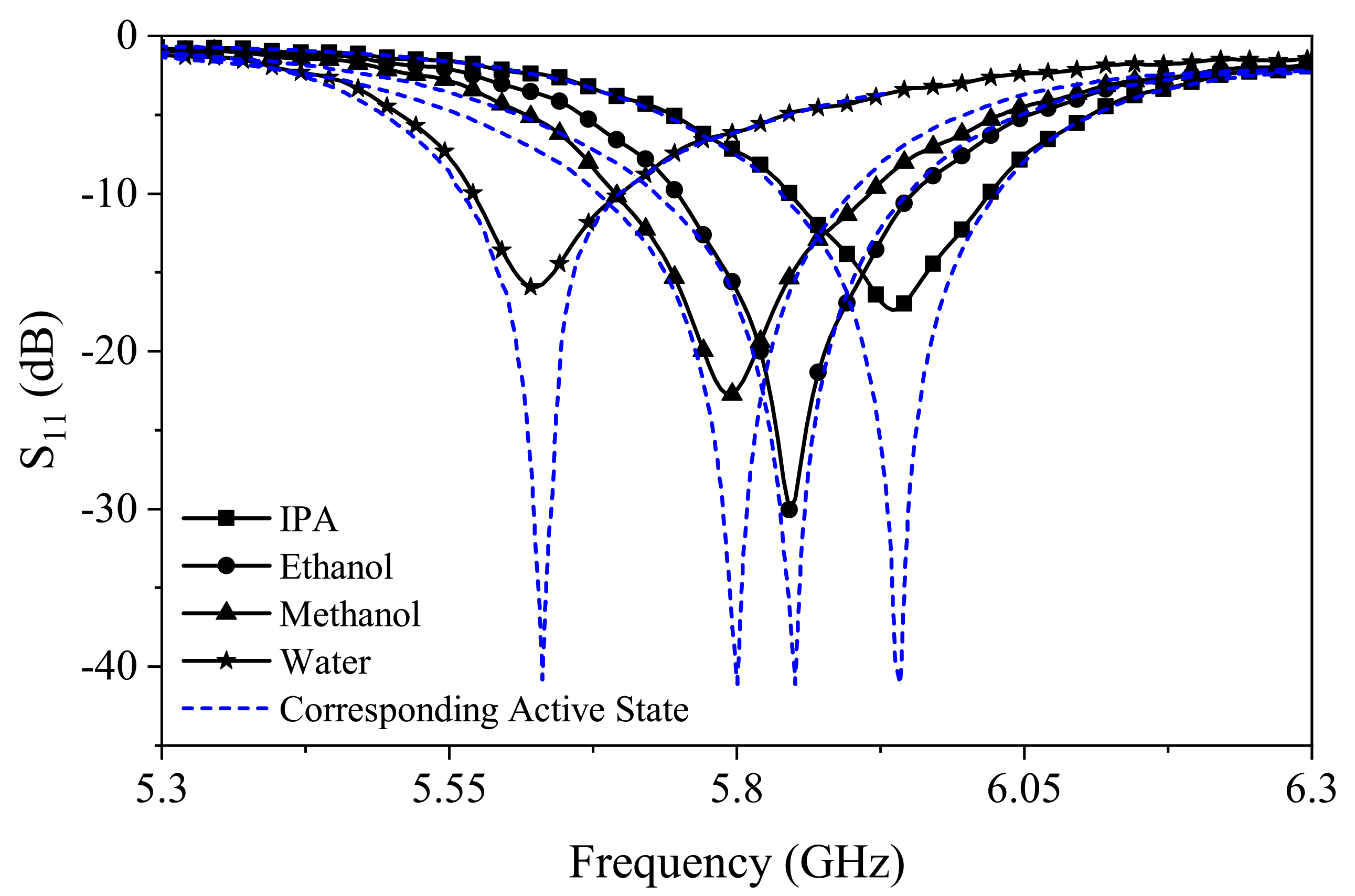
4.2. Measuring Vanadium Redox Solutions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdolrazzaghi, M.; Daneshmand, M.; Iyer, A.K. Strongly Enhanced Sensitivity in Planar Microwave Sensors Based on Metamaterial Coupling. IEEE Trans. Microw. Theory Tech. 2018, 66, 1843–1855. [Google Scholar] [CrossRef] [Green Version]
- Abdolrazzaghi, M.; Daneshmand, M. Exploiting Sensitivity Enhancement in Micro-wave Planar Sensors Using Intermodulation Products With Phase Noise Analysis. IEEE Trans. Circ. Syst. I Regul. Pap. 2020, 67, 4382–4395. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Kazemi, N.; Daneshmand, M. An SIW Oscillator for Microfluidic Lossy Medium Characterization. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020; pp. 221–224. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Kazemi, N.; Daneshmand, M. Sensitive spectroscopy using DSRR array and Linvill negative impedance. In Proceedings of the 2019 IEEE MTT-S International Microwave Symposium (IMS), Boston, MA, USA, 2–7 June 2019; pp. 1080–1083. [Google Scholar]
- Su, L.; Muñoz-Enano, J.; Vélez, P.; Gil-Barba, M.; Casacuberta, P.; Martin, F. Highly Sensitive Reflective-Mode Phase-Variation Permittivity Sensor Based on a Coplanar Waveguide Terminated With an Open Complementary Split Ring Resonator (OCSRR). IEEE Access 2021, 9, 27928–27944. [Google Scholar] [CrossRef]
- Vélez, P.; Munoz-Enano, J.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martín, F. Split ring resonator-based microwave fluidic sensors for electrolyte concentration measurements. IEEE Sens. J. 2018, 19, 2562–2569. [Google Scholar] [CrossRef]
- Albishi, A.M.; El Badawe, M.K.; Nayyeri, V.; Ramahi, O.M. Enhancing the sensitivity of dielectric sensors with multiple coupled complementary split-ring resonators. IEEE Trans. Microw. Theory Tech. 2020, 68, 4340–4347. [Google Scholar] [CrossRef]
- Mosavirik, T.; Soleimani, M.; Nayyeri, V.; Mirjahanmardi, S.H.; Ramahi, O.M. Permittivity Characterization of Dispersive Materials Using Power Measurements. IEEE Trans. Instrum. Meas. 2021. [Google Scholar] [CrossRef]
- Albishi, A.M.; Mirjahanmardi, S.H.; Ali, A.M.; Nayyeri, V.; Wasly, S.M.; Ramahi, O.M. Intelligent sensing using multiple sensors for material characterization. Sensors 2019, 19, 4766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yeo, J.; Lee, J.I. High-sensitivity microwave sensor based on an interdigital-capacitor-shaped defected ground structure for permittivity characterization. Sensors 2019, 19, 498. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martín, F.; Vélez, P.; Gil, M. Microwave Sensors Based on Resonant Elements. Sensors 2020, 20, 3375. [Google Scholar] [CrossRef] [PubMed]
- Alahnomi, R.A.; Zakaria, Z.; Yussof, Z.M.; Althuwayb, A.A.; Alhegazi, A.; Alsariera, H.; Rahman, N.A. Review of Recent Microwave Planar Resonator-Based Sensors: Techniques of Complex Permittivity Extraction, Applications, Open Challenges and Future Research Directions. Sensors 2021, 21, 2267. [Google Scholar] [CrossRef]
- Muñoz-Enano, J.; Coromina, J.; Vélez, P.; Su, L.; Gil, M.; Casacuberta, P.; Martín, F. Planar Phase-Variation Microwave Sensors for Material Characterization: A Review and Comparison of Various Approaches. Sensors 2021, 21, 1542. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Tovar-Lopez, F.J.; Scott, J.; Ghorbani, K. Differential microwave sensor for characterization of glycerol–water solutions. Sens. Actuators B Chem. 2020, 321, 128561. [Google Scholar] [CrossRef]
- Muñoz-Enano, J.; Vélez, P.; Gil, M.; Martín, F. Microfluidic reflective-mode differential sensor based on open split ring resonators (OSRRs). Int. J. Microw. Wirel. Technol. 2020, 12, 588–597. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Microwave reflective biosensor for glucose level detection in aqueous solutions. Sens. Actuators A Phys. 2020, 301, 111662. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Dual-mode resonator for simultaneous permittivity and thickness measurement of dielectrics. IEEE Sens. J. 2019, 20, 185–192. [Google Scholar] [CrossRef]
- Su, L.; Mata-Contreras, J.; Vélez, P.; Martín, F. Splitter/combiner microstrip sections loaded with pairs of complementary split ring resonators (CSRRs): Modeling and optimization for differential sensing applications. IEEE Trans. Microw. Theory Tech. 2016, 64, 4362–4370. [Google Scholar] [CrossRef]
- Baghelani, M.; Abbasi, Z.; Daneshmand, M.; Light, P.E. Non-invasive continuous-time glucose monitoring system using a chipless printable sensor based on split ring microwave resonators. Sci. Rep. 2020, 10, 1–15. [Google Scholar]
- Abbasi, Z.; Niazi, H.; Abdolrazzaghi, M.; Chen, W.; Daneshmand, M. Monitoring pH level using high-resolution microwave sensor for mitigation of stress corrosion cracking in steel pipelines. IEEE Sens. J. 2020, 20, 7033–7043. [Google Scholar] [CrossRef]
- Baghelani, M.; Abbasi, Z.; Daneshmand, M. Noncontact high sensitivity chipless tag microwave resonator for bitumen concentration measurement at high temperatures. Fuel 2020, 265, 116916. [Google Scholar] [CrossRef]
- Hosseini, N.; Baghelani, M. Selective Real-Time Non-Contact Multi-Variable Water-Alcohol-Sugar Concentration Analysis during Fermentation Process using Microwave Split-Ring Resonator Based Sensor. Sens. Actuators A Phys. 2021, 325, 112695. [Google Scholar] [CrossRef]
- Yaroshenko, I.; Kirsanov, D.; Marjanovic, M.; Lieberzeit, P.A.; Korostynska, O.; Mason, A.; Frau, I.; Legin, A. Real-time wáter quality monitoring with chemical sensors. Sensors 2020, 20, 3432. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.K.; Tiwari, N.K.; Yadav, A.K.; Akhtar, M.J.; Kar, K.K. Design of ZnO/N-doped graphene nanohybrid incorporated RF complementary split ring resonator sensor for ammonia gas detection. IEEE Sens. J. 2019, 19, 7968–7975. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Daneshmand, M. Multifunctional ultrahigh sensitive microwave planar sensor to monitor mechanical Motion: Rotation, displacement and Stretch. Sensors 2020, 20, 1184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kazemi, N.; Abdolrazzaghi, M.; Musilek, P.; Daneshmand, M. A Temperature-Compensated High-Resolution Microwave Sensor Using Artificial Neural Network. IEEE Microw. Wirel. Components Lett. 2020, 30, 919–922. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Kazemi, N.; Daneshmand, M. Machine Learning to Immune Microwave Sensors from Temperature Impact. In Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting, Montréal, QC, Canada, 5–10 July 2020; pp. 843–844. [Google Scholar]
- Cui, Y.; Ge, A. A Tunable High-Q Microwave Detector for On-Column Capillary Liquid Chromatography. IEEE Trans. Instrum. Meas. 2020, 69, 5978–5980. [Google Scholar] [CrossRef]
- Fan, L.C.; Zhao, W.S.; Gan, H.Y.; He, L.; Liu, Q.; Dong, L.; Wang, G. A high-Q active substrate integrated waveguide based sensor for fully characterizing magneto-dielectric (MD) materials. Sens. Actuators A Phys. 2020, 301, 111778. [Google Scholar] [CrossRef]
- Chen, Z.; Hong, W.; Chen, J. High-Q planar active resonator based on substrate integrated waveguide technique. Electron. Lett. 2012, 48, 575–577. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M.; Kazacos, M. State of charge monitoring methods for vanadium redox flow battery control. J. Power Sources 2011, 196, 8822–8827. [Google Scholar] [CrossRef]
- Sum, E.; Skyllas-Kazacos, M. A study of the V (II)/V (III) redox couple for redox flow cell applications. J. Power Sources 1985, 15, 179–190. [Google Scholar] [CrossRef]
- Sum, E.; Rychcik, M.; Skyllas-Kazacos, M. Investigation of the V (V)/V (IV) system for use in the positive half-cell of a redox battery. J. Power Sources 1985, 16. [Google Scholar] [CrossRef]
- Ngamsai, K.; Arpornwichanop, A. Measuring the state of charge of the electrolyte solution in a vanadium redox flow battery using a four-pole cell device. J. Power Sources 2015, 298, 150–157. [Google Scholar] [CrossRef]
- Tang, Z.; Aaron, D.S.; Papandrew, A.B.; Zawodzinski, T.A. Monitoring the state of charge of operating vanadium redox flow batteries. ECS Trans. 2012, 41, 1. [Google Scholar] [CrossRef]
- Shin, K.H.; Jin, C.S.; So, J.Y.; Park, S.K.; Kim, D.H.; Yeon, S.H. Real-time monitoring of the state of charge (SOC) in vanadium redox-flow batteries using UV–Vis spectroscopy in operando mode. J. Energy Storage 2020, 27, 101066. [Google Scholar] [CrossRef]
- Snihir, I.; Rey, W.; Verbitskiy, E.; Belfadhel-Ayeb, A.; Notten, P.H. Battery open-circuit voltage estimation by a method of statistical analysis. J. Power Sources 2006, 159, 1484–1487. [Google Scholar] [CrossRef] [Green Version]
- Ressel, S.; Bill, F.; Holtz, L.; Janshen, N.; Chica, A.; Flower, T.; Weidlich, C.; Struckmann, T. State of charge monitoring of vanadium redox flow batteries using half cell potentials and electrolyte density. J. Power Sources 2018, 378, 776–783. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Daneshmand, M. Monitoring solid particle deposition in lossy medium using planar resonator sensor. IEEE Sens. J. 2017, 17, 7981–7989. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Wiltshire, B.; Mahdi, N.; Kar, P.; Shankar, K.; Daneshmand, M. Ultraviolet sensing using a TiO2 nanotube integrated high resolution planar microwave resonator device. Nanoscale 2018, 10, 4882–4889. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Daneshmand, M. High-resolution RFID liquid sensing using a chipless tag. IEEE Microw. Wirel. Components Lett. 2017, 27, 311–313. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Shariaty, P.; Hashisho, Z.; Daneshmand, M. A non-contact microwave sensor for monitoring the interaction of zeolite 13X with CO2 and CH4 in gaseous streams. Sens. Actuators B Chem. 2017, 238, 1240–1247. [Google Scholar] [CrossRef]
- Sharafadinzadeh, N.; Abdolrazzaghi, M.; Daneshmand, M. Investigation on planar microwave sensors with enhanced sensitivity from microfluidic integration. Sens. Actuators A Phys. 2020, 301, 111752. [Google Scholar] [CrossRef]



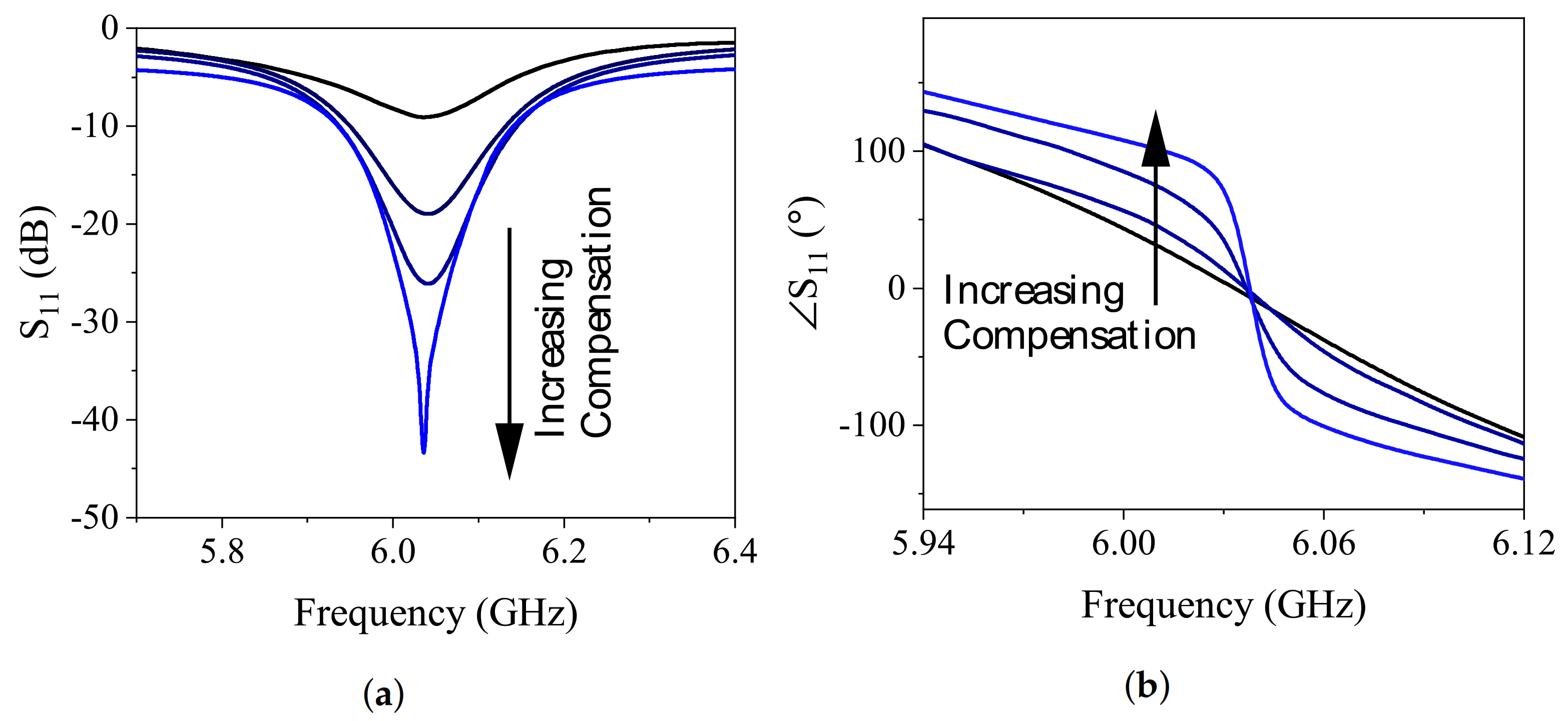

| 220 | 1.8 | 50 | 50 | 10 | 75 |
| l | |||||
| 0.1 | 100 | 5 | 1 | 2 | 0.4 |
| Parameter | Passive | |||
|---|---|---|---|---|
| Depth of | −9 | −18.9 | −26 | −43.3 |
| 3-dB BW | 175 | 83 | 57.5 | 3.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazemi, N.; Schofield, K.; Musilek, P. A High-Resolution Reflective Microwave Planar Sensor for Sensing of Vanadium Electrolyte. Sensors 2021, 21, 3759. https://doi.org/10.3390/s21113759
Kazemi N, Schofield K, Musilek P. A High-Resolution Reflective Microwave Planar Sensor for Sensing of Vanadium Electrolyte. Sensors. 2021; 21(11):3759. https://doi.org/10.3390/s21113759
Chicago/Turabian StyleKazemi, Nazli, Kalvin Schofield, and Petr Musilek. 2021. "A High-Resolution Reflective Microwave Planar Sensor for Sensing of Vanadium Electrolyte" Sensors 21, no. 11: 3759. https://doi.org/10.3390/s21113759
APA StyleKazemi, N., Schofield, K., & Musilek, P. (2021). A High-Resolution Reflective Microwave Planar Sensor for Sensing of Vanadium Electrolyte. Sensors, 21(11), 3759. https://doi.org/10.3390/s21113759







