A Highly Sensitive Refractive Index Sensor Based on a V-Shaped Photonic Crystal Fiber with a High Refractive Index Range
Abstract
:1. Introduction
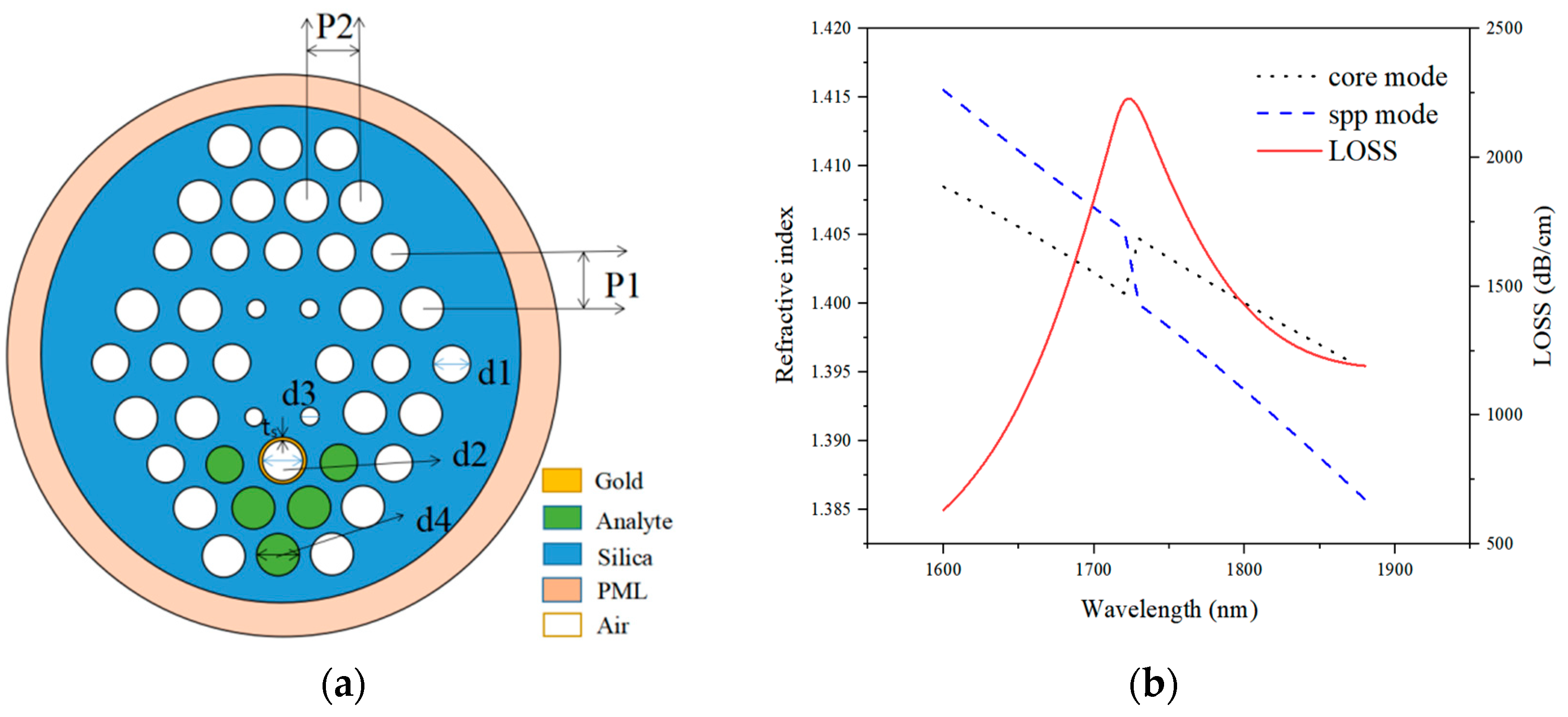
2. Proposed Structure Design and Working Principle
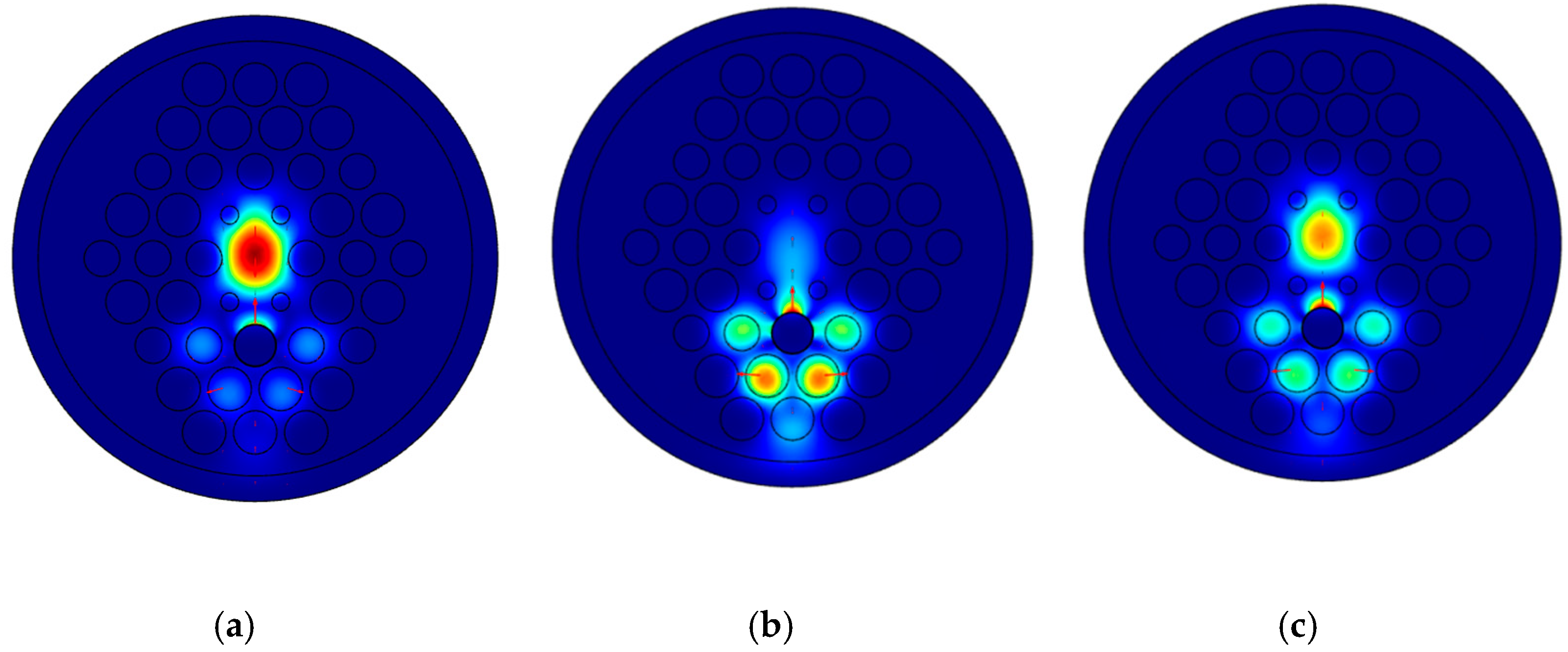
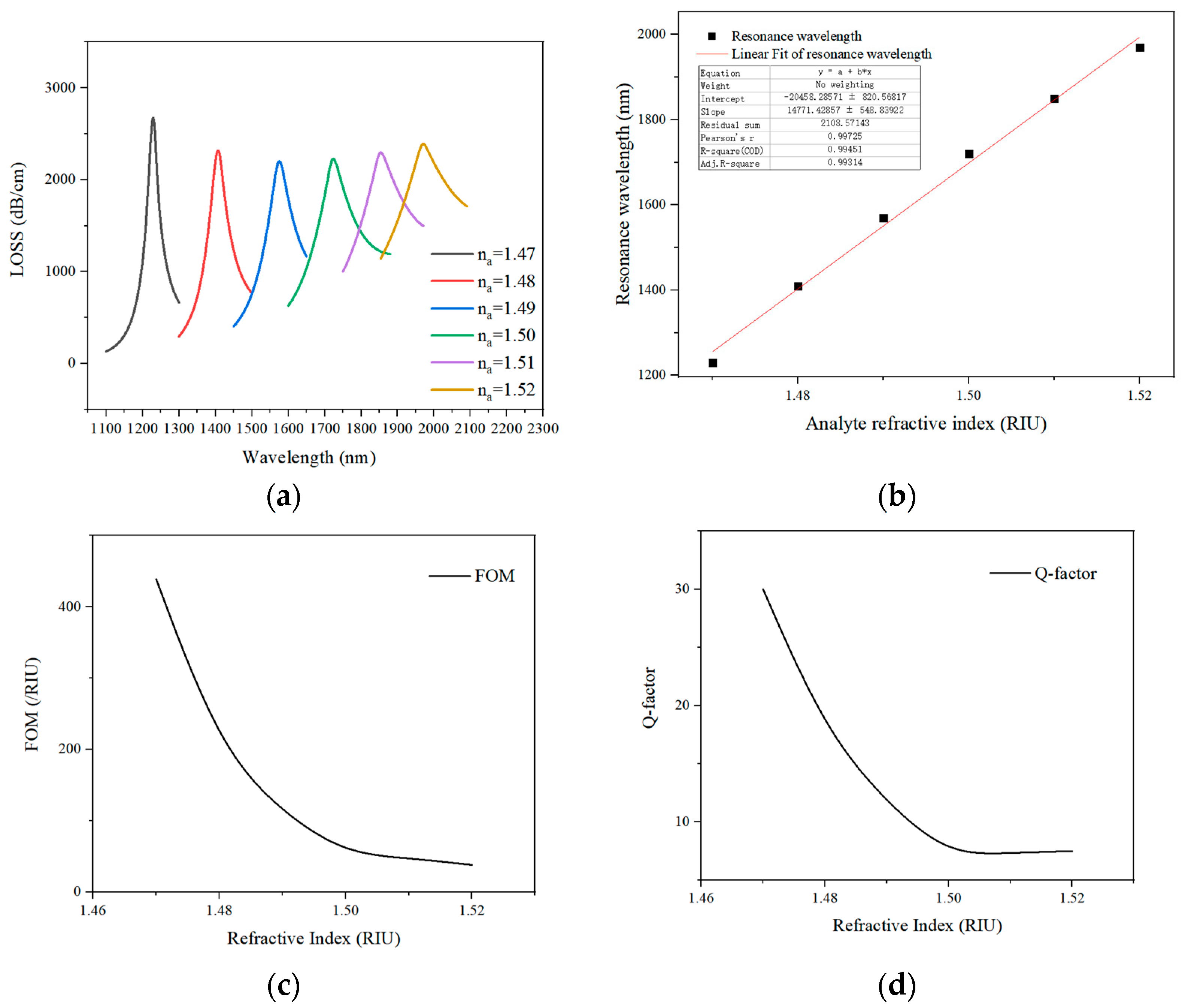
3. Simulation Result Analysis and Discussion
3.1. Discussion on Different Structural Parameter
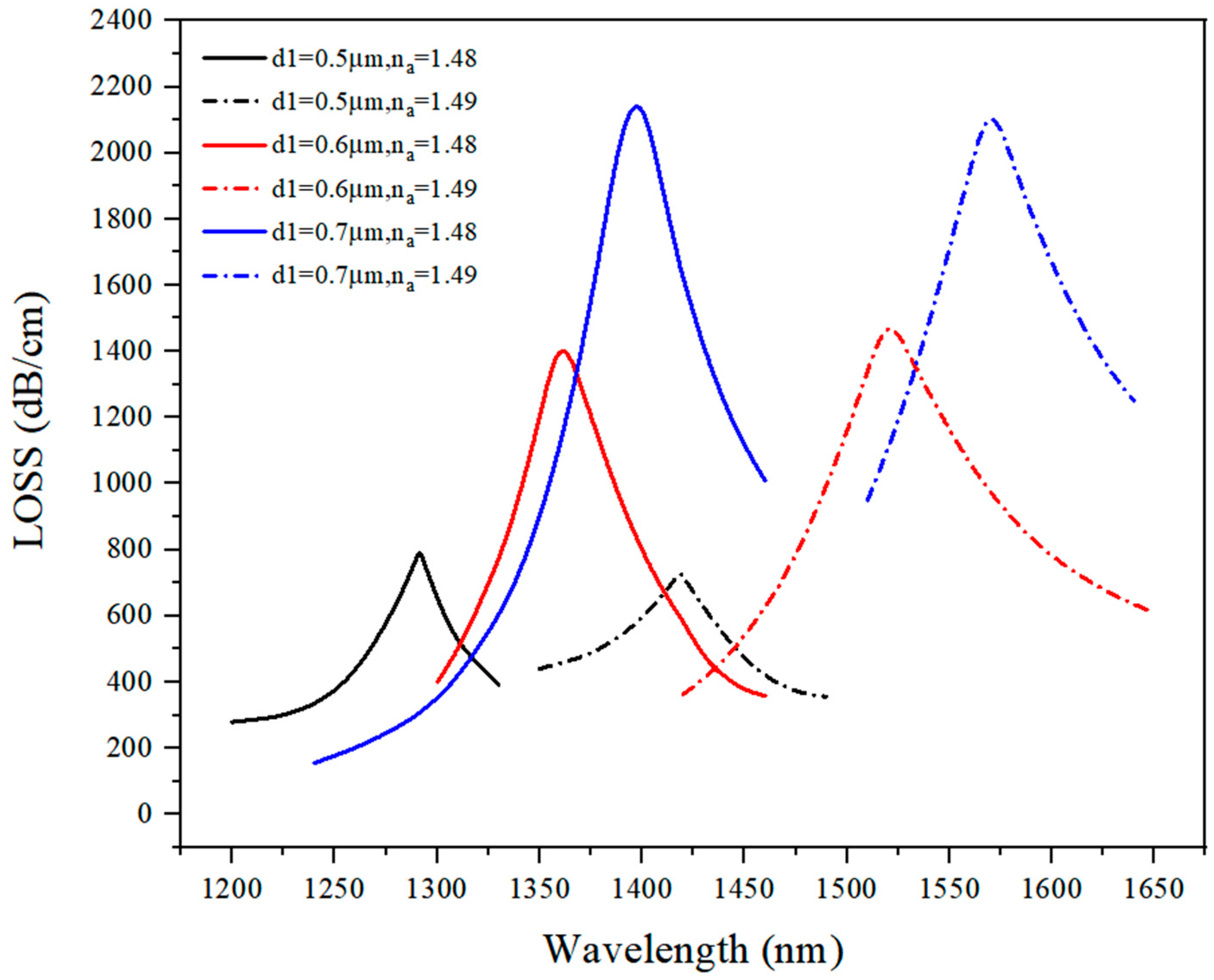
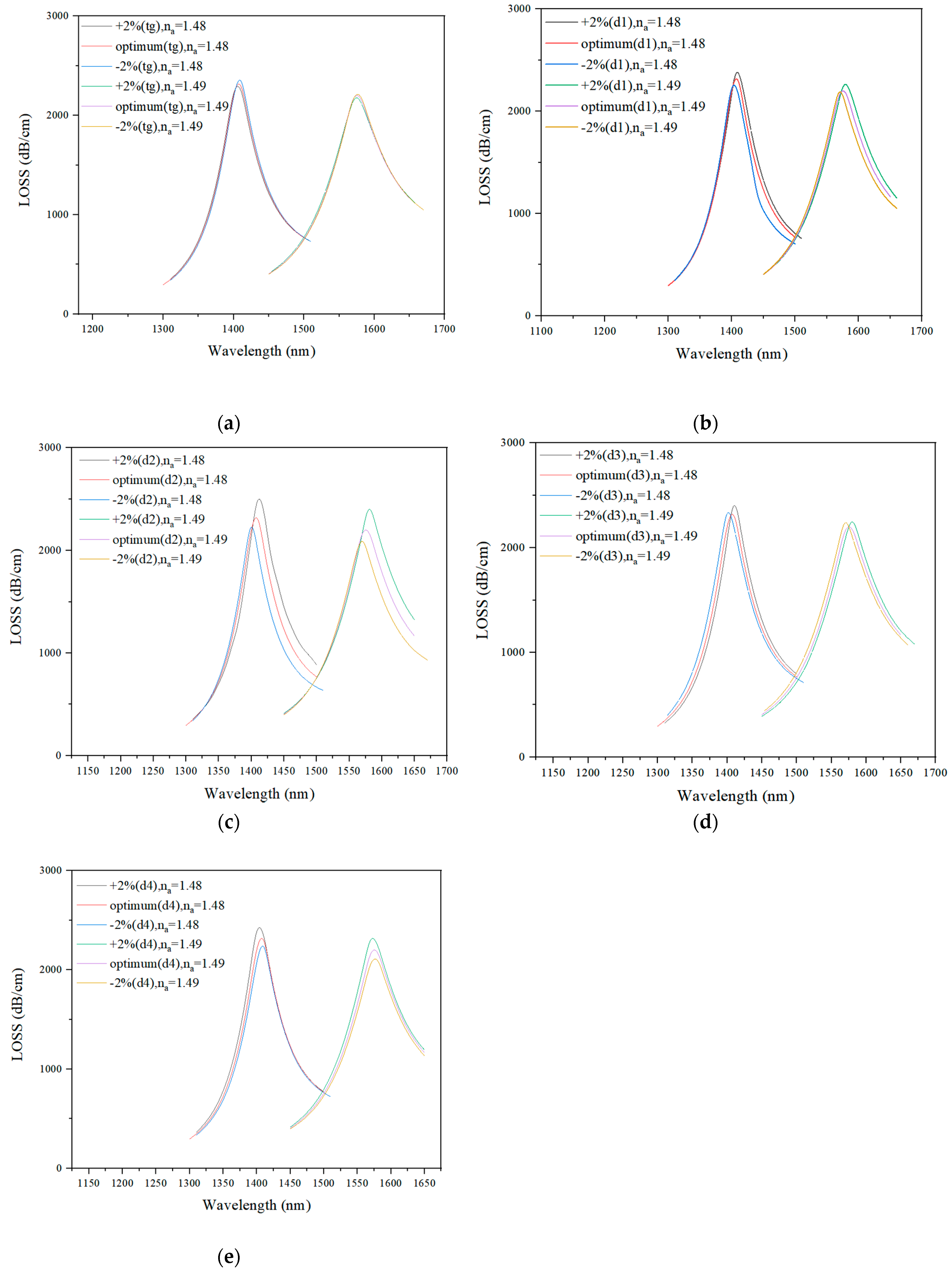
3.1.1. Discussion on d1 Optimal Value
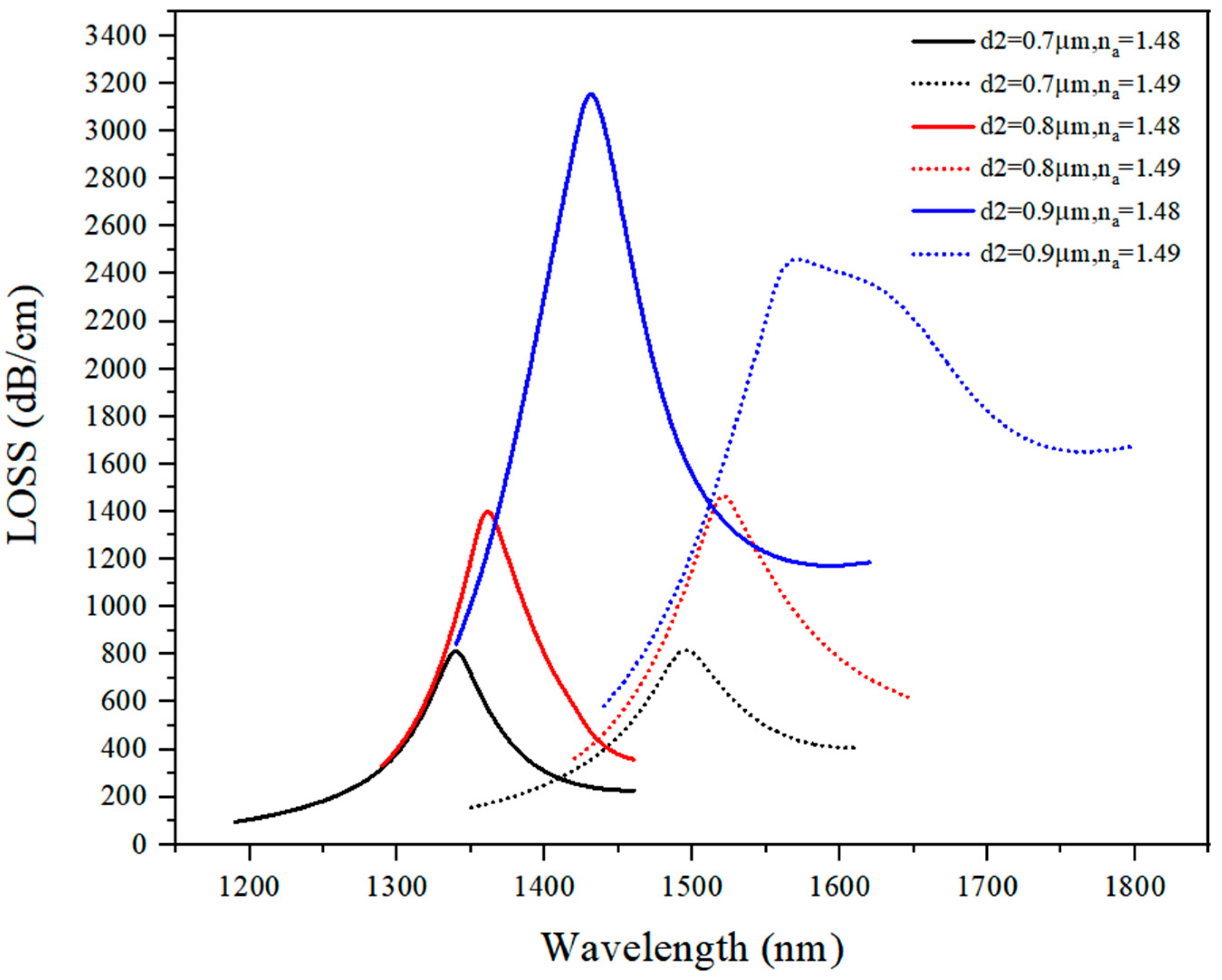
3.1.2. Discussion on d2 Optimal Value
3.1.3. Discussion on d3 Optimal Value
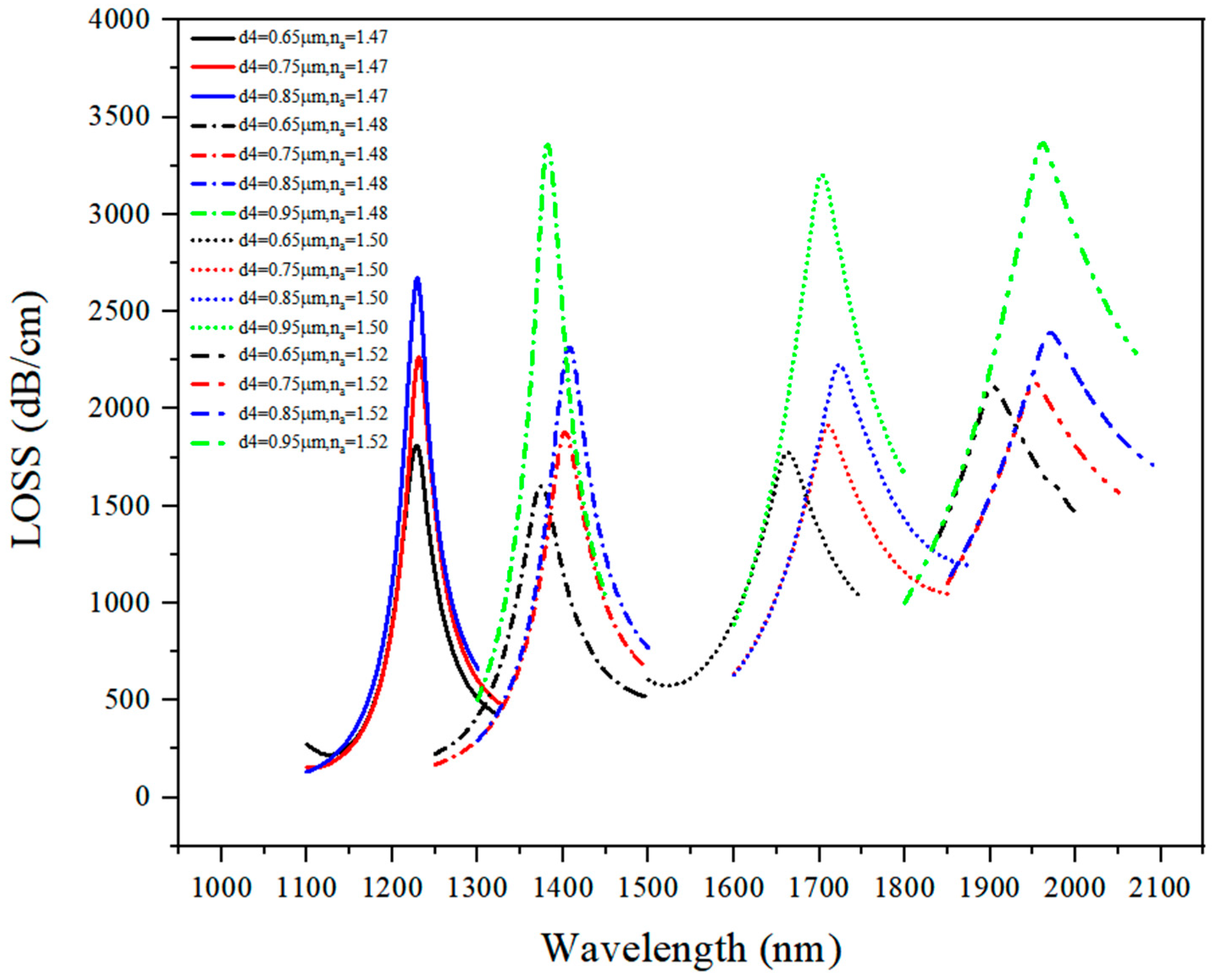
3.1.4. Discussion on d4 Optimal Value
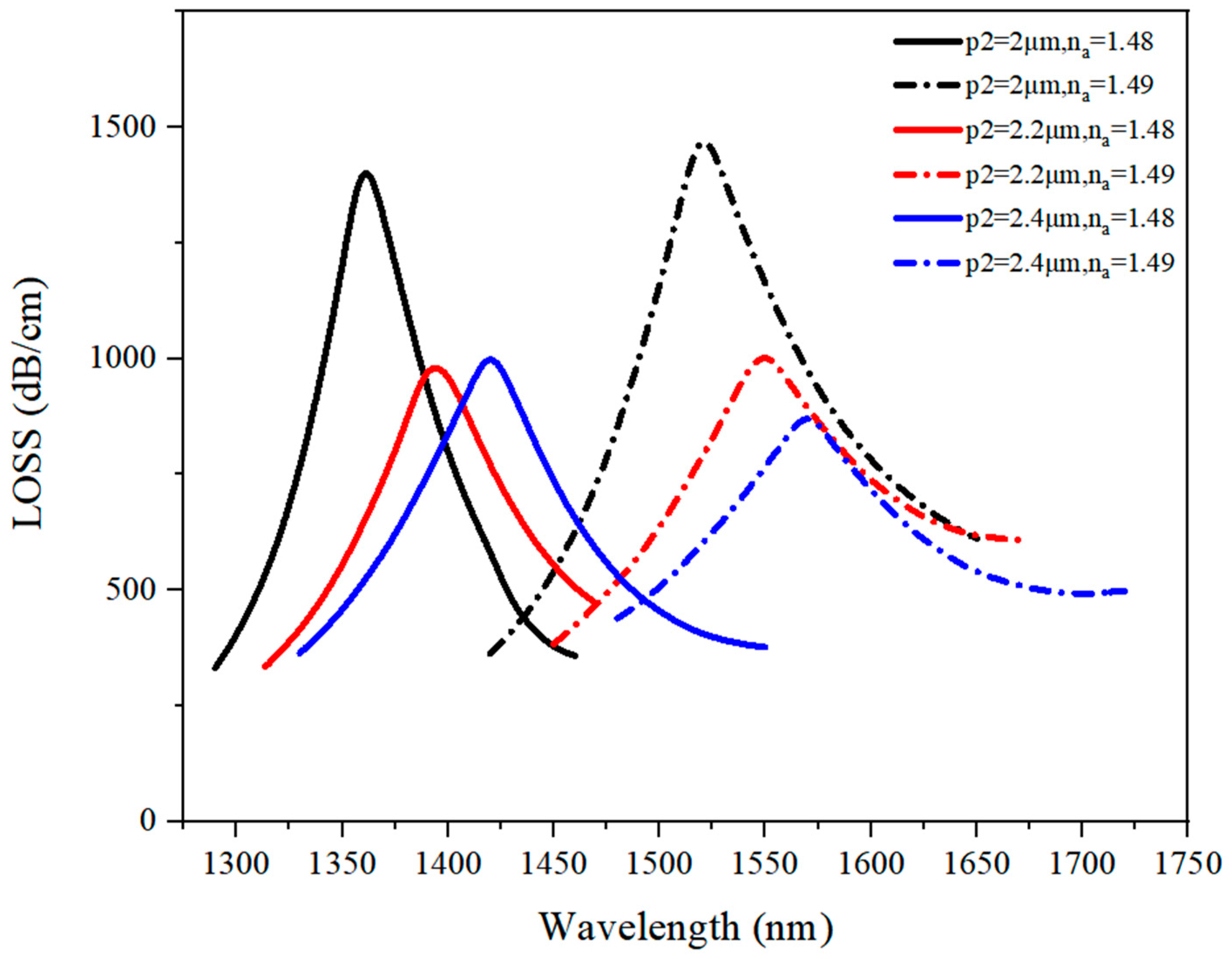
3.1.5. Discussion on p2 Optimal Value
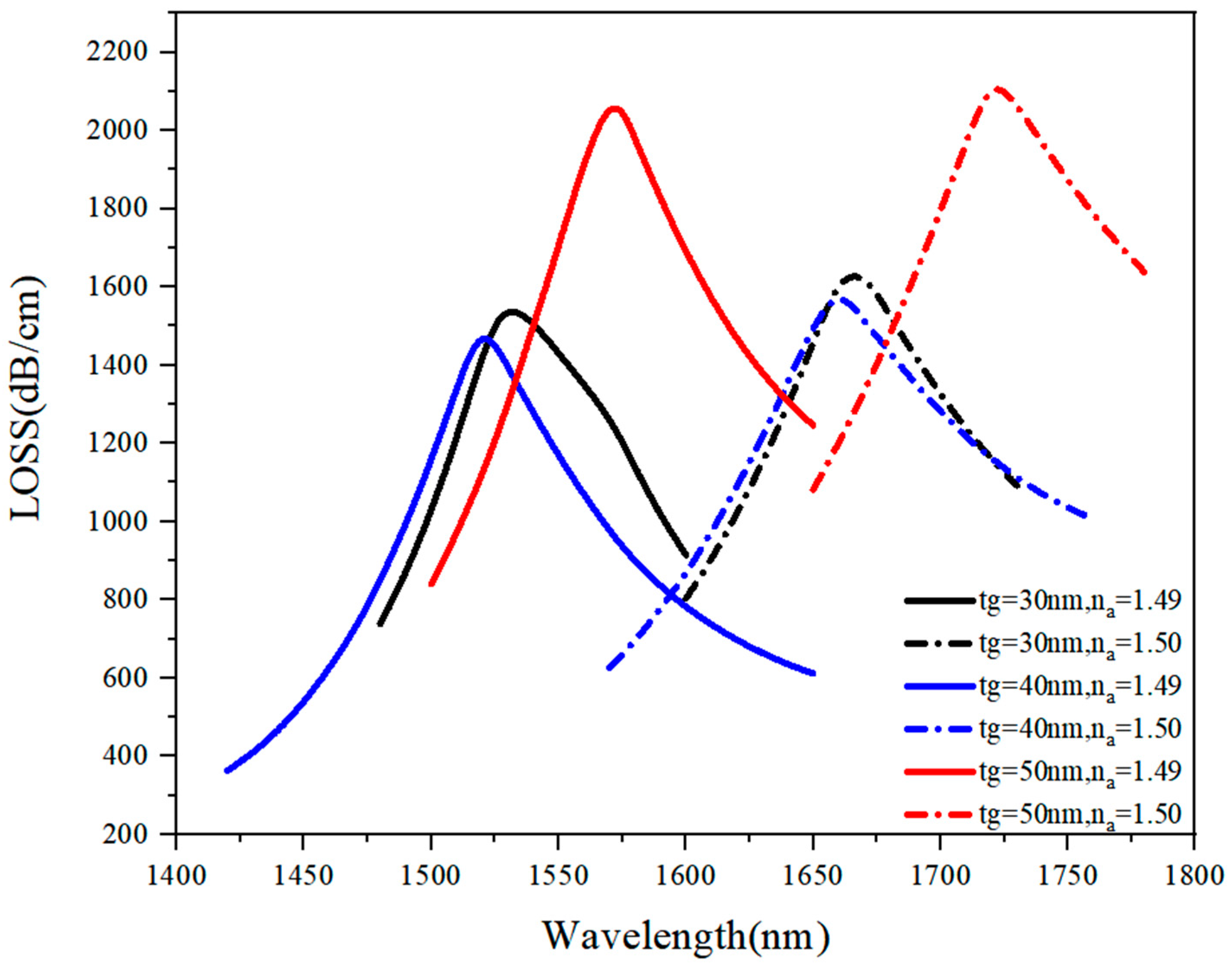
3.1.6. Discussion on tg optimal value
3.2. Fabrication Tolerance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, Z.; Fan, Z.; Kong, X.; Meng, Z. Photonic crystal fiber based wide-range of refractive index sensor with phase matching between core mode and metal defect mode. Opt. Commun. 2020, 461, 125233. [Google Scholar] [CrossRef]
- Liu, C.; Wang, F.M.; Lv, J.W.; Sun, T.; Liu, Q.; Fu, C.F.; Mu, H.W.; Chu, P.K. A highly temperature-sensitive photonic crystalfiber based on surfaceplasmon resonance. Opt. Commun. 2016, 359, 378–382. [Google Scholar] [CrossRef]
- Hossain, M.B.; Mahendiran, T.V.; Abdulrazak, L.F.; Mehedi, I.M.; Hossain, M.A.; Rana, M.M. Numerical analysis of gold coating based quasi D shape dual core PCF SPR sensor. Opt. Quantum Electron. 2020, 52, 446. [Google Scholar] [CrossRef]
- Yan, X.; Li, B.; Cheng, T.L.; Li, S.G. Analysis of High Sensitivity Photonic Crystal Fiber Sensor Based on Surface Plasmon Resonance of Refractive Indexes of Liquids. Sensors 2018, 18, 2922. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, B.; Cheng, T.; Chen, J.; Yan, X. Graphene-Enhanced Surface Plasmon Resonance Liquid Refractive Index Sensor Based on Photonic Crystal Fiber. Sensors 2019, 19, 3666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- An, G.; Li, S.; Cheng, T.; Yan, X.; Zhang, X.; Zhou, X.; Yuan, Z. Ultra-stable D-shaped Optical Fiber Refractive Index Sensor with Graphene-Gold Deposited Platform. Plasmonics 2019, 14, 155–163. [Google Scholar] [CrossRef]
- Desmet, C.; Vindas, K.; Meza, R.A.; Garrigue, P.; Voci, S.; Sojic, N.; Maziz, A.; Courson, R.; Malaquin, L.; Leichle, L.; et al. Multiplexed Remote SPR Detection of Biological Interactions through Optical Fiber Bundles. Sensors 2020, 20, 511. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Pu, S.; Li, X. Gold-Film-Thickness Dependent SPR Refractive Index and Temperature Sensing with Hetero-Core Optical Fiber Structure. Sensors 2019, 19, 4345. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singh, S.; Prajapati, Y. Highly sensitive dual-core symmetrical side-polished modified D-shaped SPR based PCF refractive index sensor with deeply etched micro openings. Optik 2021, 235, 166657. [Google Scholar] [CrossRef]
- Li, J.-X.; Zhang, W.-H.; Tong, Z.-R.; Liu, J.-W. Fiber optic sensor modified by graphene oxide–glucose oxidase for glucose detection. Opt. Commun. 2021, 492, 126983. [Google Scholar] [CrossRef]
- Butt, M.; Khonina, S.; Kazanskiy, N. Plasmonics: A Necessity in the Field of Sensing—A Review (Invited). Fiber Integr. Opt. 2021, 40, 14–47. [Google Scholar] [CrossRef]
- Liu, S.; Cao, S.; Zhang, Z.; Wang, Y.; Liao, C.; Wang, Y. Temperature Sensor Based on Side-Polished Fiber SPR Device Coated with Polymer. Sensors 2019, 19, 4063. [Google Scholar] [CrossRef] [Green Version]
- Qu, Y.; Yuan, J.; Zhou, X.; Li, F.; Yan, B.; Wu, Q.; Wang, K.; Sang, X.; Long, K.; Yu, C. Mid-infrared silicon photonic crystal fiber polarization filter based on surface plasmon resonance effect. Opt. Commun. 2020, 463, 125387. [Google Scholar] [CrossRef]
- Liang, H.; Shen, T.; Feng, Y.; Liu, H.C.; Han, W. A D-Shaped Photonic Crystal Fiber Refractive Index Sensor Coated with Graphene and Zinc Oxide. Sensors 2021, 21, 71. [Google Scholar] [CrossRef] [PubMed]
- Mahfuz, M.A.; Mollah, M.A.; Momota, M.R.; Paul, A.K.; Masud, A.; Akter, S.; Hasan, M.R. Highly sensitive photonic crystal fiber plasmonic biosensor: Design and analysis. Opt. Mater. 2019, 90, 315–321. [Google Scholar] [CrossRef]
- Wang, G.; Lu, Y.; Duan, L.; Yao, J. A Refractive Index Sensor Based on PCF with Ultra-Wide Detection Range. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 1–8. [Google Scholar] [CrossRef]
- Yang, H.; Liu, M.; Chen, Y.; Guo, L.; Xiao, G.; Liu, H.; Li, J.; Yuan, L. Highly Sensitive Graphene-Au Coated Plasmon Resonance PCF Sensor. Sensors 2021, 21, 818. [Google Scholar] [CrossRef]
- Lou, J.; Li, S.; Cheng, T.; Yan, X.; Zhang, X.; Shao, Y. Plasmonic photonic crystal fiber polarization filter with asymmetry around Au-coated and liquid-filled air holes. Opt. Quantum Electron. 2017, 49, 415. [Google Scholar] [CrossRef]
- Li, C.-Y.; Song, B.-B.; Wu, J.-X.; Huang, W.; Wu, X.-J.; Jin, C. Dual-demodulation large-scope high-sensitivity refractive index sensor based on twin-core PCF. Optoelectron. Lett. 2021, 17, 193–198. [Google Scholar] [CrossRef]
- Qiu, S.; Yuan, J.; Zhou, X.; Qu, Y.; Yan, B.; Wu, Q.; Wang, K.; Sang, X.; Long, K.; Yu, C. Highly sensitive temperature sensing based on all-solid cladding dual-core photonic crystal fiber filled with the toluene and ethanol. Opt. Commun. 2020, 477, 126357. [Google Scholar] [CrossRef]
- Qu, Y.; Yuan, J.; Zhou, X.; Li, F.; Mei, C.; Yan, B.; Wu, Q.; Wang, K.; Sang, X.; Long, K.; et al. A V-shape photonic crystal fiber polarization filter based on surface plasmon resonance effect. Opt. Commun. 2019, 452, 1–6. [Google Scholar] [CrossRef]
- Gamal, Y.; Younis, B.; Hegazy, S.; Badr, Y.; Hameed, M.F.O.; Obayya, S. Highly efficient modified dual D-shaped PCF polarization filter. Opt. Fiber Technol. 2021, 62, 102459. [Google Scholar] [CrossRef]
- Akter, S.; Ahmed, K.; El-Naggar, S.A.; Taya, S.A.; Nguyen, T.K.; Dhasarathan, V. Highly Sensitive Refractive Index Sensor for Temperature and Salinity Measurement of Seawater. Opt. Int. J. Light Electron. Opt. 2020, 216, 164901. [Google Scholar] [CrossRef]
- Guo, X.; Han, L.; Liu, F.; Li, S. Refractive index sensing characteristics of dual-core PCF based on surface plasmon resonance. Opt. Int. J. Light Electron Opt. 2020, 218, 164796. [Google Scholar] [CrossRef]
- Wu, J.; Li, S.; Shi, M.; Feng, X. Photonic crystal fiber temperature sensor with high sensitivity based on surface plasmon resonance. Opt. Fiber Technol. 2018, 43, 90–94. [Google Scholar] [CrossRef]
- Wang, S.; Sun, X.; Luo, Y.; Peng, G. Surface plasmon resonance sensor based on D-shaped Hi-Bi photonic crystal fiber. Opt. Commun. 2020, 467, 125675. [Google Scholar] [CrossRef]
- Danlard, I.; Akowuah, E.K. Assaying with PCF-based SPR refractive index biosensors: From recent configurations to outstanding detection limits. Opt. Fiber Technol. 2020, 54, 102083. [Google Scholar] [CrossRef]
- Lou, J.; Cheng, T.; Li, S.; Zhang, X. Surface plasmon resonance photonic crystal fiber biosensor based on gold-graphene layers. Opt. Fiber Technol. 2019, 50, 206–211. [Google Scholar] [CrossRef]
- Chao, C.-T.C.; Chau, Y.-F.C.; Huang, H.J.; Kumara, N.T.R.N.; Kooh, M.R.R.; Lim, C.M.; Chiang, H.-P. Highly Sensitive and Tunable Plasmonic Sensor Based on a Nanoring Resonator with Silver Nanorods. Nanomaterials 2020, 10, 1399. [Google Scholar] [CrossRef]

| d3 (μm) | na (RIU) | |||||
|---|---|---|---|---|---|---|
| 1.47 | 1.48 | 1.49 | 1.50 | 1.51 | 1.52 | |
| 0.35 | 1230.3 | 1410.1 | 1570.4 | 1720.1 | 1850.7 | 1970.9 |
| 0.45 | 1280.4 | 1470.0 | 1640.3 | 1780.2 | 1910.1 | 2020.6 |
| 0.55 | 1345.6 | 1540.5 | 1710.1 | 1850.2 | 1960.9 | 2060.4 |
| d4 (μm) | na (RIU) | Average Sensitivity (nm/RIU) | |||||
|---|---|---|---|---|---|---|---|
| 1.47 | 1.48 | 1.49 | 1.50 | 1.51 | 1.52 | ||
| 0.65 | 1230.1 | 1370.2 | 1520.8 | 1660.7 | 1790.1 | 1900.0 | 13,571.4 |
| 0.75 | 1230.2 | 1400.7 | 1570.1 | 1710.4 | 1840.4 | 1950.1 | 14,457.1 |
| 0.85 | 1230.1 | 1410.9 | 1570.5 | 1720.6 | 1850.5 | 1970.5 | 14,771.4 |
| 0.95 | 1380.8 | 1550.4 | 1700.1 | 1850.5 | 1960.6 | 14,600.0 | |
| d4 (μm) | na (RIU) | Average Sensitivity (nm/RIU) | ||||||
|---|---|---|---|---|---|---|---|---|
| 1.47 | 1.48 | 1.49 | 1.50 | 1.51 | 1.52 | 1.53 | ||
| 20 | 1420.4 | 1560.4 | 1690.3 | 1810.6 | 1910.9 | 2010.1 | 11,771.42 | |
| 30 | 1230.1 | 1410.1 | 1570.2 | 1720.5 | 1850.4 | 1970.7 | 14,771.43 | |
| 40 | 1205.3 | 1400.1 | 1570.1 | 1720.2 | 1850.3 | 1970.1 | 15,214.29 | |
| 60 | 1350.5 | 1520.7 | 1660.4 | 1780.7 | 1890.0 | 1990.1 | 12,657.14 | |
| Feature | RI Range (RIU) | Average Sensitivity (nm/RIU) | Maximum Sensitivity (nm/RIU) | Reference |
|---|---|---|---|---|
| D-Shaped coated with Graphene and Zinc Oxide | 1.36–1.47 | 4485.7 | 6000 | [11] |
| Graphene-Enhanced Liquid Refractive Index Sensor | 1.3330–1.3688 | 2290 | - | [5] |
| Wide-Range of Refractive Index Sensor | 1.35–1.46 | 1931.03 | - | [1] |
| Graphene-Au Coated Plasmon Resonance PCF Sensor | 1.32–1.41 | 3900 | 4200 | [14] |
| Highly sensitive photonic crystal fiber plasmonic biosensor | 1.33–1.40 | - | 12,000 | [12] |
| Proposed Sensor | 1.47–1.52 | 14,771.4 | 18,000.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Fu, R.; Cheng, T.; Li, S. A Highly Sensitive Refractive Index Sensor Based on a V-Shaped Photonic Crystal Fiber with a High Refractive Index Range. Sensors 2021, 21, 3782. https://doi.org/10.3390/s21113782
Yan X, Fu R, Cheng T, Li S. A Highly Sensitive Refractive Index Sensor Based on a V-Shaped Photonic Crystal Fiber with a High Refractive Index Range. Sensors. 2021; 21(11):3782. https://doi.org/10.3390/s21113782
Chicago/Turabian StyleYan, Xin, Rao Fu, Tonglei Cheng, and Shuguang Li. 2021. "A Highly Sensitive Refractive Index Sensor Based on a V-Shaped Photonic Crystal Fiber with a High Refractive Index Range" Sensors 21, no. 11: 3782. https://doi.org/10.3390/s21113782
APA StyleYan, X., Fu, R., Cheng, T., & Li, S. (2021). A Highly Sensitive Refractive Index Sensor Based on a V-Shaped Photonic Crystal Fiber with a High Refractive Index Range. Sensors, 21(11), 3782. https://doi.org/10.3390/s21113782






