Denoising and Motion Artifact Removal Using Deformable Kernel Prediction Neural Network for Color-Intensified CMOS
Abstract
:1. Introduction
- (1)
- Spatial-filter-based denoising methods
- (2)
- CNN-based denoising methods
- (1)
- A data generation strategy for color-channel motion artifacts;
- (2)
- A DKPNN which achieves joint denoising and motion artifact removal, suitable for color ICMOS/ICCD;
- (3)
- An LCTF-ICMOS low-light-level color imaging system with high integration.
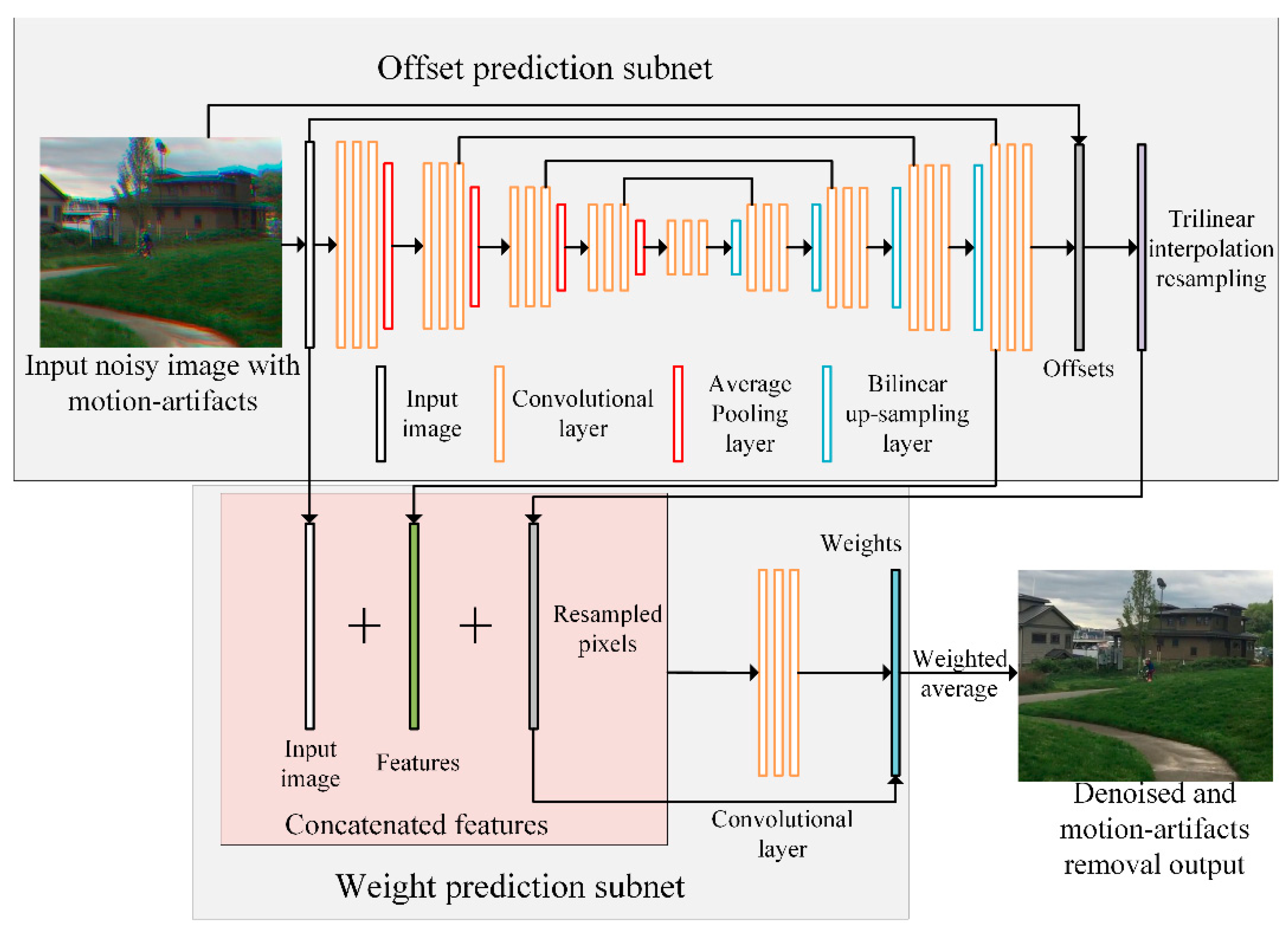
2. Joint Denoising and Motion Artifact Removal Using DKPNN for Color LCTF-ICMOS
2.1. Joint Denoising and Motion Artifact Removal Using DKPNN
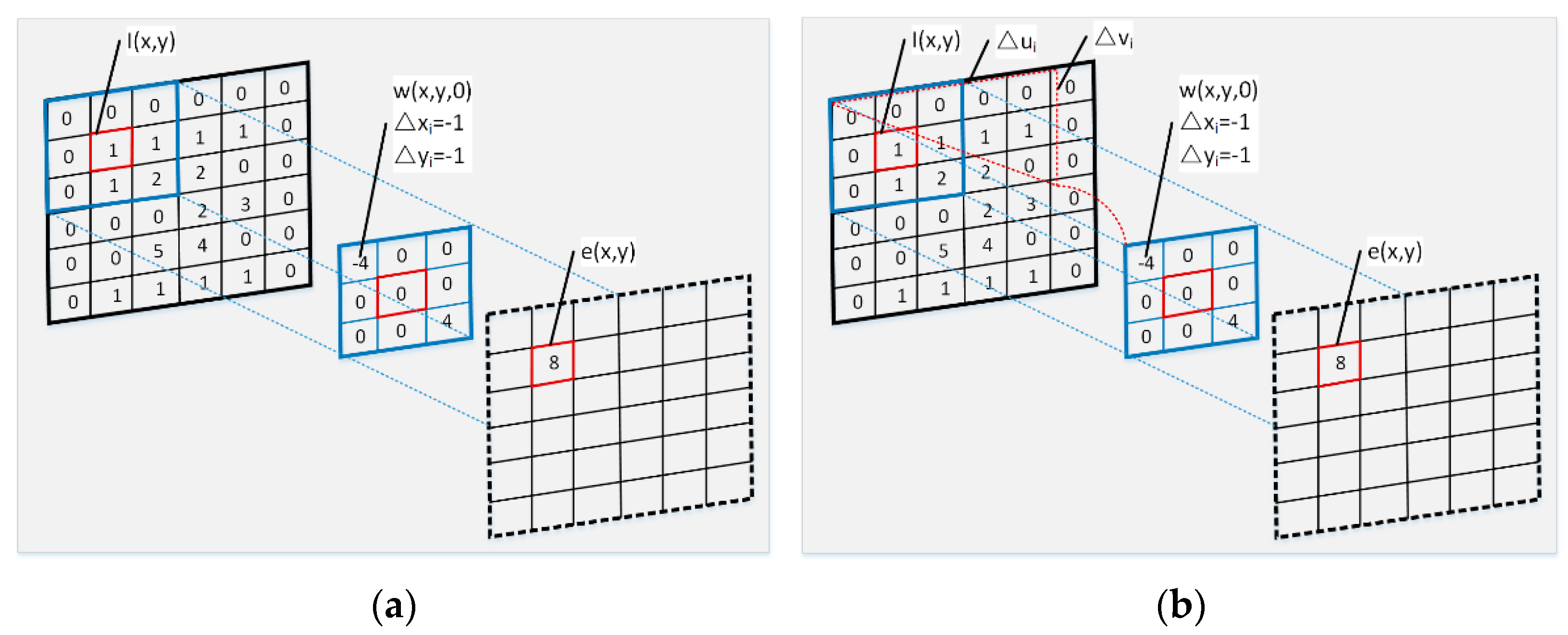
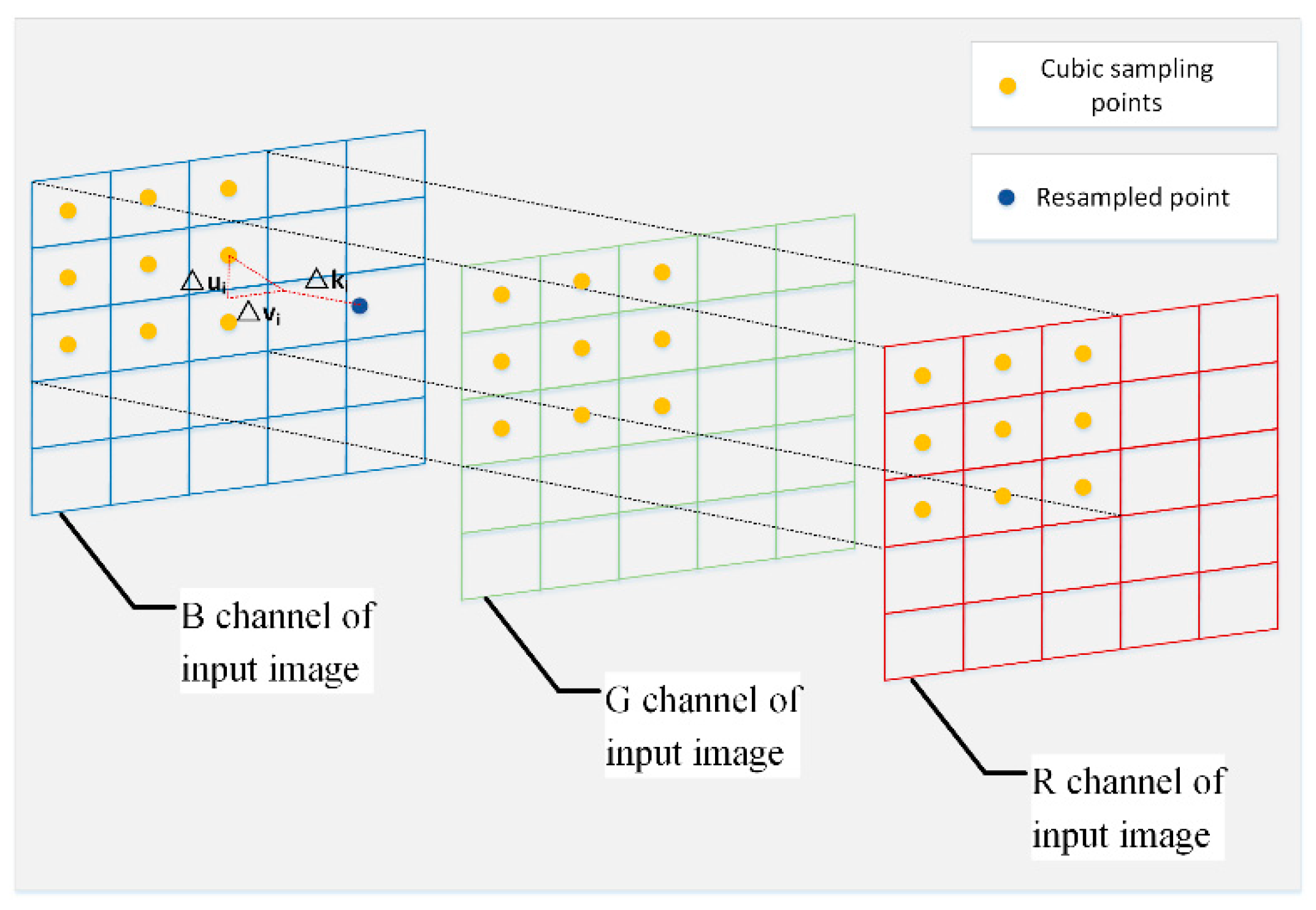
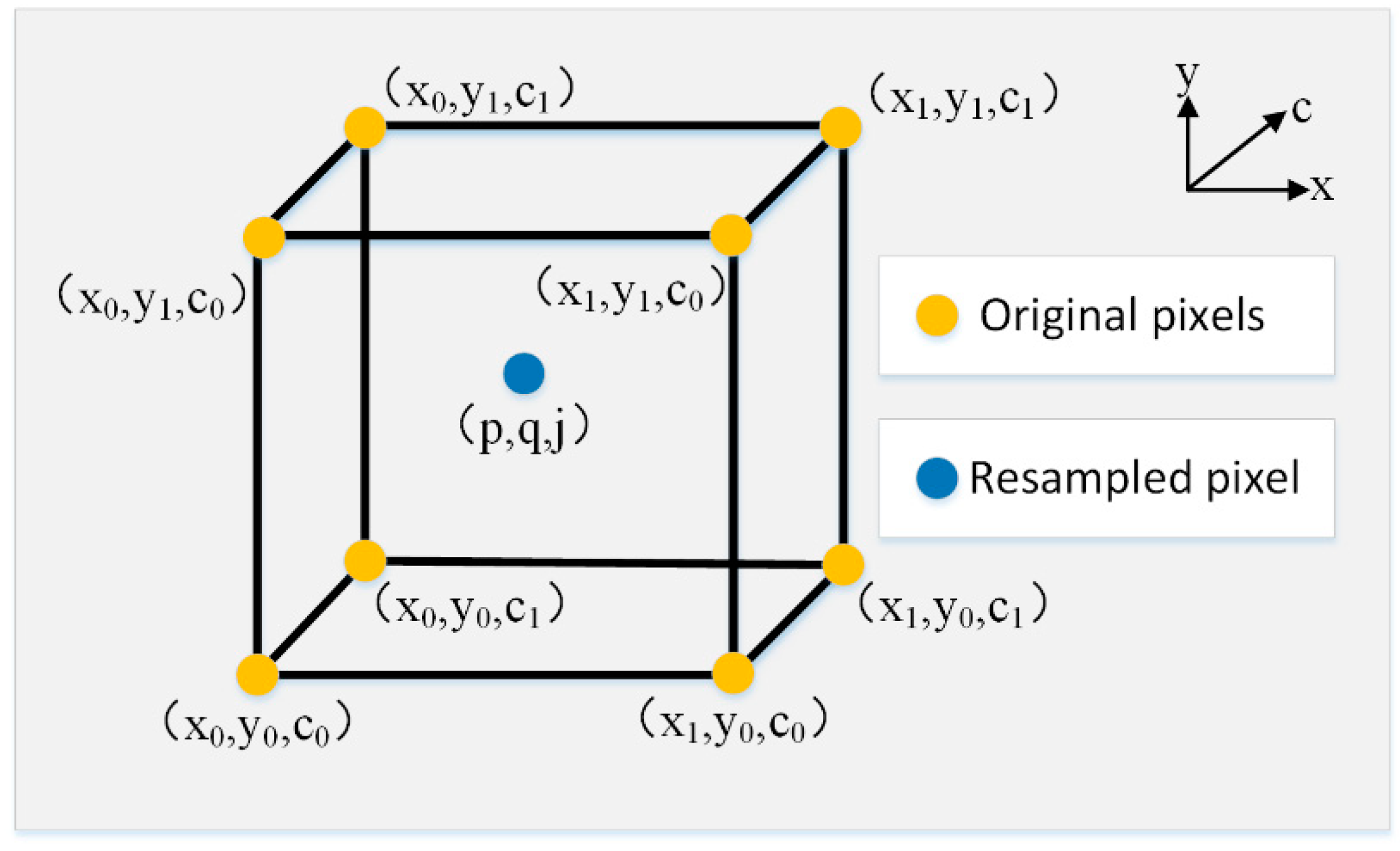
2.1.1. Offset-Prediction Subnet
2.1.2. Weight-Prediction Subnet
2.2. Data Generation Method for Color-Channel Motion Artifacts
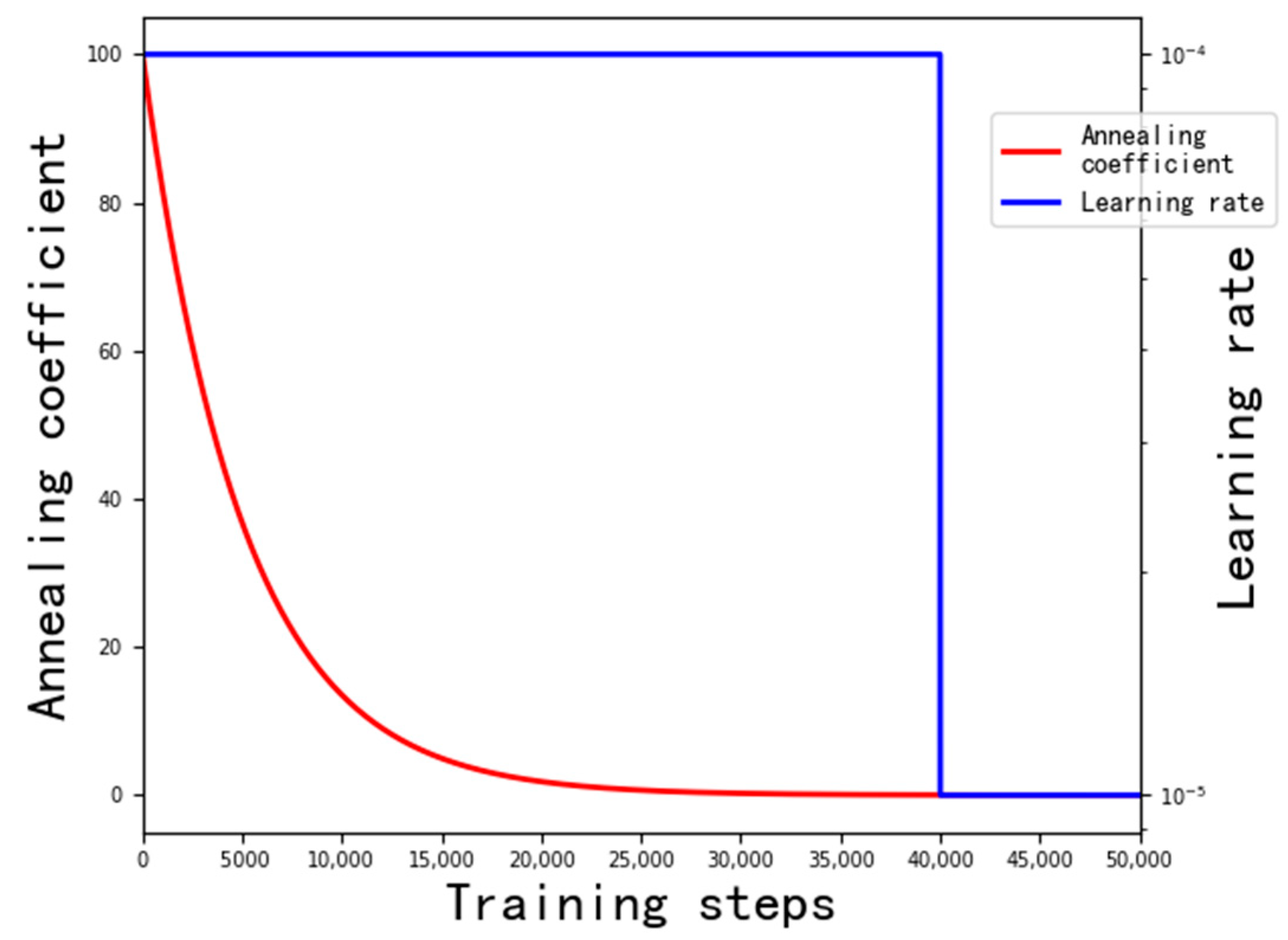
2.3. Training
3. Experimental Setup
4. Results and Discussion
4.1. Generated Noisy Data
4.2. LCTF-ICMOS Noisy Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Toet, A.; Hogervorst, M.A. Progress in color night vision. Opt. Eng. 2012, 51, 010901. [Google Scholar] [CrossRef]
- ColorPath CCNVD Color Capable Night Vision. Available online: https://armament.com/tenebraex/ (accessed on 25 April 2021).
- Chen, Y.; Hu, W.; Wu, D.; He, Y.; Zhang, D.; Zhang, Y. Spectrum matching optimization study on tri-band color night vision technology. Opt. Instrum. 2016, 38, 313–319. [Google Scholar]
- Wu, H.; Tao, S.; Gu, G.; Wang, S. Study on color night vision image fusion method based on quadruple-based images. Acta Photonica Sin. 2017, 46, 175–184. [Google Scholar]
- Kriesel, J.; Gat, N. True-Color. Night Vision Cameras, Optics and Photonics in Global Homeland Security III; International Society for Optics and Photonics: Orlando, FL, USA, 2007; p. 65400D. [Google Scholar]
- Yuan, T.; Han, Z.; Li, L.; Jin, W.; Wang, X.; Wang, H.; Bai, X. Tunable-liquid-crystal-filter-based low-light-level color night vision system and its image processing method. Appl. Opt. 2019, 58, 4947–4955. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.-M. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K.O. Image restoration by sparse 3D transform-domain collaborative filtering. In Image Processing: Algorithms and Systems VI; International Society for Optics and Photonics: San Jose, CA, USA, 2008; p. 681207. [Google Scholar]
- Knaus, C.; Zwicker, M. Progressive Image Denoising. IEEE Trans. Image Process. 2014, 23, 3114–3125. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.J.; Shen, C.; Yang, Y.B. Image Restoration Using Very Deep Convolutional Encoder-Decoder Networks with Symmetric Skip Connections. arXiv 2016, arXiv:1603.09056. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention; Munich, Germany, 5–9 October 2015, Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. MemNet: A persistent memory network for image restoration. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4549–4557. [Google Scholar]
- Liu, P.; Fang, R. Learning pixel-distribution prior with wider convolution for image denoising. arXiv 2017, arXiv:1707.09135. [Google Scholar]
- Lefkimmiatis, S. Non-local color image denoising with convolutional neural networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5882–5891. [Google Scholar]
- Lefkimmiatis, S. Universal denoising networks: A novel CNN architecture for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 19–21 June 2018; pp. 3204–3213. [Google Scholar]
- Kligvasser, I.; Shaham, T.R.; Michaeli, T. xUnit: Learning a spatial activation function for efficient image restoration. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2433–2442. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9446–9454. [Google Scholar]
- Cha, S.; Moon, T. Fully convolutional pixel adaptive image denoiser. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 17 October–2 November 2019; pp. 4160–4169. [Google Scholar]
- Liu, P.; Zhang, H.; Zhang, K.; Lin, L.; Zuo, W. Multi-level wavelet-CNN for image restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 773–782. [Google Scholar]
- Mildenhall, B.; Barron, J.T.; Chen, J.; Sharlet, D.; Ng, R.; Carroll, R. Burst denoising with kernel prediction networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2502–2510. [Google Scholar]
- Plötz, T.; Roth, S. Neural nearest neighbors networks. Adv. Neural Inf. Process. Syst. 2018, 31, 1087–1098. [Google Scholar]
- Liu, D.; Wen, B.; Fan, Y.; Loy, C.C.; Huang, T.S. Non-local recurrent network for image restoration. arXiv 2018, arXiv:1806.02919. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a Fast and Flexible Solution for CNN-Based Image Denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lehtinen, J.; Munkberg, J.; Hasselgren, J.; Laine, S.; Karras, T.; Aittala, M.; Aila, T. Noise2noise: Learning image restoration without clean data. arXiv 2018, arXiv:1803.04189. [Google Scholar]
- Liu, J.; Wu, C.-H.; Wang, Y.; Xu, Q.; Zhou, Y.; Huang, H.; Wang, C.; Cai, S.; Ding, Y.; Fan, H.; et al. Learning raw image denoising with bayer pattern unification and bayer preserving augmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–17 June 2019; pp. 2070–2077. [Google Scholar]
- Wang, X.; Chan, K.C.; Yu, K.; Dong, C.; Loy, C.C. EDVR: Video restoration with enhanced deformable convolutional networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–17 June 2019; pp. 1954–1963. [Google Scholar]
- Guo, S.; Yan, Z.; Zhang, K.; Zuo, W.; Zhang, L. Toward convolutional blind denoising of real photographs. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–17 June 2019; pp. 1712–1722. [Google Scholar]
- Marinc, T.; Srinivasan, V.; Gul, S.; Hellge, C.; Samek, W. Multi-kernel prediction networks for denoising of burst images. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 2404–2408. [Google Scholar]
- Xu, X.; Li, M.; Sun, W. Learning deformable kernels for image and video denoising. arXiv 2019, arXiv:1904.06903. [Google Scholar]
- Xu, X.; Li, M.; Sun, W.; Yang, M.-H. Learning Spatial and Spatio-Temporal Pixel Aggregations for Image and Video Denoising. IEEE Trans. Image Process. 2020, 29, 7153–7165. [Google Scholar] [CrossRef]
- Tassano, M.; Delon, J.; Veit, T. DVDNET: A fast network for deep video denoising. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1805–1809. [Google Scholar]
- Tassano, M.; Delon, J.; Veit, T. FastDVDnet: Towards real-time deep video denoising without flow estimation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 1351–1360. [Google Scholar]
- Brooks, T.; Mildenhall, B.; Xue, T.; Chen, J.; Sharlet, D.; Barron, J.T. Unprocessing images for learned raw denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Taipei, Taiwan, 22–25 September 2019; pp. 11036–11045. [Google Scholar]
- Jaroensri, R.; Biscarrat, C.; Aittala, M.; Durand, F. Generating training data for denoising real rgb images via camera pipeline simulation. arXiv 2019, arXiv:1904.08825. [Google Scholar]
- Foi, A.; Trimeche, M.; Katkovnik, V.; Egiazarian, K. Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data. IEEE Trans. Image Process. 2008, 17, 1737–1754. [Google Scholar] [CrossRef] [Green Version]
- Hasinoff, S.W.; Durand, F.; Freeman, W.T. Noise-optimal capture for high dynamic range photography. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 553–560. [Google Scholar]
- Hasinoff, S.W. Photon, Poisson Noise. 2014. Available online: http://people.csail.mit.edu/hasinoff/pubs/hasinoff-photon-2011-preprint.pdf (accessed on 25 April 2021).
- Su, S.; Delbracio, M.; Wang, J.; Sapiro, G.; Heidrich, W.; Wang, O. Deep video deblurring for hand-held cameras. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 237–246. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Wang, Z.; Simoncelli, E.; Bovik, A. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 1398–1402. [Google Scholar] [CrossRef] [Green Version]
- Farnebäck, G. Two-frame motion estimation based on polynomial expansion. In Proceedings of the Scandinavian Conference on Image Analysis, Halmstad, Sweden, 29 June–2 July 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 363–370. [Google Scholar]
- Hayat, M.M.; Torres, S.N.; Armstrong, E.; Cain, S.C.; Yasuda, B. Statistical algorithm for nonuniformity correction in focal-plane arrays. Appl. Opt. 1999, 38, 772–780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peli, E. Contrast in complex images. J. Opt. Soc. Am. A 1990, 7, 2032–2040. [Google Scholar] [CrossRef] [PubMed]
- Adjabi, I.; Ouahabi, A.; Benzaoui, A.; Jacques, S. Multi-Block Color-Binarized Statistical Images for Single-Sample Face Recognition. Sensors 2021, 21, 728. [Google Scholar] [CrossRef] [PubMed]
- Khaldi, Y.; Benzaoui, A. A new framework for grayscale ear images recognition using generative adversarial networks under unconstrained conditions. Evol. Syst. 2020, 1–12. [Google Scholar] [CrossRef]









| Convolutional Layers | L1–3 | L4–6 | L7–9 | L10–12 | L13–15 | L16–18 | L19–21 | L22–24 | L25–26 | L27 |
|---|---|---|---|---|---|---|---|---|---|---|
| Number of channels | 64 | 128 | 256 | 512 | 512 | 512 | 256 | 128 | 128 | n × 3 × 3 |
| Convolutional Layers | L1 | L2 | L3 |
|---|---|---|---|
| Number of channels | 64 | 64 | n × 3 |
| Noise Level | Metrics | BM3D | DnCNN | fDnCNN | FFDNet | BM3D + FE | DnCNN + FE | fDnCNN + FE | FFDNet + FE | DKPNN |
|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | 22.68 | 23.02 | 22.88 | 22.84 | 25.06 | 26.50 | 26.58 | 26.51 | 29.33 | |
| SSIM | 0.721 | 0.732 | 0.726 | 0.725 | 0.818 | 0.831 | 0.834 | 0.832 | 0.887 | |
| PSNR | 21.56 | 22.33 | 22.01 | 22.11 | 24.34 | 25.78 | 25.80 | 25.74 | 28.68 | |
| SSIM | 0.712 | 0.722 | 0.715 | 0.716 | 0.806 | 0.820 | 0.826 | 0.823 | 0.878 |
| Metrics | Scene | Illuminant Levels (lx) | Algorithms | |||||
|---|---|---|---|---|---|---|---|---|
| Noisy Input | BM3D | DnCNN | fDnCNN | FFDNet | Proposed | |||
| ρ | 1 | 5 × 10−2 | 0.0412 | 0.0117 | 0.0248 | 0.0079 | 0.0079 | 0.0059 |
| 1 × 10−2 | 0.0577 | 0.0128 | 0.0286 | 0.0103 | 0.0103 | 0.0081 | ||
| 5 × 10−3 | 0.0719 | 0.0144 | 0.0291 | 0.0111 | 0.0108 | 0.01 | ||
| 1 × 10−3 | 0.0778 | 0.0148 | 0.0302 | 0.0114 | 0.0113 | 0.0108 | ||
| 2 | 5 × 10−2 | 0.0436 | 0.0099 | 0.0269 | 0.0059 | 0.0058 | 0.0042 | |
| 1 × 10−2 | 0.0601 | 0.0153 | 0.0273 | 0.0112 | 0.0113 | 0.0086 | ||
| 5 × 10−3 | 0.0721 | 0.0154 | 0.0306 | 0.013 | 0.0131 | 0.0111 | ||
| 1 × 10−3 | 0.0807 | 0.0165 | 0.0308 | 0.0133 | 0.0132 | 0.0125 | ||
| RMSC | 1 | 5 × 10−2 | 8.1287 | 5.6751 | 7.299 | 5.6361 | 5.7168 | 5.4267 |
| 1 × 10−2 | 10.8123 | 6.5564 | 8.972 | 6.0954 | 6.2002 | 5.4395 | ||
| 5 × 10−3 | 14.2621 | 8.7327 | 11.3297 | 7.9825 | 8.206 | 6.9467 | ||
| 1 × 10−3 | 17.2388 | 11.8769 | 14.0814 | 10.9492 | 11.3108 | 9.9249 | ||
| 2 | 5 × 10−2 | 8.8464 | 3.7097 | 7.0186 | 2.3180 | 2.2060 | 1.9741 | |
| 1 × 10−2 | 11.9845 | 5.5569 | 9.2652 | 3.7849 | 3.7955 | 2.1758 | ||
| 5 × 10−3 | 13.5307 | 6.2826 | 10.0309 | 4.5214 | 4.5867 | 2.5442 | ||
| 1 × 10−3 | 15.3455 | 7.8517 | 11.7887 | 5.8253 | 5.7143 | 3.5552 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Li, L.; Jin, W.; Wang, X.; Jiao, G.; Liu, X.; Wang, H. Denoising and Motion Artifact Removal Using Deformable Kernel Prediction Neural Network for Color-Intensified CMOS. Sensors 2021, 21, 3891. https://doi.org/10.3390/s21113891
Han Z, Li L, Jin W, Wang X, Jiao G, Liu X, Wang H. Denoising and Motion Artifact Removal Using Deformable Kernel Prediction Neural Network for Color-Intensified CMOS. Sensors. 2021; 21(11):3891. https://doi.org/10.3390/s21113891
Chicago/Turabian StyleHan, Zhenghao, Li Li, Weiqi Jin, Xia Wang, Gangcheng Jiao, Xuan Liu, and Hailin Wang. 2021. "Denoising and Motion Artifact Removal Using Deformable Kernel Prediction Neural Network for Color-Intensified CMOS" Sensors 21, no. 11: 3891. https://doi.org/10.3390/s21113891
APA StyleHan, Z., Li, L., Jin, W., Wang, X., Jiao, G., Liu, X., & Wang, H. (2021). Denoising and Motion Artifact Removal Using Deformable Kernel Prediction Neural Network for Color-Intensified CMOS. Sensors, 21(11), 3891. https://doi.org/10.3390/s21113891





