Unified pH Measurements of Ethanol, Methanol, and Acetonitrile, and Their Mixtures with Water
Abstract
:1. Introduction
2. Materials and Methods
3. Results
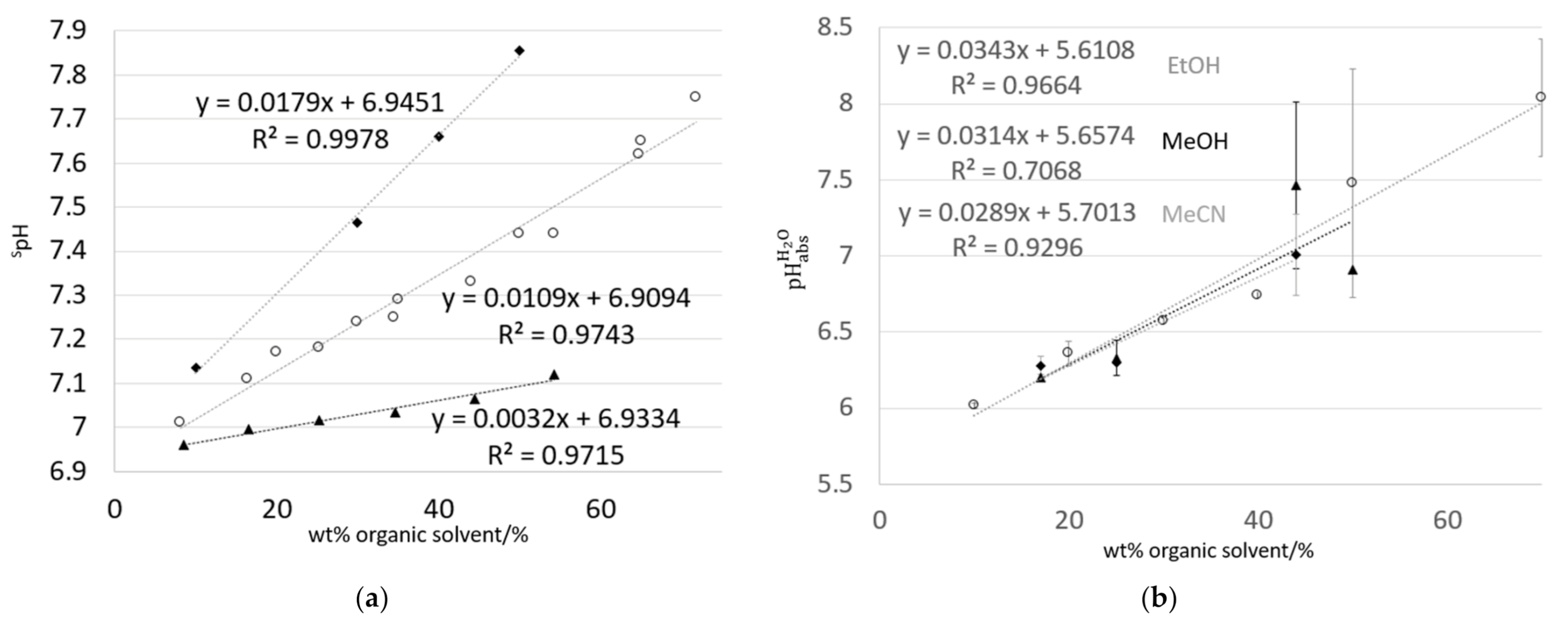
3.1. spH Values of Water–Solvent Mixtures
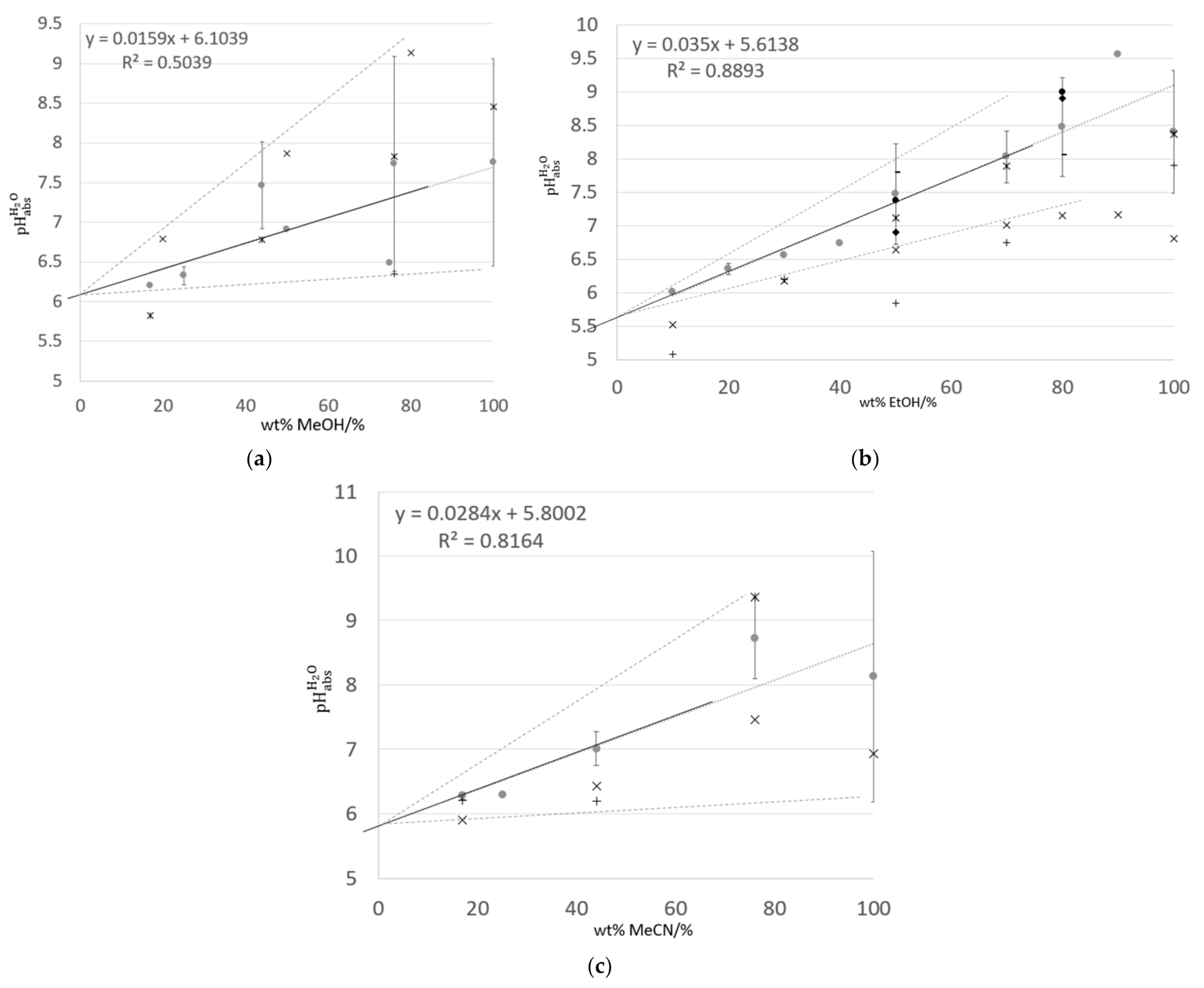
3.2. Values of Water–Organic Solvent Mixtures
4. Discussion
4.1. Solvent
4.2. Interaction with ILSB
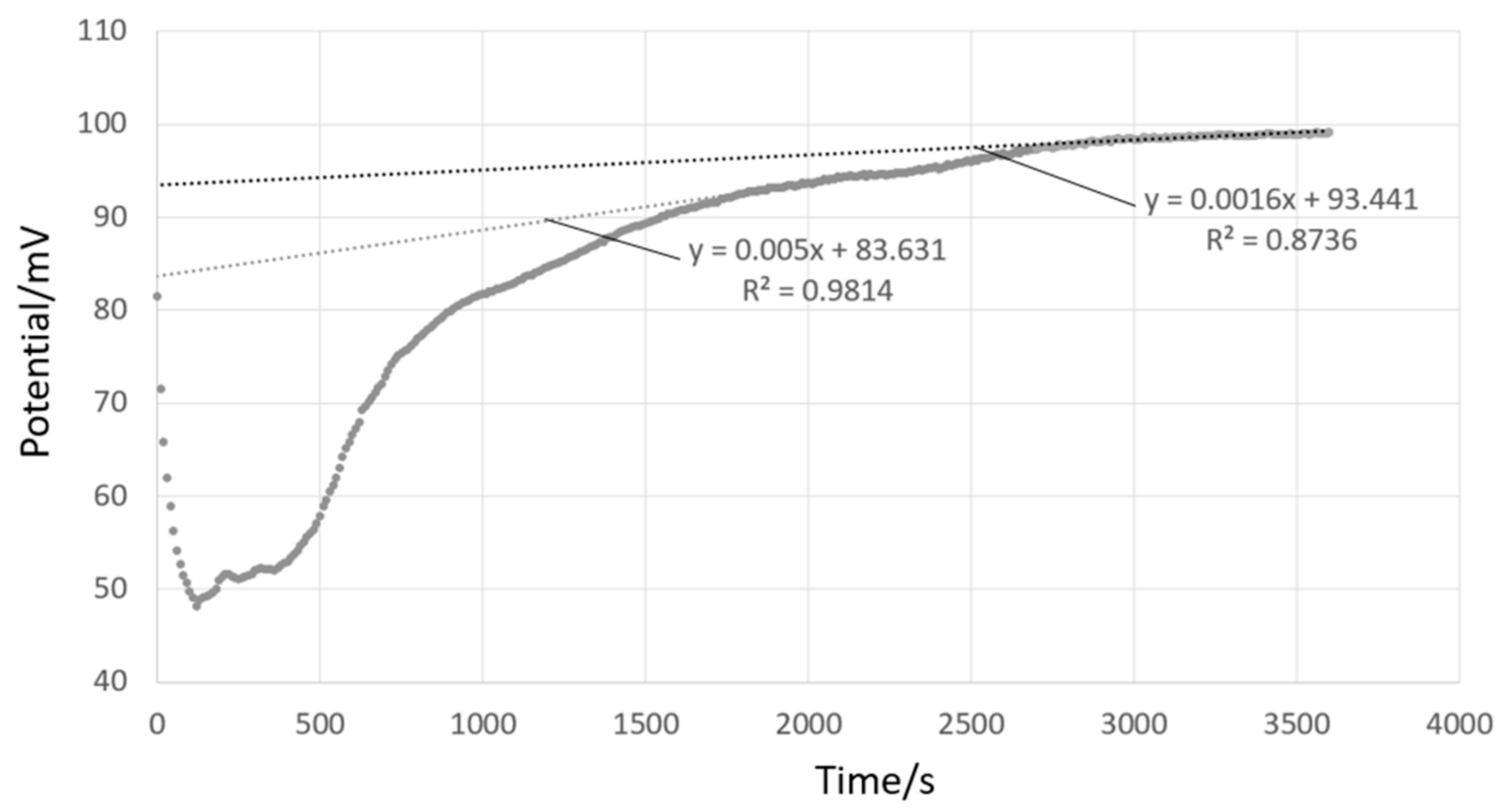
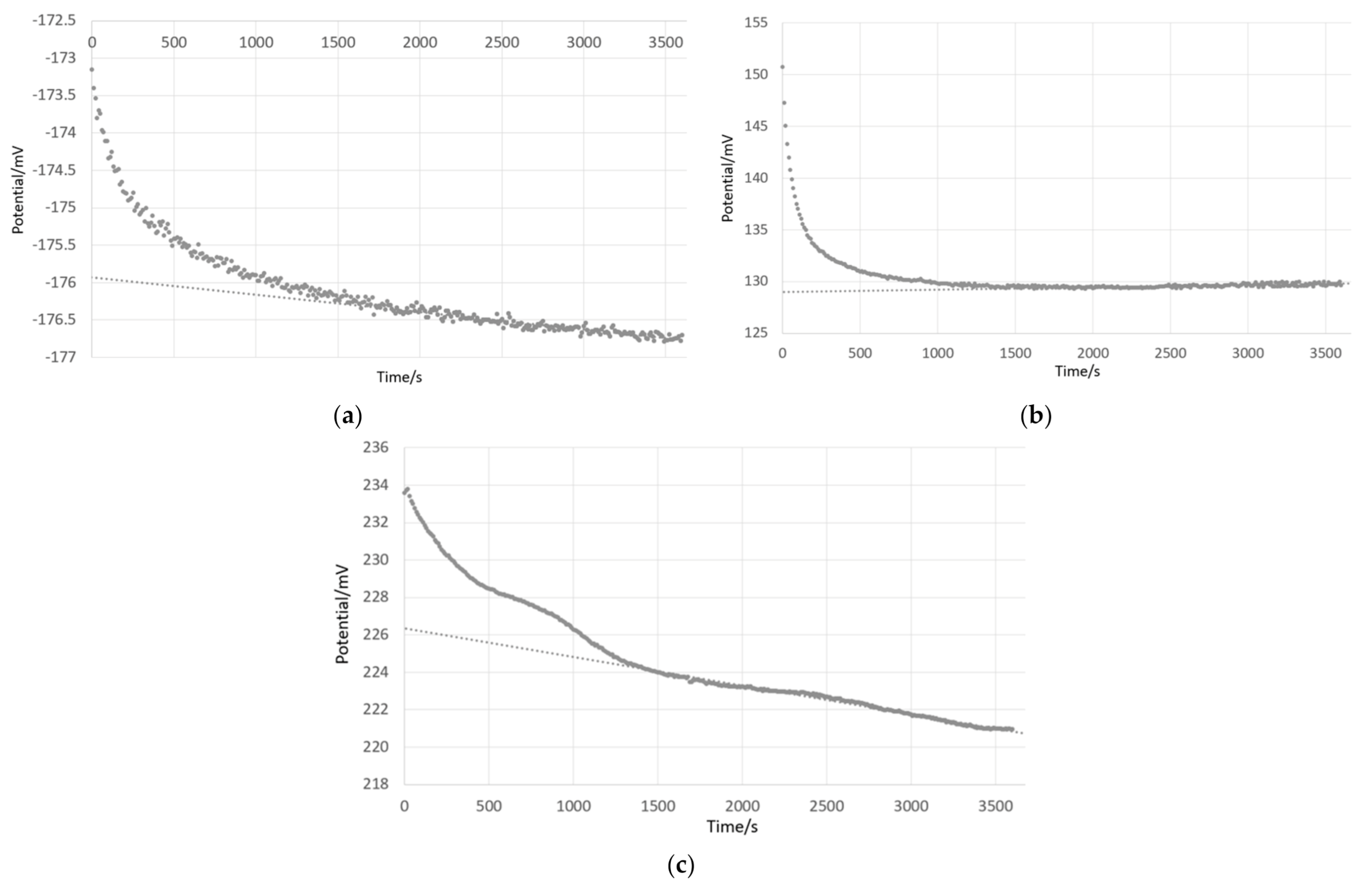
4.3. Data Analysis Methodology
4.4. Variability between GE
4.5. Metrological Comparability of Values
4.6. Ranges for Unbuffered Solvent–Water Mixtures
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Buck, R.P.; Rondinini, S.; Covington, A.K.; Baucke, F.G.K.; Brett, C.M.A.; Camoes, M.F.; Milton, M.J.T.; Mussini, T.; Naumann, R.; Pratt, K.W.; et al. Measurement of pH. Definition, standards, and procedures (IUPAC Recommendations 2002). Pure Appl. Chem. 2002, 74, 2169–2200. [Google Scholar] [CrossRef] [Green Version]
- Radiometer Analytical, pH Theory and Practice. Available online: http://www.electro.fisica.unlp.edu.ar/temas/pnolo/p3_ph_theory.pdf (accessed on 11 March 2021).
- Rondinini, S. pH measurements in non-aqueous and aqueous-organic solvents-definition of standard procedures. Anal. Bioanal. Chem. 2002, 374, 813–816. [Google Scholar] [CrossRef] [PubMed]
- Mussini, T.; Covington, A.K.; Longhi, P.; Rondinini, S. Criteria for standardization of pH measurements in organic solvents and water + organic solvent mixtures of moderate to high permittivities. Pure Appl. Chem. 1985, 57, 865–876. [Google Scholar] [CrossRef]
- Bates, R.G.; Vijh, A.K. Determination of pH: Theory and Practice. J. Electrochem. Soc. 1973, 120, 263C. [Google Scholar] [CrossRef]
- Wang, J. Potentiometry. In Analytical Electrochemistry, 2nd ed.; Wang, J., Ed.; Wiley-VCH: New York, NY, USA, 2006; pp. 140–170. [Google Scholar]
- ThermoFisher Scientific, pH Measurement Handbook. Available online: https://assets.thermofisher.com/TFS-Assets/LSG/brochures/pH-Measurement-Handbook-S-PHREFBK-E.pdf (accessed on 11 March 2021).
- Metrohm, Tips for Handling the Solvotrode, Metrohm Information Issue 1/2007. Available online: https://partners.metrohm.com/GetDocumentPublic?action=get_dms_document&docid=1196146 (accessed on 11 March 2021).
- Horiba Laqua Electrodes pH, Determination of pH in Non-Aqueous Solutions, Application Note. Available online: https://www.horiba.com/fileadmin/uploads/Scientific/water_quality/Documents/Application_Notes/HIS/21_-_Determination_of_pH_in_Non-Aqueous_Solutions__Low-Res_.pdf (accessed on 11 March 2021).
- Mettler-Toledo, pH of Non-Aqueous Samples–Measurement in Organic Solvents, White Paper. Available online: https://www.mt.com/dk/da/home/library/applications/lab-analytical-instruments/measurement-pH-organic-solvents.html (accessed on 11 March 2021).
- Brown, R.J.C.; Keates, A.C.; Brewer, P.J. Sensitivities of a Standard Test Method for the Determination of the pHe of Bioethanol and Suggestions for Improvement. Sensors 2010, 10, 9982–9993. [Google Scholar] [CrossRef]
- ASTM D6423-14: Standard Test Method for Determination of pHe of Denatured Fuel Ethanol and Ethanol Fuel Blends, ASTM International. Available online: https://www.astm.org/DATABASE.CART/HISTORICAL/D6423-14.htm (accessed on 1 June 2017).
- European Standard. NF EN 15490:2007-10: Ethanol as a blending component for petrol–Determination of pHe, October 2007. Available online: https://standards.iteh.ai/catalog/standards/cen/c624ad1e-f052-45ba-94c4-c45ae67db58d/en-15490-2007 (accessed on 1 June 2017).
- Norma Brasileira. NBR 10891: 2017–Hydrous Fuel Ethanol–Determination of pH–Potentiometric Method. Available online: https://www.abntcatalogo.com.br/norma.aspx?ID=382244 (accessed on 1 June 2017).
- Tripartite Task Force: Brazil, European Union & United States of America, White Paper on International Compatible Biofuel Standards. Available online: https://www.nist.gov/system/files/documents/2017/05/09/biofuels_report.pdf (accessed on 1 May 2018).
- Ugo, P.; Daniele, S.; Mazzocchin, G.-A.; Bontempelli, G. Acid-base equilibria in organic solvents: Part 3. An Absolute pH Scale from Proton Basicity Evaluated by Cyclic Voltammetry. Anal. Chim. Acta 1988, 208, 207–217. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Fara, D.C.; Yang, A.H.; Tämm, K.; Tamm, T.; Karelson, M. Quantitative Measures of Solvent Polarity. Chem. Rev. 2004, 104, 175–198. [Google Scholar] [CrossRef]
- Himmel, D.; Goll, S.K.; Leito, I.; Krossing, I. A Unified pH Scale for All Phases. Angew. Chem. 2010, 49, 6885–6888. [Google Scholar] [CrossRef]
- Suu, A.; Jalukse, L.; Liigand, J.; Kruve-Viil, A.; Himmel, D.; Krossing, I.; Roses, M.; Leito, I. Unified pH Values of Liquid Chromatography Mobile Phases. Anal. Chem. 2015, 87, 2623–2630. [Google Scholar] [CrossRef]
- Heering, A.; Bastkowski, F.; Seitz, S. Glass electrode half-cells for measuring unified pH in ethanol–water mixtures. J. Sensors Sens. Syst. 2020, 9, 383–389. [Google Scholar] [CrossRef]
- Radtke, V.; Ermantraut, A.; Himmel, D.; Koslowski, T.; Leito, I.; Krossing, I. The Ideal Ionic Liquid Salt Bridge for the Direct Determination of Gibbs Energies of Transfer of Single Ions, Part I: The Concept. Angew. Chem. 2018, 57, 2344–2347. [Google Scholar] [CrossRef]
- Ermantraut, A.; Radtke, V.; Gebel, N.; Himmel, D.; Koslowski, T.; Leito, I.; Krossing, I. The Ideal Ionic Liquid Salt Bridge for Direct Determination of Gibbs Energies of Transfer of Single Ions, Part II: Evaluation of the Role of Ion Solvation and Ion Mobilities. Angew. Chem. 2018, 57, 2348–2352. [Google Scholar] [CrossRef]
- Radtke, V.; Gebel, N.; Priester, D.; Ermantraut, A.; Bauerle, M.; Himmel, D.; Koslowski, T.; Leito, I.; Krossing, I. The ideal ionic liquid salt bridge for the direct determination of Gibbs energies of transfer of single ions, Part III: Evidence and implications of the absence of solvent-solvent interactions. Chem. Eur. J. 2021, 57, 2344–2347. [Google Scholar]
- Beliustin, A.A.; Pisarevsky, A.M.; Lepnev, G.P.; Sergeyev, A.S.; Shultz, M.M. Glass electrodes: A new generation. Sens. Actuat. B 1992, 10, 61–66. [Google Scholar] [CrossRef]
- Heering, A.; Stoica, D.; Camões, F.; Anes, B.; Nagy, D.; Szilágyi, Z.N.; Quendera, R.; Ribeiro, L.; Bastkowski, F.; Born, R.; et al. Symmetric Potentiometric Cells for the Measurement of Unified pH Values. Symmetry 2020, 12, 1150. [Google Scholar] [CrossRef]
- Borges, P.P.; Fraga, I.C.S.; Marques, B.S.R.; Dias, J.C.; Cunha, V.S.; Canale, L.; Narazaki, M.; Dean, S.W. pH Measurement in Bioethanol by Using Different Electrodes and according to International Standards. J. ASTM Int. 2010, 7, 1–6. [Google Scholar] [CrossRef]
- Dean, S.W.; Da Silva, R.M.; Borges, P.P.; Fraga, I.C.S.; Stradiotto, N.R. New Methodology for pH Measurements in Fuel Ethanol Using Glass Electrode. J. ASTM Int. 2011, 8. [Google Scholar] [CrossRef]
- Gelsema, W.J.; De Ligny, C.L.; Remijnse, A.G.; Blijleven, H.A. pH-Measurements in alcohol-water mixtures, using aqueous standard buffer solutions for calibration. Recl. Trav. Chim. Pays-Bas 2010, 85, 647–660. [Google Scholar] [CrossRef]
- Moldoveanu, S.C.; David, V. Solvents, Buffers, and Additives Used in the Mobile Phase. In Selection of the HPLC Method in Chemical Analysis; Elsevier BV: Amsterdam, The Netherlands, 2017; pp. 393–450. [Google Scholar]
- Van Der Veen, A.M.H.; Ent, H.; Baldan, A.; Da Cunha, V.S.; Daroda, R.J.; Lang, B.; Schantz, M.; Ulberth-Buchgraber, M.; Held, A.; Hearn, R.; et al. The BIOREMA project—Part 3: International interlaboratory comparison for bio-ethanol test methods. Accred. Qual. Assur. 2013, 18, 41–50. [Google Scholar] [CrossRef]
- Sanz-Nebot, V. Assignment of reference pH-values to primary standard buffer solutions for standardization of potentiometric sensors in acetonitrile-water mixtures. Anal. Bioanal. Chem. 1995, 353, 148–155. [Google Scholar] [CrossRef]
- Mussini, P.R. Reference value standards and primary standards for pH measurements in D2O and aqueous-organic solvent mix-tures: New accessions and assessments. Pure Appl. Chem. 1997, 69, 1007–1014. [Google Scholar] [CrossRef] [Green Version]
- Luecke, J.; McCormick, R.L. Electrical Conductivity and pHe Response of Fuel Ethanol Contaminants. Energy Fuels 2014, 28, 5222–5228. [Google Scholar] [CrossRef]
- Camões, M.F. Realisation of a unified pH scale. Chem. Int. 2018, 40, 29–30. [Google Scholar] [CrossRef]
- Pungor, E.; Toth, K.; Klatsmanyi, P.G.; Izutsu, K. Applications of ion-selective electrodes in nonaqueous and mixed solvents. Pure Appl. Chem. 1983, 55, 2029–2065. [Google Scholar] [CrossRef]
- Bastkowski, F.; Heering, A. EMPIR JRP FUN-09 Realisation of a unified pH scale–Deliverable 2–Report on interlaboratory comparison to evaluate the performance of measurement procedures. 2021; Unpublished work. [Google Scholar]
- Roses, M.; Rafols, C.; Bosch, E. Autoprotolysis in aqueous organic solvent mixtures. Anal. Chem. 1993, 65, 2294–2299. [Google Scholar] [CrossRef]
- Rondinini, S.; Longhi, P.; Mussini, P.R.; Mussini, T. Autoprotolysis constants in nonaqueous solvents and aqueous organic solvent mixtures. Pure Appl. Chem. 1987, 59, 1693–1702. [Google Scholar] [CrossRef] [Green Version]
- Farajtabar, A.; Gharib, F. Autoprotolysis constants determination of water-methanol mixtures and solvent effect. J. Taibah Univ. Sci. 2009, 2, 7–13. [Google Scholar] [CrossRef] [Green Version]
- Canals, I.; Oumada, F.Z.; Rosés, M.; Bosch, E. Retention of ionizable compounds on HPLC. 6. pH measurements with the glass electrode in methanol-water mixtures. J. Chromatogr. A 2001, 911, 191–202. [Google Scholar] [CrossRef]
- Kotrba, M.; Schilling, L.-H. Measurement of pH in ethanol, distilled water, and their mixtures: On the assessment of pH in etha-nol-based natural history wet collections and the detrimental aspects of dilution with distilled water. Collect. Forum 2018, 31, 84–101. [Google Scholar] [CrossRef]
- Faraji, M.; Farajtabar, A.; Gharib, F. Determination of water-ethanol autoprotolysis constants and solvent effect. J. Appl. Chem. Res. 2009, 9, 7–12. [Google Scholar]
- Espinosa, S.; Bosch, E.; Rosés, M. Retention of ionizable compounds on HPLC. 5. pH scales and the retention of acids and bases with acetonitrile-water mobile phases. Anal. Chem. 2000, 72, 5193–5200. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, J.; Nebot, V.S. Autoprotolysis constants and standardization of the glass electrode in acetonitrile-water mixtures. Effect of solvent composition. Anal. Chim. Acta 1991, 244, 183–191. [Google Scholar] [CrossRef]
- Bax, D.; De Ligny, C.L.; Remijnse, A.G. Activity coefficients of single ions IV.: The difference between the standard chemical potentials of single ions in ethanol and ethanol-water mixtures and in water at 25°, and some related quantities. Recl. Trav. Chim. Pays-Bas 2010, 91, 965–988. [Google Scholar] [CrossRef]
- Davison, W.; Woof, C. Performance tests for the measurement of pH with glass electrodes in low ionic strength solutions including natural waters. Anal. Chem. 1985, 57, 2567–2570. [Google Scholar] [CrossRef]
- Himmel, D.; Radtke, V.; Butschke, B.; Krossing, I. Basic Remarks on Acidity. Angew. Chem. 2018, 57, 4386–4411. [Google Scholar] [CrossRef]
- Midgley, D.; Torrance, K. Assessment of glass electrodes for determining pH in boiler feed water. Analyst 1979, 104, 63–72. [Google Scholar] [CrossRef]
- Liigand, P.; Heering, A.; Kaupmees, K.; Leito, I.; Girod, M.; Antoine, R.; Kruve-Viil, A. The Evolution of Electrospray Generated Droplets is Not Affected by Ionization Mode. J. Am. Soc. Mass Spectrom. 2017, 28, 2124–2131. [Google Scholar] [CrossRef]
- Veigure, R.; Lossmann, K.; Hecht, M.; Parman, E.; Born, R.; Leito, I.; Herodes, K.; Kipper, K. Retention of acidic and basic analytes in reversed phase column using fluorinated and novel eluent additives for liquid chromatography-tandem mass spectrometry. J. Chromatogr. A 2020, 1613, 460667. [Google Scholar] [CrossRef]
- Lõkov, M.; Tshepelevitsh, S.; Heering, A.; Plieger, P.G.; Vianello, R.; Leito, I. On the Basicity of Conjugated Nitrogen Heterocycles in Different Media. Eur. J. Org. Chem. 2017, 2017, 4475–4489. [Google Scholar] [CrossRef]
- Fondriest Environmental, Inc. pH of Water. Fundamentals of Environmental Measurements. 19 November 2013. Available online: https://www.fondriest.com/environmental-measurements/parameters/water-quality/ph/ (accessed on 1 February 2021).
- Institute for Reference Materials and Measurements (IRMM). Certification Report: Certification of the Mass Concentrations of Calcium, Chloride, Magnesium, Ortho-Phosphate, Potassium, Sodium, and of pH and Conductivity in Groundwater–Certified Reference Material ERM-CA616, EUR 24424 EN–2010, JRC European Commission. Available online: https://op.europa.eu/da/publication-detail/-/publication/70189188-ea83-4b65-beff-c6bc03c0154e (accessed on 19 February 2021).
- Elhajj, J.; Al-Hindi, M.; Azizi, F. A Review of the Absorption and Desorption Processes of Carbon Dioxide in Water Systems. Ind. Eng. Chem. Res. 2013, 53, 2–22. [Google Scholar] [CrossRef]
- ISO 10523: 2008, Water Quality–Determination of pH, Annex D. Available online: https://www.iso.org/standard/51994.html (accessed on 1 June 2017).


| Electrode Type | Electrode | Institute | |
|---|---|---|---|
| A | SCGE | EST-0601, Izmeritelnaya Tekhnika | CMI; DFM; IPQ; PTB; UT |
| B | Combination | 6.0229.100, Metrohm | BFKH |
| C | Ross Orion SureFlow, Thermo Fischer Scientific | CMI | |
| D | P11/KJ/LICL, Sentek | CMI | |
| E | Polylyte Plus, Hamilton | DFM | |
| F | Metrohm 6.0269.100 | PTB | |
| G | Half-cell | E11M001, Radiometer | DFM |
| H | 6.0150.100, Metrohm | IPQ; PTB 1 | |
| I | DG300-SC, Mettler-Toledo | PTB 1 | |
| J | Model 1076-10C, Horiba Scientific/Laqua | PTB 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deleebeeck, L.; Snedden, A.; Nagy, D.; Szilágyi Nagyné, Z.; Roziková, M.; Vičarová, M.; Heering, A.; Bastkowski, F.; Leito, I.; Quendera, R.; et al. Unified pH Measurements of Ethanol, Methanol, and Acetonitrile, and Their Mixtures with Water. Sensors 2021, 21, 3935. https://doi.org/10.3390/s21113935
Deleebeeck L, Snedden A, Nagy D, Szilágyi Nagyné Z, Roziková M, Vičarová M, Heering A, Bastkowski F, Leito I, Quendera R, et al. Unified pH Measurements of Ethanol, Methanol, and Acetonitrile, and Their Mixtures with Water. Sensors. 2021; 21(11):3935. https://doi.org/10.3390/s21113935
Chicago/Turabian StyleDeleebeeck, Lisa, Alan Snedden, Dániel Nagy, Zsófia Szilágyi Nagyné, Matilda Roziková, Martina Vičarová, Agnes Heering, Frank Bastkowski, Ivo Leito, Raquel Quendera, and et al. 2021. "Unified pH Measurements of Ethanol, Methanol, and Acetonitrile, and Their Mixtures with Water" Sensors 21, no. 11: 3935. https://doi.org/10.3390/s21113935
APA StyleDeleebeeck, L., Snedden, A., Nagy, D., Szilágyi Nagyné, Z., Roziková, M., Vičarová, M., Heering, A., Bastkowski, F., Leito, I., Quendera, R., Cabral, V., & Stoica, D. (2021). Unified pH Measurements of Ethanol, Methanol, and Acetonitrile, and Their Mixtures with Water. Sensors, 21(11), 3935. https://doi.org/10.3390/s21113935






