Forecasting Air Temperature on Edge Devices with Embedded AI †
Abstract
:1. Introduction
- First, (sensor) data related to relevant environmental variables internal to the greenhouse, which have to be maintained within suitable ranges (e.g., air humidity and temperature), are collected through devices equipped with sensors (denoted as IoT sensing nodes, or sensor nodes, SNs), generally organized as Wireless Sensor Networks (WSNs). Moreover, internal greenhouse data gathered by SNs are usually sent to less constrained nodes, denoted as gateways (GWs) and connected to the Internet. GWs forward SNs’ data to processing and storing infrastructures located in the Cloud [6]. Then, data can be retrieved and visualized (through appropriate User Interfaces, UIs), as well as kept as input data for further processing. Hence, monitoring of relevant variables inside the greenhouse is relevant for both end-users (farmers) and for researchers [7,8,9,10,11].
- Secondly, additional control devices (i.e., actuator nodes), installed inside the greenhouse in order to regulate its internal climate [12,13], can be integrated within the aforementioned collection system. As an example, if a dangerous air humidity index is detected by SNs, a ventilation system would automatically be activated in order to lower the air humidity.
- Thirdly, complex models and/or forecasting algorithms are developed with the goal of predicting the future values of the monitored environmental variables, for example allowing us to preemptively schedule some operations (e.g., the activation of a warming system) to avoid these internal variables reaching undesired conditions (i.e., too low temperatures). To this end, the greenhouse’s internal variables have been satisfactorily forecast through Deep Learning (DL) algorithms, e.g., based on Neural Networks (NNs) [14,15,16], and selecting data collected from different sources as input (namely, internal and external variables of a greenhouse, possibly measured by SNs).
2. Background
2.1. Overview on Neural Networks
2.2. Evaluation Metrics
3. Related Work
4. Methodology
- Relevant air temperature data, measured with sensors inside a greenhouse associated with an Italian demonstrator of the H2020 project AFarCloud [30], are collected and processed to remove outliers and spurious data (Section 4.1).
- The greenhouse indoor temperature sensor data collected with a sampling period min are arranged in a time series. Furthermore, from this original time series, six additional time series are derived downsampling the first time series with longer sampling periods (Section 4.2).
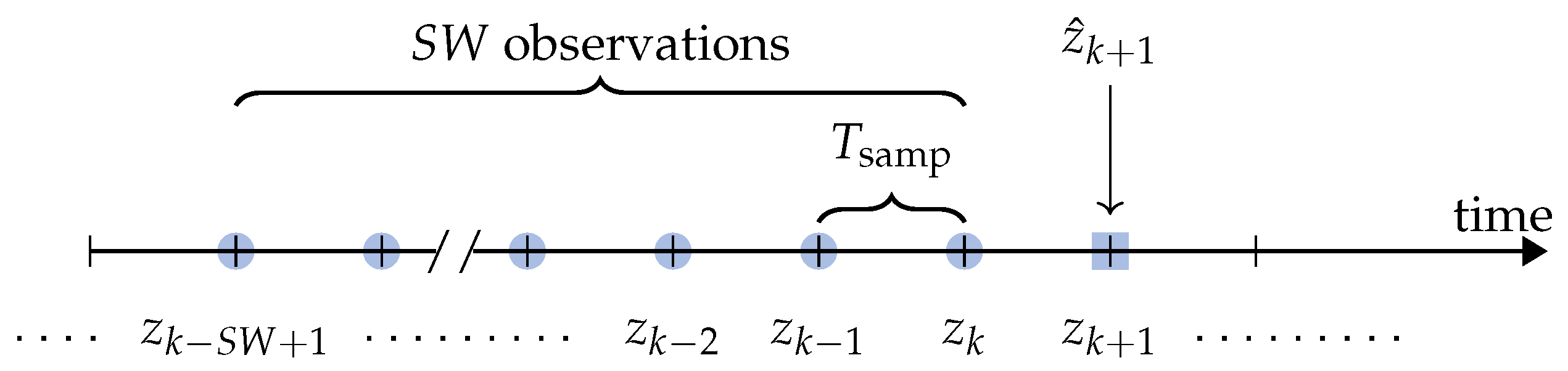
- The number of input variables of the model and the sampling period are defined as the two design parameters. Moreover, is reintegrated as the prediction time horizon; in fact, the predicted temperature value is the one corresponding to the next temperature value after the most recent one of the sliding window: this samples is, by construction, ahead. Furthermore, a proper set of values related to these parameters is selected for testing purposes (Section 4.3).
- Starting from the collected sensor data and according to the number of parameters’ values to be tested, multiple data sets are created. Furthermore, each data set is split into training and test subsets (Section 4.4).
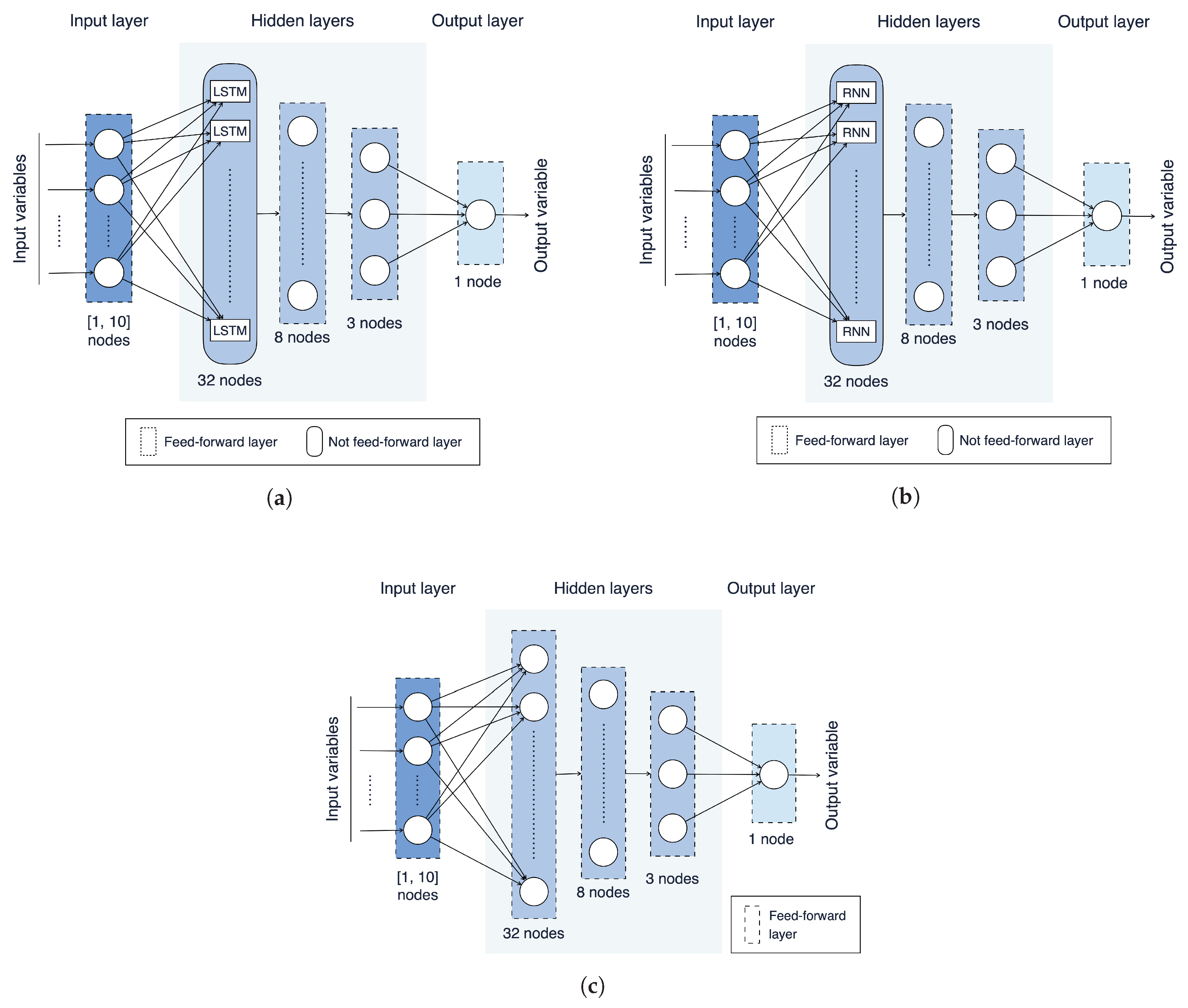
- Three NN architectures, based on an ANN, a RNN, and a LSTM, are introduced and trained with the data sets resulting from the previous steps (Section 4.5).
- The NN model presented in [19] is re-trained with a significantly larger data set—including data from 6 more months (Section 4.6).
- All models are evaluated on the test subsets and their performances are compared in terms of RMSE, MAPE, R, and NetScore (Section 5).
- Finally, the best three models (among a total of 210) on the considered engineered data sets (step 4) are performance-wise compared with relevant literature approaches (Section 5).
4.1. Data Collection and Cleaning
4.2. Engineering Time Series from Sensor Data
4.3. Sliding Window-Based Prediction
4.4. Data Pre-Processing and Data Sets Creation
4.5. Models Training
4.6. “Old Model” Re-Training
5. Experimental Results
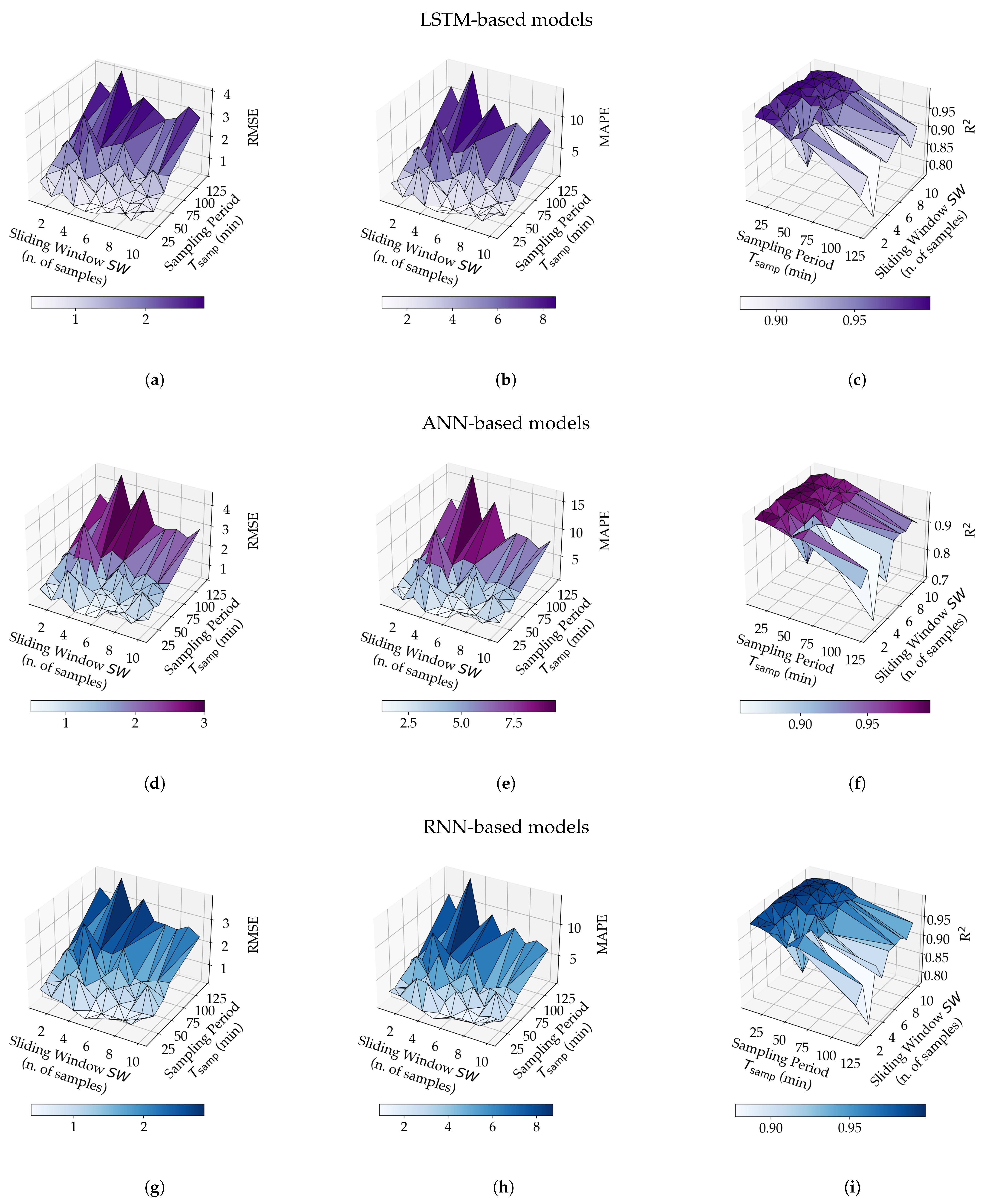
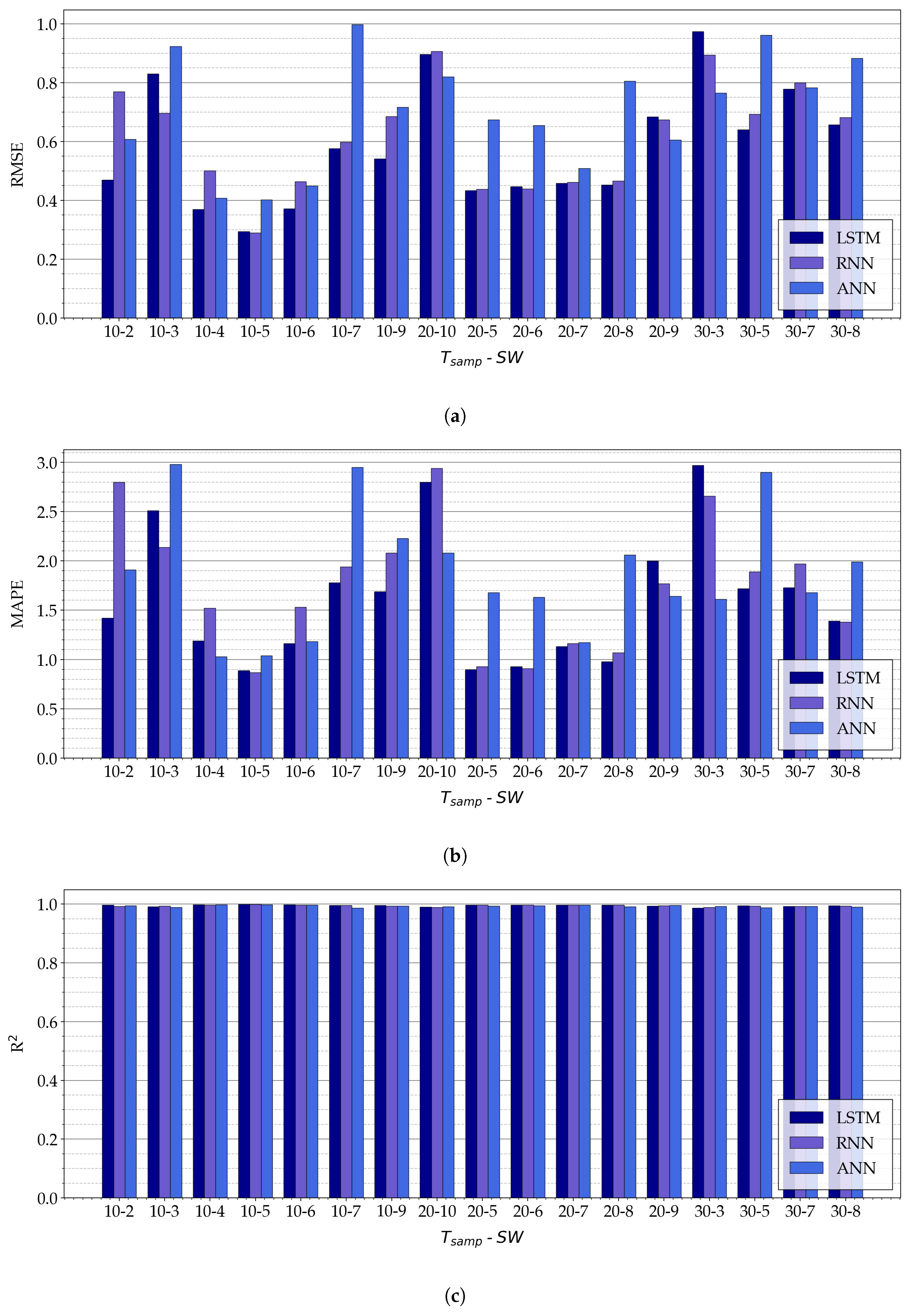
5.1. Sliding Window and Sampling Interval
5.2. NN Architecture
5.3. Performance Analysis and Literature Comparison
- the value of R of the considered NN-based models is higher than those of all the references listed in Table 1.
5.4. Possible Application Scenario and Reference Architecture
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFarCloud | Aggregate Farming in the Cloud |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| BP | Back Propagation |
| CGA | Conjugate Gradient Algorithm |
| DL | Deep Learning |
| DNN | Deep Neural Network |
| FaaS | Farm-as-a-Service |
| GW | Gateway |
| ICT | Information and Communication Technology |
| IoT | Internet of Things |
| LM | Levenberg-Marquardt |
| LSTM | Long Short-Term Memory |
| MAC | Multiply–ACcumulate |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| MLP | Multi-Layer Perceptron |
| NARX | Nonlinear AutoRegressive with eXternal input |
| NN | Neural Network |
| PSO | Particle Swarm Optimization |
| R | Coefficient of determination |
| RBF | Radial Basis Function |
| ReLU | Rectified Linear Unit |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Network |
| SA | Smart Agriculture |
| SBC | Single Board Computer |
| SF | Smart Farming |
| SN | Sensor Node |
| UI | User Interface |
| WSN | Wireless Sensor Network |
References
- Codeluppi, G.; Cilfone, A.; Davoli, L.; Ferrari, G. VegIoT Garden: A modular IoT Management Platform for Urban Vegetable Gardens. In Proceedings of the IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Portici, Italy, 24–26 October 2019; pp. 121–126. [Google Scholar] [CrossRef]
- Kumar, A.; Tiwari, G.N.; Kumar, S.; Pandey, M. Role of Greenhouse Technology in Agricultural Engineering. Int. J. Agric. Res. 2010, 5, 779–787. [Google Scholar] [CrossRef] [Green Version]
- Francik, S.; Kurpaska, S. The Use of Artificial Neural Networks for Forecasting of Air Temperature inside a Heated Foil Tunnel. Sensors 2020, 20, 652. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Escamilla-García, A.; Soto-Zarazúa, G.M.; Toledano-Ayala, M.; Rivas-Araiza, E.; Gastélum-Barrios, A. Applications of Artificial Neural Networks in Greenhouse Technology and Overview for Smart Agriculture Development. Appl. Sci. 2020, 10, 3835. [Google Scholar] [CrossRef]
- Bot, G. Physical Modeling of Greenhouse Climate. IFAC Proc. Vol. 1991, 24, 7–12. [Google Scholar] [CrossRef]
- Belli, L.; Cirani, S.; Davoli, L.; Melegari, L.; Mónton, M.; Picone, M. An Open-Source Cloud Architecture for Big Stream IoT Applications. In Interoperability and Open-Source Solutions for the Internet of Things: International Workshop, FP7 OpenIoT Project, Held in Conjunction with SoftCOM 2014, Split, Croatia, 18 September 2014, Invited Papers; Podnar Žarko, I., Pripužić, K., Serrano, M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 73–88. [Google Scholar] [CrossRef]
- Kochhar, A.; Kumar, N. Wireless sensor networks for greenhouses: An end-to-end review. Comput. Electron. Agric. 2019, 163, 104877. [Google Scholar] [CrossRef]
- Codeluppi, G.; Cilfone, A.; Davoli, L.; Ferrari, G. LoRaFarM: A LoRaWAN-Based Smart Farming Modular IoT Architecture. Sensors 2020, 20, 2028. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbasi, M.; Yaghmaee, M.H.; Rahnama, F. Internet of Things in agriculture: A survey. In Proceedings of the 3rd International Conference on Internet of Things and Applications (IoT), Isfahan, Iran, 17–18 April 2019; pp. 1–12. [Google Scholar] [CrossRef]
- Davoli, L.; Belli, L.; Cilfone, A.; Ferrari, G. Integration of Wi-Fi mobile nodes in a Web of Things Testbed. ICT Express 2016, 2, 95–99. [Google Scholar] [CrossRef] [Green Version]
- Tafa, Z.; Ramadani, F.; Cakolli, B. The Design of a ZigBee-Based Greenhouse Monitoring System. In Proceedings of the 7th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 10–14 June 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Wiboonjaroen, M.T.W.; Sooknuan, T. The Implementation of PI Controller for Evaporative Cooling System in Controlled Environment Greenhouse. In Proceedings of the 17th International Conference on Control, Automation and Systems (ICCAS), Jeju, Korea, 18–21 October 2017; pp. 852–855. [Google Scholar] [CrossRef]
- Zou, Z.; Bie, Y.; Zhou, M. Design of an Intelligent Control System for Greenhouse. In Proceedings of the 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 1–1635. [Google Scholar] [CrossRef]
- Moon, T.; Hong, S.; Young Choi, H.; Ho Jung, D.; Hong Chang, S.; Eek Son, J. Interpolation of Greenhouse Environment Data using Multilayer Perceptron. Comput. Electron. Agric. 2019, 166, 105023. [Google Scholar] [CrossRef]
- Taki, M.; Abdanan Mehdizadeh, S.; Rohani, A.; Rahnama, M.; Rahmati-Joneidabad, M. Applied machine learning in greenhouse simulation; New application and analysis. Inf. Process. Agric. 2018, 5, 253–268. [Google Scholar] [CrossRef]
- Yue, Y.; Quan, J.; Zhao, H.; Wang, H. The Prediction of Greenhouse Temperature and Humidity Based on LM-RBF Network. In Proceedings of the IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 1537–1541. [Google Scholar] [CrossRef]
- Lee, Y.; Tsung, P.; Wu, M. Techology Trend of Edge AI. In Proceedings of the International Symposium on VLSI Design, Automation and Test (VLSI-DAT), Hsinchu, Taiwan, 16–19 April 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Wong, A. NetScore: Towards Universal Metrics for Large-Scale Performance Analysis of Deep Neural Networks for Practical On-Device Edge Usage. In Image Analysis and Recognition; Karray, F., Campilho, A., Yu, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 15–26. [Google Scholar] [CrossRef] [Green Version]
- Codeluppi, G.; Cilfone, A.; Davoli, L.; Ferrari, G. AI at the Edge: A Smart Gateway for Greenhouse Air Temperature Forecasting. In Proceedings of the IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Trento, Italy, 4–6 November 2020; pp. 348–353. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cifuentes, J.; Marulanda, G.; Bello, A.; Reneses, J. Air Temperature Forecasting Using Machine Learning Techniques: A Review. Energies 2020, 13, 4215. [Google Scholar] [CrossRef]
- Kavlakoglu, E. AI vs. Machine Learning vs. Deep Learning vs. Neural Networks: What’s the Difference? Available online: https://www.ibm.com/cloud/blog/ai-vs-machine-learning-vs-deep-learning-vs-neural-networks (accessed on 2 March 2021).
- Ferrero Bermejo, J.; Gómez Fernández, J.F.; Olivencia Polo, F.; Crespo Márquez, A. A Review of the Use of Artificial Neural Network Models for Energy and Reliability Prediction. A Study of the Solar PV, Hydraulic and Wind Energy Sources. Appl. Sci 2019, 8, 1844. [Google Scholar] [CrossRef] [Green Version]
- Gardner, M.; Dorling, S. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Hongkang, W.; Li, L.; Yong, W.; Fanjia, M.; Haihua, W.; Sigrimis, N. Recurrent Neural Network Model for Prediction of Microclimate in Solar Greenhouse. IFAC-PapersOnLine 2018, 51, 790–795. [Google Scholar] [CrossRef]
- Jung, D.H.; Seok Kim, H.; Jhin, C.; Kim, H.J.; Hyun Park, S. Time-serial analysis of deep neural network models for prediction of climatic conditions inside a greenhouse. Comput. Electron. Agric. 2020, 173, 105402. [Google Scholar] [CrossRef]
- Taki, M.; Ajabshirchi, Y.; Ranjbar, S.F.; Rohani, A.; Matloobi, M. Heat transfer and MLP neural network models to predict inside environment variables and energy lost in a semi-solar greenhouse. Energy Build. 2016, 110, 314–329. [Google Scholar] [CrossRef]
- Aggregate Farming in the Cloud (AFarCloud) H2020 Project. Available online: http://www.afarcloud.eu (accessed on 14 February 2021).
- Podere Campáz—Produzioni Biologiche. Available online: https://www.poderecampaz.com (accessed on 1 February 2020).
- Chollet, F. Keras5. 2015. Available online: https://keras.io (accessed on 15 May 2021).
- Raspberry Pi. Available online: https://www.raspberrypi.org/ (accessed on 1 June 2021).
- Mazzia, V.; Khaliq, A.; Salvetti, F.; Chiaberge, M. Real-Time Apple Detection System Using Embedded Systems With Hardware Accelerators: An Edge AI Application. IEEE Access 2020, 8, 9102–9114. [Google Scholar] [CrossRef]
- Shadrin, D.; Menshchikov, A.; Ermilov, D.; Somov, A. Designing Future Precision Agriculture: Detection of Seeds Germination Using Artificial Intelligence on a Low-Power Embedded System. IEEE Sens. J. 2019, 19, 11573–11582. [Google Scholar] [CrossRef]








| Ref. | NN Model | Performances (on Test Set) | Data Set Details | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Input Variables | Architectural Type | Training Algorithm | RMSE (C) | MAPE (%) | R | Size (Samples No) | Collection Interval | Sampling Interval | |
| [3] | External temperature and solar radiation, wind speed, heater temperature, datetime reference | ANN | BP, CGA | – | N/A | N/A | 1368 | ≈2 months | 1 h |
| [14] | Internal solar radiation, air temperature and humidity, and soil moisture, CO, atmospheric pressure, datetime reference | ANN | BP | N/A | ≈87,408 | 19 months | 10 min | ||
| [15] | External solar radiation and temperature, wind speed | ANN, RBF | BP | , | , | , | N/A | N/A | N/A |
| [16] | External solar radiation, heater temperature, internal air temperature and humidity, wind speed, history of actuators, shadow screen | RBF | BP, LM | N/A | N/A | 1728 | 12 days | 10 min | |
| [19] | External apparent temperature, dew point, air humidity, air temperature and UV index, datetime reference | ANN | BP | 5346 | 10 months | 1 h | |||
| [28] | External temperature, solar radiation and humidity, wind speed and direction, history of actuators | ANN, RNN-LSTM, NARX | BP | –, –, – | N/A | , –, – | ≈470,000 | 1 year | 5, 10, 15, 20, 25, 30 min |
| [27] | Internal air and soil temperature, internal solar radiation, humidity and CO | RNN | BP | 1152 | 8 days | 10 min | |||
| Data Set | [min] | [Samples] | Size [Samples] | Training Subset Size [Samples] | Test Subset Size [Samples] | Data Set | [min] | [Samples] | Size [Samples] | Training Subset Size [Samples] | Test Subset Size [Samples] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 1 | 27,248 | 9082 | 10 | 10 | 8174 | |||||
| 10 | 2 | 8957 | 10 | 3 | 8840 | ||||||
| 10 | 4 | 8730 | 10 | 5 | 8628 | ||||||
| 10 | 6 | 8529 | 10 | 7 | 8433 | ||||||
| 10 | 8 | 8341 | 10 | 9 | 8255 | ||||||
| 120 | 1 | 2985 | 2239 | 746 | 120 | 10 | 2457 | 1843 | 614 | ||
| 120 | 2 | 2912 | 2184 | 728 | 120 | 3 | 2843 | 2133 | 710 | ||
| 120 | 4 | 2781 | 2086 | 695 | 120 | 5 | 2723 | 2043 | 680 | ||
| 120 | 6 | 2666 | 2000 | 666 | 120 | 7 | 2611 | 1959 | 652 | ||
| 120 | 8 | 2558 | 1919 | 639 | 120 | 9 | 2507 | 1881 | 626 | ||
| 20 | 1 | 4525 | 20 | 10 | 4001 | ||||||
| 20 | 2 | 4453 | 20 | 3 | 4384 | ||||||
| 20 | 4 | 4321 | 20 | 5 | 4262 | ||||||
| 20 | 6 | 4205 | 20 | 7 | 4151 | ||||||
| 20 | 8 | 4099 | 20 | 9 | 4049 | ||||||
| 30 | 1 | 9051 | 3016 | 30 | 10 | 7964 | 2654 | ||||
| 30 | 2 | 8897 | 2965 | 30 | 3 | 8759 | 2919 | ||||
| 30 | 4 | 8628 | 2876 | 30 | 5 | 8506 | 2835 | ||||
| 30 | 6 | 11184 | 8388 | 2796 | 30 | 7 | 8273 | 2757 | |||
| 30 | 8 | 8164 | 2721 | 30 | 9 | 8062 | 2687 | ||||
| 40 | 1 | 9008 | 6756 | 2252 | 40 | 10 | 7690 | 5768 | 1922 | ||
| 40 | 2 | 8829 | 6622 | 2207 | 40 | 3 | 8656 | 6492 | 2164 | ||
| 40 | 4 | 8495 | 6372 | 2123 | 40 | 5 | 8341 | 6256 | 2085 | ||
| 40 | 6 | 8196 | 6147 | 2049 | 40 | 7 | 8062 | 6047 | 2015 | ||
| 40 | 8 | 7931 | 5949 | 1982 | 40 | 9 | 7806 | 5855 | 1951 | ||
| 50 | 1 | 7220 | 5415 | 1805 | 50 | 10 | 6185 | 4639 | 1546 | ||
| 50 | 2 | 7079 | 5310 | 1769 | 50 | 3 | 6944 | 5208 | 1736 | ||
| 50 | 4 | 6816 | 5112 | 1704 | 50 | 5 | 6695 | 5022 | 1673 | ||
| 50 | 6 | 6584 | 4938 | 1646 | 50 | 7 | 6479 | 4860 | 1619 | ||
| 50 | 8 | 6376 | 4782 | 1594 | 50 | 9 | 6280 | 4710 | 1570 | ||
| 60 | 1 | 6006 | 4505 | 1501 | 60 | 10 | 5146 | 3860 | 1286 | ||
| 60 | 2 | 5886 | 4415 | 1471 | 60 | 3 | 5772 | 4329 | 1443 | ||
| 60 | 4 | 5668 | 4251 | 1417 | 60 | 5 | 5570 | 4178 | 1392 | ||
| 60 | 6 | 5478 | 4109 | 1369 | 60 | 7 | 5389 | 4042 | 1347 | ||
| 60 | 8 | 5306 | 3980 | 1326 | 60 | 9 | 5224 | 3918 | 1306 |
| NN Arch. Type | RMSE [C] | MAPE [%] | R | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Value | Value | Value | ||||||||
| ANN | Min | 10 | 5 | 10 | 4 | 120 | 3 | |||
| Max | 120 | 3 | 120 | 3 | 10 | 4, 5 | ||||
| Avg | N/A | N/A | N/A | N/A | N/A | N/A | ||||
| RNN | Min | 10 | 5 | 10 | 5 | 120 | 3 | |||
| Max | 120 | 3 | 120 | 3 | 10 | 5 | ||||
| Avg | N/A | N/A | N/A | N/A | N/A | N/A | ||||
| LSTM | Min | 10 | 5 | 10 | 5 | 120 | 3 | |||
| Max | 120 | 3 | 120 | 3 | 10 | 5 | ||||
| Avg | N/A | N/A | N/A | N/A | N/A | N/A | ||||
| Data Set | RMSE [C] | MAPE [%] | R | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| LSTM | RNN | ANN | LSTM | RNN | ANN | LSTM | RNN | ANN | |||
| 10 | 2 | ||||||||||
| 10 | 3 | ||||||||||
| 10 | 4 | ||||||||||
| 10 | 5 | ||||||||||
| 10 | 6 | ||||||||||
| 10 | 7 | ||||||||||
| 10 | 9 | ||||||||||
| 20 | 5 | ||||||||||
| 20 | 6 | ||||||||||
| 20 | 7 | ||||||||||
| 20 | 8 | ||||||||||
| 20 | 9 | ||||||||||
| 20 | 10 | ||||||||||
| 30 | 3 | ||||||||||
| 30 | 5 | ||||||||||
| 30 | 7 | ||||||||||
| 30 | 8 | ||||||||||
| Model | RMSE [C] | MAPE [%] | R | Accuracy [%] | MAC Operations | Parameters Number | NetScore |
|---|---|---|---|---|---|---|---|
| Model in [19] | 1018 | 1018 | |||||
| Re-trained [19] | 1018 | 1018 | |||||
| 22,192 | 4625 | ||||||
| 5712 | 1361 | ||||||
| 464 | 464 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Codeluppi, G.; Davoli, L.; Ferrari, G. Forecasting Air Temperature on Edge Devices with Embedded AI. Sensors 2021, 21, 3973. https://doi.org/10.3390/s21123973
Codeluppi G, Davoli L, Ferrari G. Forecasting Air Temperature on Edge Devices with Embedded AI. Sensors. 2021; 21(12):3973. https://doi.org/10.3390/s21123973
Chicago/Turabian StyleCodeluppi, Gaia, Luca Davoli, and Gianluigi Ferrari. 2021. "Forecasting Air Temperature on Edge Devices with Embedded AI" Sensors 21, no. 12: 3973. https://doi.org/10.3390/s21123973
APA StyleCodeluppi, G., Davoli, L., & Ferrari, G. (2021). Forecasting Air Temperature on Edge Devices with Embedded AI. Sensors, 21(12), 3973. https://doi.org/10.3390/s21123973








