Optimization of Fiber Bragg Gratings Inscribed in Thin Films Deposited on D-Shaped Optical Fibers
Abstract
:1. Introduction
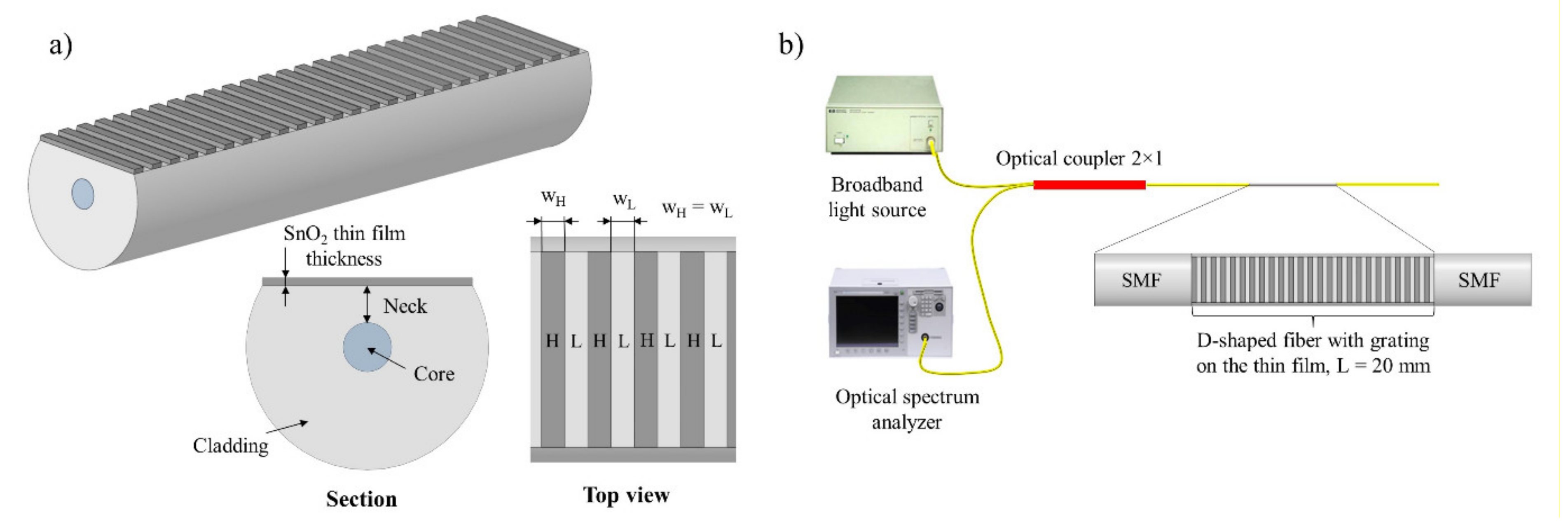
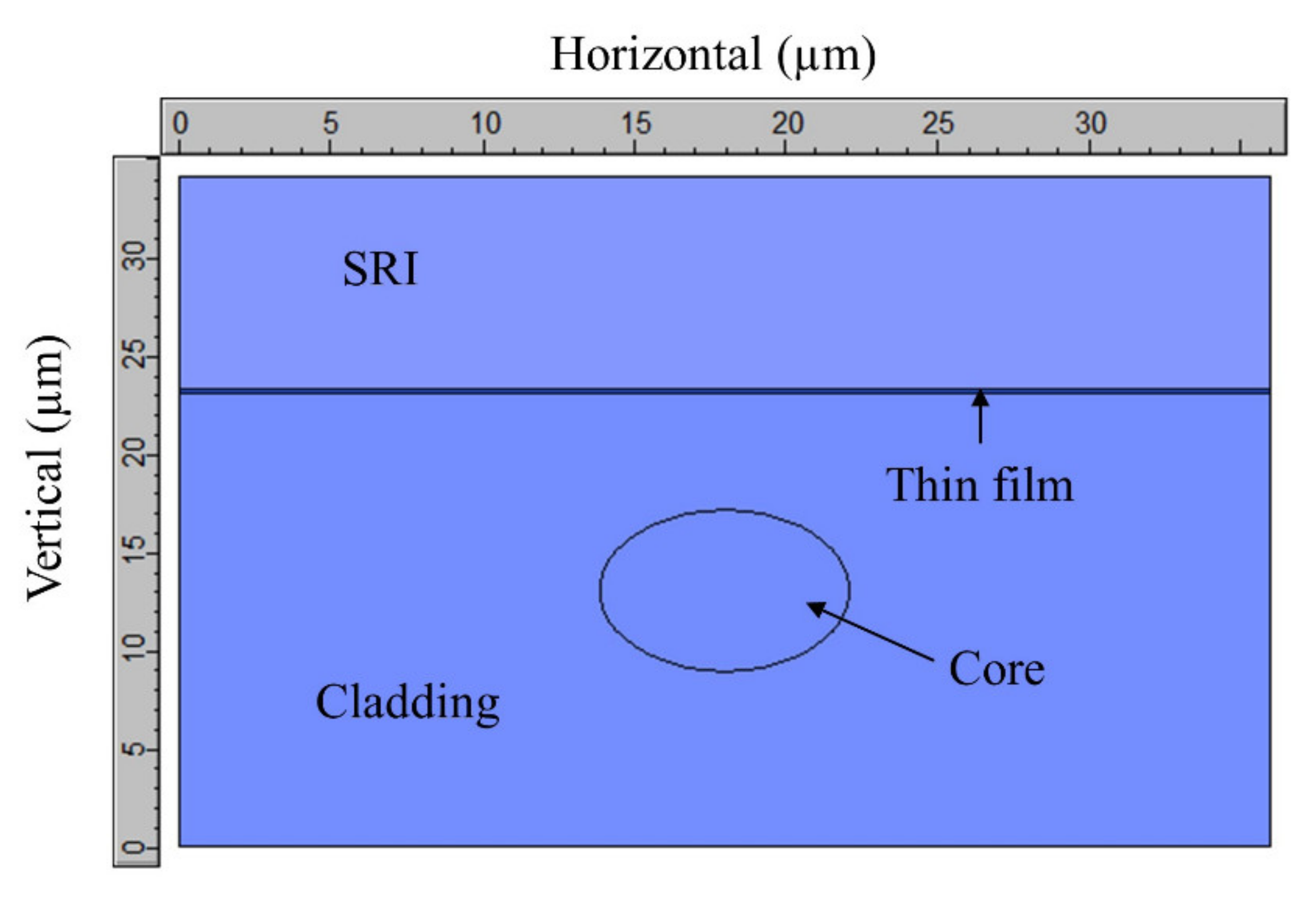
2. Theory
3. Results
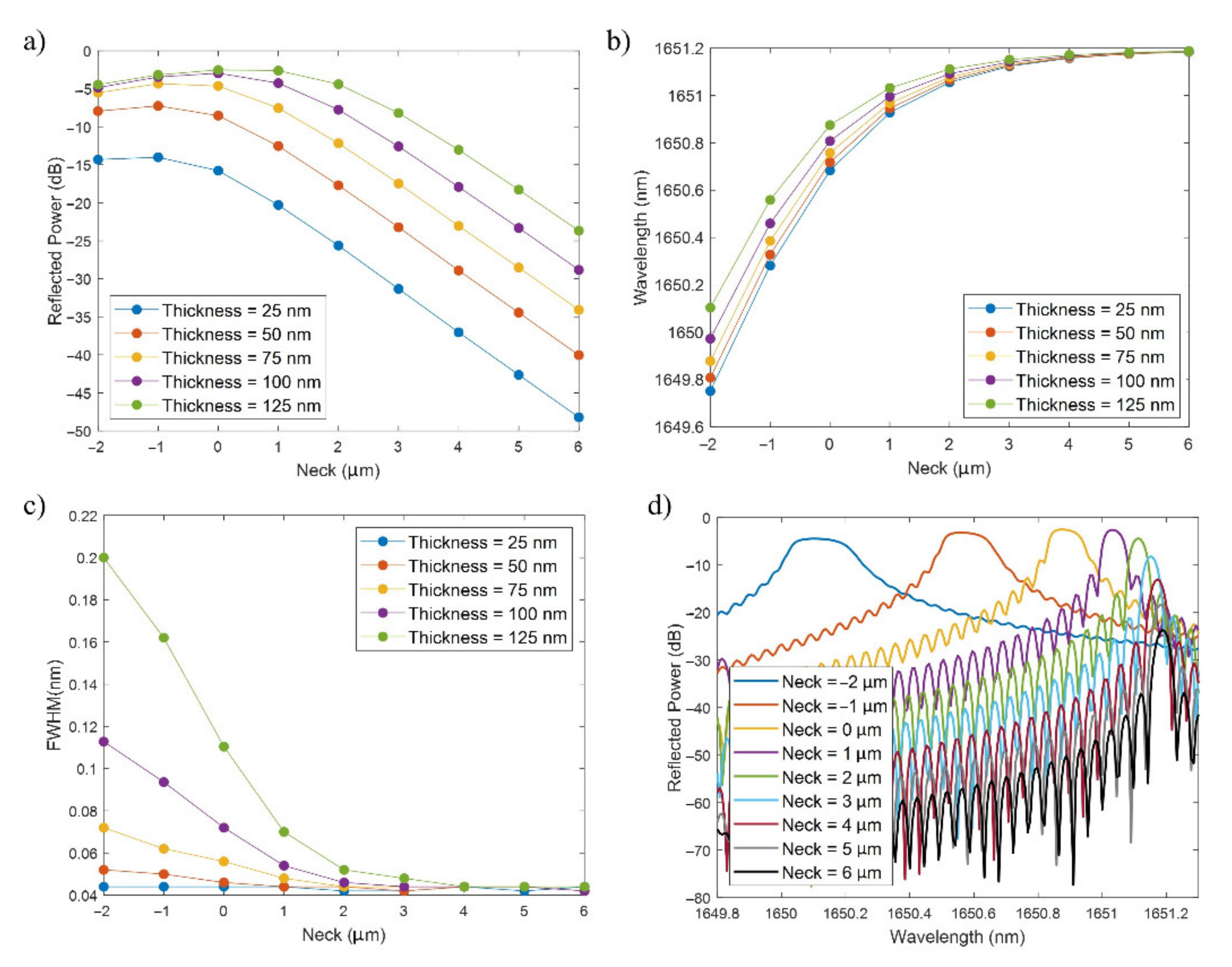
3.1. Study of the FBGs Bands for Variations of the Thin Film Thickness and the Neck
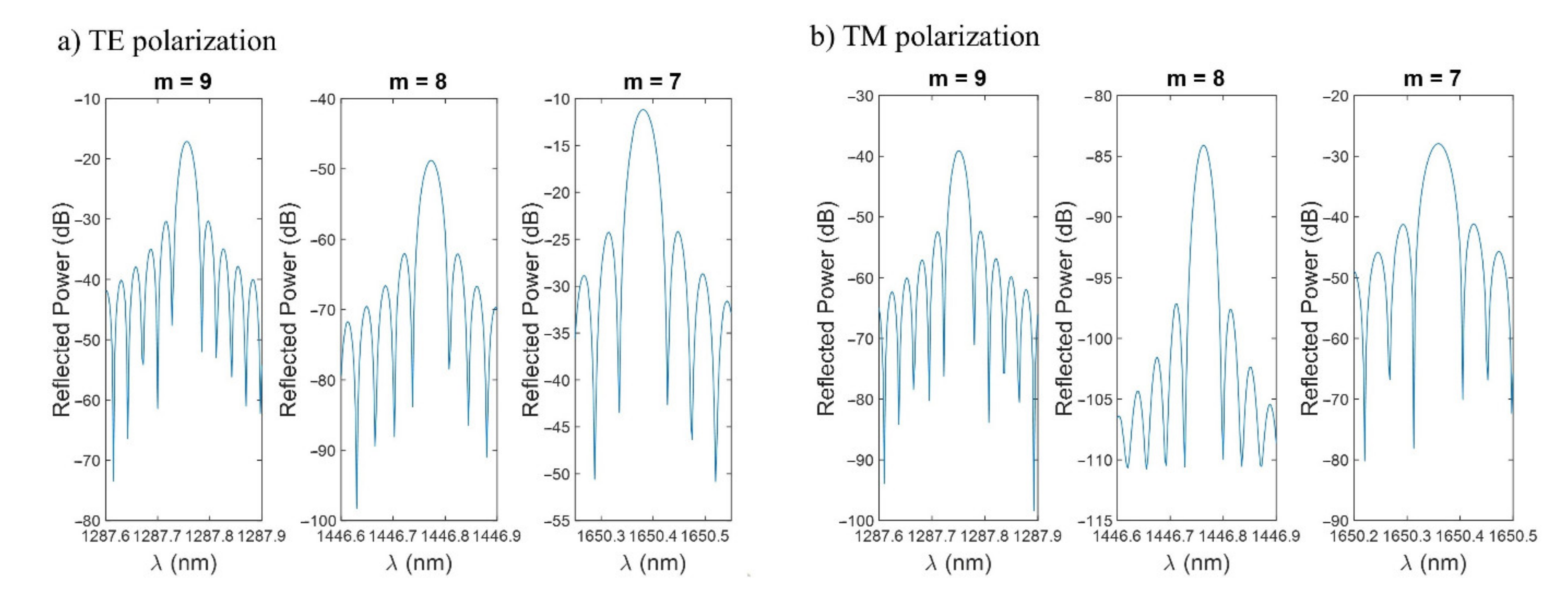
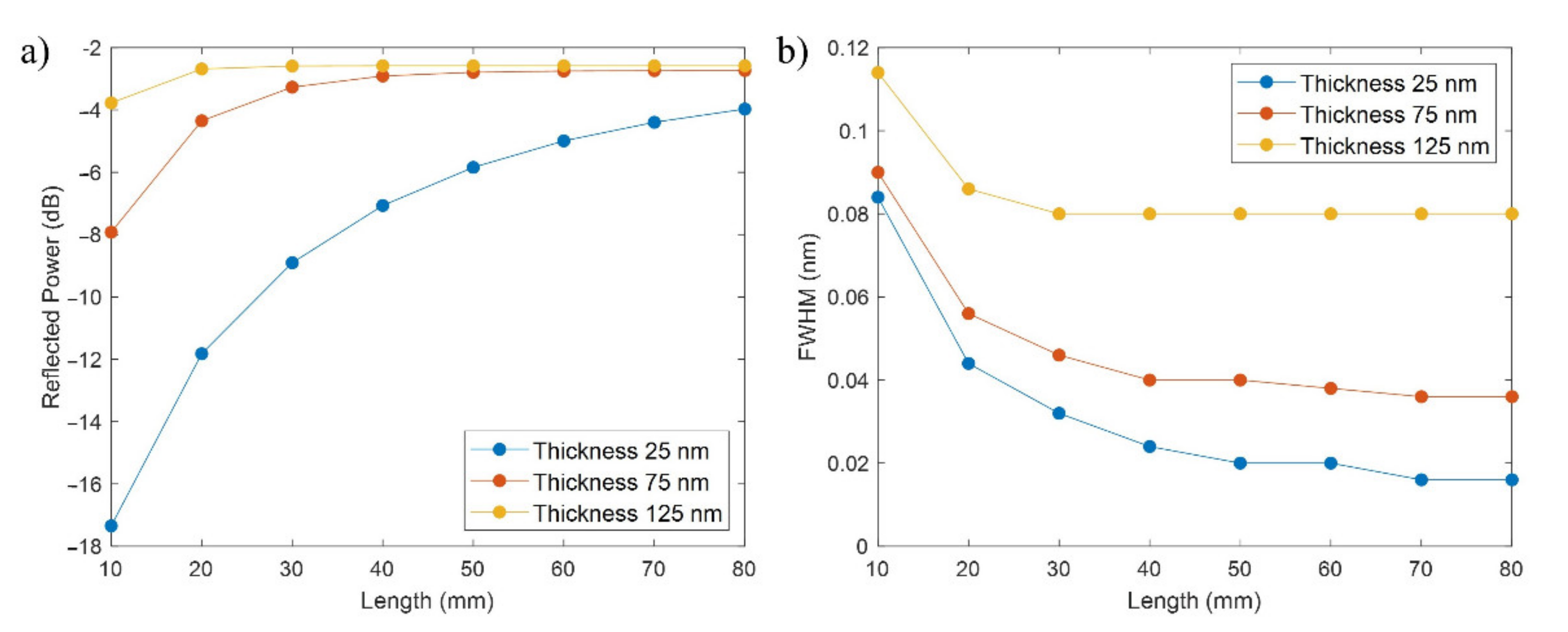
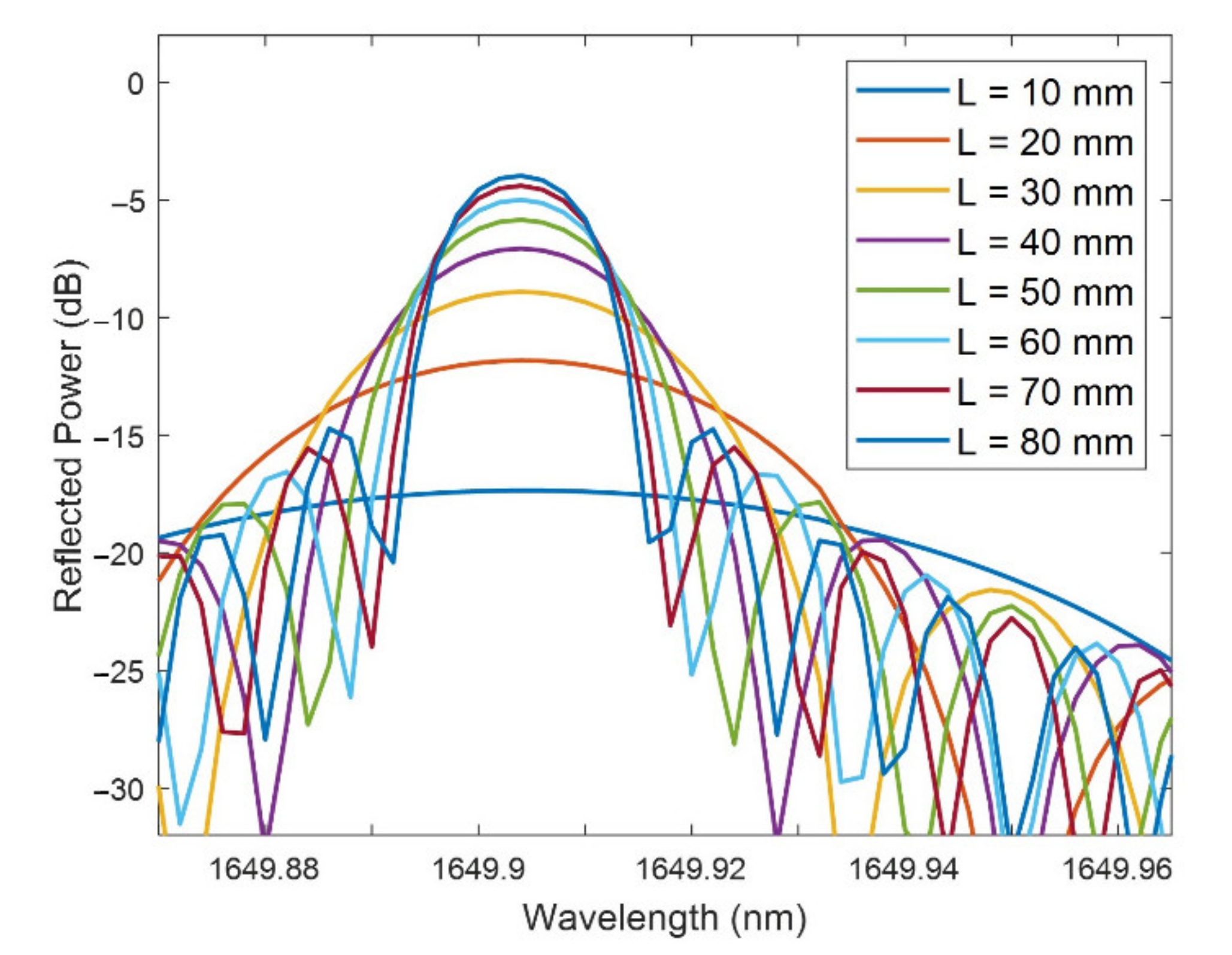
3.2. Study of the FBGs Bands for Variations of the Length of the D-Shaped Zone
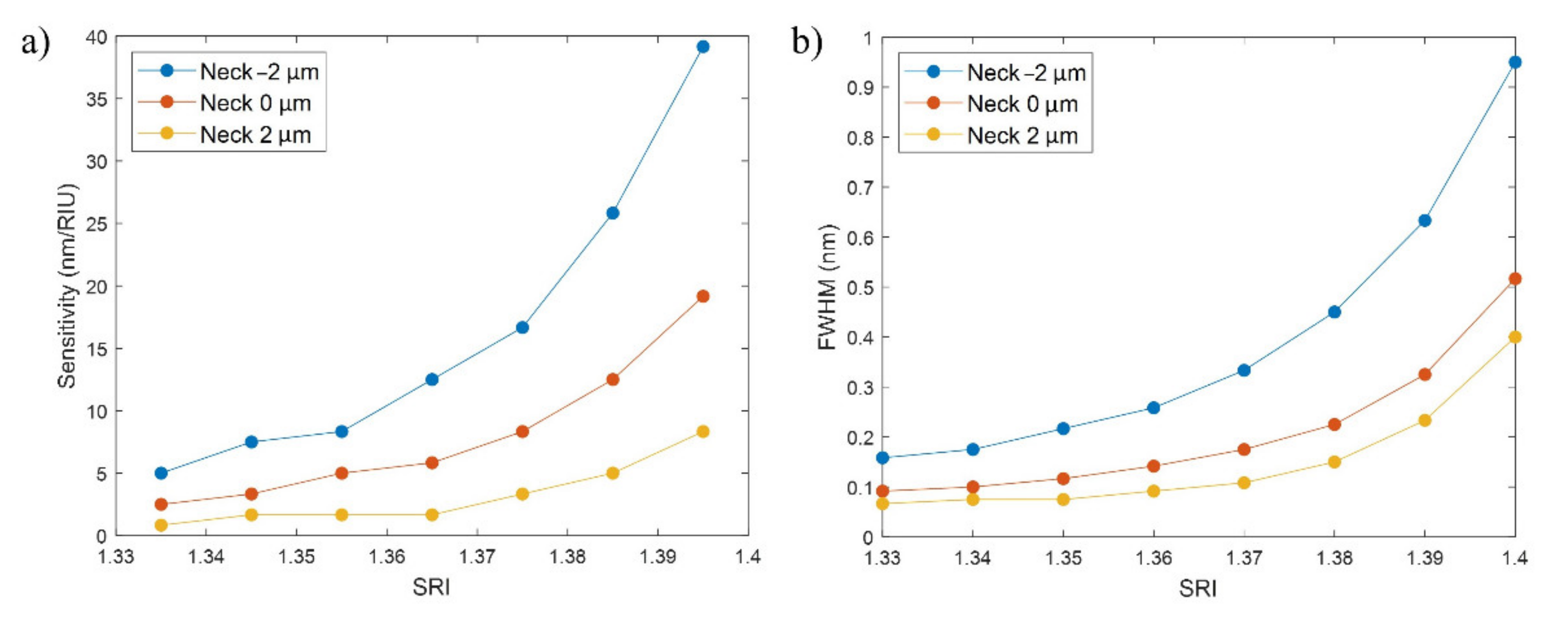
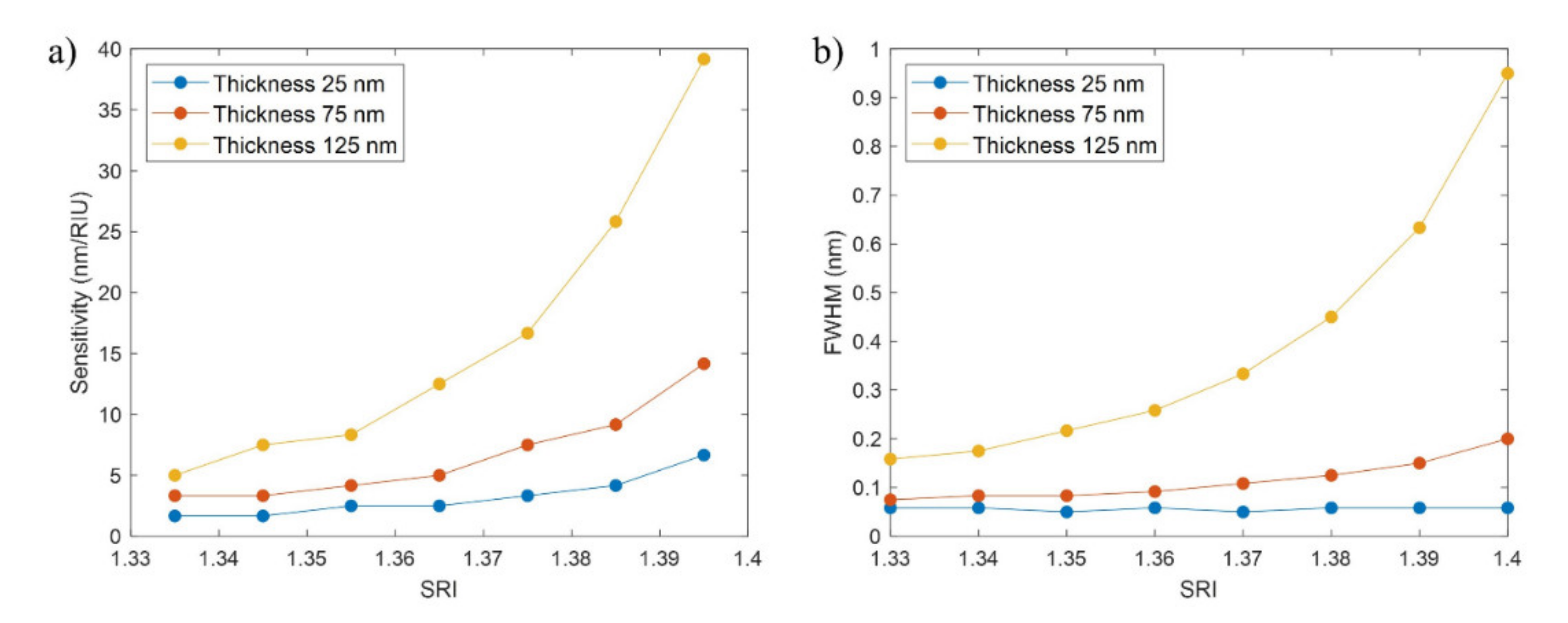
3.3. Study of the FBGs Bands for Variations of the SRI
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hill, K.O.; Meltz, G. Fiber bragg grating technology fundamentals and overview. J. Light. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef] [Green Version]
- Urrutia, A.; Del Villar, I.; Zubiate, P.; Zamarreño, C.R. A comprehensive review of optical fiber refractometers: Toward a standard comparative criterion. Laser Photon. Rev. 2019, 13, 1900094. [Google Scholar] [CrossRef]
- Erdogan, T. Cladding-mode resonances in short- and long-period fiber gratings filters. J. Opt. Soc. Am. A 1997, 14, 1760–1773. [Google Scholar] [CrossRef]
- Albert, J.; Shao, L.-Y.; Caucheteur, C. Tilted fiber Bragg grating sensors. Laser Photon. Rev. 2012, 7, 83–108. [Google Scholar] [CrossRef]
- Libish, T.M.; Radhakrishnan, P. Design and Development of Fiber Grating Based Chemical and Bio-Sensors: Chapter 5. Fabrication of Etched FBGs and Refractive Index Sensing. Ph.D. Thesis, Cochin University of Science and Technology, Kerala, India, 2015. [Google Scholar]
- Gupta, B.D.; Kant, R. Recent advances in surface plasmon resonance based fiber optic chemical and biosensors utilizing bulk and nanostructures. Opt. Laser Technol. 2018, 101, 144–161. [Google Scholar] [CrossRef]
- Sharma, A.K.; Marques, C. Design and performance perspectives on fiber optic sensors with plasmonic nanostructures and gratings: A review. IEEE Sens. J. 2019, 19, 7168–7178. [Google Scholar] [CrossRef]
- Wei, W.; Nong, J.; Zhang, G.; Tang, L.; Jiang, X.; Chen, N.; Luo, S.; Lan, G.; Zhu, Y. Graphene-based long-period fiber grating surface plasmon resonance sensor for high-sensitivity gas sensing. Sensors 2016, 17, 2. [Google Scholar] [CrossRef] [PubMed]
- Pandey, A.K.; Sharma, A.K.; Marques, C. On the application of siO2/SiC grating on ag for high-performance fiber optic plasmonic sensing of cortisol concentration. Materials 2020, 13, 1623. [Google Scholar] [CrossRef] [Green Version]
- Ying, Y.; Si, G.-Y.; Luan, F.-J.; Xu, K.; Qi, Y.-W.; Li, H.-N. Recent research progress of optical fiber sensors based on D-shaped structure. Opt. Laser Technol. 2017, 90, 149–157. [Google Scholar] [CrossRef]
- Li, S.; Liu, J.; Zheng, Z.; Wan, Y.; Kong, W.; Sun, Y. Highly sensitive, bloch surface wave D-type fiber sensor. IEEE Sens. J. 2015, 16, 1200–1204. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, F.; Guo, T.; Guan, B.-O.; Peng, G.-D.; Albert, J. Evanescently coupled optical fiber refractometer based a tilted fiber Bragg grating and a D-shaped fiber. Opt. Express 2015, 23, 20971–20976. [Google Scholar] [CrossRef] [PubMed]
- Quero, G.; Crescitelli, A.; Paladino, D.; Consales, M.; Buosciolo, A.; Giordano, M.; Cutolo, A.; Cusano, A. Evanescent wave long-period fiber grating within D-shaped optical fibers for high sensitivity refractive index detection. Sens. Actuators B Chem. 2011, 152, 196–205. [Google Scholar] [CrossRef]
- Smith, K.H.; Ipson, B.L.; Lowder, T.L.; Hawkins, A.R.; Selfridge, R.H.; Schultz, S.M. Surface-relief fiber Bragg gratings for sensing applications. Appl. Opt. 2006, 45, 1669–1675. [Google Scholar] [CrossRef] [PubMed]
- Lowder, T.L.; Gordon, J.D.; Schultz, S.M.; Selfridge, R.H. Volatile organic compound sensing using a surface-relief D-shaped fiber Bragg grating and a polydimethylsiloxane layer. Opt. Lett. 2007, 32, 2523–2525. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.; Wang, Q.; Xu, L.; Liu, S.; He, J.; Zhao, J.; Li, Z.; Wang, Y. D-shaped fiber grating refractive index sensor induced by an ultrashort pulse laser. Appl. Opt. 2016, 55, 1525–1529. [Google Scholar] [CrossRef]
- Chiavaioli, F.; Baldini, F.; Tombelli, S.; Trono, C.; Giannetti, A. Biosensing with optical fiber gratings. Nanophotonics 2017, 6, 663–679. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, Y.; Guo, Z.; Wu, X. Design for distributed feedback laser biosensors based on the active grating model. Sensors 2019, 19, 2569. [Google Scholar] [CrossRef] [Green Version]
- Lu, M.; Choi, S.S.; Ge, C.; Wagner, C.J.; Eden, J.G.; Cunningham, B.T. Design and implementation of vertically emitting distributed feedback lasers for biological sensing. In Label-Free Technologies for Drug Discovery; John Wiley and Sons: Hoboken, NJ, USA, 2011; pp. 27–40. [Google Scholar]
- Arregui, F.J.; Del Villar, I.; Zamarreño, C.R.; Zubiate, P.; Matias, I.R. Giant sensitivity of optical fiber sensors by means of lossy mode resonance. Sens. Actuators B Chem. 2016, 232, 660–665. [Google Scholar] [CrossRef] [Green Version]
- Burnat, D.; Koba, M.; Wachnicki, Ł.; Gierałtowska, S.; Godlewski, M.; Śmietana, M. Refractive index sensitivity of optical fiber lossy-mode resonance sensors based on atomic layer deposited TiO x thin overlay. In Proceedings of the Sixth European Workshop on Optical Fibre Sensors; SPIE: Bellingham, WA, USA, 2016; Volume 9916, p. 99161G. [Google Scholar]
- Wang, Q.; Li, X.; Zhao, W.M.; Jin, S. Lossy mode resonance-based fiber optic sensor using layer-by-layer SnO2 thin film and SnO2 nanoparticles. Appl. Surf. Sci. 2019, 492, 374–381. [Google Scholar] [CrossRef]
- Pavlichenko, I.; Exner, A.T.; Guehl, M.; Lugli, P.; Scarpa, G.; Lotsch, B.V. Humidity-enhanced thermally tunable TiO2/SiO2 Bragg stacks. J. Phys. Chem. C 2012, 116, 298–305. [Google Scholar] [CrossRef]
- Del Villar, I.; Arregui, F.J.; Zamarreño, C.R.; Corres, J.M.; Bariain, C.; Goicoechea, J.; Elosua, C.; Hernaez, M.; Rivero, P.J.; Socorro, A.B.; et al. Optical sensors based on lossy-mode resonances. Sens. Actuators B Chem. 2017, 240, 174–185. [Google Scholar] [CrossRef]
- Chiavaioli, F.; Zubiate, P.; Del Villar, I.; ZamarrenÌo, C.R.; Giannetti, A.; Tombelli, S.; Trono, C.; Arregui, F.J.; Matias, I.R.; Baldini, F. Femtomolar detection by nanocoated fiber label-free biosensors. ACS Sens. 2018, 3, 936–943. [Google Scholar] [CrossRef]
- Zubiate, P.; Urrutia, A.; Zamarreño, C.R.; Egea-Urra, J.; Fernández-Irigoyen, J.; Giannetti, A.; Baldini, F.; Díaz, S.; Matias, I.R.; Arregui, F.J.; et al. Fiber-based early diagnosis of venous thromboembolic disease by label-free D-dimer detection. Biosens. Bioelectron. X 2019, 2, 100026. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Del Villar, I.; Matías, I.R.; Arregui, F.J.; Lalanne, P. Optimization of sensitivity in Long Period Fiber Gratings with overlay deposition. Opt. Express 2005, 13, 56–69. [Google Scholar] [CrossRef] [Green Version]
- Cusano, A.; Iadicicco, A.; Pilla, P.; Contessa, L.; Campopiano, S.; Cutolo, A.; Giordano, M. Mode transition in high refractive index coated long period gratings. Opt. Express 2006, 14, 19. [Google Scholar] [CrossRef] [PubMed]
- Del Villar, I.; Cruz, J.L.; Socorro, A.B.; Corres, J.M.; Matias, I.R. Sensitivity optimization with cladding-etched long period fiber gratings at the dispersion turning point. Opt. Express 2016, 24, 17680. [Google Scholar] [CrossRef] [PubMed] [Green Version]
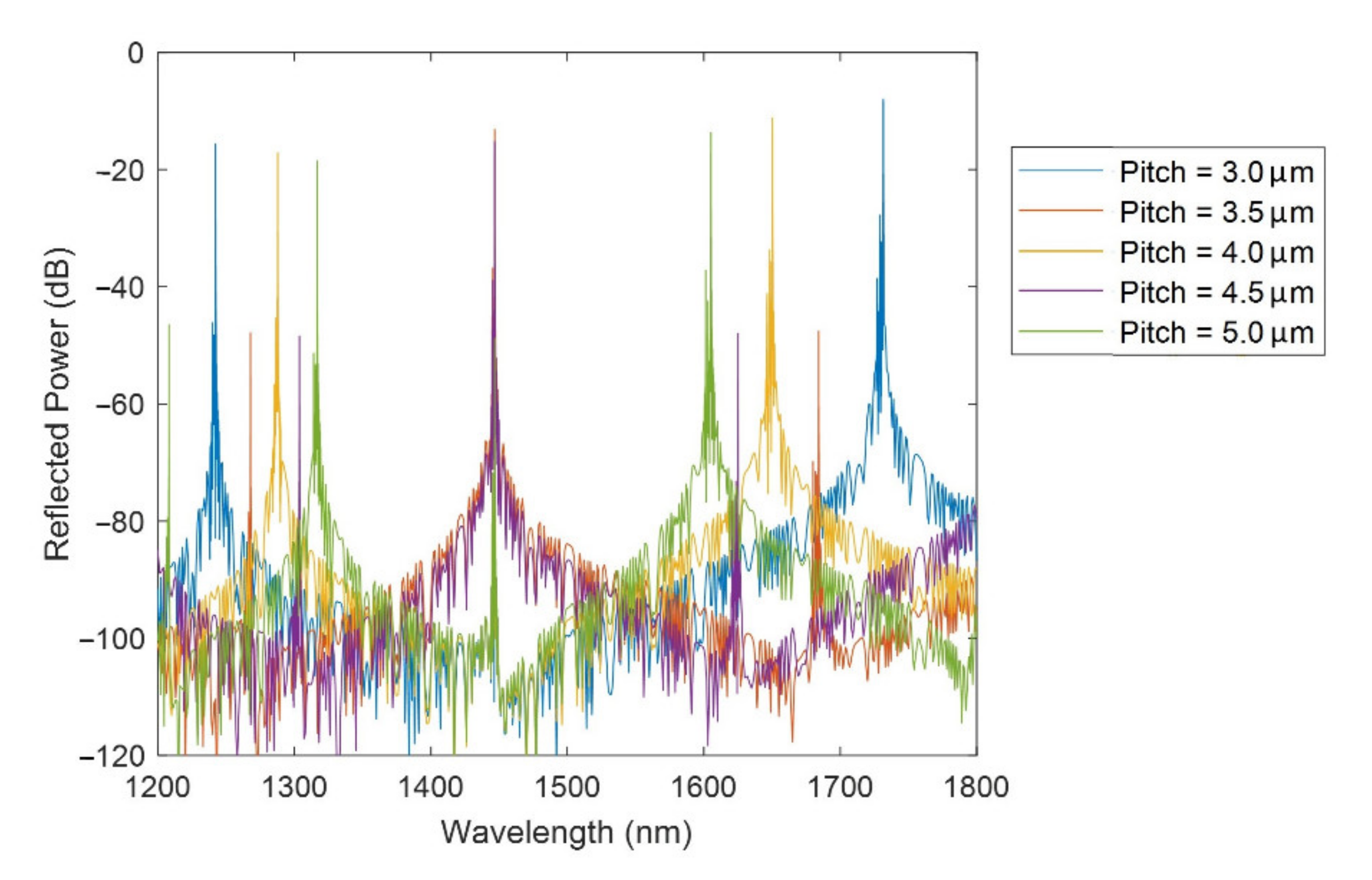


| Theoretical Wavelengths (nm) | Simulated Wavelengths (nm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| m | Pitch 3.0 µm | Pitch 3.5 µm | Pitch 4.0 µm | Pitch 4.5 µm | Pitch 5.0 µm | Pitch 3.0 µm | Pitch 3.5 µm | Pitch 4.0 µm | Pitch 4.5 µm | Pitch 5.0 µm |
| 5 | 1728 | 1731.54 | ||||||||
| 6 | 1440 | 1680 | 1446.76 | 1684.22 | ||||||
| 7 | 1234 | 1440 | 1646 | 1242.23 | 1446.77 | 1650.39 | ||||
| 8 | 1260 | 1440 | 1620 | 1800 | 1267.84 | 1446.77 | 1624.99 | 1802.40 | ||
| 9 | 1280 | 1440 | 1600 | 1287.76 | 1446.77 | 1605.21 | ||||
| 10 | 1296 | 1440 | 1303.69 | 1446.78 | ||||||
| 11 | 1309 | 1316.72 | ||||||||
| 12 | 1200 | 1208.06 | ||||||||
| SRI | Neck −2 µm | Neck 0 µm | Neck 2 µm |
|---|---|---|---|
| 1.34 | 30.00 | 26.08 | 11.76 |
| 1.40 | 49.47 | 45.54 | 26.31 |
| SRI | Thin Film Thickness | ||
|---|---|---|---|
| 25 nm | 75 nm | 125 nm | |
| 1.34 | 28.57 | 42.10 | 30.00 |
| 1.40 | 114.29 | 80.95 | 49.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imas, J.J.; Zamarreño, C.R.; del Villar, I.; Matías, I.R. Optimization of Fiber Bragg Gratings Inscribed in Thin Films Deposited on D-Shaped Optical Fibers. Sensors 2021, 21, 4056. https://doi.org/10.3390/s21124056
Imas JJ, Zamarreño CR, del Villar I, Matías IR. Optimization of Fiber Bragg Gratings Inscribed in Thin Films Deposited on D-Shaped Optical Fibers. Sensors. 2021; 21(12):4056. https://doi.org/10.3390/s21124056
Chicago/Turabian StyleImas, José Javier, Carlos R. Zamarreño, Ignacio del Villar, and Ignacio R. Matías. 2021. "Optimization of Fiber Bragg Gratings Inscribed in Thin Films Deposited on D-Shaped Optical Fibers" Sensors 21, no. 12: 4056. https://doi.org/10.3390/s21124056
APA StyleImas, J. J., Zamarreño, C. R., del Villar, I., & Matías, I. R. (2021). Optimization of Fiber Bragg Gratings Inscribed in Thin Films Deposited on D-Shaped Optical Fibers. Sensors, 21(12), 4056. https://doi.org/10.3390/s21124056









