A Fusion Algorithm for Estimating Time-Independent/-Dependent Parameters and States
Abstract
:1. Introduction
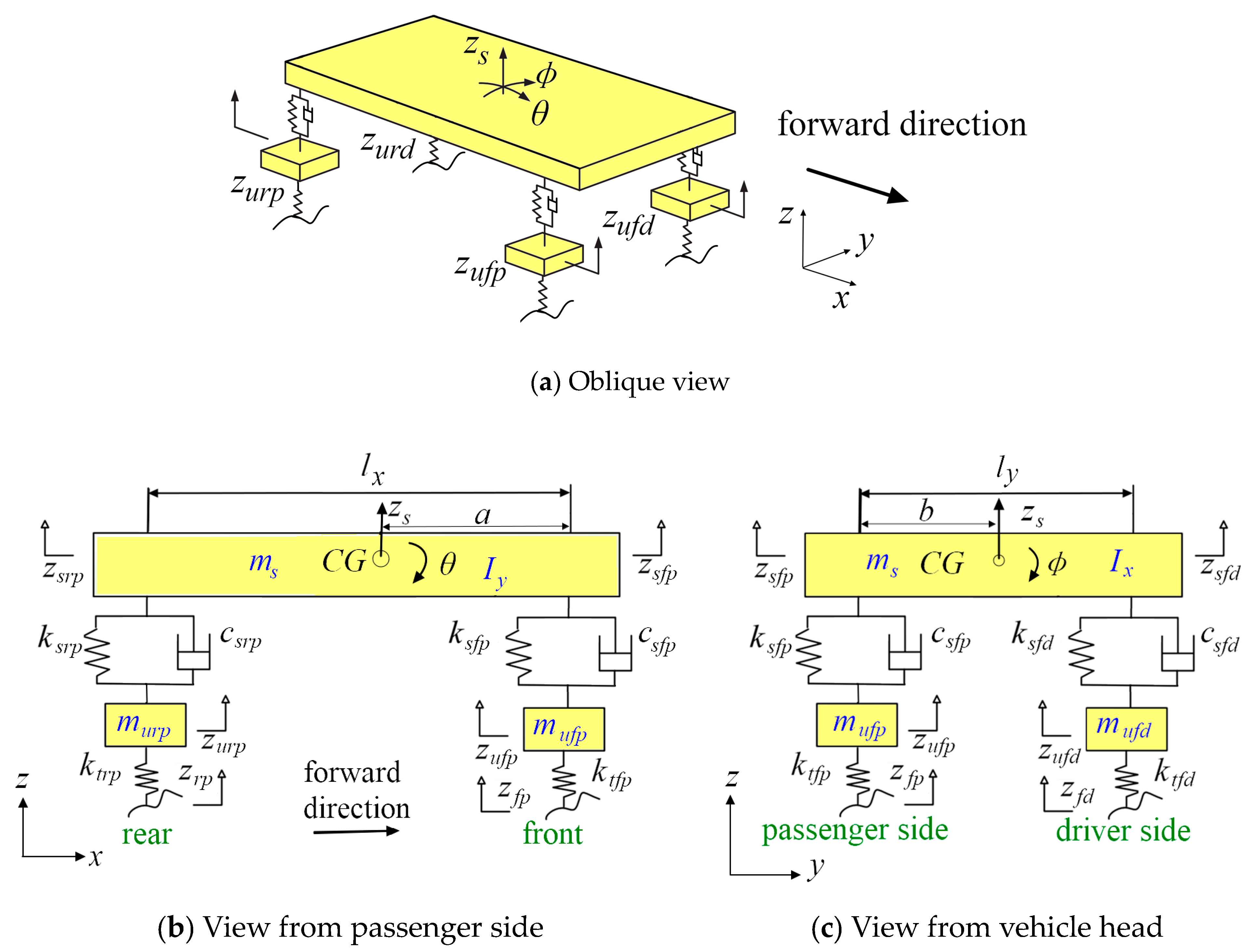
2. Vehicle Model in Vertical and Pitch Dynamics
3. HMSV for Time-Independent Parameters
3.1. State-Variable Method
3.2. Determining Parameters with HMSV Method
4. DUKF for Time-Dependent Parameters and States
4.1. Relationship between Time-Dependent Parameters
4.2. Structure of Dual Unscented Kalman Filter
5. Framework of Proposed Algorithm and Experimental Verification
6. Performance Study of the Proposed Algorithm
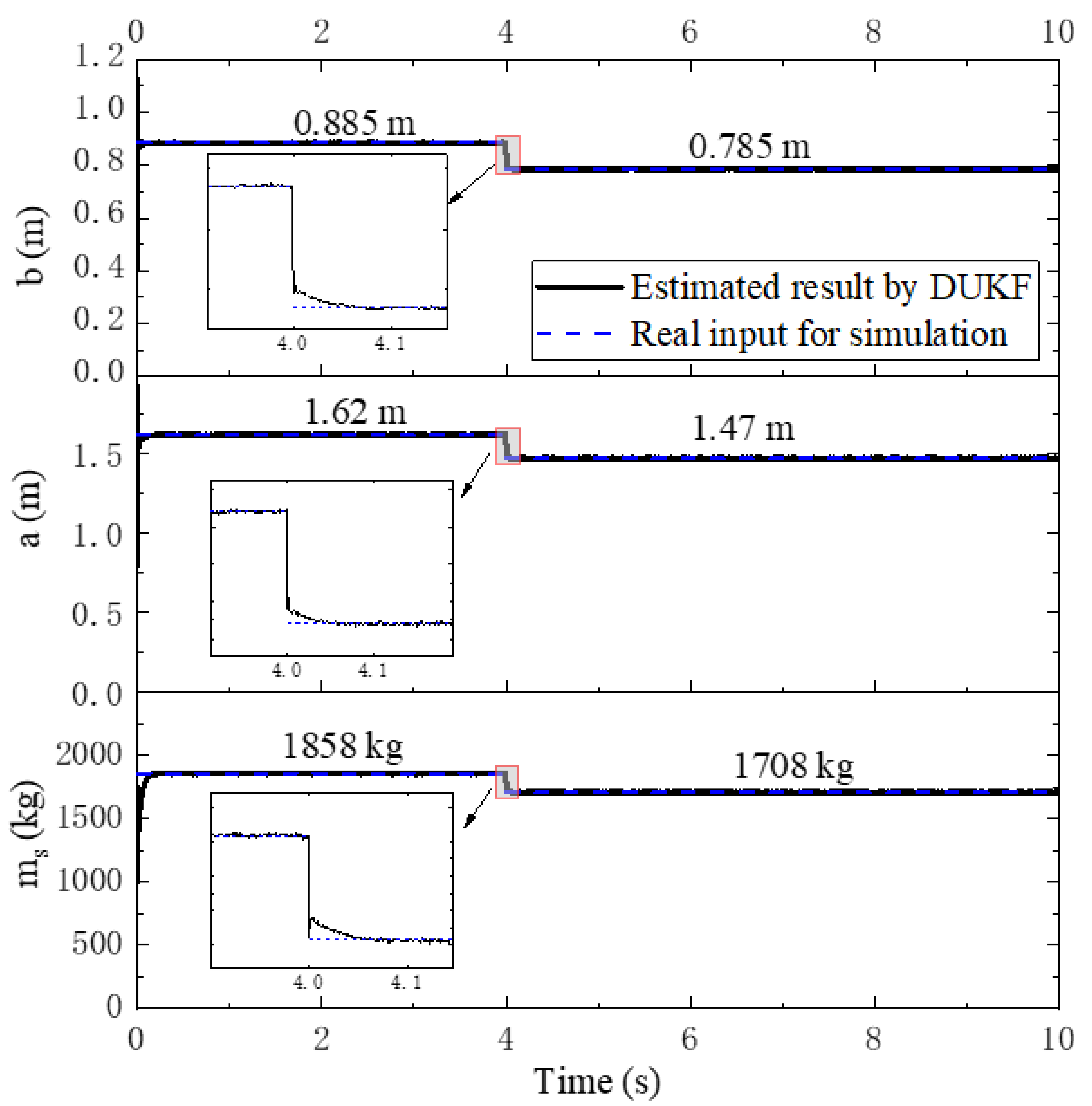
6.1. Sprung Mass Variation
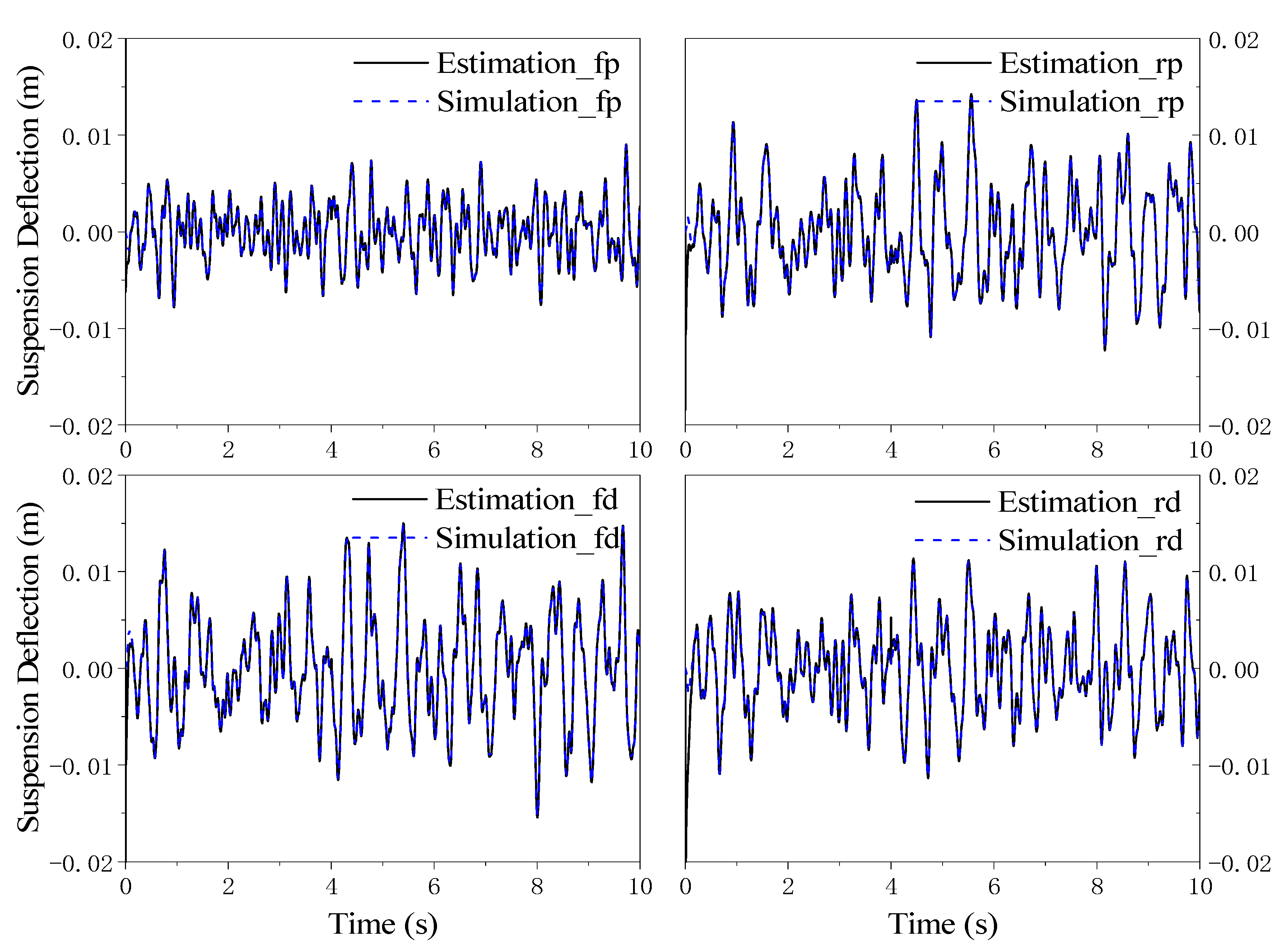
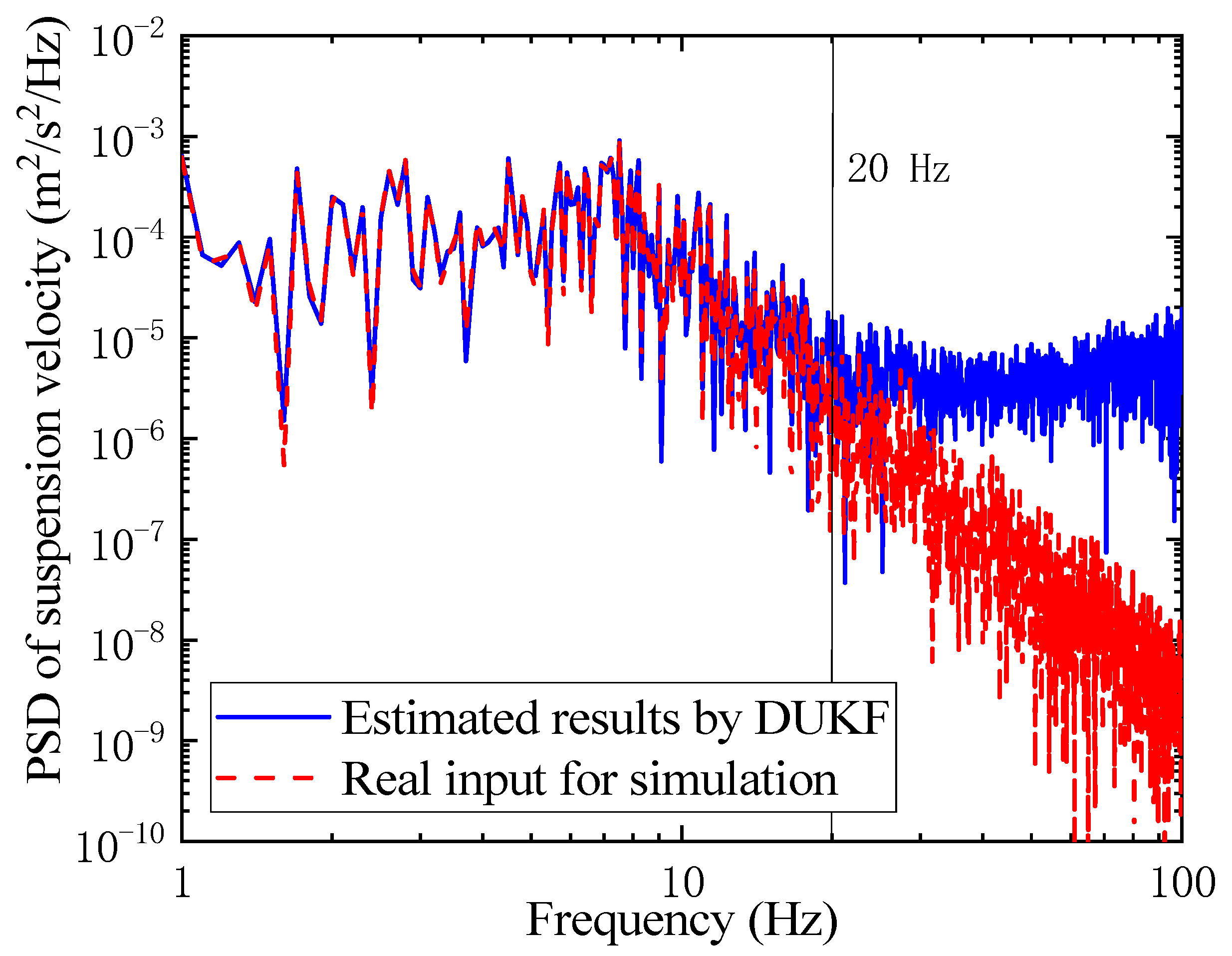
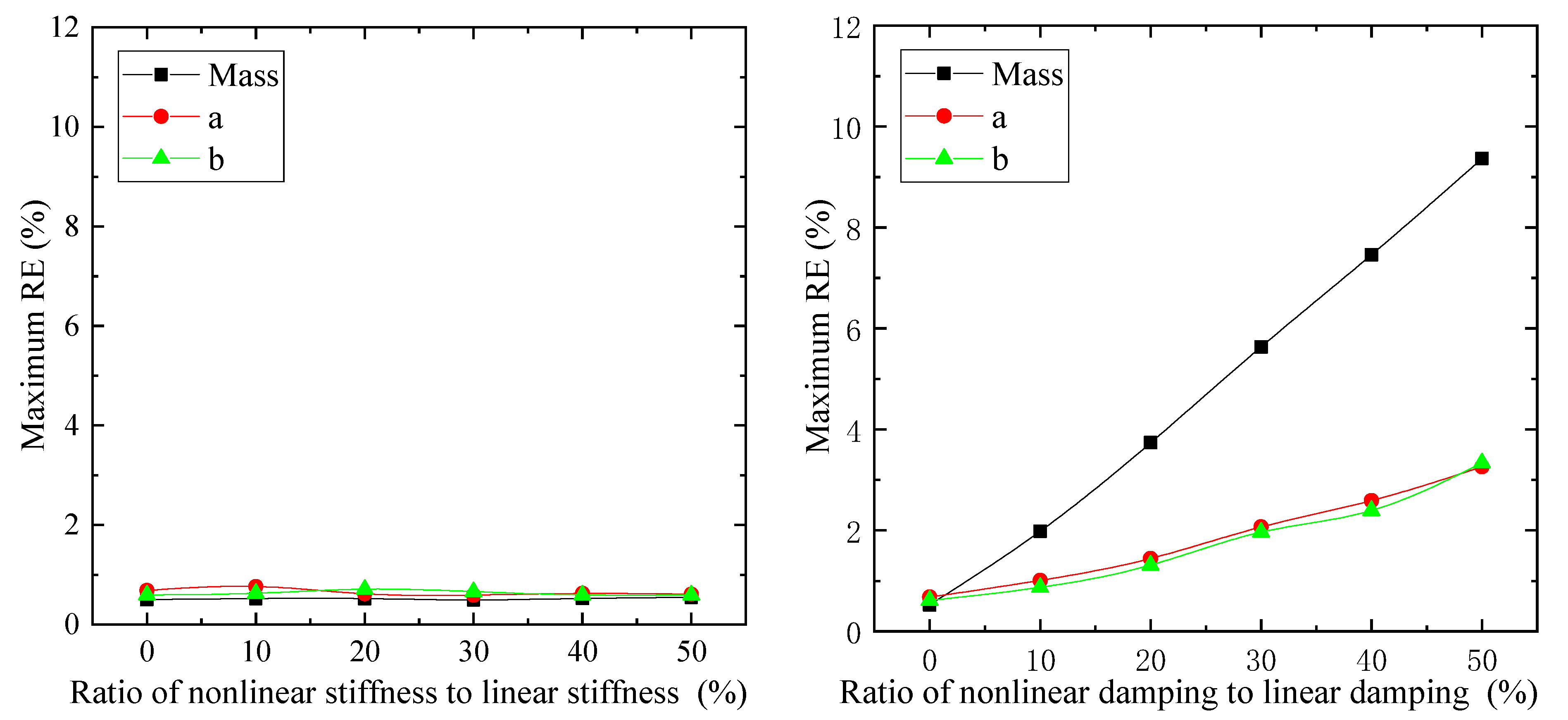
6.2. Effect of Vehicle Model Linearization
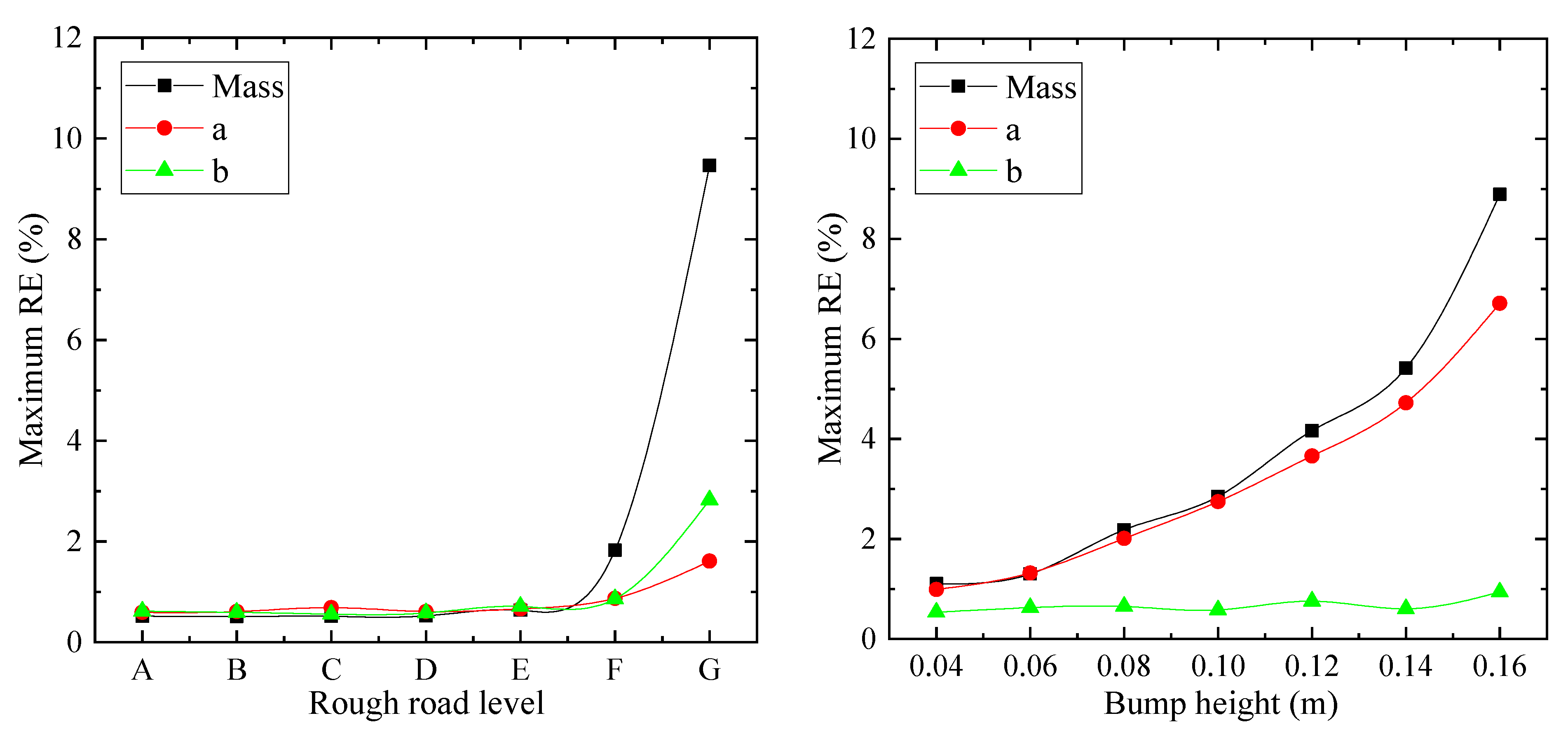
6.3. Performance under Various Road Conditions
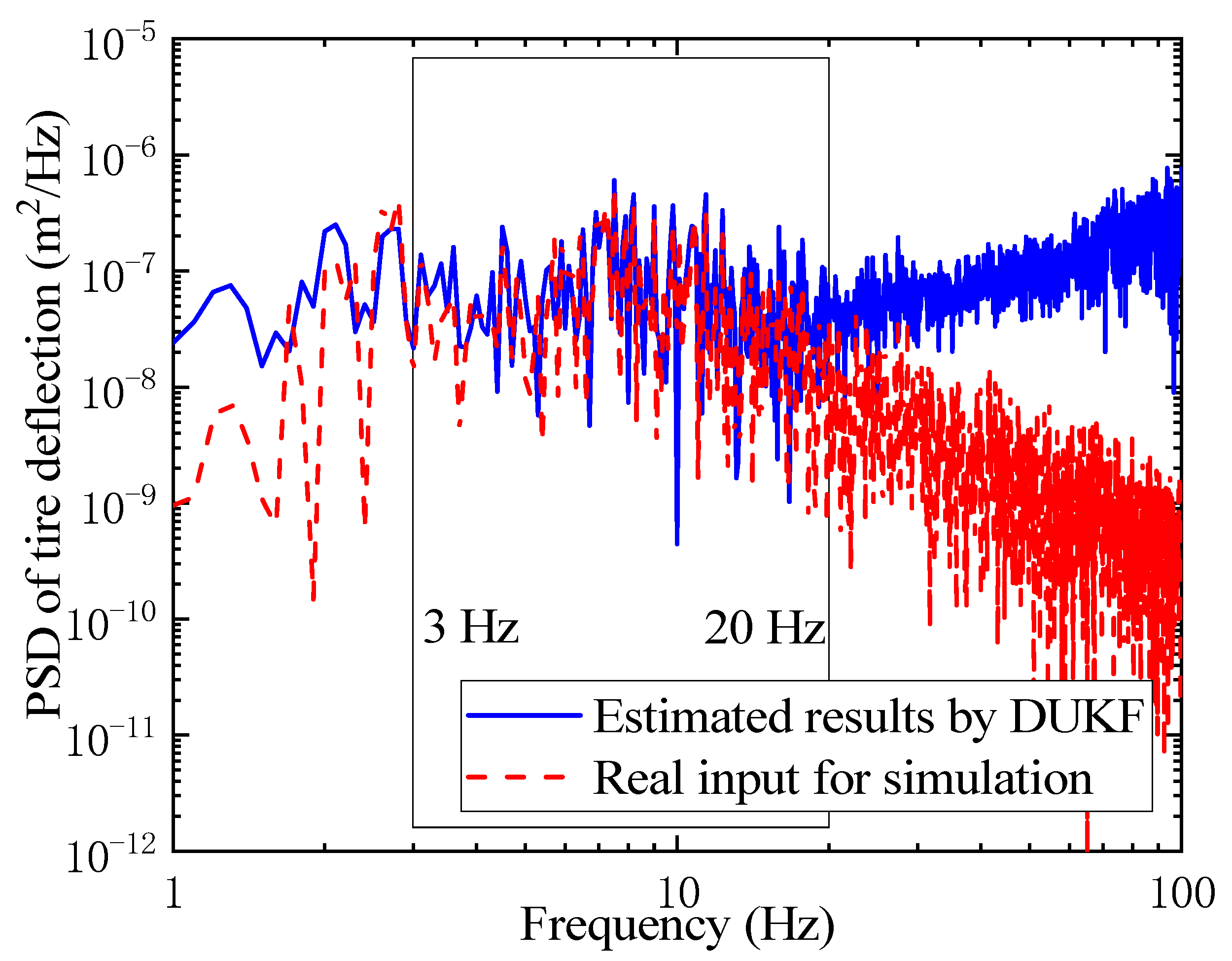
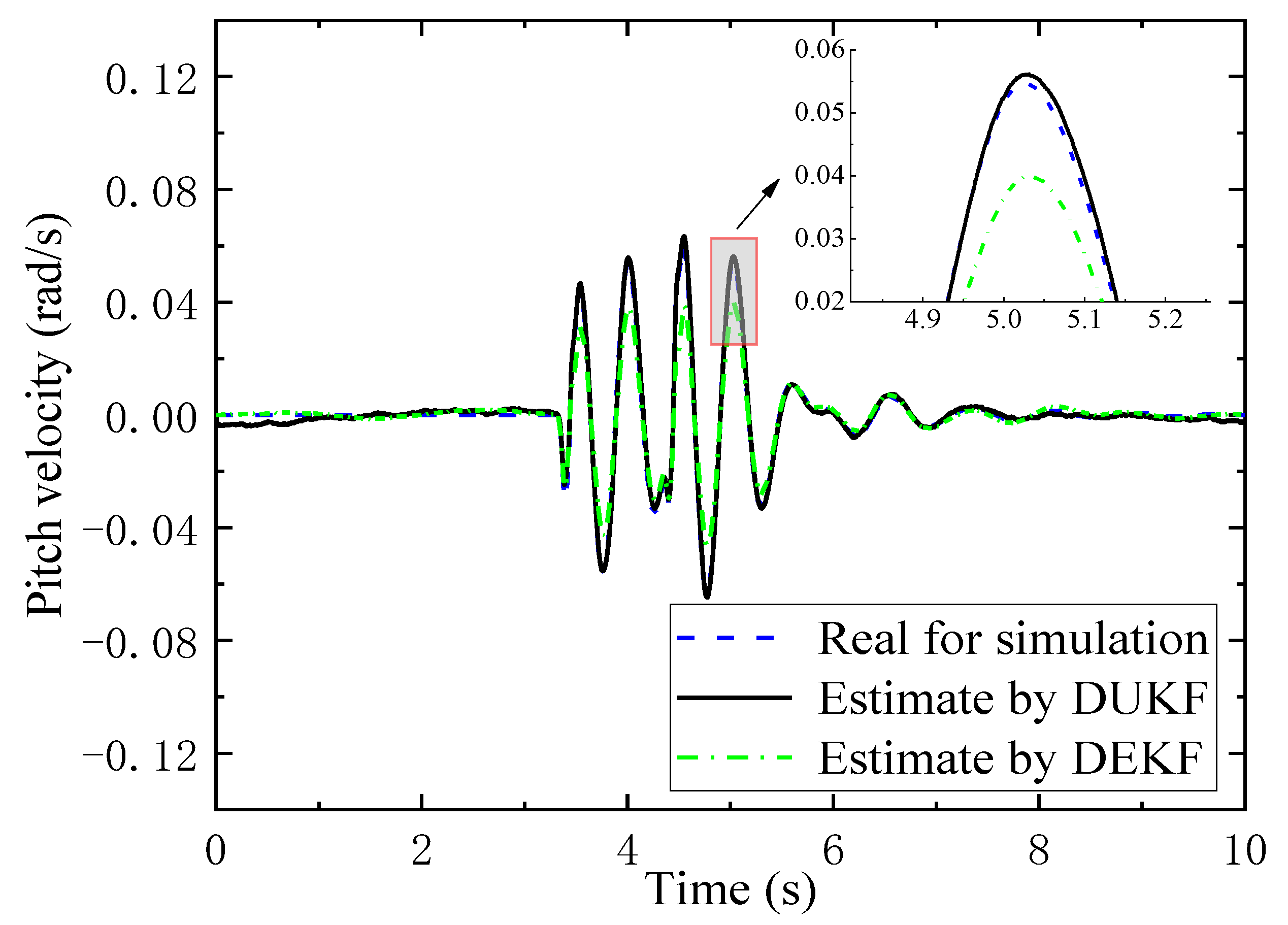
6.4. Feasibility of the Algorithm for Updating TDPs
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Notation | Description |
| Vertical Displacement | |
| Pitch Motion | |
| Roll Motion | |
| Acceleration Vector | |
| Velocity Vector | |
| Displacement Vector | |
| Mass Matrix | |
| Damping Matrix | |
| Stiffness Matrix | |
| Force Matrix | |
| State Vector | |
| Coefficient Matrix | |
| State Matrices | |
| Sampling Interval | |
| Measure Error Matrix | |
| Eigenvalue | |
| Eigenvector | |
| Subscript | |
| Sprung Mass | |
| Unsprung Mass | |
| Front Axle | |
| Real Axle | |
| Driver Side | |
| Passenger Side | |
| External Excitation | |
| Nonlinear Part | |
| New Mass | |
| Superscript | |
| Submatrices | |
| Conjugate Matrices |
Appendix A. Vehicle Parameters
| Parameter | Description | Unit |
|---|---|---|
| Empty sprung mass | kg | |
| Roll MI of empty sprung mass | ||
| Pitch MI of empty sprung mass | ||
| () | Unsprung mass | kg |
| () | Stiffness of suspension spring | N/m |
| () | Stiffness of tire | N/m |
| () | Damping of suspension | |
| Axle distance | m | |
| Wheel distance at same axle | m | |
| Distance from CG to front axle for empty vehicle | m | |
| Distance from CG to passenger side wheel line for empty vehicle | m |
| Parameter | Description | Unit |
|---|---|---|
| Total sprung mass | kg | |
| Additional sprung mass | kg | |
| Roll MI of real-time sprung mass | ||
| Pitch MI of real-time sprung mass | ||
| Distance from real-time CG to front axle | m | |
| Distance from real-time CG to passenger side wheel line | m |
Appendix B. Unscented Transform
Appendix C. Formulas of the DUKF
References
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Heidarrezaei, M.; Rahimian Koloor, S.S.; Petrů, M. A review on vehicle classification and potential use of smart vehicle-assisted techniques. Sensors 2020, 20, 3274. [Google Scholar] [CrossRef]
- Zhang, Z.; Dhanasekar, M.; Ling, L.; Thambiratnam, D.P. Effectiveness of a raised road: Rail crossing for the safety of road vehicle occupants. Eng. Fail. Anal. 2019, 97, 258–273. [Google Scholar] [CrossRef]
- Hsu, L.-Y.; Chen, T.-L. Vehicle dynamic prediction systems with on-line identification of vehicle parameters and road conditions. Sensors 2012, 12, 15778–15800. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.; Li, L.; Chen, C.-J.; Liu, C.-Z.; Hu, G.-D. A low-cost lateral active suspension system of the high-speed train for ride quality based on the resonant control method. IEEE Trans. Ind. Electron. 2017, 65, 4187–4196. [Google Scholar] [CrossRef]
- Gao, L.; Xiong, L.; Lin, X.; Xia, X.; Liu, W.; Lu, Y.; Yu, Z. Multi-sensor fusion road friction coefficient estimation during steering with lyapunov method. Sensors 2019, 19, 3816. [Google Scholar] [CrossRef] [Green Version]
- Zagorski, S.; Heydinger, G.; Coyle, J.; Jebode, M. Measured vehicle inertial parameters–NHTSA’s data through June 2020. SAE Technical Paper No. 2021-01-0970. 2021. Available online: https://saemobilus.sae.org/content/2021-01-0970/ (accessed on 12 June 2021).
- Zheng, M.; Zhang, B.; Zhang, J.; Zhang, N. Physical parameter identification method based on modal analysis for two-axis on-road vehicles: Theory and simulation. Chin. J. Mech. Eng. 2016, 29, 756–764. [Google Scholar] [CrossRef]
- Zheng, M.; Peng, P.; Zhang, B.; Zhang, N.; Wang, L.; Chen, Y. A new physical parameter identification method for two-axis on-road vehicles: Simulation and experiment. Shock. Vib. 2015, 2015, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Rozyn, M.; Zhang, N. A method for estimation of vehicle inertial parameters. Veh. Syst. Dyn. 2010, 48, 547–565. [Google Scholar] [CrossRef]
- Bae, H.S.; Ryu, J.; Gerdes, J.C. Road grade and vehicle parameter estimation for longitudinal control using GPS. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Oakland, CA, USA, 25–29 August 2001; pp. 25–29. [Google Scholar]
- Vahidi, A.; Stefanopoulou, A.; Peng, H. Recursive least squares with forgetting for online estimation of vehicle mass and road grade: Theory and experiments. Veh. Syst. Dyn. 2005, 43, 31–55. [Google Scholar] [CrossRef]
- Lin, N.; Zong, C.; Shi, S. The method of mass estimation considering system error in vehicle longitudinal dynamics. Energies 2018, 12, 52. [Google Scholar] [CrossRef] [Green Version]
- Kidambi, N.; Pietron, G.M.; Boesch, M.; Fujii, Y.; Wang, K.-W. Accuracy and robustness of parallel vehicle mass and road grade estimation. SAE Int. J. Veh. Dyn. Stability, NVH 2017, 1, 317–325. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, F.; Zhang, N.; Chen, S.; Zhang, B. A New SSUKF observer for sliding mode force tracking H∞ control of electrohydraulic active suspension. Asian J. Control. 2020, 22, 761–778. [Google Scholar] [CrossRef]
- Zhao, B.; Nagayama, T.; Xue, K. Road profile estimation, and its numerical and experimental validation, by smartphone measurement of the dynamic responses of an ordinary vehicle. J. Sound Vib. 2019, 457, 92–117. [Google Scholar] [CrossRef]
- Joa, E.; Yi, K.; Hyun, Y. Estimation of the tire slip angle under various road conditions without tire–road information for vehicle stability control. Control. Eng. Pr. 2019, 86, 129–143. [Google Scholar] [CrossRef]
- Reina, G.; Messina, A. Vehicle dynamics estimation via augmented Extended Kalman Filtering. Measurements 2019, 133, 383–395. [Google Scholar] [CrossRef]
- Salt Ducajú, J.M.; Salt Llobregat, J.J.; Cuenca, Á.; Tomizuka, M. Autonomous ground vehicle lane-keeping lpv model-based control: Dual-rate state estimation and comparison of different real-time control strategies. Sensors 2021, 21, 1531. [Google Scholar] [CrossRef]
- Wenzel, T.A.; Burnham, K.J.; Blundell, M.V.; Williams, R.A. Dual extended Kalman filter for vehicle state and parameter estimation. Veh. Syst. Dyn. 2006, 44, 153–171. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J. Real-time estimation of center of gravity position for lightweight vehicles using combined AKF–EKF method. IEEE Trans. Veh. Technol. 2014, 63, 4221–4231. [Google Scholar] [CrossRef]
- Lin, C.; Gong, X.; Xiong, R.; Cheng, X. A novel H∞ and EKF joint estimation method for determining the center of gravity position of electric vehicles. Appl. Energy 2017, 194, 609–616. [Google Scholar] [CrossRef]
- Cai, L.; Wang, H.; Jia, T.; Peng, P.; Pi, D.; Wang, E. Two-layer structure algorithm for estimation of commercial vehicle mass. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 234, 378–389. [Google Scholar] [CrossRef]
- Sun, Y.; Li, L.; Yan, B.; Yang, C.; Tang, G. A hybrid algorithm combining EKF and RLS in synchronous estimation of road grade and vehicle׳ mass for a hybrid electric bus. Mech. Syst. Signal Process. 2016, 68–69, 416–430. [Google Scholar] [CrossRef]
- Hong, S.; Lee, C.; Borrelli, F.; Hedrick, J.K. A Novel approach for vehicle inertial parameter identification using a dual kalman filter. IEEE Trans. Intell. Transp. Syst. 2014, 16, 151–161. [Google Scholar] [CrossRef]
- Astroza, R.; Alessandri, A.; Conte, J.P. A dual adaptive filtering approach for nonlinear finite element model updating accounting for modeling uncertainty. Mech. Syst. Signal Process. 2019, 115, 782–800. [Google Scholar] [CrossRef]
- Wu, Q.; Jia, Q.; Shan, J.; Meng, X. Angular velocity estimation based on adaptive simplified spherical simplex unscented Kalman filter in GFSINS. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 1375–1388. [Google Scholar] [CrossRef]
- Eftekhar Azam, S.; Chatzi, E.; Papadimitriou, C. A dual Kalman filter approach for state estimation via output-only acceleration measurements. Mech. Syst. Signal Process. 2015, 60–61, 866–886. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; Du, H.; Li, W. Two-layer structure based adaptive estimation for vehicle mass and road slope under longitudinal motion. Measurement 2017, 95, 439–455. [Google Scholar] [CrossRef]
- Boada, B.L.; Boada, M.J.L.; Zhang, H. Sensor fusion based on a dual kalman filter for estimation of road irregularities and vehicle mass under static and dynamic conditions. IEEE/ASME Trans. Mechatron. 2019, 24, 1075–1086. [Google Scholar] [CrossRef] [Green Version]
- Zhou, D.; Tan, G.; Ding, Y.; Yu, S.; Ma, X.; Wang, S.; Wang, Z. A Non-Contact Overload Identification Method Based on Vehicle Dynamics. SAE Technical Paper Series. 2019. Available online: https://saemobilus.sae.org/content/2019-01-0490/ (accessed on 12 June 2021). [CrossRef]
- Dong, G.; Chen, J.; Zhang, N. Investigation into on-road vehicle parameter identification based on subspace methods. J. Sound Vib. 2014, 333, 6760–6779. [Google Scholar] [CrossRef]
- Wan, E.A.; Merwe, R.; Nelson, A.T. Dual estimation and the unscented transformation. In Proceedings of the Neural Information Processing Systems, Denver, CO, USA, 29 November–4 December 1999; pp. 666–672. [Google Scholar]
- Wan, E.A.; Nelson, A.T. Dual Extended Kalman Filter Methods. In Kalman Filtering and Neural Networks; Wiley& Sons: Hoboken, NJ, USA, 2001; pp. 123–173. [Google Scholar]
- Vargas-Melendez, L.; Boada, B.L.; Boada, M.J.L.; Gauchia, A.; Diaz, V. Sensor Fusion Based on an Integrated Neural Network and Probability Density Function (PDF) Dual Kalman Filter for On-Line Estimation of Vehicle Parameters and States. Sensors 2017, 17, 987. [Google Scholar] [CrossRef]
- Tseng, H.E.; Hrovat, D. State of the art survey: Active and semi-active suspension control. Veh. Syst. Dyn. 2015, 53, 1034–1062. [Google Scholar] [CrossRef]
- Gohrle, C.; Schindler, A.; Wagner, A.; Sawodny, O. Road profile estimation and preview control for low-bandwidth active suspension systems. IEEE/ASME Trans. Mechatron. 2014, 20, 2299–2310. [Google Scholar] [CrossRef]
- Zhang, Z.; Dhanasekar, M.; Thambiratnam, D.P.; Ling, L. Dynamics of Tire Crossing on a Gapped Road Surface. J. Eng. Mech. 2018, 144, 04018013. [Google Scholar] [CrossRef] [Green Version]
- Deshpande, V.S.; Mohan, B.; Shendge, P.D.; Phadke, S.B. Disturbance observer based sliding mode control of active suspension systems. J. Sound Vib. 2014, 333, 2281–2296. [Google Scholar] [CrossRef]
- Gorges, C.; Öztürk, K.; Liebich, R. Impact detection using a machine learning approach and experimental road roughness classification. Mech. Syst. Signal Process. 2019, 117, 738–756. [Google Scholar] [CrossRef]
- Jin, X.; Yang, J.; Li, Y.; Zhu, B.; Wang, J.; Yin, G. Online estimation of inertial parameter for lightweight electric vehicle using dual unscented Kalman filter approach. IET Intell. Transp. Syst. 2020, 14, 412–422. [Google Scholar] [CrossRef]
- Dunik, J.; Simandl, M.; Straka, O. Unscented Kalman filter: Aspects and adaptive setting of scaling parameter. IEEE Trans. Autom. Control. 2012, 57, 2411–2416. [Google Scholar] [CrossRef]





| Parameters | Values | Units |
|---|---|---|
| 1.37 | m | |
| 2.7 | m | |
| 1.32 | m | |
| 0.685 | m |
| Parameters | Values | Units |
|---|---|---|
| 1558 | kg | |
| 2381 | kg·m2 | |
| 600 | kg·m2 | |
| 96.4 | kg | |
| 105.6 | kg | |
| 36,557 | N/m | |
| 3200 | N·s/m | |
| 42,677 | N/m | |
| 3500 | N·s/m | |
| () | 200,900 | N/m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhang, J.; Dai, J.; Zhang, B.; Qi, H. A Fusion Algorithm for Estimating Time-Independent/-Dependent Parameters and States. Sensors 2021, 21, 4068. https://doi.org/10.3390/s21124068
Zhang Z, Zhang J, Dai J, Zhang B, Qi H. A Fusion Algorithm for Estimating Time-Independent/-Dependent Parameters and States. Sensors. 2021; 21(12):4068. https://doi.org/10.3390/s21124068
Chicago/Turabian StyleZhang, Zheshuo, Jie Zhang, Jiawen Dai, Bangji Zhang, and Hengmin Qi. 2021. "A Fusion Algorithm for Estimating Time-Independent/-Dependent Parameters and States" Sensors 21, no. 12: 4068. https://doi.org/10.3390/s21124068
APA StyleZhang, Z., Zhang, J., Dai, J., Zhang, B., & Qi, H. (2021). A Fusion Algorithm for Estimating Time-Independent/-Dependent Parameters and States. Sensors, 21(12), 4068. https://doi.org/10.3390/s21124068







