Asymmetric Diffraction in Plasmonic Meta-Gratings Using an IT-Shaped Nanoslit Array
Abstract
:1. Introduction
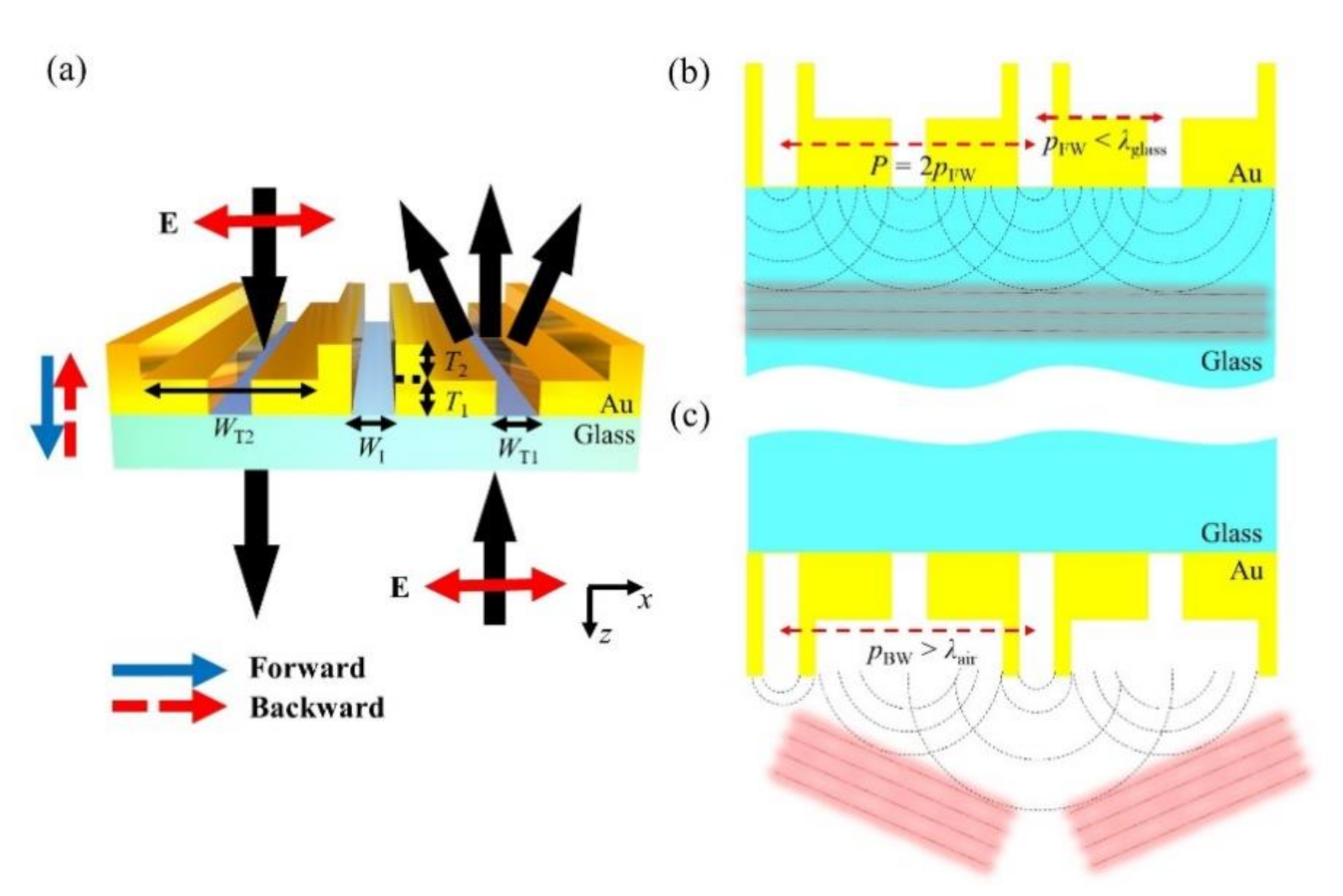
2. Basic Principle of the Proposed Structure
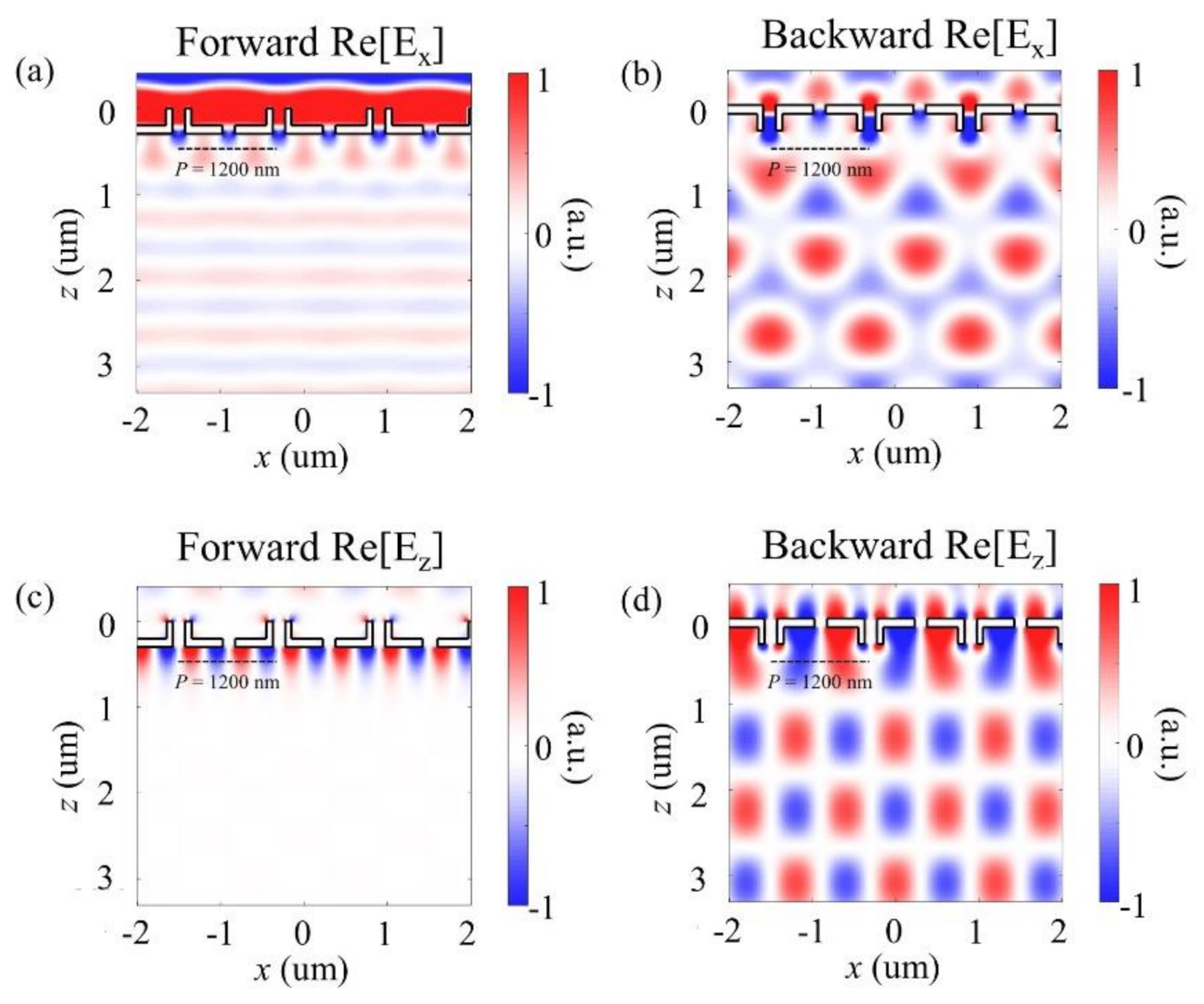
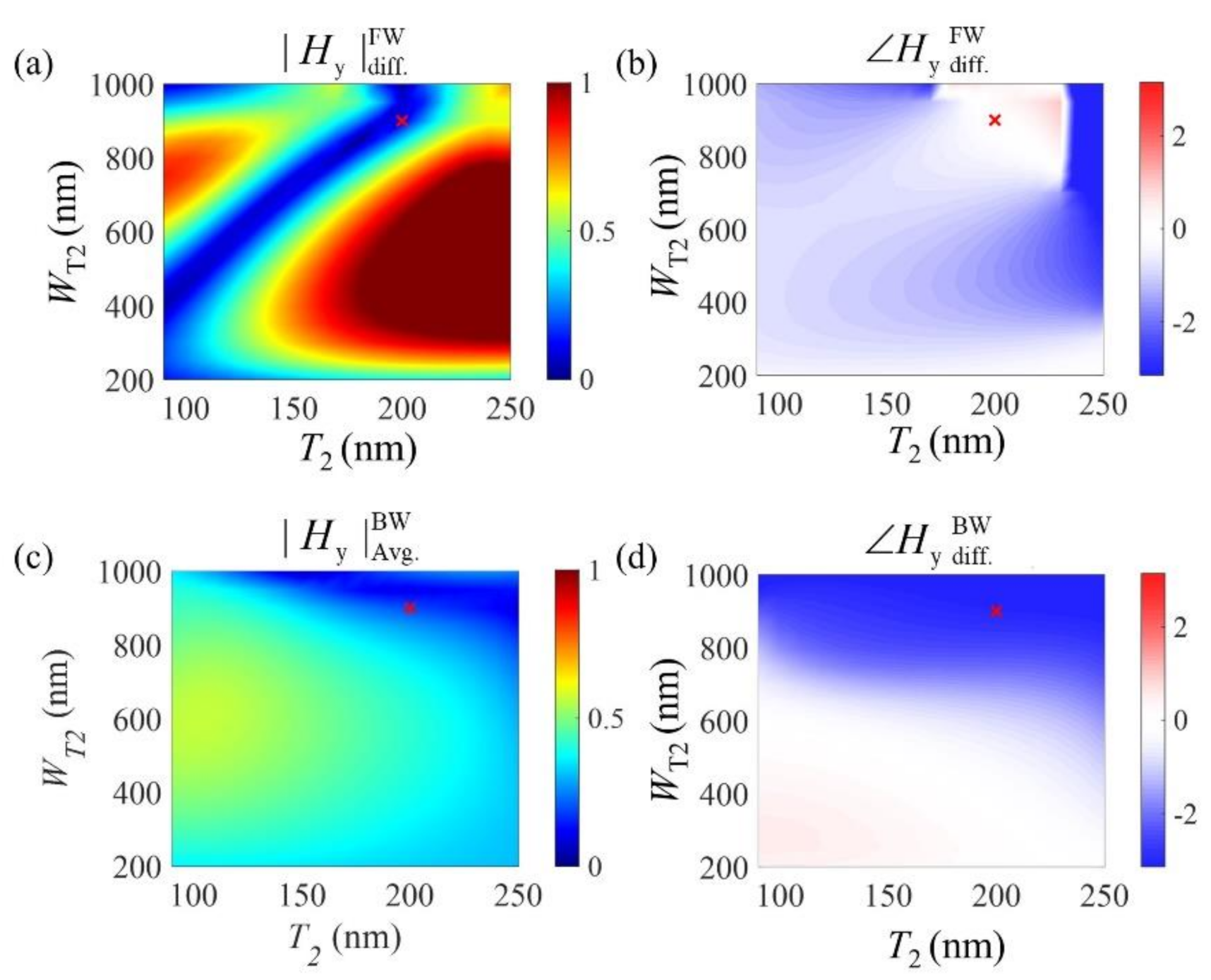
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Chang, C.; Bang, K.; Wetzstein, G.; Lee, B.; Gao, L. Toward the next-generation VR/AR optics: A review of holographic near-eye displays from a human-centric perspective. Optica 2020, 7, 1563. [Google Scholar] [CrossRef]
- Choi, W.-Y.; Lee, C.-J.; Kim, B.-S.; Oh, K.-J.; Hong, K.; Choo, H.-G.; Park, J.; Lee, S.-Y. Numerical Analysis on Viewing Angle Enhancement of Digital Hologram by Attaching a Pixelated-Random Phase Mask. Appl. Opt. 2020, 60, A54–A61. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Weng, Y.; Xu, D.; Tabiryan, N.V.; Wu, S.-T. Beam steering for virtual/augmented reality displays with a cycloidal diffractive waveplate. Opt. Express 2016, 24, 7287–7298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Wang, Q.-H.; Hu, Y. Image Encryption Using Compressive Sensing and Detour Cylindrical Diffraction. IEEE Photonics J. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Chakravarthula, P.; Dunn, D.; Aksit, K.; Fuchs, H. FocusAR: Auto-focus Augmented Reality Eyeglasses for both Real World and Virtual Imagery. IEEE Trans. Vis. Comput. Graph 2018, 24, 2906–2916. [Google Scholar] [CrossRef]
- Kumar, M.B.; Kang, D.; Jung, J.; Park, H.; Hahn, J.; Choi, M.; Bae, J.-H.; Kim, H.; Park, J. Compact vari-focal augmented real-ity display based on ultrathin, polarization-insensitive, and adaptive liquid crystal lens. Opt. Lasers Eng. 2020, 128, 106006. [Google Scholar] [CrossRef] [Green Version]
- Quan, X.; Matoba, O.; Awatsuji, Y. Single-shot incoherent digital holography using a dual-focusing lens with diffraction gratings. Opt. Lett. 2017, 42, 383–386. [Google Scholar] [CrossRef]
- Park, J.; Lee, K.; Park, Y. Ultrathin wide-angle large-area digital 3D holographic display using a non-periodic photon sieve. Nat. Commun. 2019, 10, 1304. [Google Scholar] [CrossRef] [Green Version]
- Jia, J.; Chen, J.; Yao, J.; Chu, D. A scalable diffraction-based scanning 3D colour video display as demonstrated by using tiled gratings and a vertical diffuser. Sci. Rep. 2017, 7, 44656. [Google Scholar] [CrossRef] [Green Version]
- Draper, C.T.; Blanche, P.-A. Examining aberrations due to depth of field in holographic pupil replication waveguide sys-tems. Appl. Opt. 2021, 60, 1653–1659. [Google Scholar] [CrossRef]
- Arbabi, A.; Arbabi, E.; Horie, Y.; Kamali, S.M.; Faraon, A. Planar metasurface retroreflector. Nat. Photonics 2017, 11, 415–420. [Google Scholar] [CrossRef] [Green Version]
- Akram, M.R.; Ding, G.; Chen, K.; Feng, Y.; Zhu, W. Ultrathin Single Layer Metasurfaces with Ultra-Wideband Operation for Both Transmission and Reflection. Adv. Mater. 2020, 32, e1907308. [Google Scholar] [CrossRef]
- Shirmanesh, G.K.; Sokhoyan, R.; Wu, P.C.; Atwater, H.A. Electro-optically Tunable Multifunctional Metasurfaces. ACS Nano 2020, 14, 6912–6920. [Google Scholar] [CrossRef]
- Islam, K.M.R.; Choi, S. Compact Double-Layer FR4-based Focusing Lens Using High-Efficiency Huygens’ Metasurface Unit Cells. Sensors 2020, 20, 6142. [Google Scholar] [CrossRef]
- Hao, W.; Deng, M.; Chen, S.; Chen, L. High-Efficiency Generation of Airy Beams with Huygens’ Metasurface. Phys. Rev. Appl. 2019, 11, 054012. [Google Scholar] [CrossRef]
- Park, J.; Kang, J.-H.; Kim, S.J.; Liu, X.; Brongersma, M.L. Dynamic Reflection Phase and Polarization Control in Metasurfaces. Nano Lett. 2017, 17, 407–413. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sisler, J.; Huang, Y.-W.; Yousef, K.M.A.; Lee, E.; Qiu, C.-W.; Capasso, F. Broadband achromatic metasurface-refractive optics. Nano Lett. 2018, 18, 7801–7808. [Google Scholar] [CrossRef]
- Shibanuma, T.; Maier, S.A.; Albella, P. Polarization control of high transmission/reflection switching by all-dielectric metasurfaces. Appl. Phys. Lett. 2018, 112, 063103. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef] [Green Version]
- Lesina, A.C.; Goodwill, D.; Bernier, E.; Ramunno, L.; Berini, P. Tunable plasmonic metasurfaces for optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 1. [Google Scholar] [CrossRef]
- Schlickriede, C.; Kruk, S.S.; Wang, L.; Sain, B.; Kivshar, Y.; Zentgraf, T. Nonlinear Imaging with All-Dielectric Metasurfaces. Nano Lett. 2020, 20, 4370–4376. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Huang, L.; Xu, Z.T.; Li, X.; Zentgraf, T.; Wang, Y. Four-Wave Mixing Holographic Multiplexing Based on Nonlinear Metasurfaces. Adv. Opt. Mater. 2019, 7, 1900782. [Google Scholar] [CrossRef]
- Lee, D.; Gwak, J.; Badloe, T.; Palomba, S.; Rho, J. Metasurfaces-based imaging and applications: From miniaturized optical components to functional imaging platforms. Nanoscale Adv. 2020, 2, 605–625. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.-X.; Ma, S.; Luo, W.; Cai, T.; Sun, S.; He, Q.; Zhou, L. Aberration-free and functionality-switchable meta-lenses based on tunable metasurfaces. Appl. Phys. Lett. 2016, 109, 193506. [Google Scholar] [CrossRef]
- Aieta, F.; Genevet, P.; Kats, M.A.; Yu, N.; Blanchard, R.; Gaburro, Z.; Capasso, F. Aberration-Free Ultrathin Flat Lenses and Axicons at Telecom Wavelengths Based on Plasmonic Metasurfaces. Nano Lett. 2012, 12, 4932–4936. [Google Scholar] [CrossRef]
- Wang, A.; Chen, Z.; Dan, Y. Planar metalenses in the mid-infrared. AIP Adv. 2019, 9, 085327. [Google Scholar] [CrossRef] [Green Version]
- Lee, G.-Y.; Hong, J.-Y.; Hwang, S.; Moon, S.; Kang, H.; Jeon, S.; Kim, H.; Jeong, J.-H.; Lee, B. Metasurface eyepiece for aug-mented reality. Nat. Commun. 2018, 9, 4562. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Cui, T.J.; Ji, W.; Liu, S.; Ding, J.; Wan, X.; Li, Y.B.; Jiang, M.; Qiu, C.-W.; Zhang, S. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 2017, 8, 197. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Q.; Jin, G.; Cao, L. When metasurface meets hologram: Principle and advances. Adv. Opt. Photonics 2019, 11, 518–576. [Google Scholar] [CrossRef]
- Lee, G.-Y.; Yoon, G.; Lee, S.-Y.; Yun, H.; Cho, J.; Lee, K.; Kim, H.; Rho, J.; Lee, B. Complete amplitude and phase control of light using broadband holographic metasurfaces. Nanoscale 2018, 10, 4237–4245. [Google Scholar] [CrossRef] [Green Version]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Xu, J.; Cheng, C.; Kang, M.; Chen, J.; Zheng, Z.; Fan, Y.-X.; Wang, H.-T. Unidirectional optical transmission in dual-metal gratings in the absence of anisotropic and nonlinear materials. Opt. Lett. 2011, 36, 1905–1907. [Google Scholar] [CrossRef]
- Cakmakyapan, S.; Serebryannikov, A.E.; Caglayan, H.; Ozbay, E. One-way transmission through the subwavelength slit in nonsymmetric metallic gratings. Opt. Lett. 2010, 35, 2597–2599. [Google Scholar] [CrossRef] [Green Version]
- Hadad, Y.; Soric, J.C.; Alu, A. Breaking temporal symmetries for emission and absorption. Proc. Natl. Acad. Sci. USA 2016, 113, 3471–3475. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, H.; Goto, S.; Mori, T. Optical isolation using nonreciprocal polarization rotation in Fe–InGaAlAs/InP semiconduc-tor active waveguide optical isolators. Appl. Phys. Express 2010, 3, 072201. [Google Scholar] [CrossRef]
- Xia, K.; Nori, F.; Xiao, M. Cavity-Free Optical Isolators and Circulators Using a Chiral Cross-Kerr Nonlinearity. Phys. Rev. Lett. 2018, 121, 203602. [Google Scholar] [CrossRef] [Green Version]
- Jalas, D.; Petrov, A.; Eich, M.; Freude, W.; Fan, S.; Yu, Z.; Baets, R.; Popovic, M.; Melloni, A.; Joannopoulos, J.D.; et al. What is—And what is not—An optical isolator. Nat. Photonics 2013, 7, 579–582. [Google Scholar] [CrossRef]
- Cao, Y.; Fu, Y.; Zhou, Q.; Ou, X.; Gao, L.; Chen, H.; Xu, Y. Mechanism Behind Angularly Asymmetric Diffraction in Phase-Gradient Metasurfaces. Phys. Rev. Appl. 2019, 12, 024006. [Google Scholar] [CrossRef]
- Fedotov, V.A.; Mladyonov, P.L.; Prosvirnin, S.L.; Rogacheva, A.V.; Chen, Y.; Zheludev, N.I. Asymmetric Propagation of Electromagnetic Waves through a Planar Chiral Structure. Phys. Rev. Lett. 2006, 97, 167401. [Google Scholar] [CrossRef] [Green Version]
- Zanotto, S.; Sgrignuoli, F.; Nocentini, S.; Martella, D.; Parmeggiani, C.; Wiersma, D.S. Multichannel remote polarization control enabled by nanostructured liquid crystalline networks. Appl. Phys. Lett. 2019, 114, 201103. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, M.; Barton, D.R.; Dionne, J.A. Nonreciprocal Flat Optics with Silicon Metasurfaces. Nano Lett. 2018, 18, 1104–1109. [Google Scholar] [CrossRef] [PubMed]
- Driscoll, J.B.; Astar, W.; Liu, X.; Dadap, J.I.; Green, W.M.J.; Vlasov, Y.A.; Carter, G.M.; Osgood, R.M. All-Optical Wavelength Conversion of 10 Gb/s RZ-OOK Data in a Silicon Nanowire via Cross-Phase Modulation: Experiment and Theoretical Investigation. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1448–1459. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, Y.; Hu, H.; Xue, W.; Yvind, K.; Mork, J. Nonreciprocal transmission in a nonlinear photonic-crystal Fano structure with broken symmetry. Laser Photonics Rev. 2015, 9, 241–247. [Google Scholar] [CrossRef]
- Frese, D.; Wei, Q.; Wang, Y.; Huang, L.; Zentgraf, T. Non-reciprocal asymmetric polarization encryption by layered plas-monic metasurfaces. Nano Lett. 2019, 19, 3976–3980. [Google Scholar] [CrossRef]
- Ahadi, S.; Granpayeh, N. Femtosecond all-optical switching based on asymmetric plasmonic Kerr Fabry–Perot resonators. Opt. Commun. 2015, 349, 36–41. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Chen, J.; Yue, S.; Gong, Q. A dichroic surface-plasmon-polariton splitter based on an asymmetric T-shape nanoslit. Opt. Express 2013, 21, 14548–14554. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Zhang, X.; Xiao, J.; Gong, Q. Submicron bidirectional all-optical plasmonic switches. Sci. Rep. 2013, 3, 1451. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Yue, S.; Xiao, J.; Gong, Q. Plasmon-Induced Transparency in Asymmetric T-Shape Single Slit. Nano Lett. 2012, 12, 2494–2498. [Google Scholar] [CrossRef]
- Hwi, K.; Junghyun, P.; Byoungho, L.; Lee, B.; Kim, H.; Park, J. Fourier Modal Method and Its Applications in Computational Nanophotonics; CRC Press: Boca Raton, FL, USA, 2017; p. 66. [Google Scholar]


| P [nm] | WT2 [nm] | T2 [nm] | DP0th (%) | (DP+1st + DP−1st) (%) | Diffraction Angle (°) |
|---|---|---|---|---|---|
| 1100 | 850 | 190 | 11.88 | 15.2 | 62 |
| 1150 | 900 | 180 | 0.80 | 22.16 | 58 |
| 1200 1 | 900 | 200 | 7.06 | 16.86 | 54 |
| 1250 | 950 | 210 | 2.42 | 12.96 | 51 |
| 1300 | 900 | 220 | 0.48 | 1.84 | 49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, H.-D.; Moon, S.-W.; Lee, S.-Y. Asymmetric Diffraction in Plasmonic Meta-Gratings Using an IT-Shaped Nanoslit Array. Sensors 2021, 21, 4097. https://doi.org/10.3390/s21124097
Jeong H-D, Moon S-W, Lee S-Y. Asymmetric Diffraction in Plasmonic Meta-Gratings Using an IT-Shaped Nanoslit Array. Sensors. 2021; 21(12):4097. https://doi.org/10.3390/s21124097
Chicago/Turabian StyleJeong, Hee-Dong, Seong-Won Moon, and Seung-Yeol Lee. 2021. "Asymmetric Diffraction in Plasmonic Meta-Gratings Using an IT-Shaped Nanoslit Array" Sensors 21, no. 12: 4097. https://doi.org/10.3390/s21124097
APA StyleJeong, H.-D., Moon, S.-W., & Lee, S.-Y. (2021). Asymmetric Diffraction in Plasmonic Meta-Gratings Using an IT-Shaped Nanoslit Array. Sensors, 21(12), 4097. https://doi.org/10.3390/s21124097







