Parameter Design and Performance Evaluation of a Large-Swath and High-Resolution Space Camera
Abstract
:1. Introduction
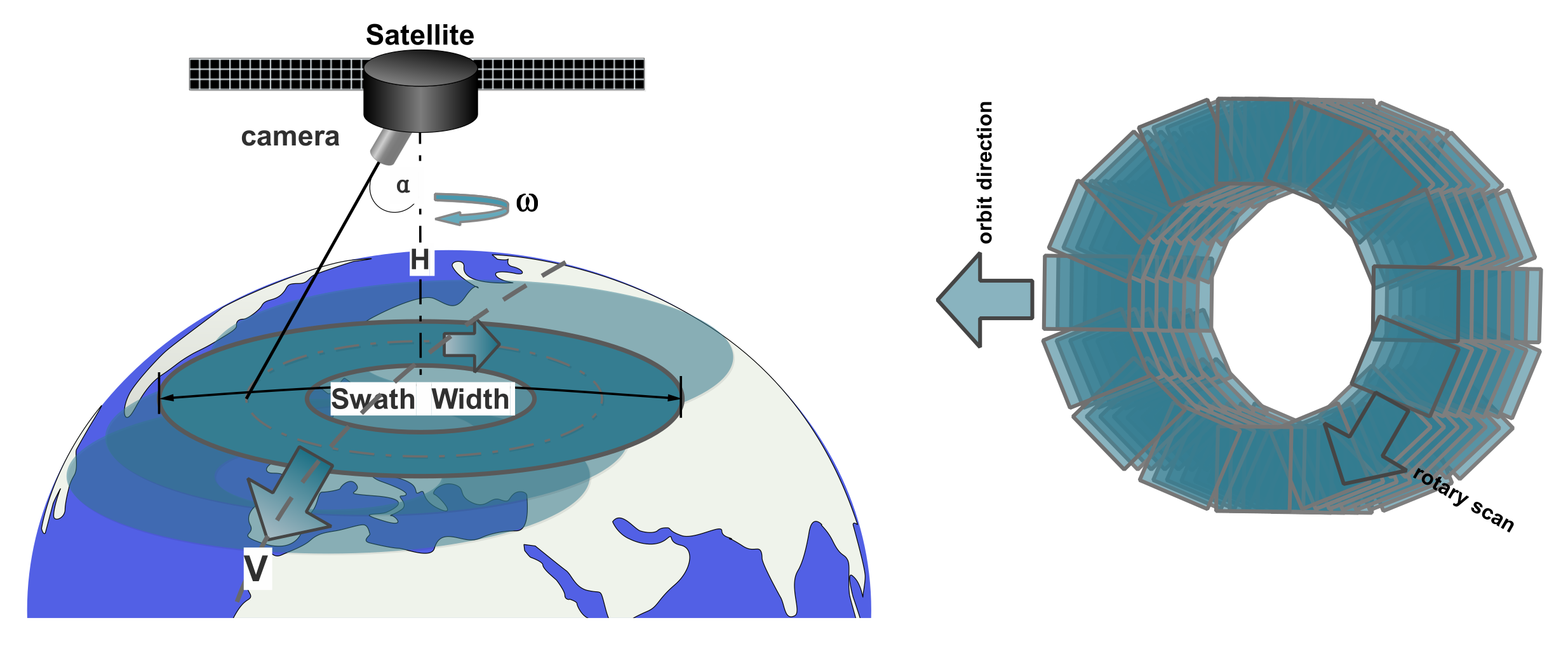
2. Low Earth Orbit Plane Array Rotary Scan Camera
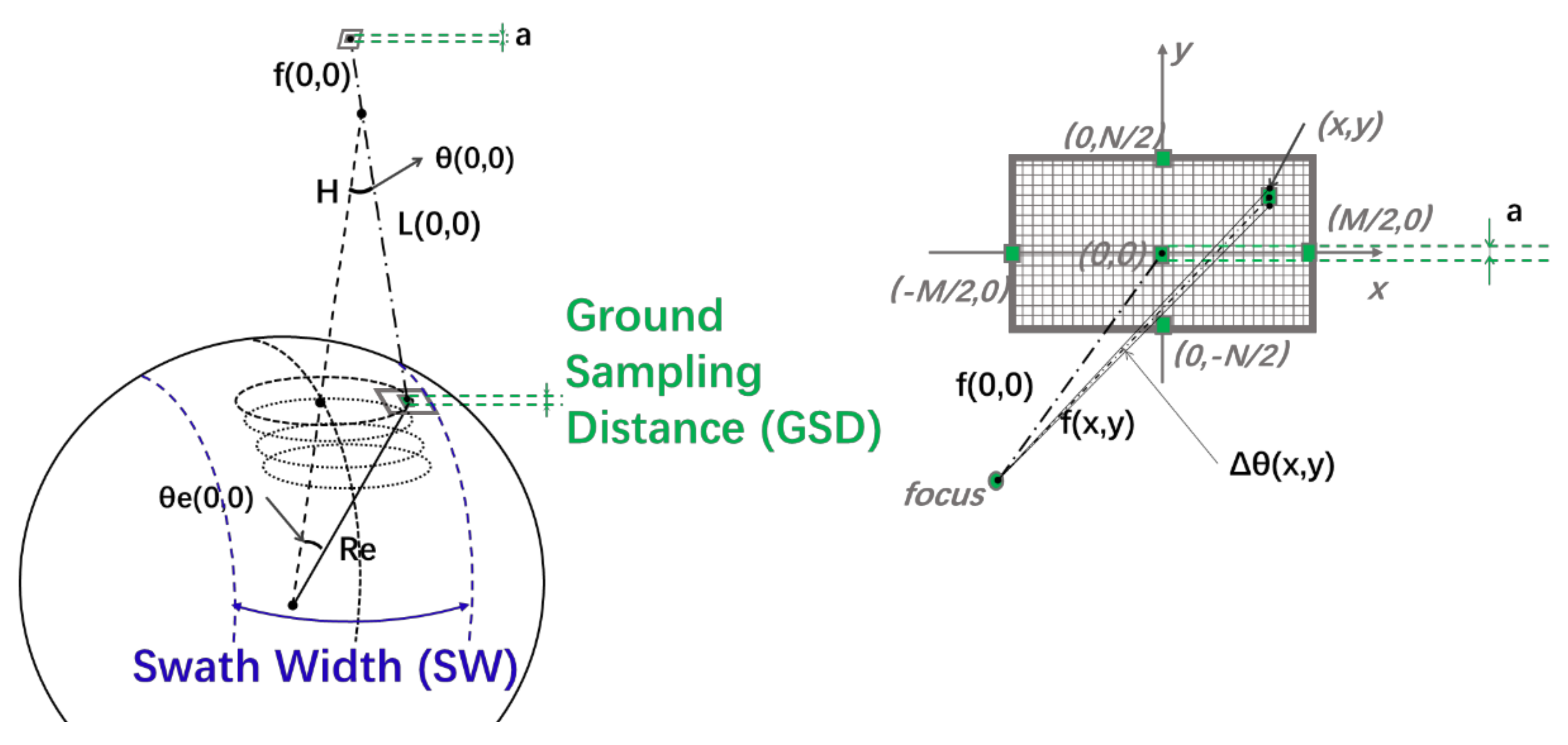
2.1. Swath and Resolution Model
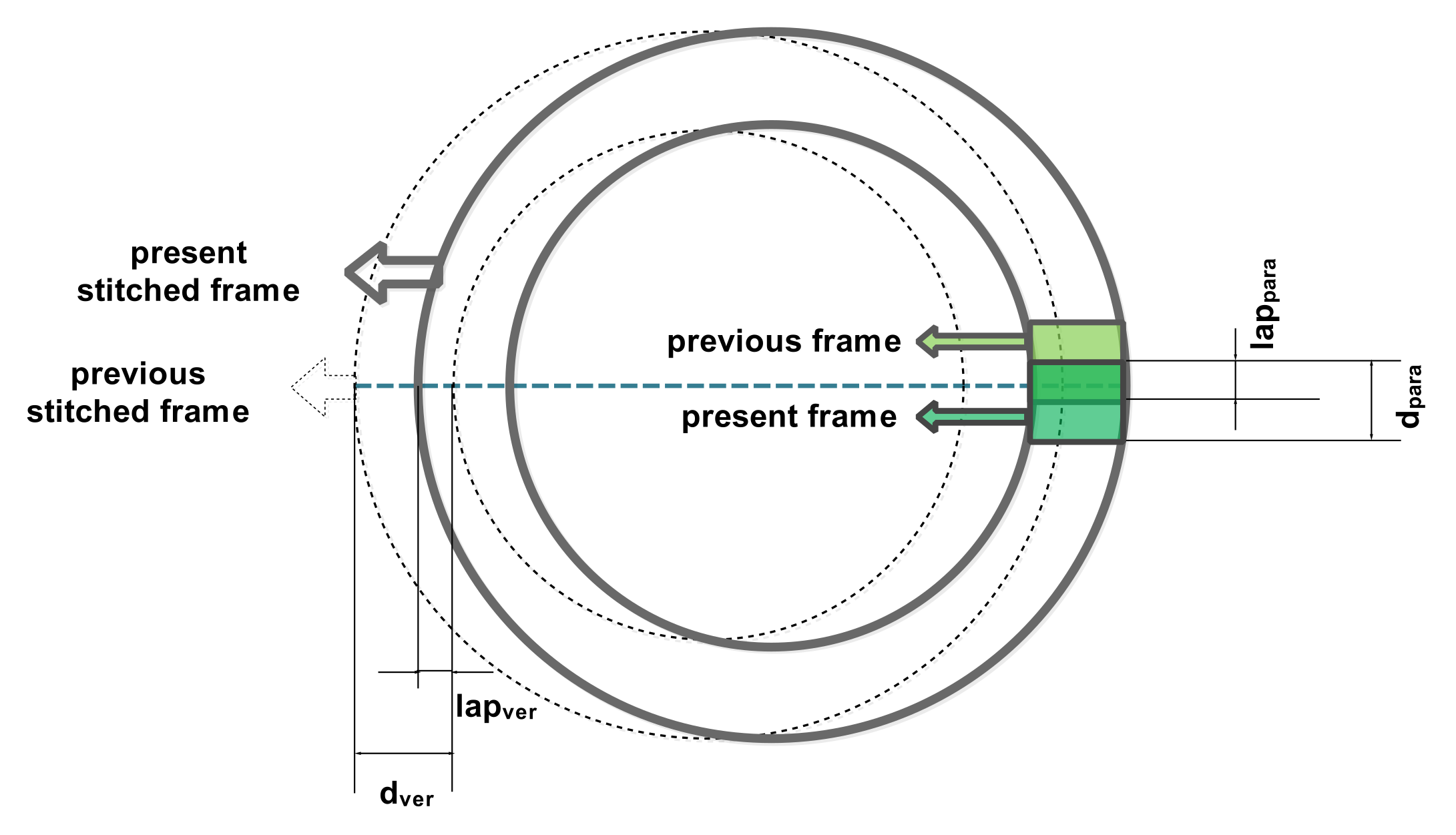
2.2. Overlap Rate
3. System Parameter Design Process
3.1. Optimization Design Modeling
3.2. Optimization Design Method
| Algorithm 1: System parameter design algorithm |
| 1: Begin 2: Initialize calculation number: i = 0; 3: Initialize feasible solution number: k = 0; 4: Input maximum calculation number: i_max; 5: Input maximum feasible solution number: k_max; 6: while (i < i_max) and (k < k_max) do 7: Update the calculation number i = i + 1; 8: Generate a set of system parameters at random: x(i) = (f, w, alpha, Mnum, Nnum); 9: if (Constraint1 in Equation (18)) and (Constraint2 in Equation (19)) == TRUE then 10: Save x(i) as a feasible solution; 11: update the feasible number: k = k + 1; 12: if object(i) ≤ object_best then 13: Update the best solution: x_best = x(i), object_best = object(i); 14: end 15: end 16: Output The best solution x_best; 17: end 18: End |
4. Example and Evaluation
4.1. Design Example
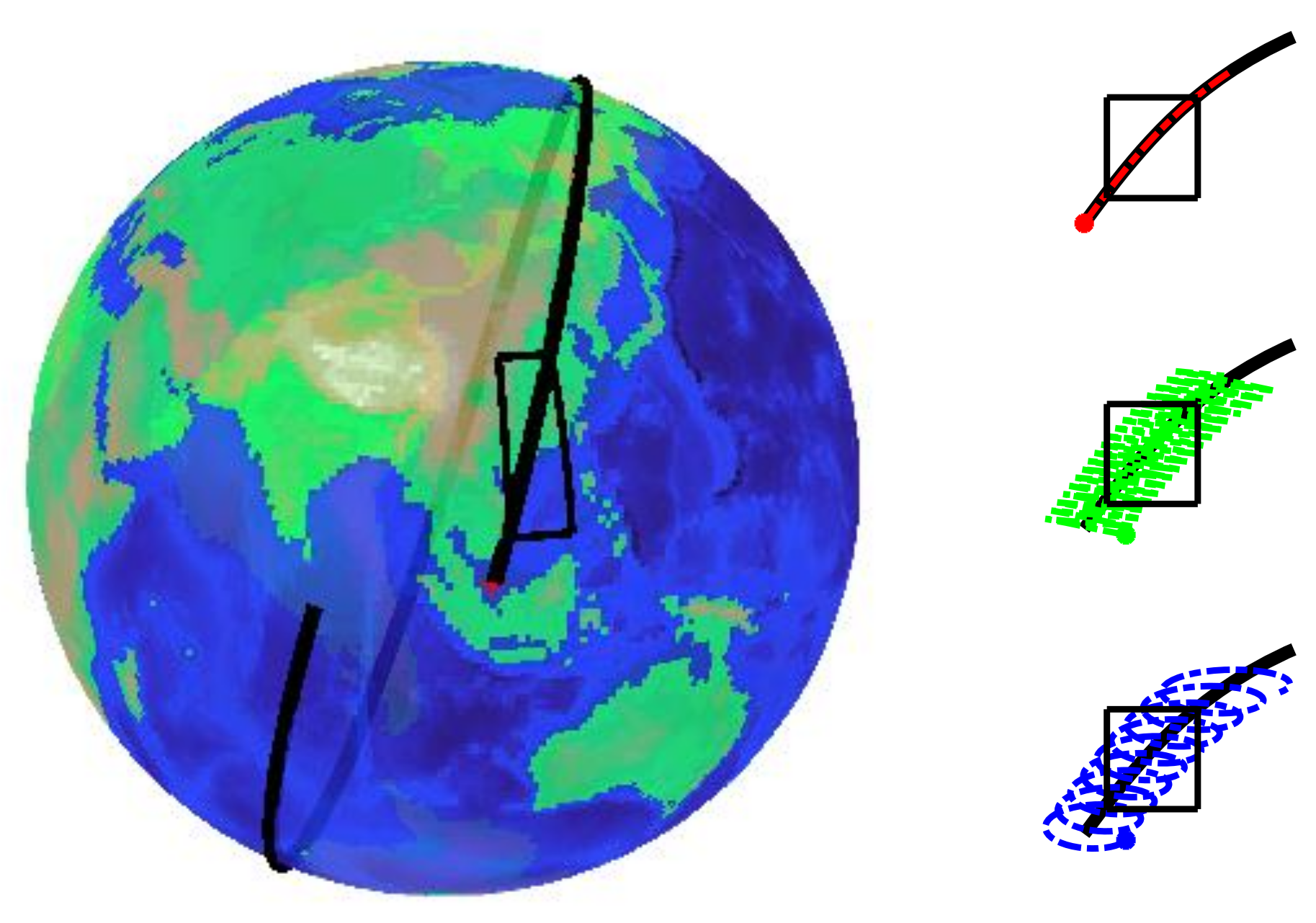
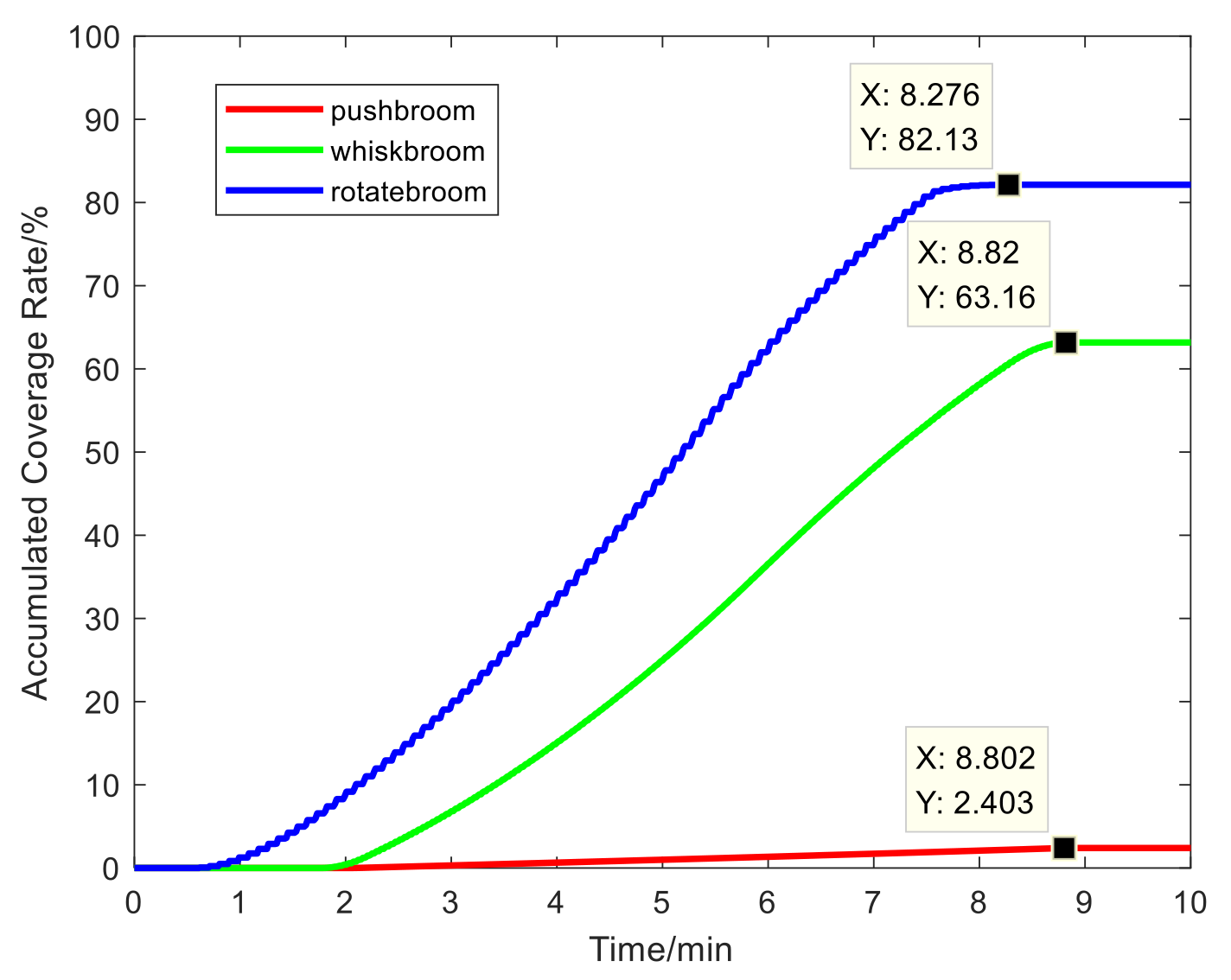
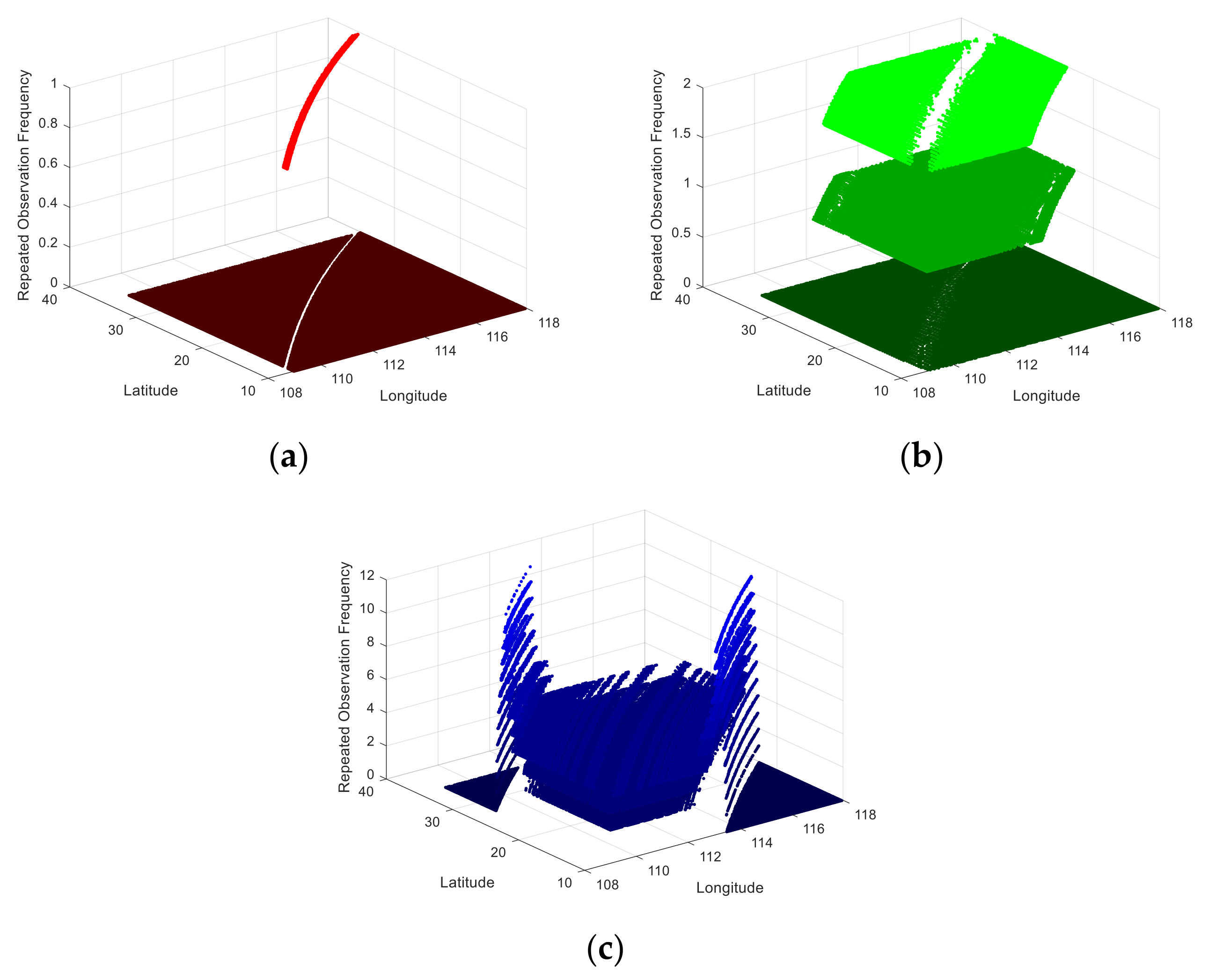
4.2. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Leininger, B. A next-generation system enables persistent surveillance of wide areas. SPIE Newsroom 2008. [Google Scholar] [CrossRef]
- Circi, C.; Ortore, E.; Bunkheila, F. Satellite constellations in sliding ground track orbits. Aerosp. Sci. Technol. 2014, 39, 395–402. [Google Scholar] [CrossRef]
- Yang, B.; Wang, M.; Jin, S.; Pan, J. An optimal imaging-scheduling algorithm for the multi-strip imaging-mode of the high-resolution agile satellites based on certain step-size search. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 339–343. [Google Scholar] [CrossRef] [Green Version]
- Jie, H.A.N.; Yong, X.I.E.; Guoxi, W.U.; Zhengzheng, Y.U.; Yuelei, Q.I.A.N.; Xiaoguo, G.U.A.N. Research on the self-adaptive matching method of GF-1 satellite imagery considering the features of multicamera mosaic imaging. Remote Sens. Land Resour. 2017, 29, 13–19. [Google Scholar]
- Tang, X.; Hu, F.; Wang, M.; Pan, J.; Jin, S.; Lu, G. Inner FoV stitching of spaceborne TDI CCD images based on sensor geometry and projection plane in object space. Remote Sens. 2014, 6, 6386–6406. [Google Scholar] [CrossRef] [Green Version]
- Wolfe, R.E.; Lin, G.; Nishihama, M.; Tewari, K.P.; Tilton, J.C.; Isaacman, A.R. Suomi NPP VIIRS prelaunch and on-orbit geo-metric calibration and characterization. J. Geophys. Res. Atmos. 2013, 118, 11–508. [Google Scholar] [CrossRef] [Green Version]
- Gale, W. The Potential of Satellites for Wide Area Surveillance of Australia; Air Power Studies Centre: New Delhi, India, 1992. [Google Scholar]
- Toutin, T. Comparison of stereo-extracted DTM from different high-resolution sensors. SPOT-5, EROS-A, IKONOS-II and QuickBird. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2121–2129. [Google Scholar] [CrossRef]
- Longbotham, N.; Pacifici, F.; Baugh, B.; Camps-Valls, G. Prelaunch assessment of worldview-3 information content. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014. [Google Scholar]
- Salomonson, V.V.; Barnes, W.L.; Maymon, P.W.; Montgomery, H.E.; Ostrow, H. MODIS: Advanced facility instrument for studies of the Earth as a system. IEEE Trans. Geosci. Remote Sens. 1989, 27, 145–153. [Google Scholar] [CrossRef]
- Ian, W. Defense Support Program (DSP). Missile Threat, Center for Strategic and International Studies. 2016. Available online: https://missilethreat.csis.org/defsys/dsp/ (accessed on 20 January 2021).
- Soumekh, M. Reconnaissance with slant plane circular SAR imaging. IEEE Trans. Image Process. 1996, 5, 1252–1265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Hu, F.; Jin, S. Study on the development of wide technology about high resolution optical remote sensing satellites. Geomat. World 2017, 24, 45–50. [Google Scholar]
- Yin, Z.; Gao, S.; Li, H.; Li, P. Rotation-Based Large-Breadth Optical Imaging Method. CN107168005B, 1 October 2019. [Google Scholar]
- Song, M.; Qu, H.; Zhang, G. Design of aerospace camera circular scanning imaging model. Infrared Laser Eng. 2018, 47, 195–202. [Google Scholar]
- Shaoyuan, C.; Li, Z.; Weijun, G.; Jinqiang, W. Geometric parameters analysis of large FOV space camera when rolling. Infrared Laser Eng. 2015, 44, 1872–1877. [Google Scholar]
- Li, S.-Y.; Zhou, S.-C. The optical scanning technology in laser scanning and tracking system. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2009: Advances in Infrared Imaging and Applications, Beijing, China, 4 August 2009; SPIE: Bellingham, WA, USA, 2009; Volume 7383, p. 73832B. [Google Scholar]
- Zhi-lai, L.; Dong-lin, X.; Xue-jun, Z.N. Optical and mechanical design for long focal length and wide-field optical system. Opt. Precis. Eng. 2008, 16, 2485–2490. [Google Scholar]
- Morrison, J.J. A System of Sixteen Synchronous Satellites for Worldwise Navigation and Surveillance; U.S. Federal Aviation Administration: Washington, DC, USA, 1973. [Google Scholar]


| No. | H | f | w | alpha | Mnum | Nnum | SW | GSD | K | ETA | Object |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 200 | 7.78 | 62.13 | 66.32 | 10 | 10 | 1,054,346 | 0.96 | 0.11 | 0.14 | 0.61 |
| 2 | 300 | 5.63 | 98.15 | 56.7 | 7 | 12 | 1,005,317 | 0.96 | 0.2 | 0.25 | 0.56 |
| 3 | 400 | 5.15 | 80.66 | 49.88 | 8 | 8 | 1,037,295 | 0.98 | 0.19 | 0.23 | 0.50 |
| 4 | 500 | 4.78 | 65.61 | 43.24 | 9 | 6 | 1,022,767 | 0.99 | 0.14 | 0.30 | 0.46 |
| 5 | 600 | 5.21 | 61.08 | 39.46 | 10 | 5 | 1,072,620 | 0.97 | 0.17 | 0.21 | 0.46 |
| 6 | 700 | 6.07 | 64.75 | 35.92 | 10 | 5 | 1,091,257 | 0.87 | 0.15 | 0.10 | 0.47 |
| 7 | 800 | 5.93 | 54.11 | 34.7 | 10 | 5 | 1,196,224 | 0.99 | 0.12 | 0.29 | 0.46 |
| 8 | 900 | 6.33 | 69.87 | 32.79 | 8 | 8 | 1,238,651 | 1.00 | 0.17 | 0.42 | 0.51 |
| 9 | 1000 | 7.34 | 67.64 | 28.64 | 9 | 6 | 1,159,952 | 0.86 | 0.14 | 0.23 | 0.51 |
| Parameter | Value |
|---|---|
| Target simulation region: | Longitude: [109° E, 118° E]; |
| The South China Sea region. | Latitude: [10° N, 35° N] |
| Grid-scale | [0.05, 0.05] |
| Orbit height | 500 km |
| Equatorial longitude of the ascending point | 105.4° E |
| Initial operating position angle | 10.6° |
| Orbit inclination | 70.2° |
| Focal length | 4.78 m |
| Detector type | CMOS-GSENSE5130 |
| Pixel size a | 4.5 μm |
| Detector Scale M*N | 5092 × 3021 |
| Frame frequency | 67Hz |
| Splicing Number Mnum*Nnum | 9 × 6 |
| Swing angle alpha | −43.24°~+43.24° |
| Swing angular velocity | 65.61°/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Rao, P.; Hu, T. Parameter Design and Performance Evaluation of a Large-Swath and High-Resolution Space Camera. Sensors 2021, 21, 4106. https://doi.org/10.3390/s21124106
Sun Y, Rao P, Hu T. Parameter Design and Performance Evaluation of a Large-Swath and High-Resolution Space Camera. Sensors. 2021; 21(12):4106. https://doi.org/10.3390/s21124106
Chicago/Turabian StyleSun, Yingying, Peng Rao, and Tingliang Hu. 2021. "Parameter Design and Performance Evaluation of a Large-Swath and High-Resolution Space Camera" Sensors 21, no. 12: 4106. https://doi.org/10.3390/s21124106
APA StyleSun, Y., Rao, P., & Hu, T. (2021). Parameter Design and Performance Evaluation of a Large-Swath and High-Resolution Space Camera. Sensors, 21(12), 4106. https://doi.org/10.3390/s21124106






