A Data-Driven Scheme for Fault Detection of Discrete-Time Switched Systems
Abstract
1. Introduction
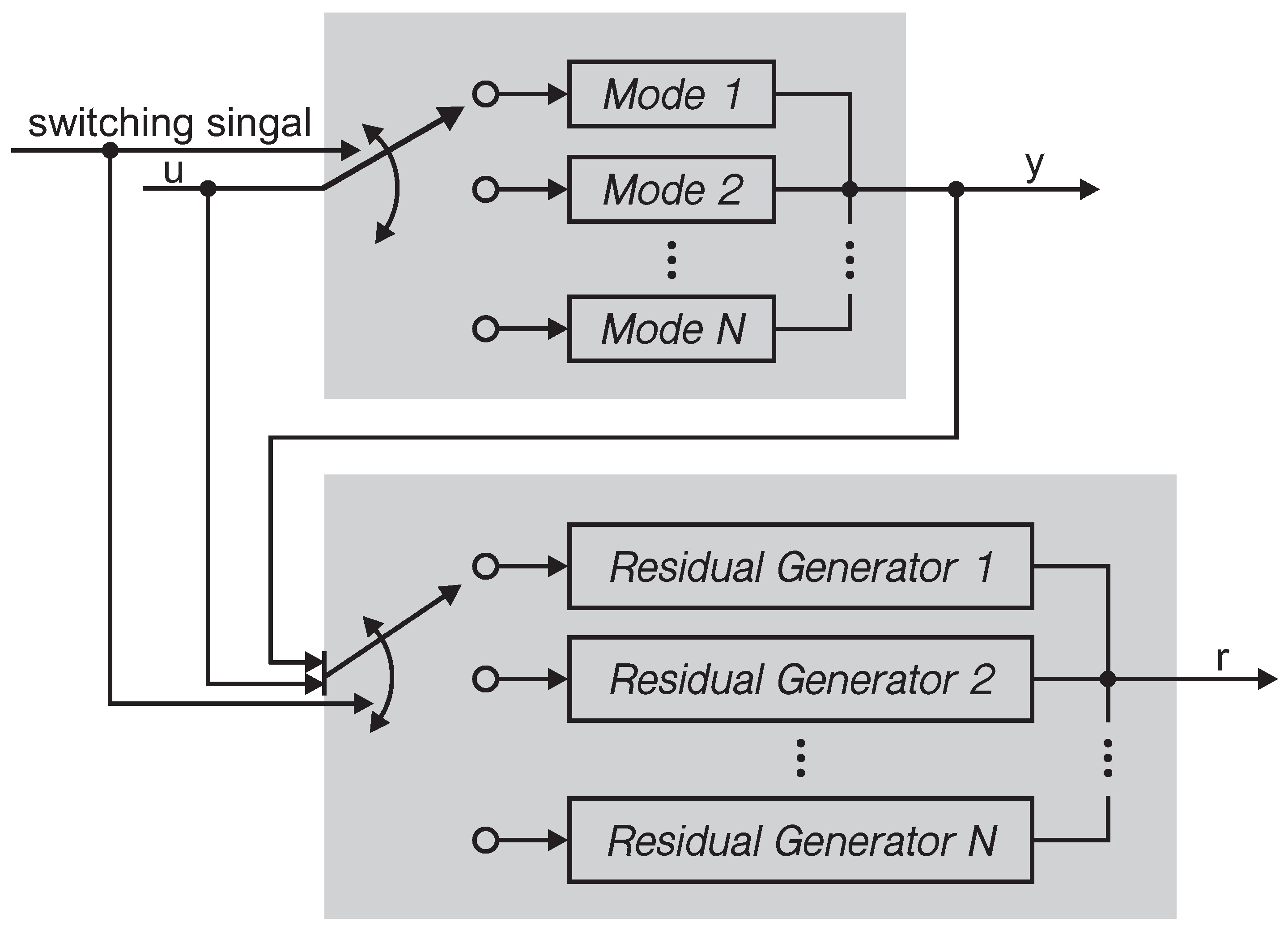
2. System Descriptions and Preliminaries
2.1. System Descriptions
2.2. SKR-Based Residual Generators
2.3. K-Gap Metric
2.4. Structure of Data Matrices
3. Main Results
3.1. Problem Descriptions
3.2. Mode Distinguishability Conditions
3.3. Mode Distinguishability Realisation
3.3.1. Normalised Data-Driven SKR in the Open-Loop Case
3.3.2. Normalised Data-Driven SKR in the Closed-Loop Case
3.3.3. Data-Driven Realisation of the K-Gap Metric
3.4. Data-Driven Fault Detection
| Algorithm 1 | Offline Data-Driven Procedure |
| Step 1: | Collect the process data of each subsystem |
| Step 2: | Choose and build the Hankel matrices for open-loop case |
| or for closed-loop case | |
| Step 3: | Perform LQ decomposition (10) or (16) and calculate the data-driven SKR |
| Step 4: | Utilise the singular value decomposition to get the normalised data-driven SKR |
| in (11) or (17) | |
| Step 5: | Calculate the K-gap metric of any two modes according to (18) and compare it |
| with given scalar | |
| Step 6: | Construct the data-driven residual generator according to (4) |
| Step 7: | Run the evaluation function (24) and set the threshold |
| Algorithm 2 | Online Fault Detection |
| Step 1: | Collect the online process data |
| Step 2: | Run the residual generator (4) with each SKR |
| Step 3: | Obtain the residual signal and the evaluation function according to (24) |
| Step 4: | Implement the decision logic (26) |
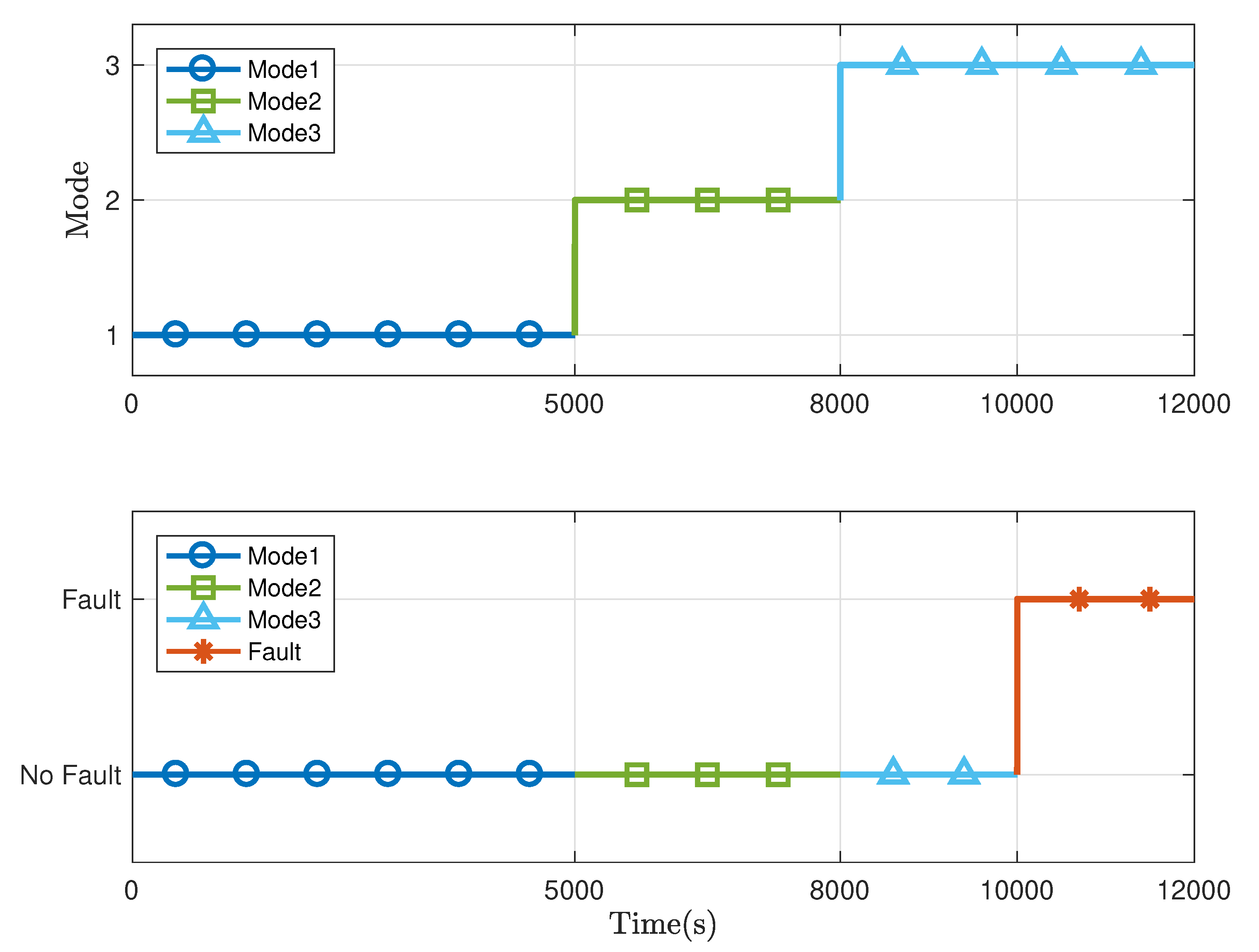
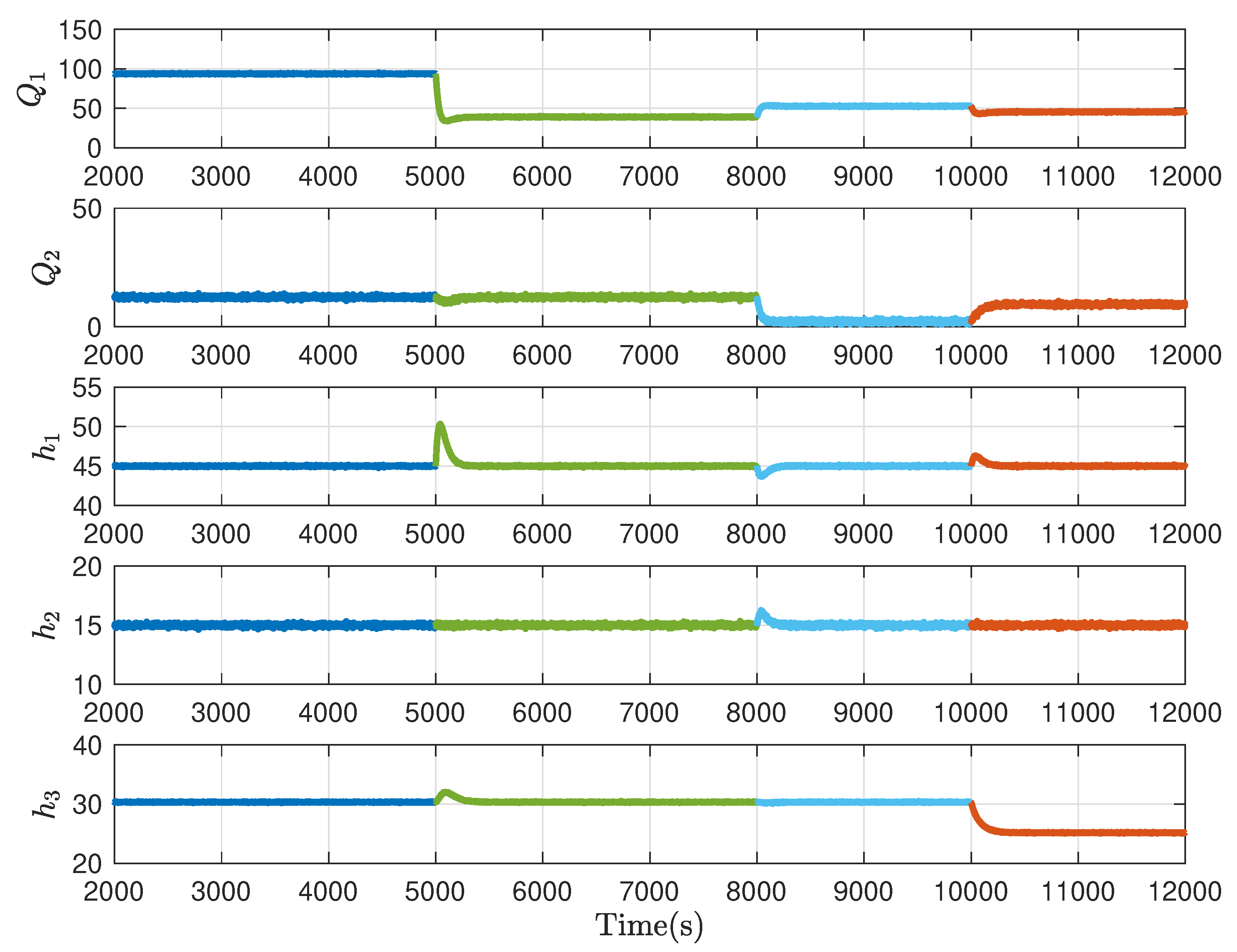
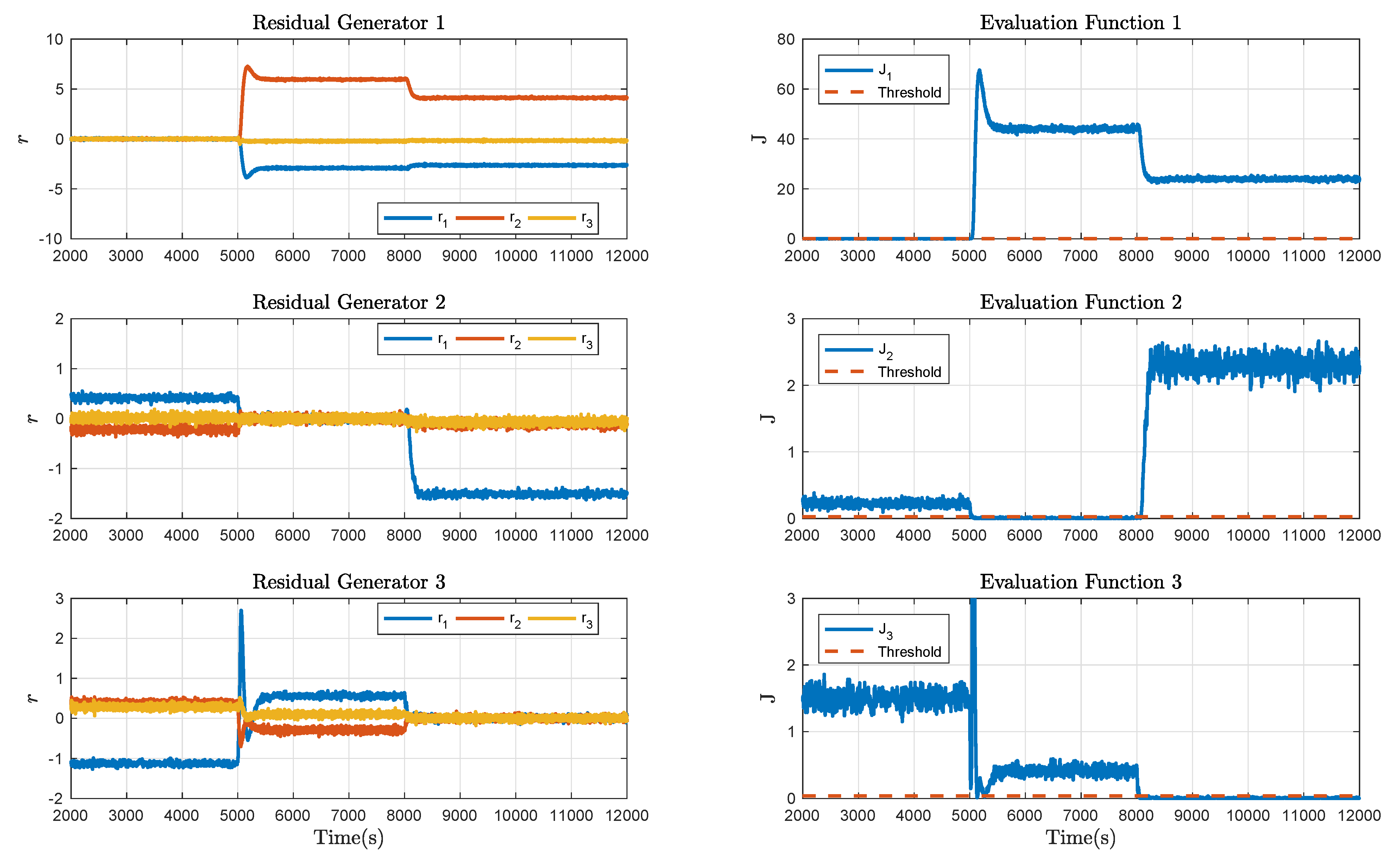
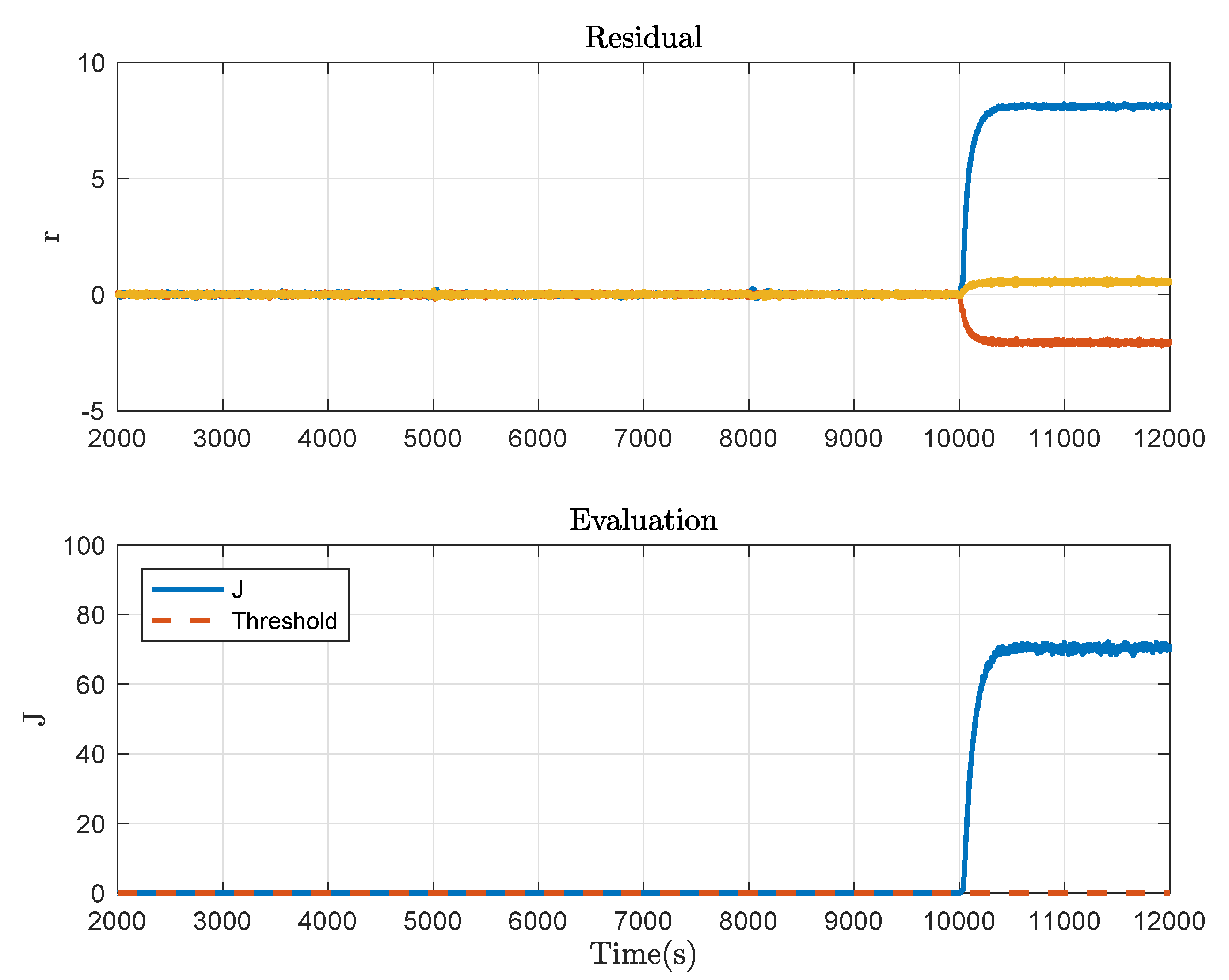
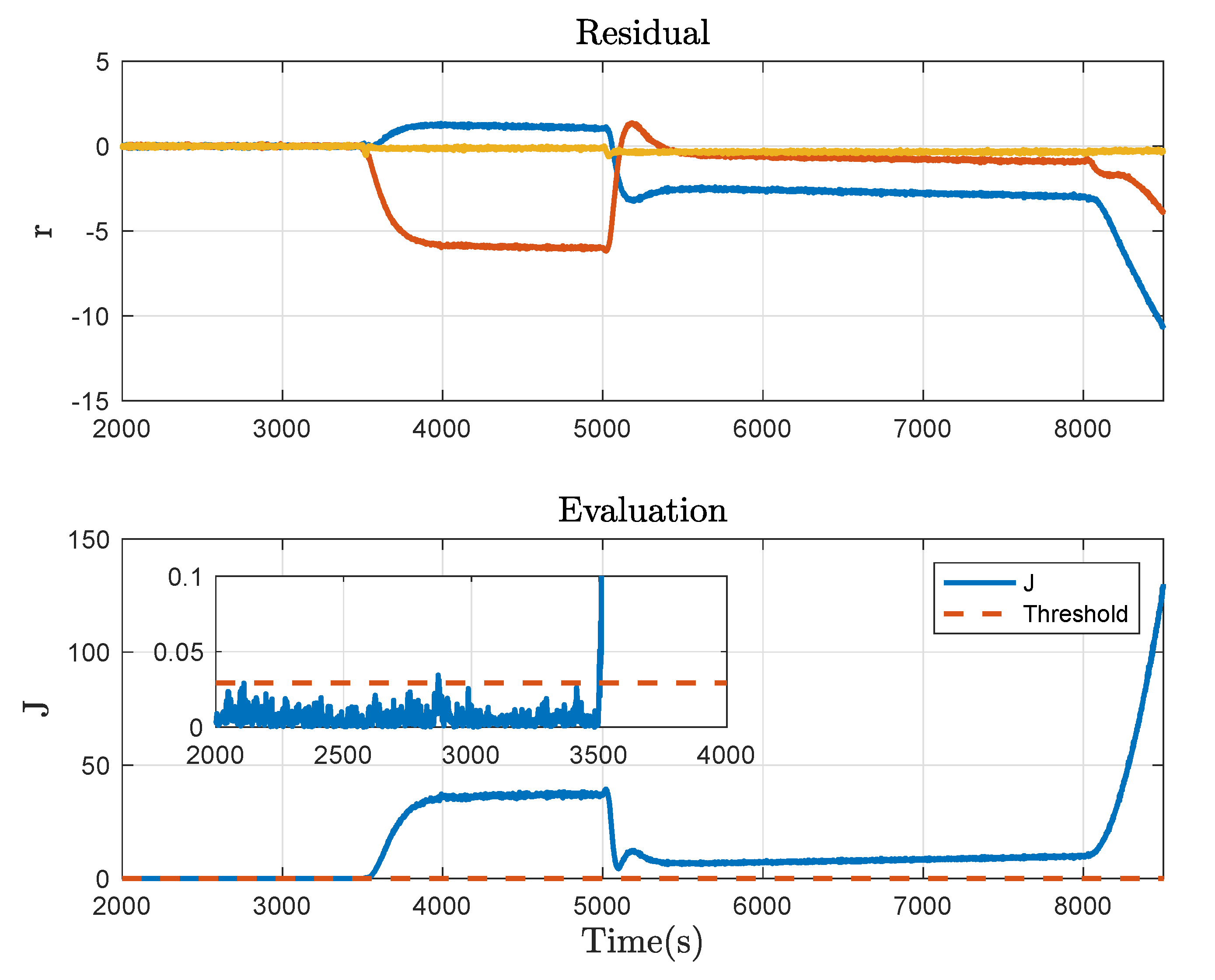
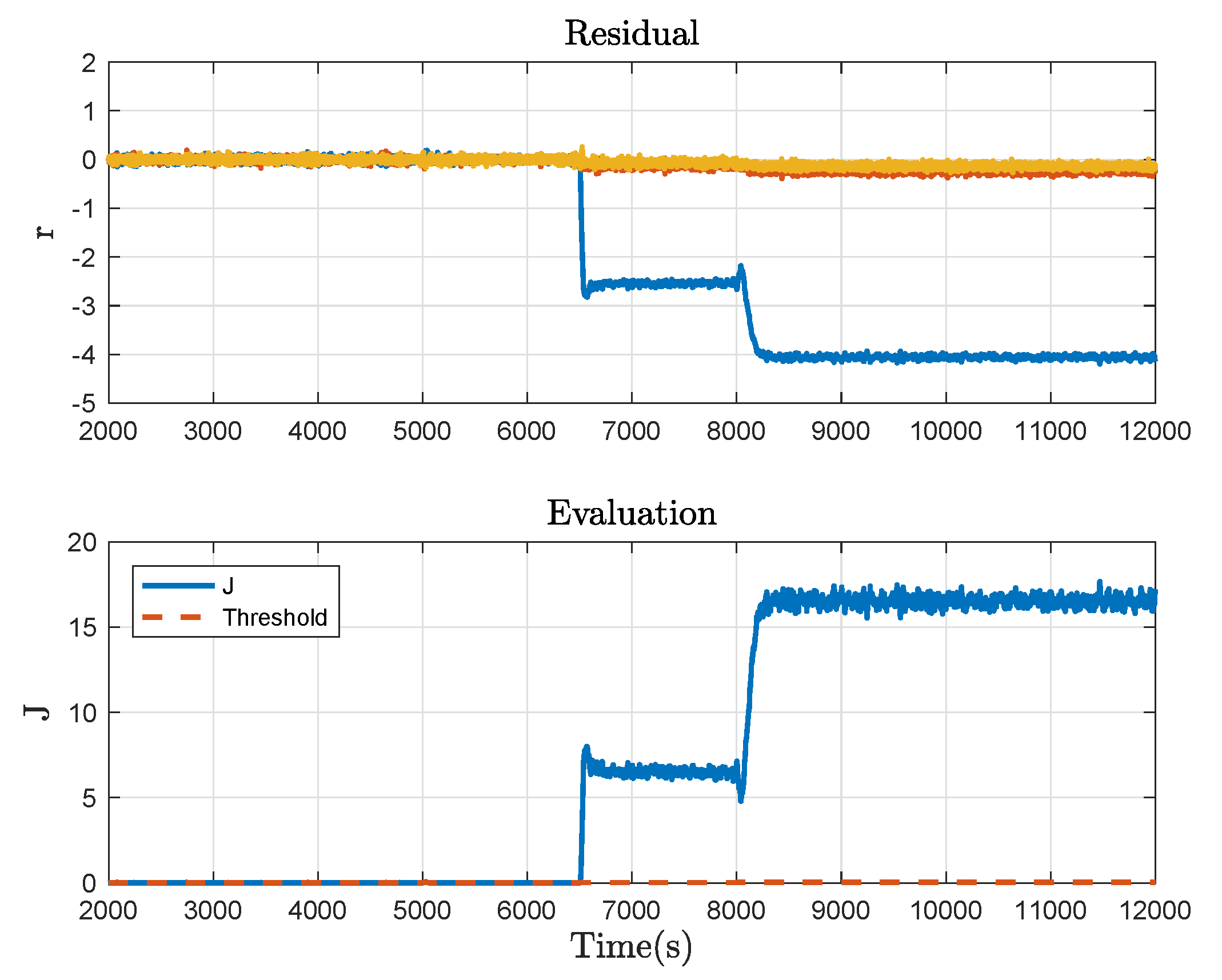
4. Benchmark Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Luo, H.; Ding, S.X.; Yang, Y.; Peng, K. Performance-based fault detection and fault-tolerant control for automatic control systems. Automatica 2019, 99, 308–316. [Google Scholar] [CrossRef]
- Shenfield, A.; Howarth, M. A novel deep learning model for the detection and identification of rolling element-bearing faults. Sensors 2020, 20, 5112. [Google Scholar] [CrossRef]
- Yang, Y.; Ding, S.X.; Li, L. Parameterization of nonlinear observer-based fault detection systems. IEEE Trans. Automat. Control 2016, 61, 3687–3692. [Google Scholar] [CrossRef]
- Mistry, P.; Lane, P.; Allen, P. Railway point-operating machine fault detection using unlabeled signaling sensor data. Sensors 2020, 20, 2692. [Google Scholar] [CrossRef]
- Yin, S.; Zhu, X. Intelligent particle filter and its application to fault detection of nonlinear system. IEEE Trans. Ind. Electron. 2015, 62, 3852–3861. [Google Scholar] [CrossRef]
- Yang, K.; Chu, R.; Zhang, R.; Xiao, J.; Tu, R. A novel methodology for series arc fault detection by temporal domain visualization and convolutional neural network. Sensors 2020, 20, 162. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, S.X.; Peng, T.; Yang, C.; Gui, W. Fault detection for non-Gaussian processes using generalized canonical correlation analysis and randomized algorithms. IEEE Trans. Ind. Electron. 2018, 65, 1559–1567. [Google Scholar] [CrossRef]
- Song, Y.; Yang, S.; Cheng, C.; Xie, P. A novel fault detection method for running gear systems based on dynamic inner slow feature analysis. IEEE Access 2020, 8, 211371–211379. [Google Scholar] [CrossRef]
- Patton, R.J.; Frank, P.M.; Clark, R.N. Issue of Fault Diagnosis for Dynamic Systems; Springer: Berlin, Germany, 2000. [Google Scholar]
- Ju, Y.; Wei, G.; Ding, D.; Zhang, S. Fault detection for discrete time-delay networked systems with round-robin protocol in finite-frequency domain. Int. J. Syst. Sci. 2019, 50, 2497–2509. [Google Scholar] [CrossRef]
- Zhai, X.; Xu, H.; Wang, G. Robust H-/H∞ fault detection observer design for polytopic spatially interconnected systems over finite frequency domain. Int. J. Robust Nonlinear Control 2020, 31, 404–426. [Google Scholar] [CrossRef]
- Liu, J.; Yang, L.; Xu, M.; Zhang, Q.; Yan, R.; Chen, X. Model-based detection of soft faults using the smoothed residual for a control system. Meas. Sci. Technol. 2020, 32, 015107. [Google Scholar] [CrossRef]
- Li, R.; Yang, Y. Fault detection for T-S fuzzy singular systems via integral sliding modes. J. Frankl. Inst. 2020, 357, 13125–13143. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, F.; Guo, S. Actuator fault detection for uncertain systems based on the combination of the interval observer and asymptotical reduced-order observer. Int. J. Control 2020, 93, 2653–2661. [Google Scholar] [CrossRef]
- Yin, S.; Gao, H.; Qiu, J.; Kaynak, O. Fault detection for nonlinear process with deterministic disturbances: A just-in-time learning based data driven method. IEEE Trans. Cybern. 2017, 47, 3649–3657. [Google Scholar] [CrossRef] [PubMed]
- Naderi, E.; Khorasani, K. Data-driven fault detection, isolation and estimation of aircraft gas turbine engine actuator and sensors. Mech. Syst. Signal Pr. 2018, 100, 415–438. [Google Scholar] [CrossRef]
- Fravolini, M.L.; del Core, G.; Papa, U.; Valigi, P.; Napolitano, M.R. Data-driven schemes for robust fault detection of air data system sensors. IEEE Trans. Control Syst. Technol. 2019, 27, 234–248. [Google Scholar] [CrossRef]
- Luo, H.; Yin, S.; Liu, T.; Khan, A.Q. A data-driven realization of the control-performance-oriented process monitoring system. IEEE Trans. Ind. Electron. 2020, 67, 521–530. [Google Scholar] [CrossRef]
- Russell, E.; Chiang, L.; Braatz, R. Data-Driven Methods for Fault Detection and Diagnosis in Chemical Processes; Springer: Berlin, Germany, 2000. [Google Scholar]
- Bazanella, A.S.; Campestrini, L.; Eckhard, D. Data-Driven Controller Design: The H2 Approach; Springer: Dordrecht, The Netherlands; New York, NY, USA, 2012. [Google Scholar]
- Cheng, C.; Qiao, X.; Luo, H.; Wang, H.; Teng, W.; Zhang, B. Data-driven incipient fault detection and diagnosis for the running gear in high-speed trains. IEEE Trans. Veh. Technol. 2020, 69, 9566–9576. [Google Scholar] [CrossRef]
- Huo, X.; Ma, L.; Zhao, X.; Zong, G. Observer-based fuzzy adaptive stabilization of uncertain switched stochastic nonlinear systems with input quantization. J. Frankl. Inst. 2019, 356, 1789–1809. [Google Scholar] [CrossRef]
- Zamani, I.; Shafiee, M.; Ibeas, A. Stability analysis of hybrid switched nonlinear singular time-delay systems with stable and unstable subsystems. Int. J. Syst. Sci. 2014, 45, 1128–1144. [Google Scholar] [CrossRef]
- Gong, C.S.A.; Li, S.W.; Shiue, M.T. A bootstrapped comparator-switched active rectifying circuit for wirelessly powered integrated miniaturized energy sensing systems. Sensors 2019, 19, 4714. [Google Scholar] [CrossRef]
- Bara, G.I. Robust switched static output feedback control for discrete-time switched linear systems. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 4986–4992. [Google Scholar]
- Yao, D.; Dou, C.; Yue, D.; Zhao, N.; Zhang, T. Event-triggered adaptive consensus tracking control for nonlinear switching multi-agent systems. Neurocomputing 2020, 415, 157–164. [Google Scholar] [CrossRef]
- Feng, C.; Wang, Q.; Liu, C.; Hu, C.; Liang, X. Variable-structure near-space vehicles with time-varying state constraints attitude control based on switched nonlinear system. Sensors 2020, 20, 848. [Google Scholar] [CrossRef] [PubMed]
- Aminsafaee, M.; Shafiei, M.H. Delayed state feedback predictive control of uncertain nonlinear discrete-time switched systems with input constraint and state delays. IET Control Theory Appl. 2020, 14, 2937–2947. [Google Scholar] [CrossRef]
- Zhao, H.; Peng, L.; Yu, H. Distributed model-free bipartite consensus tracking for unknown heterogeneous multi-agent systems with switching topology. Sensors 2020, 20, 4164. [Google Scholar] [CrossRef]
- Liberzon, D. Finite data-rate feedback stabilization of switched and hybrid linear systems. Automatica 2014, 50, 409–420. [Google Scholar] [CrossRef]
- Daafouz, J.; Riedinger, P.; Iung, C. Stability analysis and control syhthesis for switched systems: A switched Lyapunov function approach. IEEE Trans. Automat. Control 2002, 47, 1883–1887. [Google Scholar] [CrossRef]
- Zhao, X.; Yin, Y.; Niu, B.; Zheng, X. Stabilization for a class of switched nonlinear systems with novel average dwell time switching by T-S fuzzy modeling. IEEE Trans. Cybern. 2016, 46, 1952–1957. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Liu, T.; Sun, X.M. Stability analysis of cyclic switched linear systems: An average cycle dwell time approach. Inform. Sci. 2021, 544, 227–237. [Google Scholar] [CrossRef]
- Guan, C.; Fei, Z.; Karimi, H.R.; Shi, P. Finite-time synchronization for switched neural networks via quantized feedback control. IEEE Trans. Syst. Man Cybern. Syst. 2019. [Google Scholar] [CrossRef]
- Li, S.; Xiang, Z.; Zhang, J. Dwell-time conditions for exponential stability and standard L1-gain performance of discrete-time singular switched positive systems with time-varying delays. Nonlinear Anal. Hybrid Syst. 2020, 38, 100939. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, W.; Zhang, G. Finite-time stability and stabilization of Ito stochastic systems with Markovian switching: Mode-dependent parameter approach. IEEE Trans. Automat. Control 2015, 60, 2428–2433. [Google Scholar] [CrossRef]
- Vargas, A.N.; Costa, E.F.; do Val, J.B.R. On the control of Markov jump linear systems with no mode observation: Application to a DC motor device. Int. J. Robust Nonlinear Control 2013, 23, 1136–1150. [Google Scholar] [CrossRef]
- Li, K.; Mu, X. Necessary and sufficient conditions for leader-following consensus of multi-agent systems with random switching topologies. Nonlinear Anal. Hybrid Syst. 2020, 37, 100905. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Z.; Li, G.; Wang, W. Fault detection for switched positive systems under successive packet dropouts with application to the Leslie matrix model. Int. J. Robust Nonlinear Control 2016, 26, 2807–2823. [Google Scholar] [CrossRef]
- Li, J.; Pan, K.; Su, Q.; Zhao, X. Sensor fault detection and fault-tolerant control for buck converter via affine switched systems. IEEE Access 2019, 7, 47124–47134. [Google Scholar] [CrossRef]
- Du, D.; Xu, S.; Cocquempot, V. Finite-frequency fault detection filter design for discrete-time switched systems. IEEE Access 2018, 6, 70487–70496. [Google Scholar] [CrossRef]
- Liu, Y.; Arunkumar, A.; Sakthivel, R.; Nithya, V.; Alsaadi, F. Finite-time event-triggered non-fragile control and fault detection for switched networked systems with random packet losses. J. Frankl. Inst. 2020, 357, 11394–11420. [Google Scholar] [CrossRef]
- Raza, M.T.; Khan, A.Q.; Mustafa, G.; Abid, M. Design of Fault Detection and Isolation Filter for Switched Control Systems Under Asynchronous Switching. IEEE Trans. Control Syst. Technol. 2016, 24, 13–23. [Google Scholar] [CrossRef]
- Liu, X.; Su, X.; Shi, P.; Nguang, S.; Shen, C. Fault detection filtering for nonlinear switched systems via event-triggered communication approach. Automatica 2019, 101, 365–376. [Google Scholar] [CrossRef]
- Kazemi, M.G.; Montazeri, M. Fault detection of continuous time linear switched systems using combination of Bond Graph method and switching observer. ISA Trans. 2019, 94, 338–351. [Google Scholar] [CrossRef]
- Sun, T.; Zhou, D.; Zhu, Y.; Basin, M.V. Stability, l2-gain analysis, and parity space-based fault detection for discrete-time switched systems under dwell-time switching. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3358–3368. [Google Scholar] [CrossRef]
- Garbouj, Y.; Zouari, T.; Ksouri, M. Parity Space Method for Mode Detection of a Nonlinear Switching System Using Takagi-Sugeno Modeling. Int. J. Fuzzy Syst. 2019, 21, 837–851. [Google Scholar] [CrossRef]
- Li, L.; Ding, S.X. Gap metric techniques and their application to fault detection performance analysis and fault isolation schemes. Automatica 2020, 118, 109029. [Google Scholar] [CrossRef]
- Koenings, T.; Krueger, M.; Luo, H.; Ding, S.X. A data-driven computation method for the gap metric and the optimal stability margin. IEEE Trans. Automat. Control 2018, 63, 805–810. [Google Scholar] [CrossRef]
- Luo, H.; Zhao, H.; Yin, S. Data-driven design of fog-computing-aided process monitoring system for large-scale industrial processes. IEEE Trans. Ind. Inform. 2018, 14, 4631–4641. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Zhao, Z.; Zhou, J.; Liu, R. Fault detection via data-driven K-gap metric with application to ship propulsion systems. In Proceedings of the 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 6023–6027. [Google Scholar]

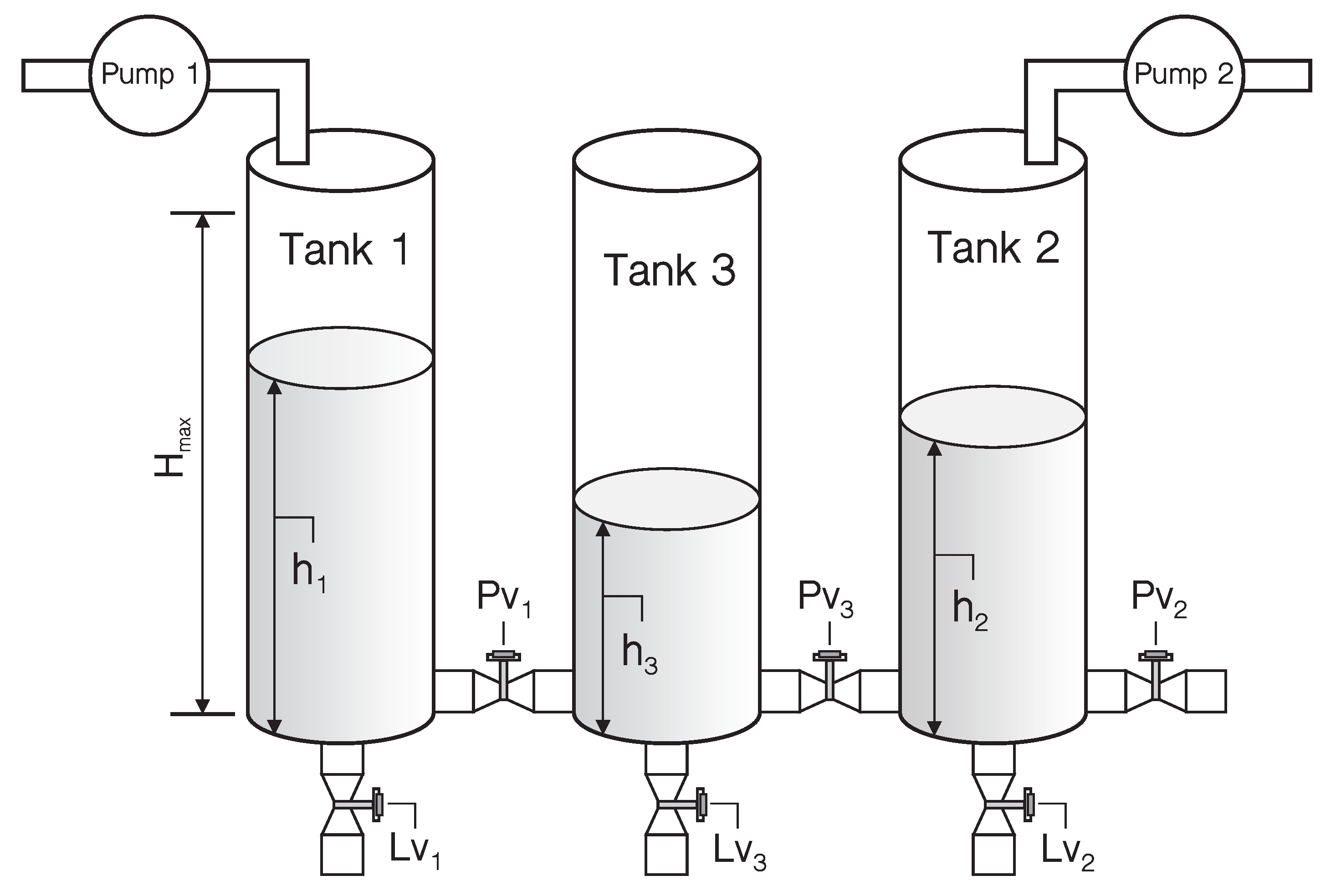

| Mode | PV | PV | PV | LV | LV | LV |
|---|---|---|---|---|---|---|
| Mode 1: | open | open | open | open | close | close |
| Mode 2: | open | open | open | close | close | close |
| Mode 3: | open | close | open | open | open | close |
| Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Cross section area of tanks | 154 | cm | |
| Cross section area of pipes | 0.5 | cm | |
| Cross section area of drain pipes | 0.5 | cm | |
| Max. height of tanks | 62 | cm | |
| Max. flow rate of pump 1 | 100 | cm | |
| Max. flow rate of pump 2 | 100 | cm | |
| Coeff. of flow for pipe 1 | 0.46 | ||
| Coeff. of flow for pipe 2 | 0.60 | ||
| Coeff. of flow for pipe 3 | 0.45 | ||
| Coeff. of flow for drain pipe 1 | 0.46 | ||
| Coeff. of flow for drain pipe 2 | 0.60 | ||
| Coeff. of flow for drain pipe 3 | 0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Luo, H.; Wu, Y. A Data-Driven Scheme for Fault Detection of Discrete-Time Switched Systems. Sensors 2021, 21, 4138. https://doi.org/10.3390/s21124138
Zhao H, Luo H, Wu Y. A Data-Driven Scheme for Fault Detection of Discrete-Time Switched Systems. Sensors. 2021; 21(12):4138. https://doi.org/10.3390/s21124138
Chicago/Turabian StyleZhao, Hao, Hao Luo, and Yunkai Wu. 2021. "A Data-Driven Scheme for Fault Detection of Discrete-Time Switched Systems" Sensors 21, no. 12: 4138. https://doi.org/10.3390/s21124138
APA StyleZhao, H., Luo, H., & Wu, Y. (2021). A Data-Driven Scheme for Fault Detection of Discrete-Time Switched Systems. Sensors, 21(12), 4138. https://doi.org/10.3390/s21124138







