Monopulse Secondary Surveillance Radar Coverage—Determinant Factors
Abstract
:1. Introduction
- Proposal of an MSSR antenna with custom geometry and feeding signals for an improved radiation pattern.
- Determination of the SUM beam radiation pattern, illustrating the horizontal, vertical, and 3D characteristics of the proposed MSSR antenna.
- Assessment of reflection and refraction events in radar coverage, highlighting the cause for the lobing phenomenon.
- Evaluation of the impact of the curvature of the Earth on the MSSR range, uniquely illustrating the perceived flight angle variation with the slant distance for an AVO in flight at constant level.
- Estimation of the link budget based on the features of the proposed MSSR antenna.
- Illustration of the theoretical findings by means of real MSSR measurements and positioning and analysis of extracted positioning data.
- MSSR coverage simulation in Radio Mobile.
2. Proposed MSSR Antenna
- -
- the SUM beam is obtained by employing the 35 front columns of the antenna and, to a small extent, the back column. It is used for the MSSR-aircraft dialogue.
- -
- the CONTROL beam is obtained by employing the back column and, through the CONTROL coupler (3 dB attenuation), the 35 front columns (with signal phase reversal). It is used for the validation of the MSSR request in the aircraft transponder and for the validation of the aircraft answer in the MSSR extractor.
- -
- the DIFFERENCE beam is the sum of the signal differences of the 17 right-left pairs of front columns for the purpose of off boresight angle (OBA) evaluation in the radar extractor [3]. It is used to improve the extracted AVO azimuth.
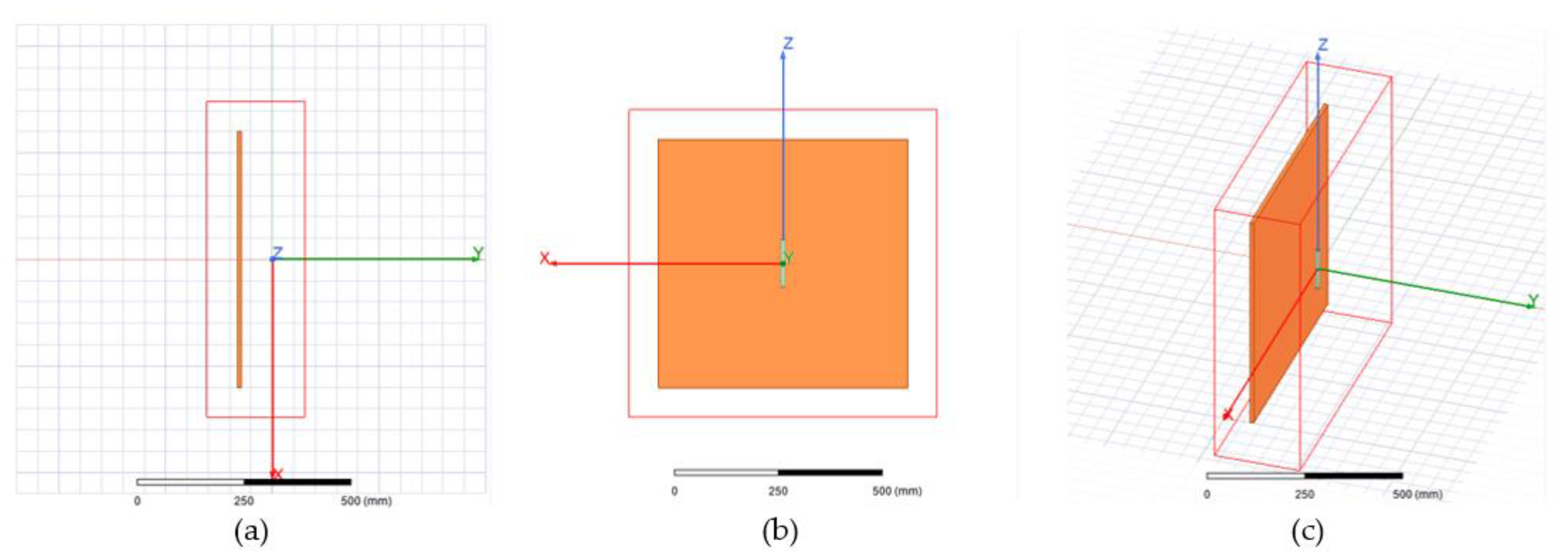
2.1. The Dipole with Reflector
2.2. Horizontal Pattern of SUM Beam
2.2.1. Currents Required for Feeding the Columns
2.2.2. The Horizontal Factor
2.3. Vertical Pattern of Sum Beam
2.3.1. Column Factor
2.3.2. Vertical Factor
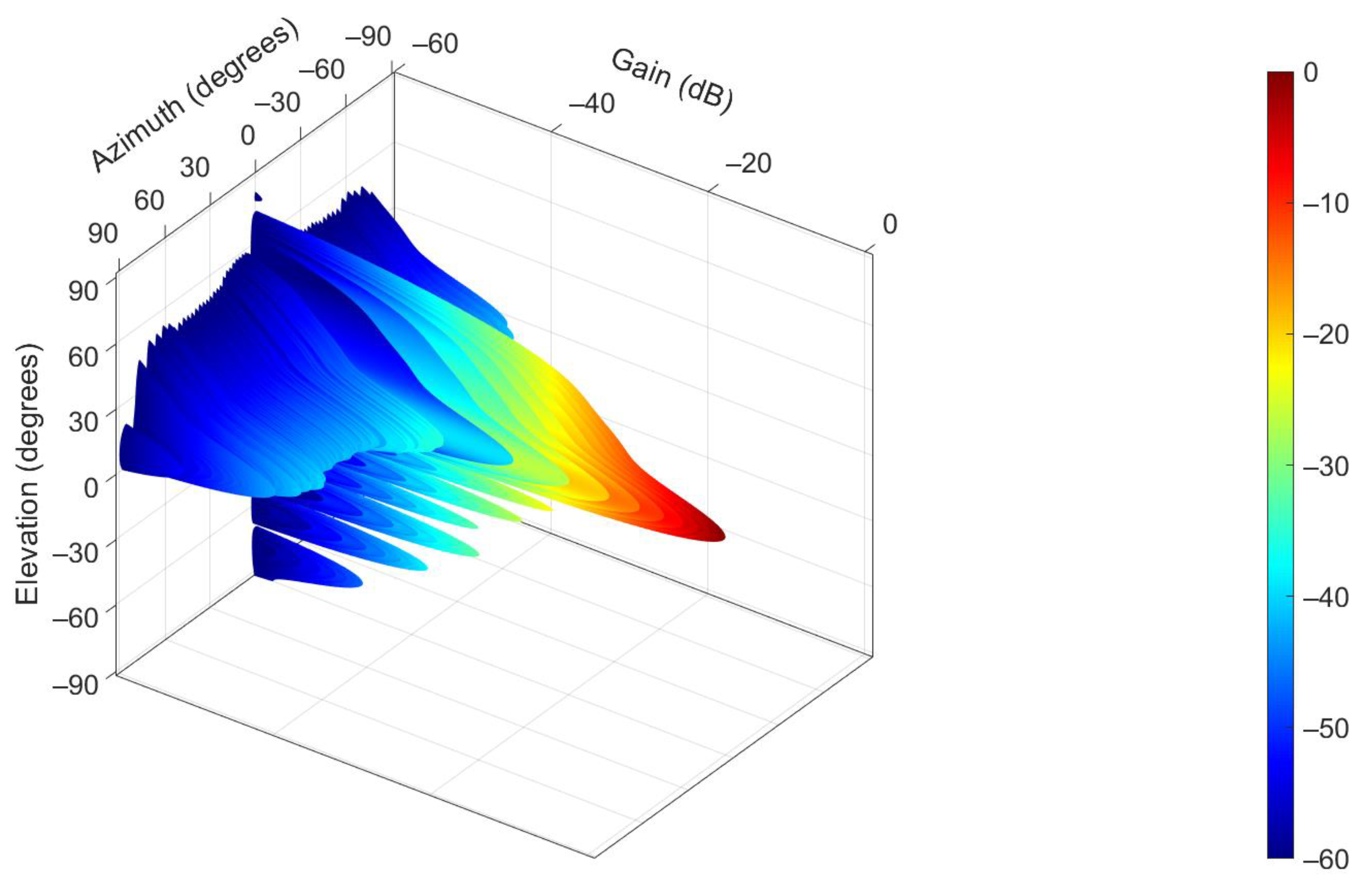
2.4. 3D Pattern of the MSSR Antenna
3. Radar coverage
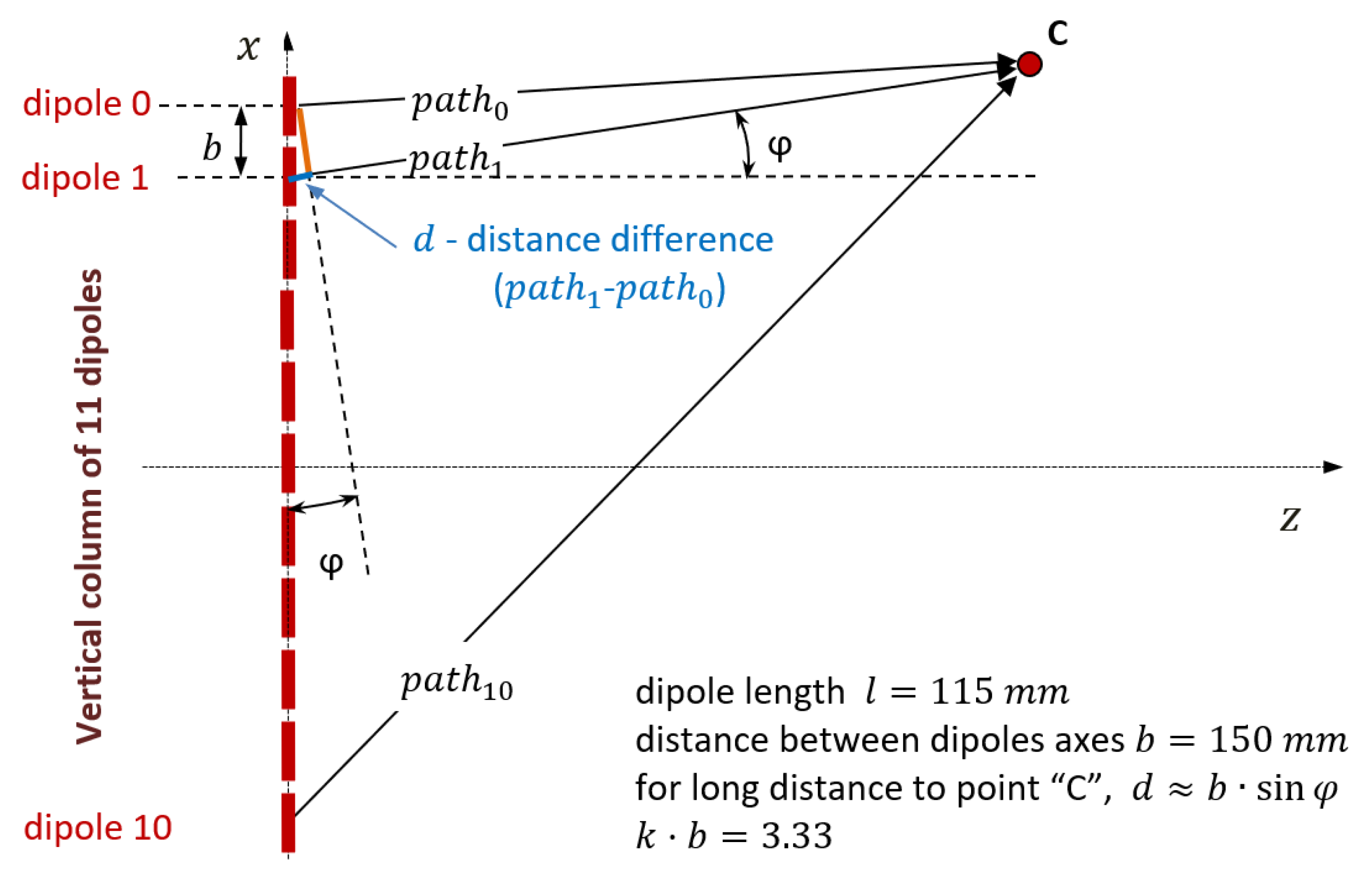
3.1. Refraction in the Earth’s Atmosphere
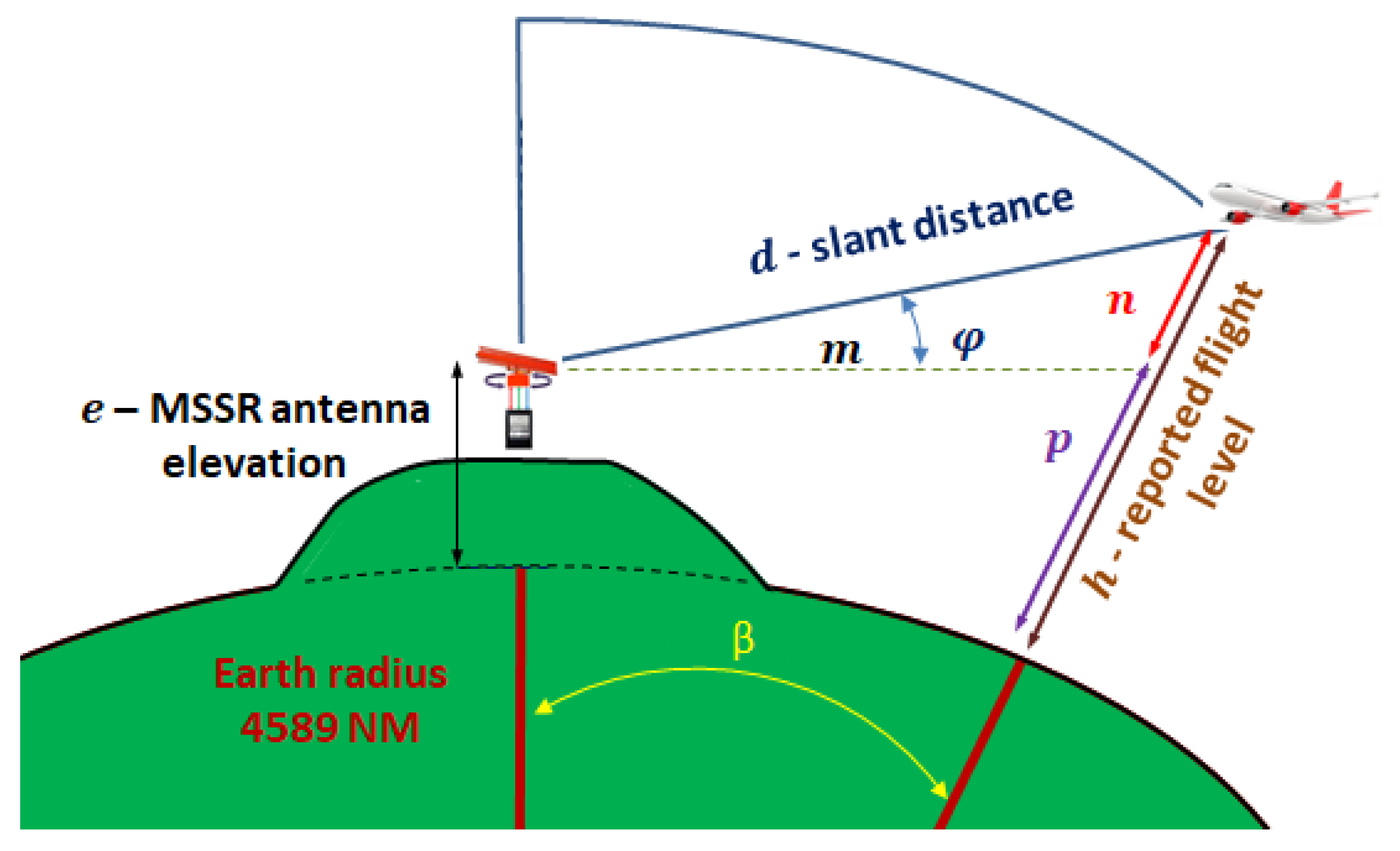
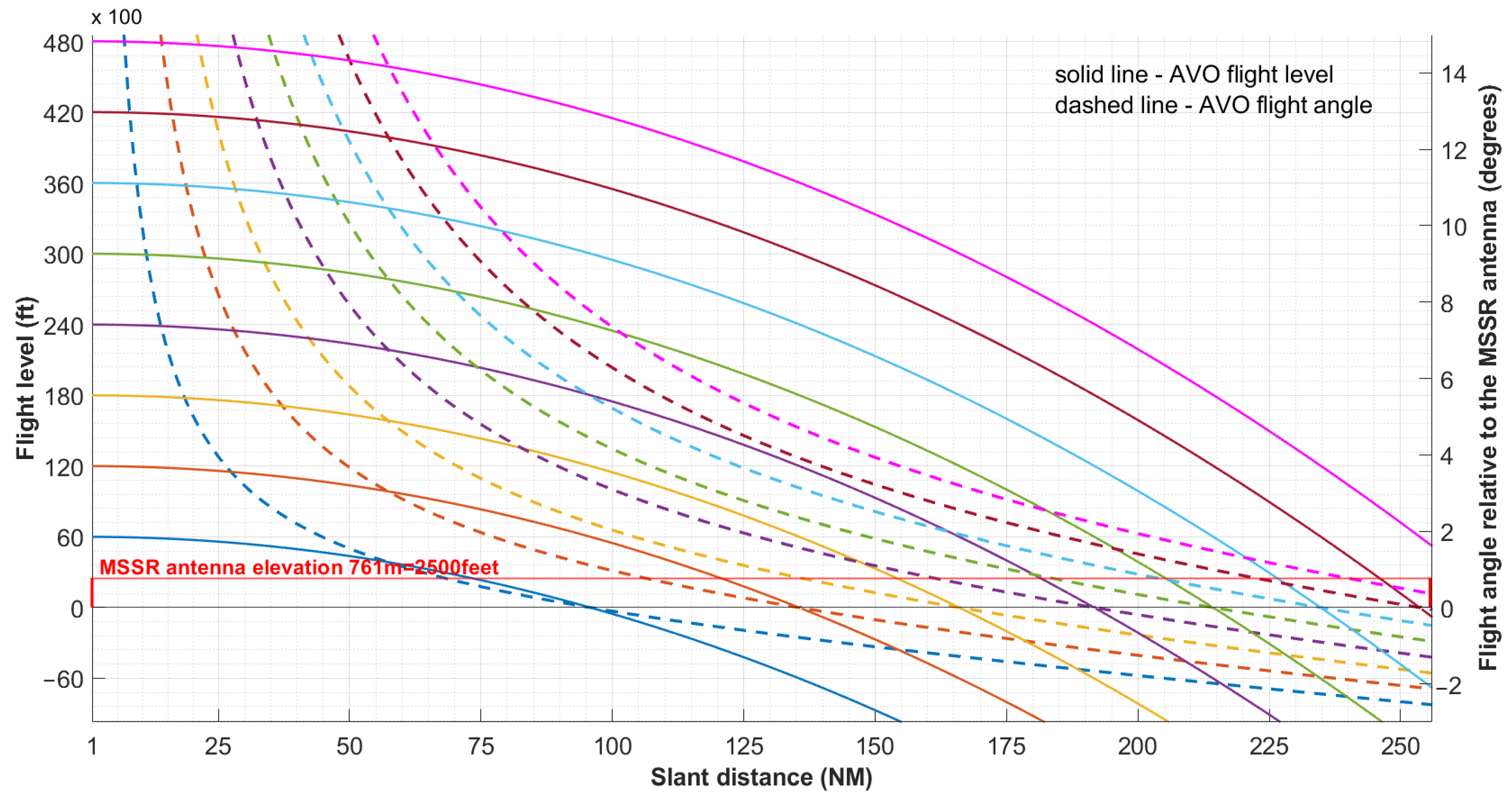
3.2. Flight at Constant Height
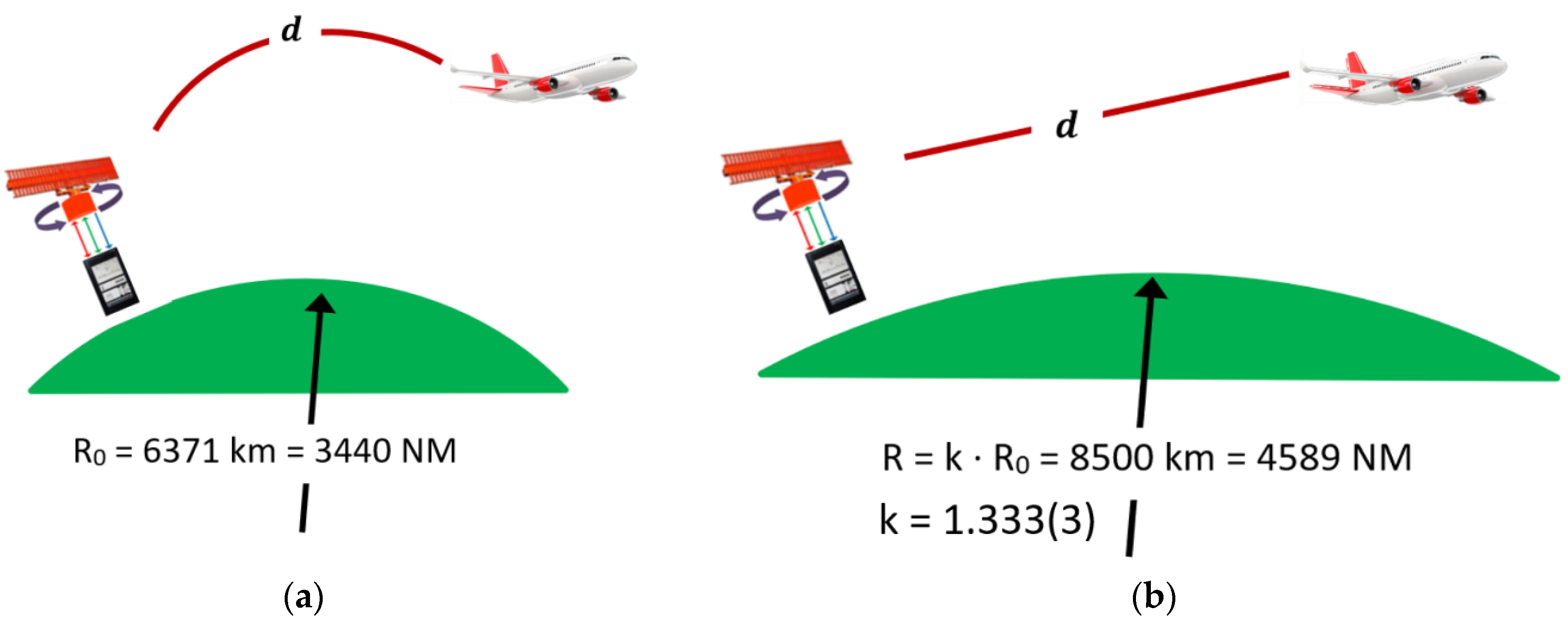
3.3. Radar Range
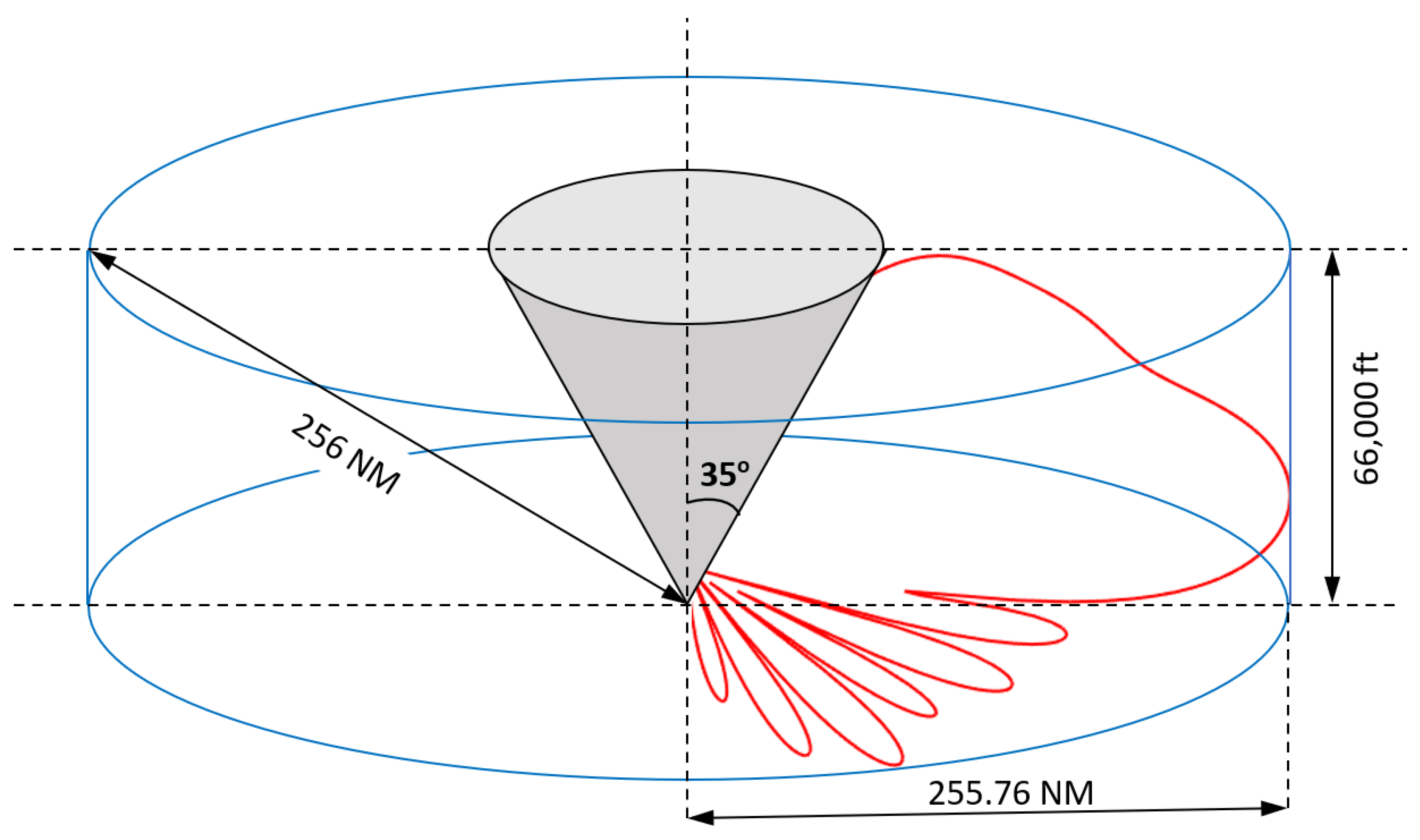
3.4. Volume Coverage
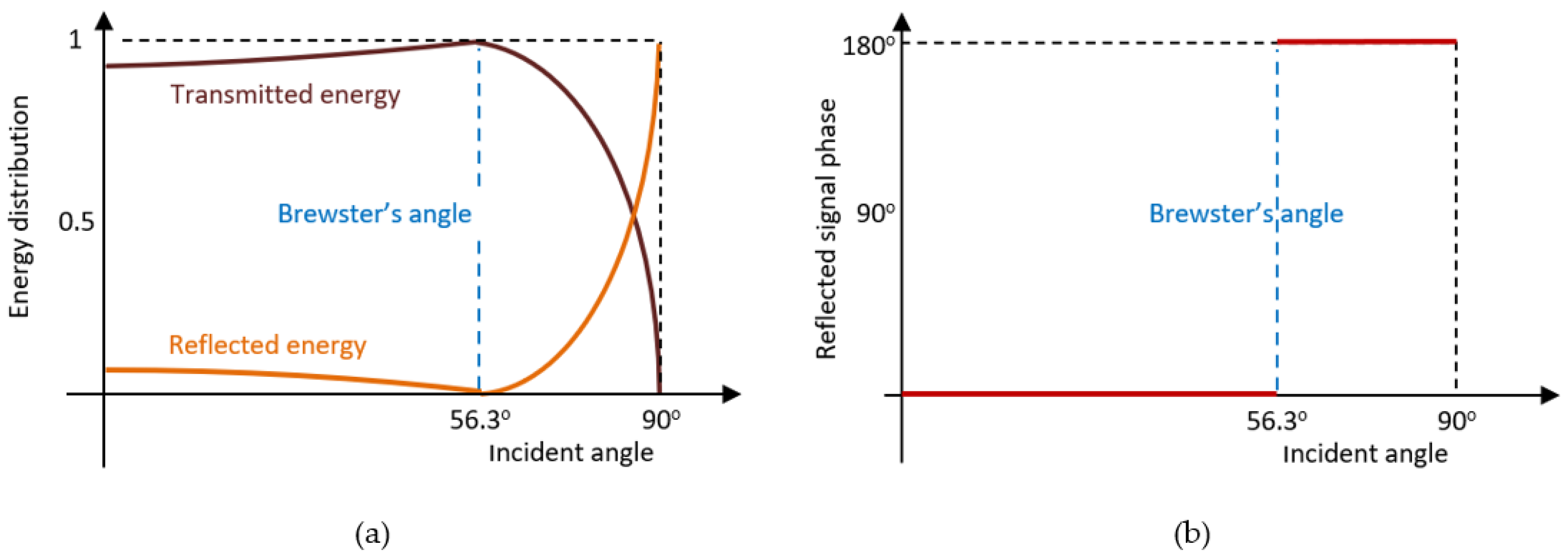
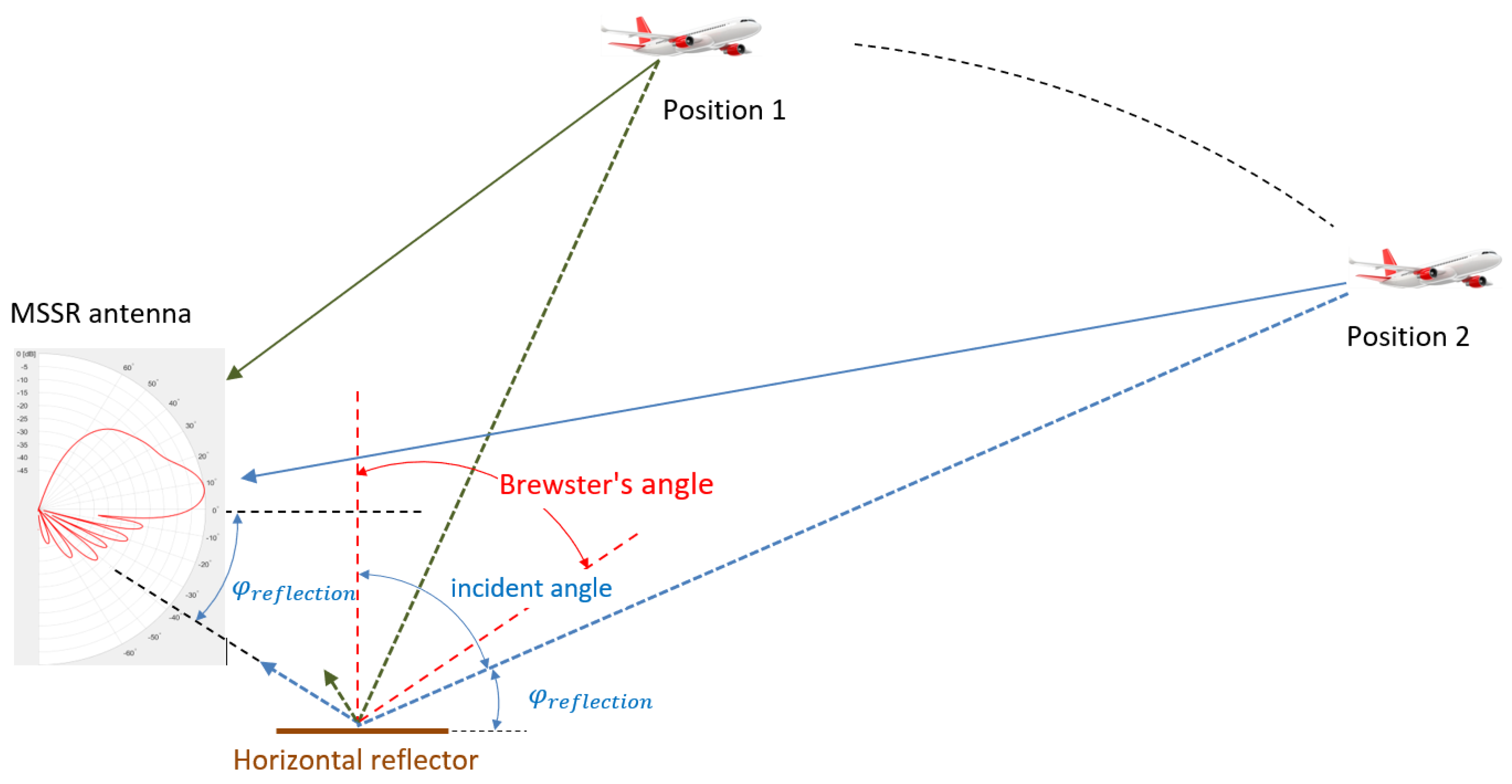
3.5. Reflections Due to Antenna Positioning
3.6. Multipath Propagation in the MSSR-Aircraft Transmission
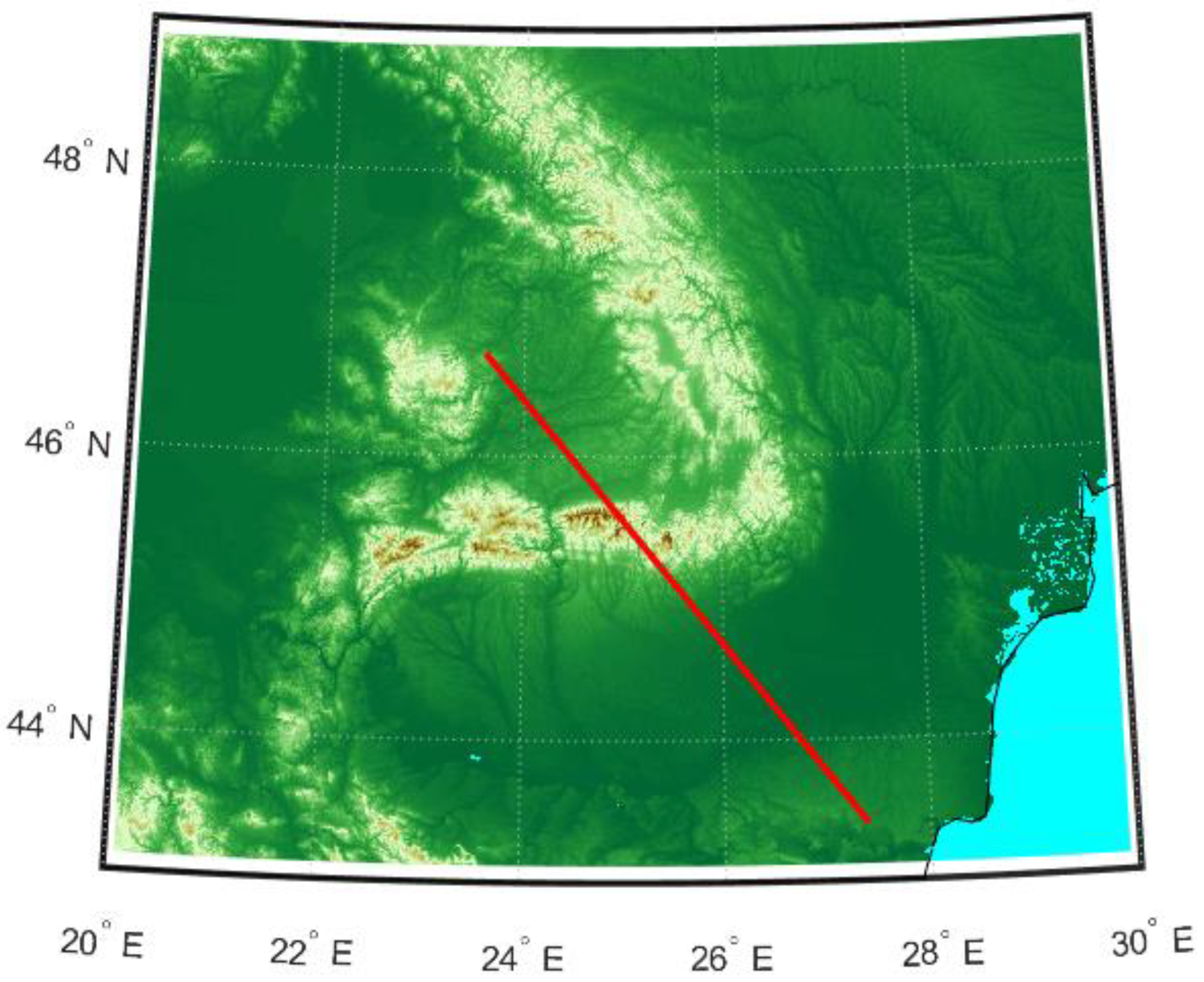
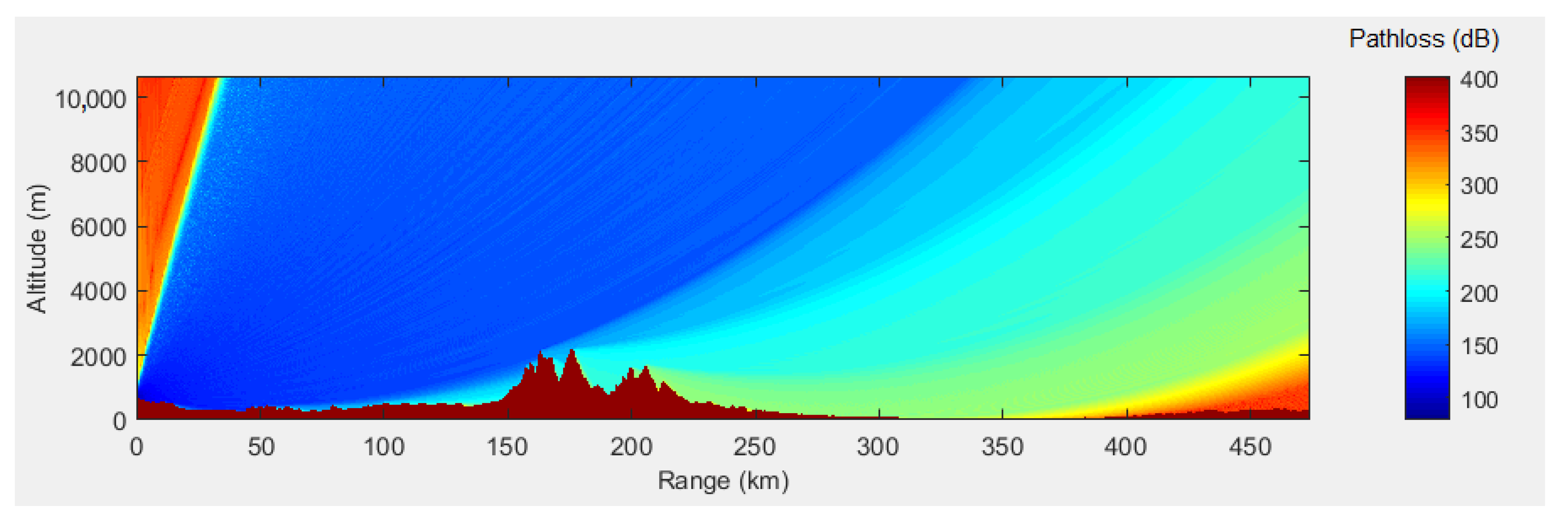
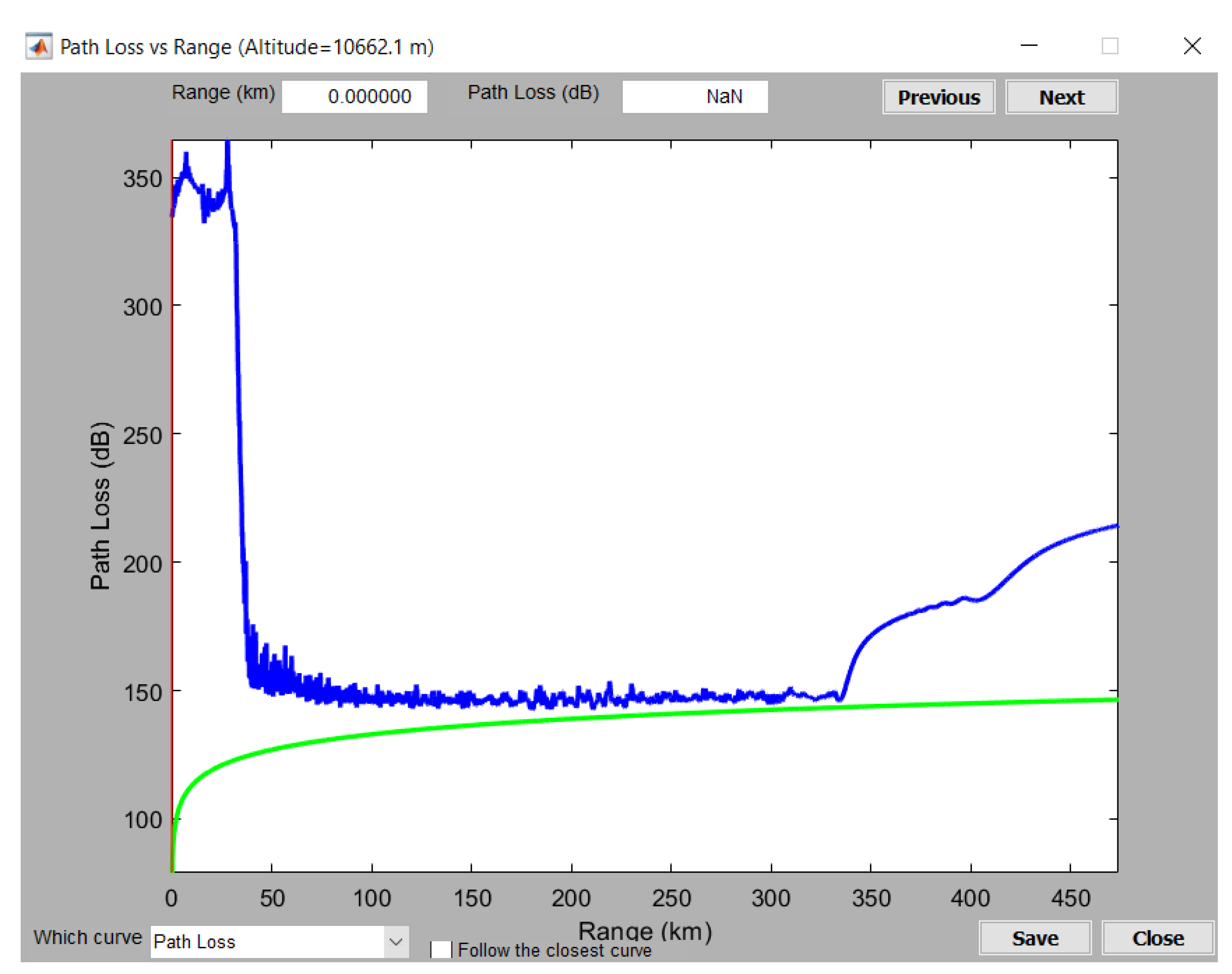
4. Experimental Measurements and Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Lim, T.H.; Go, M.; Seo, C.; Choo, H. Analysis of the Target Detection Performance of Air-to-Air Airborne Radar Using Long-Range Propagation Simulation in Abnormal Atmospheric Conditions. Appl. Sci. 2020, 10, 6440. [Google Scholar] [CrossRef]
- Stevens, M.C. Secondary Surveillance Radar; Artech House, Inc.: Norwood, MA, USA, 1988; ISBN 0-89006-292-7. [Google Scholar]
- Barton, D.K.; Leonov, S.A. Radar Technology Encyclopedia; Artech House, Inc.: Norwood, MA, USA, 1998; ISBN 0-89006-893-3. [Google Scholar]
- Skolnik, M.I. Introduction to Radar Systems, 3rd ed.; The McGraw-Hill Book Co.: Singapore, 1981. [Google Scholar]
- International Civil Aviation Organization. Surveillance and Collision Avoidance Systems. Annex 10, 4th ed.; International Civil Aviation Organization: Montréal, QC, Canada, 2007; Volume 4, ISBN 92-9194-952-3. [Google Scholar]
- International Civil Aviation Organization. Doc 8071, Manual on Testing of Radio Navigation AIDS. In Testing of Surveillance RADAR Systems; International Civil Aviation Organization: Montréal, QC, Canada, 2002; Volume 3. [Google Scholar]
- Zalabsky, T.; Hnilicka, T. An Antenna Array Synthesis for Large Vertical Aperture Antenna for Secondary Surveillance Radar. In Proceedings of the 2017 International Symposium ELMAR, Zadar, Croatia, 18–20 September 2017; IEEE: New York, NY, USA, 2017; pp. 119–122. [Google Scholar] [CrossRef]
- Schejbal, V.; Bezousek, P.; Pidanic, J.; Chyba, M. Secondary Surveillance Radar Antenna [Antenna Designer’s Notebook]. IEEE Antennas Propag. Mag. 2013, 55, 164–170. [Google Scholar] [CrossRef]
- Závodný, V. MSSR-Monopulse Secondary Surveillance Radar. Eldis Pardubice, sro., Pardubice, Czech Republic. Available online: www.urel.feec.vutbr.cz/~sebestaj/MRAR/MRAR_P_CZ06.pdf (accessed on 28 February 2020).
- Weber, M.; Wood, M.; Franz, J.; Conway, M.; Cho, J.Y.N. Secondary Surveillance Phased Array Radar (SSPAR): Initial Feasibility Study; Lincoln Laboratory, Massachusetts Institute of Technology: Lexington, MA, USA, 2014. [Google Scholar] [CrossRef]
- T-CZ, A.S. Monopulse Secondary Surveillance Radar Antenna, Pardubice, Czech Republic. 2021. Available online: https://www.tcz.cz/wp-content/uploads/2021/02/www.tcz.cz-standardizovane-produkty-t-cz-monopulse-secondary-surveillance-radar-antenna.pdf (accessed on 11 May 2021).
- Zavodny, V.; Schejbal, V.; Bezousek, P. Primary surveillance radar of RSP-10M system. In Proceedings of the 2018 28th International Conference Radioelektronika (RADIOELEKTRONIKA), Prague, Czech Republic, 19–20 April 2018; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zavodny, V.; Bezousek, P.; Schejbal, V. Secondary surveillance radar for RSP-10M system. In Proceedings of the 2018 28th International Conference Radioelektronika (RADIOELEKTRONIKA), Prague, Czech Republic, 19–20 April 2018; IEEE: New York, NY, USA, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Denney, E.; Pai, G. Safety considerations for UAS ground-based detect and avoid. In Proceedings of the 2016 IEEE/AIAA 35th Digital Avionics Systems Conference (DASC), Sacramento, CA, USA, 25–30 September 2016; IEEE: New York, NY, USA, 2016; pp. 1–10. [Google Scholar] [CrossRef]
- Eslami Nazari, M.; Ghorbani, A. Predicting a Three-Dimensional Radar Coverage Area: Introducing a new method based on propagation of radio waves. IEEE Antennas Propag. Mag. 2016, 58, 28–34. [Google Scholar] [CrossRef]
- European Aviation Safety Agency. MOSTDONT—Mode S Transponder in High Density Operational Environment. Research Project EASA.2009/2. Final Report. 2010. Available online: https://www.easa.europa.eu/document-library/research-reports/easa20092 (accessed on 1 June 2021).
- Minteuan, G.; Palade, T. Monopulse Secondary Surveillance Radar Antenna Theory. In Proceedings of the 2020 International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 5–6 November 2020; IEEE: New York, NY, USA, 2020; pp. 1–4. [Google Scholar] [CrossRef]
- International Civil Aviation Organization. Manual on the Secondary Surveillance Radar (SSR) Systems. Doc 9684. AN/951, 3rd ed.; International Civil Aviation Organization: Montréal, QC, Canada, 2004. [Google Scholar]
- INDRA. Monopulse Secondary Surveillance Mode-S Radar. Available online: https://www.indracompany.com/sites/default/files/indra-monopulse_secondary_surveillance_mode_s_radar.pdf (accessed on 18 March 2021).
- Radartutorial. Large Vertical Aperture (LVA) Antennas. Available online: https://www.radartutorial.eu/19.kartei/ka12.en.html (accessed on 11 May 2021).
- Balanis, C.A. Antenna Theory—Analysis and Design, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; ISBN 0-471-66782-X. [Google Scholar]
- Hansen, R.C. Phased Array Antennas, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 86–92. ISBN 978-0-470-40102-6. [Google Scholar]
- Taylor, T.T. Design of Line-Source Antennas for Narrow Beamwidth and Low Side Lobes. Trans. IRE Prof. Group Antennas Propag. 1955, 3, 16–28. [Google Scholar] [CrossRef]
- Mailloux, R.J. Phase Array Antenna Handbook, 2nd ed.; Artech House, Inc.: Norwood, MA, USA, 2005. [Google Scholar]
- Milligan, T.A. Modern Antenna Design, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; ISBN-13 978-0-471-45776-3. [Google Scholar]
- Volakis, J.L. Antenna Engineering Handbook, 4th ed.; The McGraw-Hill Com.: New York, NY, USA, 2007. [Google Scholar]
- Szüllő, Á.; Orbán, J.; Mikó, G. Development of a multichannel vector network analyzer for “in situ” measurement of radar antennas. In Proceedings of the 2015 Conference on Microwave Techniques (COMITE), Pardubice, Czech Republic, 22–23 April 2015; IEEE: New York, NY, USA, 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Tucker, N. Phased Array Design Toolbox v2.5, MATLAB Central File Exchange. 2021. Available online: https://www.mathworks.com/matlabcentral/fileexchange/22942-phased-array-design-toolbox-v2-5 (accessed on 2 June 2021).
- Ansys HFSS. Available online: https://www.ansys.com/products/electronics/ansys-hfss (accessed on 2 June 2021).
- Doerry, A.W. Earth Curvature and Atmospheric Refraction Effects on Radar Signal Propagation; SANDIA Report SAND2012-10690; Sandia National Laboratories: Albuquerque, NM, USA, 2013. [Google Scholar]
- Sjoberg, D. EITN90 Radar and Remote Sensing Lecture 3: Propagation Effects and Mechanisms; Department of Electrical and Information Technology, Faculty of Engineering LTH, Lund University: Lund, Sweden, 2018; Available online: https://www.eit.lth.se/fileadmin/eit/courses/eitn90/2018/lecture3.pdf (accessed on 11 May 2021).
- Raytheon. Condor Mk 3 Mode S MSSR Monopulse Secondary Surveillance Radar. Available online: https://www.raytheon.com/sites/default/files/capabilities/rtnwcm/groups/rsl/documents/content/rtn_304605.pdf (accessed on 18 March 2021).
- AeroEXPO. INTELCAN—SKYSURV Monopulse Secondary Surveillance Radar (MSSR), Catalog Excerpt. Available online: https://pdf.aeroexpo.online/pdf/intelcan/skysurv-monopulse-secondary-surveillance-radar-mssr/171084-11647.html (accessed on 11 May 2021).
- Jarama, Á.J.; López-Araquistain, J.; De Miguel, G.; Besada, J.A. Complete Systematic Error Model of SSR for Sensor Registration in ATC Surveillance Networks. Sensors 2017, 17, 2171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, F.T.S.; Yang, X. Introduction to Optical Engineering; Cambridge University Press: New York, NY, USA, 1997; ISBN 0-521-57493-5. [Google Scholar]
- Chen, Q.; Won, D.; Akos, D.M. Snow depth sensing using the GPS L2C signal with a dipole antenna. EURASIP J. Adv. Signal Process. 2014, 2014, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Von Hippel, A.R.; Morgan, S.O. Dielectric Materials and Applications. J. Electrochem. Soc. 1955, 102, 68C. [Google Scholar] [CrossRef]
- Najibi, N.; Jin, S. Physical Reflectivity and Polarization Characteristics for Snow and Ice-Covered Surfaces Interacting with GPS Signals. Remote Sens. 2013, 5, 4006–4030. [Google Scholar] [CrossRef] [Green Version]
- International Telecommunication Union-Radiocommucation Sector (ITU-R). Electrical characteristics of the surface of the Earth. In Radiowave Propagation; P Series; Recommendation ITU-R P.527-4 (06/2017); ITU: Geneva, Switzerland, 2017. [Google Scholar]
- International Civil Aviation Organization. Aeronautical Surveillance Manual, 1st ed.; International Civil Aviation Organization: Montréal, QC, Canada, 2010. [Google Scholar]
- Gundersen, R.; Norland, R.; Denby, C.R. Geometric, Environmental and Hardware Error Sources of a Ground-Based Interferometric Real-Aperture FMCW Radar System. Remote Sens. 2018, 10, 2070. [Google Scholar] [CrossRef] [Green Version]
- Johnson, R.C. Antenna Engineering Handbook, 3rd ed.; The McGraw-Hill Com.: New York, NY, USA, 1993. [Google Scholar]
- Schejbal, V.; Ondrej, F.; Zavodny, V. Study of Refraction Effects for Propagation over Terrain. In Electromagnetic Propagation and Waveguides in Photonics and Microwave Engineering; Steglich, P., Ed.; IntechOpen: Rijeka, Croatia, 2020; ISBN 978-1-83968-189-9. [Google Scholar] [CrossRef]
- Sommer, C.; Dressler, F. Using the Right Two-Ray Model? A Measurement based Evaluation of PHY Models in VANETs. In Proceedings of the 17th ACM International Conference on Mobile Computing and Networking (MobiCom 2011), Poster Session, Las Vegas, NV, USA, 19–23 September 2011. [Google Scholar]
- Ozgun, O.; Sahin, V.; Erguden, M.E.; Apaydin, G.; Yilmaz, A.E.; Kuzuoglu, M.; Sevgi, L. PETOOL v2.0: Parabolic Equation Toolbox with evaporation duct models and real environment data. Comput. Phys. Commun. 2020, 256, 107454. [Google Scholar] [CrossRef]
- Ozgun, O.; Apaydin, G.; Kuzuoglu, M.; Sevgi, L. PETOOL: MATLAB-based one-way and two-way split-step parabolic equation tool for radiowave propagation over variable terrain. Comput. Phys. Commun. 2011, 182, 2638–2654. [Google Scholar] [CrossRef]
- Lilly, B.; Cetinkaya, D.; Durak, U. Tracking Light Aircraft with Smartphones at Low Altitudes. Information 2021, 12, 105. [Google Scholar] [CrossRef]
- Coudé, R. VE2DBE. Radio Mobile. Available online: http://radiomobile.pe1mew.nl/ (accessed on 28 May 2021).
- Hufford, G.A.; Longley, A.G.; Kissick, W.A. A Guide to the Use of the ITS Irregular Terrain Model in the Area Prediction Mode; NTIA REPORT 82–100; US Department of Commerce, National Telecommunications and Information Administration: Washington, DC, USA, 1982. [Google Scholar]
- Fratu, O.; Martian, A.; Craciunescu, R.; Vulpe, A.; Halunga, S.; Zaharis, Z.; Lazaridis, P.; Kasampalis, S.; Octavian, F. Comparative study of Radio Mobile and ICS Telecom propagation prediction models for DVB-T. In Proceedings of the 2015 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, Ghent, Belgium, 17–19 June 2015; IEEE: New York, NY, USA, 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Kasampalis, S.; Lazaridis, P.I.; Zaharis, Z.; Bizopoulos, A.; Zettas, S.; Cosmas, J. Comparison of Longley-Rice, ITU-R P.1546 and Hata-Davidson propagation models for DVB-T coverage prediction. In Proceedings of the 2014 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, Beijing, China, 25–27 June 2014; IEEE: New York, NY, USA, 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Federal Aviation Administration. VOR, VOR/DME and VORTAC Siting Criteria; FAA: Washington, DC, USA, 1986.








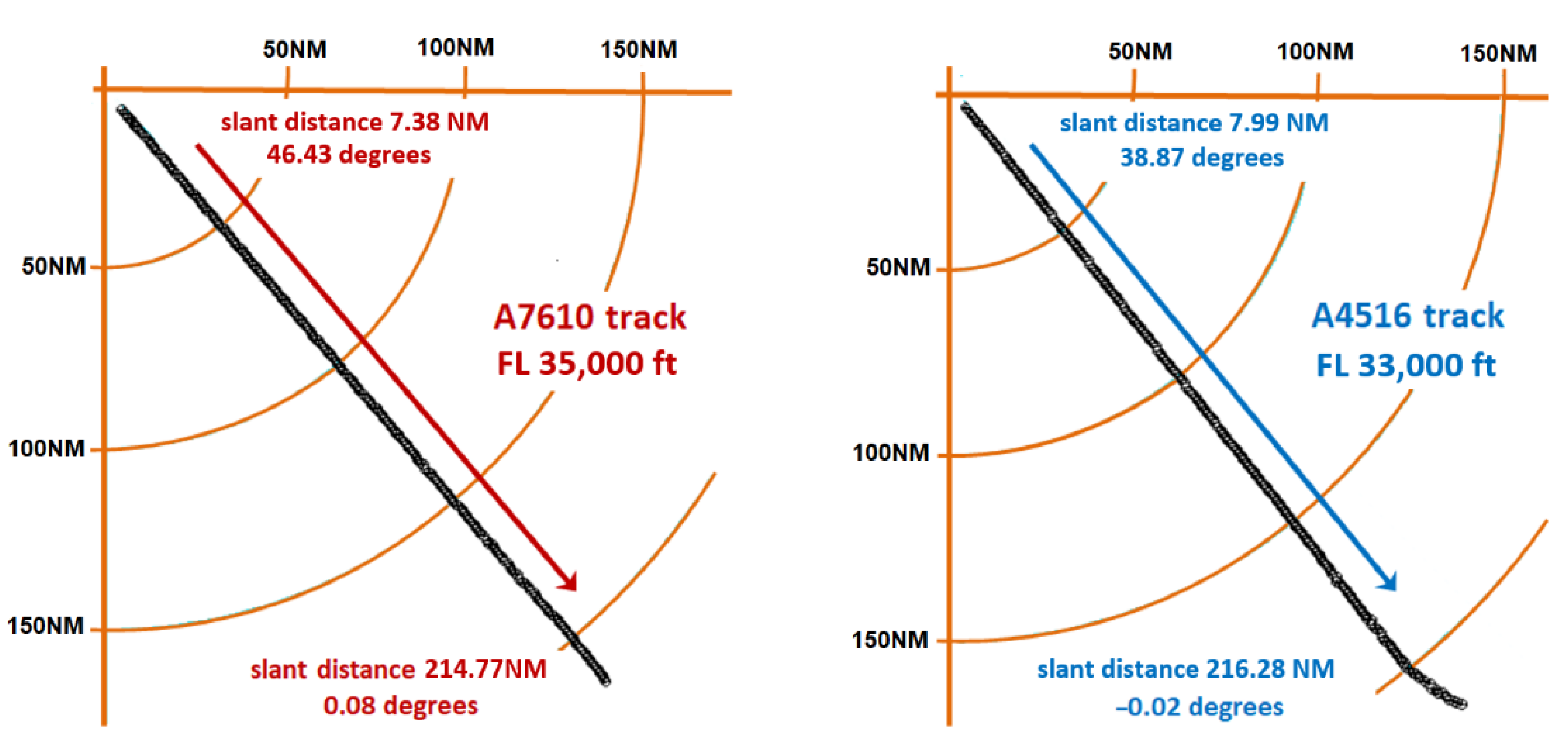
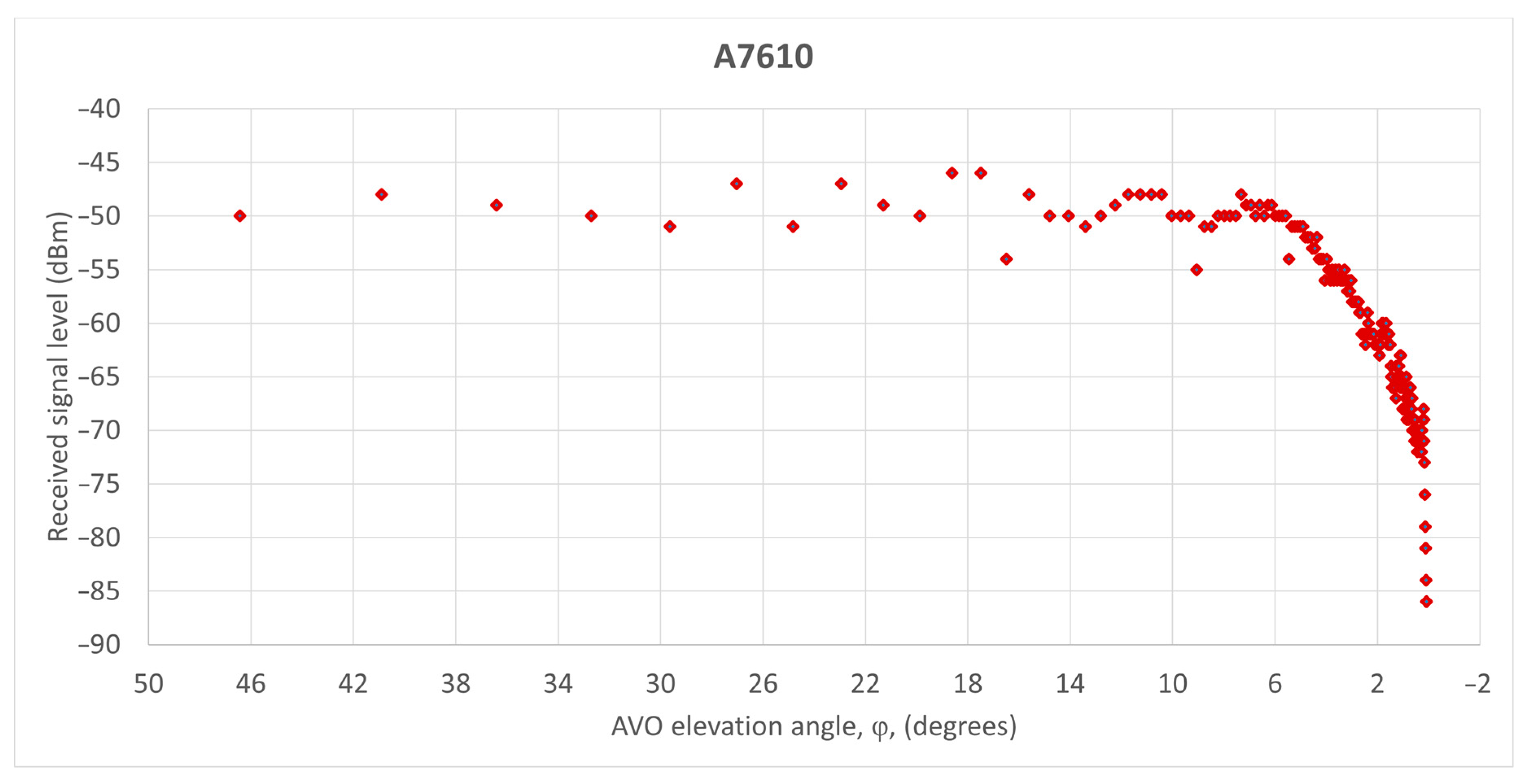
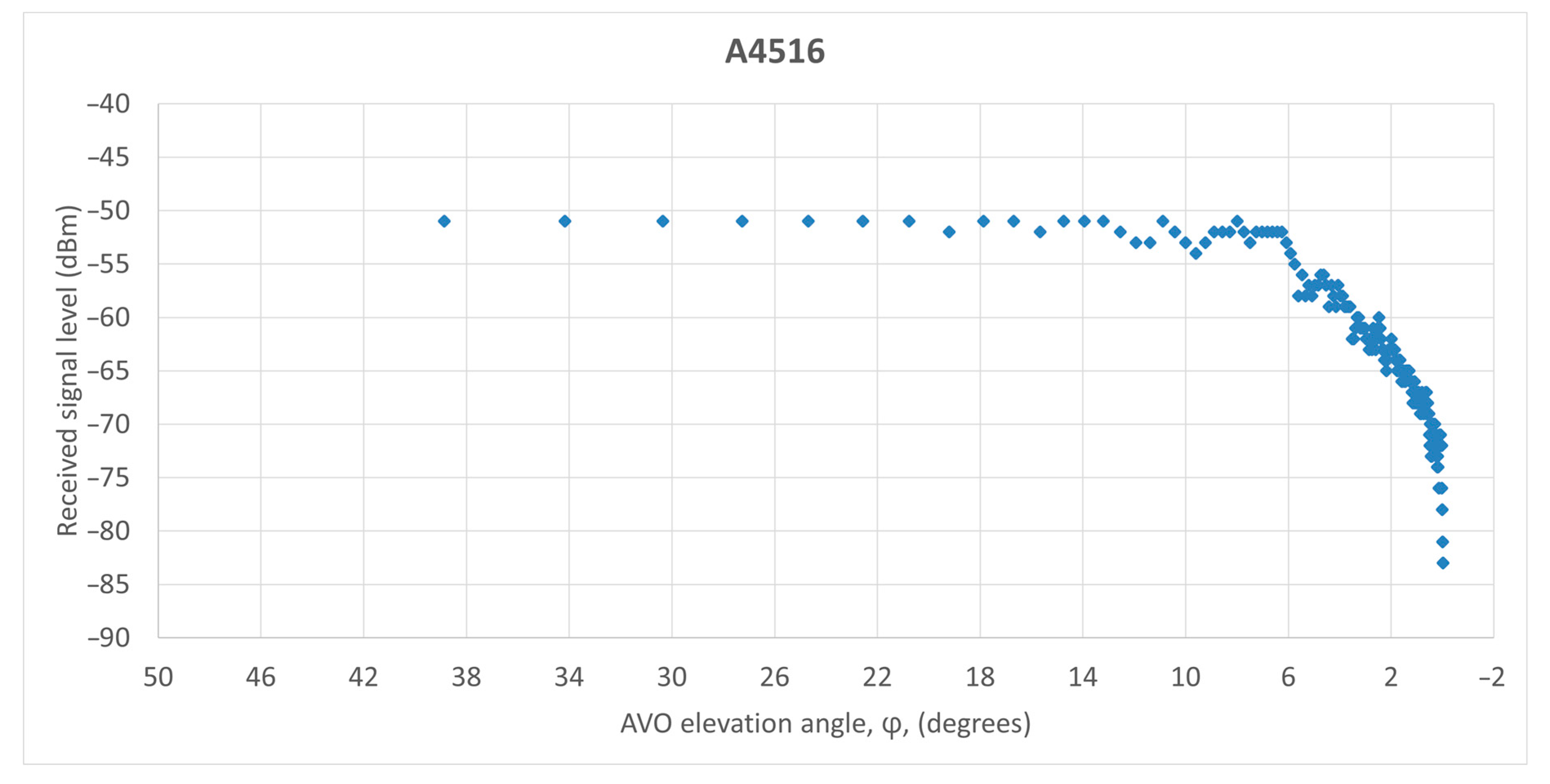

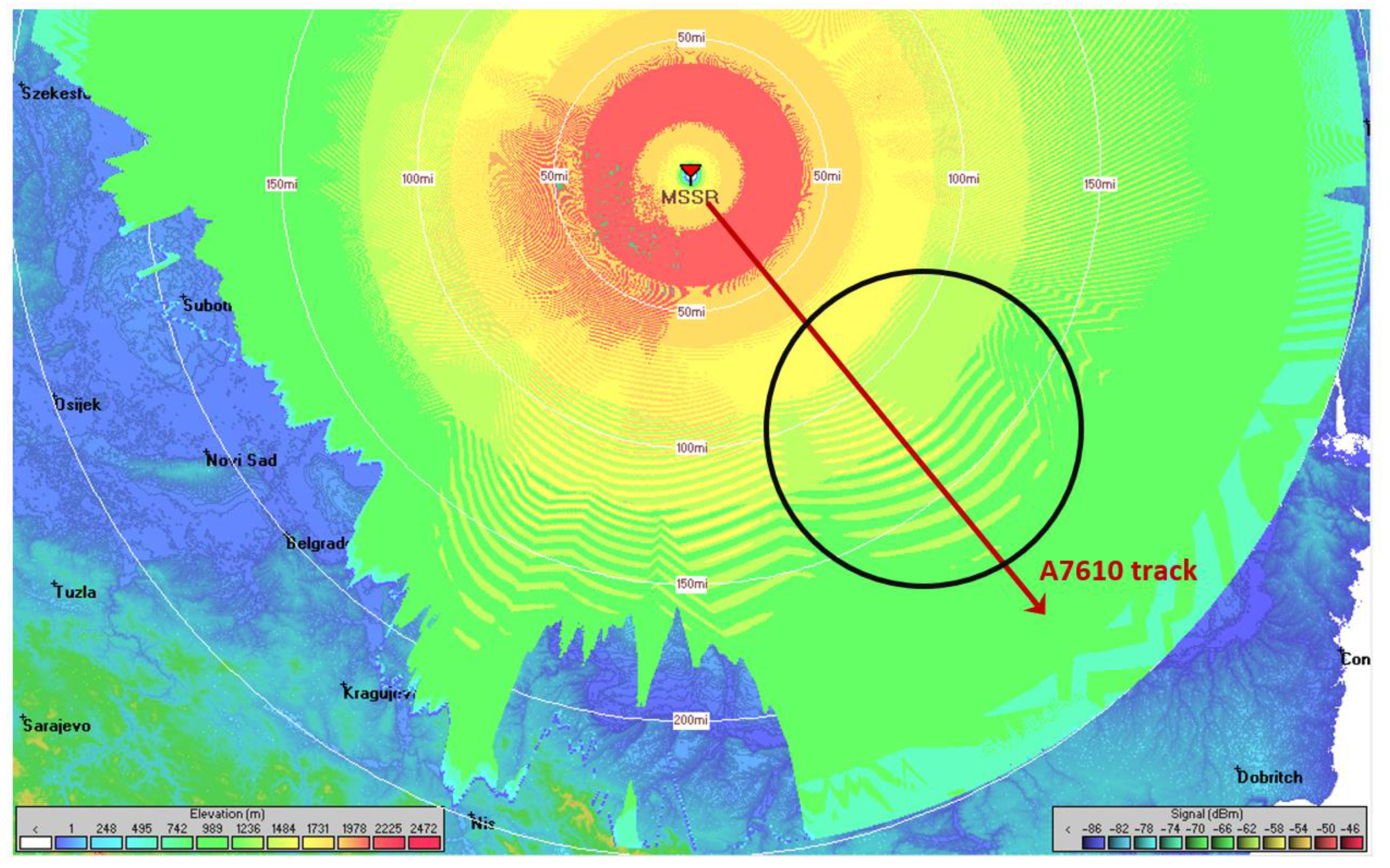
| Column y | 0 | ±1 | ±2 | ±3 | ±4 | ±5 | ±6 | ±7 | ±8 |
| Current I(y) | 1.64 | 1.63 | 1.60 | 1.55 | 1.48 | 1.40 | 1.31 | 1.20 | 1.08 |
| Column y | ±9 | ±10 | ±11 | ±12 | ±13 | ±14 | ±15 | ±16 | ±17 |
| Current I(y) | 0.97 | 0.85 | 0.73 | 0.62 | 0.51 | 0.40 | 0.34 | 0.33 | 0.33 |
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| I(dx) | 0.13 | 0.2 | 0.36 | 0.39 | 0.73 | 1 | 0.73 | 0.39 | 0.36 | 0.2 | 0.13 |
| φx(rad) | 1.47 | 1.82 | 1.34 | 1.14 | 0.86 | 0 | −0.86 | −1.14 | −1.34 | −1.82 | −1.47 |
| Parameter | Value/Setting |
|---|---|
| Centre position (MSSR antenna) | 46.71852° N, 23.60073° E |
| Elevation data source | DTED |
| Operating frequency | 1060 MHz |
| Relative ground permittivity | 15 |
| Antenna polarization | vertical |
| Climate | Continental temperate |
| Role of MSSR | Master |
| Role of AVO | Slave |
| MSSR antenna height | 20 m |
| AVO antenna height | 10,662 m |
| AVO transmit power | 54 dBm |
| MSSR sensitivity | −86 dBm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minteuan, G.; Palade, T.; Puschita, E.; Dolea, P.; Pastrav, A. Monopulse Secondary Surveillance Radar Coverage—Determinant Factors. Sensors 2021, 21, 4198. https://doi.org/10.3390/s21124198
Minteuan G, Palade T, Puschita E, Dolea P, Pastrav A. Monopulse Secondary Surveillance Radar Coverage—Determinant Factors. Sensors. 2021; 21(12):4198. https://doi.org/10.3390/s21124198
Chicago/Turabian StyleMinteuan, Gheorghe, Tudor Palade, Emanuel Puschita, Paul Dolea, and Andra Pastrav. 2021. "Monopulse Secondary Surveillance Radar Coverage—Determinant Factors" Sensors 21, no. 12: 4198. https://doi.org/10.3390/s21124198
APA StyleMinteuan, G., Palade, T., Puschita, E., Dolea, P., & Pastrav, A. (2021). Monopulse Secondary Surveillance Radar Coverage—Determinant Factors. Sensors, 21(12), 4198. https://doi.org/10.3390/s21124198







