A System for Monitoring of Broadband FMR Phenomenon in Low-Carbon Steel Films Subjected to Deformations
Abstract
:1. Introduction
2. VNA Based FMR Measuring System
2.1. DC Field Magnetization/Demagnetization Section
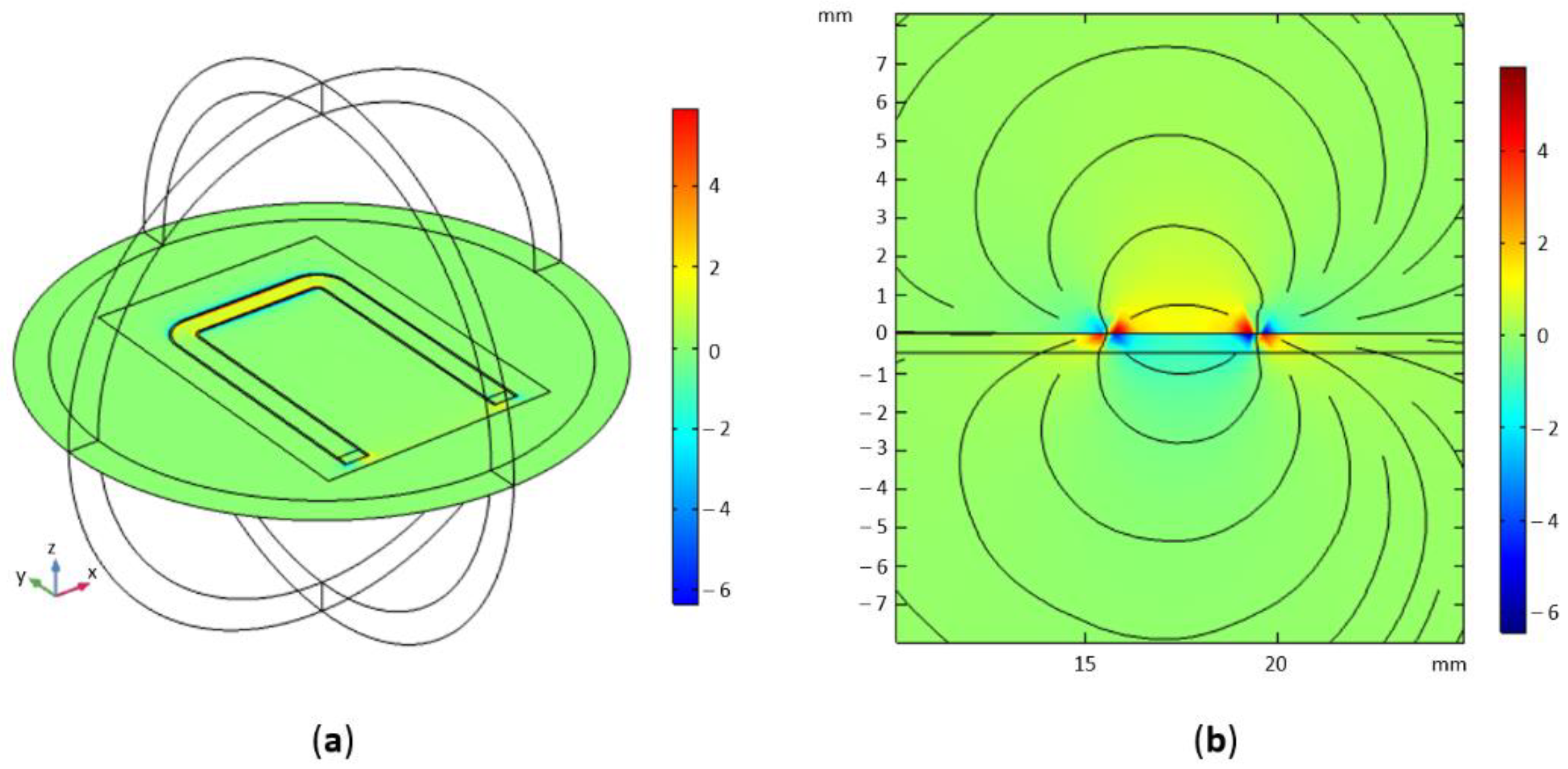
2.2. High-Frequency Electromagnetic Field Sensing Section
3. Experiment
3.1. Measuring Samples
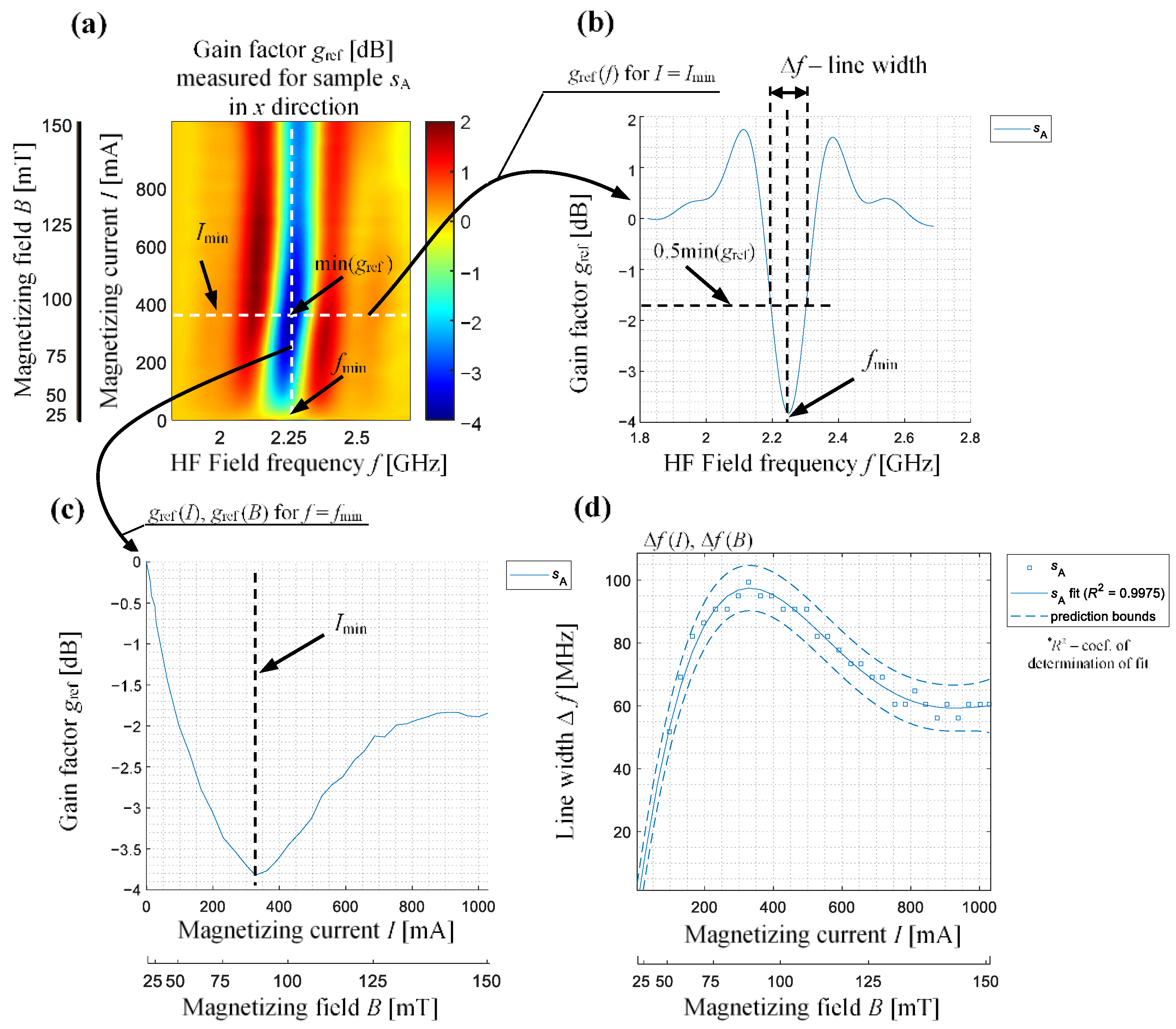
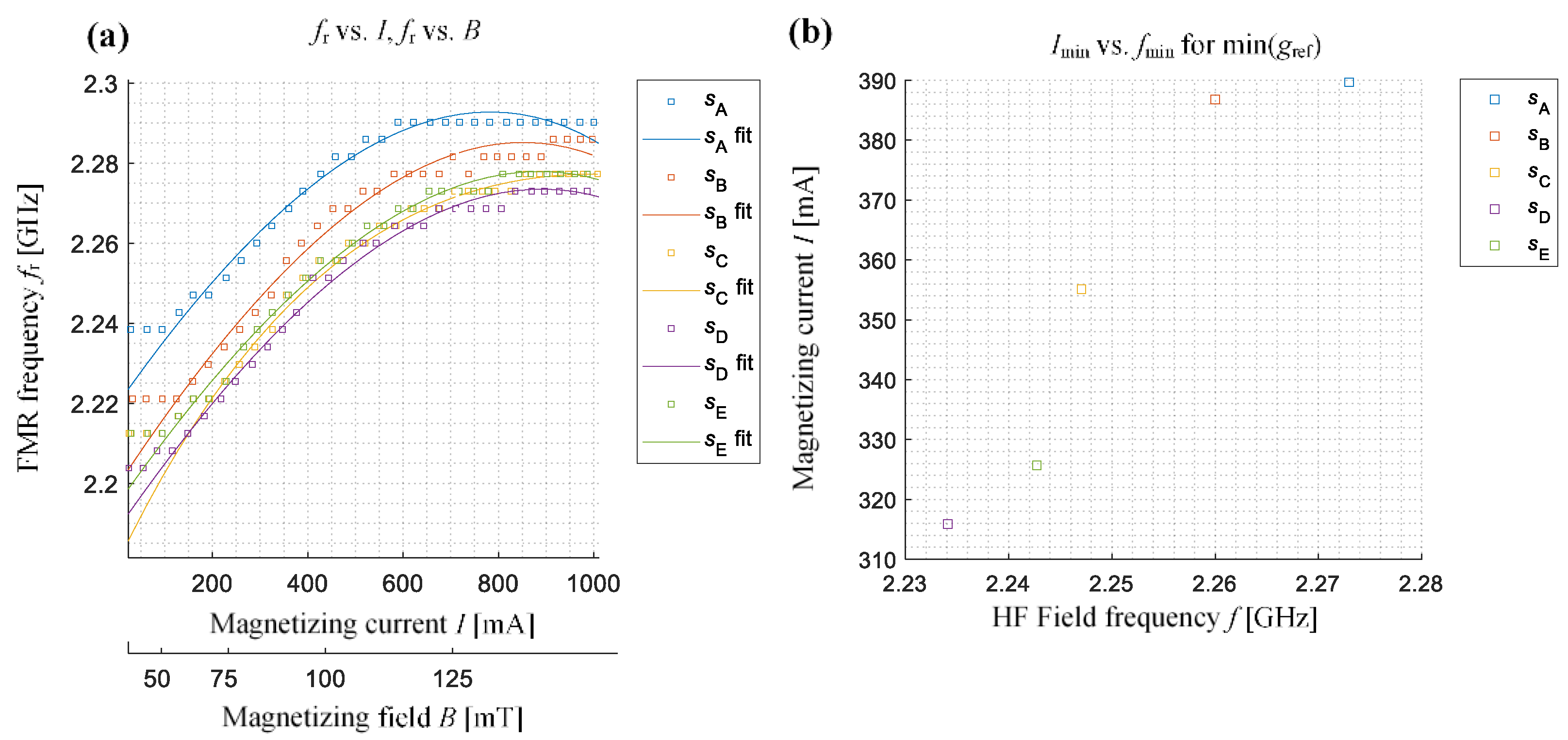
3.2. Measurements, Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiles, D.C. Dynamics of Domain Magnetization and the Barkhausen Effect. Czech. J. Phys. 2000, 50, 893–924. [Google Scholar] [CrossRef]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials, 2nd ed.; IEEE/Wiley: Hoboken, NJ, USA, 2009; ISBN 978-0-471-47741-9. [Google Scholar]
- Yamazaki, T.; Furuya, Y.; Nakao, W. Experimental Evaluation of Domain Wall Dynamics by Barkhausen Noise Analysis in Fe30Co70 Magnetostrictive Alloy Wire. J. Magn. Magn. Mater. 2019, 475, 240–248. [Google Scholar] [CrossRef]
- Ducharne, B.; Le, M.-Q.; Sebald, G.; Cottinet, P.; Guyomar, D.; Hebrard, Y. Characterization and Modeling of Magnetic Domain Wall Dynamics Using Reconstituted Hysteresis Loops from Barkhausen Noise. In Proceedings of the First World Congress on Condition Monitoring, London, UK, 13–16 June 2017. [Google Scholar]
- Maciusowicz, M.; Psuj, G. Time-Frequency Analysis of Barkhausen Noise for the Needs of Anisotropy Evaluation of Grain-Oriented Steels. Sensors 2020, 20, 768. [Google Scholar] [CrossRef] [Green Version]
- Hubert, A.; Schäfer, R. Magnetic Domains: The Analysis of Magnetic Microstructures; Springer: Berlin, Germany; New York, NY, USA, 1998; ISBN 978-3-540-64108-7. [Google Scholar]
- Bilzer, C. Microwave Susceptibility of Thin Ferromagnetic Films: Metrology and Insight into Magnetization Dynamics. Ph.D. Theses, Université Paris Sud-Paris XI, Orsay, France, 2007. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; Wiley: Hoboken, NJ, USA, 2005; ISBN 978-0-471-41526-8. [Google Scholar]
- Morrish, A.H. The Physical Principles of Magnetism; IEEE Press: New York, NY, USA, 2001; ISBN 978-0-7803-6029-7. [Google Scholar]
- Neudecker, I.; Woltersdorf, G.; Heinrich, B.; Okuno, T.; Gubbiotti, G.; Back, C.H. Comparison of Frequency, Field, and Time Domain Ferromagnetic Resonance Methods. J. Magn. Magn. Mater. 2006, 307, 148–156. [Google Scholar] [CrossRef] [Green Version]
- Kalarickal, S.S.; Krivosik, P.; Wu, M.; Patton, C.E.; Schneider, M.L.; Kabos, P.; Silva, T.J.; Nibarger, J.P. Ferromagnetic Resonance Linewidth in Metallic Thin Films: Comparison of Measurement Methods. J. Appl. Phys. 2006, 99, 093909. [Google Scholar] [CrossRef] [Green Version]
- Lo, C.-K. Instrumentation for Ferromagnetic Resonance Spectrometer. In Ferromagnetic Resonance-Theory and Applications; Yaln, O., Ed.; IntechOpen: Rijeka, Croatia, 2013; ISBN 978-953-51-1186-3. [Google Scholar]
- Chumak, O. Magnetoelastic Properties, Magnetic Anisotropy and Magnetic Damping of Co2YZ Heusler Alloy Thin Films. Ph.D. Thesis, Division of Physics of Magnetism, Institute of Physics Polish Academy of Sciences, Warsaw, Poland, 2019. [Google Scholar]
- Maksymov, I.S.; Kostylev, M. Broadband Stripline Ferromagnetic Resonance Spectroscopy of Ferromagnetic Films, Multilayers and Nanostructures. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 69, 253–293. [Google Scholar] [CrossRef] [Green Version]
- Álvarez, N.; Alejandro, G.; Gómez, J.; Goovaerts, E.; Butera, A. Relaxation Dynamics of Ferromagnetic FePt Thin Films in a Broad Frequency Range. J. Phys. Appl. Phys. 2013, 46, 505001. [Google Scholar] [CrossRef]
- Dubowik, J.; Glowinski, H. Broad-Band Ferromagnetic Resonance in Thin Magnetic Films and Nanostructures. Curr. Top. Biophys. 2010, 33, 43–45. [Google Scholar]
- Samuel, H. Frequency-Swept Ferromagnetic Resonance Characterization of Permalloy Thin Films; Department of Electrical and Computer Sciences, University of California: Berkeley, CA, USA, 2018. [Google Scholar]
- Zhu, B.; Lo, C.C.H.; Lee, S.J.; Jiles, D.C. Micromagnetic Modeling of the Effects of Stress on Magnetic Properties. J. Appl. Phys. 2001, 89, 7009–7011. [Google Scholar] [CrossRef] [Green Version]
- Kittel, C. Ferromagnetic Resonance. J. Phys. Radium 1951, 12, 297–302. [Google Scholar] [CrossRef]
- Anders, W.; Biller, E. Ferromagnetic Resonance Linewidth in Bulk Nickel for Various Angles between the Static Magnetic Field and the Surface of the Sample. J. Phys. Colloq. 1971, 32, C1-774–C1-776. [Google Scholar] [CrossRef] [Green Version]
- Schlömann, E. Ferromagnetic Resonance in Polycrystals. J. Phys. Radium 1959, 20, 327–332. [Google Scholar] [CrossRef] [Green Version]
- Tufescu, F.M.; Óvári, T.A.; Chiriac, H.; Stancu, A.; Cuza, A.I. Stress and temperature effect on the FMR response of nearly zero magnetostrictive amorphous microwires. J. Optoelectron. Adv. Mater. 2003, 5, 273–277. [Google Scholar]
- Ben Hamida, A.; Sievers, S.; Pierz, K.; Schumacher, H.W. Broadband Ferromagnetic Resonance Characterization of GaMnAs Thin Films. J. Appl. Phys. 2013, 114, 123704. [Google Scholar] [CrossRef] [Green Version]
- Guskos, N.; Glenis, S.; Zolnierkiewicz, G.; Typek, J.; Sibera, D.; Narkiewicz, U. FMR Study of Temperature Dependence of Magnetic Properties of Nanocrystalline 0.90 (Fe2O3)/0.10ZnO. Acta Phys. Pol. A 2011, 120, 1070–1073. [Google Scholar] [CrossRef]
- Merabtine, S.; Zighem, F.; Garcia-Sanchez, A.; Gunasekaran, V.; Belmeguenai, M.; Zhou, X.; Lupo, P.; Adeyeye, A.O.; Faurie, D. Origin of Relationship between Ferromagnetic Response and Damage in Stretched Systems. Sci. Rep. 2018, 8, 13695. [Google Scholar] [CrossRef]
- Finkel, P.; Lofland, S. Stress Dependence and Effect of Plastic Deformation on Magnetic Hysteresis and Anhysteretic Magnetization of FeNi32% Films. J. Appl. Phys. 2007, 101, 09C508. [Google Scholar] [CrossRef] [Green Version]
- Dubowik, J.; Załęski, K.; Glowinski, H.; Gościańska, I. Angular Dependence of Ferromagnetic Resonance Linewidth in Thin Films. Phys. Rev. B 2011, 84, 184438. [Google Scholar] [CrossRef]
- Smokotin, E.M.; Gusyatskii, G.F.; Protopopova, L.M.; Kapitonov, A.M. The Effect of Inhomogeneous Stress on the FMR in Ferrites. Phys. Status Solidi A 1978, 50, 269–274. [Google Scholar] [CrossRef]
- Sahu, B.N.; Venkataramani, N.; Prasad, S.; Krishnan, R. Effect of Thickness on Magnetic and Microwave Properties of RF-Sputtered Zn-Ferrite Thin Films. AIP Adv. 2017, 7, 056102. [Google Scholar] [CrossRef] [Green Version]
- Sievers, S.; Liebing, N.; Nass, P.; Serrano-Guisan, S.; Pasquale, M.; Schumacher, H.W. Towards Wafer Scale Inductive Determination of Magnetostatic and Dynamic Parameters of Magnetic Thin Films and Multilayers. IEEE Trans. Magn. 2013, 49, 4. [Google Scholar] [CrossRef] [Green Version]
- Liebing, N.; Serrano-Guisan, S.; Caprile, A.; Olivetti, E.S.; Celegato, F.; Pasquale, M.; Müller, A.; Schumacher, H.W. Influence of Sample Geometry on Inductive Damping Measurement Methods. IEEE Trans. Magn. 2011, 47, 2502–2504. [Google Scholar] [CrossRef] [Green Version]
- Noh, S.; Monma, D.; Miyake, K.; Doi, M.; Sahashi, M. Damping Constant Influence on Spin Dynamics in Field Generating Layer of STO for MAMR Writing Head. J. Phys. Conf. Ser. 2011, 266, 012061. [Google Scholar] [CrossRef]
- PocketVNA User Manual. Available online: http://pocketvna.com/styled (accessed on 26 April 2021).
- Simons, R.N. Coplanar Waveguide Circuits, Components, and Systems; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 978-0-471-46393-1. [Google Scholar]
- Frei, W. Modeling of Coplanar Waveguides. Available online: https://www.comsol.com/blogs/modeling-coplanar-waveguides/ (accessed on 26 April 2021).
- Lopato, P.; Herbko, M. Evaluation of Selected Metasurfaces’ Sensitivity to Planar Geometry Distortions. Appl. Sci. 2020, 10, 261. [Google Scholar] [CrossRef] [Green Version]









| C | P | S | Mn | Fe |
|---|---|---|---|---|
| 0.08 | 0.03 | 0.03 | 0.4 | as remainder |
| Young Module E [GPa] | Tensile Strength [MPa] | Elongation at Break [%] |
|---|---|---|
| 180 | 650 | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Psuj, G.; Lopato, P.; Maciusowicz, M.; Herbko, M. A System for Monitoring of Broadband FMR Phenomenon in Low-Carbon Steel Films Subjected to Deformations. Sensors 2021, 21, 4301. https://doi.org/10.3390/s21134301
Psuj G, Lopato P, Maciusowicz M, Herbko M. A System for Monitoring of Broadband FMR Phenomenon in Low-Carbon Steel Films Subjected to Deformations. Sensors. 2021; 21(13):4301. https://doi.org/10.3390/s21134301
Chicago/Turabian StylePsuj, Grzegorz, Przemyslaw Lopato, Michal Maciusowicz, and Michal Herbko. 2021. "A System for Monitoring of Broadband FMR Phenomenon in Low-Carbon Steel Films Subjected to Deformations" Sensors 21, no. 13: 4301. https://doi.org/10.3390/s21134301
APA StylePsuj, G., Lopato, P., Maciusowicz, M., & Herbko, M. (2021). A System for Monitoring of Broadband FMR Phenomenon in Low-Carbon Steel Films Subjected to Deformations. Sensors, 21(13), 4301. https://doi.org/10.3390/s21134301








