Coherence between Decomposed Components of Wrist and Finger PPG Signals by Imputing Missing Features and Resolving Ambiguous Features
Abstract
:1. Introduction
2. Methods
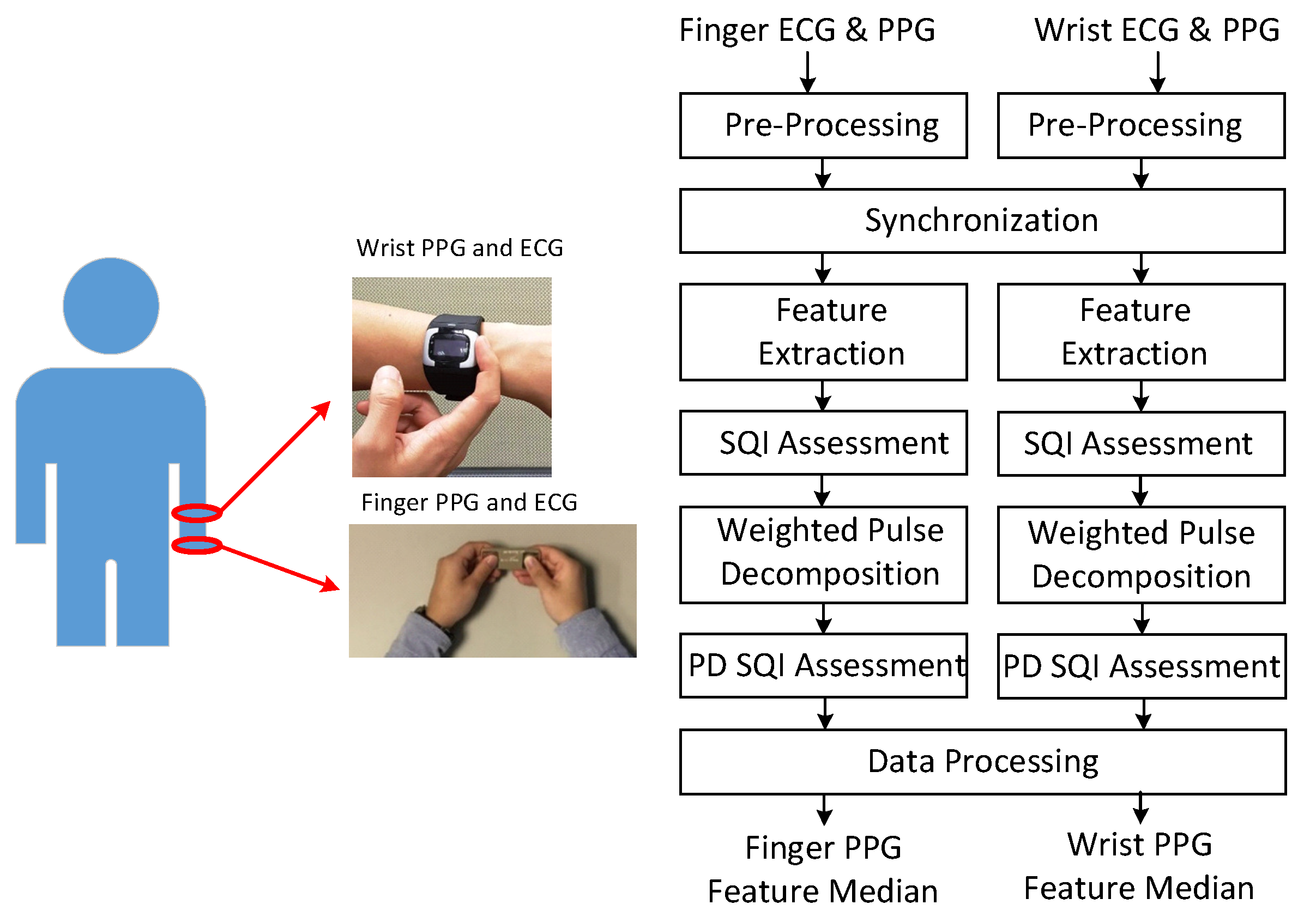
2.1. Signal Processing Flow
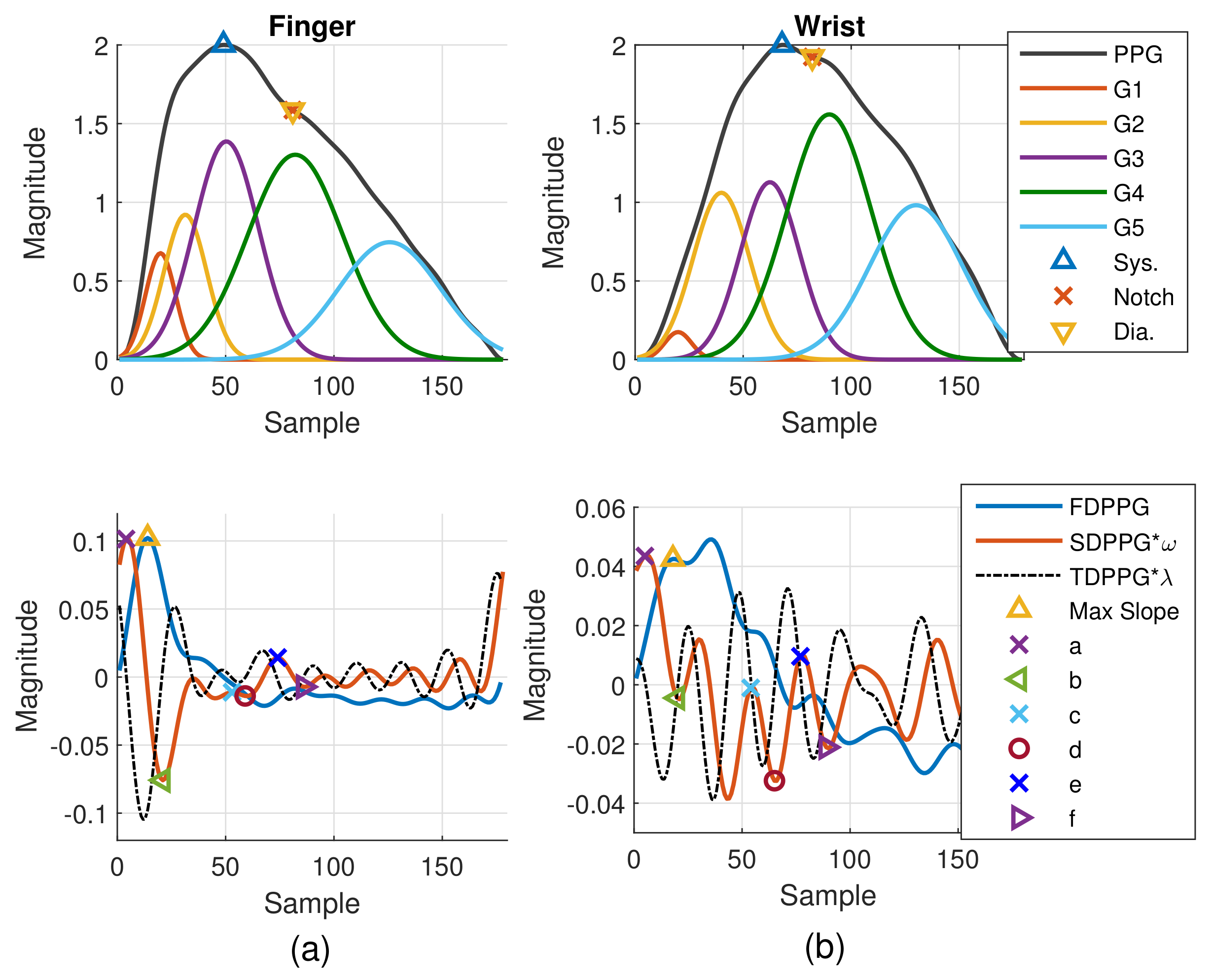
2.1.1. Feature Extraction
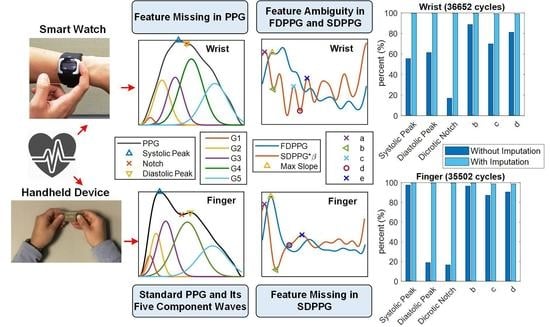
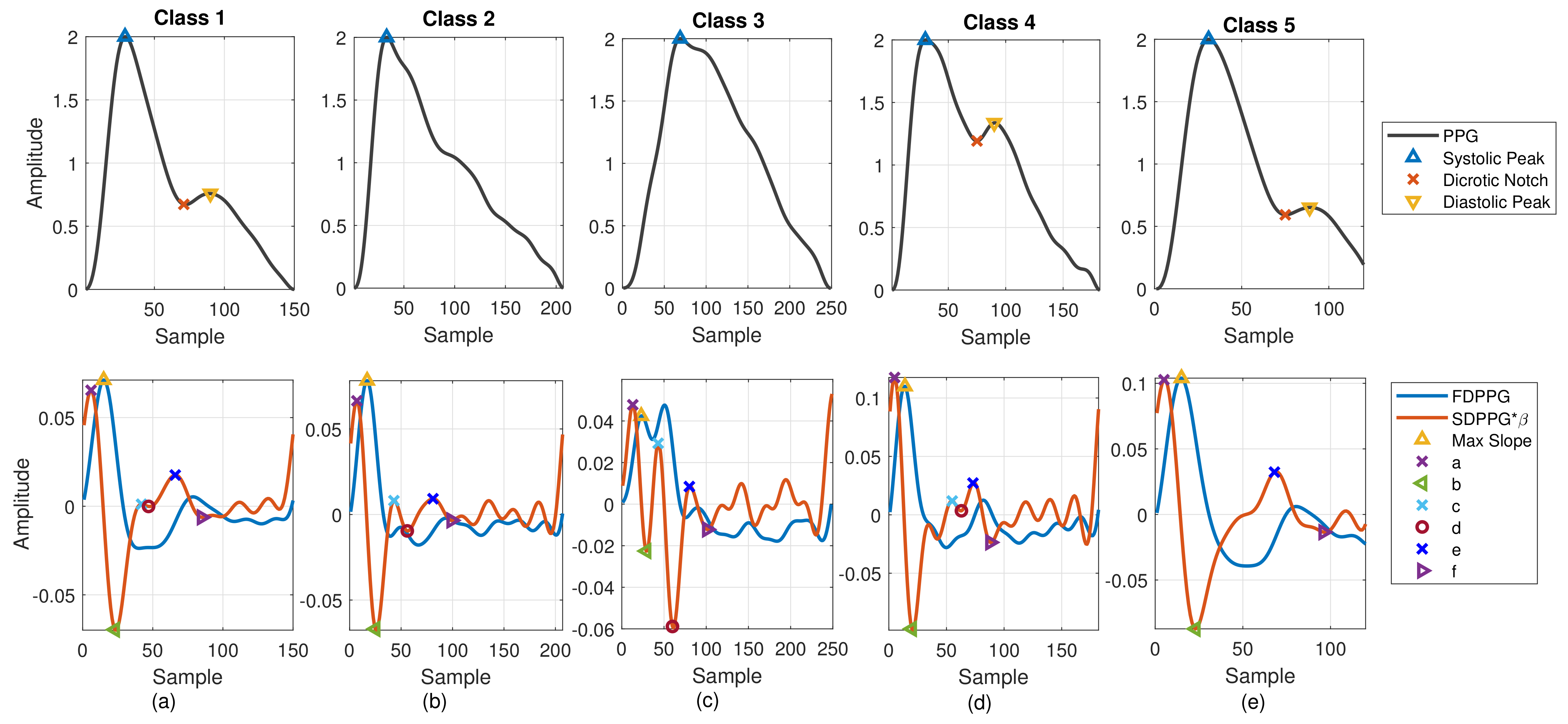
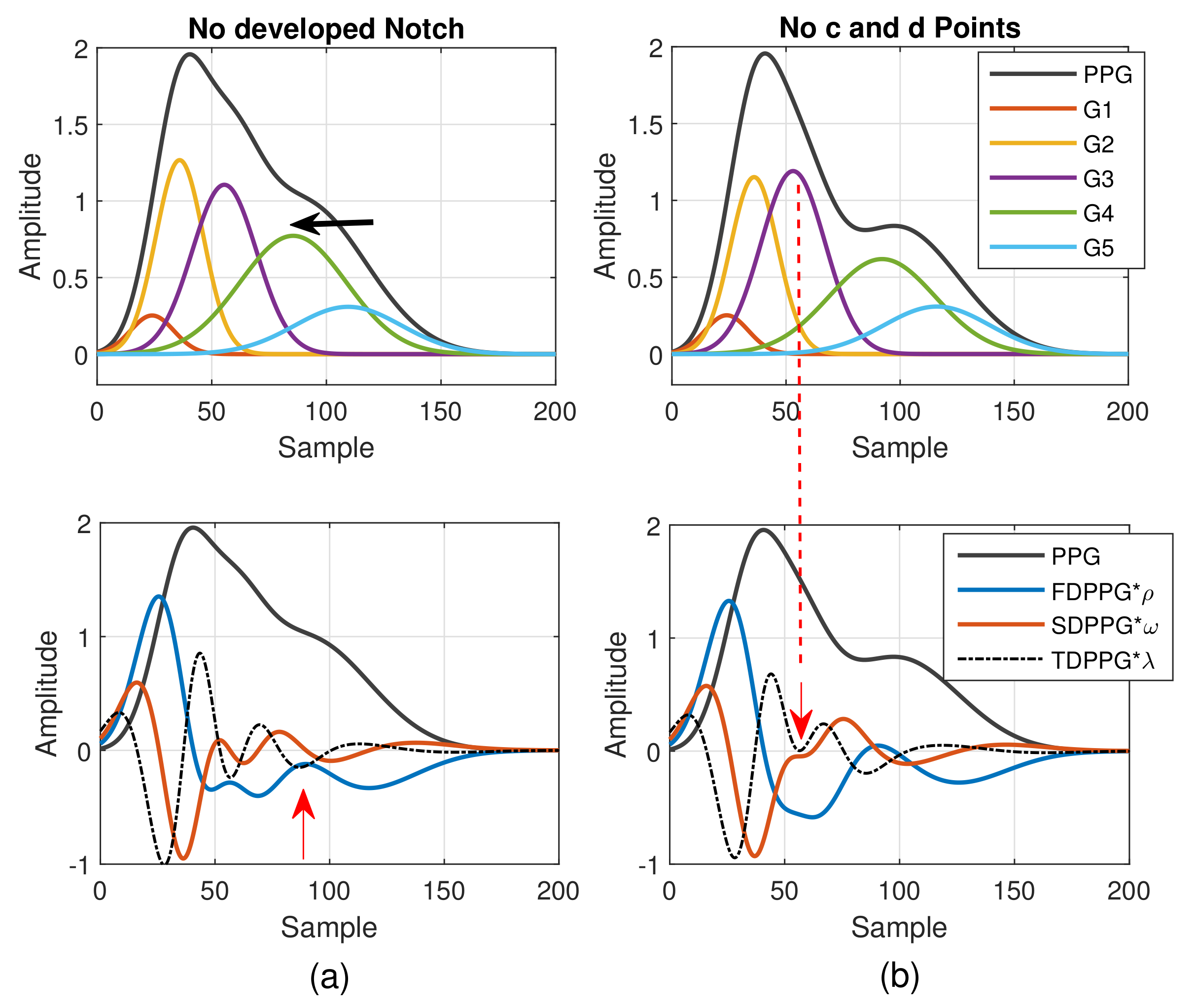
- Class 1: Standard PPG pulse contains distinguishable features including systolic peak, notch, and diastolic peak. Recognized maximum exists in FDPPG and distinguishable a to f points appear in SDPPG.
- Class 2: A single peak is shown in the PPG pulse without a recognizable notch. Usually the missing features are notch and diastolic peak in finger PPG.
- Class 3: In the FDPPG waveform, ambiguity exists for maximum selection. In the one-minute recording, sometimes, the first local maximum and the second local maximum occur before the systolic peak and become alternatively distinct depending on their strengths.
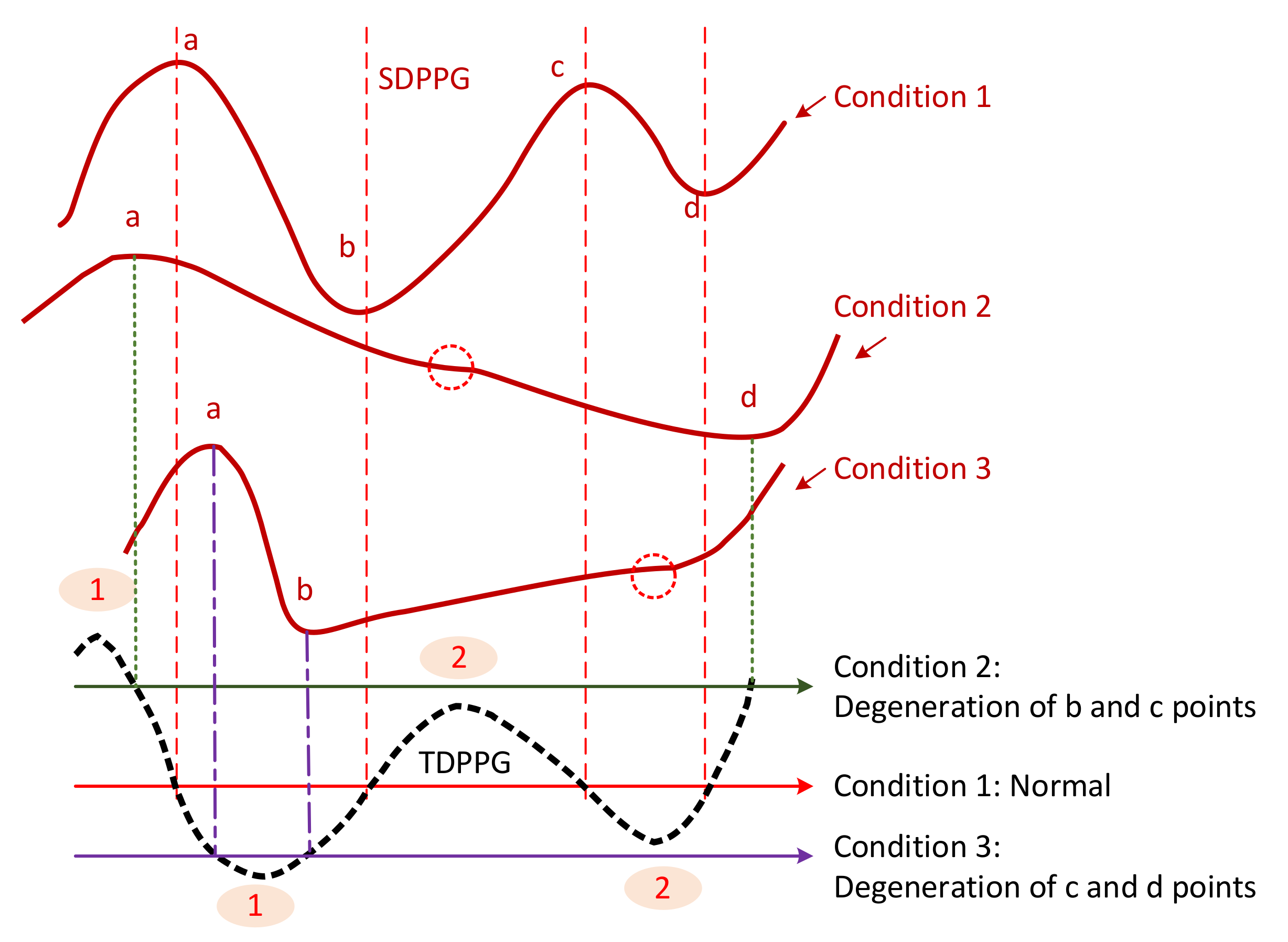
- Class 4: In the SDPPG waveform, there may be more than two maxima and two minima before point e, which was called multiple c and d points in [22]. Feature ambiguity is shown.
- Class 5: In the SDPPG waveform, the number of extrema could be less than four before e point. Usually, the missing features are c and d points.
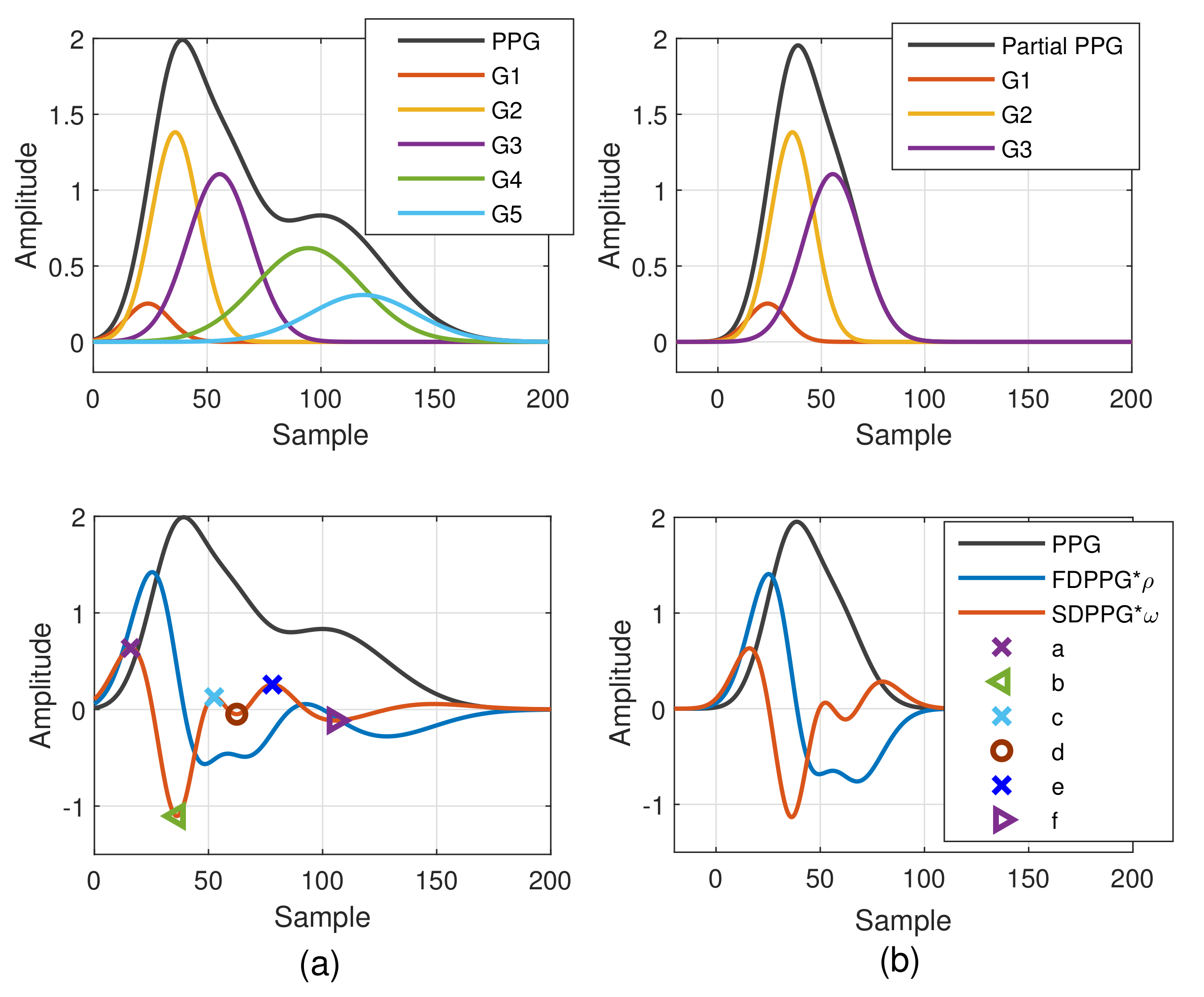
2.1.2. Weighted Pulse Decomposition Analysis (WPDA)
2.2. Missing-Feature Imputation and Ambiguous-Feature Resolution
2.2.1. Causes of Missing and Ambiguous Features
2.2.2. Feature Imputation and Resolving
- (1)
- Features in SDPPG
- (2)
- Features in PPG
- (3)
- Features in FDPPG
3. Results
3.1. Statistics of Imputed Features
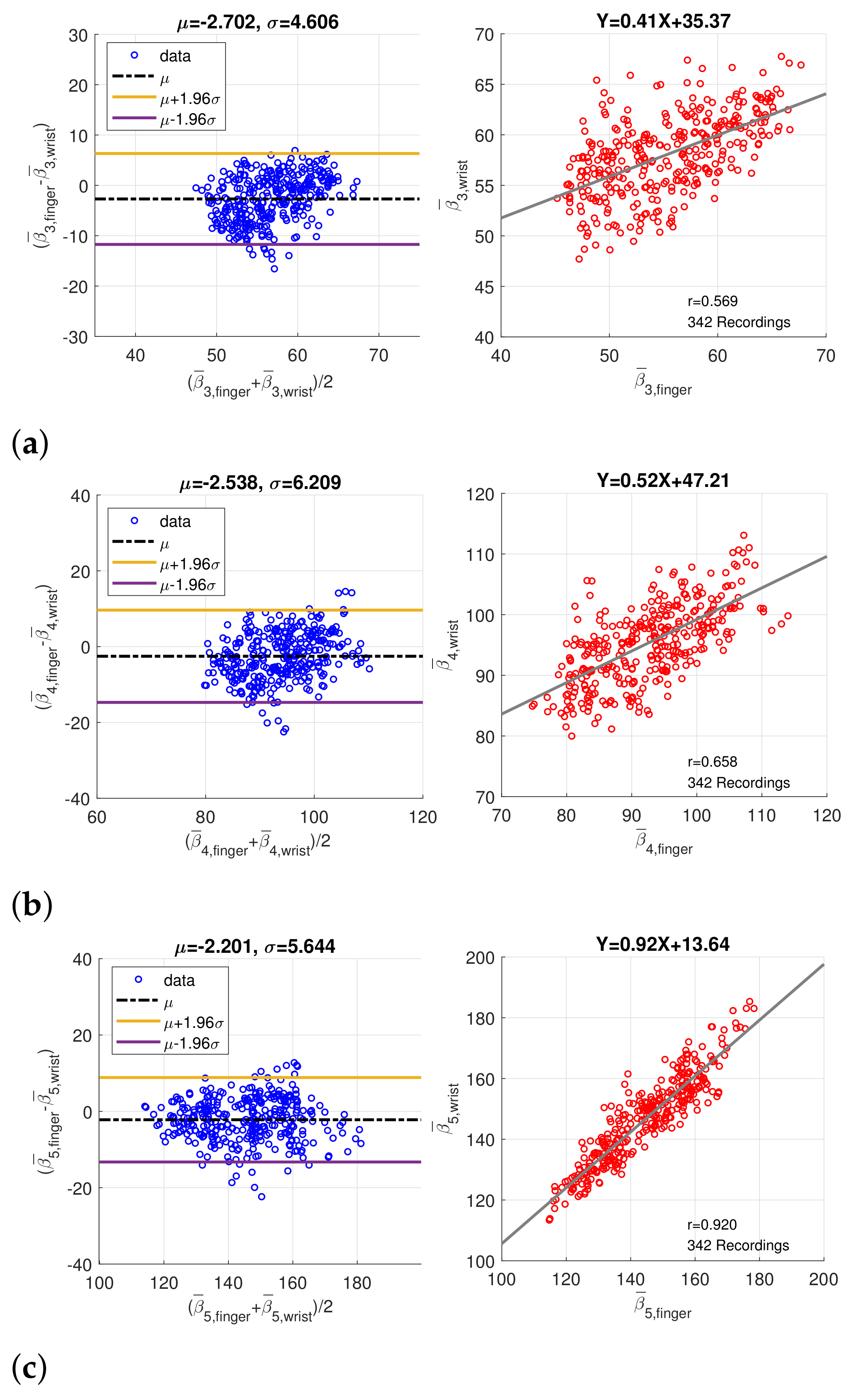
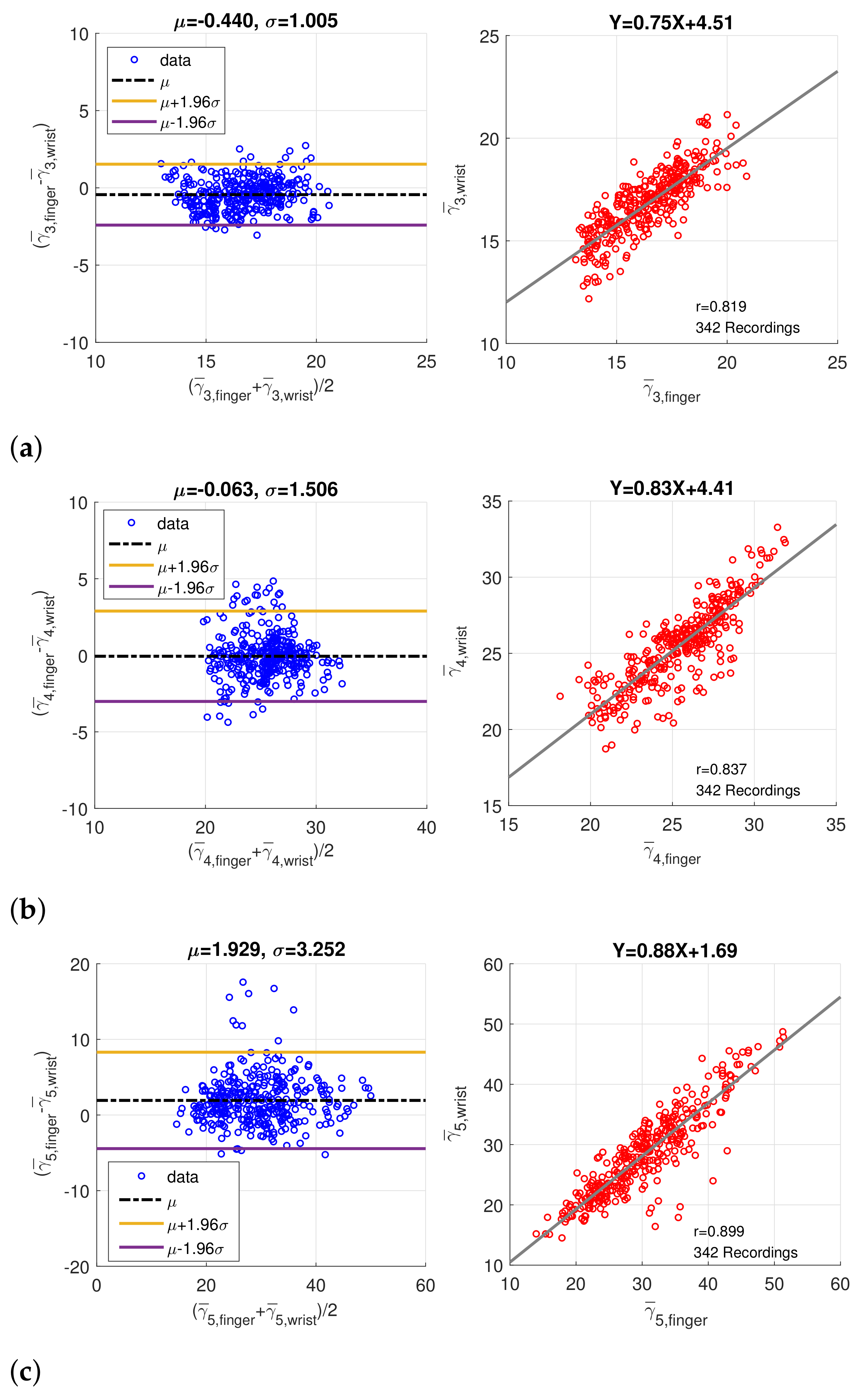
3.2. Coherence between Finger PPG and Wrist PPG
4. Discussion
- : The successful feature extraction ratios are increased for further PPG signal processing.
- : The standard deviations of feature distributions are decreased.
- : The proper boundary constraints derived from feature extraction can be set and the component waves can be located correctly to enhance the feature correlation.
- : Notable coherence of intrinsic properties between wrist and finger PPG exists, especially for the temporal properties.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ranieri, C.M.; MacLeod, S.; Dragone, M.; Vargas, P.A.; Romero, R.A.F. Activity recognition for ambient assisted living with videos, inertial units and ambient sensors. Sensors 2021, 21, 768. [Google Scholar] [CrossRef]
- Truppa, L.; Guaitolini, M.; Garofalo, P.; Castagna, C.; Mannini, A. Assessment of biomechanical response to fatigue through wearable sensors in semi-professional football referees. Sensors 2021, 21, 66. [Google Scholar] [CrossRef] [PubMed]
- Cosoli, G.; Scalise, L.; Poli, A.; Spinsante, S. Wearable devices as a valid support for diagnostic excellence: Lessons from a pandemic going forward. Health Technol. 2021, 11, 673–675. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Atef, M.; Lian, Y. Towards a continuous noninvasive cuffless blood pressure monitoring system using PPG: Systems and circuits review. IEEE Circuits Syst. 2018, 18, 6–26. [Google Scholar] [CrossRef]
- Casacanditella, L.; Cosoli, G.; Casaccia, S.; Tomasini, E.P.; Scalise, L. Indirect measurement of the carotid arterial pressure from vibrocardiographic signal: Calibration of the waveform and comparison with photoplethysmographic signal. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society, Orlando, FL, USA, 16–20 August 2016; pp. 3568–3571. [Google Scholar]
- Chan, G.S.; Middleton, P.M.; Celler, B.G.; Wang, L.; Lovell, N.H. Automatic detection of left ventricular ejection time from a finger photoplethysmographic pulse oximetry waveform: Comparison with Doppler aortic measurement. Physiol. Meas. 2007, 28, 439–452. [Google Scholar] [CrossRef]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuffless blood pressure estimation algorithms for continuous health-Care monitoring. IEEE Trans. Biomed. Eng. 2017, 64, 859–869. [Google Scholar] [CrossRef]
- Schlesinger, O.; Vigderhouse, N.; Eytan, D.; Moshe, Y. Blood pressure estimation from PPG signals using convolutional neural networks and Siamese network. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1135–1139. [Google Scholar]
- Alty, S.R.; Angarita-Jaimes, N.; Millasseau, S.C.; Chowienczyk, P.J. Predicting arterial stiffness from the digital volume pulse waveform. IEEE Trans. Biomed. Eng. 2007, 54, 2268–2275. [Google Scholar] [CrossRef] [PubMed]
- Hong, K.S.; Park, K.T.; Ahn, J.M. Aging index using photoplethysmography for a healthcare Device: Comparison with brachial-ankle pulse wave velocity. Healthc. Inform. Res. 2015, 21, 30–34. [Google Scholar] [CrossRef] [Green Version]
- Elgendi, M. On the analysis of fingertip photoplethysmogram signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef]
- Thomas, S.S.; Nathan, V.; Zong, C.; Akinbola, E.; Aroul, A.L.P.; Philipose, L.; Jafari, R. BioWatch—A wrist watch based signal acquisition system for physiological signals including blood pressure. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 2286–2289. [Google Scholar]
- Priyanka, K.N.G.; Chao, P.C.P.; Tu, T.Y.; Kao, Y.H.; Yeh, M.H.; Pandey, R.; Eka, F.P. Estimating blood Pressure via artificial neural networks based on measured photoplethysmography waveforms. In Proceedings of the IEEE Sensors, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar]
- Sola, J.; Proença, M.; Ferrario, D.; Porchet, J.A.; Falhi, A.; Grossenbacher, O.; Sartori, C. Noninvasive and nonocclusive blood pressure estimation via a chest sensor. IEEE Trans. Biomed. Eng. 2013, 60, 3505–3513. [Google Scholar] [CrossRef] [Green Version]
- Marzorati, D.; Bovio, D.; Salito, C.; Mainardi, L.; Cerveri, P. Chest wearable apparatus for cuffless continuous blood pressure measurements based on PPG and PCG signals. IEEE Access 2020, 8, 55424–55437. [Google Scholar] [CrossRef]
- Rajala, S.; Lindholm, H.; Taipalus, T. Comparison of photoplethysmogram measured from wrist and finger and the effect of measurement location on pulse arrival time. Physiol. Meas. 2018, 39, 075010. [Google Scholar] [CrossRef]
- Hartmann, V.; Liu, H.; Chen, F.; Qiu, Q.; Hughes, S.; Zheng, D. Quantitative comparison of photoplethysmographic waveform characteristics: Effect of measurement site. Front. Physiol. 2019, 10, 198. [Google Scholar] [CrossRef]
- Fujita, D.; Suzuki, A. Evaluation of the possible use of PPG waveform features measured at low sampling rate. IEEE Access 2019, 7, 58316–58322. [Google Scholar] [CrossRef]
- Che, X.; Li, M.; Kang, W.; Lai, F.; Wang, J. Continuous blood pressure estimation from two-channel PPG parameters by XGBoost. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Dali, China, 6–8 December 2019; pp. 2707–2712. [Google Scholar]
- Shimazaki, S.; Kawanaka, H.; Ishikawa, H.; Inoue, K.; Oguri, K. Cuffless blood pressure estimation from only the waveform of photoplethysmography using CNN. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 5042–5045. [Google Scholar]
- Harfiya, L.N.; Chang, C.-C.; Li, Y.-H. Continuous blood pressure estimation using exclusively photopletysmography by LSTM-based signal-to-signal translation. Sensors 2021, 21, 2952. [Google Scholar] [CrossRef]
- Huang, C.H.; Guo, J.W.; Yang, Y.C.; Tsai, P.Y.; Wu, A.Y.A.; Lin, H.J.; Wang, T.D. Weighted pulse decomposition analysis of fingertip photoplethysmogram signals for blood pressure assessment. In Proceedings of the International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 10–21 October 2020. [Google Scholar]
- Hashimoto, J.; Watabe, D.; Kimura, A.; Takahashi, H.; Ohkubo, T.; Totsune, K.; Imai, Y. Determinants of the second derivative of the finger photoplethysmogram and brachial-ankle pulse-wave velocity: The Ohasama study. Am. J. Hypertens. 2005, 18, 477–485. [Google Scholar] [CrossRef] [Green Version]
- Dawber, T.R.; THomas, H.E., Jr.; McNamara, P.M. Characteristics of the dicrotic notch of the arterial pulse wave in coronary heart disease. Angiology 1973, 24, 244–255. [Google Scholar] [CrossRef]
- Wang, L.; Xu, L.; Feng, S.; Meng, M.Q.H.; Wang, K. Multi- Gaussian fitting for pulse waveform using weighted least squares and multi-criteria decision making method. Comput. Biol. Med. 2013, 43, 1661–1672. [Google Scholar] [CrossRef] [PubMed]
- Homma, S.; Ito, S.; Koto, T.; Ikegami, H. Relationship between accelerated plethysmogram, blood pressure and arterial elasticity. Jpn. Soc. Phys. Fit. Sport Med. 1992, 41, 98–107. [Google Scholar]
- Elgendi, M. Optimal signal quality index for photoplethysmogram Signals. Bioengineering 2016, 3, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baruch, M.C.; Warburton, D.E.; Bredin, S.S.; Cote, A.; Gerdt, D.W.; Adkins, C.M. Pulse decomposition analysis of the digital arterial pulse during hemorrhage simulation. Nonlinear Biomed. Phys. 2011, 5, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Couceiro, R.; Carvalho, P.; Paiva, R.P.; Henriques, J.; Quintal, I.; Antunes, M.; Meyer, C. Assessment of cardiovascular function from multi-Gaussian fitting of a finger photoplethysmogram. Physiol. Meas. 2015, 36, 1801–1825. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Min, S.D. Feasibility Study for the non-invasive blood pressure estimation based on PPG morphology: Normotensive subject study. Biomed. Eng. Online 2017, 16, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rubins, U. Finger and ear photoplethysmogram waveform analysis by fitting with Gaussians. Med. Biol. 2008, 46, 1271–1276. [Google Scholar] [CrossRef]
- Khurana, I.; Khurana, A. Medical Physiology for Undergraduate Students-E-Book, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Chang, H.H.; Hsu, C.C.; Chen, C.Y.; Lee, W.K.; Hsu, H.T.; Shyu, K.K.; Lee, P.L. A Method for Respiration Rate Detection in Wrist PPG Signal Using Holo-Hilbert Spectrum. IEEE Sens. J. 2018, 18, 7560–7569. [Google Scholar] [CrossRef]





| Amplitude Gain | Peak Position | Wave Width | ||||
|---|---|---|---|---|---|---|
| i | ||||||
| 1 | 0 | 0 | ||||
| 2 | 0 | |||||
| 3 | 0 | |||||
| 4 | 0 | 0 | ||||
| 5 | 0 | N | 0 | |||
| Feature | Definition | Normal Condition | Imputed Condition |
|---|---|---|---|
| Systolic peak | PPG peak in systole | in systole with the largest | 1. if |
| PPG amplitude | 2. | ||
| Notch | PPG local minimum around | 1. Same as imputed systolic peak 1. | |
| systole boundary | or imputed diastolic peak 1. | ||
| 2. | |||
| Diastolic peak | PPG peak in diastole | first in diastole | 1. if |
| 2. | |||
| Maximal slope | First local maximum in FDPPG | First | |
| Point a | First local maximum in SDPPG | First | - |
| Point b | First local minimum in SDPPG | First | |
| Point c | Last local maximum in SDPPG | Last | 1. if degeneration of b and c1 |
| before | 2. if degeneration of c1 and d1 | ||
| 3. if degeneration of d1 and c2 | |||
| 4. if degeneration of c2 and d2 | |||
| Point d | Last local minimum in SDPPG | Last | 1. if degeneration of c1 and d1 |
| before | 2. if degeneration of d1 and c2 | ||
| 3. if degeneration of c2 and d2 | |||
| Point e | Local maximum in SDPPG | - | |
| around end-systolic boundary | |||
| Point f | First local minimum in SDPPG | First after | - |
| after |
| (a) | ||||||||
| Without Imputation & Resolving | With Imputation & Resolving | |||||||
| Total: 418 Recordings | Total: 519 Recordings | |||||||
| Median | Mean | Std. | Missing Rec. | Median | Mean | Std. | Missing Rec. | |
| R–R Interval (ms) | 841.80 | 832.75 | 125.02 | 0 | 832.03 | 824.07 | 121.01 | 0 |
| Systolic Peak (ms) | 222.65 | 221.83 | 42.27 | 3 | 222.66 | 220.31 | 41.01 | 0 |
| Notch (ms) | 328.13 | 328.86 | 25.66 | 389 | 347.6 | 346.52 | 31.52 | 0 |
| Diastolic Peak (ms) | 386.72 | 385.00 | 34.96 | 383 | 359.38 | 355.20 | 31.33 | 0 |
| Maximal Slope (ms) | 70.31 | 74.25 | 14.57 | 0 | 70.31 | 70.47 | 9.29 | 0 |
| b (ms) | 101.56 | 104.73 | 17.97 | 4 | 101.56 | 102.03 | 12.66 | 0 |
| c (ms) | 164.06 | 168.44 | 27.58 | 30 | 167.97 | 172.62 | 26.29 | 0 |
| d (ms) | 222.65 | 228.05 | 33.00 | 20 | 226.56 | 228.44 | 28.79 | 0 |
| (b) | ||||||||
| Without Imputation & Resolving | With Imputation & Resolving | |||||||
| Total: 465 Recordings | Total: 583 Recordings | |||||||
| Median | Mean | Std. | Missing Rec. | Median | Mean | Std. | Missing Rec. | |
| R–R Interval (ms) | 855.47 | 862.71 | 131.58 | 0 | 847.66 | 847.21 | 131.20 | 0 |
| Systolic Peak (ms) | 281.25 | 285.47 | 39.14 | 220 | 277.34 | 273.83 | 27.70 | 0 |
| Notch (ms) | 328.13 | 331.56 | 27.77 | 453 | 316.41 | 317.58 | 22.81 | 0 |
| Diastolic Peak (ms) | 378.91 | 382.23 | 33.20 | 175 | 371.09 | 370.00 | 31.29 | 0 |
| Maximal Slope (ms) | 101.56 | 106.99 | 27.07 | 0 | 78.13 | 76.99 | 12.34 | 0 |
| b (ms) | 136.72 | 140.55 | 35.66 | 12 | 89.84 | 90.46 | 17.85 | 0 |
| c (ms) | 187.50 | 190.27 | 34.84 | 116 | 187.50 | 186.84 | 28.59 | 0 |
| d (ms) | 242.19 | 242.89 | 28.98 | 35 | 244.14 | 244.34 | 21.40 | 0 |
| Correlation Coefficient (p Value) | ||
|---|---|---|
| Feature | Without Imputation | With Imputation |
| Position | 0.573 (p < 0.001) | 0.569 (p < 0.001) |
| Position | 0.530 (p < 0.001) | 0.658 (p < 0.001) |
| Position | 0.815 (p < 0.001) | 0.920 (p < 0.001) |
| Width | 0.653 (p < 0.001) | 0.819 (p < 0.001) |
| Width | 0.715 (p < 0.001) | 0.837 (p < 0.001) |
| Width | 0.733 (p < 0.001) | 0.899 (p < 0.001) |
| Systolic Peak | 0.348 (p = 0.070) | 0.480 (p < 0.001) |
| Notch | - | 0.600 (p < 0.001) |
| Diastolic Peak | - | 0.617 (p < 0.001) |
| SI | 0.324 (p < 0.001) | 0.543 (p < 0.001) |
| 0.329 (p < 0.001) | 0.391 (p < 0.001) | |
| 0.582 (p < 0.001) | 0.729 (p < 0.001) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, P.-Y.; Huang, C.-H.; Guo, J.-W.; Li, Y.-C.; Wu, A.-Y.A.; Lin, H.-J.; Wang, T.-D. Coherence between Decomposed Components of Wrist and Finger PPG Signals by Imputing Missing Features and Resolving Ambiguous Features. Sensors 2021, 21, 4315. https://doi.org/10.3390/s21134315
Tsai P-Y, Huang C-H, Guo J-W, Li Y-C, Wu A-YA, Lin H-J, Wang T-D. Coherence between Decomposed Components of Wrist and Finger PPG Signals by Imputing Missing Features and Resolving Ambiguous Features. Sensors. 2021; 21(13):4315. https://doi.org/10.3390/s21134315
Chicago/Turabian StyleTsai, Pei-Yun, Chiu-Hua Huang, Jia-Wei Guo, Yu-Chuan Li, An-Yeu Andy Wu, Hung-Ju Lin, and Tzung-Dau Wang. 2021. "Coherence between Decomposed Components of Wrist and Finger PPG Signals by Imputing Missing Features and Resolving Ambiguous Features" Sensors 21, no. 13: 4315. https://doi.org/10.3390/s21134315
APA StyleTsai, P.-Y., Huang, C.-H., Guo, J.-W., Li, Y.-C., Wu, A.-Y. A., Lin, H.-J., & Wang, T.-D. (2021). Coherence between Decomposed Components of Wrist and Finger PPG Signals by Imputing Missing Features and Resolving Ambiguous Features. Sensors, 21(13), 4315. https://doi.org/10.3390/s21134315