Method for Tunnel Displacements Calculation Based on Mobile Tunnel Monitoring System
Abstract
:1. Introduction
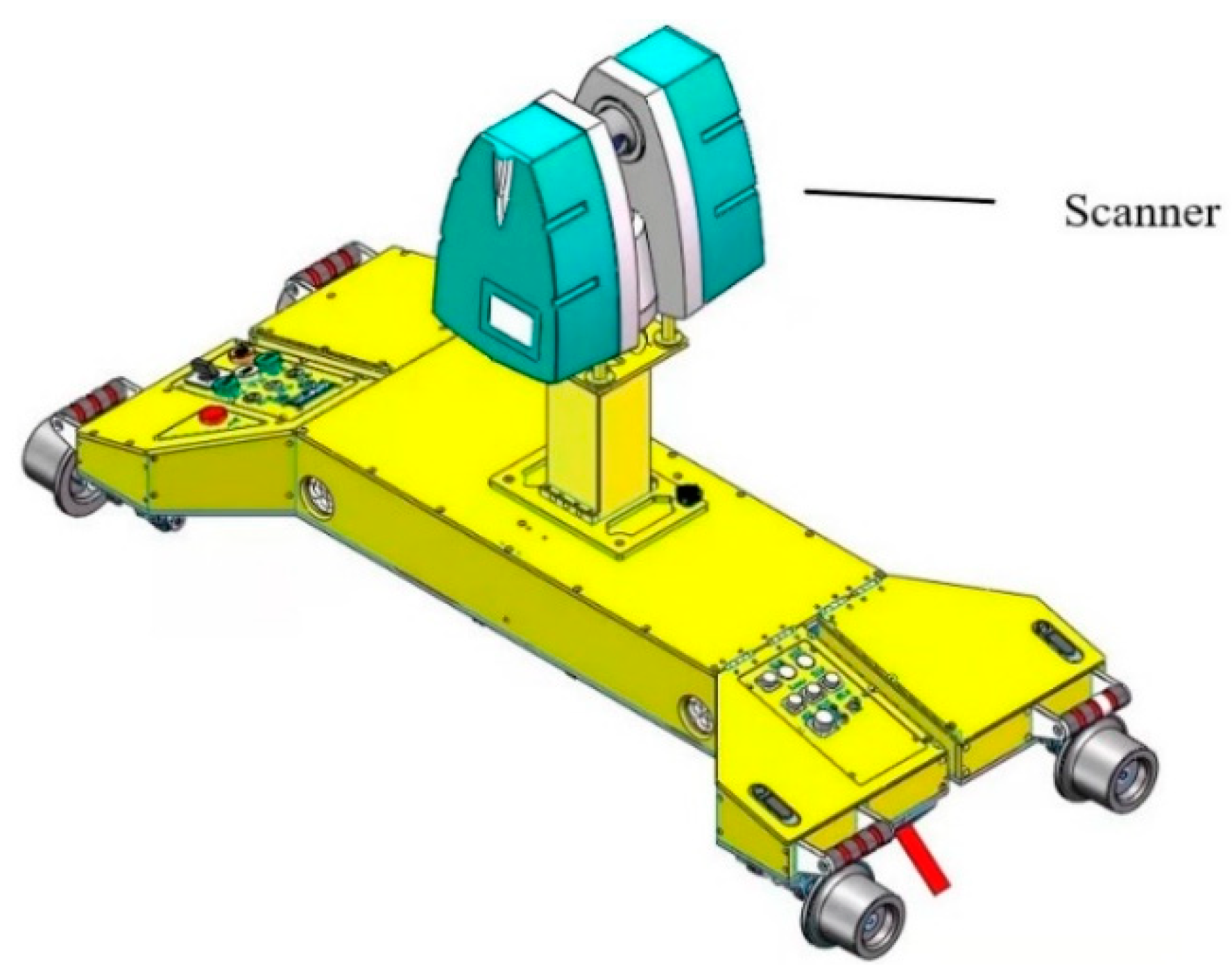
2. Mobile Tunnel Monitoring System (MTDS)
3. Methods
3.1. Orthophoto Generation
3.1.1. Point Cloud Fitting Circle
3.1.2. Point Cloud Projection According to the Tunnel Arc Length
3.1.3. Building Grid Index
3.1.4. Grid to Image
- There is only one point in the grid indexIf there is a point in the grid index corresponding to the row and column number of the matrix, and the intensity value of the point is I, then the gray value of the point is stored in the row and column numbers corresponding to the matrix.
- There are two or more points in the gridIf there are two or more points in the grid, let the grid center coordinate be and the point coordinate be . The Euclidean distance between the grid center and point was calculated as follows:If there is a point such that , then the gray value corresponding to that point is stored in the row and column numbers corresponding to the image matrix.
- No point in grid corresponding to matrixIf there are no points in the grid corresponding to the row and column numbers of the matrix, making , then the inverse distance weighted average interpolation (IDW) method was used. The reason of using IDW algorithm is to assign gray value to the grid (that is, image pixels) to prevent the existence of black spots in the image. The points in the point cloud data are regarded as discrete points in the plane, assuming that there are N discrete points , , …, . The grid center is regarded as the predicted interpolation point . The Euclidean distance formula was used as the distance function formula:where is the interpolation point coordinate, and is the coordinate of each discrete point. When the power parameter is determined, the weight function is used to calculate the weight of each discrete point.where p is the power parameter, and n is the number of discrete points; in this study, p = 3. The function for calculating the interpolation point is as follows:where is the intensity value of the interpolation point, and the gray value g of the point is stored in the row and column number corresponding to the matrix. The calculation method for g is as follows:
3.2. Longitudinal Ring Seam Identification
3.2.1. Longitudinal Ring Seam Detection
3.2.2. Transverse Seam Inspection of Capping Block
- 1.
- Canny image binarization
- 2.
- Hough line detection
3.3. Tunnel Displacement Calculation
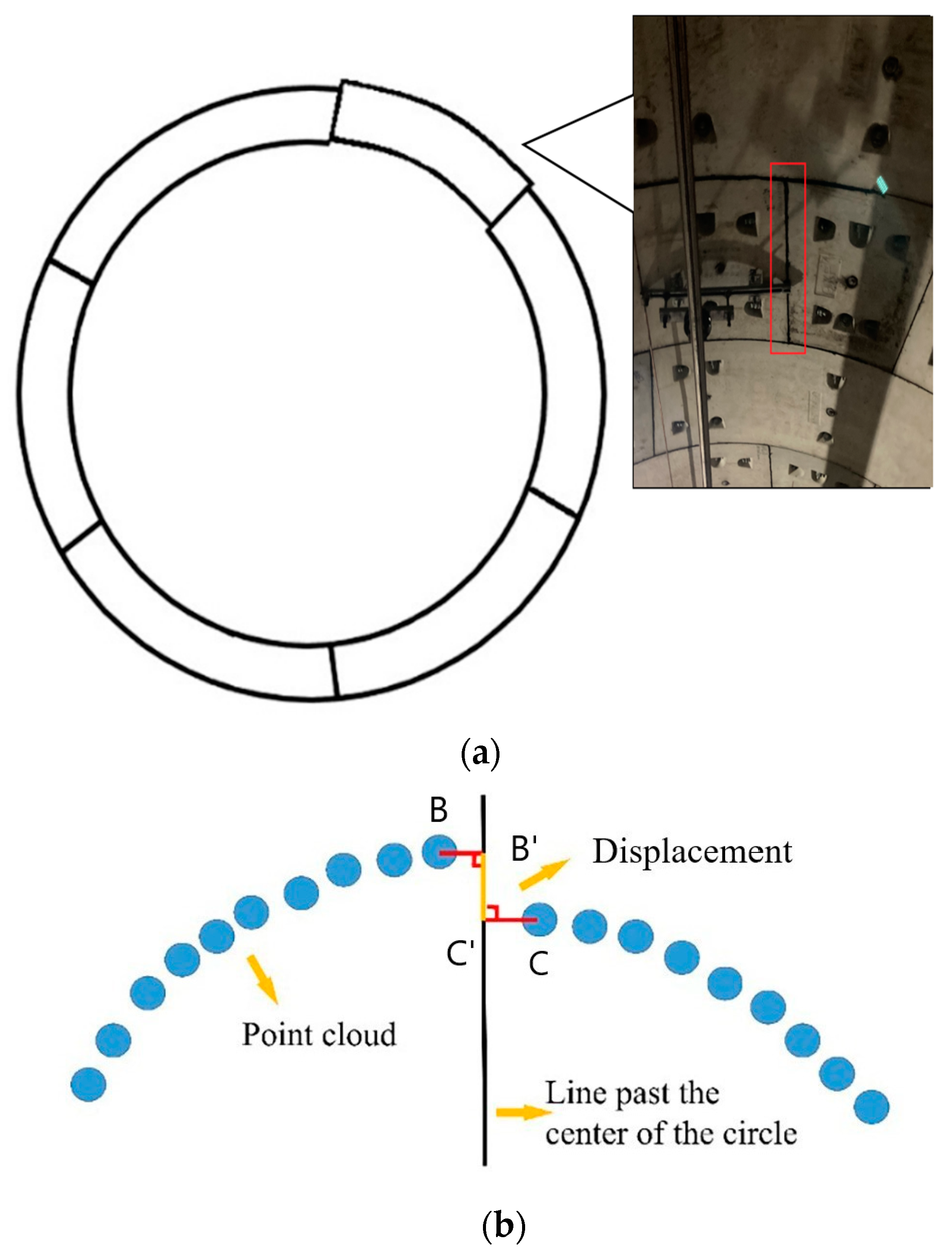
3.3.1. Tunnel Radial Displacement Calculation
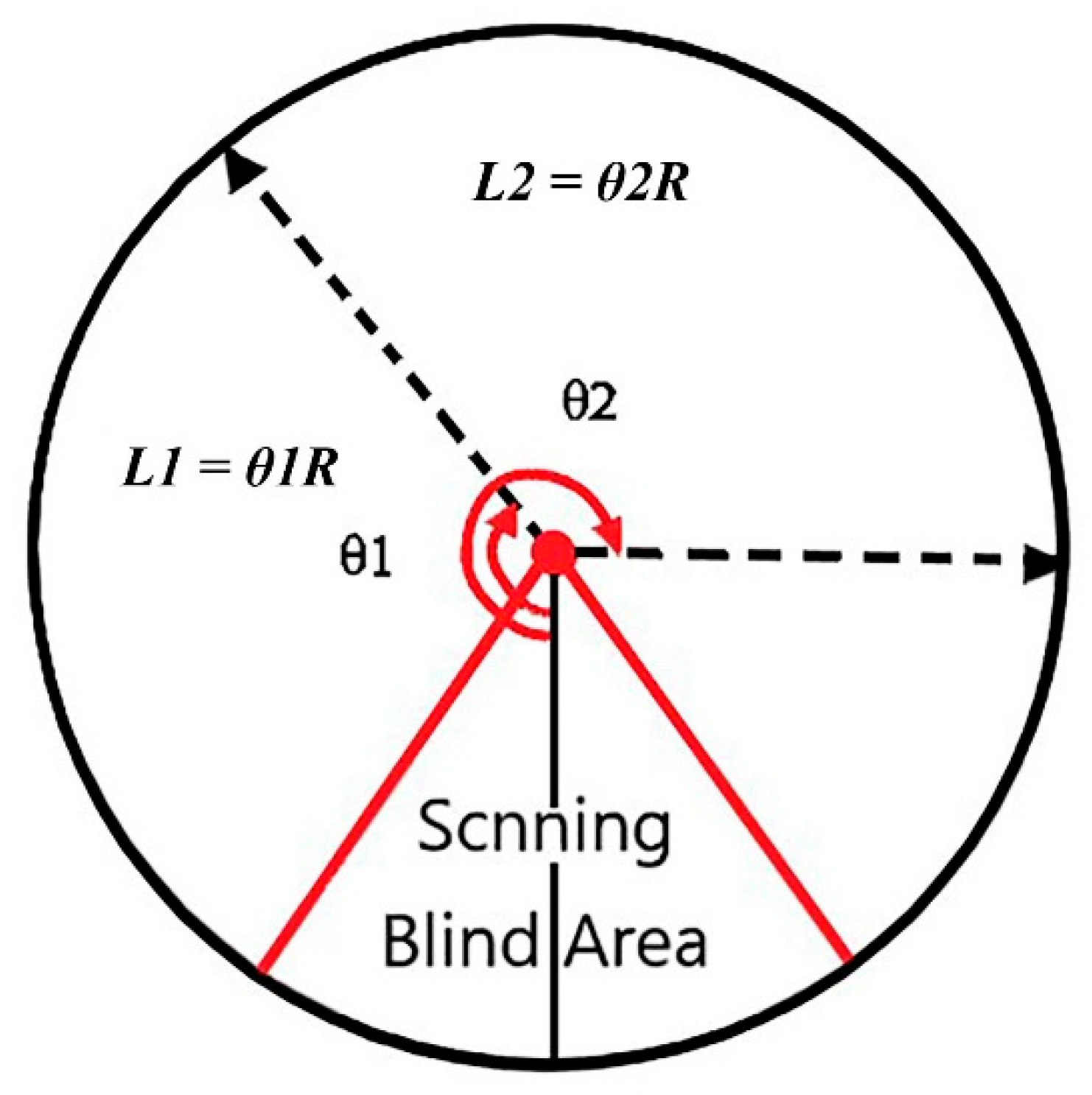
3.3.2. Circumferential Displacement Calculation
4. Method Validation
4.1. Data Sources
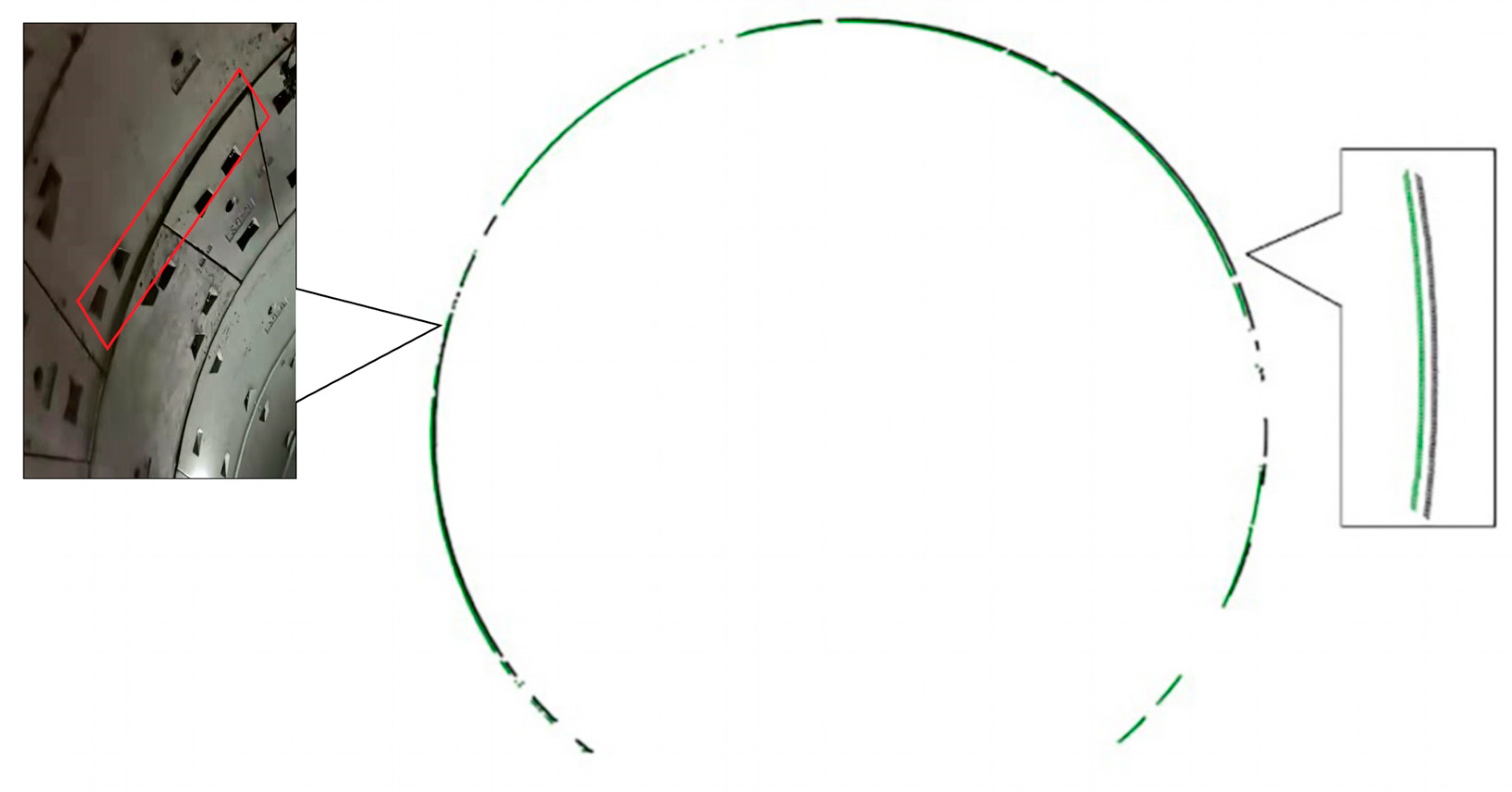
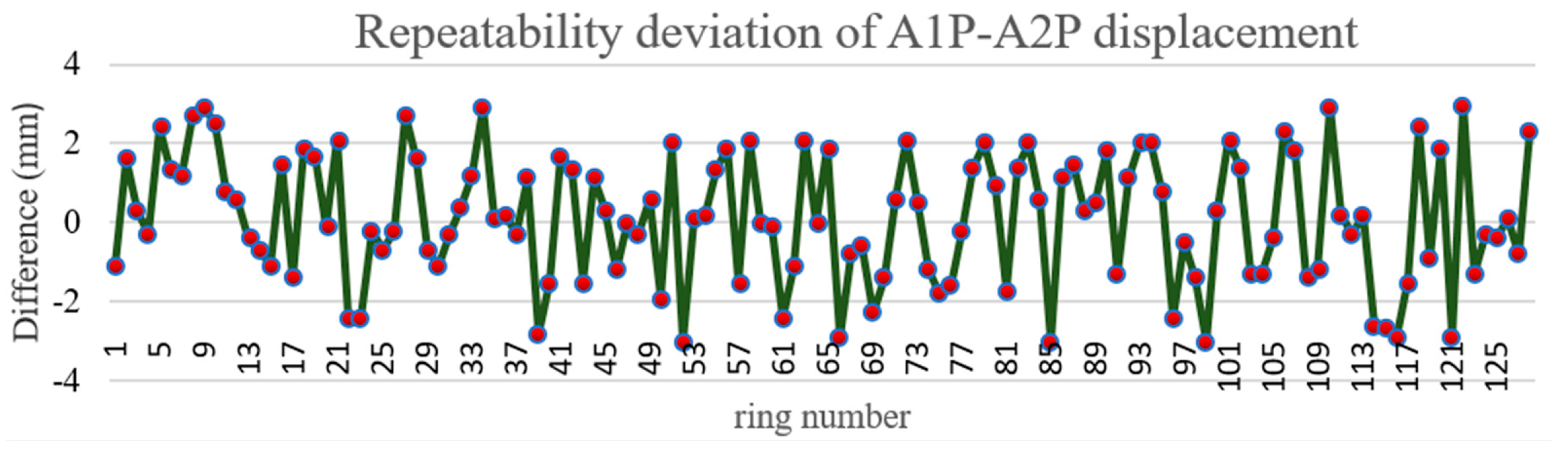
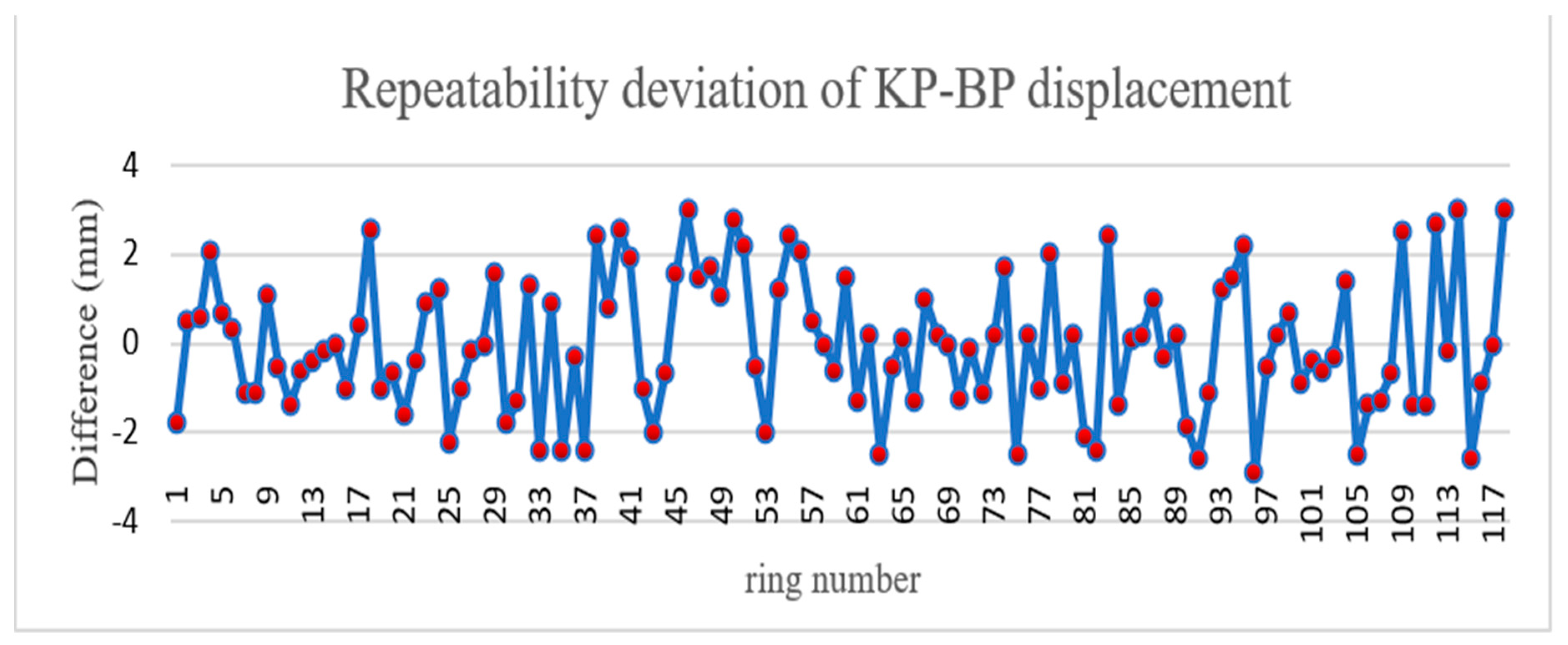
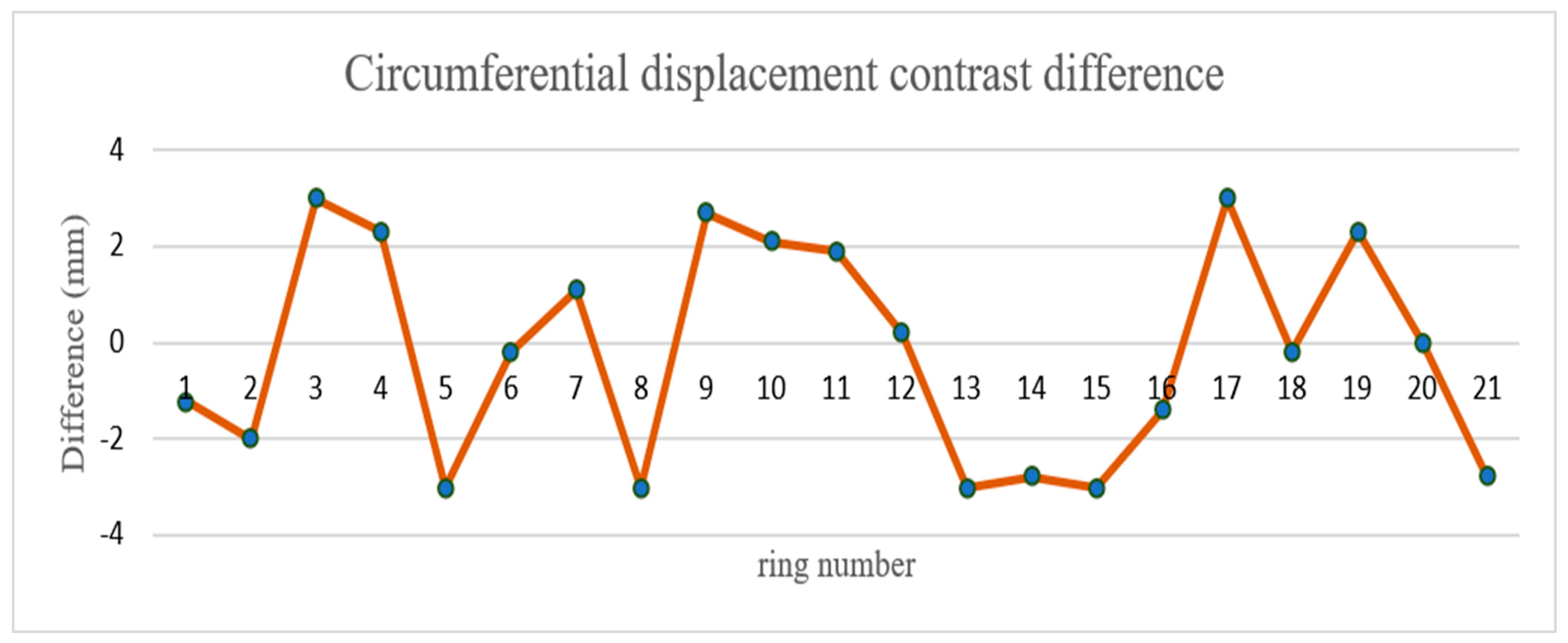
4.2. Circumferential Displacement Round-Trip Precision Verification
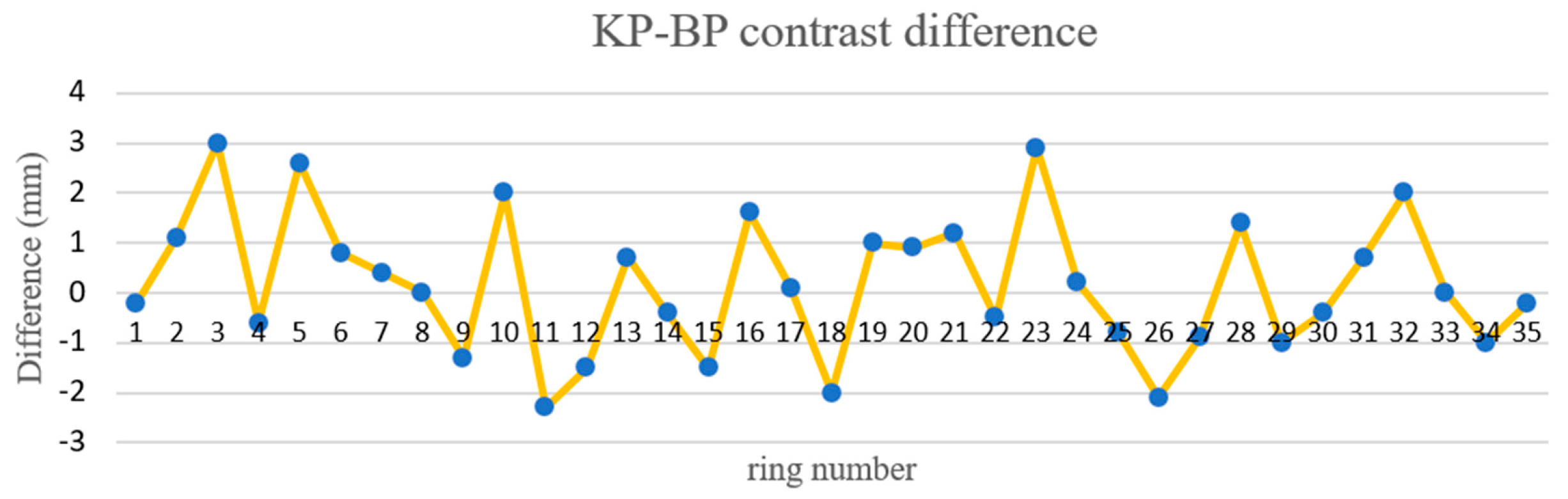
4.3. Radial Displacement Round-Trip Precision Verification
4.4. Radial Displacement Comparative Precision Verification
4.5. Radial Displacement Absolute Accuracy Verification
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, C.J.; Sun, R.Y. The Application of Three-Dimensional Laser Scanner and Vehicle Mounted Mobile Measurement System in Engineering Survey. Surv. Mapp. Spat. Geogr. Inf. 2019, 42, 188–190. [Google Scholar]
- Holgado-Barco, A.; Riveiro, B.; González-Aguilera, D.; Arias, P. Automatic Inventory of Road Cross-Sections From Mobile Laser Scanning System. Comput. Aid. Civ. Infrastruct. Eng. 2017, 32, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Xiao, W.; Vallet, B.; Brédif, M.; Paparoditis, N. Street Environment Change Detection from Mobile Laser Scanning Point Clouds. ISPRS J. Photogramm. 2015, 107, 38–49. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Z. A Shape-Based Segmentation Method for Mobile Laser Scanning Point Clouds. ISPRS J. Photogramm. 2013, 81, 19–30. [Google Scholar] [CrossRef]
- Zhou, L.; Vosselman, G. Mapping Curbstones in Airborne and Mobile Laser Scanning Data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 293–304. [Google Scholar] [CrossRef]
- Wang, Z.F.; Yao, L.B.; Zhou, B. Mobile Measurement System Design and Key Technology Research. Bull. Surv. Mapp. Suppl. 2015, 1, 231–234. [Google Scholar]
- Chang, X.J. Study on the Control Technology of Segment Relocation in Metro Shield Tunnel Construction. Mod. Urban Rail Transit 2020, 4, 37–40. [Google Scholar]
- Ma, J.; Chen, X.W.; Chen, X.H. Analysis of the Influence of Bolt Diameter on the Displacement of Pipe Segments. Pearl River Water Transp. 2020, 7, 91–92. [Google Scholar]
- Yuan, H.; Liu, C.; Lu, J.; Deng, C.; Gong, L. Measurement principle and accuracy analysis of three-dimensional free station tunnel non-contact monitoring with total station. Eng. Invest. 2012, 40, 63–67. [Google Scholar]
- Li, G.Y.; Fan, B.X. Precision engineering survey technology and its development. Acta Geod. Cartogr. Sin. 2017, 46, 1742–1751. [Google Scholar]
- Luo, Y.; Chen, J.; Xi, W.; Zhao, P.; Qiao, X.; Deng, X.; Liu, Q. Analysis of tunnel displacement accuracy with total station. Measurement 2016, 83, 29–37. [Google Scholar] [CrossRef]
- Tang, W.Y. The application of 3D laser scanning technology in the re-measurement of subway tunnel axis. Eng. Constr. Des. 2020, 2, 60–62. [Google Scholar]
- Tang, K.; Hua, X.H.; Cheng, W.; Xia, Z. Research on the Monitoring Method of Building Deformation Based on Three-Dimensional Laser Scanning. Geogr. Inf. Surv. Mapp. 2013, 38, 54–55. [Google Scholar]
- Yin, H.; Feng, Q.H.; Liao, Z.H.; Jiang, L.L.; Cai, J. Disease Tunnel Monitoring Based on 3D Laser Scanning Technology. Undergr. Space Eng. 2014, 10, 895–901. [Google Scholar]
- Zhang, M.Z.; Zhang, M.D. Application of 3D Laser Scanning Technology in Deformation Monitoring of Subway Tunnels. City Surv. 2018, 3, 144–147. [Google Scholar]
- Cheng, Z.C. Application of 3D Laser Scanning Technology in Deformation Monitoring of Rectangular Tunnel Segments. Construction 2017, 39, 1409–1411. [Google Scholar]
- Cheng, Y.J.; Qiu, W.; Lei, J. Automatic extraction of tunnel lining cross-sections from terrestrial laser scanning point clouds. Sensors 2016, 16, 1648. [Google Scholar] [CrossRef]
- Gao, H.; Li, K.; Ma, Q.M.; Han, Z.S.; Sun, P.C. Application research of mobile three-dimensional laser measurement system in disease monitoring of subway operating tunnels. Bull. Surv. Mapp. 2019, 8, 101–161. [Google Scholar]
- Shen, Z.Y.; Tan, Z. Application Research of grp5000 Tunnel Inspection Car in Shanghai Metro. Shanxi Archit. 2013, 39, 158–159. [Google Scholar]
- Dianyou, B. The Application of Three-Dimensional Laser Scanning Technology in the Investigation of Subway Structure Status. Urban Geotech. Invest. Surv. 2019, 4, 126–128. [Google Scholar]
- Cui, H.; Ren, X.; Mao, Q.; Hu, Q.; Wang, W. Shield Subway Tunnel Deformation Detection Based on Mobile Laser Scanning. Autom. Constr. 2019, 106, 102889. [Google Scholar] [CrossRef]
- Lueprasert, P.; Jongpradist, P.; Jongpradist, P.; Suwansawat, S. Numerical investigation of tunnel deformation due to adjacent loaded pile and pile-soil-tunnel interaction. Tunn. Undergr. Space Technol. 2017, 70, 166–181. [Google Scholar] [CrossRef]
- Parsapour, D.; Fahimifar, A. Semi-analytical solution for time-dependent deformations in swelling rocks around circular tunnels. Geosci. J. 2016, 20, 517–528. [Google Scholar] [CrossRef]
- Paraskevopoulou, C.; Diederichs, M. Analysis of time-dependent deformation in tunnels using the Convergence-Confinement Method. Tunn. Undergr. Space Eng. 2018, 71, 62–80. [Google Scholar] [CrossRef]
- Sainoki, A.; Tabata, S.; Mitri, H.; Fukuda, D.; Kodama, J. Time-dependent tunnel deformations in homogeneous and heterogeneous weak rock formations. Comput. Geotech. 2017, 92, 186–200. [Google Scholar] [CrossRef]
- Janda, T.; Šejnoha, M.; Šejnoha, J. Applying Bayesian approach to predict deformations during tunnel construction. Int. J. Numer. Anal. Methods Géoméch. 2018, 42, 1765–1784. [Google Scholar]
- Sun, H.; Xu, Z.; Yao, L.; Zhong, R.; Du, L.; Wu, H. Tunnel Monitoring and Measuring System Using Mobile Laser Scanning: Design and Deployment. Remote Sens. 2020, 12, 730. [Google Scholar] [CrossRef] [Green Version]
- Du, L.M.; Zhong, R.F.; Sun, H.L.; Zhu, Q.; Zhang, Z. Study of the Integration of the CNU-TS-1 Mobile Tunnel Monitoring System. Sensors 2018, 18, 420. [Google Scholar] [CrossRef] [Green Version]
- Arastounia, M. Automated As-Built Model Generation of Subway Tunnels From Mobile Lidar Data. Sensors 2016, 16, 1486. [Google Scholar] [CrossRef] [Green Version]
- Du, L.M.; Zhong, R.F.; Sun, H.L.; Liu, Y.J.; Wu, Q. Cross-Section Positioning Based on a Dynamic Mls Tunnel Monitoring System. Photogramm. Rec. 2019, 34, 244–265. [Google Scholar] [CrossRef]
- Du, L.; Zhong, R.; Sun, H.; Wu, Q. Automatic Monitoring of Tunnel Deformation Based on High Density Point Clouds Data. ISPRS—International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2017, 42, 353. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Sun, H.L.; Zhong, R.F.; Han, Y.L. Deformation Detection Method of Mine Tunnel Based on Mobile Detection System. Sensors 2020, 20, 5400. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Zhong, R.F.; Sun, H.; Du, L.M.; Zhen, Z. Tunnel Boundary Detection Method of Mobile Laser Detection System. Sci. Surv. Mapp. 2020, 45, 118–125. [Google Scholar]
- Xu, D.S.; Zhao, Y.M.; Liu, H.B.; Zhu, H.H. Deformation Monitoring of Metro Tunnel with a New Ultrasonic-Based System. Sensors 2017, 17, 1758. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yertutanol, K.; Akgün, H.; Sopacı, E. Displacement monitoring, displacement verification and stability assessment of the critical sections of the Konak tunnel, İzmir, Turkey. Tunn. Undergr. Space Technol. 2020, 101, 103357. [Google Scholar] [CrossRef]
- Jiang, H.; Cheng, J.; Zhang, J.; Zhang, J.; Su, Y.; Zheng, Y. Principle and application of in-situ monitoring system for ground displacement induced by shield tunnelling. Tunn. Undergr. Space Technol. 2021, 112, 103905. [Google Scholar] [CrossRef]
- Sun, H.; Liu, S.; Zhong, R.; Du, L. Cross-Section Deformation Analysis and Visualization of Shield Tunnel Based on Mobile Tunnel Monitoring System. Sensors 2020, 20, 1006. [Google Scholar] [CrossRef] [Green Version]









| Number | Forward Displacement (mm) | Backward Displacement (mm) | Absolute Deviation (mm) |
|---|---|---|---|
| 1 | 7.7 | 10.1 | 2.4 |
| 2 | 8.7 | 9.4 | 0.7 |
| 3 | 9.7 | 12.1 | 2.4 |
| 4 | 7.1 | 9.9 | 2.8 |
| 5 | 12.5 | 10.7 | 1.8 |
| 6 | 9.1 | 9.3 | 0.2 |
| 7 | 10.8 | 14.0 | 3.2 |
| 8 | 9.9 | 8.6 | 1.3 |
| 9 | 7.2 | 10.1 | 2.9 |
| 10 | 7.5 | 9.1 | 1.6 |
| 11 | 10.8 | 10.5 | 0.3 |
| 12 | 15.7 | 18.0 | 2.3 |
| 13 | 10.1 | 9.6 | 0.5 |
| 14 | 7.8 | 7.8 | 0.0 |
| 15 | 11.2 | 12.0 | 0.8 |
| 16 | 8.6 | 9.3 | 0.7 |
| 17 | 7.7 | 9.1 | 1.4 |
| 18 | 8.7 | 8.0 | 0.7 |
| 19 | 11.2 | 13.8 | 2.6 |
| 20 | 7.7 | 9.5 | 1.8 |
| 21 | 12.1 | 11.3 | 0.8 |
| 22 | 13.2 | 11.4 | 1.8 |
| 23 | 12.1 | 12.4 | 0.3 |
| 24 | 8.0 | 7.8 | 0.2 |
| 25 | 9.8 | 7.4 | 2.4 |
| Absolute Mean Deviation (mm) | 1.4 | ||
| Number | Measured Value of Vernier Calipers (mm) | Radial Displacement Measured by Proposed Method (mm) | Absolute Deviation (mm) |
|---|---|---|---|
| 1 | 3.5 | 4.5 | 1.2 |
| 2 | 5.3 | 3.0 | 2.3 |
| 3 | 2.1 | 5.1 | 3.0 |
| 4 | 7.4 | 4.9 | 2.5 |
| 5 | 1.5 | 3.7 | 2.2 |
| 6 | 3.8 | 6.0 | 2.2 |
| 7 | 4.9 | 2.2 | 2.7 |
| 8 | 1.9 | 1.6 | 0.3 |
| 9 | 3.6 | 6.1 | 2.5 |
| 10 | 3.2 | 4.1 | 0.9 |
| Absolute Mean Deviation (mm) | 1.98 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, Z.; Sun, H.; Zhong, R.; Du, L. Method for Tunnel Displacements Calculation Based on Mobile Tunnel Monitoring System. Sensors 2021, 21, 4407. https://doi.org/10.3390/s21134407
Yue Z, Sun H, Zhong R, Du L. Method for Tunnel Displacements Calculation Based on Mobile Tunnel Monitoring System. Sensors. 2021; 21(13):4407. https://doi.org/10.3390/s21134407
Chicago/Turabian StyleYue, Zeyu, Haili Sun, Ruofei Zhong, and Liming Du. 2021. "Method for Tunnel Displacements Calculation Based on Mobile Tunnel Monitoring System" Sensors 21, no. 13: 4407. https://doi.org/10.3390/s21134407
APA StyleYue, Z., Sun, H., Zhong, R., & Du, L. (2021). Method for Tunnel Displacements Calculation Based on Mobile Tunnel Monitoring System. Sensors, 21(13), 4407. https://doi.org/10.3390/s21134407






