Modeling and Imaging of Ultrasonic Array Inspection of Side Drilled Holes in Layered Anisotropic Media
Abstract
:1. Introduction
2. Background Theory
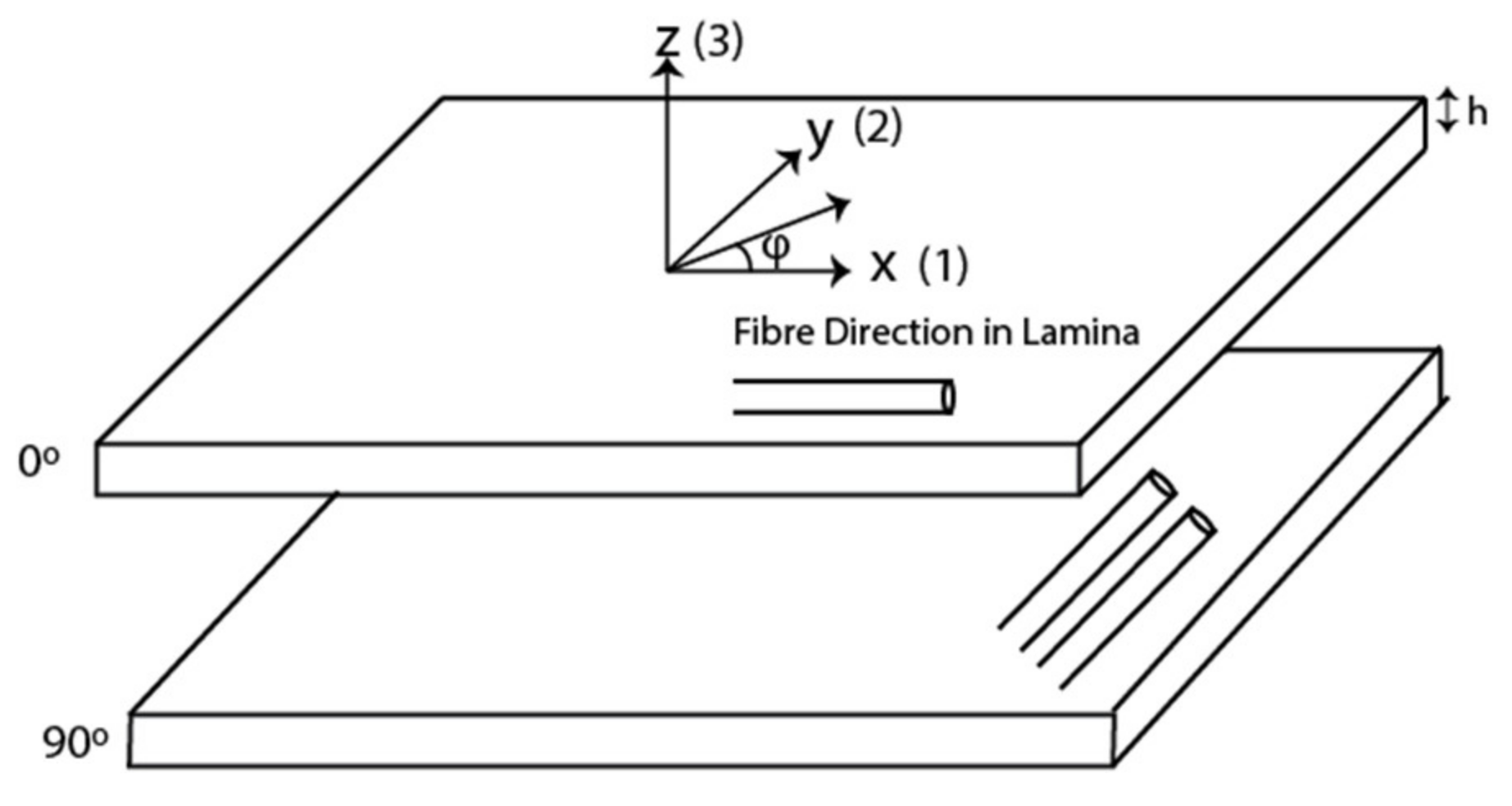
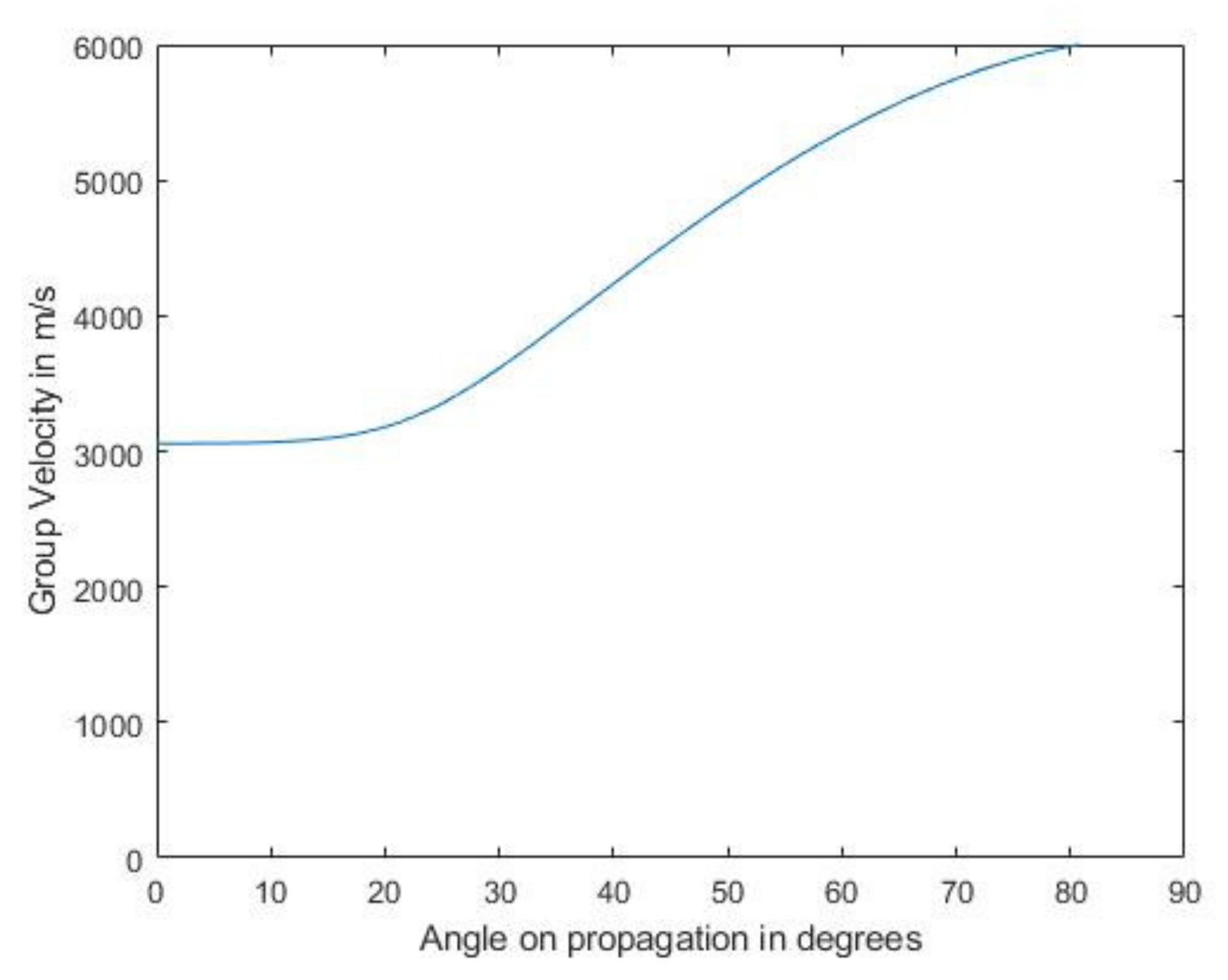
2.1. Transfer and Stiffness Matrix Method for Multilayer Wave Propagation
2.2. Modeling of the Transducer Gaussian Beams
2.3. Equivalent Homogeneous Anisotropic Properties of a Thick Laminate
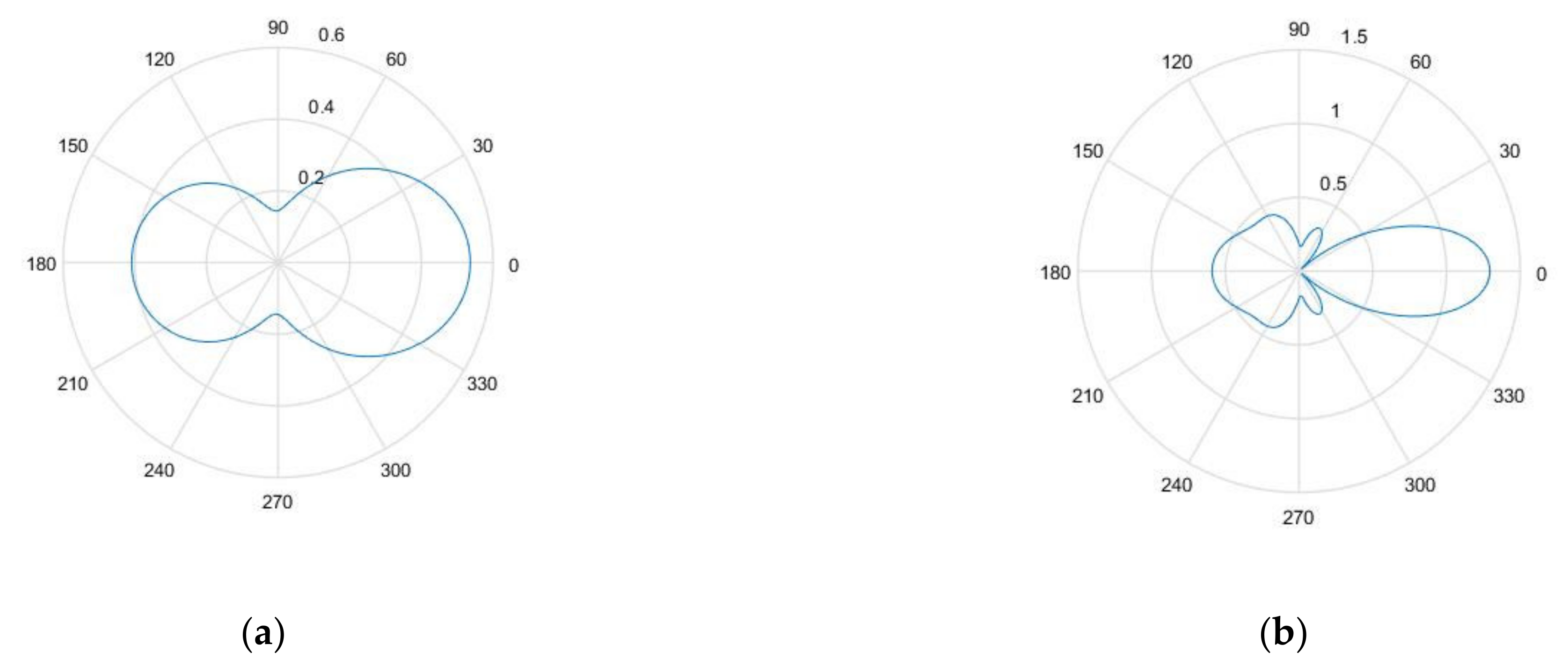
2.4. Scattering Coefficient of a SDH
3. Development of a Model to Facilitate Scattering of SDH in a Layered Anisotropic Medium
3.1. Reflection and Transmission Coefficients of Layered Structure Bounded by Anisotropic Media
3.2. Calculation of the Scattering from SDH Embedded in the Medium
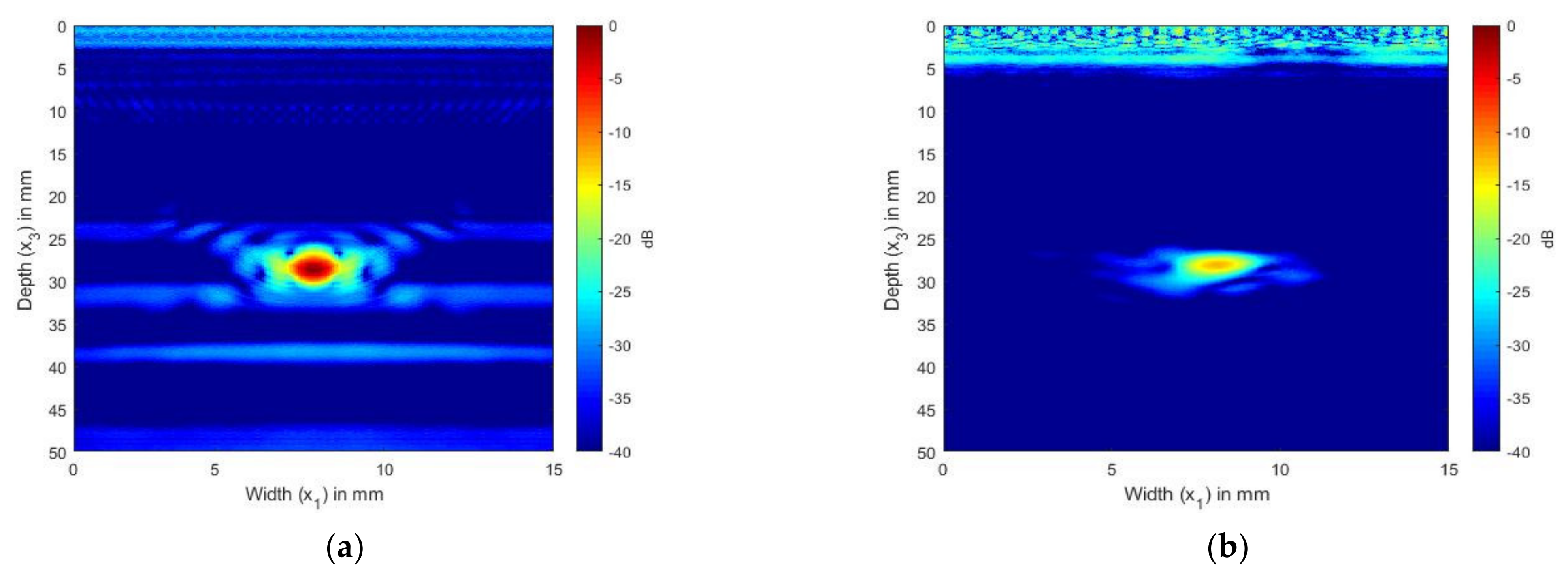
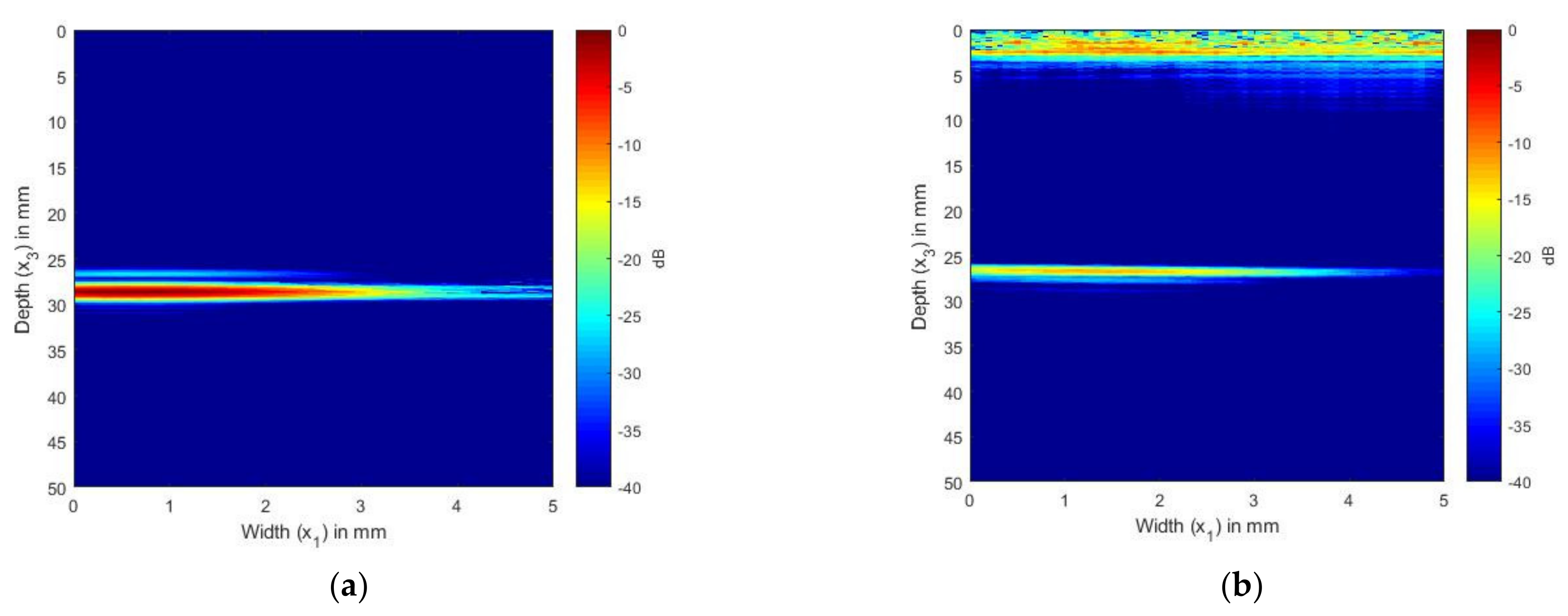
3.3. TFM Imaging
3.4. Quantitative Comparison of the Images
- Simulate the response from the embedded scatterer and calculate the peak amplitude of the scatterer.
- Simulate the response of the laminate without the scatterer and calculate the root mean square of the amplitudes of the signal in a chosen region around the scatterer, which is the “noise” of the image.
- Use Equation (57) to calculate the SNR of the SDH. The same procedure is carried out for the experimental TFM image, wherein the laminate FMC signals are processed before and after the SDH has been drilled into the laminate.
4. Simulation and Results
4.1. Calculation of Equivalent Homogeneous Properties
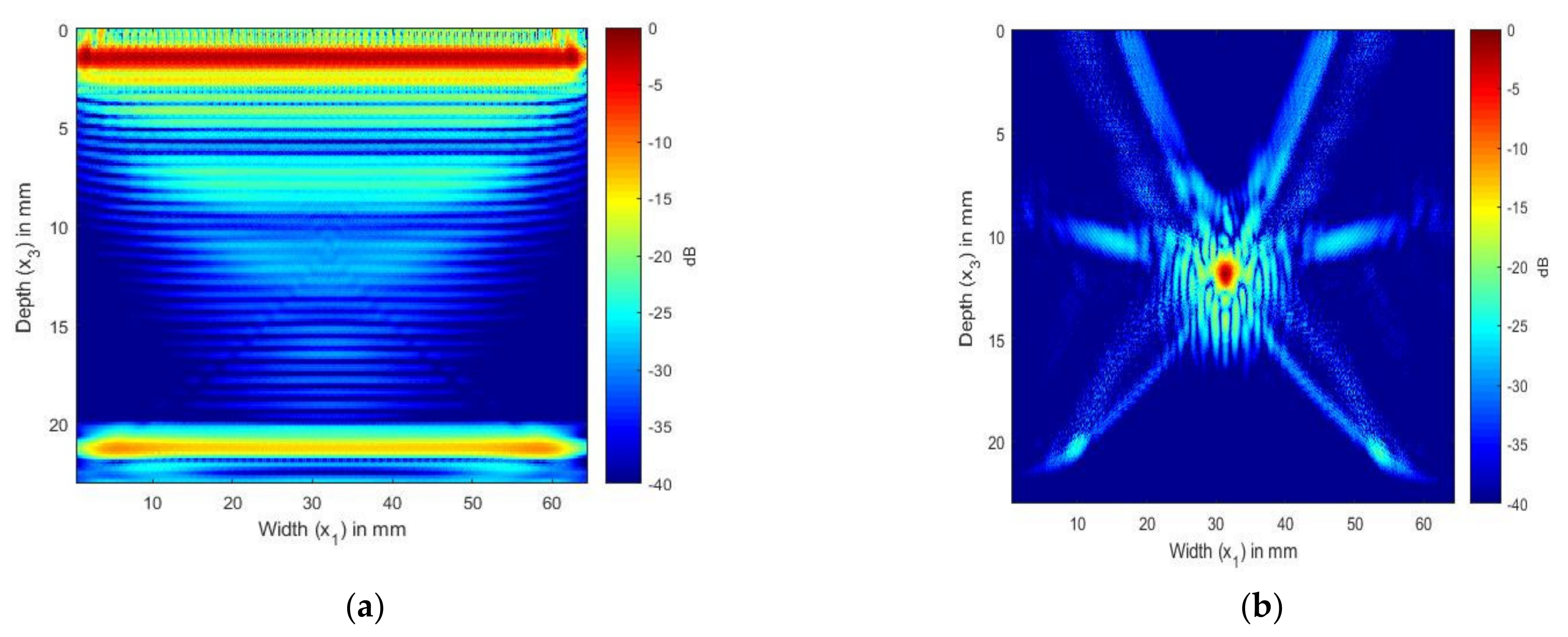
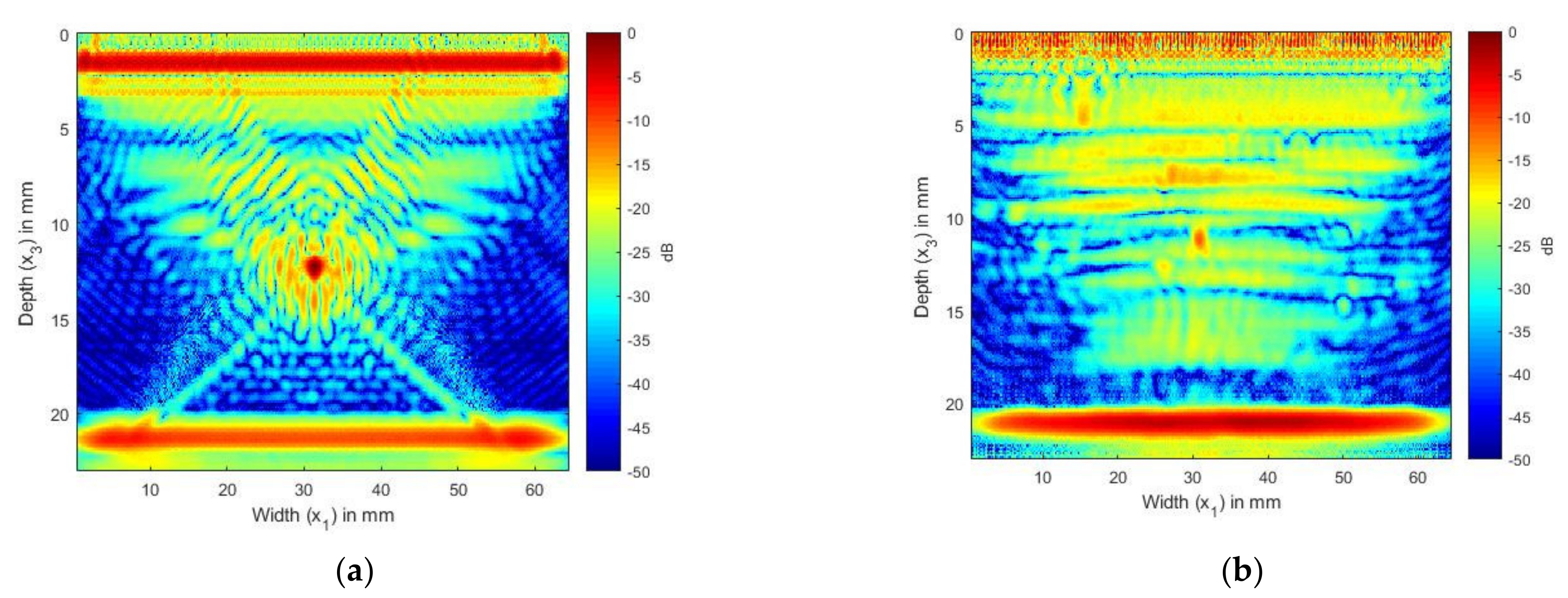
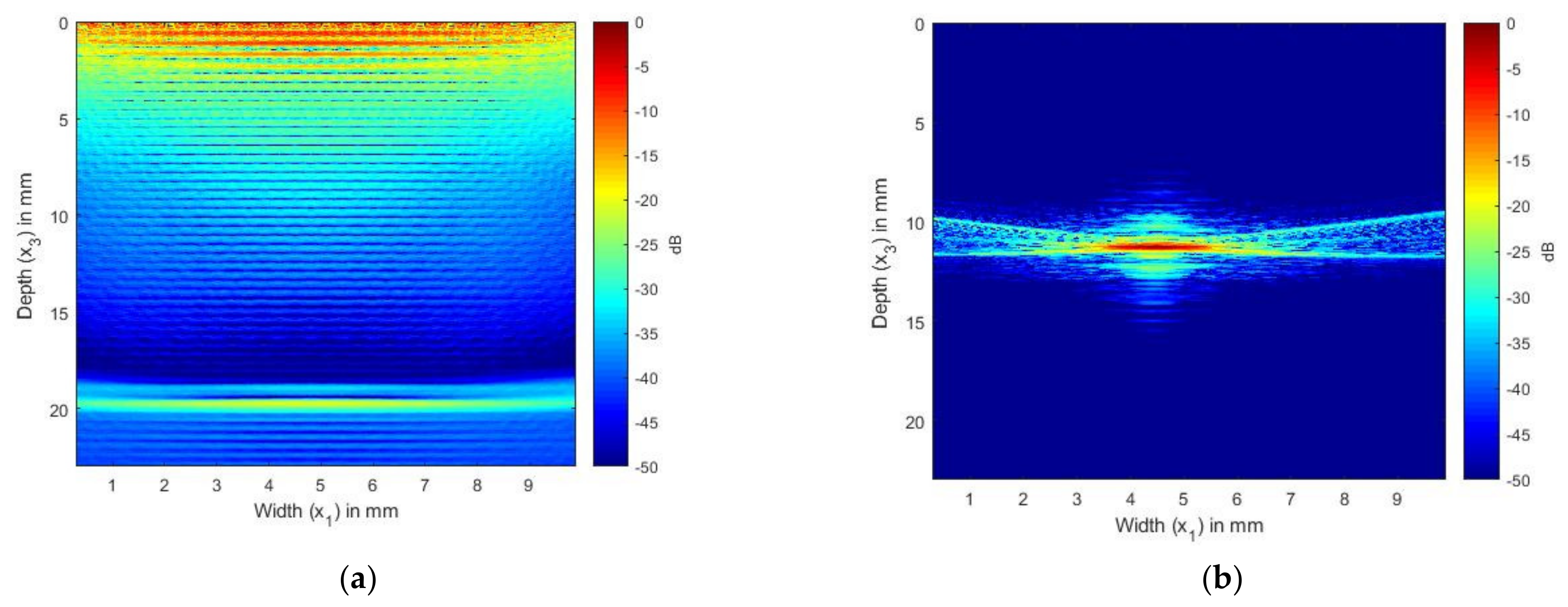
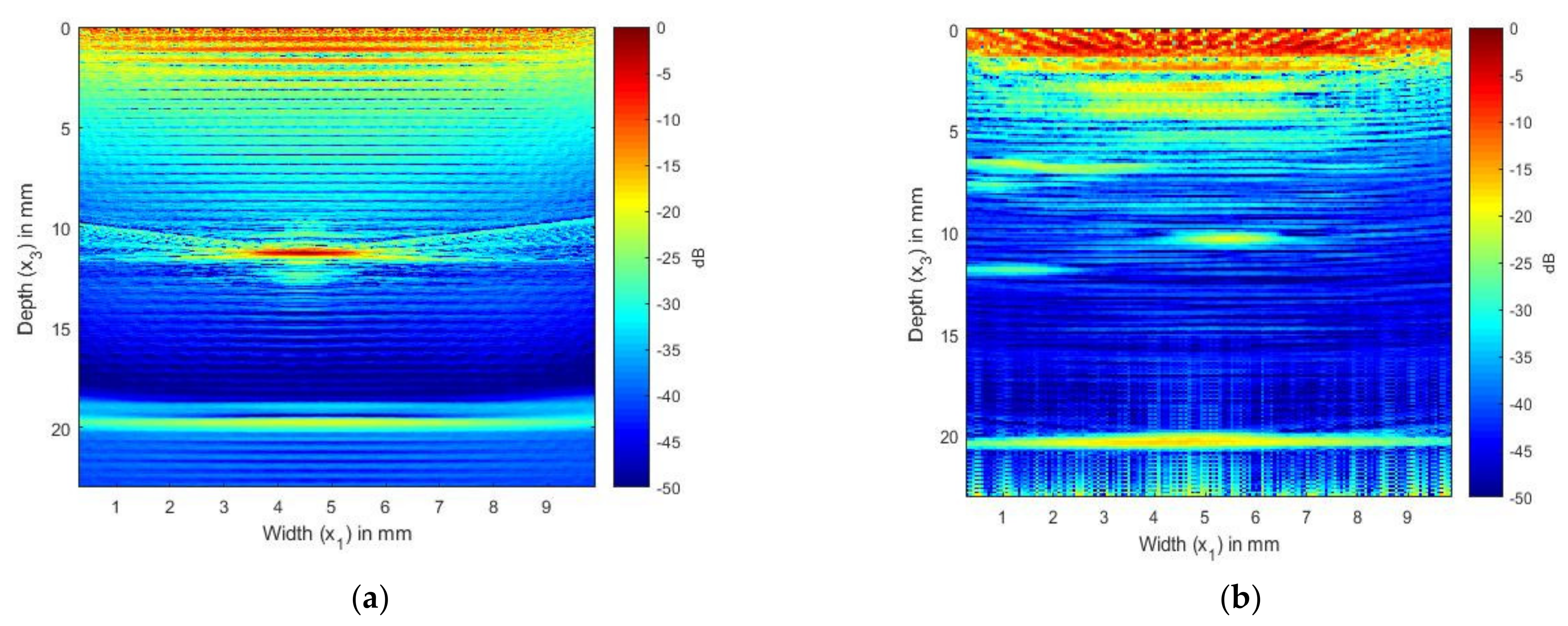
4.2. SDH Embedded in Aluminum Inspected by a 2.25 and 5 MHz Array
4.3. SDH Embedded in CFRP Inspected by Arrays with Center Frequencies of 2.25 and 5 MHz
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- McIlhagger, A.; Archer, E.; McIlhagger, R. Manufacturing processes for composite materials and components for aerospace applications. In Polymer Composites in the Aerospace Industry; Elsevier Inc.: Amsterdam, The Netherlands, 2015; pp. 53–75. ISBN 9780857099181. [Google Scholar]
- Garnier, C.; Pastor, M.L.; Eyma, F.; Lorrain, B. The detection of aeronautical defects in situ on composite structures using non destructive testing. Compos. Struct. 2011, 93, 1328–1336. [Google Scholar] [CrossRef] [Green Version]
- Smith, R. Composite Defects and their Detection. Mater. Sci. Eng. 2009, 3, 103–143. [Google Scholar]
- Soutis, C. Introduction: Engineering Requirements for Aerospace Composite Materials. In Polymer Composites in the Aerospace Industry; Elsevier Inc.: Amsterdam, The Netherlands, 2015; ISBN 9780857099181. [Google Scholar]
- Cantwell, W.J.; Morton, J. The significance of damage and defects and their detection in composite materials: A review. J. Strain Anal. Eng. Des. 1992, 27, 29–42. [Google Scholar] [CrossRef]
- Pagodinas, D. Ultrasonic signal processing methods for detection of defects in composite materials. Ultragarsas 2002, 45, 47–54. Available online: https://www.ultragarsas.ktu.lt/index.php/USnd/article/view/8157 (accessed on 30 November 2020).
- La Malfa Ribolla, E.; Rezaee Hajidehi, M.; Rizzo, P.; Fileccia Scimemi, G.; Spada, A.; Giambanco, G. Ultrasonic inspection for the detection of debonding in CFRP-reinforced concrete. Struct. Infrastruct. Eng. 2018, 14, 807–816. [Google Scholar] [CrossRef]
- Deydier, S.; Leymarie, N.; Calmon, P.; Mengeling, V. Modeling of the ultrasonic propagation into carbon-fiber-reinforced epoxy composites, using a ray theory based homogenization method. In Proceedings of the AIP Conference, New England, ME, USA, 31 July 2006. [Google Scholar] [CrossRef]
- Jezzine, K.; Ségur, D.; Ecault, R.; Dominguez, N.; Calmon, P. Hybrid ray-FDTD model for the simulation of the ultrasonic inspection of CFRP parts. In Proceedings of the AIP Conference, Atlanta, GE, USA, 16 February 2017; p. 090016. [Google Scholar] [CrossRef] [Green Version]
- Huang, R.; Schmerr, L.W.; Sedov, A. Multi-Gaussian Ultrasonic Beam Modeling for Multiple Curved Interfaces—An ABCD Matrix Approach; Research in NonDestructive Evaluation; Taylor & Francis: London, UK, 2005; Volume 16, ISBN 0934984050. [Google Scholar]
- Anand, C.; Delrue, S.; Jeong, H.; Shroff, S.; Groves, R.M.; Benedictus, R. Simulation of ultrasonic beam propagation from phased arrays in anisotropic media using linearly phased multi-Gaussian beams. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 106–116. [Google Scholar] [CrossRef]
- Knopoff, L. A Matrix Method for Elastic Wave Problems. Bull. Seismol. Soc. Am. 1964, 54, 431–438. [Google Scholar]
- Haskell, N.A. The dispersion of surface waves on multilayered media. Bull. Seismol. Soc. Am. 1953, 43, 17–34. [Google Scholar] [CrossRef]
- Thomson, W.T. Transmission of elastic waves through a stratified solid medium. J. Appl. Phys. 1950, 21, 89–93. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Wang, L. Ultrasonic waves in layered anisotropic media: Characterization of multidirectional composites. Int. J. Solids Struct. 2002, 39, 5529–5545. [Google Scholar] [CrossRef]
- Anand, C.; Groves, R.; Benedictus, R. A Gaussian Beam Based Recursive Stiffness Matrix Model to Simulate Ultrasonic Array Signals from Multi-Layered Media. Sensors 2020, 20, 4371. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Chimenti, D.E.; Nagy, P.B. Physical Ultrasonics of Composites; Oxford University Press: Oxford, UK, 2011; ISBN 9780195079609. [Google Scholar]
- Dobson, J.; Tweedie, A.; Harvey, G.; O’Leary, R.; Mulholland, A.; Tant, K.; Gachagan, A. Finite element analysis simulations for ultrasonic array NDE inspections. In Proceedings of the AIP Conference, Minneapolis, MN, USA, 26 July 2015; Volume 1706, p. 040005. [Google Scholar] [CrossRef] [Green Version]
- Schmerr, L.W. Fundamentals of Ultrasonic Nondestructive Evaluation: A Modeling Approach; Springer Series in Measurement Science and Technology; Springer: New York, NY, USA, 2016; ISBN 3319304615. [Google Scholar]
- Sun, C.T.; Li, S. Three-Dimensional Effective Elastic Constants for Thick Laminates. J. Compos. Mater. 1988, 22, 629–639. [Google Scholar] [CrossRef]
- Schmerr, L.W. Fundamentals of Ultrasonic Phased Arrays; Springer International Publishing: Cham, Switzerland, 2015; Volume 215, ISBN 978-3-319-07271-5. [Google Scholar]
- Nayfeh, A.H. The general problem of elastic wave propagation in multilayered anisotropic media. J. Acoust. Soc. Am. 1991, 89, 1521–1531. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Wang, L. Stable recursive algorithm for elastic wave propagation in layered anisotropic media: Stiffness matrix method. J. Acoust. Soc. Am. 2002, 112, 822–834. [Google Scholar] [CrossRef]
- Huang, R.; Schmerr, L.W.; Sedov, A. Modeling the radiation of ultrasonic phased-array transducers with Gaussian beams. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2692–2702. [Google Scholar] [CrossRef]
- Wen, J.J.; Breazeale, M.A. A diffraction beam field expressed as the superposition of Gaussian beams. J. Acoust. Soc. Am. 1988, 83, 1752–1756. [Google Scholar] [CrossRef]
- Postma, G.W. Wave propagation in a stratified medium. Geophysics 1955, 20, 780–806. [Google Scholar] [CrossRef]
- Isaac, M.; Daniel, O.I. Engineering Mechanics of Composite Materials; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Liu, D.; Li, X. An overall view of laminate theories based on displacement hypothesis. J. Compos. Mater. 1996, 30, 1539–1561. [Google Scholar] [CrossRef]
- Backus, G.E. Long-wave elastic anisotropy produced by horizontal layering. J. Geophys. Res. 1962, 67, 4427–4440. [Google Scholar] [CrossRef] [Green Version]
- Schmerr, L.W. Modeling Ultrasonic Problems for the 2002 Benchmark Session. In Proceedings of the AIP Conference, Bellingham, WA, USA, 14 July 2002; Volume 657, pp. 1776–1783. [Google Scholar] [CrossRef]
- Lopez-Sanchez, A.L.; Kim, H.J.; Schmerr, L.W.; Sedov, A. Measurement models and scattering models for predicting the ultrasonic pulse-echo response from side-drilled holes. J. Nondestruct. Eval. 2005, 24, 83–96. [Google Scholar] [CrossRef]
- Huang, R. Ultrasonic Modeling for Complex Geometries and Materials. 2006. Available online: http://adsabs.harvard.edu/abs/2006PhDT54H (accessed on 1 January 2021).
- Auld, B.A. General electromechanical reciprocity relations applied to the calculation of elastic wave scattering coefficients. Wave Motion 1979, 1, 3–10. [Google Scholar] [CrossRef]
- Holmes, C.; Drinkwater, B.W.; Wilcox, P.D. Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation. NDT E Int. 2005, 38, 701–711. [Google Scholar] [CrossRef]
- Hosten, B.; Castaings, M. Transfer matrix of multilayered absorbing and anisotropic media. Measurements and simulations of ultrasonic wave propagation through composite materials. J. Acoust. Soc. Am. 1993, 94, 1488–1495. [Google Scholar] [CrossRef]
- Lopez-Sanchez, A.L.; Kim, H.J.; Schmerr, L.W.; Gray, T.A. Modeling the response of ultrasonic reference reflectors. Res. Nondestruct. Eval. 2006, 17, 49–69. [Google Scholar] [CrossRef]


| Centre Frequency (MHz) | Pitch (mm) | Number of Elements | |
|---|---|---|---|
| Array 1 | 2.25 | 1 | 64 |
| Array 2 | 5 | 0.6 | 16 |
| Properties | Aluminum (GPa) | Carbon/Epoxy >65% Fiber-Volume Fraction (GPa) |
|---|---|---|
| C11 | 110 | 13.89(1+0.02i) |
| C22 | 110 | 13.89(1+0.02i) |
| C33 | 110 | 121.7(1+0.001i) |
| C12=C21 | 60 | 6.43(1+0.011i) |
| C13=C31 | 60 | 5.5(1+0.007i) |
| C23=C32 | 60 | 5.5(1+0.007i) |
| C44 | 25 | 5.1(1+0.066i) |
| C55 | 25 | 5.1(1+0.066i) |
| C66 | 25 | 3.73(1+0.027i) |
| Properties | Values in GPa |
|---|---|
| 54.76(1+0.002i) | |
| 54.76(1+0.002i) | |
| 13.89(1+0.02i) | |
| 18.53(1+0.01i) | |
| 5.96(1+0.004i) | |
| 5.96(1+0.005i) | |
| 4.3(1+0.06i) | |
| 4.3(1+0.06i) | |
| 18.12(1+0.03i) |
| Central Frequency of Array | SNR of SDH in Simulated Image | SNR of SDH in Experimental Image | Difference |
|---|---|---|---|
| 2.25 MHz | −42.9 dB | −39.5 dB | −3.4 dB |
| 5 MHz | −26.1 dB | −33.4 dB | −7.3 dB |
| Central Frequency of Array | SNR of SDH in Simulated Image | SNR of SDH in Experimental Image | Difference |
|---|---|---|---|
| 2.25 MHz | −42.9 dB | −25.6 dB | −17.3 dB |
| 5 MHz | −35.48 dB | −21 dB | −14.48 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anand, C.; Groves, R.M.; Benedictus, R. Modeling and Imaging of Ultrasonic Array Inspection of Side Drilled Holes in Layered Anisotropic Media. Sensors 2021, 21, 4640. https://doi.org/10.3390/s21144640
Anand C, Groves RM, Benedictus R. Modeling and Imaging of Ultrasonic Array Inspection of Side Drilled Holes in Layered Anisotropic Media. Sensors. 2021; 21(14):4640. https://doi.org/10.3390/s21144640
Chicago/Turabian StyleAnand, Chirag, Roger M. Groves, and Rinze Benedictus. 2021. "Modeling and Imaging of Ultrasonic Array Inspection of Side Drilled Holes in Layered Anisotropic Media" Sensors 21, no. 14: 4640. https://doi.org/10.3390/s21144640
APA StyleAnand, C., Groves, R. M., & Benedictus, R. (2021). Modeling and Imaging of Ultrasonic Array Inspection of Side Drilled Holes in Layered Anisotropic Media. Sensors, 21(14), 4640. https://doi.org/10.3390/s21144640







