Abstract
The compressive sensing (CS)-based sparse channel estimator is recognized as the most effective solution to the excessive pilot overhead in massive MIMO systems. However, due to the complex signal processing in the wireless communication systems, the measurement matrix in the CS-based channel estimation is sometimes “unfriendly” to the channel recovery. To overcome this problem, in this paper, the state-of-the-art sparse Bayesian learning using approximate message passing with unitary transformation (UTAMP-SBL), which is robust to various measurement matrices, is leveraged to address the multi-user uplink channel estimation for hybrid architecture millimeter wave massive MIMO systems. Specifically, the sparsity of channels in the angular domain is exploited to reduce the pilot overhead. Simulation results demonstrate that the UTAMP-SBL is able to achieve effective performance improvement than other competitors with low pilot overhead.
1. Introduction
Massive MIMO is a key technology for the fifth-generation (5G) communication systems [1]. Thanks to the shorter wavelength of the millimeter wave (mmWave) signal, the numerous antennas are packed into a compact-size array, which facilitates the commercial deployment of massive MIMO systems [2], but under the consideration of the high power consumption of Analog-to-Digital Converters (ADCs), the hybrid beamforming architecture, that divides the precoder and the combiner into the analog and digital domains, is developed to solve it and regarded as an effective alternative [3,4]. In this hybrid architecture system, the precoding is crucial and dependent on the acquisition of accurate channel state information (CSI). However, the number of pilots used for channel estimation will increase linearly with that of antennas and users in the wireless systems. As a result, the channel estimation with fewer pilots is a significant challenge in the hybrid mmWave massive MIMO systems [3].
The compressive sensing (CS)-based channel estimator is capable of exploiting the sparsity of channels to reduce the pilot overhead greatly and a lot of studies on this topic have been done. Some studies focus on the sparsity in the delay domain. In [5], the orthogonal matching pursuit (OMP) algorithm is utilized to estimate the wideband mmWave delay-domain sparse channels. In [6], an adaptive structured subspace pursuit algorithm at the user is proposed to estimate the delay-domain MIMO channels with the spatio-temporal common sparsity. The authors of [7] propose a sparse channel recovery algorithm based on the vector approximate message passing (VAMP) for the massive MIMO delay-domain channels. Some works concentrate on the sparsity in the angular domain. For example, a distributed sparsity adaptive matching pursuit (DSAMP) algorithm is proposed in [8], whereby the spatially common sparsity is exploited. In [9], a novel sparse Bayesian learning (SBL) approach is utilized to recover the angular-domain block-sparse channels. In [10], a structured turbo-CS algorithm is proposed to estimate the angular-domain massive MIMO channels which are modeled by a Markov chain prior. Furthermore, the work [11] even jointly exploits the 3-D clustered structure of channels in the angular-delay domain and proposes an approximate message passing (AMP)-based estimation algorithm. However, all of above angular-domain sparse channel estimation schemes are based on the assumption that the angles exactly lie on the grids, or ignore the power leakage caused by grid mismatch. Recently, there are many off-grid channel estimation techniques. In [12], the authors utilize the low-rank structure along with the sparsity in angular domain to improve the channel estimation performance, and the off-grid angles can be recovered with their algorithm successfully. In [13], the angles are treated as random parameters and the grid-less quantized variational Bayesian channel estimation algorithm is proposed for antenna array systems with low resolution ADCs. Besides, the multi-dimensional variational line spectral estimation algorithm proposed in [14] can be effectively applied for multi-dimensional off-grid angle estimation. In addition, a novel super-resolution downlink channel estimation approach developed from the SBL is provided in [15], where the sampled angular grid points are treated as the underlying parameters.
The performance of these CS-based algorithms is affected by the measurement matrix which is usually associated with the signal processing operations in the system. If these operations are not carefully designed, the measurement matrix perhaps becomes detrimental to channel recovery. Recently, a CS algorithm, termed the SBL using approximate message passing with unitary transformation (UTAMP-SBL), is proposed by Luo et al. and it outperforms the state-of-the-art AMP-based SBL algorithms, the Gaussian generalized AMP-based SBL (GGAMP-SBL), in terms of robustness, speed and recovery accuracy for difficult measurement matrices [16]. In this paper, we apply UTAMP-SBL to the sparse channel estimation to improve the performance. Specifically, the multi-user uplink channel estimation for hybrid architecture mmWave massive MIMO systems is studied as an example. And the angular-domain sparsity of the mmWave channels is fully exploited in our estimation. Additionally, this algorithm can be extended to other sparse channel estimation for the performance improvement. Simulation results verify that the UTAMP-SBL outperforms the other competitors.
The remainder of this paper is organized as follows. In Section 2, the hybrid millimeter wave massive MIMO system model is introduced. In Section 3, the uplink sparse channel estimation with UTAMP-SBL is described. In Section 4, the Cramér-Rao bound (CRB) is provided as a performance benchmark. Simulation results are provided and the performance is discussed in Section 5. Conclusions are given in Section 6.
Notations: and ⊗ denote the conjugate transpose operation and the Kronecker product. ⊙ and ⊘ represent the componentwise vector multiplication and the componentwise vector division. denotes vectorizing the matrix as a vector. , and denote the identity matrix, the all-one column vector and the all-zero column vector, respectively. returns a diagonal matrix with the elements of vector on its main diagonal. represents the Gaussian distribution of the complex vector with mean and covariance matrix . denotes a Gamma distribution with shape parameter and rate parameter . denotes the expectation of the function with respect to probability density . Finally, denotes equality up to a constant scale factor.
2. System Model
2.1. Millimeter Wave MIMO Channel Model
We consider a mmWave MIMO-OFDM system where the base station (BS) is equipped with antennas and serves K multi-antenna user equipments (UEs), and each UE has antennas. The frequency-domain channel between the BS and the kth UE at the pth subcarrier can be modeled as [17]
where L is the number of physical paths, is the complex path gain, is the sampling rate, is the path delay, and are the steering vectors at the BS and the UE, respectively, and are the azimuth angles of departure and arrival (AoD/AoA) uniformly distributed in .
For each UE in the system, we generate one line of sight (LoS) path and non-LoS (NLoS) paths. The path gains follow the complex Gaussian distribution and the ratio of the power of LOS path to that of NLoS path is 10 dB [18]. In the OFDM system, the cyclic prefix (CP) is introduced to mitigate the inter-symbol interference and we have , where is the maximum path delay and is the length of CP. So we generate and . For the steering vectors, assuming the uniform linear arrays are adopted at the BS and the UE, they can be shown as
where is the wavelength and is the antenna spacing.
2.2. Uplink Pilot Transmission
We consider the typical hybrid analog digital precoding and combining architecture in the mmWave massive MIMO systems, where the BS and each UE are assumed to have RF chains and RF chains, respectively. We focus on the uplink pilot training. The kth UE transmits the pilot at the pth pilot subcarrier and the tth OFDM symbol to the BS, where is the number of data streams. At the BS, the receiver receives pilots from all UEs in the same time-frequency resources and the received signal can be written as
where and are the digital precoder and the analog precoder of the kth user, and are the digital combiner and the analog combiner of the BS and is the additive white Gaussian noise (AWGN). Note that the analog precoder and the analog combiner are frequency-flat, while the digital precoder and the digital combiner are different for each subcarrier. This is because the RF phase shifters can provide constant response over the wide frequency band when the fully connected network is used.
2.3. Sparse Channel Estimation Formulation
In the multi-user uplink channel estimation, the channels of K users, , , need to be estimated from the received signal . It is clear that there are non-zero elements in these K channel matrices. Because there are only elements in , we have to arrange pilots for channel estimation and the pilot overhead is unacceptable. Fortunately, we benefit from the inherent sparse characteristic of millimeter wave channels and apply the CS algorithms in the channel estimation to reduce the pilot overhead.
In order to formulate the sparse channel estimation problem, we first rewrite the frequency-domain channel matrix as
where is the virtual angle-domain channel matrix, and are the partial discrete Fourier transform (DFT) matrices, and are the numbers of grids at the BS and the UE. Because of the domination of the LOS path in the multipath channel, the virtual angle-domain mmWave channel appears the sparsity, i.e., there are only a few non-zero elements in the channel matrix and other components are zero. Actually, these zeros are not strictly equal to zero but are only close to zero owing to the power leakage problem [19], which is ignored in this paper for simplification and it will be disscussed in the future research. The frequency-domain channel and the transformed virtual angle-domain channel are shown in Figure 1, where the frequency-domain channel is generated according to (1) and the virtual angle-domain channel is derived from (4). Obviously, from Figure 1b, the power of the channel is concentrated in a few virtual angles and these channel components can be estimated from the low-overhead pilot.
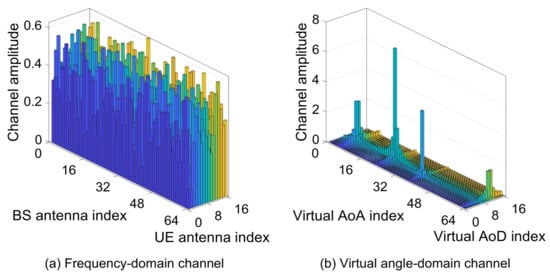
Figure 1.
The illustration of the frequency-domain channel and the virtual angle-domain channel.
Substituting (4) in (3), we have
where is the combiner at the BS, is the pilot after precoding at the UE and is the noise after combining at the BS. Note that usually the channel is invariant in some successive OFDM symbols. Rewrite (5) in matrix form as
where , , and . Using the result , (6) can be equivalently expressed as
where , . We stack the received signals that are transmited on G successive symbols, and we have
where , and .
As shown above, in the channel estimation, the measurement matrix derives from pilots, precoders, combiners and the partial DFT matrices, so it is a difficult matrix in all probability. With the difficult measurement matrix, the existing sparse channel estimation algorithms can fail to recover channels. As a result, the UTAMP-SBL which is robust to difficult measurement matrix is a wise choice.
3. Uplink Channel Estimation with UTAMP-SBL
Focus on the channel estimation of the single subcarrier and the subscript p is omitted for conciseness,
Let , , so the sizes of , and are , and , respectively, where . In order to characterize the sparsity of , the Gaussian prior model is adopted, i.e.,
where and . Define the singular value decomposition (SVD) of is , where is an orthogonal matrix and . Perform unitary transformation to (9) and we have
where , and follows . Define and the likelihood function of is
According to the Bayesian rule, the joint probability density function is
where the Dirac function factor is adopted first in [20] to facilitate the derivation of the algorithm. The factor graph of the factorization (13) is shown in Figure 2. The UTAMP-SBL algorithm will be derived from message-passing on this graph and applied to the channel estimation.

Figure 2.
The factor graph of uplink sparse channel estimation.
Firstly, we consider the massages between node and node . According to the sum-product algorithm, the massage from function node to variable node is . The massage from variable node to function node is defined as . So the belief can be calculated as , where the mean and variance are
Then, we focus on the massages between node and node . Similarly, the massage from function node to variable node is defined as . And the massage from variable node to function node is defined as . So the belief is calculated as , where the mean and variance are
For the sparse channel estimation, the mean of the belief is the estimated channel.
Next, the variable , , and mentioned above can be updated with the UTAMP which is derived from the AMP. In the UTAMP, the means and variances are calculated by [16]
where the intermediate variables and are given by [16]
Besides, there are several model parameters need to be learned at each iteration. For the noise precision , it can be updated with the expectation-maximization (EM) algorithm [16]
For the variable , according to the sum-product algorithm, the componentwise massage from function node to variable node is
The message from variable node to function node is . Consequently, the belief is expressed as
So, is the mean of this distribution, i.e.,
when we set . For the parameter , it is difficult to renewed, but there is an effective way found in [16] and we use it directly. As a result, is calculated by
The process of the channel estimation with UTAMP-SBL is given in Algorithm 1. In this algorithm, the iteration will be halted if the number of it reaches the maximum value or .
| Algorithm 1 Uplink channel estimation with UTAMP-SBL. |
| Input: The received signal and the matrix . Output: The estimated sparse channel .
|
The computational complexity of the UTAMP-SBL is dominated by the complex multiplications required for matrix-vector operations. At the stage of initialization, the complexity of SVD is [21]. The matrix-vector product of is . At the stage of iteration, the complexity of calculating and are respectively and in the step 3 of Algorithm 1. The calculations of remaining steps only involve the component-wise vector multiplication or scalar operations which bring a small amount of complex multiplication compared with matrix-vector product. Therefore, the computational complexity of them is omitted. When the iteration reaches T, the total complexity is . Discarding the low-order terms, the total complexity is .
4. Cramér-Rao Bound Analysis
In this section, the CRB is provided as a performance benchmark of the channel estimation. From Section 3, the sparse channel estimation is modeled as an SBL problem and the CRBs for SBL derived in [22] can be adopted directly.
5. Simulation Results
The simulation parameters are chosen as follows, , , , , , and . The pilots, precoders and combiners are generated according to [17]. In order to evaluate the performance, the normalized MSE (NMSE) between the estimated channel and the real channel is introduced. We compare the NMSE performance for the OMP [5], SBL [9], EM-BBG-VAMP [7], SuRe-CSBL [15], TurboCS [10], UTAMP-SBL, and the CRB derived in Section 4.
Figure 3 shows the NMSE versus the pilot overhead at . As defined in Section 3, N is the dimension of the received signal and M is the dimension of the sparse channel . In this simulation, the pilot overhead is denoted as . We can find that the off-grid algorithm, SuRe-CSBL, could not achieve the desired performance when the pilot is insufficient in spite of it is the winners in [15]. The SBL, EM-BBG-VAMP and UTAMP-SBL work well with 9.38% pilot overhead compared with other algorithms. Thus, when the pilot overhead is extremely low, the SuRe-CSBL, TurboCS and OMP are not sensible choices. It is also shown that the UTAMP-SBL performs distinctly better than the other estimators with the same pilot overhead. From another side, it is also concluded that the UTAMP-SBL can accurately estimate the channels with fewer pilots. For example, when the NMSE performance meets −10 dB, the OMP, SBL and EM-BBG-VAMP respectively need 22.66%, 21.88%, 16.41% pilot overhead. However, the UTAMP-SBL only needs 11.72% overhead, which means the pilot overhead is reduced by 28.58% compared with the EM-BBG-VAMP.
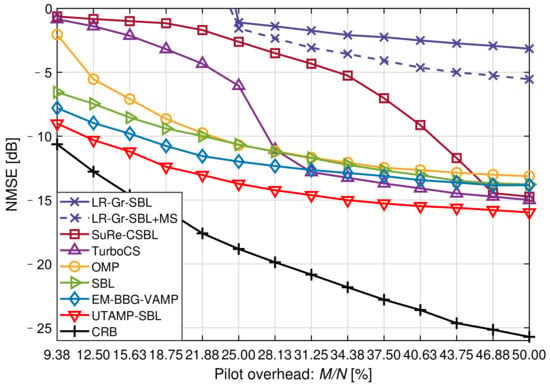
Figure 3.
The NMSE versus the pilot overhead at SNR = 20 dB.
Figure 4 shows the NMSE versus the SNR with 25.00% pilot overhead. Due to insufficient of pilots, the SuRe-CSBL and TurboCS could not estimate the channels well, even if their NMSEs are lower than CRB at low SNRs. It is observed that the UTAMP-SBL has the best performance compared with the other competitors. This is because the UTAMP-SBL is robust to different types of difficult measurement matrices, such as non-zero mean, rank-deficient, correlated, or ill-conditioned matrix [16]. This feature is crucial for the practical application of this algorithm. In the channel estimation, the measurement matrix is usually related to the complex signal processing operations as described in Section 2.3, so it can be a difficult matrix. Therefore, the UTAMP-SBL with strong robustness performs better in the channel estimation. Moreover, the matrix inversion step of SBL causing the high complexity is avoided by replacing the E-step in the EM with UTAMP, and the algorithm complexity is reduced [16].
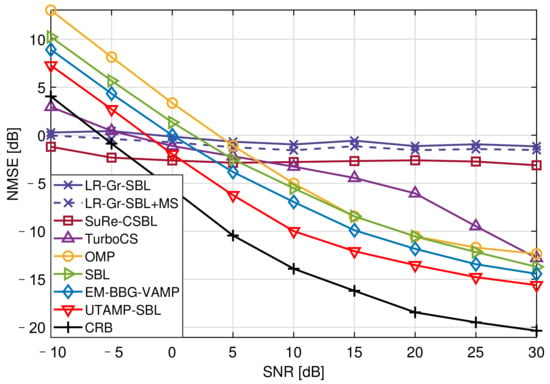
Figure 4.
The NMSE versus the SNR with 25.00% pilot overhead.
Figure 5 provides the NMSE versus the number of iterations at different SNRs with 25.00% pilot overhead, which illustrates the convergences of the algorithms. Since the algorithms, SuRe-CSBL, TurboCS, are not suitable for our channel estimation when the pilot overhead is 25.00%, only the convergences of the OMP, SBL, EM-BBG-VAMP and UTAMP-SBL are compared. When , the OMP fails to converge even if the number of iterations reaches 300, and the NMSE performance decreases with the increasing iterations. This shows that the OMP is not suitable for the low SNR cases. The SBL, EM-BBG-VAMP and UTAMP-SBL require about 100 iterations to converge. When , the OMP is still with the worst convergence and the UTAMP-SBL is with the best convergence. However, when , the EM-BBG-VAMP converges slightly faster than the UTAMP-SBL. From the results, the EM-BBG-VAMP converges within 20 iterations while the UTAMP-SBL requires about 40 iterations. And these two algorithms are both faster than the SBL and the OMP. Additionally, in this figure, only the performance of the UTAMP-SBL becomes better with the iteration at all SNRs, while that of other algorithms sometimes deteriorates with the iteration. This further demonstrates the advantage of the UTAMP-SBL in convergence. From above observation and analysis, the UTAMP-SBL is superior to the comparison algorithms in the convergence speed and the NMSE performance.
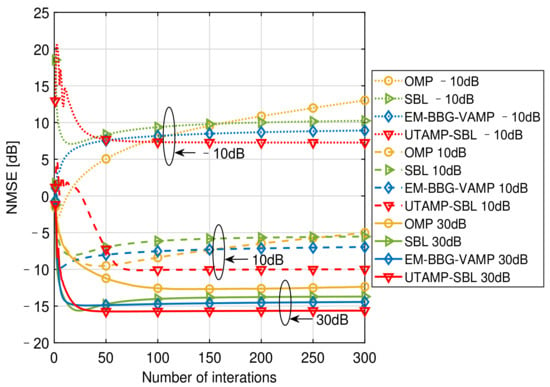
Figure 5.
The NMSE versus the number of iterations at different SNRs with 25.00% pilot overhead.
6. Conclusions
In this paper, the UTAMP-SBL algorithm is applied to estimate the sparse channels for improving the performance. In order to evaluate the effect of this algorithm in practical channel estimation, we study the multi-user uplink channel estimation for hybrid architecture mmWave massive MIMO systems. Simulation results demonstrate the superiority of the UTAMP-SBL in terms of NMSE performance and pilot overhead reduction.
Author Contributions
Conceptualization, S.H. and Y.W.; methodology, S.H.; software, S.H.; validation, S.H., Y.W. and C.L.; formal analysis, S.H. and C.L.; investigation, S.H.; data curation, S.H. and C.L.; writing—original draft preparation, S.H.; writing—review and editing, Y.W. and C.L.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Education and China Mobile Joint Scientific Research Fund (No. MCM20180201).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Xiao, M.; Mumtaz, S.; Huang, Y.; Dai, L.; Li, Y.; Matthaiou, M.; Karagiannidis, G.K.; Björnson, E.; Yang, K.; Chih-Lin, I.; et al. Millimeter Wave Communications for Future Mobile Networks. IEEE J. Sel. Areas Commun. 2017, 35, 1909–1935. [Google Scholar] [CrossRef] [Green Version]
- Heath, R.W.; González-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An Overview of Signal Processing Techniques for Millimeter Wave MIMO Systems. IEEE J. Sel. Topics Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Ayach, O.E.; Leus, G.; Heath, R.W. Channel Estimation and Hybrid Precoding for Millimeter Wave Cellular Systems. IEEE J. Sel. Topics Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef] [Green Version]
- Venugopal, K.; Alkhateeb, A.; Prelcic, N.G.; Heath, R.W. Channel Estimation for Hybrid Architecture-Based Wideband Millimeter Wave Systems. IEEE J. Sel. Areas Commun. 2017, 35, 1996–2009. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Dai, W.; Shim, B.; Wang, Z. Structured Compressive Sensing-Based Spatio-Temporal Joint Channel Estimation for FDD Massive MIMO. IEEE Trans. Commun. 2016, 64, 601–617. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Yao, H.; Jiang, C.; Chen, X.; Kuang, L.; Hanzo, L. Downlink Channel Estimation for Massive MIMO Systems Relying on Vector Approximate Message Passing. IEEE Trans. Veh. Technol. 2019, 68, 5145–5148. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Dai, L.; Wang, Z.; Chen, S. Spatially Common Sparsity Based Adaptive Channel Estimation and Feedback for FDD Massive MIMO. IEEE Trans. Signal Process. 2015, 63, 6169–6183. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, S.; Mishra, A.; Rajoriya, A.; Jagannatham, A.K.; Ascheid, G. Quasi-Static and Time-Selective Channel Estimation for Block-Sparse Millimeter Wave Hybrid MIMO Systems: Sparse Bayesian Learning (SBL) Based Approaches. IEEE Trans. Signal Process. 2018, 67, 1251–1266. [Google Scholar] [CrossRef]
- Chen, L.; Liu, A.; Yuan, X. Structured Turbo Compressed Sensing for Massive MIMO Channel Estimation Using a Markov Prior. IEEE Trans. Veh. Technol. 2018, 67, 4635–4639. [Google Scholar] [CrossRef]
- Lin, X.; Wu, S.; Jiang, C.; Kuang, L.; Yan, J.; Hanzo, L. Estimation of Broadband Multiuser Millimeter Wave Massive MIMO-OFDM Channels by Exploiting Their Sparse Structure. IEEE Trans. Wireless Commun. 2018, 17, 3959–3973. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Liu, Z.; Song, C.; Xu, Z.; Zhong, C. Low-rank and Angular Structures aided mmWave MIMO Channel Estimation with Few-bit ADCs. In Proceedings of the 2020 IEEE 11th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hangzhou, China, 8–11 June 2020; pp. 1–5. [Google Scholar]
- Zhu, J.; Wen, C.-K.; Tong, J.; Xu, C.; Jin, S. Grid-Less Variational Bayesian Channel Estimation for Antenna Array Systems With Low Resolution ADCs. IEEE Trans. Wireless Commun. 2020, 19, 1549–1562. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, J.; Zhang, N.; Xu, Z. Multidimensional Variational Line Spectra Estimation. IEEE Signal Process. Lett. 2020, 27, 945–949. [Google Scholar] [CrossRef]
- He, Z.-Q.; Yuan, X.; Chen, L. Super-Resolution Channel Estimation for Massive MIMO via Clustered Sparse Bayesian Learning. IEEE Trans. Veh. Technol. 2019, 68, 6156–6160. [Google Scholar] [CrossRef]
- Luo, M.; Guo, Q.; Huang, D.; Xi, J. Sparse Bayesian Learning Based on Approximate Message Passing with Unitary Transformation. In Proceedings of the 2019 IEEE VTS Asia Pacific Wireless Communications Symposium (APWCS), Singapore, 28–30 August 2019; pp. 1–5. [Google Scholar]
- Gao, Z.; Hu, C.; Dai, L.; Wang, Z. Channel Estimation for Millimeter-Wave Massive MIMO With Hybrid Precoding Over Frequency-Selective Fading Channels. IEEE Commun. Lett. 2016, 20, 1259–1262. [Google Scholar] [CrossRef] [Green Version]
- Muhi-Eldeen, Z.; Ivrissimtzis, L.P.; Al-Nuaimi, M. Modelling and Measurements of Millimetre Wavelength Propagation in Urban Environments. IET Microwaves Antennas Propag. 2010, 4, 1300–1309. [Google Scholar] [CrossRef]
- Hu, C.; Dai, L.; Mir, T.; Gao, Z.; Fang, J. Super-Resolution Channel Estimation for MmWave Massive MIMO With Hybrid Precoding. IEEE Trans. Veh. Technol. 2018, 67, 8954–8958. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Wu, S.; Zhu, J. A Unified Bayesian Inference Framework for Generalized Linear Models. IEEE Signal Process. Lett. 2018, 25, 398–402. [Google Scholar] [CrossRef]
- Rangan, S.; Schniter, P.; Fletcher, A.K. Vector Approximate Message Passing. IEEE Trans. Inf. Theory 2019, 65, 6664–6684. [Google Scholar] [CrossRef] [Green Version]
- Prasad, R.; Murthy, C.R. Cramér-Rao-Type Bounds for Sparse Bayesian Learning. IEEE Trans. Signal Process. 2013, 61, 622–632. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).