Arc-Induced Long-Period Fiber Gratings at INESC TEC. Part I: Fabrication, Characterization and Mechanisms of Formation
Abstract
:1. Introduction
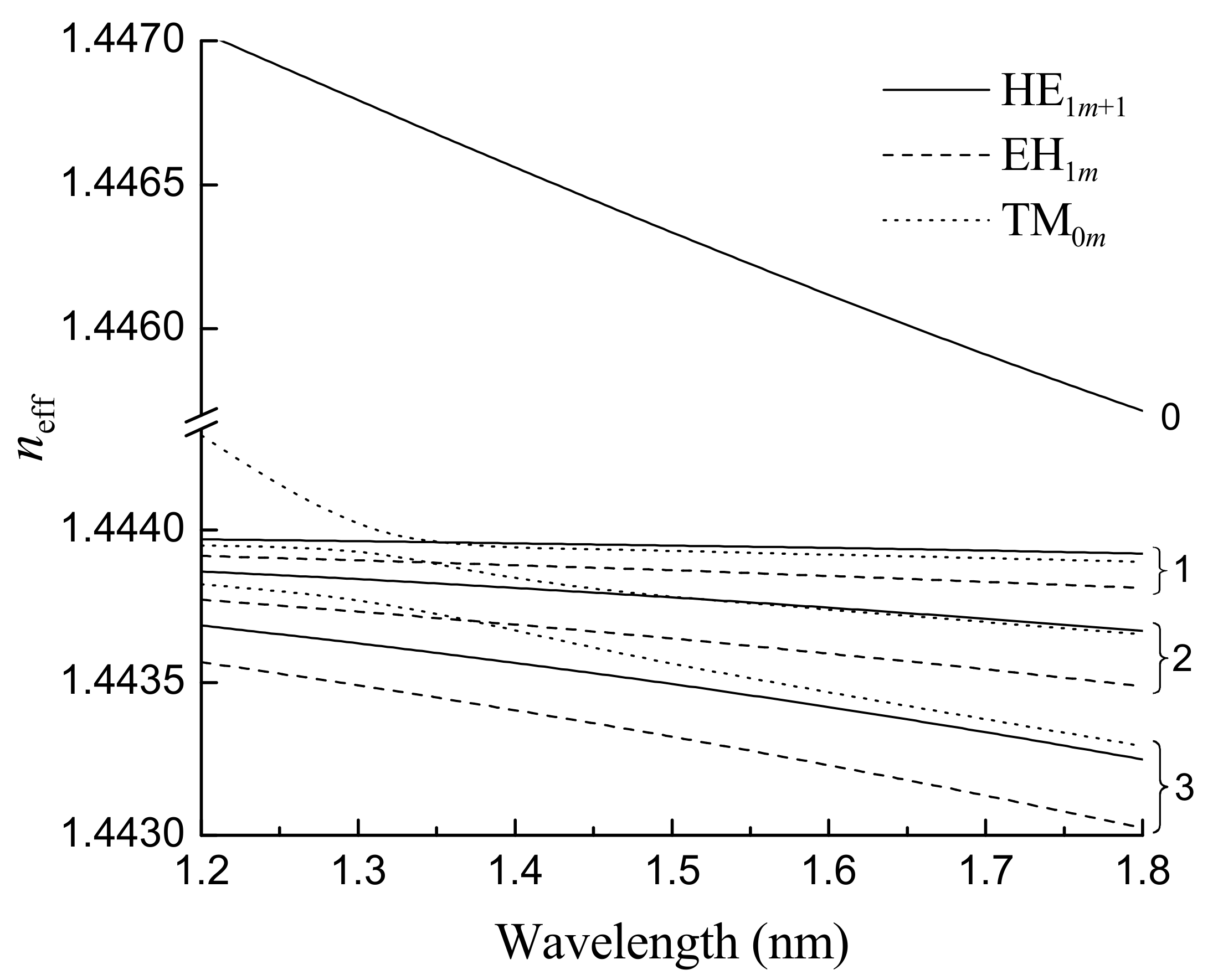
2. Theory of Long-Period Fiber Gratings
3. Fabrication and Characterization of Long-Period Fiber Gratings
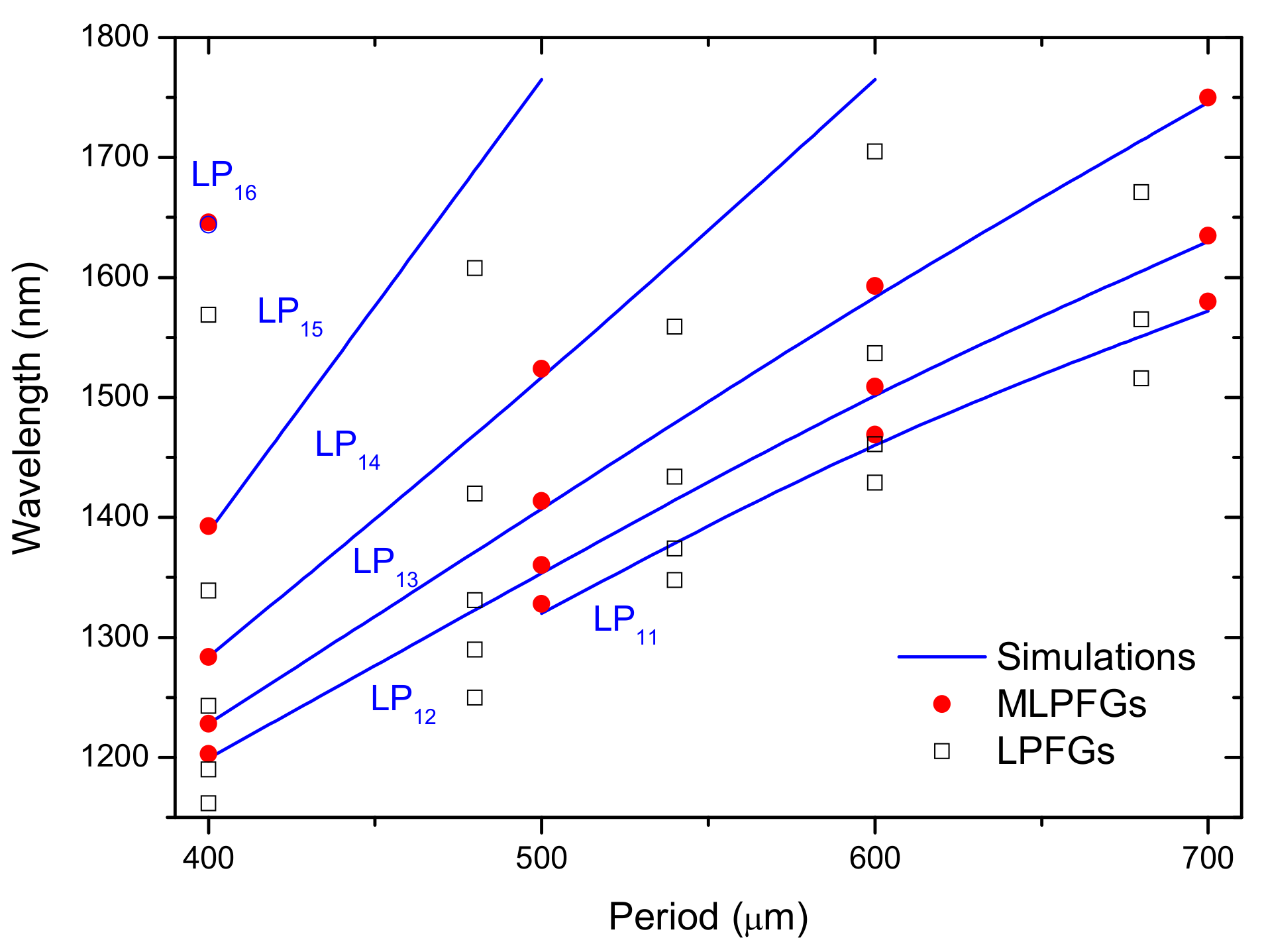
3.1. LPFGs Fabrication
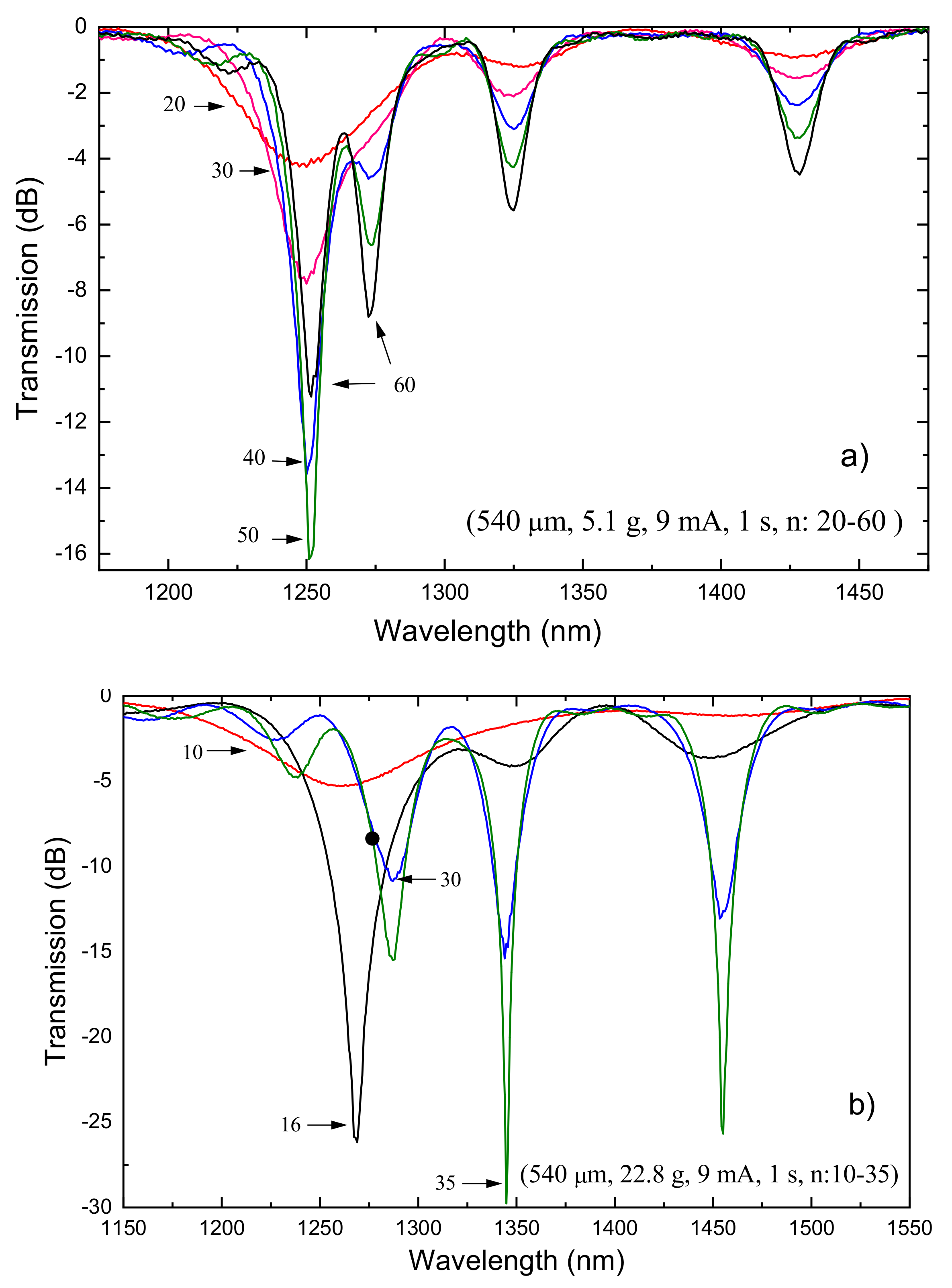
3.2. LPFGs Characterization
4. Mechanisms of Gratings Formation
4.1. Fiber Temperature
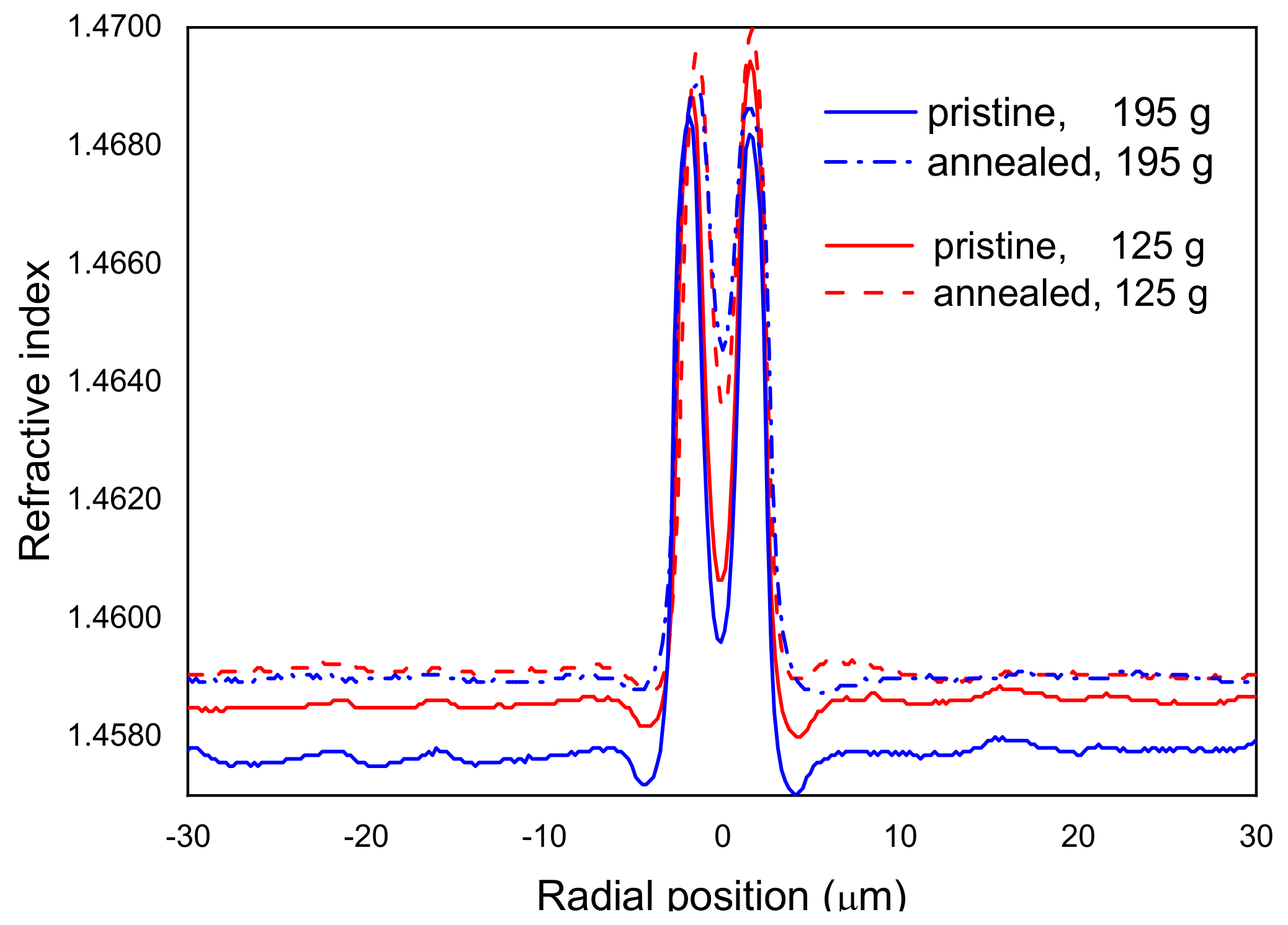
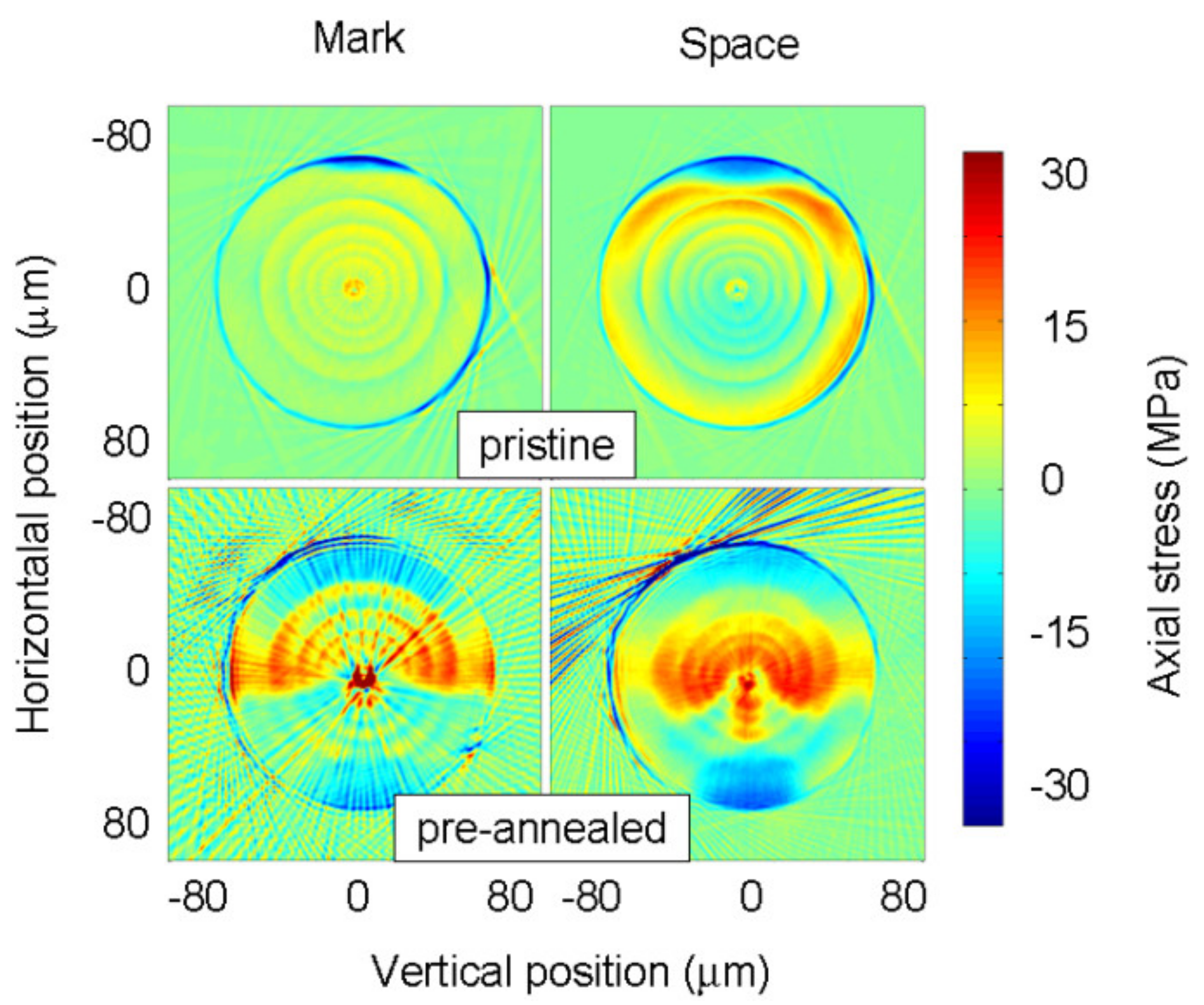
4.2. Elastic and Viscoelastic Stresses
4.3. Microdeformations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vengsarkar, A.M.; Lemaire, P.J.; Judkins, J.B.; Bhatia, V.; Erdogan, T.; Sipe, J.E. Long-period fiber gratings as band-rejection filters. J. Lightwave Technol. 1996, 14, 58–65. [Google Scholar] [CrossRef]
- An, H.; Ashton, B.; Fleming, S. Long-period-grating-assisted optical add–drop filter based on mismatched twin-core photosensitive-cladding fiber. Opt. Lett. 2004, 29, 343–345. [Google Scholar] [CrossRef] [PubMed]
- Abramov, A.; Eggleton, B.; Rogers, J.; Espindola, R.; Hale, A.; Windeler, R.; Strasser, T. Electrically tunable efficient broad-band fiber filter. IEEE Photonics Technol. Lett. 1999, 11, 445–447. [Google Scholar] [CrossRef]
- Costantini, D.; Muller, C.; Vasiliev, S.; Limberger, H.; Salathe, R. Tunable loss filter based on metal-coated long-period fiber grating. IEEE Photonics Technol. Lett. 1999, 11, 1458–1460. [Google Scholar] [CrossRef]
- Vengsarkar, A.M.; Bergano, N.S.; Davidson, C.R.; Pedrazzani, J.R.; Judkins, J.B.; Lemaire, P.J. Long-period fiber-grating-based gain equalizers. Opt. Lett. 1996, 21, 336–338. [Google Scholar] [CrossRef] [PubMed]
- Wysocki, P.F.; Judkins, J.B.; Espindola, R.P.; Andrejco, M.; Vengsarkar, A.M. Broad-band erbium-doped fiber amplifier flattened beyond 40 nm using long-period grating filter. IEEE Photonics Technol. Lett. 1997, 9, 1343–1345. [Google Scholar] [CrossRef]
- Patrick, H.; Kersey, A.; Burns, W.; Moeller, R. Erbium-doped superfluorescent fibre source with long period fibre grating wavelength stabilisation. Electron. Lett. 1997, 33, 2061. [Google Scholar] [CrossRef]
- Dong, X.; Yang, X.; Shum, P.; Chan, C.C. Tunable WDM filter with 0.8-nm channel spacing using a pair of long-period fiber gratings. IEEE Photonics Technol. Lett. 2005, 17, 795–797. [Google Scholar] [CrossRef]
- Gu, X.J. Wavelength-division multiplexing isolation fiber filter and light source using cascaded long-period fiber gratings. Opt. Lett. 1998, 23, 509–510. [Google Scholar] [CrossRef]
- Kim, M.J.; Eom, T.J.; Paek, U.-C.; Lee, B.H. Lens-free optical fiber connector having a long working distance assisted by matched long-period fiber gratings. J. Light. Technol. 2005, 23, 588–596. [Google Scholar] [CrossRef]
- Perlin, V.; Winful, H. Nonlinear pulse switching using long-period fiber gratings. J. Light. Technol. 2000, 18, 329–333. [Google Scholar] [CrossRef]
- Kim, Y.H.; Kim, N.S.; Chung, Y.; Paek, U.-C.; Han, W.-T. All-optical switching application based on optical nonlinearity of Yb(3+) doped aluminosilicate glass fiber with a long-period fiber gratings pair. Opt. Express 2004, 12, 651–656. [Google Scholar] [CrossRef] [PubMed]
- Kulishov, M.; Azaña, J. Long-period fiber gratings as ultrafast optical differentiators. Opt. Lett. 2005, 30, 2700–2702. [Google Scholar] [CrossRef] [PubMed]
- Das, M.; Thyagarajan, K. Dispersion compensation in transmission using uniform long period fiber gratings. Opt. Commun. 2001, 190, 159–163. [Google Scholar] [CrossRef]
- Han, Y.-G.; Kim, C.-S.; Kang, J.; Paek, U.-C.; Chung, Y. Multiwavelength Raman fiber-ring laser based on tunable cascaded long-period fiber gratings. IEEE Photonics Technol. Lett. 2003, 15, 383–385. [Google Scholar] [CrossRef]
- Patrick, H.J.; Chang, C.C.; Vohra, S.T. Long period fibre gratings for structural bend sensing. Electron. Lett. 1998, 34, 1773. [Google Scholar] [CrossRef]
- Patrick, H.; Kersey, A.; Bucholtz, F. Analysis of the response of long period fiber gratings to external index of refraction. J. Light. Technol. 1998, 16, 1606–1612. [Google Scholar] [CrossRef]
- Bhatia, V.; Campbell, D.; Claus, R.O.; Vengsarkar, A.M. Simultaneous strain and temperature measurement with long-period gratings. Opt. Lett. 1997, 22, 648–650. [Google Scholar] [CrossRef]
- Bhatia, V. Applications of long-period gratings to single and multi-parameter sensing. Opt. Express 1999, 4, 457–466. [Google Scholar] [CrossRef]
- Shu, X.; Zhang, L.; Bennion, I. Sensitivity characteristics near the dispersion turning points of long-period fiber gratings in B/Ge codoped fiber. Opt. Lett. 2001, 26, 1755–1757. [Google Scholar] [CrossRef]
- Han, Y.-G.; Lee, S.B.; Kim, C.-S.; Kang, J.U.; Chung, Y.; Paek, U.-C. Simultaneous measurement of temperature and strain using dual long-period fiber gratings with controlled temperature and strain sensitivities. Opt. Express 2003, 11, 476–481. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frazão, O.; Romero, R.; Rego, G.; Marques, P.V.S.; Salgado, H.; Santos, J.L. Sampled fibre Bragg grating sensors for simultaneous strain and temperature measurement. Electron. Lett. 2002, 38, 693. [Google Scholar] [CrossRef]
- Allsop, T.; Zhang, L.; Bennion, I. Detection of organic aromatic compounds in paraffin by a long-period fiber grating optical sensor with optimized sensitivity. Opt. Commun. 2001, 191, 181–190. [Google Scholar] [CrossRef]
- Falate, R.; Kamikawachi, R.; Muller, M.; Kalinowski, H.; Fabris, J. Fiber optic sensors for hydrocarbon detection. Sens. Actuators B Chem. 2005, 105, 430–436. [Google Scholar] [CrossRef]
- Khaliq, S.; James, S.; Tatam, R. Fiber-optic liquid-level sensor using a long-period grating. Opt. Lett. 2001, 26, 1224–1226. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.M.; Tay, C.M.; Tjin, S.C.; Chan, C.C.; Rahardjo, H. High relative humidity measurements using gelatin coated long-period grating sensors. Sens. Actuators B Chem. 2005, 110, 335–341. [Google Scholar] [CrossRef]
- Del Villar, I.; Matias, I.R.; Arregui, F.J. Long-period fiber gratings with overlay of variable refractive index. IEEE Photonics Technol. Lett. 2005, 17, 1893–1895. [Google Scholar] [CrossRef]
- Martins, R.; Caldas, P.; Teixeira, B.; Azevedo, J.; Monteiro, J.; Belo, J.H.; de Araújo, J.P.E.; Santos, J.L.; Rego, G. Cryogenic Temperature Response of Reflection-Based Phase-Shifted Long-Period Fiber Gratings. J. Light. Technol. 2014, 33, 2511–2517. [Google Scholar] [CrossRef]
- Huang, J.; Lan, X.; Kaur, A.; Wang, H.; Yuan, L.; Xiao, H. Reflection-based phase-shifted long period fiber grating for simultaneous measurement of temperature and refractive index. Opt. Eng. 2013, 52, 014404. [Google Scholar] [CrossRef]
- James, S.; Tatam, R. Optical fibre long-period grating sensors: Characteristics and application. Meas. Sci. Technol. 2003, 14, R49–R61. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.W.; Wang, Q. Mini review: Recent advances in long period fiber grating biological and chemical sensors. Instrum. Sci. Technol. 2019, 47, 140–169. [Google Scholar] [CrossRef]
- Rego, G. A Review of Refractometric Sensors Based on Long Period Fibre Gratings. Sci. World J. 2013, 2013, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Debowska, A.K.; Smietana, M.; Mikulic, P.; Bock, W.J. High temperature nano-coated electric-arc-induced long-period gratings working at the dispersion turning point for refractive index sensing. Jpn. J. Appl. Phys. 2014, 53, 08ME01. [Google Scholar] [CrossRef]
- Coelho, L.; Viegas, D.; Santos, J.L.; De Almeida, J.M.M.M.; De Almeida, J.M.M.M. Detection of Extra Virgin Olive Oil Thermal Deterioration Using a Long Period Fibre Grating Sensor Coated with Titanium Dioxide. Food Bioprocess Technol. 2015, 8, 1211–1217. [Google Scholar] [CrossRef]
- Petrovic, J.S.; Dobb, H.; Mezentsev, V.K.; Kalli, K.; Webb, D.J.; Bennion, I. Sensitivity of LPGs in PCFs Fabricated by an Electric Arc to Temperature, Strain, and External Refractive Index. J. Light. Technol. 2007, 25, 1306–1312. [Google Scholar] [CrossRef]
- Fu, C.; Wang, Y.; Liu, S.; Bai, Z.; Liao, C.; He, J.; Wang, Y. Recent Progress in Fabrications and Applications of Heating-Induced Long Period Fiber Gratings. Sensors 2019, 19, 4473. [Google Scholar] [CrossRef] [Green Version]
- Kosinski, S.G.; Vengsarkar, A.M. Splice-based long-period fiber gratings. In Proceedings of the Optical Fiber Communications Conference, San Jose, CA, USA, 22 February 1998. [Google Scholar]
- Dianov, E. Thermo-induced long-period fibre gratings. In Proceedings of the 11th International Conference on Integrated Optics and Optical Fibre Communications and 23rd European Conference on Optical Communications IOOC-ECOC97, Edinburgh, UK, 22–25 September 1997; Volume 1997. [Google Scholar]
- Davis, D.; Gaylord, T.; Glytsis, E.; Kosinski, S.; Mettler, S.; Vengsarkar, A. Long-period fibre grating fabrication with focused CO2 laser pulses. Electron. Lett. 1998, 34, 302–303. [Google Scholar] [CrossRef]
- Guan, B.-O.; Tam, H.Y.; Ho, S.L.; Liu, S.-Y.; Dong, X.-Y. Growth of long-period gratings in H2-loaded fiber after 193-nm UV inscription. IEEE Photonics Technol. Lett. 2000, 12, 642–644. [Google Scholar] [CrossRef]
- Kalachev, A.; Nikogosyan, D.; Brambilla, G. Long-period fiber grating fabrication by high-intensity femtosecond pulses at 211 nm. J. Light. Technol. 2005, 23, 2568–2578. [Google Scholar] [CrossRef]
- Slattery, S.A.; Nikogosyan, D.N. Long-period fiber grating inscription under high-intensity 352 nm femtosecond irradiation: Three-photon absorption and energy deposition in cladding. Opt. Commun. 2005, 255, 81–90. [Google Scholar] [CrossRef]
- Zagorul’ko, K.A.E.; Kryukov, P.G.; Larionov, Y.V.; Rybaltovsky, A.A.; Dianov, E.M.; Vorob’Ev, N.S.; Smirnov, A.V.; Schelev, M.Y.; Prokhorov, A.M. Fabrication of a long-period grating in a fibre by second-harmonic radiation from a femtosecond Ti:sapphire laser. Quantum Electron. 2001, 31, 999–1002. [Google Scholar] [CrossRef]
- Kryukov, P.; Larionov, Y.; Rybaltovskii, A.; Zagorul’Ko, K.; Dragomir, A.; Nikogosyan, D.; Ruth, A. Long-period fibre grating fabrication with femtosecond pulse radiation at different wavelengths. Microelectron. Eng. 2003, 69, 248–255. [Google Scholar] [CrossRef]
- Li, X.; Yue, C.; Xia, L.; Chen, X.; Xie, S. Novel technique for long period gratings fabrication using broad spectrum ultraviolet source. Microw. Opt. Technol. Lett. 2002, 33, 368–370. [Google Scholar] [CrossRef]
- Dianov, E.M.; Stardubov, D.S.; Vasiliev, S.; Frolov, A.A.; Medvedkov, O.I. Refractive-index gratings written by near-ultraviolet radiation. Opt. Lett. 1997, 22, 221–223. [Google Scholar] [CrossRef]
- Blows, J.; Tang, D. Gratings written with tripled output of Q-switched Nd:YAG laser. Electron. Lett. 2000, 36, 1837–1839. [Google Scholar] [CrossRef]
- Chen, K.P.; Herman, P.R.; Zhang, J.; Tam, R. Fabrication of strong long-period gratings in hydrogen-free fibers with 157-nm F2-laser radiation. Opt. Lett. 2001, 26, 771–773. [Google Scholar] [CrossRef] [Green Version]
- Kondo, Y.; Nouchi, K.; Mitsuyu, T.; Watanabe, M.; Kazansky, P.; Hirao, K. Fabrication of long-period fiber gratings by focused irradiation of infrared femtosecond laser pulses. Opt. Lett. 1999, 24, 646–648. [Google Scholar] [CrossRef] [PubMed]
- Rao, Y.-J.; Wang, Y.-P.; Ran, Z.-L.; Zhu, T. Novel fiber-optic sensors based on long-period fiber gratings written by high-frequency CO2 laser pulses. J. Light. Technol. 2003, 21, 1320–1327. [Google Scholar] [CrossRef]
- Hwang, I.K.; Yun, S.H.; Kim, B.Y. Long-period fiber gratings based on periodic microbends. Opt. Lett. 1999, 24, 1263–1265. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, O.V. Fabrication of long-period fiber gratings by twisting a standard single-mode fiber. Opt. Lett. 2005, 30, 3290–3292. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.; Lee, K.R.; Paek, U.-C.; Chung, Y. Fabrication of helical long-period fiber gratings by use of a CO2 laser. Opt. Lett. 2004, 29, 1464–1466. [Google Scholar] [CrossRef]
- Kopp, V.I.; Churikov, V.M.; Singer, J.; Chao, N.; Neugroschl, D.; Genack, A.Z. Chiral Fiber Gratings. Science 2004, 305, 74–75. [Google Scholar] [CrossRef]
- Lin, C.; Wang, L. Loss-tunable long period fibre grating made from etched corrugation structure. Electron. Lett. 1999, 35, 1872. [Google Scholar] [CrossRef]
- Fujimaki, M.; Ohki, Y.; Brebner, J.L.; Roorda, S. Fabrication of long-period optical fiber gratings by use of ion implantation. Opt. Lett. 2000, 25, 88–89. [Google Scholar] [CrossRef] [PubMed]
- Von Bibra, M.L.; Roberts, A.; Canning, J. Fabrication of long-period fiber gratings by use of focused ion-beam irradiation. Opt. Lett. 2001, 26, 765–767. [Google Scholar] [CrossRef] [PubMed]
- Jáuregui, C.; Lopez-Higuera, J.M. Virtual long-period gratings. Opt. Lett. 2005, 30, 14–16. [Google Scholar] [CrossRef] [PubMed]
- Savin, S.; Digonnet, M.J.F.; Kino, G.S.; Shaw, H.J. Tunable mechanically induced long-period fiber gratings. Opt. Lett. 2000, 25, 710–712. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Gaylord, T.K. Dissimilar-fiber long-period fiber gratings: Concept and demonstration. Appl. Opt. 2017, 56, 1142. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Liu, S.; Bai, Z.; He, J.; Liao, C.; Wang, Y.; Li, Z.; Zhang, Y.; Yang, K.; Bin, Y.; et al. Orbital Angular Momentum Mode Converter Based on Helical Long Period Fiber Grating Inscribed by Hydrogen—Oxygen Flame. J. Light. Technol. 2018, 36, 1683–1688. [Google Scholar] [CrossRef]
- Viveiros, D.; De Almeida, J.M.; Coelho, L.; Vasconcelos, H.; Maia, J.M.; Amorim, V.A.; Jorge, P.A.S.; Marques, P.V.S. Temperature Stability and Spectral Tuning of Long Period Fiber Gratings Fabricated by Femtosecond Laser Direct Writing. Sensors 2020, 20, 3898. [Google Scholar] [CrossRef]
- Bai, Y.; He, Z.; Bai, J.; Dang, S. The study of second-order coupling of cladding modes of helical long-period gratings inscribed by commercial welding machine. Appl. Phys. A 2021, 127, 1–4. [Google Scholar] [CrossRef]
- Rego, G.; Okhotnikov, O.; Dianov, E.; Sulimov, V. High-temperature stability of long-period fiber gratings produced using an electric arc. J. Light. Technol. 2001, 19, 1574–1579. [Google Scholar] [CrossRef]
- Rego, G.; Falate, R.; Santos, J.L.; Salgado, H.; Fabris, J.L.; Semjonov, S.L.; Dianov, E.M. Arc-induced long-period gratings in aluminosilicate glass fibers. Opt. Lett. 2005, 30, 2065–2067. [Google Scholar] [CrossRef]
- Rego, G.; Fernandez, A.F.; Gusarov, A.; Brichard, B.; Berghmans, F.; Santos, J.L.; Salgado, H.M. Effect of ionizing radiation on the properties of arc-induced long-period fiber gratings. Appl. Opt. 2005, 44, 6258–6263. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morishita, K.; Miyake, Y.; Morishita, K.; Miyake, Y. Fabrication and Resonance Wavelengths of Long-Period Gratings Written in a Pure-Silica Photonic Crystal Fiber by the Glass Structure Change. J. Light. Technol. 2004, 22, 625–630. [Google Scholar] [CrossRef]
- Humbert, G.; Malki, A.; Février, S.; Roy, P.; Pagnoux, D. Electric arc-induced long-period gratings in Ge-free air-silica microstructure fibres. Electron. Lett. 2003, 39, 349–350. [Google Scholar] [CrossRef]
- Humbert, G.; Malki, A.; Février, S.; Roy, P.; Auguste, J.-L.; Blondy, J.-M. Long period grating filters fabricated with electric arc in dual concentric core fibers. Opt. Commun. 2003, 225, 47–53. [Google Scholar] [CrossRef]
- Smietana, M.; Bock, W.J.; Mikulic, P.; Chen, J. Increasing sensitivity of arc-induced long-period gratings—pushing the fabrication technique toward its limits. Meas. Sci. Technol. 2010, 22, 015201. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Rios, A.; Salceda-Delgado, G.; Monzón-Hernández, D.; Anzueto-Sánchez, G. Arc-induced long-period fiber gratings inscribed in asymmetric adiabatic tapers. Opt. Eng. 2013, 52, 086111. [Google Scholar] [CrossRef]
- Ladicicco, A.; Ranjan, R.; Campopiano, S. Fabrication and Characterization of Long-Period Gratings in Hollow Core Fibers by Electric Arc Discharge. IEEE Sens. J. 2014, 15, 3014–3020. [Google Scholar] [CrossRef]
- Srivastava, A.; Esposito, F.; Pereira, J.M.B.; Campopiano, S.; Iadicicco, A. Fabrication and characterization of arc-induced long period gratings in optical fibers with micro-channels. In Proceedings of the 2020 IEEE Sensors, Rotterdam, The Netherlands, 25–28 October 2020. [Google Scholar]
- Esposito, F.; Ranjan, R.; Campopiano, S.; Iadicicco, A. Arc-Induced Long Period Gratings from Standard to Polarization-Maintaining and Photonic Crystal Fibers. Sensors 2018, 18, 918. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ranjan, R.; Esposito, F.; Iadicicco, A.; Campopiano, S. Arc-Induced Long Period Gratings in Phosphorus-Doped Fiber. IEEE Photonics Technol. Lett. 2017, 29, 611–614. [Google Scholar] [CrossRef]
- Huo, L.; Wang, R.; Tang, M.; Wu, Q.; Fu, S.; Liu, D. Reconfigurable Inter-Core Signal Switching Within Multicore Fibers Based on Long-Period Gratings. J. Light. Technol. 2019, 37, 6025–6032. [Google Scholar] [CrossRef]
- Iadicicco, A.; Campopiano, S.; Cusano, A. Long-Period Gratings in Hollow Core Fibers by Pressure-Assisted Arc Discharge Technique. IEEE Photonics Technol. Lett. 2011, 23, 1567–1569. [Google Scholar] [CrossRef]
- Ranjan, R.; Esposito, F.; Iadicicco, A.; Stancalie, A.; Sporea, D.; Campopiano, S. Comparative Study of Long-Period Gratings Written in Standard and Fluorine-Doped Fibers by Electric Arc Discharge. IEEE Sens. J. 2016, 16, 4265–4273. [Google Scholar] [CrossRef]
- Esposito, F.; Campopiano, S.; Iadicicco, A. Arc-Induced Long Period Gratings in Erbium-Doped Fiber. IEEE Photonics J. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Davis, D.; Gaylord, T.; Glytsis, E.; Mettler, S. Very-high-temperature stable CO2-laser-induced long-period fibre gratings. Electron. Lett. 1999, 35, 740–742. [Google Scholar] [CrossRef]
- Humbert, G.; Malki, A. Electric-arc-induced gratings in non-hydrogenated fibres: Fabrication and high-temperature char-acterizations. J. Opt. Pure Appl. Opt. 2002, 4, 194–198. [Google Scholar] [CrossRef]
- Rego, G.; Marques, P.V.S.; Santos, J.L.; Salgado, H.M. Arc-Induced Long-Period Gratings. Fiber Integr. Opt. 2005, 24, 245–259. [Google Scholar] [CrossRef]
- Yablon, A.D. Optical Fiber Fusion Splicer; Springer: Berlin/Heidelberg, Germany, 2005; Volume 103. [Google Scholar]
- Rego, G. Fibre optic devices produced by arc discharges. J. Opt. 2010, 12, 113002. [Google Scholar] [CrossRef]
- Poole, C.D.; Poole, C.D.; Presby, H.M.; Meester, J.P. 2-Mode Fiber Spatial-Mode Converter Using Periodic Core Deformation. Electron. Lett. 1994, 30, 1437–1438. [Google Scholar] [CrossRef]
- Rego, G. Arc-Induced Long Period Fiber Gratings. J. Sens. 2016, 2016, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Tsao, C. Multilayered cylindrical waveguides. In Optical Fibre Waveguide Analysis; Oxford University Press: Oxford, UK, 1992; p. 243. [Google Scholar]
- Erdogan, T. Cladding-mode resonances in short- and long-period fiber grating filters. J. Opt. Soc. Am. A 1997, 14, 1760–1773. [Google Scholar] [CrossRef]
- Ivanov, O.; Nikitov, S.A.; Gulyaev, Y.V. Cladding modes of optical fibers: Properties and applications. Phys. Uspekhi 2006, 49, 167–191. [Google Scholar] [CrossRef]
- Zhao, Y.; Palais, J. Simulation and characteristics of long-period fiber Bragg grating coherence spectrum. J. Light. Technol. 1998, 16, 554–561. [Google Scholar] [CrossRef]
- Yamada, M.; Sakuda, K. Analysis of almost-periodic distributed feedback slab waveguides via a fundamental matrix approach. Appl. Opt. 1987, 26, 3474–3478. [Google Scholar] [CrossRef]
- Morishita, K.; Kaino, A. Adjusting resonance wavelengths of long-period fiber gratings by the glass-structure change. Appl. Opt. 2005, 44, 5018–5023. [Google Scholar] [CrossRef]
- Palai, P.; Satyanarayan, M.N.; Das, M.; Thyagarajan, K.; Pal, B.P. Characterization and simulation of long period gratings fabricated using electric discharge. Opt. Commun. 2001, 193, 181–185. [Google Scholar] [CrossRef]
- Godbout, N.; Daxhelet, X.; Maurier, A.; Lacroix, S. Long-period fiber grating by electrical discharge. In Proceedings of the 24th European Conference on Optical Communication. ECOC’98 (IEEE Cat. No.98TH8398), Madrid, Spain, 20–24 September 1998. [Google Scholar]
- Nam, S.H.; Zhan, C.; Lee, J.; Hahn, C.; Reichard, K.; Ruffin, P.; Deng, K.-L.; Yin, S. Bend-insensitive ultra short long-period gratings by the electric arc method and their applications to harsh environment sensing and communication. Opt. Express 2005, 13, 731–737. [Google Scholar] [CrossRef] [PubMed]
- Iredale, T.B.; Steinvurzel, P.; Eggleton, B.J. Eggleton Electric-arc-induced long-period gratings in fluid-filled photonic bandgap fibre. Electron. Lett. 2006, 42, 739–740. [Google Scholar] [CrossRef]
- Martinez-Rios, A.; Monzon-Hernandez, D.; Torres-Gomez, I. Highly sensitive cladding-etched arc-induced long-period fiber gratings for refractive index sensing. Opt. Commun. 2010, 283, 958–962. [Google Scholar] [CrossRef]
- Colaco, C.; Caldas, P.; Del Villar, I.; Chibante, R.; Rego, G. Arc-Induced Long-Period Fiber Gratings in the Dispersion Turning Points. J. Light. Technol. 2016, 34, 4584–4590. [Google Scholar] [CrossRef]
- Kim, M.W.; Lee, D.W.; Hong, B.I.; Chung, H.Y. Performance characteristics of long-period fiber-gratings made from periodic tapers induced by electric-arc discharge. J. Korean Phys. Soc. 2002, 40, 369–373. [Google Scholar]
- Cho, M.P.; Lin, H.S.; Yong, Y.T.; Phua, Y.N.; Yong, T.K.; Rahman, F.A. Characterisation of continuous arc discharge system as a fusion heat source for fused fiber components. In Proceedings of the the 4th Annual IEEE International Conference on Cyber Technology in Automation, Control and Intelligent, Hong-Kong, China, 4–7 June 2014; pp. 270–273. [Google Scholar]
- Yin, G.; Tang, J.; Liao, C.; Wang, Y. Automatic arc discharge technology for inscribing long period fiber gratings. Appl. Opt. 2016, 55, 3873–3878. [Google Scholar] [CrossRef] [PubMed]
- Do Rego, G.M. Arc-Induced Long-Period Fibre Gratings: Fabrication and Their Applications in Optical Communications and Sensing, in Engineering Faculty. Ph.D. Thesis, Porto University, Porto, Portugal, 2006. [Google Scholar]
- Ivanov, O.V.; Rego, G. Origin of coupling to antisymmetric modes in arc-induced long-period fiber gratings. Opt. Express 2007, 15, 13936–13941. [Google Scholar] [CrossRef]
- Mesonero-Santos, P.; Fernández-Medina, A.; Coelho, L.; Viveiros, D.; Jorge, P.; Belenguer, T.; Heredero, R.L. Effect of Low-Doses of Gamma Radiation on Electric Arc-Induced Long Period Fiber Gratings. Sensors 2021, 21, 2318. [Google Scholar] [CrossRef]
- Vasconcelos, H.; De Almeida, J.M.M.M.; Saraiva, C.M.T.; Jorge, P.; Coelho, L.C.C. Mach–Zehnder Interferometers Based on Long Period Fiber Grating Coated With Titanium Dioxide for Refractive Index Sensing. J. Light. Technol. 2019, 37, 4584–4589. [Google Scholar] [CrossRef]
- Gonçalves, H.; Moreira, L.; Pereira, M.L.G.; Jorge, P.; Gouveia, C.; Martins-Lopes, P.; Fernandes, J.R. Biosensor for label-free DNA quantification based on functionalized LPGs. Biosens. Bioelectron. 2016, 84, 30–36. [Google Scholar] [CrossRef] [Green Version]
- Simões, E.; Abe, I.; Oliveira, J.; Frazão, O.; Caldas, P.; Pinto, J. Characterization of optical fiber long period grating refractometer with nanocoating. Sen. Actuators B Chem. 2011, 153, 335–339. [Google Scholar] [CrossRef]
- Trifanov, I.; Caldas, P.; Neagu, L.; Romero, R.; Berendt, M.O.; Salcedo, J.A.R.; Podoleanu, A.G.; Ribeiro, A.B.L. Combined Neodymium–Ytterbium-Doped ASE Fiber-Optic Source for Optical Coherence Tomography Applications. IEEE Photonics Technol. Lett. 2010, 23, 21–23. [Google Scholar] [CrossRef]
- Frazão, O.; Falate, R.; Fabris, J.L.; Santos, J.L.; Ferreira, L.A.; Araújo, F.M. Optical inclinometer based on a single long-period fiber grating combined with a fused taper. Opt. Lett. 2006, 31, 2960–2962. [Google Scholar] [CrossRef]
- Falate, R.; Frazão, O.; Baptista, J.M.; Fabris, J.L.; Santos, J.L. Optical bend sensor based on a long-period fiber grating monitored by an optical time-domain reflectometer. Opt. Eng. 2005, 44, 110502. [Google Scholar] [CrossRef] [Green Version]
- Magalhães, R.; Silva, S.; Frazão, O. Curvature Sensor Based on a Long-Period Grating in a Fiber Ring Resonator Interro-gated by an OTDR. Photonic Sens. 2020, 10, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Silva, L.H.; Santos, P.; Coelho, L.C.C.; Jorge, P.; Baptista, J.M. Development of a Long Period Fiber Grating Interrogation System Using A Multimode Laser Diode. Sensors 2021, 21, 749. [Google Scholar] [CrossRef] [PubMed]
- Rego, G.; Santos, L.; Schroder, B.; Marques, P.V.S.; Santos, J.L.; Salgado, H. In Situ Temperature Measurement of an Optical Fiber Submitted to Electric Arc Discharges. IEEE Photonics Technol. Lett. 2004, 16, 2111–2113. [Google Scholar] [CrossRef]
- Rego, G.; Santos, L.; Schröder, B. Estimation of the fiber temperature during an arc-discharge. Microw. Opt. Technol. Lett. 2008, 50, 2020–2025. [Google Scholar] [CrossRef]
- Rego, G.M.; Marques, P.V.S.; Santos, J.L.; Salgado, H.M. Estimation of the fibre temperature during the inscription of arc-induced long-period gratings. Opt. Commun. 2006, 259, 620–625. [Google Scholar] [CrossRef] [Green Version]
- Rego, G. Annealing of arc-induced gratings at high temperatures. Electron. Lett. 2009, 45, 972. [Google Scholar] [CrossRef] [Green Version]
- Enomoto, T.; Shigehara, M.; Ishikawa, S.; Danzuka, T.; Kanamori, H. Long-period fiber grating in a pure-silica-core fiber written by residual stress relaxation. In Proceedings of the OFC ’Optical Fiber Communication Conference and Exhibit. Technical Digest 1998 OSA Technical Digest Series Vol.2 (IEEE Cat. No.98CH36177), San Jose, CA, USA, 22–27 February 1998; pp. 277–278. [Google Scholar]
- Durr, F.; Rego, G.; Marques, P.V.S.; Semjonov, S.; Dianov, E.; Limberger, H.; Salathe, R. Tomographic stress profiling of arc-induced long-period fiber gratings. J. Light. Technol. 2005, 23, 3947–3953. [Google Scholar] [CrossRef]
- Wang, P.; Jenkins, M.H.; Gaylord, T.K. Arc-discharge effects on residual stress and refractive index in single-mode optical fibers. Appl. Opt. 2016, 55, 2451–2456. [Google Scholar] [CrossRef]
- Yablon, A.D.; Yan, M.F.; Wisk, P.; DiMarcello, F.V.; Fleming, J.W.; Reed, W.A.; Monberg, E.M.; DiGiovanni, D.J.; Jasapara, J.; Lines, M.E. Refractive index perturbations in optical fibers resulting from frozen-in viscoelasticity. Appl. Phys. Lett. 2004, 84, 19–21. [Google Scholar] [CrossRef]
- Mohanna, Y.; Saugrain, J.-M.; Rousseau, J.-C.; LeDoux, P. Relaxation of internal stresses in optical fibers. J. Light. Technol. 1990, 8, 1799–1802. [Google Scholar] [CrossRef]
- Shin, I.H.; Ju, S.; Veetil, S.P.; Han, W.-T.; Kim, D.Y. Simple model for frozen-in viscoelastic stress in optical fibers. Opt. Commun. 2008, 281, 2504–2508. [Google Scholar] [CrossRef]
- Rego, G.; Dürr, F.; Marques, P.V.S.; Limberger, H. Strong asymmetric stresses arc-induced in pre-annealed nitrogen-doped fibres. Electron. Lett. 2006, 42, 334. [Google Scholar] [CrossRef] [Green Version]
- Abrishamian, F.; Dragomir, N.; Morishita, K. Refractive index profile changes caused by arc discharge in long-period fiber gratings fabricated by a point-by-point method. Appl. Opt. 2012, 51, 8271–8276. [Google Scholar] [CrossRef]
- Berthold, J. Historical review of microbend fiber-optic sensors. J. Light. Technol. 1995, 13, 1193–1199. [Google Scholar] [CrossRef]
- Probst, C.; Bjarklev, A.; Andreasen, S. Experimental verification of microbending theory using mode coupling to discrete cladding modes. J. Light. Technol. 1989, 7, 55–61. [Google Scholar] [CrossRef] [Green Version]
- Rego, G.; Fernandes, J.R.A.; Santos, J.L.; Salgado, H.M.; Marques, P.V.S. New technique to mechanically induce long-period fibre gratings. Opt. Commun. 2003, 220, 111–118. [Google Scholar] [CrossRef]
- Martínez-Ríos, A.; Torres-Gómez, I.; Anzueto-Sánchez, G.; Selvas-Aguilar, R.; Duran-Ramirez, V.; Guerrero-Viramontes, J.; Toral-Acosta, D.; Delgado, G.S.; Castillo-Guzman, A. Asymmetric mode coupling in arc-induced long-period fiber gratings. Opt. Commun. 2016, 364, 37–43. [Google Scholar] [CrossRef]
- Rego, G.; Ivanov, O.V.; Marques, P.V.S. Demonstration of coupling to symmetric and antisymmetric cladding modes in arc-induced long-period fiber gratings. Opt. Express 2006, 14, 9594–9599. [Google Scholar] [CrossRef]
- Rego, G.; Ivanov, O.V. Two types of resonances in long-period gratings induced by arc discharges in boron/ germanium co-doped fibers. Opt. Lett. 2007, 32, 2984–2986. [Google Scholar] [CrossRef]
- Rego, G. Long-period fiber gratings mechanically induced by winding a string around a fiber/grooved tube set. Microw. Opt. Technol. Lett. 2008, 50, 2064–2068. [Google Scholar] [CrossRef]
- Rego, G.M.; Salgado, H.M.; Santos, J.L. Interrogation of a Fiber Bragg Grating Using a Mechanically Induced Long-Period Fiber Grating. IEEE Sens. J. 2006, 6, 1592–1595. [Google Scholar] [CrossRef]
- Rego, G. Optical filters for fiber lasers and amplifiers. Microw. Opt. Technol. Lett. 2008, 50, 890–894. [Google Scholar] [CrossRef]











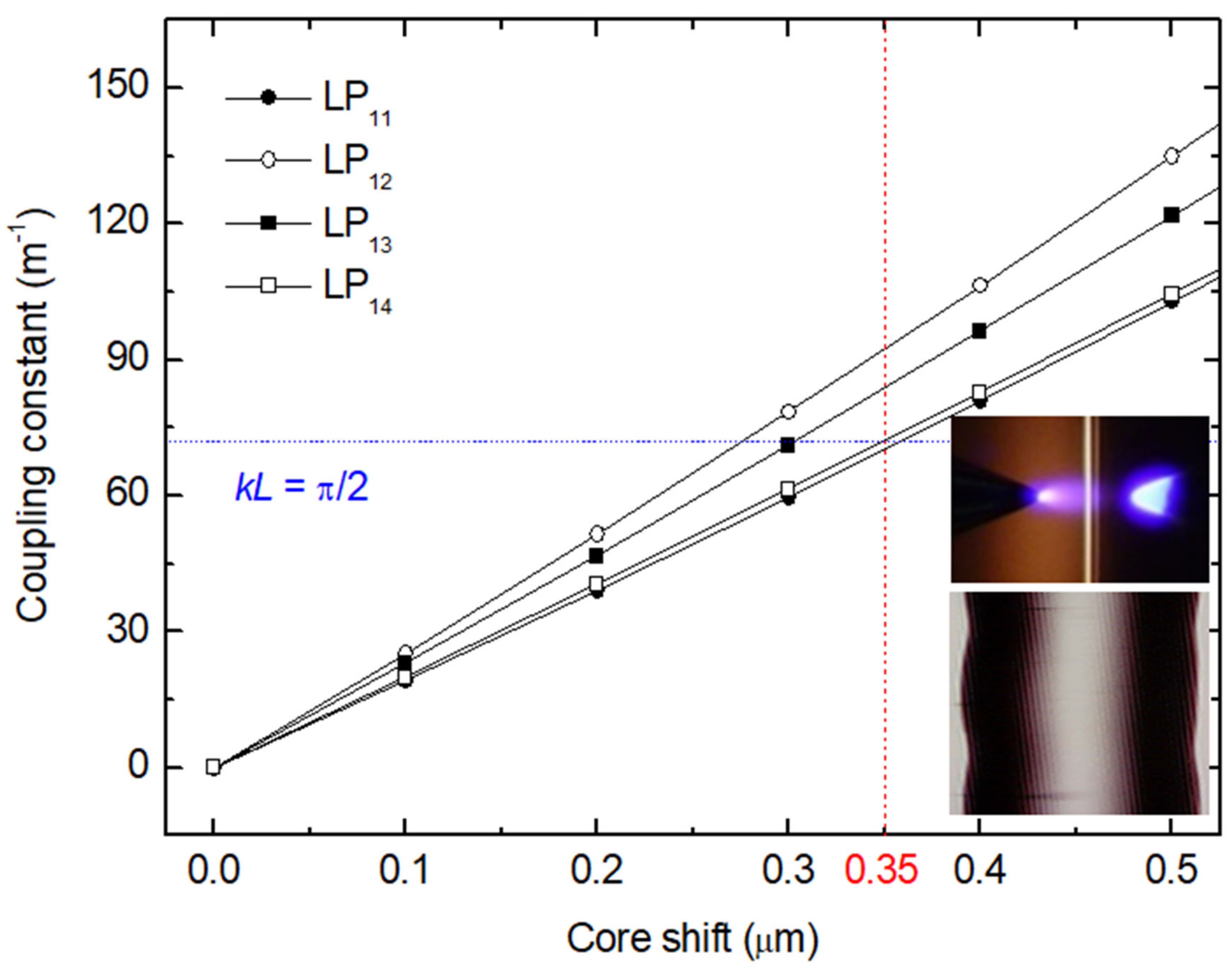
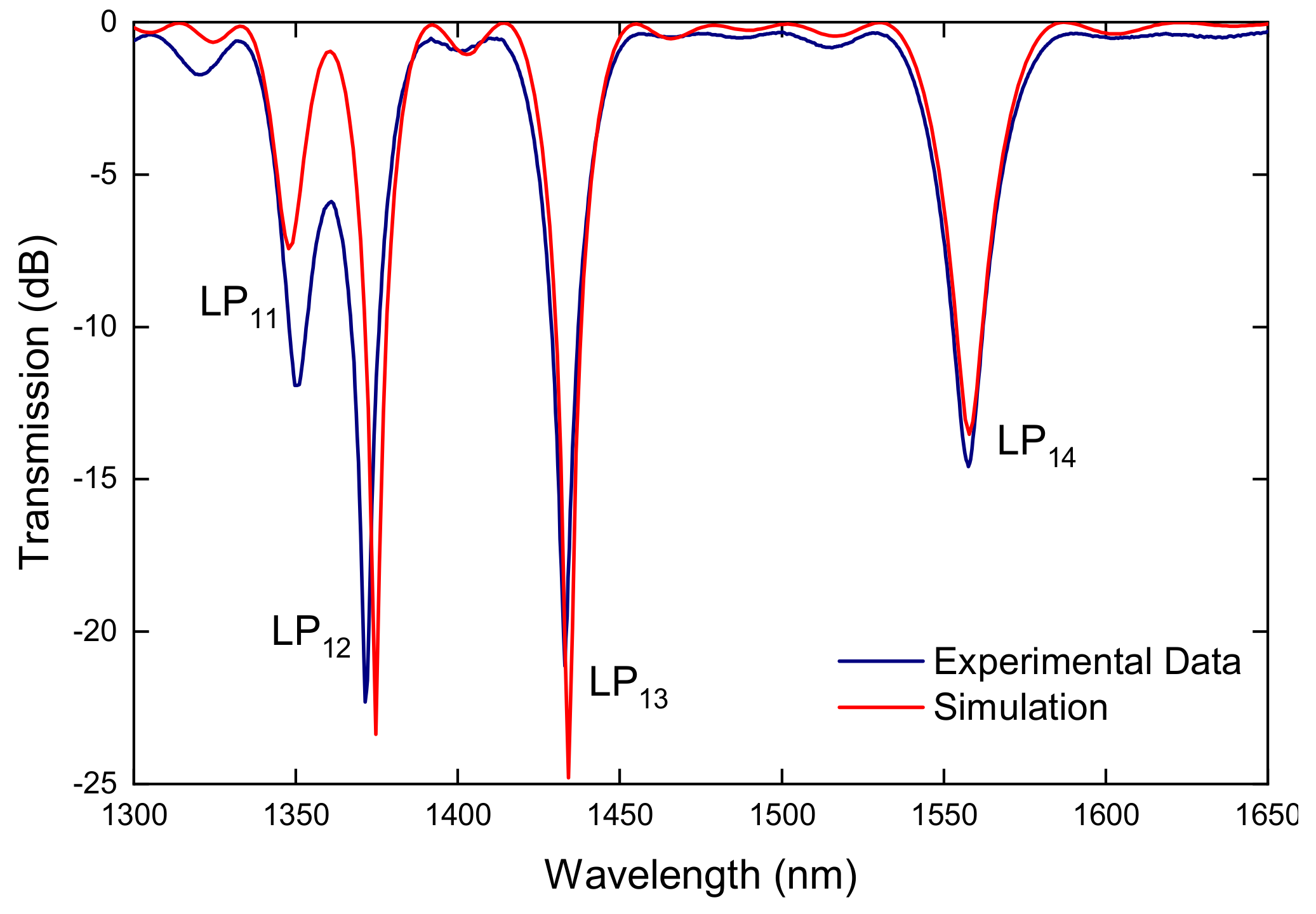
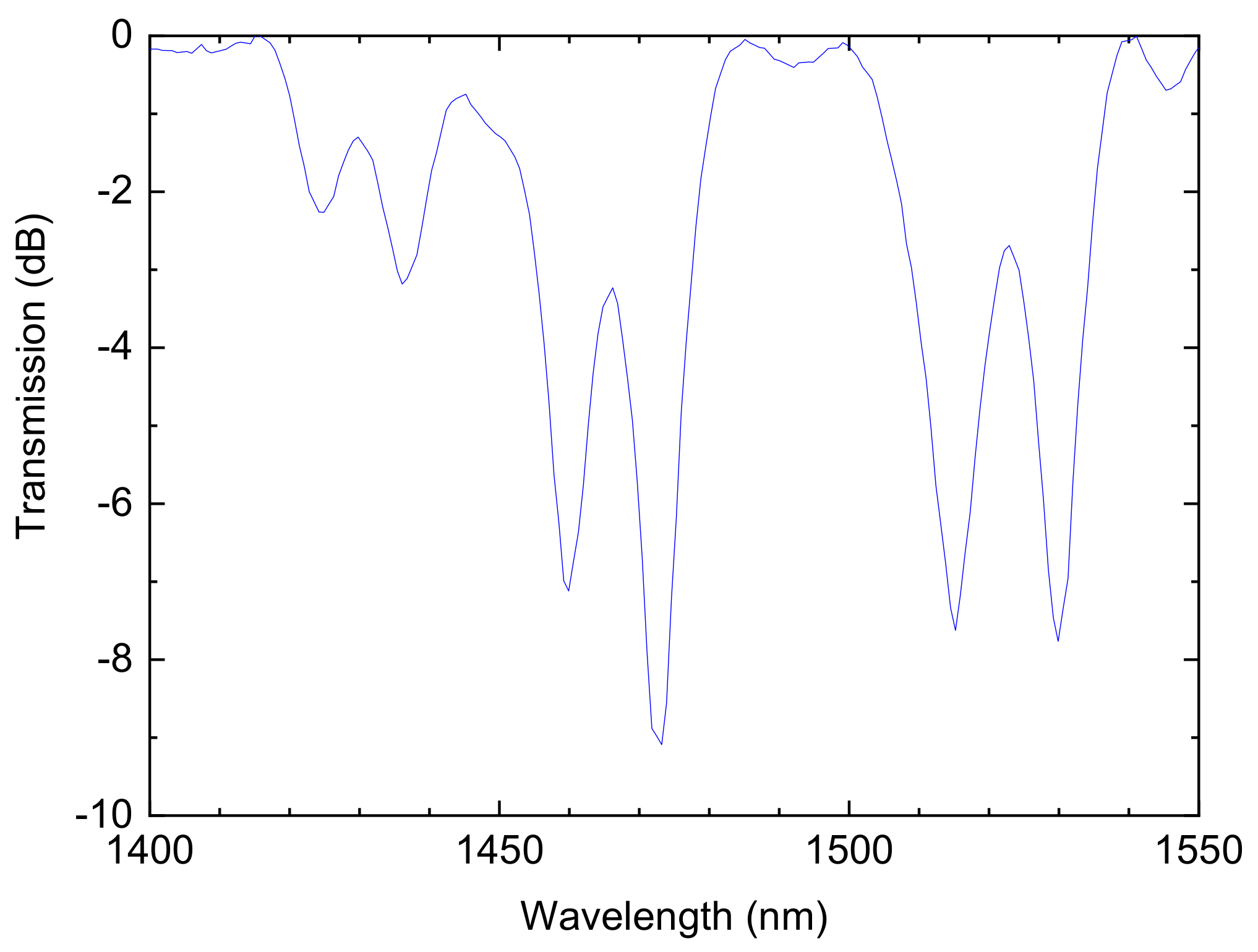
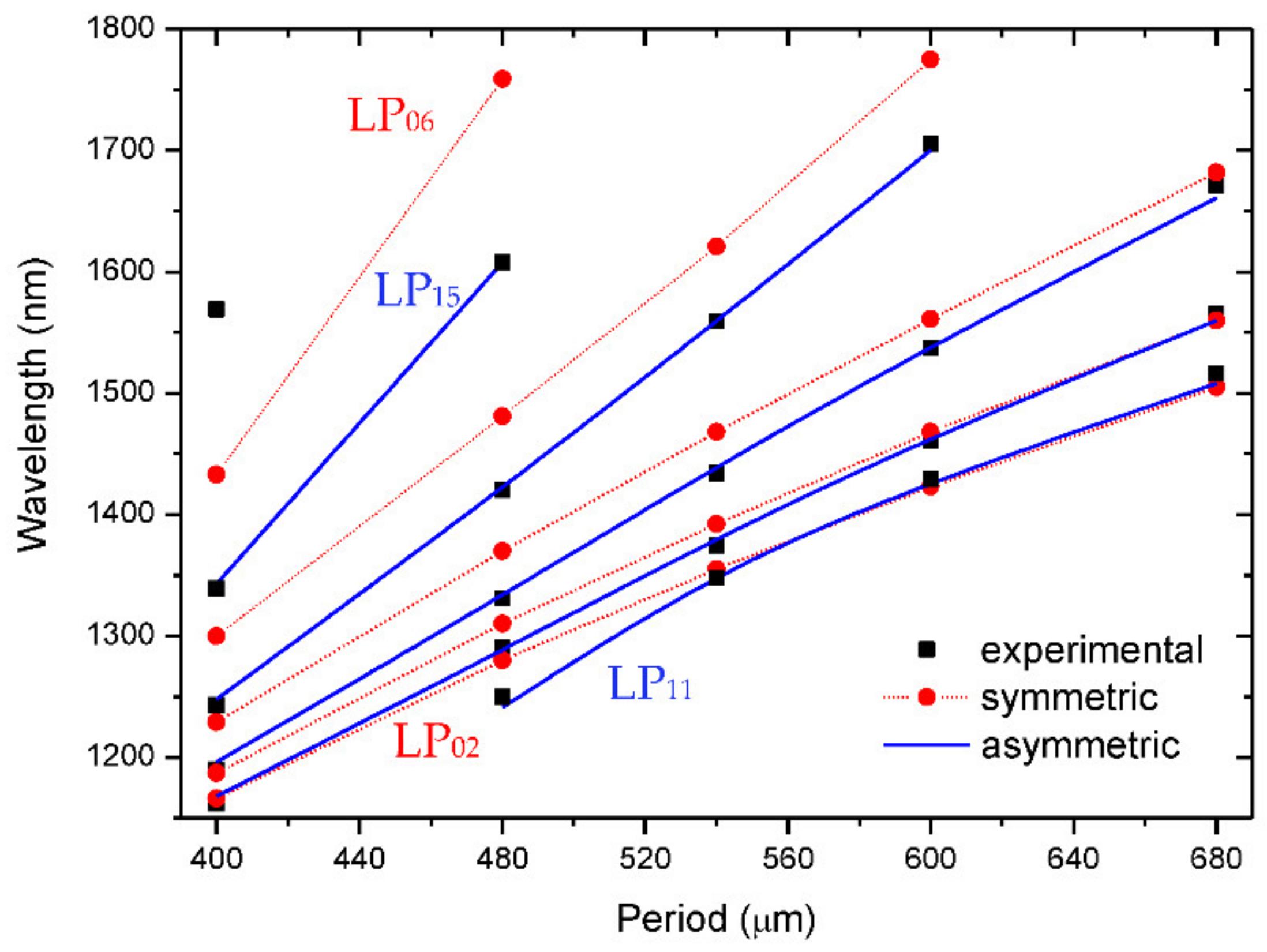
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rego, G.; Caldas, P.; Ivanov, O.V. Arc-Induced Long-Period Fiber Gratings at INESC TEC. Part I: Fabrication, Characterization and Mechanisms of Formation. Sensors 2021, 21, 4914. https://doi.org/10.3390/s21144914
Rego G, Caldas P, Ivanov OV. Arc-Induced Long-Period Fiber Gratings at INESC TEC. Part I: Fabrication, Characterization and Mechanisms of Formation. Sensors. 2021; 21(14):4914. https://doi.org/10.3390/s21144914
Chicago/Turabian StyleRego, Gaspar, Paulo Caldas, and Oleg V. Ivanov. 2021. "Arc-Induced Long-Period Fiber Gratings at INESC TEC. Part I: Fabrication, Characterization and Mechanisms of Formation" Sensors 21, no. 14: 4914. https://doi.org/10.3390/s21144914
APA StyleRego, G., Caldas, P., & Ivanov, O. V. (2021). Arc-Induced Long-Period Fiber Gratings at INESC TEC. Part I: Fabrication, Characterization and Mechanisms of Formation. Sensors, 21(14), 4914. https://doi.org/10.3390/s21144914






