Towards Measuring Terahertz Photon Statistics by a Superconducting Bolometer
Abstract
:1. Introduction
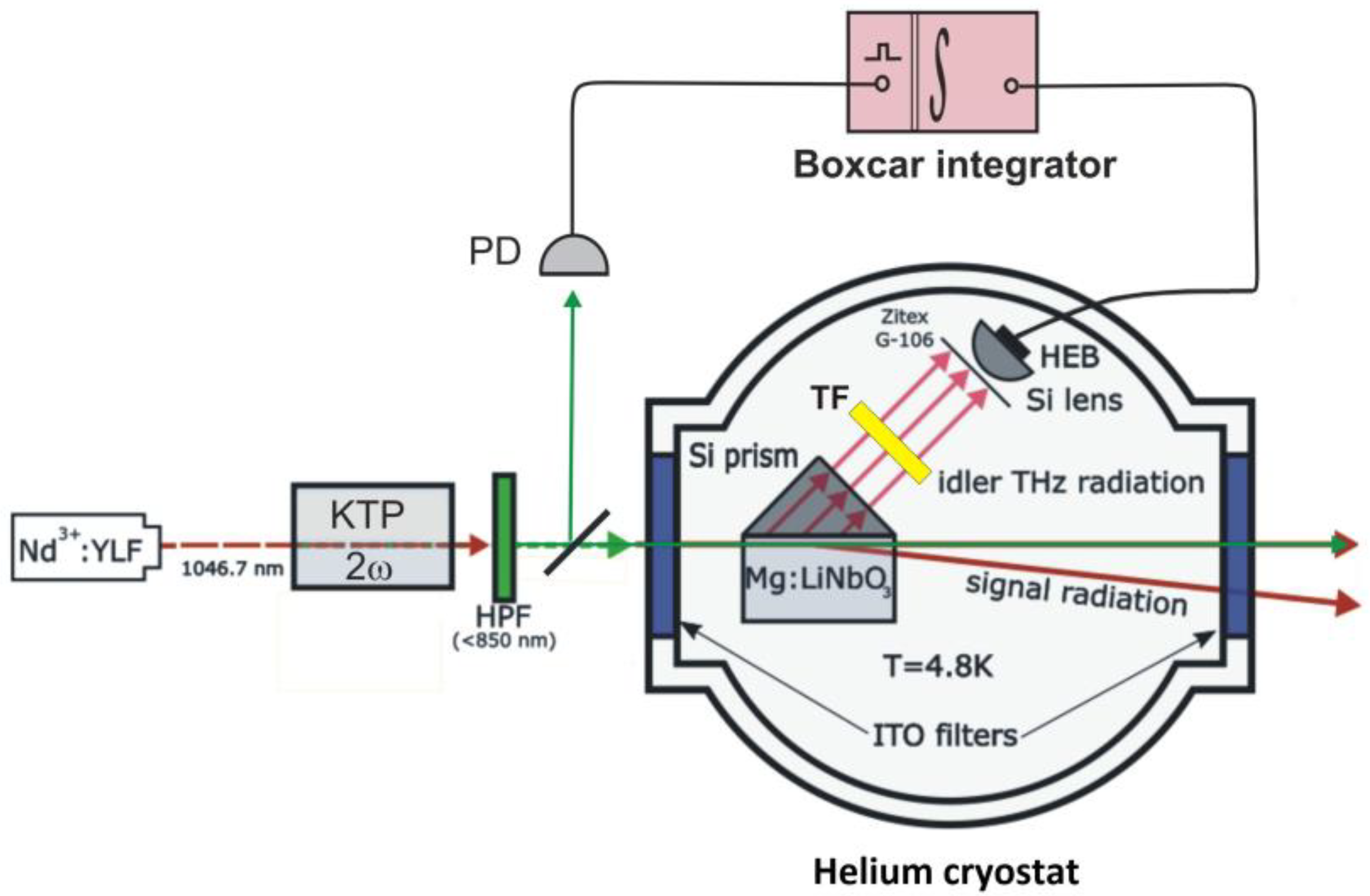
2. Materials and Methods
3. Results and Discussion
4. Conclusions
- (1)
- any reading consists of a number of discrete single counts with Poisson statistical distribution,
- (2)
- contributions of individual counts (“single charges”) to each total reading are statistically distributed according to the normal law,
- (3)
- the average values of contributions (“mean single charges”) depend on the number of counts in each reading.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kitaeva, G.K.; Yakunin, P.V.; Kornienko, V.V.; Penin, A.N. Absolute brightness measurements in the terahertz frequency range using vacuum and thermal fluctuations as references. Appl. Phys. B 2014, 116, 929–937. [Google Scholar] [CrossRef]
- Riek, C.; Seletskiy, D.V.; Moskalenko, A.S.; Schmidt, J.F.; Krauspe, P.; Eckart, S.; Eggert, S.; Burkard, G.; Leitenstorfer, A. Direct sampling of electric-field vacuum fluctuations. Science 2015, 350, 420–423. [Google Scholar] [CrossRef] [Green Version]
- Kornienko, V.V.; Kitaeva, G.K.; Sedlmeir, F.; Leuchs, G.; Schwefel, H.G.L. Towards terahertz detection and calibration through spontaneous parametric down-conversion in the terahertz idler-frequency range generated by a 795 nm diode laser system. APL Photonics 2018, 3, 051704. [Google Scholar] [CrossRef]
- Kitaeva, G.K.; Kornienko, V.V.; Leontyev, A.A.; Shepelev, A.V. Generation of optical signal and terahertz idler photons by spontaneous parametric down-conversion. Phys. Rev. A 2018, 98, 063844. [Google Scholar] [CrossRef]
- Kitaeva, G.K.; Kornienko, V.V.; Kuznetsov, K.A.; Pentin, I.V.; Smirnov, K.V.; Vakhtomin, Y.B. Direct detection of the idler THz radiation generated by spontaneous parametric down-conversion. Opt. Lett. 2019, 44, 1198–1201. [Google Scholar] [CrossRef]
- Haase, B.; Kutas, M.; Riexinger, F.; Bickert, P.; Keil, A.; Molter, D.; Bortz, M.; von Freymann, G. Spontaneous parametric down-conversion of photons at 660 nm to the terahertz and sub-terahertz frequency range. Opt. Express 2019, 27, 7458. [Google Scholar] [CrossRef] [PubMed]
- Benea-Chelmus, I.-C.; Settembrini, F.F.; Scalari, G.; Faist, J. Electric field correlation measurements on the electromagnetic vacuum state. Nature 2019, 568, 202–206. [Google Scholar] [CrossRef]
- Kuznetsov, K.A.; Malkova, E.I.; Zakharov, R.V.; Tikhonova, O.V.; Kitaeva, G.K. Nonlinear interference in strongly non-degenerate regime and Schmidt mode analysis. Phys. Rev. A 2020, 101, 053843. [Google Scholar] [CrossRef]
- Kutas, M.; Haase, B.; Bickert, P.; Riexinger, F.; Molter, D.; von Freymann, G. Terahertz quantum sensing. Sci. Adv. 2020, 6, eaaz8065. [Google Scholar] [CrossRef] [Green Version]
- Kitaeva, G.K.; Leontyev, A.A.; Prudkovskii, P.A. Quantum correlation between optical and terahertz photons generated under multimode spontaneous parametric down-conversion. Phys. Rev. A 2020, 101, 053810. [Google Scholar] [CrossRef]
- Novikova, T.I.; Kuznetsov, K.A.; Leontyev, A.A.; Kitaeva, G.K. Study of SPDC spectra to reveal temperature dependences for optical-terahertz biphotons. Appl. Phys. Lett. 2020, 116, 264003. [Google Scholar] [CrossRef]
- Lemos, G.B.; Borish, V.; Cole, G.D.; Ramelow, S.; Lapkiewicz, R.; Zeilinger, A. Quantum imaging with undetected photons. Nature 2014, 512, 409. [Google Scholar] [CrossRef] [Green Version]
- Nomerotski, A.; Keach, M.; Stankus, P.; Svihra, P.; Vintskevich, S. Counting of Hong-Ou-Mandel bunched optical photons using a fast pixel camera. Sensors 2020, 20, 3475. [Google Scholar] [CrossRef]
- Clark, A.S.; Chekhova, M.; Matthews, J.C.F.; Rarity, J.G.; Oulton, R.F. Special Topic: Quantum sensing with correlated light sources. Appl. Phys. Lett. 2021, 118, 060401. [Google Scholar] [CrossRef]
- Moreau, P.-A.; Toninelli, E.; Gregory, T.; Padgett, M.J. Ghost Imaging Using Optical Correlations. Laser Photonics Rev. 2018, 12, 1700143. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.-Z.; Li, M.-F.; Chen, X.-X.; Yu, W.-K.; Zhang, A.-N. Single-photon quantum imaging via single-photon illumination. Appl. Phys. Lett. 2020, 117, 214001. [Google Scholar] [CrossRef]
- Kitaeva, G.K.; Penin, A.N. Spontaneous parametric down-conversion. JETP Lett. 2005, 82, 350–355. [Google Scholar] [CrossRef]
- Kalashnikov, D.A.; Paterova, A.V.; Kulik, S.P.; Krivitsky, L.A. Infrared spectroscopy with visible light. Nat. Photonics 2016, 10, 98. [Google Scholar] [CrossRef] [Green Version]
- Polyakov, S.V.; Migdall, A.L. High accuracy verificatio;n of a correlated photon-based method for determining photoncounting detection efficiency. Opt. Express 2007, 15, 1390–1407. [Google Scholar] [CrossRef] [Green Version]
- Avella, A.; Ruo-Berchera, I.; Degiovanni, I.P.; Brida, G.; Genovese, M. Absolute calibration of an EMCCD camera by quantum correlation, linking photon counting to the analog regime. Opt. Lett. 2016, 41, 1841–1844. [Google Scholar] [CrossRef] [Green Version]
- Kuznetsov, K.A.; Kitaeva, G.K.; Kovalev, S.P.; Germansky, S.A.; Buryakov, A.M.; Tuchak, A.N.; Penin, A.N. Complex extraordinary dielectric function of Mg-doped lithium niobate crystals at terahertz frequencies . Appl. Phys. B 2016, 122, 223. [Google Scholar] [CrossRef]
- Karasik, B.S.; Sergeev, A.V. THz hot-electron photon counter. IEEE Trans. Appl. Supercond. 2005, 15, 618–621. [Google Scholar] [CrossRef]
- McKitterick, C.B.; Vora, H.; Du, X.; Karasik, B.S.; Prober, D.E. Graphene microbolometers with superconducting contacts for terahertz photon detection. J. Low Temp. Phys. 2014, 176, 291–298. [Google Scholar] [CrossRef] [Green Version]
- Williams, J.O.D.; Alexander-Webber, J.A.; Lapington, J.S.; Roy, M.; Hutchinson, I.B.; Sagade, A.A.; Martin, M.-B.; Braeuninger-Weimer, P.; Cabrero-Vilatela, A.; Wang, R.; et al. Towards a graphene-based low intensity photon counting photodetector. Sensors 2016, 16, 1351. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Echternach, P.M.; Pepper, B.J.; Reck, T.; Bradford, C.M. Single photon detection of 1 5 THz radiation with the quantum capacitance detector. Nat. Astron. 2018, 2, 90–97. [Google Scholar] [CrossRef]
- Jahanmirinejad, S.; Frucci, G.; Mattioli, F.; Sahin, D.; Gaggero, A.; Leoni, R.; Fiore, A. Photon-number resolving detector based on a series array of superconducting nanowires. Appl. Phys. Lett. 2012, 101, 072602. [Google Scholar] [CrossRef] [Green Version]
- Burenkov, I.A.; Sharma, A.K.; Gerrits, T.; Harder, G.; Bartley, T.J.; Silberhorn, C.; Goldschmidt, E.A.; Polyakov, S.V. Full statistical mode reconstruction of a light field via a photon-number-resolved measurement. Phys. Rev. A 2017, 95, 053806. [Google Scholar] [CrossRef] [Green Version]
- Lolli, L.; Taralli, E.; Portesi, C.; Rajteri, M.; Monticone, E. Aluminum–titanium bilayer for near-infrared transition edge sensors. Sensors 2016, 16, 953. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santavicca, D.F.; Reulet, B.; Karasik, B.S.; Pereverzev, S.V.; Olaya, D.; Gershenson, M.E.; Frunzio, L.; Prober, D.E. Energy resolution of terahertz single-photon-sensitive bolometric detectors. Appl. Phys. Lett. 2010, 96, 083505. [Google Scholar] [CrossRef] [Green Version]
- Shurakov, A.; Lobanov, Y.; Goltsman, G. Superconducting hot-electron bolometer: From the discovery of hot-electron phenomena to practical application. Supercond. Sci. Technol. 2015, 29, 023001. [Google Scholar] [CrossRef]
- Pentin, I.; Vakhtomin, Y.; Seleznev, V.; Smirnov, K. Hot electron energy relaxation time in vanadium nitride superconducting film structures under THz and IR radiation. Sci. Rep. 2020, 10, 16819. [Google Scholar] [CrossRef]
- Seliverstov, S.; Maslennikov, S.; Ryabchun, S.; Finkel, M.; Klapwijk, T.; Kaurova, N.; Vakhtomin, Y.; Smirnov, K.; Voronov, B.; Goltsman, G. Fast and sensitive terahertz direct detector based on superconducting antenna-coupled hot electron bolometer. IEEE Trans. Appl. Supercond. 2015, 25, 2300304. [Google Scholar] [CrossRef]
- Shurakov, A.; Seliverstov, S.; Kaurova, N.; Finkel, M.; Voronov, B.; Goltsman, G. Input bandwidth of hot electron bolometer with spiral antenna. IEEE Trans. Terahertz Sci. Technol. 2012, 2, 400. [Google Scholar] [CrossRef]
- Wang, T.; Zalkovskij, M.; Iwaszczuk, K.; Lavrinenko, A.V.; Naik, G.V.; Kim, J.; Boltasseva, A.; Jepsen, P.U. Ultrabroadband terahertz conductivity of highly doped ZnO and ITO. Opt. Mat. Express 2015, 5, 566. [Google Scholar] [CrossRef]
- Suizu, K.; Koketsu, K.; Shibuya, T.; Tsutsui, T.; Akiba, T.; Kawase, K. Extremely frequency-widened terahertz wave generation using Cherenkov-type radiation. Opt. Express 2009, 17, 6676. [Google Scholar] [CrossRef]
- Komenou, K.; Yamashita, T.; Onodera, Y. Energy gap measurement of niobium nitride. Phys. Lett. A 1968, 28, 335. [Google Scholar] [CrossRef]
- Klyshko, D.N. Photons and Nonlinear Optics; Gordon and Breach: New York, NY, USA, 1988. [Google Scholar]
- Sultanov, V.D.; Kuznetsov, K.A.; Leontyev, A.A.; Kitaeva, G.K. Generation of optical–terahertz biphotons and detection of their terahertz component under frequency-nondegenerate parametric down-conversion. JETP Lett. 2020, 112, 269–273. [Google Scholar] [CrossRef]
- Barends, R.; Hajenius, M.; Gao, J.R.; Klapwijk, T.M. Current-induced vortex unbinding in bolometer mixers. Appl. Phys. Lett. 2005, 87, 263506. [Google Scholar] [CrossRef]
- Miao, W.; Delorme, Y.; Feret, A.; Lefevre, R.; Lecomte, B.; Dauplay, F.; Krieg, J.-M.; Beaudin, G.; Zhang, W.; Ren, Y.; et al. Comparison between hot spot modeling and measurement of a superconducting hot electron bolometer mixer at submillimeter wavelengths. J. Appl. Phys. 2009, 106, 10390. [Google Scholar] [CrossRef]
- Miao, W.; Zhang, W.; Zhong, J.Q.; Shi, S.C.; Delorme, Y.; Lefevre, R.; Feret, A.; Vacelet, T. Non-uniform absorption of terahertz radiation on superconducting hot electron bolometer microbridges. Appl. Phys. Lett. 2014, 104, 052605. [Google Scholar] [CrossRef]
- Scully, M.O.; Lamb, V.E. Quantum Theory of an Optical Maser. III. Theory of Photoelectron Counting Statistics. Phys. Rev. 1969, 179, 368–373. [Google Scholar] [CrossRef]
- Tatarskii, V.I. Corrections to the theory of photocounting. Phys. Lett. A 1990, 144, 491. [Google Scholar] [CrossRef]


| Bolometer Current | Pump Power | Number of Counts <m> | Mean Single Current <e1>/τ, arb.un. | Single-Current Deviation σ, arb.un. | |||
|---|---|---|---|---|---|---|---|
| Equation (6) | Equation (7) | Equation (6) | Equation (7) | Equation (6) | Equation (7) | ||
| 64 μA | 29.6 mW | 7.04 ± 0.14 | 4.58 ± 0.12 | 22.9 ± 0.5 | 46.4 ± 1.9 | 44.9 ± 0.2 | 56.6 ± 1.0 |
| 53.4 mW | 8.95 ± 0.7 | 9.22 ± 0.06 | 43.8 ± 3.6 | 35.1 ± 0.4 | 37.7 ± 2.6 | 16.4 ± 0.5 | |
| 76.6 mW | 11.9 ± 5.7 | 13.82 ± 0.03 | 45 ± 23 | 29.7 ± 0.15 | 35 ± 20 | 11.3 ± 0.2 | |
| 69 μA | 53.4 mW | 8.9 ± 1.2 | 9.07 ± 0.06 | 80 ± 12 | 66.5 ± 0.5 | 66.8 ± 9.2 | 30.3 ± 1.2 |
| 76.6 mW | 12.4 ± 8.8 | 14.3 ± 0.2 | 71 ± 53 | 48.3 ± 1.0 | 54.7 ± 48.3 | 19.7 ± 1.6 | |
| 92.8 mW | 17.91 ± 0.03 | 16.1 ± 0.8 | 87.9 ± 0.2 | 156 ± 4 | 19.7 ± 0.6 | 115 ± 4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prudkovskii, P.; Leontyev, A.; Kuznetsov, K.; Kitaeva, G. Towards Measuring Terahertz Photon Statistics by a Superconducting Bolometer. Sensors 2021, 21, 4964. https://doi.org/10.3390/s21154964
Prudkovskii P, Leontyev A, Kuznetsov K, Kitaeva G. Towards Measuring Terahertz Photon Statistics by a Superconducting Bolometer. Sensors. 2021; 21(15):4964. https://doi.org/10.3390/s21154964
Chicago/Turabian StylePrudkovskii, Pavel, Andrey Leontyev, Kirill Kuznetsov, and Galiya Kitaeva. 2021. "Towards Measuring Terahertz Photon Statistics by a Superconducting Bolometer" Sensors 21, no. 15: 4964. https://doi.org/10.3390/s21154964
APA StylePrudkovskii, P., Leontyev, A., Kuznetsov, K., & Kitaeva, G. (2021). Towards Measuring Terahertz Photon Statistics by a Superconducting Bolometer. Sensors, 21(15), 4964. https://doi.org/10.3390/s21154964






