Recent Advances in Generation and Detection of Orbital Angular Momentum Optical Beams—A Review
Abstract
:1. Introduction
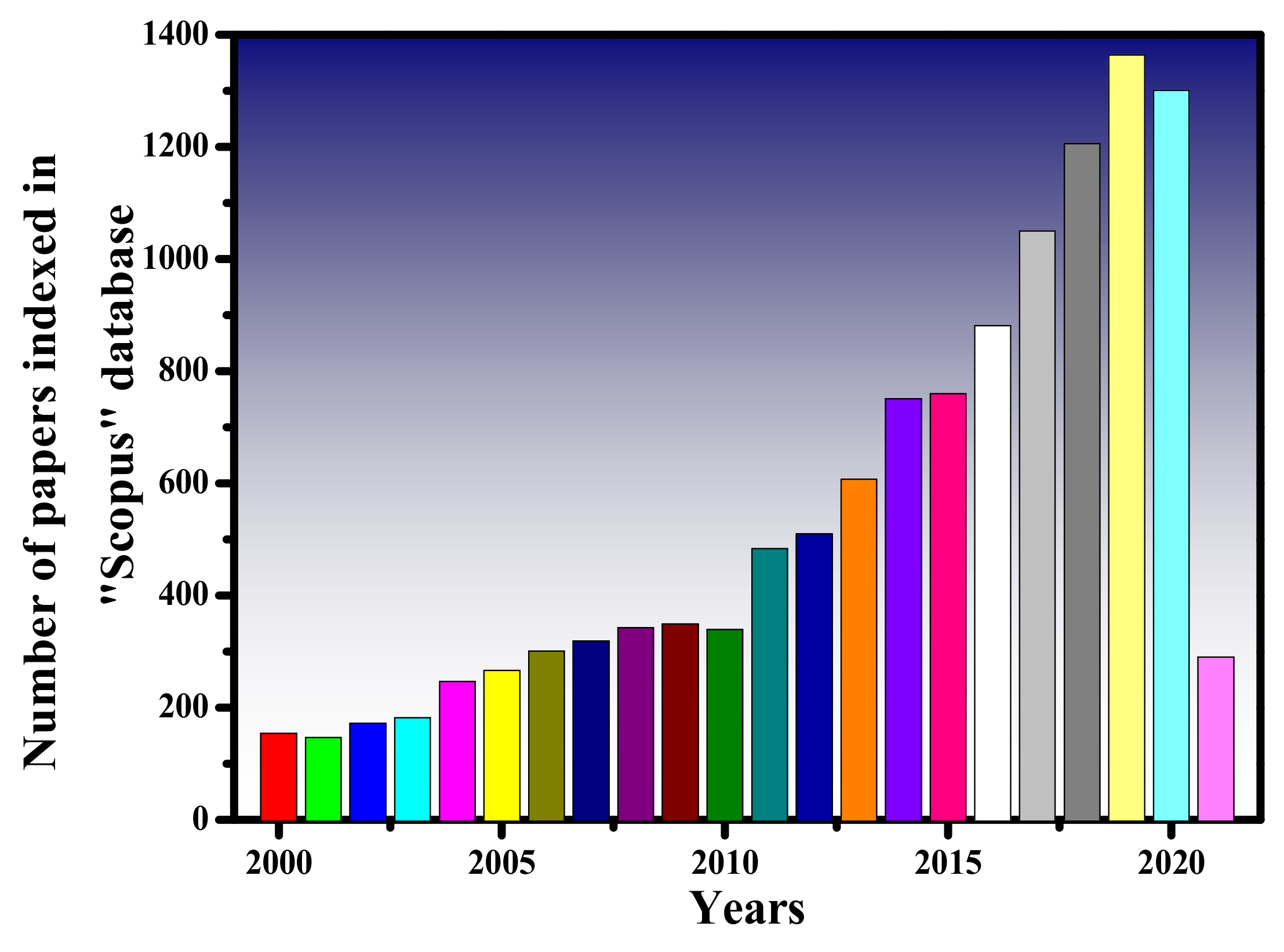
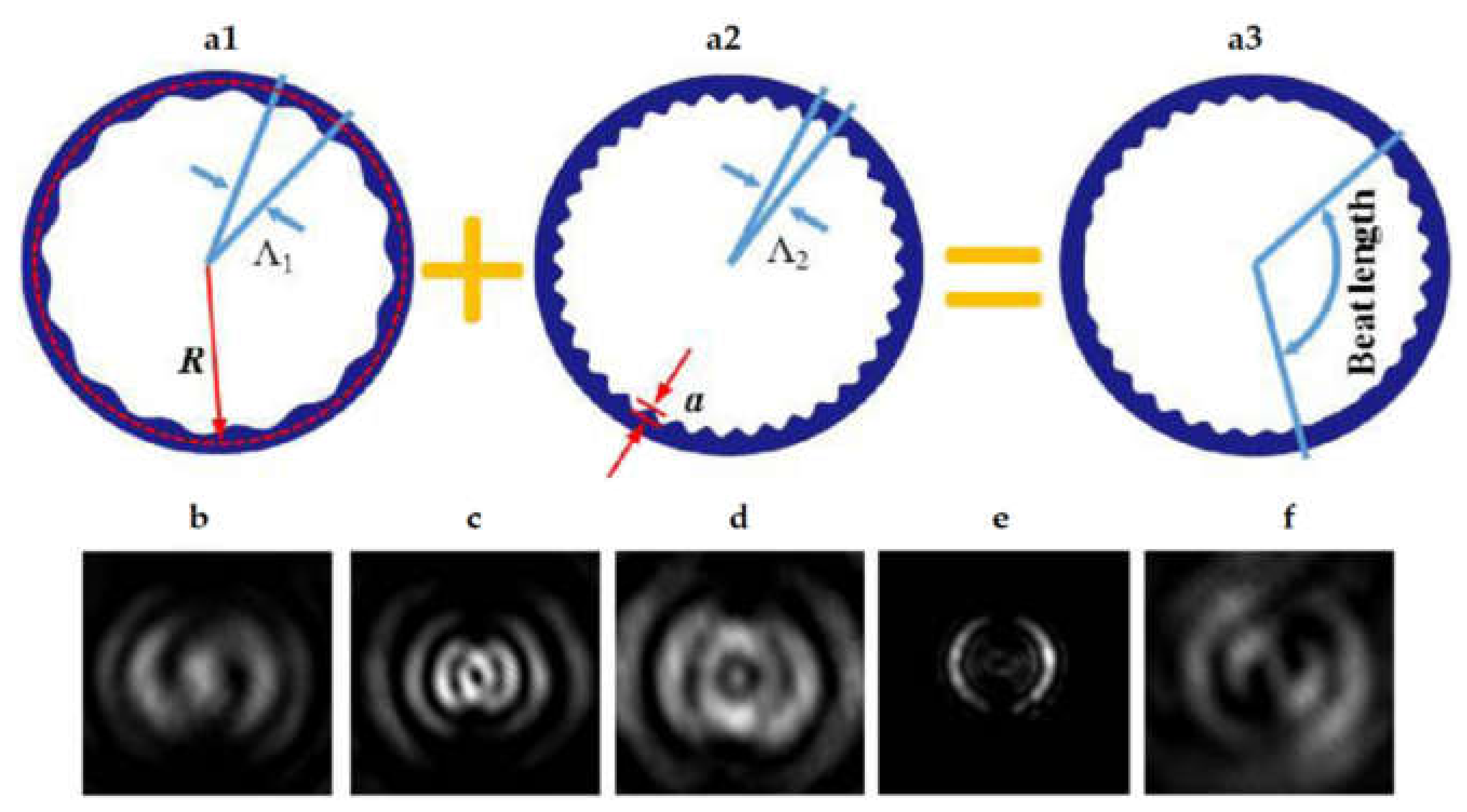
2. OAM Emitters Based on Diffractive Optic Elements
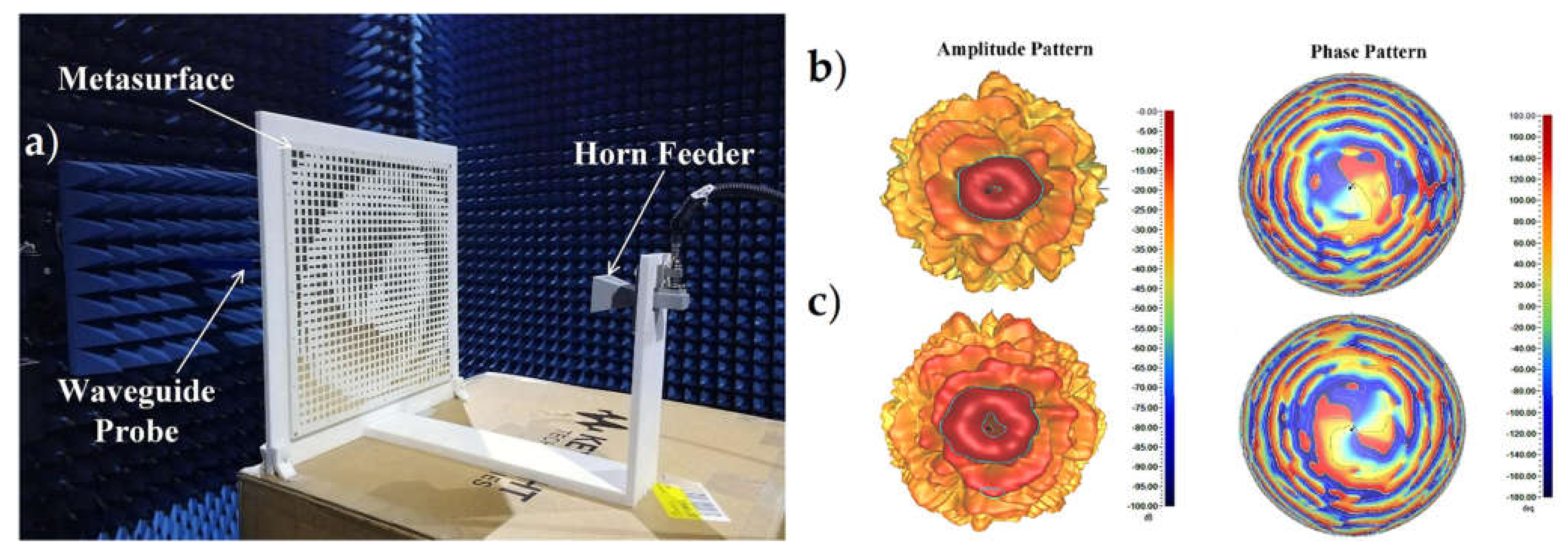
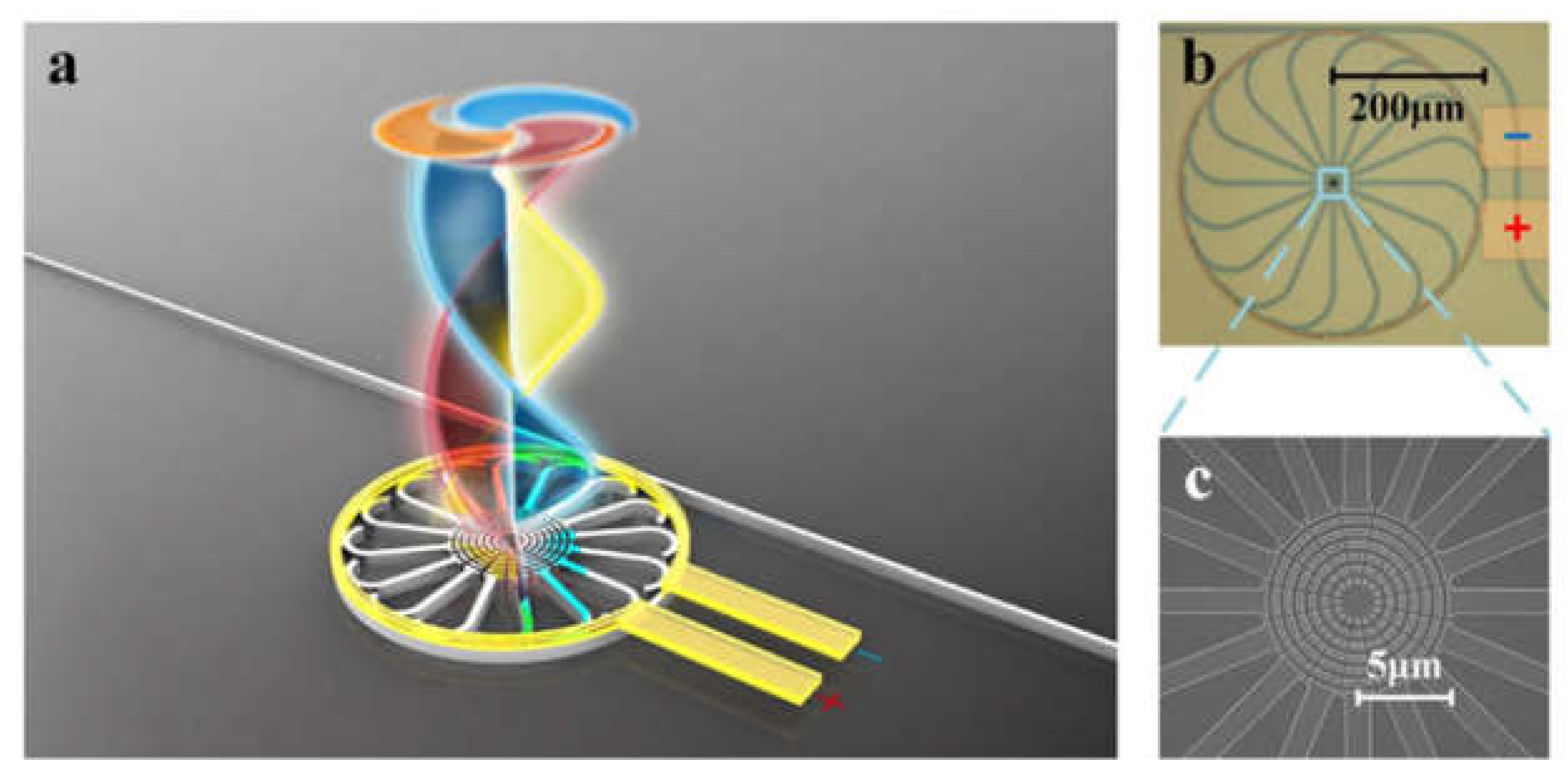
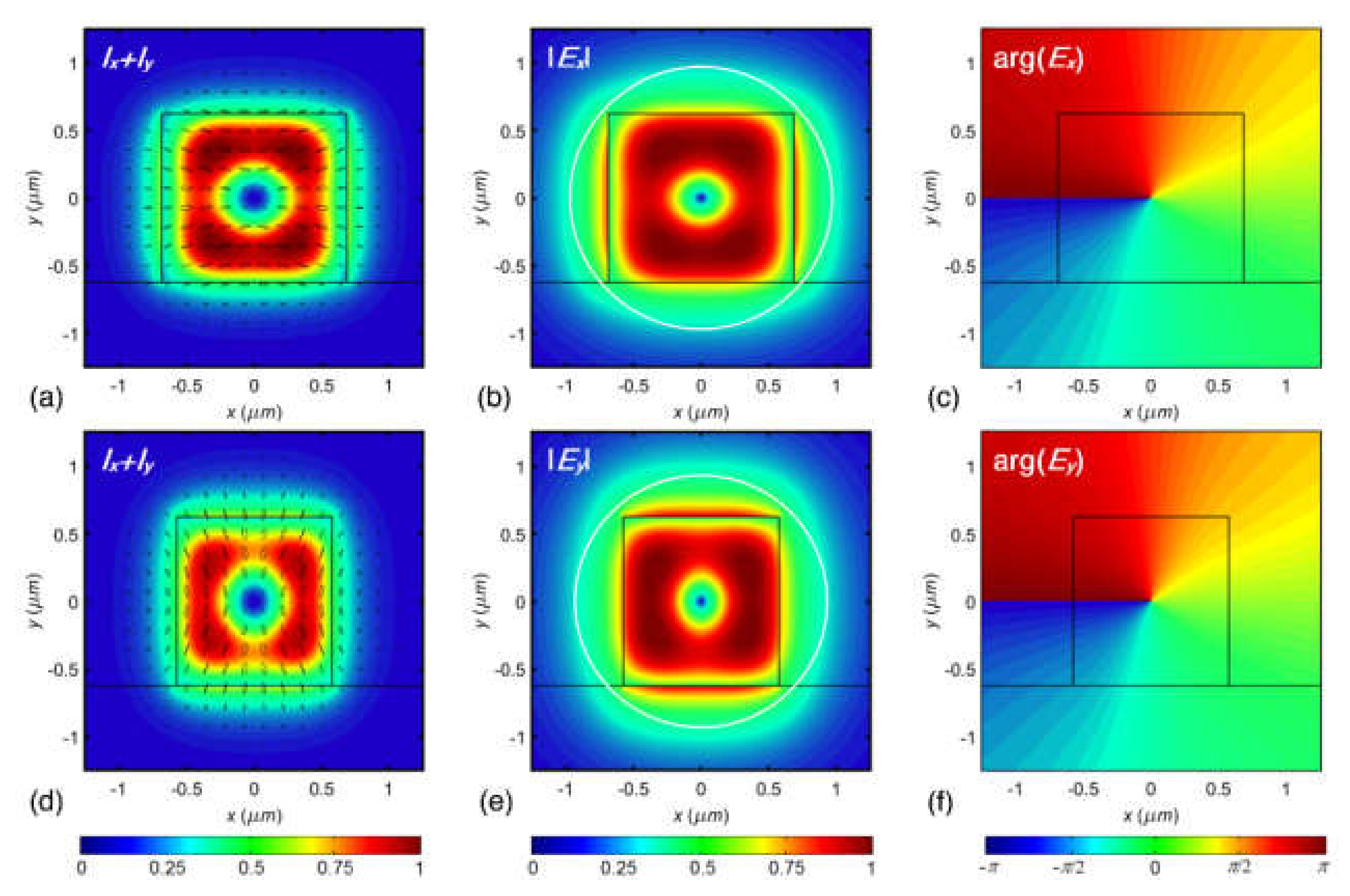
3. MSs for Generation of Vector OV Beams
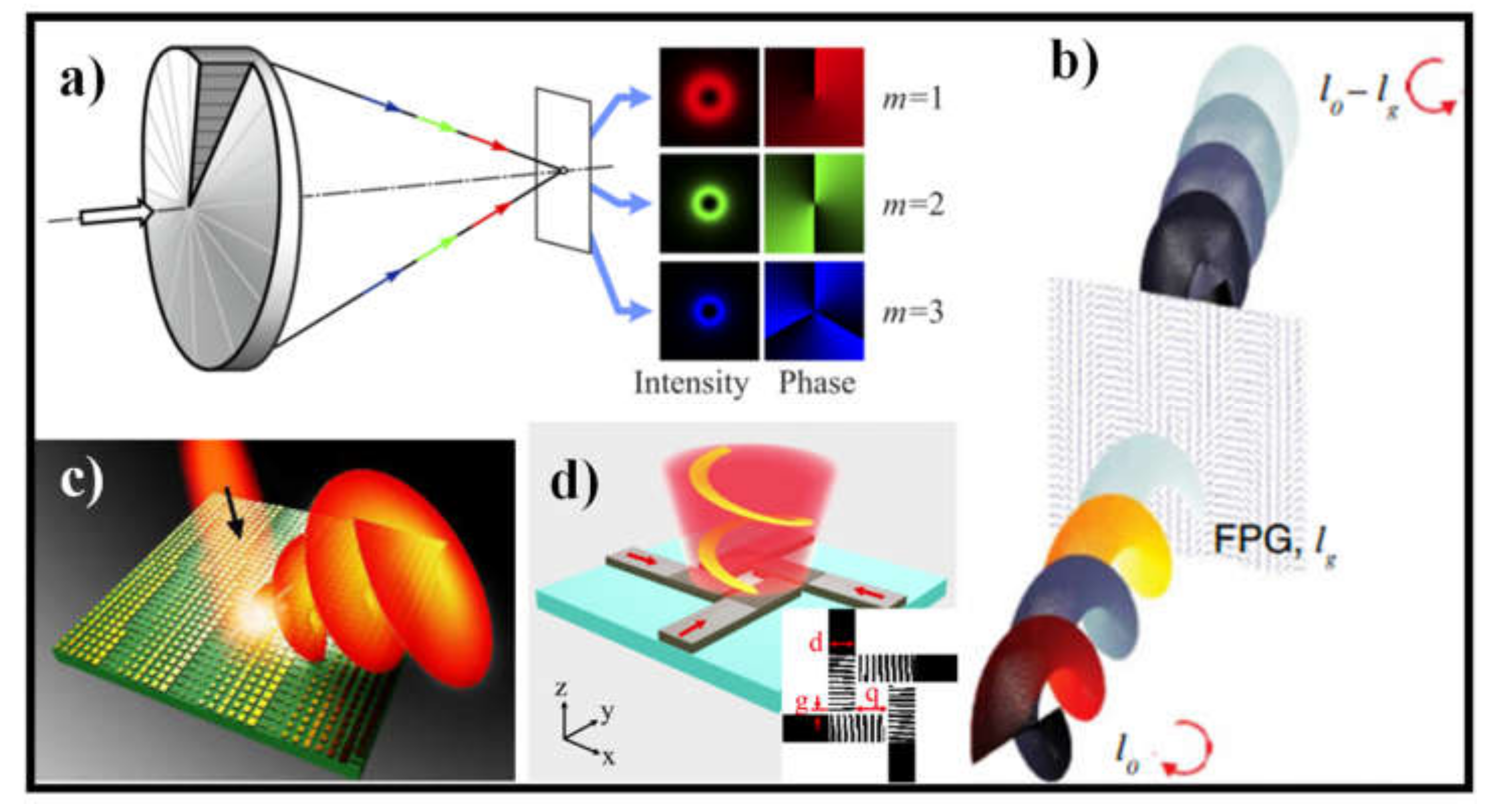
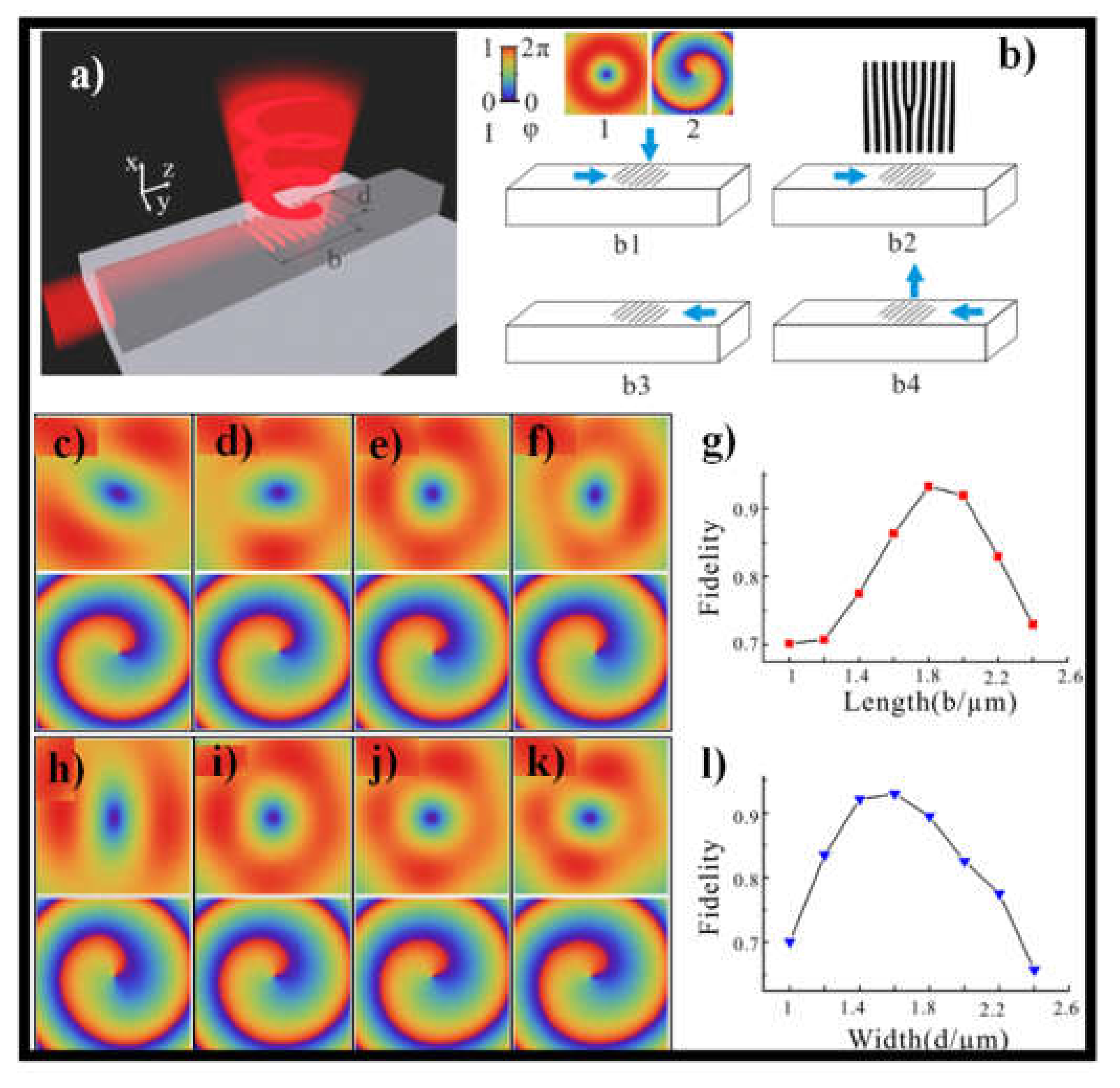
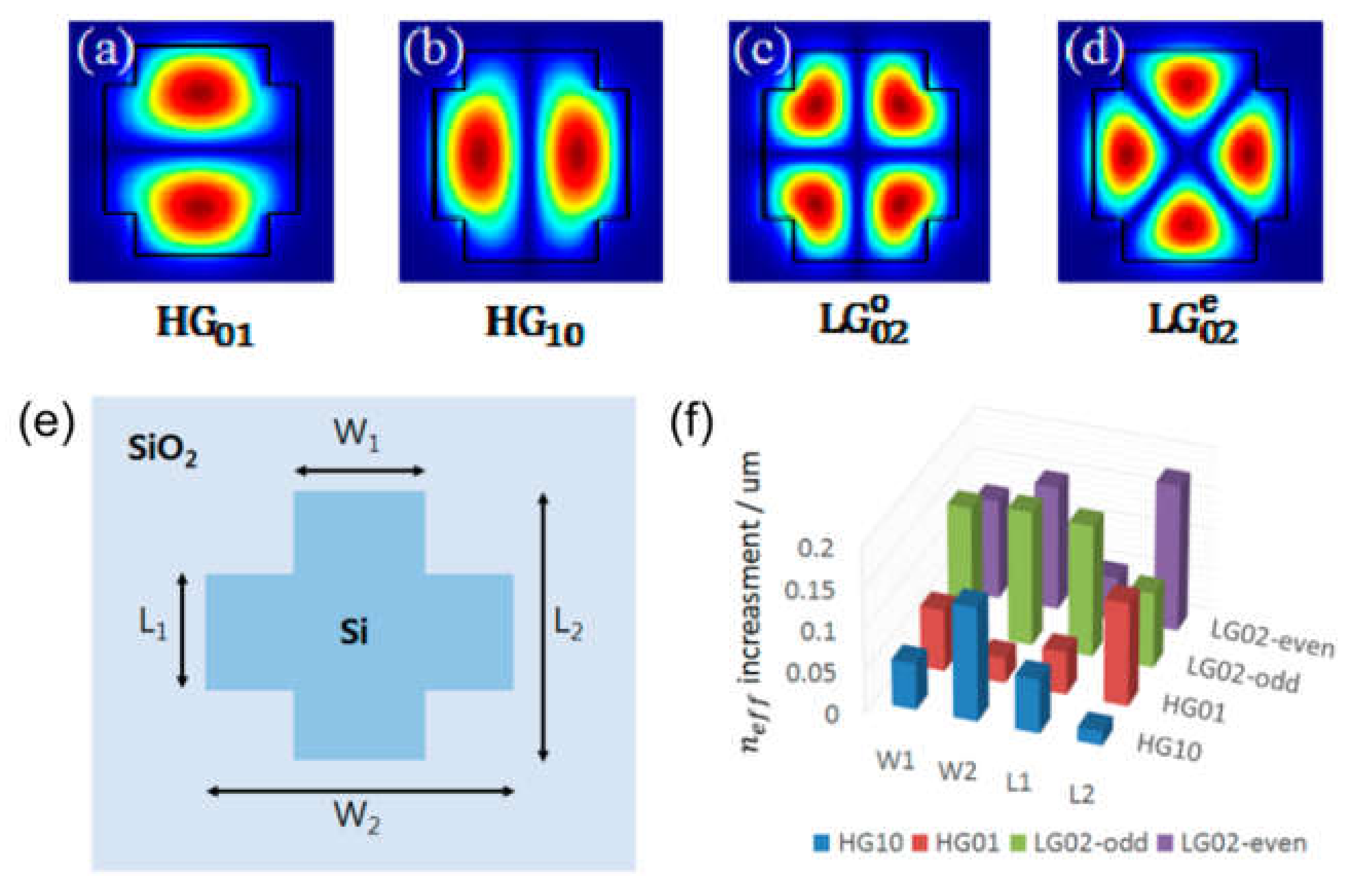
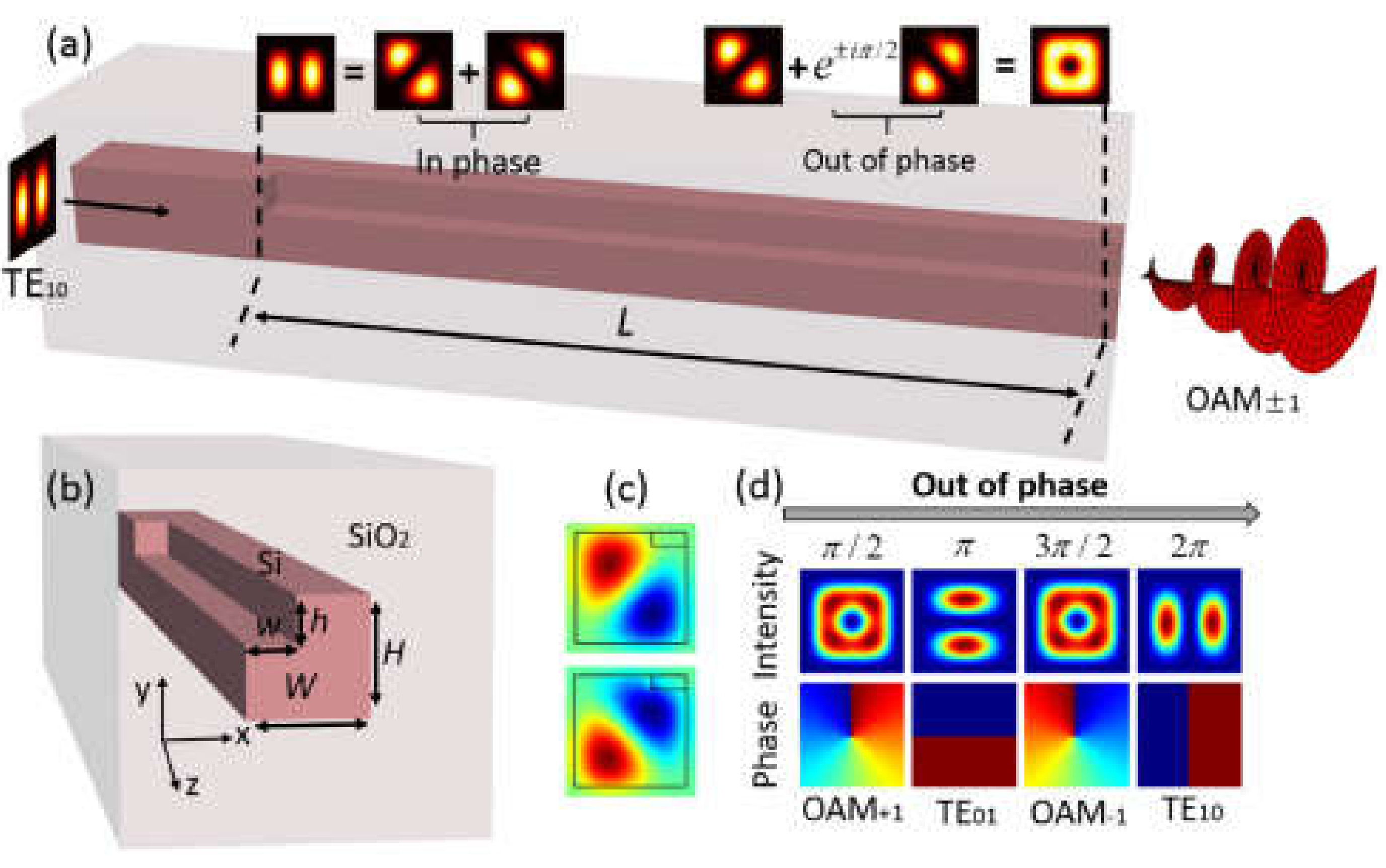
4. OAM Beams Generation with Photonic Integrated Circuits
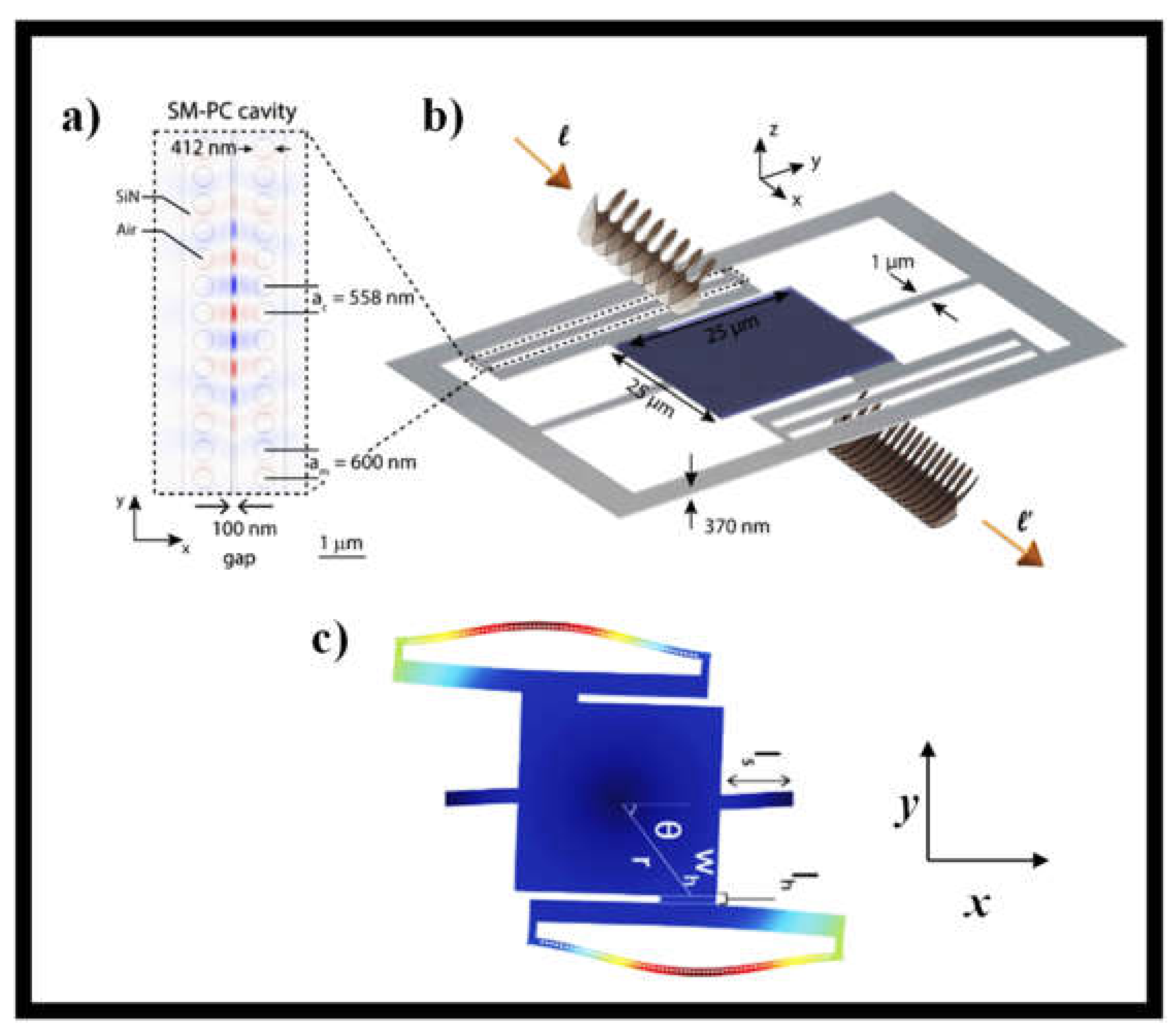
5. Detection of Light with OAM
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef] [Green Version]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [Green Version]
- Nicolas, A.; Veissier, L.; Giner, L.; Giacobino, E.; Maxein, D.; Laurat, J. A quantum memory for orbital angular momentum photonic qubits. Nat. Photonics 2014, 8, 234–238. [Google Scholar] [CrossRef] [Green Version]
- Moreno, I.; Davis, J.; Ruiz, I.; Cottrell, D. Decomposition of radially and azimuthally polarized beams using a circular-polarization and vortex-sensing diffraction grating. Opt. Express 2010, 18, 7173–7183. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Savelyev, D.; Kazanskiy, N.L. Vortex phase elements as detectors of polarization state. Opt. Express 2015, 23, 17845–17859. [Google Scholar] [CrossRef] [PubMed]
- Moreno, I.; Davis, J.; Badham, K.; Sanchez-Lopez, M.M.; Holland, J.; Cottrell, D. Vector beam polarization state spectrum analyzer. Sci. Rep. 2017, 7, 2216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khonina, S.N.; Porfirev, A.P.; Karpeev, S. Recognition of polarization and phase states of light based on the interaction of nonuniformly polarized laser beams with singular phase structures. Opt. Express 2019, 27, 18484–18492. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Chapin, S.C.; Germain, V.; Dufresne, E.R. Automated trapping, assembly, and sorting with holographic optical tweezers. Opt. Express 2006, 14, 13095–13100. [Google Scholar] [CrossRef] [Green Version]
- Gong, L.; Gu, B.; Rui, G.; Cui, Y.; Zhu, Z.; Zhan, Q. Optical forces of focused femtosecond laser pulses on nonlinear optical Rayleigh particles. Photonics Res. 2018, 6, 138–143. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, J.; Min, C.; Jin, Y.; Jiang, Y.; Liu, J.; Zhu, S.; Sheng, Y.; Zayats, A.V.; Yuan, X. Nonlinearity-induced multiplexed optical trapping and manipulation with femtosecond vector beams. Nano Lett. 2018, 18, 5538–5543. [Google Scholar] [CrossRef] [PubMed]
- Reddy, S.G.; Vaity, C.P.P.; Aadhi, A.; Prabhakar, S.; Singh, R.P. Non-diffracting speckles of a perfect vortex beam. J. Opt. 2016, 18, 055602. [Google Scholar] [CrossRef]
- Furhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694. [Google Scholar] [CrossRef] [Green Version]
- Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh criterion limit with optical vortices. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef] [Green Version]
- Jesacher, A.; Ritsch-Marte, M.; Piestun, R. Three-dimensional information from two-dimensional scans: A scanning microscope with postacquisition refocusing capability. Optica 2015, 2, 210–213. [Google Scholar] [CrossRef]
- Willig, K.I.; Rizzoli, S.O.; Westphal, V.; Jahn, R.; Hell, S.W. STED microscopy reveals that synaptotagmin remains clustered after synaptic vesicle exocytosis. Nature 2006, 440, 935–939. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Askarpour, A.N.; Sun, L.; Shi, J.; Li, X.; Alu, A. Chirality detection of enantiomers using twisted optical metamaterials. Nat. Commun. 2017, 8, 1–8. [Google Scholar] [CrossRef]
- Xie, Z.; Lei, T.; Si, G.; Du, L.; Lin, J.; Min, C.; Yuan, X. On-chip spin-controlled orbital angular momentum directional coupling. J. Phys. D Appl. Phys. 2017, 51, 014002. [Google Scholar] [CrossRef]
- Xie, G.; Song, H.; Zhao, Z.; Milione, G.; Ren, Y.; Liu, Y.; Zhang, R.; Bao, C.; Li, L.; Wang, Z.; et al. Using a complex optical orbital-angular-momentum spectrum to measure object parameters. Opt. Lett. 2017, 42, 4482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qin, Y.; Li, Y.; Deng, D.; Liu, Y.; Sun, M. Ultracompact biosensor based on a metalens with a longitudinally structured vector beam. Appl. Opt. 2019, 58, 4438–4442. [Google Scholar] [CrossRef]
- Dorrah, A.H.; Zamboni-Rached, M.; Mojahedi, M. Experimental demonstration of tunable refractometer based on orbital angular momentum of longitudinally structured light. Light Sci. Appl. 2018, 7, 40. [Google Scholar] [CrossRef] [Green Version]
- Cvijetic, N.; Milione, G.; Ip, E.; Wang, T. Detecting lateral motion using light’s orbital angular momentum. Sci. Rep. 2015, 5, 15422. [Google Scholar] [CrossRef]
- Lavery, M.P.; Speirits, F.; Barnett, S.; Padgett, M. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Padgett, M.J. Orbital angular momentum 25 years on. Opt. Express 2017, 25, 11265–11274. [Google Scholar] [CrossRef] [PubMed]
- Cojoc, D.; Garbin, V.; Ferrari, E.; Businaro, L.; Romanato, F.; Fabrizio, E. Laser trapping and micromanipulation using optical vortices. Microelectron. Eng. 2005, 78–79, 125–131. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, W.; Xie, M.; Zhao, F. Optical rotational self-assembly at air-water surface by a single vortex beam. Results Phys. 2019, 12, 1172–1176. [Google Scholar] [CrossRef]
- Barbieri, C.; Tamburini, F.; Anzolin, G.; Bianchini, A.; Mari, E.; Sponselli, A.; Umbriaco, G.; Prasciolu, M.; Romanato, F.; Villoresi, P. Light’s orbital angular momentum and optical vortices for astronomical coronagraphy from ground and space telescopes. Earth Moon Planets 2009, 105, 283–288. [Google Scholar] [CrossRef]
- Huang, H.; Milione, G.; Lavery, M.J.; Xie, G.; Ren, Y.; Cao, Y.; Ahmed, N.; Nguyen, T.A.; Nolan, D.A.; Li, M.-J.; et al. Mode division multiplexing using an orbital angular momentum mode sorter and MIMO-DSP over a graded-index few-mode optical fibre. Sci. Rep. 2015, 5, 14931. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high security encryption. Nat. Photonics 2020, 14, 102–108. [Google Scholar] [CrossRef]
- Zhang, H.; Mao, B.; Han, Y.; Wang, Z.; Yue, Y.; Liu, Y. Generation of orbital angular momentum modes using fiber systems. Appl. Sci. 2019, 9, 1033. [Google Scholar] [CrossRef] [Green Version]
- Ruffato, G.; Massari, M.; Romanato, F. Diffractive optics for OAM-mode division multiplexing of optical vortices design, fabrication and optical characterization. In Proceedings of the IEEE 7th International Conference on Advance Optoelectronics and Lasers (CAOL), Odessa, Ukraine, 12–15 September 2016; pp. 148–150. [Google Scholar]
- Khonina, S.N.; Porfirev, A.P.; Volotovskiy, S.G.; Ustinov, A.V.; Fomchenkov, S.A.; Pavelyev, V.S.; Schroter, S.; Duparre, M. Generation of Multiple Vector Optical Bottle Beams. Photonics 2021, 8, 218. [Google Scholar] [CrossRef]
- Courtial, J.; Padgett, M.J. Performance of a cylindrical lens mode converter for producing Laguerre-Gaussian laser modes. Opt. Commun. 1999, 159, 13–18. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.C.; Kristensen, M.; Woerdman, J.P. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Uchida, M.; Tonomura, A. Generation of electron beams carrying orbital angular momentum. Nature 2010, 464, 737–739. [Google Scholar] [CrossRef]
- Dyson, J. Circular and spiral diffraction gratings. Proc. R. Soc. Lond. Ser. A 1958, 248, 93–106. [Google Scholar]
- Forbes, A.; Dudley, A.; McLaren, M. Creation and detection of optical modes with spatial light modulators. Adv. Opt. Photonics 2016, 8, 200–227. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Li, S.; Willner, A.E. Metamaterials-based broadband generation of orbital angular momentum carrying vector beams. Opt. Lett. 2013, 38, 932–934. [Google Scholar] [CrossRef] [PubMed]
- Marrucci, L.; Karimi, E.; Slussarenko, S.; Piccirillo, B.; Santamato, E.; Nagali, E.; Sciarrino, F. Spin-to-orbital conversion of the angular momentum of light and its classical and quantum applications. J. Opt. 2011, 13, 064001. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Go, S.; Huang, B.; Feng, Y.; Huang, X.; Liu, W.; Li, Z. All-fiber second-order optical vortex generation based on strong modulated long-period grating in a four-mode fiber. Opt. Lett. 2017, 42, 5210. [Google Scholar] [CrossRef]
- Ma, X.; Liu, C.-H.; Chang, G.; Galvanauskas, A. Angular-momentum coupled optical waves in chirally-coupled-core fibers. Opt. Express 2011, 19, 26515. [Google Scholar] [CrossRef]
- Zeng, X.; Li, Y.; Feng, L.; Wu, S.; Yang, C.; Li, W.; Tong, W.; Wu, J. All-fiber optical angular momentum mode multiplexer based on a mode-selective photonic lantern and a mode polarization controller. Opt. Lett. 2018, 43, 4779. [Google Scholar] [CrossRef]
- Ruffato, G.; Rossi, R.; Massari, M.; Mafakheri, E.; Capaldo, P.; Romanato, F. Design, fabrication and characterization of computer generated holograms for anti-counterfeiting applications using OAM beams as light decoders. Sci. Rep. 2017, 7, 18011. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heckenberg, N.R.; McDuff, R.; Smith, C.P.; White, A.G. Generation of optical phase insinglarities by computer-generated holograms. Opt. Commun. 1992, 91, 158–162. [Google Scholar]
- Cohen, G.B.; Pogreb, R.; Vinokur, K.; Davidov, D. Spatial light modulator based on a deformed-helix ferroelectric liquid crystal and a thin a-Si:H amorphous photoconductor. Appl. Opt. 1997, 36, 455–459. [Google Scholar] [CrossRef] [PubMed]
- Genevet, P.; Yu, N.F.; Aieta, Y.F.; Lin, J.; Kats, M.A.; Blanchard, R.; Scully, M.O.; Gaburro, Z.; Capasso, F. Ultra-thin plasmonic optical vortex plate based on phase discontinuities. Appl. Phys. Lett. 2012, 100, 013101. [Google Scholar] [CrossRef] [Green Version]
- Yu, N.F.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, W.; Xue, Q.; Che, W. Low-profile wideband dual-circularly polarized orbital angular momentum antenna array using metasurface. Microw. Opt. Technol. Lett. 2020, 63, 1207–1212. [Google Scholar] [CrossRef]
- Sun, Z.; Shi, Y.; Sun, X.; Jia, H.; Jin, Z.; Deng, K.; Yang, J. Underwater acoustic multiplexing communication by pentamodemetasurface. J. Phys. D Appl. Phys. 2020, 54, 205303. [Google Scholar] [CrossRef]
- Wang, D.; Liu, F.; Liu, T.; Sun, S.; He, Q.; Zhou, L. Efficient generation of complex vectorial optical fields with metasurfaces. Light Sci. Appl. 2021, 10, 67. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Zhang, S.; Pu, M.; He, Q.; Jin, J.; Xu, M.; Zhang, Y.; Gao, P.; Luo, X. Spin-decoupled metasurface for simultaneous detection of spin and orbital angular momenta via momentum transformation. Light Sci. Appl. 2021, 10, 63. [Google Scholar] [CrossRef]
- Munk, B. Frequency Selective Surfaces: Theory and Design; John Wiley: New York, NY, USA, 2000. [Google Scholar]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Carbon dioxide gas sensor based on polyhexamethylene biguanide polymer deposited on silicon nano-cylinders metasurface. Sensors 2021, 21, 378. [Google Scholar] [CrossRef]
- Li, J.; Wu, T.; Xu, W.; Liu, Y.; Liu, C.; Wang, Y.; Yu, Z.; Zhu, D.; Yu, L.; Ye, H. Mechanisms of 2π phase control in dielectric metasurface and transmission enhancement effect. Opt. Express 2019, 27, 23186–23196. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, C.; Grbic, A. Metamaterial Huygens’ surfaces: Tailoring wave fronts with reflectionless sheets. Phys. Rev. Lett. 2013, 110, 197401. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Podlipnov, V.V.; Karpeev, S.V.; Ustinov, A.V.; Volotovsky, S.G.; Ganchevskaya, S.V. Spectral control of the orbital angular momentum of a laser beam based on 3D properties of spiral phase plates fabricated for an infrared wavelength. Opt. Express 2020, 28, 18407. [Google Scholar] [CrossRef]
- Li, Y.; Kim, J.; Escuti, M.J. Orbital angular momentum generation and mode transformation with high efficiency using forked polarization gratings. Appl. Opt. 2012, 51, 8236–8245. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.; Kim, D.; Sawant, A.; Lee, I.; Choi, E.; Lee, J. Generation of E-band metasurface-based vortex beam with reduced divergence angle. Sci. Rep. 2020, 10, 8289. [Google Scholar] [CrossRef]
- Liu, A.; Wu, M.; Zhuang, R.; Hong, J.; Wang, Q.; Ren, X. On-chip generation of the reconfigurable orbital angular momentum with high order. Opt. Express 2020, 28, 17957. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, X.; Zhang, D.; Zhao, P.; Li, X.; Cui, K.; Liu, F.; Huang, Y. Generating optical superimposed vortex beam with tunable orbital momentum using integrated devices. Sci. Rep. 2015, 5, 10958. [Google Scholar] [CrossRef] [Green Version]
- Fontaine, N.K.; Doerr, C.R.; Buhl, L.L. Efficient multiplexing and demultiplexing of free-space orbital angular momentum using photonic integrated circuits. In Proceedings of the Optical Fiber Communication Conference, OSA Technical Digest, Los Angeles, CA, USA, 4–8 March 2012. [Google Scholar]
- Guan, B.; Scott, R.P.; Fontaine, N.K.; Ferrari, T.C.; Cappuzzo, M.; Klemens, F.; Keller, B.; Earnshaw, M.; Yoo, S.B. Integrated optical orbital angular momentum multiplexing device using 3-D waveguides and a silica PLC. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 9–14 June 2013. [Google Scholar]
- Li, H.; Phillips, D.B.; Wang, X.; Ho, D.; Chen, L.; Zhou, X.; Zhu, J.; Yu, S.; Cai, X. Orbital angular momentum vertical-cavity surface-emitting lasers. Optica 2015, 2, 547–552. [Google Scholar] [CrossRef] [Green Version]
- Zheng, S.; Wang, J. On-chip orbital angular momentum modes generator and (de)multiplexer based on trench silicon waveguides. Opt. Express 2017, 25, 18492. [Google Scholar] [CrossRef]
- Krenn, M.; Fickler, R.; Fink, M.; Handsteiner, J.; Malik, M.; Scheidl, T.; Ursin, R.; Zeilinger, A. Communication with spatially modulated light through turbulent air across Vienna. New J. Phys. 2014, 16, 113028. [Google Scholar] [CrossRef]
- Yan, Y.; Xie, G.; Lavery, M.P.; Huang, H.; Ahmed, N.; Bao, C.; Ren, Y.; Cao, Y.; Li, L.; Zhao, Z.; et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5876, 4876. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Xie, G.; Yan, Y.; Ahmed, N.; Ren, Y.; Yue, Y.; Rogawski, D.; Willner, M.; Erkmen, B.; Birnbaum, K.M.; et al. 100 Tbit/s free-space data link enabled by three-dimensional multiplexing of orbital angular momentum, polarization, and wavelength. Opt. Express 2014, 39, 197–200. [Google Scholar] [CrossRef] [Green Version]
- Gbur, G.; Tyson, R.K. Vortex beam propagation through atmospheric turbulence and topological charge conservation. J. Opt. Soc. Am. A 2008, 25, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Pu, J.; Chen, Z.; Wang, T.; Pu, J.; Chen, Z. Beam-spreading and topological charge of vortex beams propagating in a turbulent atmosphere. Opt. Commun. 2009, 282, 1255–1259. [Google Scholar] [CrossRef]
- Malik, M.; O’Sullivan, M.; Rodenburg, B.; Mirhosseini, M.; Leach, J.; Lavery, M.P.; Padgett, M.; Boyd, R.W. Influence of atmospheric turbulence on optical communications using orbital angular momentum for encoding. Opt. Express 2012, 20, 13195–13200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Porfirev, A.; Kirilenko, M.; Khonina, S.N.; Skidanov, R.; Soifer, V. Study of propagation of vortex beams in aerosol optical medium. Appl. Opt. 2017, 56, E5–E15. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Striletz, A.; Kovalev, A.; Kotlyar, V. Propagation of laser vortex beams in a parabolic optical fiber. Proc. SPIE 2010, 7523. [Google Scholar] [CrossRef]
- Ye, J.; Li, Y.; Han, Y.; Deng, D.; Guo, Z.; Gao, J.; Sun, Q.; Liu, Y.; Qu, S. Excitation and separation of vortex modes in twisted air-core fiber. Opt. Express 2016, 24, 8310–8316. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Chremmos, I.; Chen, Y.; Zhu, G.; Zhang, J.; Zhu, J.; Zhang, Y.; Liu, J.; Yu, S. Compact and high-performance vortex mode sorter for multi-dimensional multiplexed fiber communication systems. Optica 2020, 7, 254–262. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Almazov, A.A.; Khonina, S.N.; Soifer, V.A.; Elfstrom, H.; Turunen, J. Generation of phase singularity through diffracting a plane or Gaussian beam by a spiral phase plate. J. Opt. Soc. Am. A 2005, 22, 849–861. [Google Scholar] [CrossRef] [PubMed]
- Oraizi, H.; Emamian, H. Generation of orbital angular momentum modes via holographic leaky-wave metasurfaces. Sci. Rep. 2020, 10, 7358. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Ustinov, A.V.; Logachev, V.I.; Porfirev, A.P. Properties of vortex light fields generated by generalized spiral phase plates. Phys. Rev. A 2020, 101, 043829. [Google Scholar] [CrossRef]
- Isakov, D.; Wu, Y.; Allen, B.; Grant, P.S.; Stevens, C.J.; Gibbons, G.J. Evaluation of the Laguerre-Gaussian mode purity produced by three-dimensional-printed microwave spiral phase plates. R. Soc. Open Sci. 2020, 7, 200493. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Kotlyar, V.V.; Soifer, V.A.; Skinkaryev, M.V.; Uspleniev, G.V. Trochoson. Opt. Commun. 1992, 91, 158–162. [Google Scholar] [CrossRef]
- Musigmann, M.; Jahns, J.; Bock, M.; Grunwald, R. Refractive-diffractive dispersion compensation for optical vortex beams with ultrashort pulse durations. Appl. Opt. 2014, 53, 7304–7311. [Google Scholar] [CrossRef]
- Degtyarev, S.A.; Porfirev, A.P.; Khonina, S.N. Photonic nanohelix generated by a binary spiral axicon. Appl. Opt. 2016, 55, B44–B48. [Google Scholar] [CrossRef]
- Soskin, M.S.; Polyanskii, P.V.; Arkhelyuk, O.O. Computer-synthesized hologram-based rainbow optical vortices. New J. Phys. 2004, 6, 196. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, C.; Jia, W.; Hu, A.; Cao, W.; Wu, J.; Wang, S. Generation of dipole vortex array using spiral Dammann zone plates. Appl. Opt. 2012, 51, 6799–6804. [Google Scholar] [CrossRef]
- Janicijevic, L.; Topuzoski, S. Gaussian laser beam transformation into an optical vortex beam by helical lens. J. Mod. Opt. 2016, 63, 164–176. [Google Scholar] [CrossRef] [Green Version]
- Davis, J.A.; Cottrell, D.M.; Sand, D. Abruptly autofocusing vortex beam. Opt. Express 2012, 20, 13302–13310. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhao, S.; Yu, W.; Zhu, X. Abruptly autofocusing property of circular Airy vortex beams with different initial launch angles. J. Opt. Soc. Am. A 2018, 35, 890–894. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P.; Ustinov, A.V.; Butt, M.A. Generation of complex transverse energy flow distributions with autofocusing optical vortex beams. Micromachines 2021, 12, 297. [Google Scholar] [CrossRef]
- Bazhenov, V.Y.; Vasnetsov, M.V.; Soskin, M.S. Laser beams with screw dislocations in their wavefronts. JTP Lett. 1990, 52, 429–431. [Google Scholar]
- Heckenberg, N.R.; McDuff, R.; Smith, C.P.; Rubinstein-Dunlop, H.; Wegener, M.J. Laser beams with phase singularities. Opt. Quantum Electron. 1992, 24, S951–S962. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kotlyar, V.V.; Soifer, V.A.; Lautanen, J.; Honkanen, M.; Turunen, J. Generating a couple of rotating nondiffracting beams using a binary-phase DOE. Optik 1999, 110, 137–144. [Google Scholar]
- Janicijevic, L.; Topuzoski, S. Fresnel and Fraunhofer diffraction of a Gaussian laser beam by fork-shaped gratings. J. Opt. Soc. Am. A 2008, 25, 2659–2669. [Google Scholar] [CrossRef] [PubMed]
- Topuzoski, S. Generation of optical vortices with curved fork-shaped holograms. Opt. Quantum Electron. 2016, 48, 1–6. [Google Scholar] [CrossRef]
- Saad, F.; El Halba, E.M.; Belafhal, A. Generation of generalized spiraling Bessel beams of arbitrary order by curved fork-shaped holograms. Opt. Quantum Electron. 2016, 48, 454. [Google Scholar] [CrossRef]
- Khonina, S.N.; Usinov, A.V.; Kirilenko, M.S.; Kuchmizhak, A.A.; Porfirev, A.P. Application of a binary curved fork grating for the generation and detection of optical vortices outside the focal plane. J. Opt. Soc. Am. B 2020, 37, 1714–1721. [Google Scholar] [CrossRef]
- Wang, D.; Jin, L.; Rosales-Guzman, C.; Gao, W. Generating arbitrary arrays of circular Airy Gaussian vortex beams with a single digital hologram. Appl. Phys. B 2021, 127, 22. [Google Scholar] [CrossRef]
- Khonina, S.N.; Balalayev, S.A.; Skidanov, R.V.; Kotlyar, V.V.; Paivanranta, B.; Turunen, J. Encoded binary diffractive element to form hyper-geometric laser beams. J. Opt. A Pure Appl. Opt. 2009, 11, 065702. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kotlyar, V.V.; Soifer, V.A.; Honkanen, M.; Lautanen, J.; Turunen, J. Generation of rotating Gauss-Laguerre modes with binary-phase diffractive optics. J. Mod. Opt. 2009, 46, 227–238. [Google Scholar]
- Lerner, V.; Shwa, D.; Drori, Y.; Katz, N. Shaping Laguerre-Gaussian laser modes with binary gratings using a digital micromirror device. Opt. Lett. 2012, 37, 4826–4848. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mirhosseini, M.; Magana-Loaiza, O.S.; Chen, C.; Rodenburg, B.; Malik, M.; Boyd, R.W. Rapid generation of light beams carrying orbital angular momentum. Opt. Express 2013, 21, 30204–30211. [Google Scholar] [CrossRef] [Green Version]
- Kotlyar, V.V.; Soifer, V.A.; Khonina, S.N. Rotation of multimodal Gauss-Laguerre light beams in free space and in a fiber. Opt. Lasers Eng. 1998, 29, 343–350. [Google Scholar] [CrossRef]
- Almazov, A.A.; Khonina, S.N.; Kotlyar, V.V. Using phase diffraction optical elements to shape and select laser beams consisting of a superposition of an arbitrary number of angular harmonics. J. Opt. Technol. 2005, 72, 391–399. [Google Scholar] [CrossRef]
- Caley, A.J.; Thomson, M.J.; Liu, J.; Waddie, A.J.; Taghizadeh, M.R. Diffractive optical elements for high gain lasers with arbitrary output beam profiles. Opt. Express 2007, 15, 10699–10704. [Google Scholar] [CrossRef]
- Jia, W.; Chen, Z.; Wen, F.J.; Zhou, C.; Chow, Y.T.; Chung, P.S. Coaxial holographic encoding based on pure phase modulation. Appl. Opt. 2011, 50, H10–H15. [Google Scholar] [CrossRef]
- Gerchberg, R.W.; Saxton, W.D. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Khonina, S.N.; Kotlyar, V.V.; Soifer, V.A. Techniques for encoding composite diffractive optical elements. Proc. SPIE Int. Soc. Opt. Eng. 2003, 5036, 493–498. [Google Scholar]
- Meister, M.; Winfield, R.J. Novel approaches to direct search algorithms for the design of diffractive optical elements. Opt. Commun. 2002, 203, 39–49. [Google Scholar] [CrossRef]
- Hsu, W.-F.; Lin, S.-C. Iternative pixelwise approach applied to computer-generated holograms and diffractive optical elements. Appl. Opt. 2018, 57, A189–A196. [Google Scholar] [CrossRef] [PubMed]
- Swartzlander, G.A. Achromatic optical vortex lens. Opt. Lett. 2006, 31, 2042–2044. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Zhao, D. Optical vortices generated by multi-level achromatic spiral phase plates for broadband beams. Opt. Commun. 2008, 281, 7–11. [Google Scholar] [CrossRef]
- Fadeyeva, T.A.; Shvedov, V.G.; Izdebskaya, Y.V.; Volyar, A.V.; Brasselet, E.; Neshev, D.N.; Desyatnikov, A.S.; Krolikowski, W.; Kivshar, Y.S. Spatially engineered polarization states and optical vortices in uniaxial crystals. Opt. Express 2010, 18, 10848–10863. [Google Scholar]
- Loussert, C.; Brasselet, E. Efficient scalar and vectorial singular beam shaping using homogeneous anisotropic media. Opt. Lett. 2010, 35, 7–9. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Alferov, S.V.; Soifer, V.A. Generation of cylindrical vector beams of high orders using uniaxial crystals. J. Opt. 2015, 17, 065001. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Paranin, V.D.; Morozov, A.A. Polarization conversion under focusing of vortex laser beams along the axis of anisotropic crystals. Phys. Lett. A 2017, 381, 2444–2455. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P.; Kazanskiy, N.L. Variable transformation of singular cylindrical vector beams using anisotropic crystals. Sci. Rep. 2020, 10, 5590. [Google Scholar] [CrossRef]
- Wang, X.; Ding, J.; Ni, W.; Guo, C.; Wang, H. Generation of arbitrary vector beams with a spatial light modulator and a common path interferometric arrangement. Opt. Lett. 2007, 32, 3549. [Google Scholar] [CrossRef] [PubMed]
- Cancula, M.; Ravnik, M.; Zumer, S. Generation of vector beams with liquid crystal disclination lines. Phys. Rev. E 2014, 90, 022503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hsu, W.-L.; Balakrishnan, K.; Ibn-Elhaj, M.; Pau, S. Infrared liquid crystal polymer micropolarizer. Appl. Opt. 2014, 53, 5252–5258. [Google Scholar] [CrossRef]
- Alpmann, C.; Schlickriede, C.; Otte, E.; Denz, C. Dynamic modulation of Poincare beams. Sci. Rep. 2017, 7, 8076. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, H.; Fu, S.; Zhai, Y.; Yin, C.; Gao, C. Spatial light modulator-based programmable J-plate for the arbitrary spin-to-orbital angular momentum conversion of lights. Appl. Phys. B 2019, 125, 42. [Google Scholar] [CrossRef]
- Beck, R.J.; Parry, J.P.; MacPherson, W.N.; Waddie, A.; Weston, N.J.; Shephard, J.D.; Hand, D.P. Application of cooled spatial light modulator for high power nanosecond laser micromachining. Opt. Express 2010, 18, 17059–17065. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, D.; Gui, L.; Akram, M.R. Generation of OAM radio waves using a slot antenna array. In Proceedings of the Asia-Pacific Microwave Conference (APMC), Nanjing, China, 6–9 December 2015; pp. 1–3. [Google Scholar]
- Yu, S.X.; Li, L.; Shi, G.M.; Zhu, C.; Shi, Y. Generating multiple orbital angular momentum vortex beams using a metasurface in radio frequency domain. Appl. Phys. Lett. 2016, 108, 241901. [Google Scholar] [CrossRef]
- Wang, L.Y.; Shi, H.Y.; Zhu, S.T.; Li, J.X.; Zhang, A.X.; Li, L.M. Generation of multiple modes microwave vortex beams using tunable metasurface. In Proceedings of the 7th IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies, Xi’an, China, 24–27 October 2017; pp. 379–381. [Google Scholar]
- Bai, X. High-efficiency transmissive metasurface for dual-polarized dual-mode OAM generation. Results Phys. 2020, 18, 103334. [Google Scholar] [CrossRef]
- Barnett, S.M.; Allen, L. Orbital angular momentum and nonparaxial light beams. Opt. Commun. 1994, 10, 670. [Google Scholar] [CrossRef]
- Devlin, R.C.; Ambrosio, A.; Rubin, N.A.; Mueller, J.P.B.; Capasso, F. Arbitrary spin-to-orbital angular momentum conversion of light. Science 2017, 358, 896–901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, C.-H.; Fuh, A.Y.-G. Complex beam shaping based on an equivalent q-plate system and analysis of its properties using digital holography polarization imaging. Sci. Rep. 2017, 7, 2769. [Google Scholar] [CrossRef] [Green Version]
- Karimi, E.; Piccirillo, B.; Nagali, E.; Marrucci, L.; Santamato, E. Efficient generation and sorting of orbital angular momentum eigenmodes of light by thermally tuned q-plates. Appl. Phys. Lett. 2009, 94, 231123. [Google Scholar] [CrossRef]
- Li, G.X.; Kang, M.; Chen, S.M.; Zhang, S.; Pun, E.B.; Cheah, K.; Li, J.S. Spin-enabled plasmonic metasurfaces for manipulating orbital angular momentum of light. Nano Lett. 2013, 13, 4148–4151. [Google Scholar] [CrossRef]
- Zhang, Y.; Lyu, Y.; Liao, D.; Wang, H. Reflective metasurface for generating orbital angular momentum of microwave. In Proceedings of the International Applied Computational Electromagnetics Society Symposium (ACES), Firenze, Italy, 29–30 March 2017; pp. 1–2. [Google Scholar]
- Chen, M.N.; Jiang, L.J.; Sha, W.I. Orbital angular momentum generation and detection by geometric-phase based metasurfaces. Appl. Sci. 2018, 8, 362. [Google Scholar] [CrossRef] [Green Version]
- Yue, F.; Wen, D.; Xin, J.; Gerardot, B.D.; Li, J.; Chen, X. Vector vortex beam generation with a single plasmonic metasurface. ACS Photonics 2016, 3, 1558–1563. [Google Scholar] [CrossRef]
- Mehmood, M.Q.; Mei, S.; Hussain, S.; Huang, K.; Siew, S.Y.; Zhang, L.; Zhang, T.; Ling, X.; Liu, H.; Teng, J.; et al. Visible-frequency metasurface for structuring and spatially multiplexing optical vortices. Adv. Mater. 2016, 28, 2533–2539. [Google Scholar] [CrossRef]
- Yang, Y.M.; Wang, W.Y.; Moitra, P.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation. Nano Lett. 2014, 14, 1394–1399. [Google Scholar] [CrossRef]
- He, Y.; Li, Y.; Liu, J.; Zhang, X.; Cai, Y.; Chen, Y.; Chen, S.; Fan, D. Switchable phase and polarization singular beams generation using dielectric metasurfaces. Sci. Rep. 2017, 7, 6814. [Google Scholar] [CrossRef] [PubMed]
- Stafeev, S.S.; Kotlyar, V.V.; Nalimov, A.G.; Kotlyar, M.V.; O’Faolain, L. Subwavelength gratings for polarization conversion and focusing of laser light. Photonics Nanostruct. 2017, 27, 32–41. [Google Scholar] [CrossRef]
- Degtyarev, S.A.; Volotovsky, S.G.; Khonina, S.N. Sublinearly chirped metalenses for forming abruptly autofocusing cylindrically polarized beams. J. Opt. Soc. Am. B 2018, 35, 1963–1969. [Google Scholar] [CrossRef]
- Schemmel, P.; Pisano, G.; Maffei, B. Modular spiral phase plate design for orbital angular momentum generation at millimetre wavelengths. Opt. Express 2014, 22, 14712–14726. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Bai, Z.; Zhu, G.; Fu, C.; Li, Y.; Liu, S.; Liao, C.; Wang, Y. 3D nanoprintedkinoform spiral zone plates on fiber facets for high-efficiency focused vortex beam generation. Opt. Express 2020, 28, 38127–38139. [Google Scholar] [CrossRef]
- Doerr, C.R.; Buhl, L.L. Circular grating coupler for creating focused azimuthally and radially polarized beams. Opt. Lett. 2011, 36, 1209–1211. [Google Scholar] [CrossRef]
- Su, T.; Scott, R.; Djordjevic, S.; Fontaine, N.; Geisler, D.; Cai, Z.; Yoo, S. Demonstration of free space coherent optical communication using integrated silicon photonic orbital angular momentum devices. Opt. Express 2012, 20, 9396–9402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, D.; Feng, X.; Huang, Y. Encoding and decoding of orbital angular momentum for wireless optical interconnects on chip. Opt. Express 2012, 20, 26986–26995. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, P.; Feng, X.; Xu, Y.; Cui, K.; Liu, F.; Zhang, W.; Huang, Y. Integrated photonic emitter with a wide switching range of orbital angular momentum modes. Sci. Rep. 2016, 6, 22512. [Google Scholar] [CrossRef] [PubMed]
- Taillaert, D.; Laere, F.V.; Ayre, M.; Bogaerts, W.; Thourhout, D.V.; Bienstman, P.; Baets, R. Grating couplers for coupling between optical fibers and nanophotonic waveguides. Jpn. J. Appl. Phys. 2006, 45, 6071. [Google Scholar] [CrossRef] [Green Version]
- Cognee, K.D.H.L.P.K.A. Generation of pure OAM beams with a single state of polarization by antenna-decorated microdisk resonators. ACS Photonics 2020, 7, 43. [Google Scholar] [CrossRef]
- Cai, X.; Wang, J.; Strain, M.J.; Johnson-Morris, B.; Zhu, J.; Sorel, M.; Brien, J.L.; Thompson, M.G.; Yu, S. Integrated compact optical vortex beam emitters. Science 2012, 338, 363–366. [Google Scholar] [CrossRef]
- Li, R.; Feng, X.; Zhang, D.; Cui, K.; Liu, F.; Huang, Y. Radially polarized orbital angular momentum beam emitter based on shallow-ridge silicon microring cavity. IEEE Photonics J. 2014, 6, 2200710. [Google Scholar] [CrossRef]
- Scaffardi, M.; Malik, M.M.; Lazzeri, E.; Klitis, C.; Meriggi, L.; Zhang, N.; Sorel, M.; Bogoni, A. 3x3 optical switch by exploiting vortex beam emitters based on silicon microrings with superimposed gratings. Opt. Lett. 2017, 42, 3749. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Q.; Klitis, C.; Li, S.; Chen, Y.; Cai, X.; Sorel, M.; Yu, S. Generation of photonic orbital angular momentum superposition states using vortex beam emitters with superimposed gratings. Opt. Express 2016, 24, 3168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, A.; Zou, C.-L.; Ren, X.; Wang, Q.; Guo, G.-C. On-chip generation and control of the vortex beam. Appl. Phys. Lett. 2016, 108, 181103. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Hu, X.; Jin, L.; Fu, X.; Chen, Q. Generation of in-plane light beam with orbital angular momentum with an asymmetrical plasmonic waveguide. Plasmonics 2016, 11, 1323–1329. [Google Scholar] [CrossRef]
- Xie, Z.; Lei, T.; Li, F.; Qiu, H.; Zhang, Z.; Wang, H.; Min, C.; Du, L.; Li, Z.; Yuan, X. Ultra-broadband on-chip twisted light emitter for optical communications. Light Sci. Appl. 2018, 7, 18001. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation. Nanophotonics 2018, 7, 1533–1556. [Google Scholar] [CrossRef]
- Zhao, Z.; Fan, S. Design principles of apodized grating couplers. J. Lightwave Technol. 2020, 38, 4435–4446. [Google Scholar] [CrossRef]
- Liu, J.; Li, S.; Ding, Y.; Chen, S.; Du, C.; Mo, Q.; Morioka, T.; Yvind, K.; Oxenlowe, K.; Yu, S.; et al. Orbital angular momentum modes emission from a silicon photonic integrated device for km-scale data-carrying fiber transmission. Opt. Express 2018, 26, 15471–15479. [Google Scholar] [CrossRef]
- Li, S.; Nong, Z.; Wu, X.; Yu, W.; He, M.; Klitis, C.; Zhu, Y.; Gao, S.; Liu, J.; Li, Z.; et al. Orbital angular momentum vector modes (de)multiplexer based on multimode micro-ring. Opt. Express 2018, 26, 29895–29905. [Google Scholar] [CrossRef]
- Paul, S.; Lyubopytov, V.S.; Schumann, M.F.; Cesar, J.; Chipouline, A.; Wegener, M.; Küppers, F. Wavelength-selective orbital-angular-momentum beam generation using MEMS tunable Fabry-Perot filter. Opt. Lett. 2016, 41, 3249. [Google Scholar] [CrossRef]
- Lyubopytov, V.S.; Porfirev, A.P.; Gurbatov, S.O.; Paul, S.; Schumann, M.F.; Cesar, J.; Malekizandi, M.; Haidar, M.T.; Wegener, M.; Chipouline, A.; et al. Simultaneous wavelength and orbital angular momentum demultiplexing using tunable MEMS-based Fabry-Perot filter. Opt. Express 2017, 25, 9634–9646. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Feng, X.; Cui, K.; Liu, F.; Huang, Y. Generating in-plane orbital angular momentum beams with silicon waveguides. IEEE Photonics J. 2013, 5, 2201206. [Google Scholar] [CrossRef]
- Zhang, D. Angular momentum of optical modes in a silicon channel waveguide. Phys. Rev. Res. 2020, 2, 33454. [Google Scholar] [CrossRef]
- Lee, I.J.; Kim, S. On-chip guiding of higher-order orbital angular momentum modes. Photonics 2019, 6, 72. [Google Scholar] [CrossRef] [Green Version]
- Lee, I.J.; Kim, S. Directional coupler design for orbital angular momentum mode-based photonic integrated circuits. Opt. Express 2020, 28, 30085. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhao, L.; Hao, Y.; Liu, W.; Wu, Y.; Wei, Z.; Xu, N.; Qin, S.; Yang, X.; Liu, H. Metasurface spiral focusing generators with tunable orbital angular momentum based on slab silicon nitride waveguide and vanadium dioxide (VO2). Nanomaterials 2020, 10, 1864. [Google Scholar] [CrossRef]
- Lyubopytov, V.S.; Kutluyarov, R.V.; Bagmanov, V.K.; Neumann, N.; Sultanov, A.K. Modeling and optimization of vortex modes propagation in rectangular dielectric waveguides. IEEE Photonics J. 2020, 12, 6100117. [Google Scholar] [CrossRef]
- Meng, Y.; Liu, Z.; Xie, Z.; Wang, R.; Qi, T.; Hu, F.; Kim, H.; Xiao, Q.; Fu, X.; Wu, Q.; et al. Versatile on-chip light coupling and (de)multiplexing from arbitrary polarizations to controlled waveguide modes using an integrated dielectric metasurface. Photonics Res. 2020, 8, 564. [Google Scholar] [CrossRef]
- Liang, Y.; Wu, H.W.; Huang, B.J.; Huang, X.G. Light beams with selective angular momentum generated by hybrid plasmonic waveguides. Nanoscale 2014, 6, 12360–12365. [Google Scholar] [CrossRef]
- Lyubopytov, V.S.; Chipouline, A.; Zywietz, U.; Chichkov, B.; Sokolovskii, G.S.; Averkiev, N.S.; Savchenko, G.M.; Bougrov, V.E.; Monroy, I.T.; Kuppers, F. Optical vortex propagation in few-mode rectangular polymer waveguides. In Proceedings of the 2017 Opto-Electronics and Communications Conference (OECC) and Photonics Global Conference (PGC), Singapore, 31 July–4 August 2017. [Google Scholar]
- Lyubopytov, V.S.; Chipouline, A.; Sokolovskii, G.S.; Averkiev, N.S.; Savchenko, G.M.; Zywietz, U.; Chichkov, B.; Monroy, I.T.; Bougrov, V.E.; Kuppers, F. Demonstration of optical vortex propagation in on-chip rectangular dielectric waveguides. In Proceedings of the 2017 European Conference on Lasers and Electro-Optics and European Quantum Electronics Conference, Munich, Germany, 25–29 June 2017. [Google Scholar]
- Ma, Z.; Chen, H.; Wu, K.; Zhang, Y.; Chen, Y.; Yu, S. Self-imaging of orbital angular momentum (OAM) modes in rectangular multimode interference waveguides. Opt. Express 2015, 23, 5014. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Hybrid plasmonic waveguide-assisted metal-insulator-metal ring resonator for refractive index sensing. J. Mod. Opt. 2018, 65, 1135–1140. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Device performance of standard strip, slot and hybrid plasmonic micro-ring resonator: A comparative study. Waves Random Complex Media 2020. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, F.; Gu, J.; Huang, X.G.; Liu, S. Integratable quarter-wave plates enable one-way angular momentum conversion. Sci. Rep. 2016, 6, 24959. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kutluyarov, R.V.; Fatkhiev, D.M.; Stepanov, I.V.; Grakhova, E.P.; Lyubopytov, V.S.; Sultanov, A.K. Design and modeling of a photonic integrated device for optical vortex generation in a silicon waveguide. Comput. Opt. 2021, 45, 324–330. [Google Scholar] [CrossRef]
- Fatkhiev, D.M.; Lyubopytov, V.S.; Kutluyarov, R.V.; Grakhova, E.P.; Sultanov, A.K. A grating coupler design for optical vortex mode generation in rectangular waveguides. IEEE Photonics J. 2021. [Google Scholar] [CrossRef]
- Schulze, C.; Dudley, A.; Flamm, D.; Duparre, M.; Forbes, A. Measurement of the orbital angular momentum density of light by modal decomposition. New J. Phys. 2013, 15, 073025. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.; Xia, H.; Xie, W.; Peng, Y. Orbital angular momentum mode detection of the combined vortex beam generated by coherent combining technology. Opt. Express 2020, 28, 35795–35806. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Ma, L. Detecting the orbital angular momentum of electro-magnetic waves using virtual rotational antenna. Sci. Rep. 2017, 7, 4585. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Chu, H.; Giddens, H.; Li, R.; Hao, Y. Experimental observation of linear and rotational doppler shifts from several designer surfaces. Sci. Rep. 2019, 9, 8971. [Google Scholar] [CrossRef] [Green Version]
- Genevet, P.; Lin, J.; Kats, M.A.; Capasso, F. Holographic detection of the orbital angular momentum of light with plasmonic photodiodes. Nat. Commun. 2012, 3, 1278. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, S.M.; Daldorff, L.S.; Forozesh, K.; Thide, B.; Bergman, J.S.; Isham, B.; Karlsson, R.; Carozzi, T.D. Orbital angular momentum in radio: Measurement methods. Radio Sci. 2010, 45, 1–14. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef] [Green Version]
- Kotlyar, V.V.; Khonina, S.N.; Soifer, V. Light field decomposition in angular harmonics by means of diffractive optics. J. Mod. Opt. 1998, 45, 1495–1506. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kotlyar, V.; Soifer, V.; Paakkonen, P.; Simonen, J.; Turunen, J. An analysis of the angular momentum of a light field in terms of angular harmonics. J. Mod. Opt. 2001, 48, 1543–1557. [Google Scholar] [CrossRef]
- Moreno, I.; Davis, J.A.; Pascoguin, B.L.; Mitry, M.J.; Cottrell, D.M. Vortex sensing diffraction gratings. Opt. Lett. 2009, 34, 2927–2929. [Google Scholar] [CrossRef] [PubMed]
- Kazanskiy, N.L.; Khonina, S.N.; Karpeev, S.V.; Porfirev, A.P. Diffractive optical elements for multiplexing structured laser beams. Quantum Electron. 2020, 50, 629–635. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Paranin, V.D. A technique for simultaneous detection of individual vortex states of Laguerre-Gaussian beams transmitted through an aqueous suspension of microparticles. Opt. Lasers Eng. 2018, 105, 68–74. [Google Scholar] [CrossRef]
- Khonina, S.N.; Skidanov, R.V.; Kotlyar, V.V.; Jefimovs, K.; Turunen, J. Phase diffractive filter to analyze an output step-index fiber beam. Proc. SPIE Int. Soc. Opt. Eng. 2004, 5182, 251–259. [Google Scholar]
- Lei, T.; Zhang, M.; Li, Y.; Jia, P.; Liu, G.N.; Xu, X.; Li, Z.; Min, C.; Lin, J.; Yu, C.; et al. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci. Appl. 2015, 4, e257. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, S.; Wang, T.; Gao, C. Measurement of orbital angular momentum spectra of multiplexing optical vortices. Opt. Express 2016, 24, 6240–6248. [Google Scholar] [CrossRef]
- D’Errico, A.; D’Amelio, R.; Piccirillo, B.; Cardano, F.; Marrucci, L. Measuring the complex orbital angular momentum spectrum and spatial mode decomposition of structured light beams. Optica 2017, 4, 1350–1357. [Google Scholar] [CrossRef] [Green Version]
- Fu, S.; Zhai, Y.; Wang, T.; Yin, C.; Gao, C. Orbital angular momentum channel monitoring of coaxially multiplexed vortices by diffraction pattern analysis. Appl. Opt. 2018, 57, 1056–1060. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Butt, M.A. Spatial-light-modulator-based multichannel data transmission by vortex beams of various orders. Sensors 2021, 21, 2988. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.; Wong, P.; Cheah, K.; et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mueller, J.P.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface polarization optics: Independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 2017, 118, 133901. [Google Scholar]
- Bao, Y.; Ni, J.; Qiu, C.W. A minimalist single-layer metasurface for arbitrary and full control of vector vortex beams. Adv. Mater. 2020, 32, 1905659. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Wang, P.; Wang, C.; Liu, J.; Ye, H.; Zhou, X.; Li, Y.; Chen, S.; Fan, D. All-optical signal processing in structured light multiplexing with dielectric meta-optics. ACS Photonics 2020, 7, 135–146. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Zhang, L.; Wang, G.; Zhang, L.; Liu, M.; Zeng, C.; Wang, L.; Sun, Q.; Zhao, W.; et al. Efficient optical angular momentum manipulation for compact multiplexing and demultiplexing using a dielectric metasurface. Adv. Opt. Mater. 2020, 8, 1901666. [Google Scholar] [CrossRef]
- Rui, G.; Gu, B.; Cui, Y.; Zhan, Q. Detection of orbital angular momentum using a photonic integrated circuit. Sci. Rep. 2016, 6, 28262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, A.; Jones, R.; Liao, L.; Samara-Rubio, D.; Rubin, D.; Cohen, O.; Nicolaescu, R.; Paniccia, M. A high-speed silicon optical modulator based on a metal-oxide-semiconductor capacitor. Nature 2004, 427, 615–618. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Ultrashort inverted tapered silicon ridge-to-slot waveguide coupler at 1.55 μm and 3.392 μm wavelength. Appl. Opt. 2020, 59, 7821–7828. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. 2D-Photonic crystal heterostructures for the realization of compact photonic devices. Photonics Nanostruct.-Fundam. Appl. 2021, 44, 100903. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Silicon photonic devices realized on refractive index engineered subwavelength grating waveguides-A review. Opt. Laser Technol. 2021, 138, 106863. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Butt, M.A. Spectral characteristics of broad band-rejection filter based on Bragg grating, one-dimensional photonic crystal, and subwavelength grating waveguide. Phys. Scr. 2021, 96, 055505. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L. Narrowband perfect metasurface absorber based on impedance matching. Photonics Lett. Pol. 2020, 12, 88–90. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, W.; Chen, L. Experimental detection of high-order or fractional orbital angular momentum of light based on a robust mode converter. Appl. Phys. Lett. 2016, 108, 111108. [Google Scholar] [CrossRef]
- Ma, A.; Intaravanne, Y.; Han, J.; Wang, R.; Chen, X. Polarization detection using light’s orbital angular momentum. Adv. Opt. Mater. 2020, 8, 2000484. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Malaney, R.; Green, J. Detecting orbital angular momentum of light in Satellite-to-Ground Quantum communications. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Kaviani, H.; Ghobadi, R.; Behera, B.; Wu, M.; Hryciw, A.; Vo, S.; Fattal, D.; Barclay, P. Optomechanical detection of light with orbital angular momentum. Opt. Express 2020, 28, 15482–15496. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatkhiev, D.M.; Butt, M.A.; Grakhova, E.P.; Kutluyarov, R.V.; Stepanov, I.V.; Kazanskiy, N.L.; Khonina, S.N.; Lyubopytov, V.S.; Sultanov, A.K. Recent Advances in Generation and Detection of Orbital Angular Momentum Optical Beams—A Review. Sensors 2021, 21, 4988. https://doi.org/10.3390/s21154988
Fatkhiev DM, Butt MA, Grakhova EP, Kutluyarov RV, Stepanov IV, Kazanskiy NL, Khonina SN, Lyubopytov VS, Sultanov AK. Recent Advances in Generation and Detection of Orbital Angular Momentum Optical Beams—A Review. Sensors. 2021; 21(15):4988. https://doi.org/10.3390/s21154988
Chicago/Turabian StyleFatkhiev, Denis M., Muhammad A. Butt, Elizaveta P. Grakhova, Ruslan V. Kutluyarov, Ivan V. Stepanov, Nikolay L. Kazanskiy, Svetlana N. Khonina, Vladimir S. Lyubopytov, and Albert K. Sultanov. 2021. "Recent Advances in Generation and Detection of Orbital Angular Momentum Optical Beams—A Review" Sensors 21, no. 15: 4988. https://doi.org/10.3390/s21154988
APA StyleFatkhiev, D. M., Butt, M. A., Grakhova, E. P., Kutluyarov, R. V., Stepanov, I. V., Kazanskiy, N. L., Khonina, S. N., Lyubopytov, V. S., & Sultanov, A. K. (2021). Recent Advances in Generation and Detection of Orbital Angular Momentum Optical Beams—A Review. Sensors, 21(15), 4988. https://doi.org/10.3390/s21154988








