Energy-Efficient Time Synchronization Based on Nonlinear Clock Skew Tracking for Underwater Acoustic Networks
Abstract
:1. Introduction
- First, to characterize time-varying clock skews, a nonlinear model based on the temperature data collected from sea trials and the crystal oscillators’ temperature–frequency characteristics is established. It compensates for the estimation error introduced by clock skews and increases the TS accuracy.
- Second, based on a receive-only (RO) paradigm, a single-way communication scheme is used to reduce the energy consumption of UANs. By receiving the periodical broadcast signals from the reference node, any sensor node in the communication range can measure the time of arrival (TOA) of the received packets and obtain a series of observation equations that are used to calibrate the clock parameters. The impulsive noises are considered during communication processes and the Gaussian Mixture Model (GMM) is adopted to fit the noise in this paper.
- Last, to solve the nonlinear and non-Gaussian problems, an improved particle filter (PF) algorithm is employed. Moreover, the particles’ weights are revised under the GMM noise model and thus, accurate clock parameters can be estimated.
2. Algorithm Description
2.1. System Model
2.1.1. Nonlinear Clock Skew Model
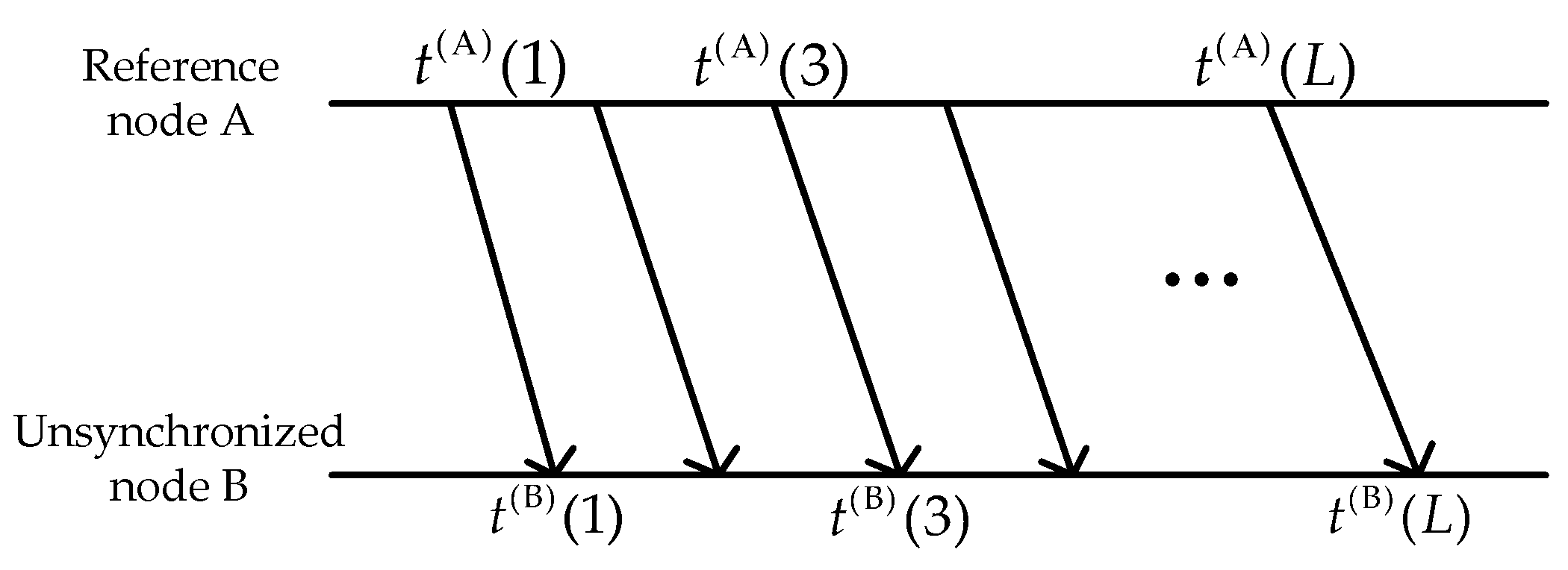
2.1.2. Single-Way Communication Scheme under the GMM Noise Model
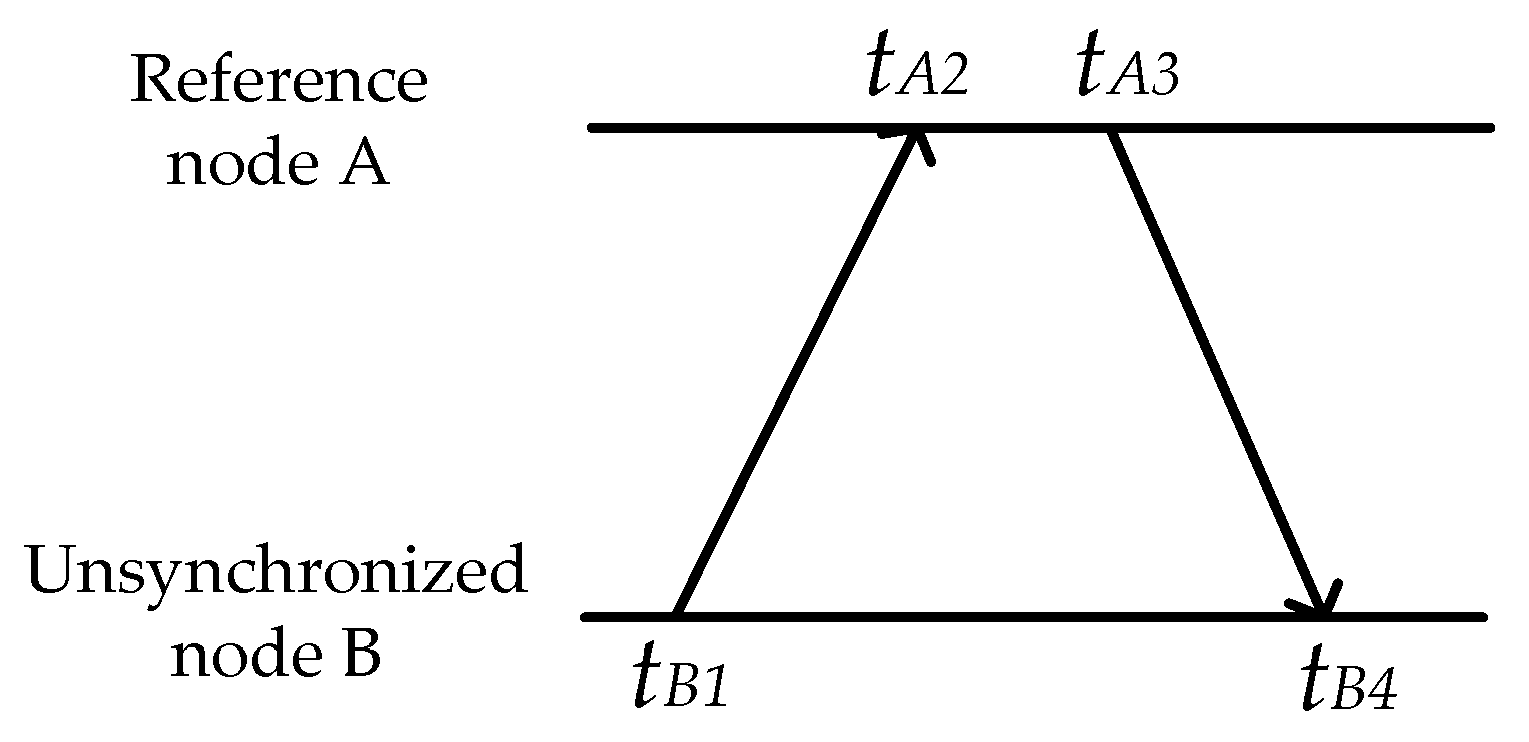
2.1.3. Calibration of the Clock offset
2.2. Nonlinear Clock Skew Tracking Based on PF
3. Performance Evaluation
3.1. Simulation Setup
3.2. Simulation Results and Analysis
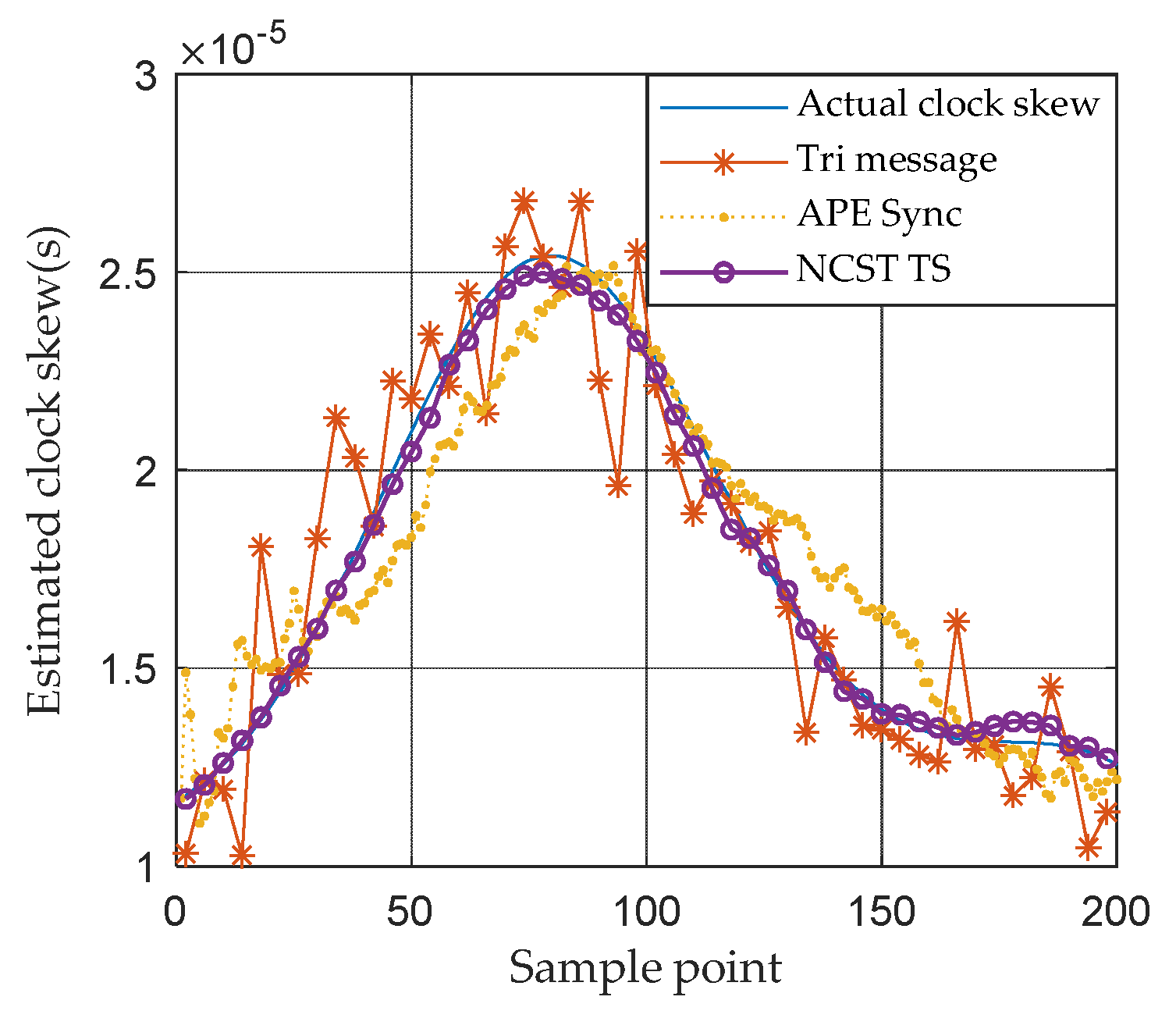
3.2.1. Performance of Tracking Results and RMSE Based on the Gaussian Noise Model
3.2.2. Performance on Tracking Results and RMSE Based on the GMM Noise Model
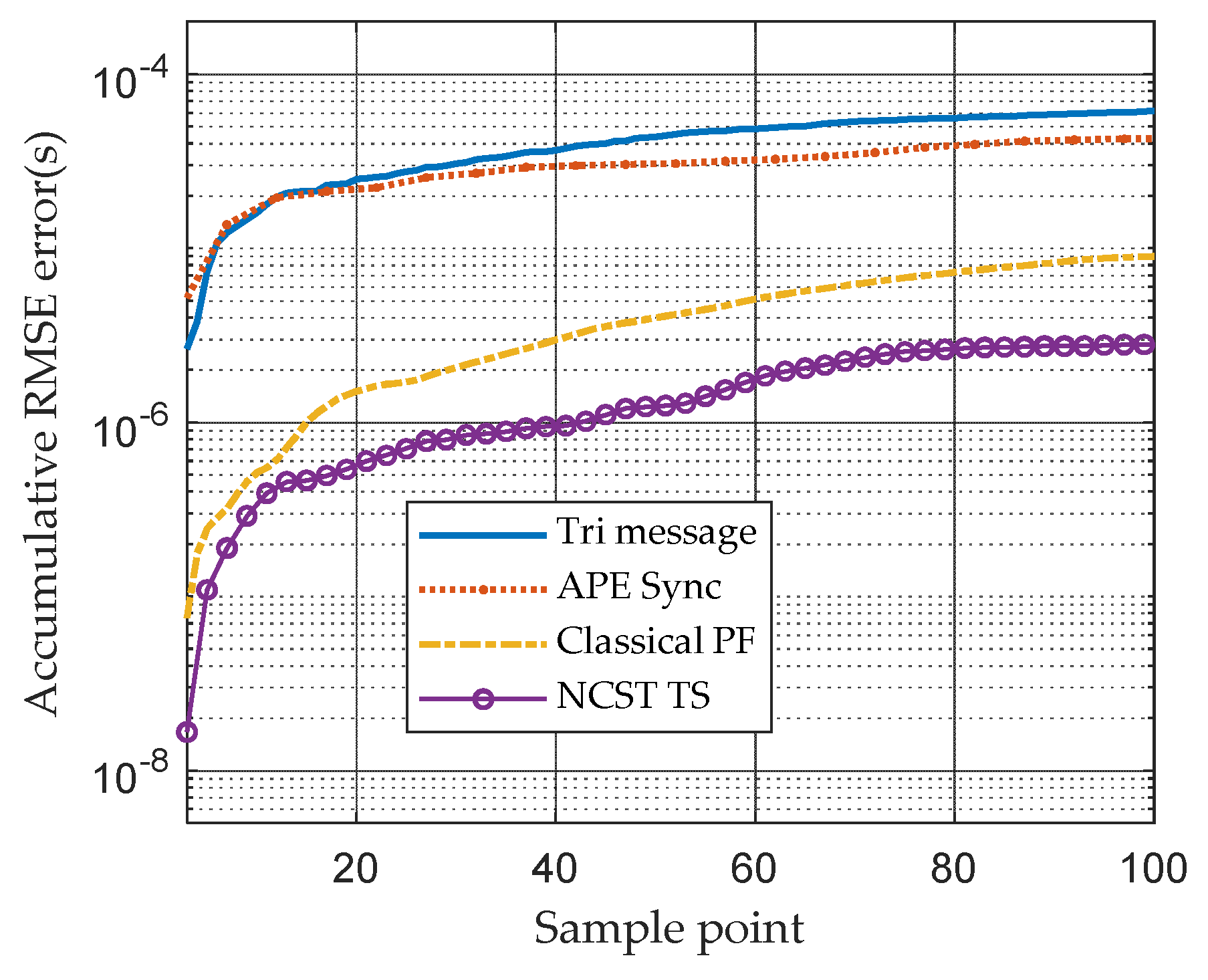
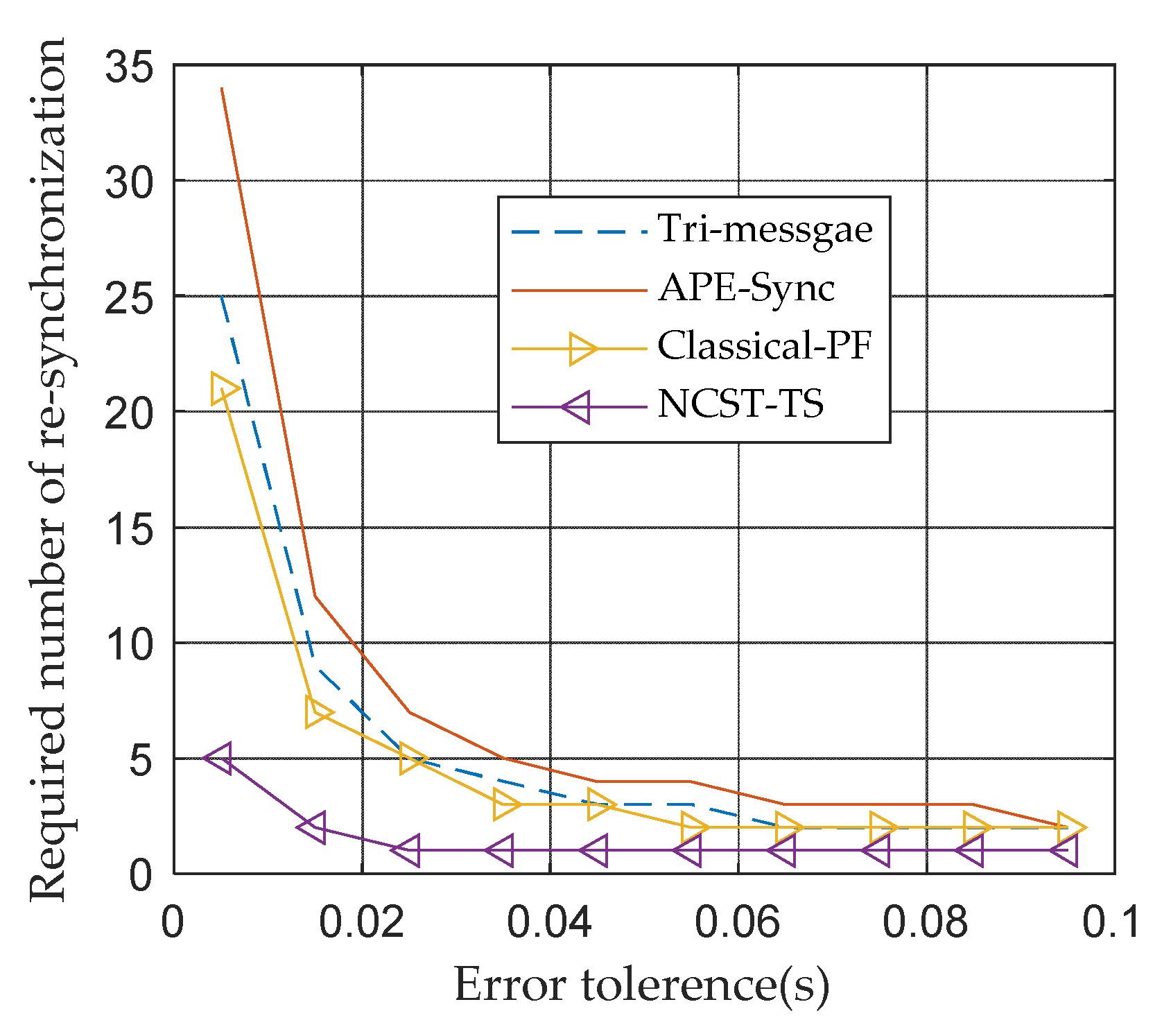
3.2.3. Comparison of Different Algorithms in Terms of Energy Efficiency
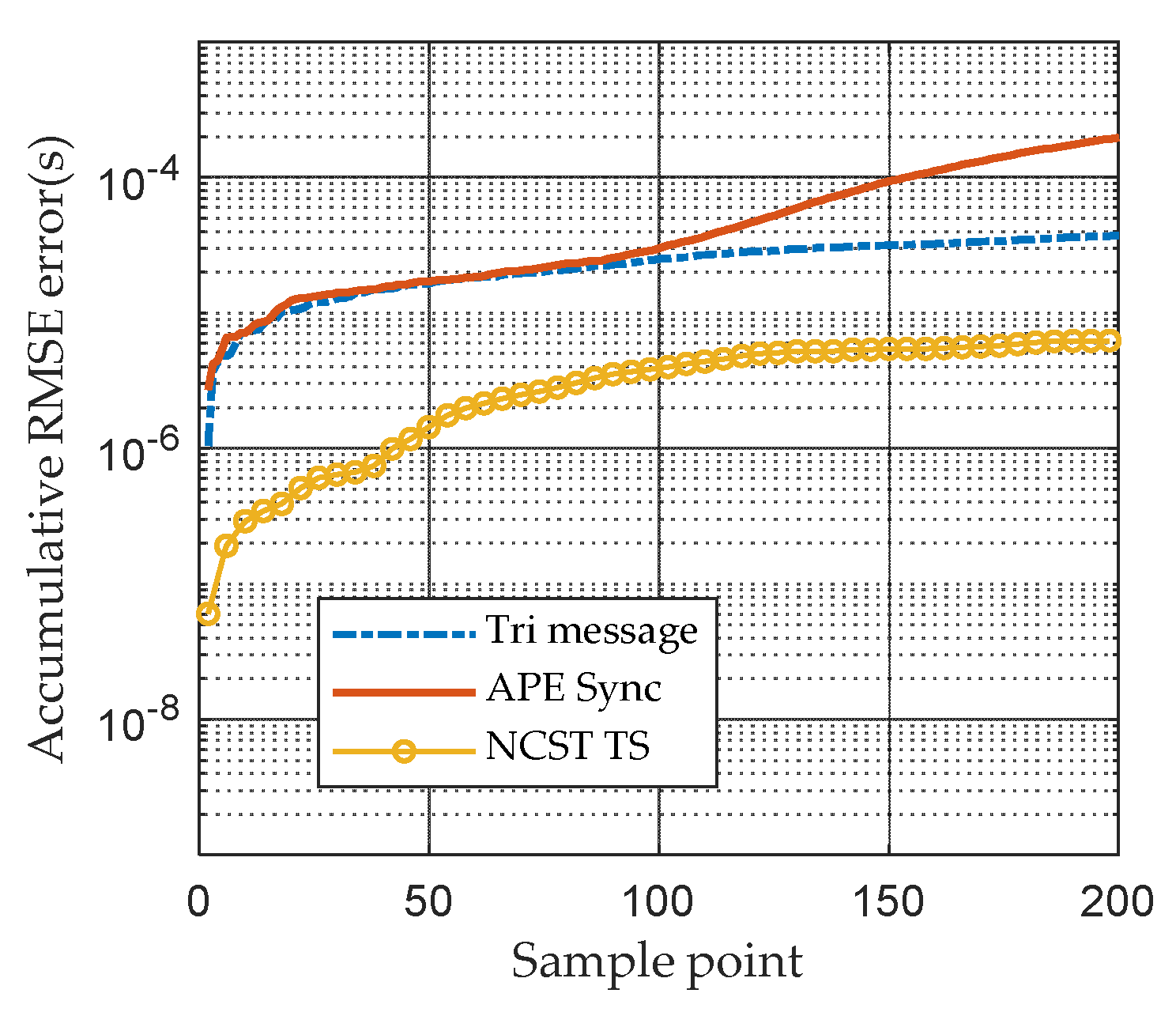
3.2.4. Comparison of Different Algorithms in Terms of Time Error after TS
3.2.5. Comparison of Different TS Algorithms in Terms of Consumed Energy
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, Y. Underwater Acoustic Sensor Networks with Cost Efficiency for Internet of Underwater Things. IEEE Trans. Ind. Electron. 2020, 68, 1707–1716. [Google Scholar] [CrossRef]
- Pallares, O.; Bouvet, P.-J.; Del Rio, J. TS-MUWSN: Time Synchronization for Mobile Underwater Sensor Networks. IEEE J. Ocean. Eng. 2016, 41, 763–775. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Zheng, L.; Li, G.; Xie, H.; Sun, X. Simulation and Analysis of Time Synchronization System for Seafloor Observatory Network Using OMNeT++. In Proceedings of the 2020 12th International Conference on Communication Software and Networks (ICCSN), Chongqing, China, 12–15 June 2020; pp. 318–323. [Google Scholar] [CrossRef]
- Liu, G.; Yan, S.; Mao, L. Receiver-Only-Based Time Synchronization Under Exponential Delays in Underwater Wireless Sensor Networks. IEEE Internet Things J. 2020, 7, 9995–10009. [Google Scholar] [CrossRef]
- Diamant, R.; Lampe, L. Underwater Localization with Time-Synchronization and Propagation Speed Uncertainties. IEEE Trans. Mob. Comput. 2012, 12, 1257–1269. [Google Scholar] [CrossRef]
- Sun, S.; Qin, S.; Hao, Y.; Zhang, G.; Zhao, C. Underwater Acoustic Localization of the Black Box Based on Generalized Second-Order Time Difference of Arrival (GSTDOA). In IEEE Transactions on Geoscience and Remote Sensing; IEEE: Piscataway, NJ, USA, 2020; pp. 1–11. [Google Scholar] [CrossRef]
- Pan, X.; Shen, Y.; Zhang, J. IoUT Based Underwater Target Localization in the Presence of Time Synchronization Attacks. IEEE Trans. Wirel. Commun. 2021, 20, 3958–3973. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, X.; Leus, G. Robust Time-Based Localization for Asynchronous Networks. IEEE Trans. Signal Process. 2011, 59, 4397–4410. [Google Scholar] [CrossRef]
- Gardner, A.T.; Collins, J.A. A second look at Chip Scale Atomic Clocks for long term precision timing. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Elson, J.; Girod, L.; Estrin, D. Fine-grained network time synchronization using reference broadcasts. In Proceedings of the 5th Symposium on Operating Systems Design and Implementation, Boston, MA, USA, 9–11 December 2002; pp. 147–163. [Google Scholar]
- Ganeriwal, S.; Ram, K.; Mani, B.S. Timing-sync protocol for sensor networks. In Proceedings of the 1st International Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, 5–7 November 2003; pp. 138–149. [Google Scholar]
- Maroti, M.; Kusy, B.; Simon, G.; Ledeczi, A. The flooding time synchronization protocol. In Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems, Baltimore, MD, USA, 3–5 November 2004; pp. 39–49. [Google Scholar]
- Cho, H.; Kim, J.; Baek, Y. Enhanced Precision Time Synchronization for Wireless Sensor Networks. Sensors 2011, 11, 7625–7643. [Google Scholar] [CrossRef] [Green Version]
- Bruscato, L.T.; Heimfarth, T.; De Freitas, E.P. Enhancing Time Synchronization Support in Wireless Sensor Networks. Sensors 2017, 17, 2956. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zeng, P.; Zhou, M.; Li, D.; Wang, J. Cluster-Based Maximum Consensus Time Synchronization for Industrial Wireless Sensor Networks. Sensors 2017, 17, 141. [Google Scholar] [CrossRef] [Green Version]
- Rhee, I.-K.; Lee, J.; Kim, J.; Serpedin, E.; Wu, Y.-C. Clock Synchronization in Wireless Sensor Networks: An Overview. Sensors 2009, 9, 56–85. [Google Scholar] [CrossRef] [Green Version]
- Jin, Z.; Ding, M.; Luo, Y.; Li, S. Integrated Time Synchronization and Multiple Access Protocol for Underwater Acoustic Sensor Networks. IEEE Access 2019, 7, 101844–101854. [Google Scholar] [CrossRef]
- Xing, G.; Chen, Y.; He, L.; Su, W.; Hou, R.; Li, W.; Zhang, C.; Chen, X. Energy Consumption in Relay Underwater Acoustic Sensor Networks for NDN. IEEE Access 2019, 7, 42694–42702. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, Z.; Peng, Z.; Cui, J.-H.; Zuba, M.; Fiondella, L. Mobi-Sync: Efficient Time Synchronization for Mobile Underwater Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2012, 24, 406–416. [Google Scholar] [CrossRef]
- Uddin, M.B.; Castelluccis, C. Toward clock skew based wireless sensor node services. In Proceedings of the Wireless Internet Conference (WICON), Singapore, Singapore, 1–3 March 2010; pp. 1–6. [Google Scholar]
- Li, D.; Wu, Y.; Zhu, M. Nonbinary LDPC code for noncoherent underwater acoustic communication under non-Gaussian noise. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Cario, G.; Casavola, A.; Djapic, V.; Gjanci, P.; Lupia, M.; Petrioli, C.; Spaccini, D. Clock synchronization and ranging estimation for control and cooperation of multiple UUVs. In Proceedings of the OCEANS 2016—Shanghai, Shanghai, China, 10–13 April 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Syed, A.A.; Heidemann, J. Time synchronization for high latency acoustic networks. In Proceedings of the IEEE INFOCOM 2006. 25TH IEEE International Conference on Computer Communications, Barcelona, Catalunya, Spain, 23–29 April 2006; pp. 1–12. [Google Scholar]
- Tian, C.; Jiang, H.; Liu, X.; Wang, X.; Liu, W.; Wang, Y. Tri-Message: A Lightweight Time Synchronization Protocol for High Latency and Resource-Constrained Networks. In Proceedings of the 2009 IEEE International Conference on Communications, Dresden, Germany, 14–18 June 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Lu, F.; Mirza, D.; Schurgers, C. D-Sync: Doppler-based time synchronization for mobile underwater sensor networks. In Proceedings of the Fifth ACM International Workshop on Underwater Networks, Woods Hole, MA, USA, 30 September–1 October 2010; pp. 1–8. [Google Scholar]
- Feng, X.; Wang, Z.; Zhu, X.L. Doppler auxiliary time synchronization algorithm for underwater acoustic sensor network. J. Commun. 2017, 38, 9–15. [Google Scholar]
- Liu, J.; Wang, Z.; Zuba, M.; Peng, Z.; Cui, J.-H.; Zhou, S. DA-Sync: A Doppler-Assisted Time-Synchronization Scheme for Mobile Underwater Sensor Networks. IEEE Trans. Mob. Comput. 2013, 13, 582–595. [Google Scholar] [CrossRef]
- Zhou, F.; Wang, Q.; Han, G.; Qiao, G.; Sun, Z.; Niaz, A. APE-Sync: An Adaptive Power Efficient Time Synchronization for Mobile Underwater Sensor Networks. IEEE Access 2019, 7, 52379–52389. [Google Scholar] [CrossRef]
- Zhou, F.; Wang, Q.; Nie, D.; Qiao, G. DE-Sync: A Doppler-Enhanced Time Synchronization for Mobile Underwater Sensor Networks. Sensors 2018, 18, 1710. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Pan, J.; Cai, L. Adaptive Clock Skew Estimation with Interactive Multi-Model Kalman Filters for Sensor Networks. In Proceedings of the 2010 IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Li, J.; Mechitov, K.A.; Kim, R.E.; Spencer, B.F. Efficient time synchronization for structural health monitoring using wireless smart sensor networks. Struct. Control. Health Monit. 2015, 23, 470–486. [Google Scholar] [CrossRef]
- Wen, J.; Sun, X.-M.; Zhan, C.; Zhong, Y.-H.; Wang, J. An Analysis of Frequency-Temperature Relations of At-Cut Quartz Crystal Resonators by Finite Element Method with Comsol. In Proceedings of the 2019 13th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Harbin, China, 11–14 January 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Zennaro, D.; Tomasi, B.; Vangelista, L.; Zorzi, M. Light-Sync: A low overhead synchronization algorithm for underwater acoustic networks. In Proceedings of the 2012 Oceans—Yeosu, Yeosu, Korea, 21–24 May 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Dai, Q.; Xu, H.; Huang, D. Gaussian mixture filter algorithm considering non-Gaussian colored noise. J. Geod. Geodynamics 2020, 40, 1308–1312. [Google Scholar] [CrossRef]
- Chang, D.-C.; Fang, M.-W. Bearing-Only Maneuvering Mobile Tracking with Nonlinear Filtering Algorithms in Wireless Sensor Networks. IEEE Syst. J. 2013, 8, 160–170. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Song, W.; Wang, Z.; Wang, J.; Alsaadi, F.E.; Shan, J. Particle Filtering for Nonlinear/Non-Gaussian Systems with Energy Harvesting Sensors Subject to Randomly Occurring Sensor Saturations. IEEE Trans. Signal Process. 2020, 69, 15–27. [Google Scholar] [CrossRef]
- Jin, Z.; Ding, M.; Su, Y.; Yang, Q.; Wu, T. Joint time synchronization and multiple access mechanism for underwater glider networks. Syst. Eng. Electron. 2019, 41, 659–666. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| Distance | 1500 m |
| Speed of sound | 1500 m/s |
| Maximum skew of | 40 ppm |
| Maximum offset of | 0.01 s |
| Interval between transmit messages | 2 s |
| Number of message L | 30 |
| Granularity of clock | 0.1 μs |
| random delay X | 10 μs |
| Algorithm | Run Time (ms) | Number of Transmitting Time Stamps | Number of Receiving Time Stamps | Energy Consumed by Processing (J) | Energy Consumed by Trans and Revs Activities (J) |
|---|---|---|---|---|---|
| NCST-TS | 7.4 | 1 | 21 | 0.333 | 12.425 |
| APE-Sync | 3.5 | 11 | 11 | 0.158 | 21.175 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Zhu, M.; Li, D.; Fang, X.; Wu, Y. Energy-Efficient Time Synchronization Based on Nonlinear Clock Skew Tracking for Underwater Acoustic Networks. Sensors 2021, 21, 5018. https://doi.org/10.3390/s21155018
Liu D, Zhu M, Li D, Fang X, Wu Y. Energy-Efficient Time Synchronization Based on Nonlinear Clock Skew Tracking for Underwater Acoustic Networks. Sensors. 2021; 21(15):5018. https://doi.org/10.3390/s21155018
Chicago/Turabian StyleLiu, Di, Min Zhu, Dong Li, Xiaofang Fang, and Yanbo Wu. 2021. "Energy-Efficient Time Synchronization Based on Nonlinear Clock Skew Tracking for Underwater Acoustic Networks" Sensors 21, no. 15: 5018. https://doi.org/10.3390/s21155018
APA StyleLiu, D., Zhu, M., Li, D., Fang, X., & Wu, Y. (2021). Energy-Efficient Time Synchronization Based on Nonlinear Clock Skew Tracking for Underwater Acoustic Networks. Sensors, 21(15), 5018. https://doi.org/10.3390/s21155018







