Comparative Experimental Investigation on Optimal Parametric Array Types
Abstract
:1. Introduction
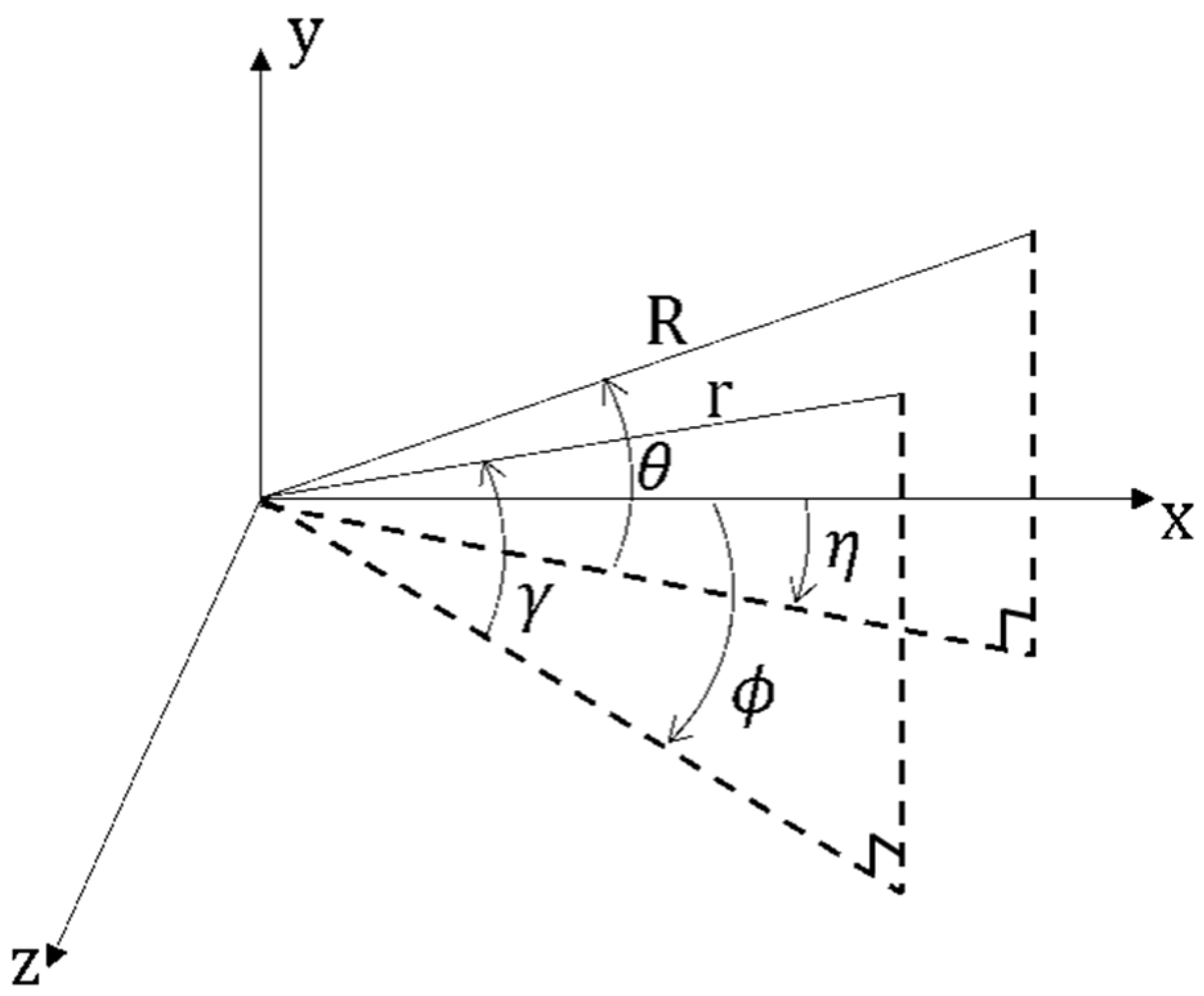
2. Fundamental Principle of the Parametric Array
2.1. Dual-Frequency Parametric Array
2.2. Broadband Parametric Array
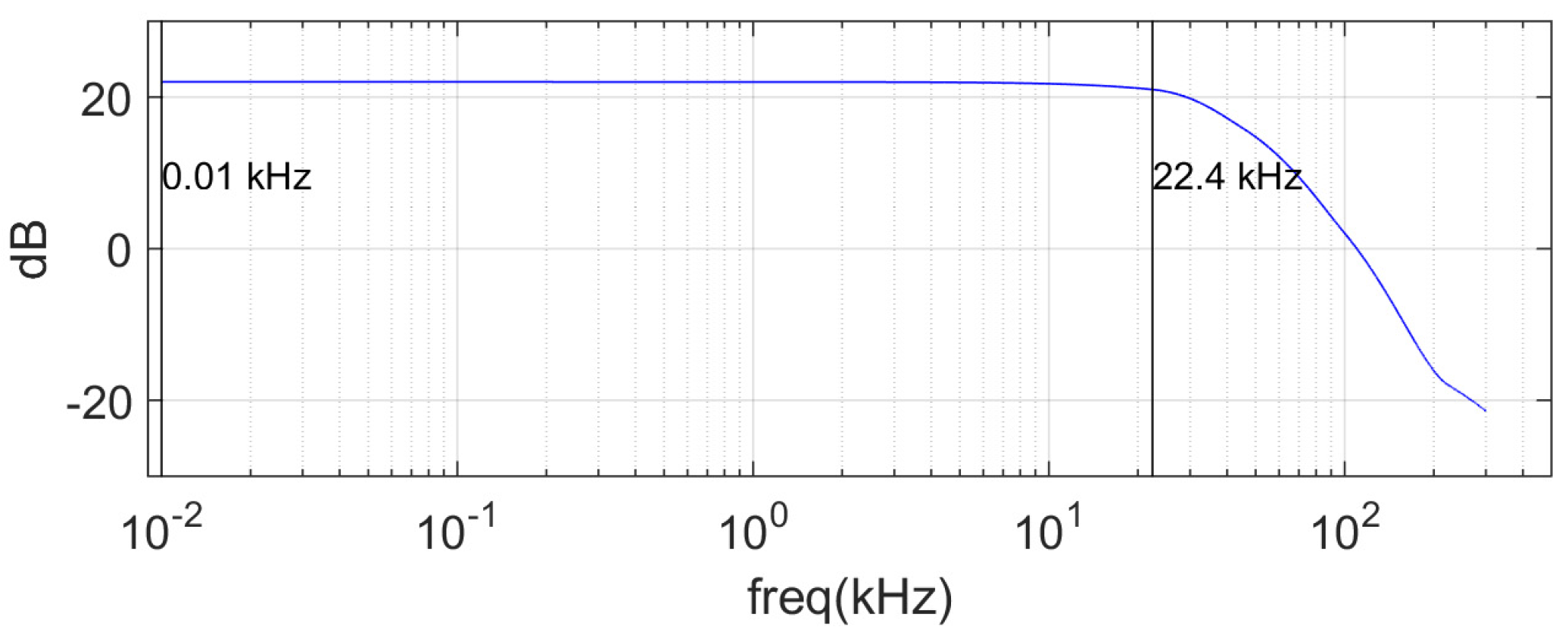
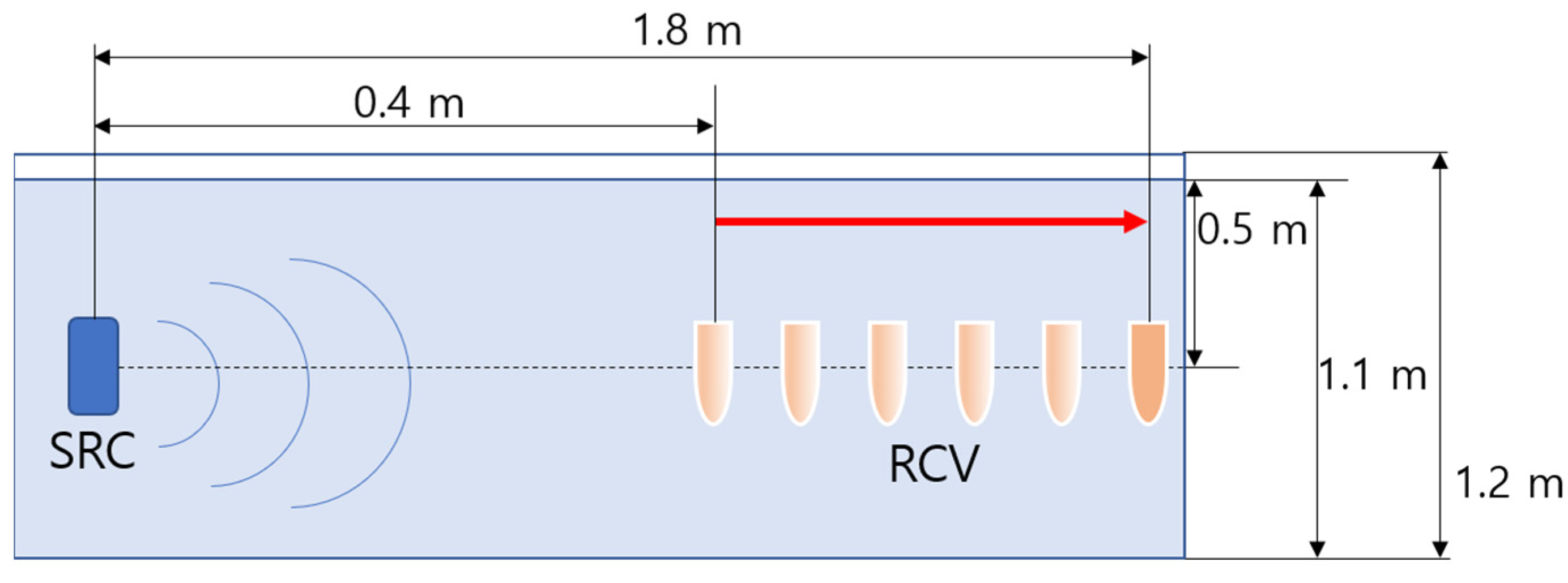
3. Experimental Setup
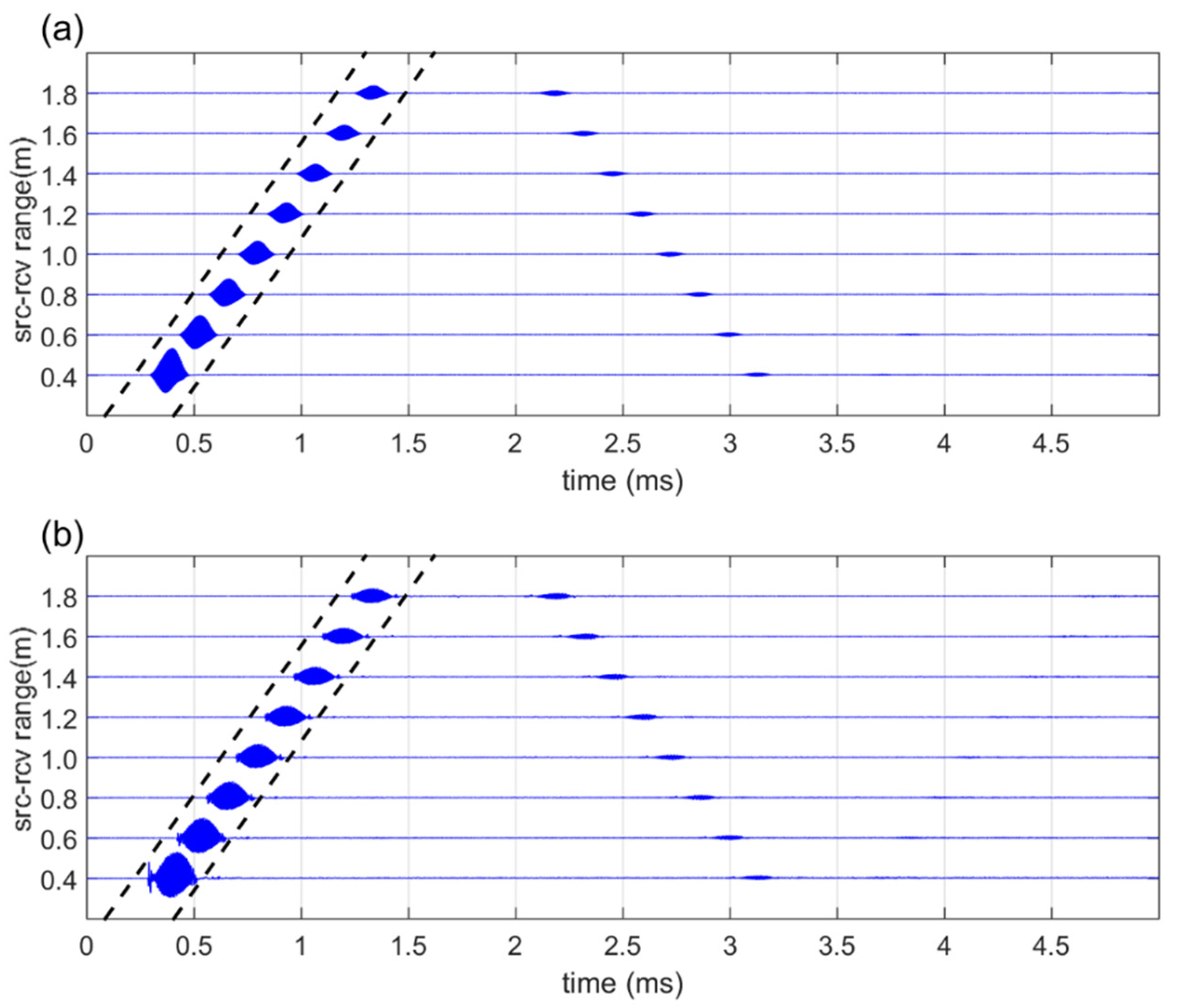
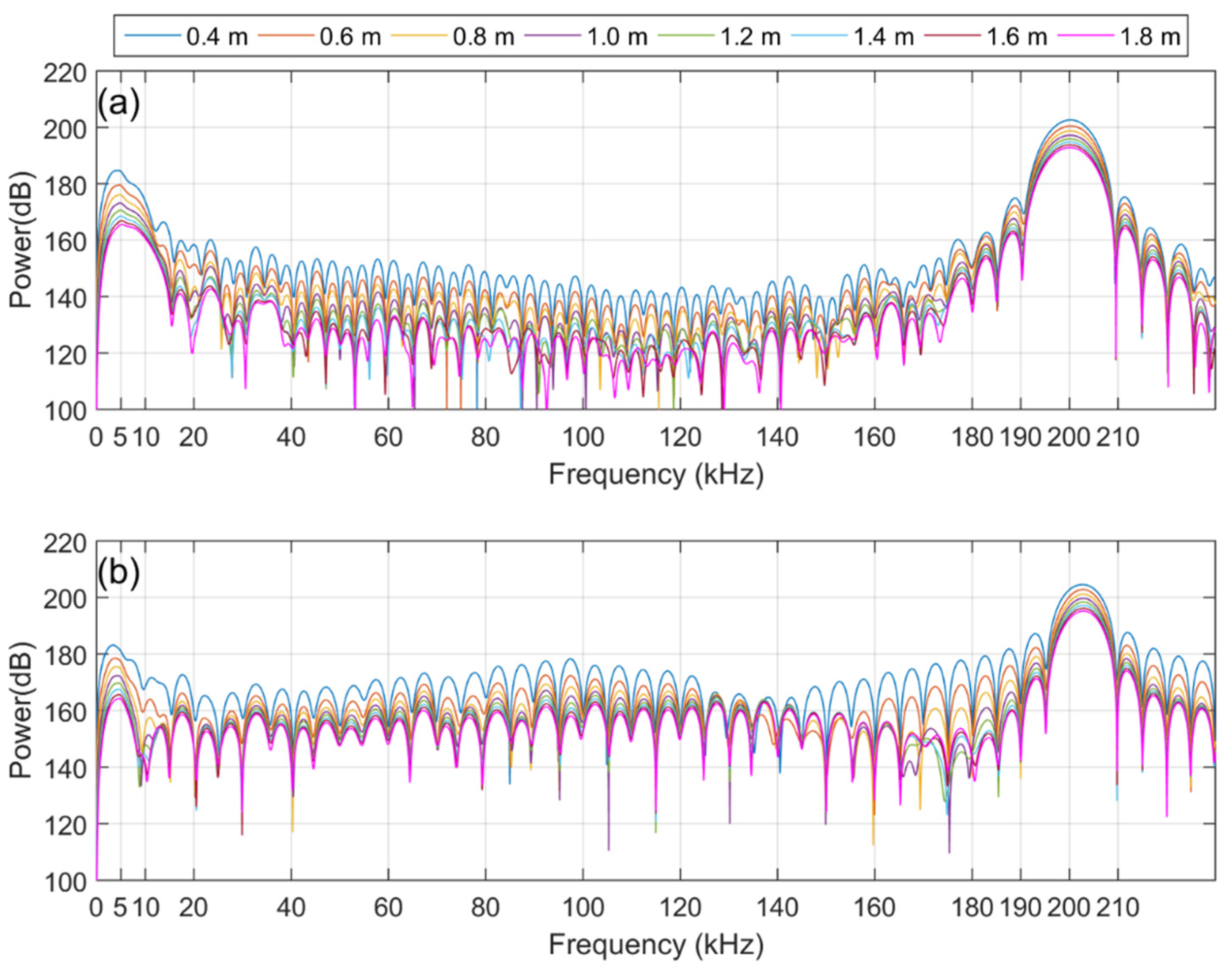
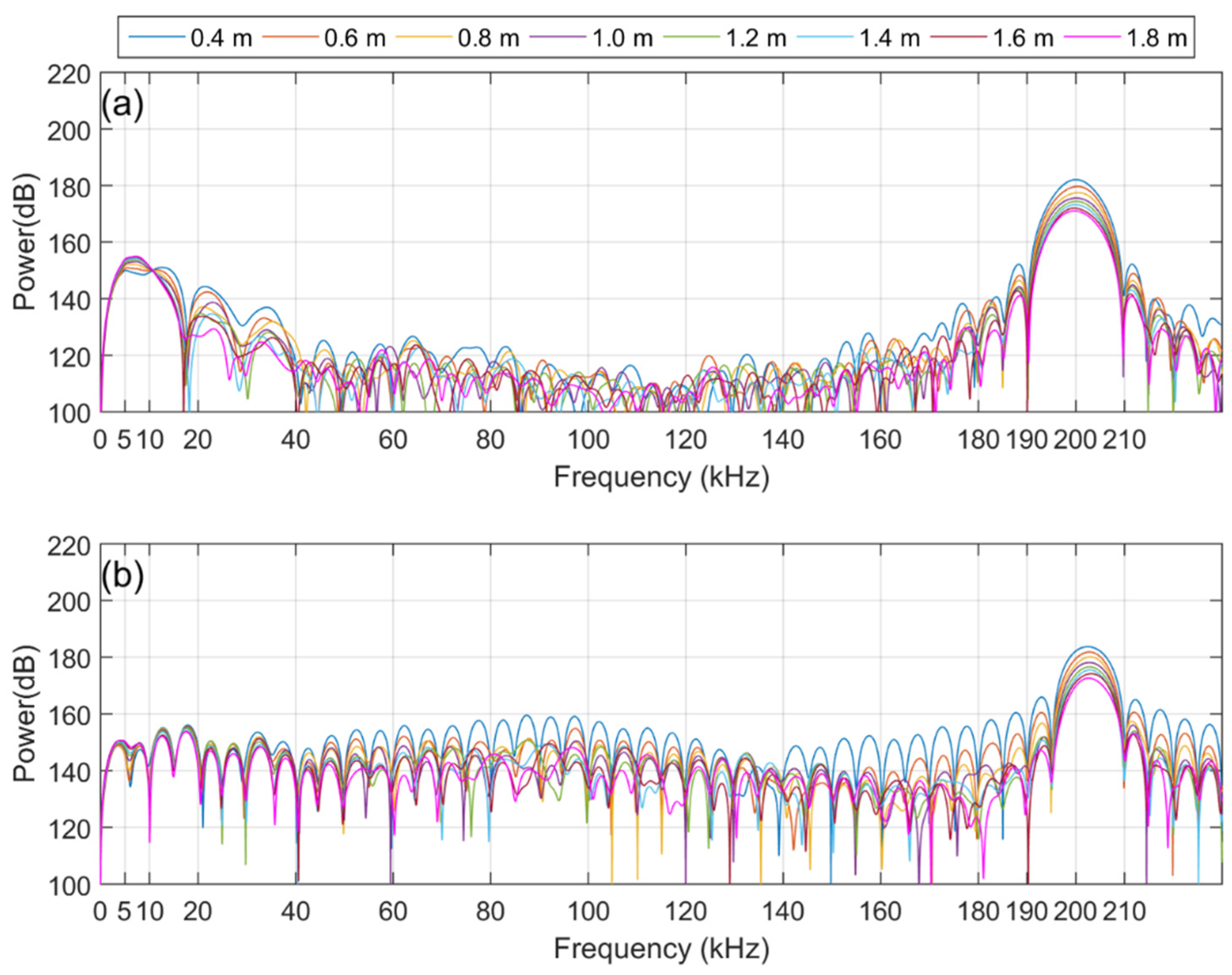
4. Results and Discussion
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Capps, R.N.; Weber, F.J. Handbook of sonar transducer passive materials. J. Acoust. Soc. Am. 1981, 70, 622–623. [Google Scholar] [CrossRef]
- Bobber, R.J. Underwater Electroacoustic Measurements; Peninsula Publishing: Newport Beach, CA, USA, 1988; ISBN 0932146198. [Google Scholar]
- Mikeska, E.E.; Behrens, J.A. Evaluation of transducer window materials. J. Acoust. Soc. Am. 1976, 59, 1294–1298. [Google Scholar] [CrossRef]
- Rudgers, A.J.; Solvold, C.A. Apparatus-independent acoustical-material characteristics obtained from panel-test measurements. J. Acoust. Soc. Am. 1984, 76, 926–934. [Google Scholar] [CrossRef]
- Jung, D. Experimental Investigation of Parametric Array for Low Frequency Measurement System of Acoustic Materials; Department of Ocean Engineering Graduate School of Korea Maritime and Ocean University: Busan, Korea, in press.
- Humphrey, V.F. The measurement of acoustic properties of limited size panels by use of a parametric source. J. Sound Vib. 1985, 98, 67–81. [Google Scholar] [CrossRef]
- Humphrey, V.F.; Robinson, S.P.; Smith, J.D.; Martin, M.J.; Beamiss, G.A.; Hayman, G.; Carroll, N.L. Acoustic characterization of panel materials under simulated ocean conditions using a parametric array source. J. Acoust. Soc. Am. 2008, 124, 803–814. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, V.F.; Berktay, H.O. The transmission coefficient of a panel measured with a parametric source. J. Sound Vib. 1985, 101, 85–106. [Google Scholar] [CrossRef]
- Kim, W.-H. A Consideration on the Results of Sound Field Measurement for the Parametric Array. In Proceedings of the Korean Society for Noise and Vibration Engineering Conference, Seoul, Korea, 26 April 2012; pp. 202–203. [Google Scholar]
- Merklinger, H.M. Improved efficiency in the parametric transmitting array. J. Acoust. Soc. Am. 1975, 58, 784–787. [Google Scholar] [CrossRef]
- Moffett, M.B.; Mello, P. Parametric Acoustic Sources Of Transient Signals. J. Acoust. Soc. Am. 1979, 66, 1182–1187. [Google Scholar] [CrossRef]
- Moffett, M.B.; Mellen, R.H. Effective lengths of parametric acoustic sources. J. Acoust. Soc. Am. 1981, 70, 1424–1426. [Google Scholar] [CrossRef]
- Ju, H.-S.; Kim, Y. Directional characteristics of parametric loudspeakers in near-field. In Proceedings of the Korean Society for Noise and Vibration Engineering Conference, Seoul, Korea, 1 November 2005; pp. 545–550. [Google Scholar]
- Rudenko, O.V.; Soluyan, S.I. Scattering of Sound By Sound. Sov. Phys. Acoust. 1973, 18, 352–355. [Google Scholar]
- Westervelt, P.J. Parametric Acoustic Array. J. Acoust. Soc. Am. 1963, 35, 535–537. [Google Scholar] [CrossRef]
- Berktay, H.O. Nonlinear Interaction of Two Sound Beams. J. Acoust. Soc. Am. 1965, 38, 480–481. [Google Scholar] [CrossRef]
- Naze, J.; Tjøtta, S. Nonlinear Interaction of Two Sound Beams. J. Acoust. Soc. Am. 1965, 37, 174–175. [Google Scholar] [CrossRef]
- Moffett, M.B.; Mellen, R.H. Model for parametric acoustic sources. J. Acoust. Soc. Am. 1977, 61, 325–337. [Google Scholar] [CrossRef]
- Moffett, M.B.; Konrad, W.L. Parametric acoustic source with an endfire primary projector. J. Acoust. Soc. Am. 1982, 72, 993–997. [Google Scholar] [CrossRef]
- Fenlon, F.H. On the performance of a dual frequency parametric source via matched asymptotic solutions of Burgers’ equation. J. Acoust. Soc. Am. 1974, 55, 35–46. [Google Scholar] [CrossRef]
- Rolleigh, R.L. Difference frequency pressure within the interaction region of a parametric array. J. Acoust. Soc. Am. 1975, 58, 964–971. [Google Scholar] [CrossRef]
- Pederson, T.B. A Parametric Sonar Performance Calculator. Le J. Phys. Colloq. 1979, 40, C8-137–C8-139. [Google Scholar] [CrossRef]
- Moffett, M.B.; Mellen, R.H. Nearfield characteristics of parametric acoustic sources. J. Acoust. Soc. Am. 1981, 69, 404–409. [Google Scholar] [CrossRef]
- Berktay, H.O.; Leahy, D.J. Farfield performance of parametric transmitters. J. Acoust. Soc. Am. 1974, 55, 539–546. [Google Scholar] [CrossRef]
- Berktay, H.O. Possible exploitation of non-linear acoustics in underwater transmitting applications. J. Sound Vib. 1965, 2, 435–461. [Google Scholar] [CrossRef]
- Zhou, H.; Huang, S.H.; Li, W. Parametric acoustic array and its application in underwater acoustic engineering. Sensors 2020, 20, 2148. [Google Scholar] [CrossRef] [Green Version]
- Pantea, C.; Osterhoudt, C.F.; Sinha, D.N. Determination of acoustical nonlinear parameter β of water using the finite amplitude method. Ultrasonics 2013, 53, 1012–1019. [Google Scholar] [CrossRef]
- Rolleigh, R.L. Analysis of the broadband parametric array with Gaussian primary directivity patterns. J. Acoust. Soc. Am. 1980, 68, 649–654. [Google Scholar] [CrossRef]
- Hatano, Y.; Shi, C.; Kinoshita, S.; Kajikawa, Y. Linearization of the parametric array loudspeaker upon varying input amplitudes. In Proceedings of the 2015 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Hong Kong, China, 16–19 December 2015. [Google Scholar]
- Shi, C.; Kajikawa, Y. Effect of the ultrasonic emitter on the distortion performance of the parametric array loudspeaker. Appl. Acoust. 2016, 112, 108–115. [Google Scholar] [CrossRef]
- Farias, F.; Abdulla, W. A method for selecting a proper modulation technique for the parametric acoustic array. J. Phys. Conf. Ser. 2018, 1075, 012035. [Google Scholar] [CrossRef]
- Szabo, J.P.; Bent, A.D. Reduction in edge effects for small panels characterized by a parametric array source. J. Acoust. Soc. Am. 2019, 145, 795–804. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, V.F. Laboratory applications of truncated parametric arrays. J. Acoust. Soc. Am. 2009, 125, 2689. [Google Scholar] [CrossRef]
- Pantea, C.; Sinha, D.N. Broad-band acoustic low frequency collimated beam for ultrasonic imaging. J. Acoust. Soc. Am. 2013, 133, 3423. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, D.; Song, J.; Kim, J.; Lee, J. Comparative Experimental Investigation on Optimal Parametric Array Types. Sensors 2021, 21, 5085. https://doi.org/10.3390/s21155085
Jung D, Song J, Kim J, Lee J. Comparative Experimental Investigation on Optimal Parametric Array Types. Sensors. 2021; 21(15):5085. https://doi.org/10.3390/s21155085
Chicago/Turabian StyleJung, Donghwan, Jiyoung Song, Jeasoo Kim, and Jaehyuk Lee. 2021. "Comparative Experimental Investigation on Optimal Parametric Array Types" Sensors 21, no. 15: 5085. https://doi.org/10.3390/s21155085
APA StyleJung, D., Song, J., Kim, J., & Lee, J. (2021). Comparative Experimental Investigation on Optimal Parametric Array Types. Sensors, 21(15), 5085. https://doi.org/10.3390/s21155085





