DC Voltage Sensorless Predictive Control of a High-Efficiency PFC Single-Phase Rectifier Based on the Versatile Buck-Boost Converter
Abstract
:1. Introduction
- An AC voltage sensor: is employed to detect the phase angle of the source voltage, which is then used to generate the unitary sine current reference for the power factor control;
- A DC voltage sensor: is used to regulate the converter output voltage and provide load overvoltage protection;
- A DC current sensor: is utilized to achieve closed-loop power factor control, DC voltage regulation, and overcurrent protection to the load.
- Increase of the complexity and cost of the control circuit that is a problem for applications with very stringent cost and space requirements.
- Reduction of the power converter reliability.
- Increase in noise coupling and grounding issues of mixed-signal printed circuit board (PCB) from the connection between the power converter and the controller.
- A novel PFC single-phase rectifier based on the VBB converter is presented. Its many advantages tested in DC-DC applications are now meant to be proved in an AC-DC PFC application.
- A high-reliability is obtained by reducing the number of sensors, as critical components in reliability of the converter [33]. This reliability improvement does not compromise the control performance [34]. The ideal voltage conversion ratio of the proposed rectifier converter is used to estimate the DC output voltage. In this way, the controller senses only input variables (DC current and AC voltage), which reduce the noise coupling between the converter input and output terminals.
- A high-efficiency converter topology operating as PFC single-phase rectifier is achieved. Its power conversion efficiency is compared with other classical PFC rectifiers as the SEPIC and the noninverting buck-boost converter.
- A converter topology with a wide bandwidth and, consequently, with fast control loops, is proposed. The design of two nested control loops corresponds to a predictive-based current controller (inner loop for the DC input current) and a proportional-integral (PI) voltage controller (outer loop for the DC output voltage). These controllers operate along with output voltage estimation and grid-synchronising phase-locked loop (PLL) running in a low-cost microcontroller. Each of the proposed controllers ensure fast-tracking of the control set-points, and low steady-state error under demanding tests that include changes in the output voltage reference and the resistive load.
2. Modeling of DC-DC Buck-Boost Converters
2.1. SEPIC Converter
2.2. Noninverting Buck-Boost Converter (BB)
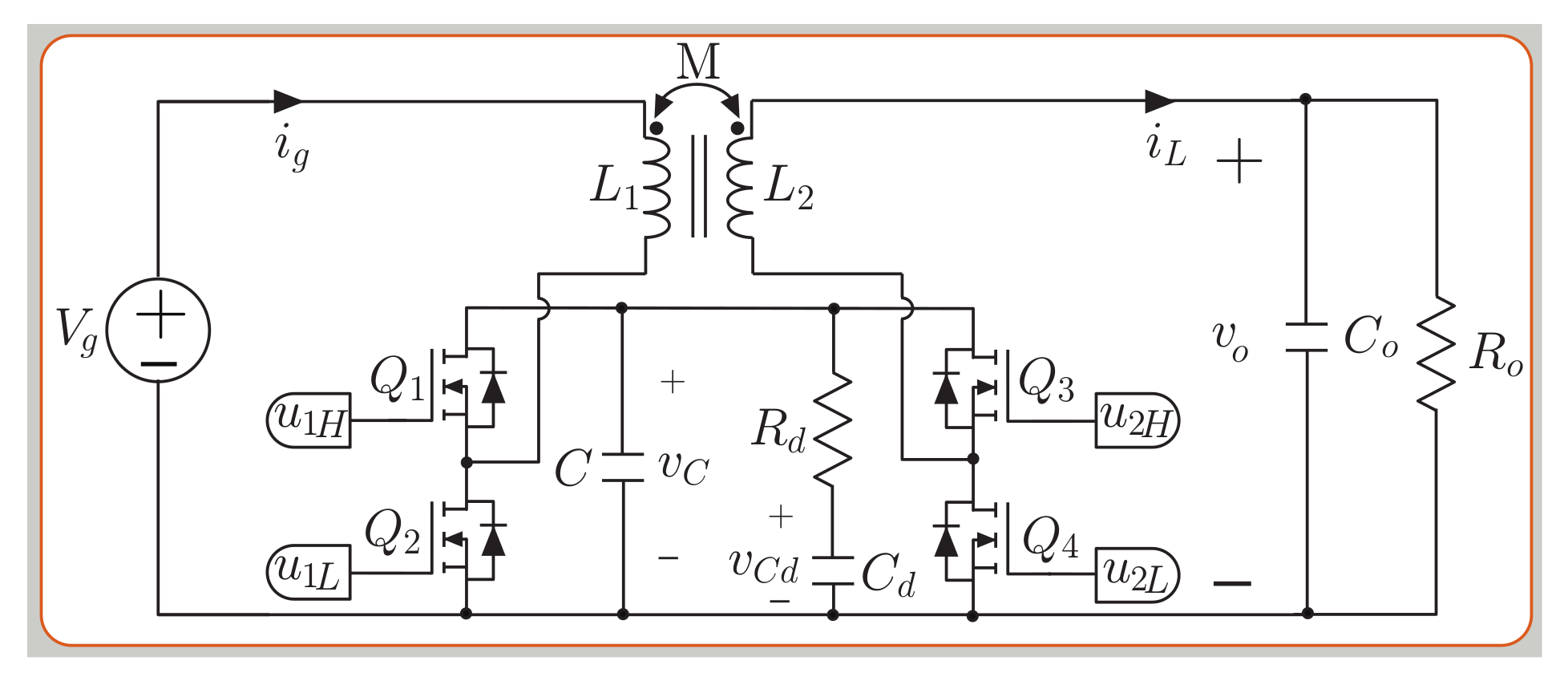
2.3. Versatile Buck-Boost Converter (VBB)
3. Power Losses Methods
3.1. Electro-Thermal Model
3.2. Power Inductor Losses Calculation
4. Voltage-Sensorless Predictive Controller for a Single Phase AC-DC Converter
4.1. Proportional-Integral Voltage Controller
4.2. Predictive Digital Current Programmed Control
5. Simulation and Real-Time HIL Results
5.1. Efficiency Results
5.2. Experimental Results
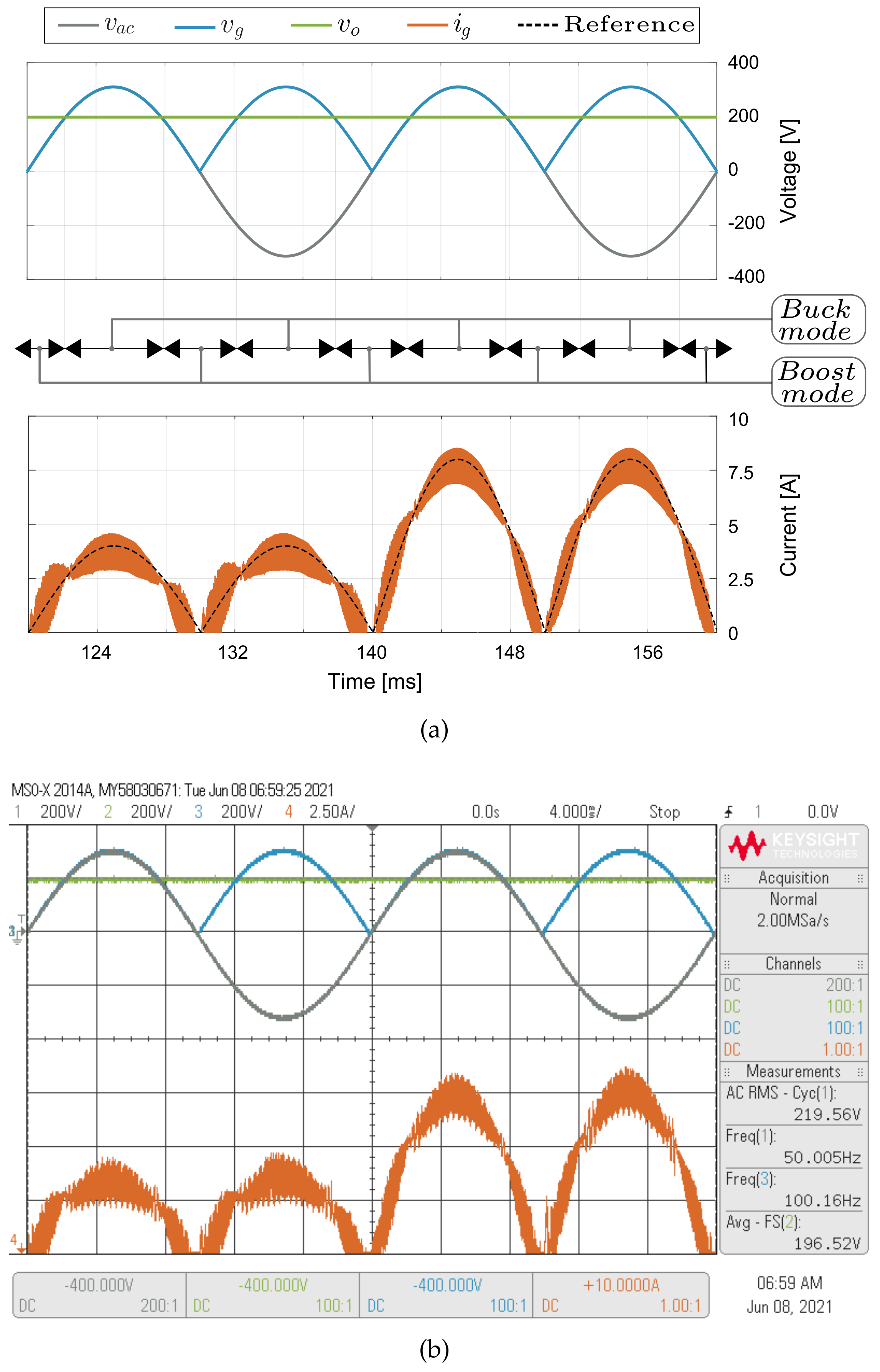
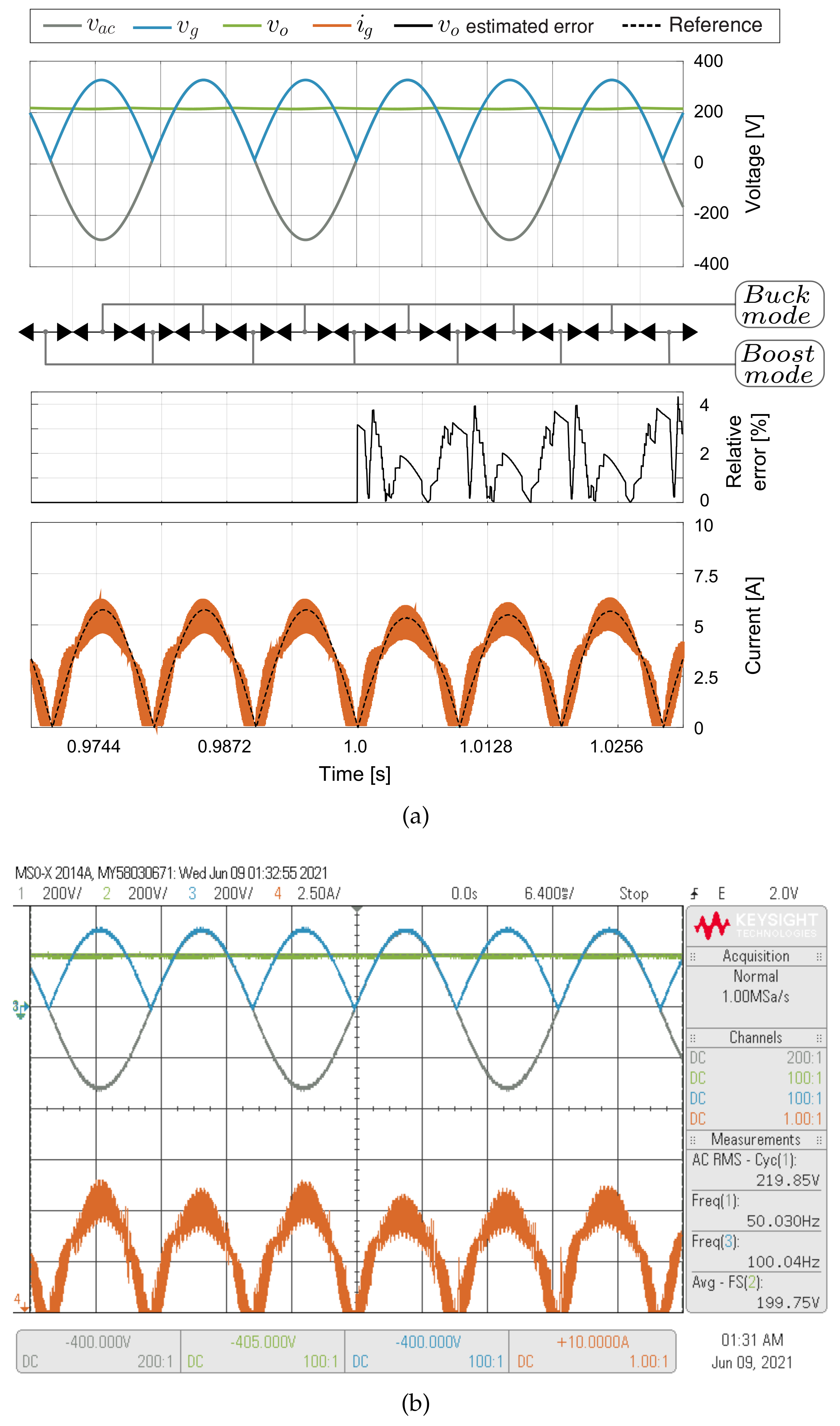
5.3. Inner Loop Current Control Results
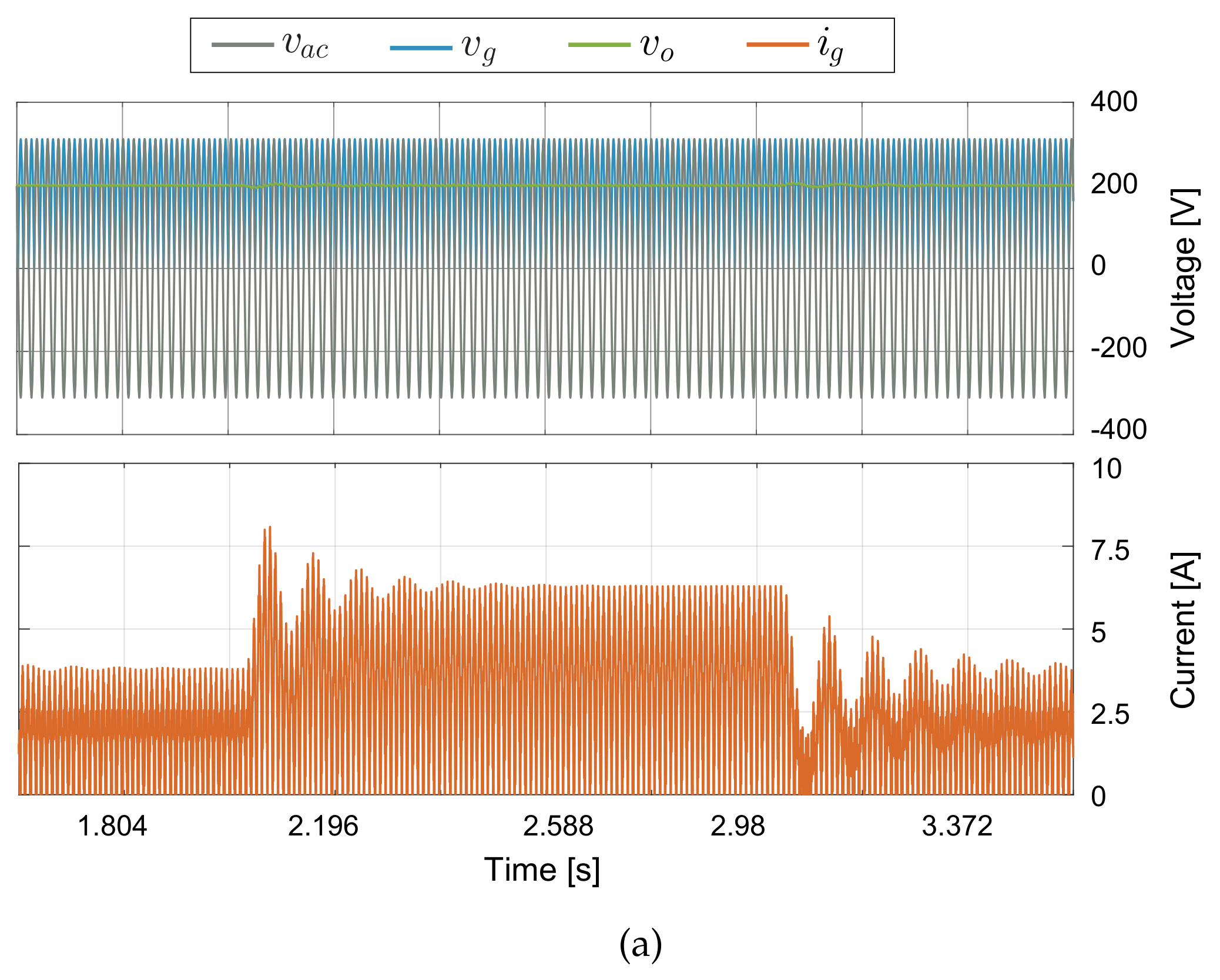
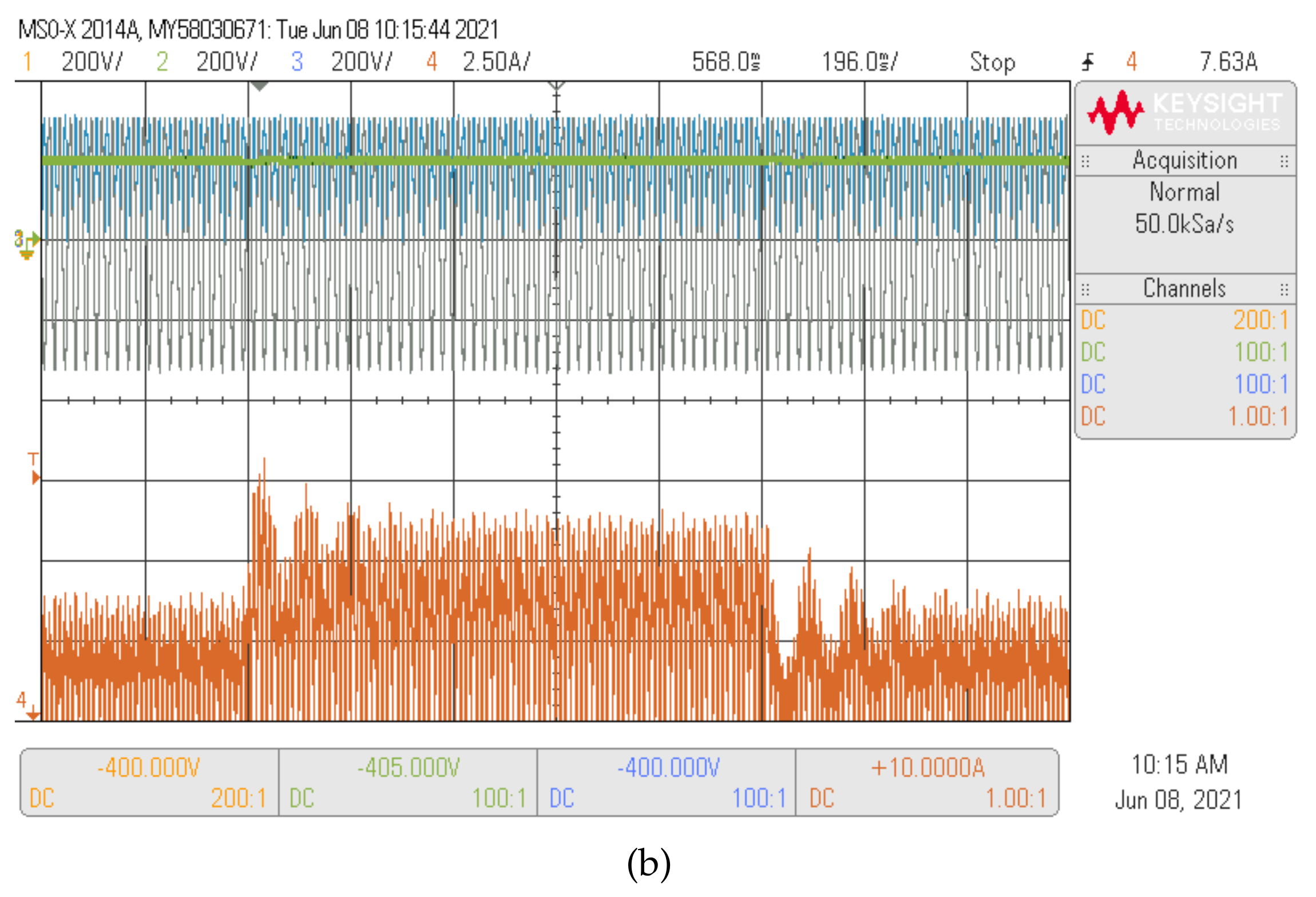
5.4. DC Voltage Sensorless Control Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, D.; Wang, B.; Zhang, G.; Wang, G.; Yu, Y. A review of sensorless control methods for AC motor drives. CES Trans. Electr. Mach. Syst. 2018, 2, 104–115. [Google Scholar] [CrossRef]
- Yin, Z.; Gao, F.; Zhang, Y.; Du, C.; Li, G.; Sun, X. A review of nonlinear Kalman filter appling to sensorless control for AC motor drives. CES Trans. Electr. Mach. Syst. 2019, 3, 351–362. [Google Scholar] [CrossRef]
- Wang, G.; Valla, M.; Solsona, J. Position Sensorless Permanent Magnet Synchronous Machine Drives—A Review. IEEE Trans. Ind. Electron. 2020, 67, 5830–5842. [Google Scholar] [CrossRef]
- Li, Y.; Wu, H.; Xu, X.; Sun, X.; Zhao, J. Rotor position estimation approaches for sensorless control of permanent magnet traction motor in electric vehicles: A review. World Electr. Veh. J. 2021, 12, 9. [Google Scholar] [CrossRef]
- Liang, C.M.; Lin, Y.J.; Chen, J.Y.; Chen, G.R.; Yang, S.C. Sensorless LC Filter Implementation for Permanent Magnet Machine Drive Using Observer-Based Voltage and Current Estimation. Sensors 2021, 21, 3596. [Google Scholar] [CrossRef]
- Yan, Y.; Yang, M.; Yang, T.; Ye, S.; Jiang, W. Speed Sensorless Control of Linear Ultrasonic Motors Based on Stator Vibration Amplitude Compensation. Sensors 2020, 20, 6705. [Google Scholar] [CrossRef]
- Kim, G.; Hirata, K. Motion Control of a Two-Degree-of-Freedom Linear Resonant Actuator without a Mechanical Spring. Sensors 2020, 20, 1954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Urbanski, K.; Janiszewski, D. Sensorless Control of the Permanent Magnet Synchronous Motor. Sensors 2019, 19, 3546. [Google Scholar] [CrossRef] [Green Version]
- Gutierrez-Villalobos, J.M.; Rodriguez-Resendiz, J.; Rivas-Araiza, E.A.; Martínez-Hernández, M.A. Sensorless FOC Performance Improved with On-Line Speed and Rotor Resistance Estimator Based on an Artificial Neural Network for an Induction Motor Drive. Sensors 2015, 15, 15311–15325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S.Y.; Tseng, C.L.; Lin, S.C.; Chiu, C.J.; Chou, J.H. An Adaptive Supervisory Sliding Fuzzy Cerebellar Model Articulation Controller for Sensorless Vector-Controlled Induction Motor Drive Systems. Sensors 2015, 15, 7323–7348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gamazo-Real, J.C.; Vázquez-Sánchez, E.; Gómez-Gil, J. Position and Speed Control of Brushless DC Motors Using Sensorless Techniques and Application Trends. Sensors 2010, 10, 6901–6947. [Google Scholar] [CrossRef] [Green Version]
- López, F.; López-Martín, V.M.; Azcondo, F.J.; Corradini, L.; Pigazo, A. Current-Sensorless Power Factor Correction With Predictive Controllers. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 891–900. [Google Scholar] [CrossRef]
- Ohnishi, T.; Hojo, M. DC voltage sensorless single-phase PFC converter. IEEE Trans. Power Electron. 2004, 19, 404–410. [Google Scholar] [CrossRef]
- Yip, S.; Qiu, D.; Chung, H.S.H.; Hui, S. A novel voltage sensorless control technique for a bidirectional AC/DC converter. IEEE Trans. Power Electron. 2003, 18, 1346–1355. [Google Scholar] [CrossRef]
- Qi, W.; Li, S.; Tan, S.C.; Hui, S.Y. Design Considerations for Voltage Sensorless Control of a PFC Single-Phase Rectifier Without Electrolytic Capacitors. IEEE Trans. Ind. Electron. 2020, 67, 1878–1889. [Google Scholar] [CrossRef]
- Wang, Y.; de Haan, S.W.H.; Ferreira, J.A. Potential of Improving PWM Converter Power Density with Advanced Components. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Rodríguez, M.; Rodríguez, A.; Miaja, P.F.; Lamar, D.G.; Zúniga, J.S. An Insight into the Switching Process of Power MOSFETs: An Improved Analytical Losses Model. IEEE Trans. Power Electron. 2010, 25, 1626–1640. [Google Scholar] [CrossRef]
- Hartmann, M.; Ertl, H.; Kolar, J.W. On the Tradeoff Between Input Current Quality and Efficiency of High Switching Frequency PWM Rectifiers. IEEE Trans. Power Electron. 2012, 27, 3137–3149. [Google Scholar] [CrossRef]
- Stupar, A.; Friedli, T.; Minibock, J.; Kolar, J.W. Towards a 99% Efficient Three-Phase Buck-Type PFC Rectifier for 400-V DC Distribution Systems. IEEE Trans. Power Electron. 2012, 27, 1732–1744. [Google Scholar] [CrossRef]
- Qi, W.; Li, S.; Yuan, H.; Tan, S.C.; Hui, S.Y. High-Power-Density Single-Phase Three-Level Flying-Capacitor Buck PFC Rectifier. IEEE Trans. Power Electron. 2019, 34, 10833–10844. [Google Scholar] [CrossRef]
- Abdel-Rahman, S.; Stückler, F.; Siu, K. PFC Boost Converter Design Guide; Infineon Application Note; Infineon Technologies AG: Munich, Germany, 2016; Volume 2. [Google Scholar]
- Baek, J.; Park, M.H.; Kim, T.; Youn, H.S. Modified Power Factor Correction (PFC) Control and Printed Circuit Board (PCB) Design for High-Efficiency and High-Power Density On-Board Charger. Energies 2021, 14, 605. [Google Scholar] [CrossRef]
- Restrepo, C.; Calvente, J.; Cid-Pastor, A.; Aroudi, A.E.; Giral, R. A Noninverting Buck–Boost DC–DC Switching Converter with High Efficiency and Wide Bandwidth. IEEE Trans. Power Electron. 2011, 26, 2490–2503. [Google Scholar] [CrossRef]
- Restrepo, C.; Calvente, J.; Romero, A.; Vidal-Idiarte, E.; Giral, R. Current-Mode Control of a Coupled-Inductor Buck–Boost DC–DC Switching Converter. IEEE Trans. Power Electron. 2012, 27, 2536–2549. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Calvente, J.; Milanovic, M.; Giral, R. Fast Transitions Between Current Control Loops of the Coupled-Inductor Buck–Boost DC–DC Switching Converter. IEEE Trans. Power Electron. 2013, 28, 3648–3652. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Member, S.; Calvente, J.; Giral, R.; Member, S. Hysteretic transition method for avoiding the dead-zone effect and subharmonics in a non-inverting buck-boost converter. IEEE Trans. Power Electron. 2014, 30, 3418–3430. [Google Scholar] [CrossRef] [Green Version]
- Ordono, A.; Unamuno, E.; Barrena, J.A.; Paniagua, J. Interlinking converters and their contribution to primary regulation: A review. Int. J. Electr. Power Energy Syst. 2019, 111, 44–57. [Google Scholar] [CrossRef]
- Meenadevi, R.; Premalatha, L. A novel bridgeless SEPIC converter for power factor correction. Energy Procedia 2017, 117, 991–998. [Google Scholar] [CrossRef]
- Jassim, B.M. SEPIC AC-DC Converter for Aircraft Application. In Proceedings of the MELECON 2014–2014 17th IEEE Mediterranean Electrotechnical Conference, Beirut, Lebanon, 13–16 April 2014; pp. 12–16. [Google Scholar]
- Rosa, A.H.; De Souza, T.M.; Morais, L.M.; Seleme, S.I. Adaptive and nonlinear control techniques applied to sepic converter in DC-DC, pfc, ccm and dcm modes using hil simulation. Energies 2018, 11, 602. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.Y.; Chen, H.C. A comparison study of boost and Buck-boost power factor corrector for ultra-wide input voltage range applications. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 2719–2726. [Google Scholar]
- Chandran, C.; Chandran, L.R. Two switch buck boost converter for power factor correction. In Proceedings of the 2015 International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 24–26 June 2015; pp. 454–459. [Google Scholar]
- Bae, S.; Kim, M. Effect of Sensors on the Reliability and Control Performance of Power Circuits in the Web of Things (WoT). Sensors 2016, 16, 1430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adinolfi, G.; Graditi, G. Reliability Prediction of Smart Maximum Power Point Converter for PV Applications. In System Reliability; InTech: London, UK, 2017. [Google Scholar] [CrossRef] [Green Version]
- Song, Q.; Wang, L.; Chen, J. A Decentralized Energy Management Strategy for a Fuel Cell–Battery Hybrid Electric Vehicle Based on Composite Control. IEEE Trans. Ind. Electron. 2021, 68, 5486–5496. [Google Scholar] [CrossRef]
- Mishra, P.; Pradhan, A.K.; Bajpai, P. Adaptive Distance Relaying for Distribution Lines Connecting Inverter-Interfaced Solar PV Plant. IEEE Trans. Ind. Electron. 2021, 68, 2300–2309. [Google Scholar] [CrossRef]
- Khalghani, M.R.; Solanki, J.; Solanki, S.K.; Khooban, M.H.; Sargolzaei, A. Resilient Frequency Control Design for Microgrids Under False Data Injection. IEEE Trans. Ind. Electron. 2021, 68, 2151–2162. [Google Scholar] [CrossRef]
- Xu, Y.; Nian, H.; Chen, L. Small-Signal Modeling and Analysis of DC-Link Dynamics in Type-IV Wind Turbine System. IEEE Trans. Ind. Electron. 2021, 68, 1423–1433. [Google Scholar] [CrossRef]
- He, H.; Quan, S.; Sun, F.; Wang, Y. Model Predictive Control With Lifetime Constraints Based Energy Management Strategy for Proton Exchange Membrane Fuel Cell Hybrid Power Systems. IEEE Trans. Ind. Electron. 2020, 67, 9012–9023. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Q.; Williams, H.; Xu, H. Back-to-Back Competitive Learning Mechanism for Fuzzy Logic Based Supervisory Control System of Hybrid Electric Vehicles. IEEE Trans. Ind. Electron. 2020, 67, 8900–8909. [Google Scholar] [CrossRef]
- Liu, C.; Bai, H.; Zhuo, S.; Zhang, X.; Ma, R.; Gao, F. Real-Time Simulation of Power Electronic Systems Based on Predictive Behavior. IEEE Trans. Ind. Electron. 2020, 67, 8044–8053. [Google Scholar] [CrossRef]
- Ling, Y.; Li, Y.; Xiang, J. Load Support by Droop-controlled Distributed Generations. IEEE Trans. Ind. Electron. 2021, 68, 8345–8355. [Google Scholar] [CrossRef]
- Hren, A.; Slibar, P. Full order dynamic model of SEPIC converter. In Proceedings of the IEEE International Symposium on Industrial Electronics, ISIE 2005, Dubrovnik, Croatia, 20–23 June 2005; Volume 2, pp. 553–558. [Google Scholar]
- Chang, C.W.; Wei, C.L. Single-inductor four-switch non-inverting buck-boost dc-dc converter. In Proceedings of the 2011 International Symposium on VLSI Design, Automation and Test, Hsinchu, Taiwan, 25–28 April 2011; pp. 1–4. [Google Scholar]
- Mendez-Diaz, F.; Pico, B.; Vidal-Idiarte, E.; Calvente, J.; Giral, R. HM/PWM Seamless Control of a Bidirectional Buck–Boost Converter for a Photovoltaic Application. IEEE Trans. Power Electron. 2019, 34, 2887–2899. [Google Scholar] [CrossRef]
- González-Castaño, C.; Restrepo, C.; Giral, R.; García-Amoros, J.; Vidal-Idiarte, E.; Calvente, J. Coupled inductors design of the bidirectional non-inverting buck–boost converter for high-voltage applications. IET Power Electron. 2020, 13, 3188–3198. [Google Scholar] [CrossRef]
- Górecki, P.; Wojciechowski, D. Accurate Computation of IGBT Junction Temperature in PLECS. IEEE Trans. Electron. Dev. 2020, 67, 2865–2871. [Google Scholar] [CrossRef]
- Imaoka, J.; Okamoto, K.; Shoyama, M.; Ishikura, Y.; Noah, M.; Yamamoto, M. Modeling, magnetic design, simulation methods, and experimental evaluation of various powder cores used in power converters considering their DC superimposition characteristics. IEEE Trans. Power Electron. 2018, 34, 9033–9051. [Google Scholar] [CrossRef]
- Kazimierczuk, M.K. High-Frequency Magnetic Components; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 29. [Google Scholar]
- Corradini, L.; Maksimovic, D.; Mattavelli, P.; Zane, R. Digital Control of High-Frequency Switched-Mode Power Converters; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Calvente, J.; Ramirez-Murillo, H.; Vidal-Idiarte, E.; Giral, R.; Restrepo, C. Multisampled average current control of switching power converters. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 2120–2124. [Google Scholar]
- Chen, J.; Prodic, A.; Erickson, R.W.; Maksimovic, D. Predictive digital current programmed control. IEEE Trans. Power Electron. 2003, 18, 411–419. [Google Scholar] [CrossRef] [Green Version]
- Restrepo, C.; Konjedic, T.; Flores-Bahamonde, F.; Vidal-Idiarte, E.; Calvente, J.; Giral, R. Multisampled digital average current controls of the versatile buck–boost converter. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 879–890. [Google Scholar] [CrossRef]
- Patiño, C.R. Pem Fuel Cell Modeling and Converters Design for a 48 vs. dc Power Bus. Ph.D. Thesis, Universitat Rovira i Virgili, Tarragona, Spain, 2012. [Google Scholar]
- Jackiewicz, D.; Kachniarz, M.; Bieńkowski, A. Temperature Influence on the Functional Properties of Inductive Components with Mn–Zn Ferrite Cores. In Proceedings of the International Conference on Oxide Materials for Electronic Engineering, Lviv, Ukraine, 29 May–2 June 2017; Volume 59. [Google Scholar]







| BB Converter | Buck Mode | Boost Mode | ||
|---|---|---|---|---|
| VBB Converter | Buck Mode | Boost Mode | ||
| Parameter | Value or Type |
|---|---|
| Input voltage Vg | 0–400 V |
| Output voltage Vo | 100–400 V |
| Rated Power | 3.2 kW |
| Switching frequency fs | 100 kHz |
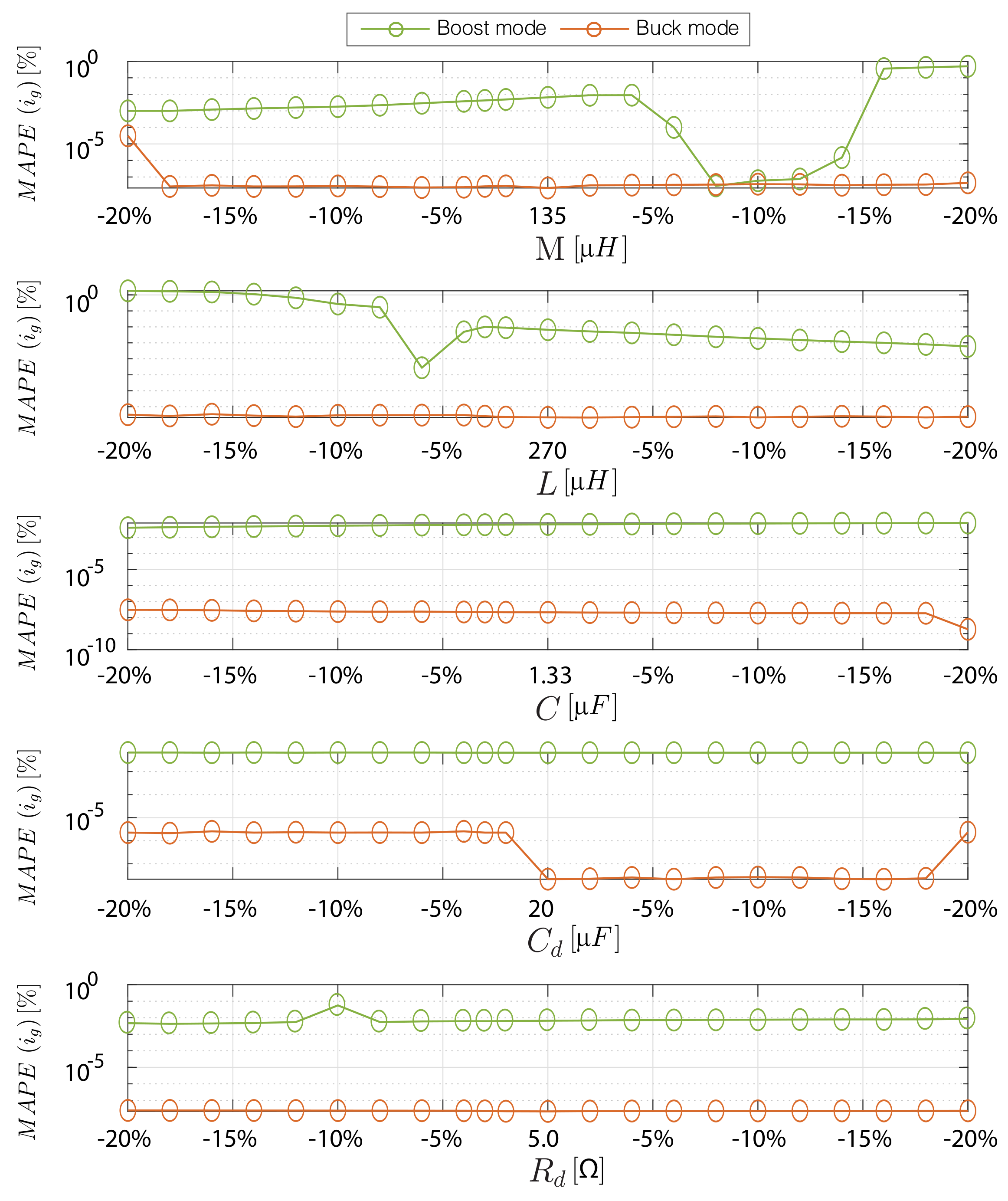
| Output capacitor Co | 28 μF |
| Damping capacitor Cd | 20 μF |
| Intermediate capacitor C | 1.32 μF |
| Coupled inductor | M = 135 μH and L = 270 μH |
| Damping resistance Rd | 5 Ω |
| SEPIC | ||
|---|---|---|
| converter | ||
| BB converter | ||
| Buck | ||
| Boost | ||
| VBB converter | ||
| Buck | ||
| Boost |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Castaño, C.; Restrepo, C.; Sanz, F.; Chub, A.; Giral, R. DC Voltage Sensorless Predictive Control of a High-Efficiency PFC Single-Phase Rectifier Based on the Versatile Buck-Boost Converter. Sensors 2021, 21, 5107. https://doi.org/10.3390/s21155107
González-Castaño C, Restrepo C, Sanz F, Chub A, Giral R. DC Voltage Sensorless Predictive Control of a High-Efficiency PFC Single-Phase Rectifier Based on the Versatile Buck-Boost Converter. Sensors. 2021; 21(15):5107. https://doi.org/10.3390/s21155107
Chicago/Turabian StyleGonzález-Castaño, Catalina, Carlos Restrepo, Fredy Sanz, Andrii Chub, and Roberto Giral. 2021. "DC Voltage Sensorless Predictive Control of a High-Efficiency PFC Single-Phase Rectifier Based on the Versatile Buck-Boost Converter" Sensors 21, no. 15: 5107. https://doi.org/10.3390/s21155107
APA StyleGonzález-Castaño, C., Restrepo, C., Sanz, F., Chub, A., & Giral, R. (2021). DC Voltage Sensorless Predictive Control of a High-Efficiency PFC Single-Phase Rectifier Based on the Versatile Buck-Boost Converter. Sensors, 21(15), 5107. https://doi.org/10.3390/s21155107








