Novel Road Traffic Management Strategy for Rapid Clarification of the Emergency Vehicle Route Based on V2V Communications
Abstract
:1. Introduction
- The proposed approach allows the emergency vehicles to communicate with the nearest vehicle in the crowded area to effectively send an emergency message to other vehicles, containing the information that there is an emergency vehicle on its way. Upon receiving this information, all the vehicles on the road will change their paths and clear the path for the oncoming emergency vehicle.
- The proposed approach developed an efficient method to enhance transmission efficiency and system reliability, and reduce the travel time of the emergency vehicles to drive safely to their destination, which saves people’s lives. This can be achieved by finding the nearest vehicles to communicate with and efficiently relay messages to the other vehicles on the road.
- An optimization problem to ascertain that the communication among all the vehicles is reliable, and to achieve the required system QoS was formulated.
- The proposed technique was evaluated in terms of packet delivery ratio, average end-to-end delay, and travel time under different conditions, such as differing transmission power, channel conditions (path loss exponent), and interference due to the other transmission sources. The interference can be, for example, from vehicles or devices, vehicle mobility, vehicle density, and vehicle speed. These findings can optimize the system performance for the whole network in a vibrant environment.
2. Literature Review
3. Proposed Model and Problem Formulation
3.1. System Model
3.2. Problem Formulation
s.t. C1: {pout ≤ poutmax}
C2: {Pv ≤ Pvmax}
3.3. Vehicle Communication Scenario
3.3.1. First Stage
3.3.2. Second Stage
- ,
- , and
| Algorithm 1: Finding the nearest vehicle with which to communicate |
| Input: Number of vehicles in the transmission area (V), emergency vehicle position, emergency vheicle transmisson power (PE), channel fade coefficient (hEVN), different interfence devices, interference transmission power (PD, PC, Pvi), interference channel fade coefficient (hDVN, hCVN, hVVN), channel noise (N), the required outage probability (poutEVN), and the path loss exponent (α) Output: Finding the nearest vehicle with which to communicate 1: Establish the required poutEVN 2: for different values of PE, PD, PC, Pv, hEVN, hDVN, hCVN, hVVN, α do 3: Determine the nearest receiving vehicle using 4: Send emergency message to the nearest receiver directly 5: end for |
| Algorithm 2: System performance evaluation |
| Input: Number of lanes (L), initial number of vehicles (ni) in each lane lane, emergency vehicle position, emergency vehicle transmisson power (PE), vehicle transmisson power (Pv), channel fade coefficient (hEVN, hVNV1), different interfence devices, interference transmission power (PD, PC, Pvi), interference channel fade coefficient (hDV1, hCV1, hVV1), channel noise (N), path loss exponent (α), and the initial vehicle velocity (vi) Output: PDR, E2E, v, number of vehicles in each lane (n), poutLi, Pv 1: Establish the required 2: Establish L, ni, vi 3: for different values of PE, PD, PC, Pv, hEVN, hDVN, hCVN, hVVN, α, v, N do 4: Calculate the velocity of the vehicles in each lane after receiving the emergency message ; 5: Calculate required number of vehicles in each lane 6: Construct the Lagrange function 7: Calculate the partial derivatives ,, and 8: Let , , 9: Determine 𝛌, μ, poutLi, Pv 10: Calculate PDR 11: Calculate E2E 12: end for |
- 4
- Packet delivery ratio (PDR): This is the ratio of the successful number of packets received by the destinations to the total number of the packets sent by the source. The system is considered reliable and efficient when the value of PDR increases. Thus, PDR can be given as [37]:
- 5
- Average end-to-end delay (E2E): The average end-to-end delay can be defined as the total time needed to successfully receive the transmitted packets over a network. The average end-to-end delay can be measured as the sum of the amount of time spent from sending a packet until it reaches its destination over the total number of packets received by the destination [37]:
4. Numerical Results and Discussion
4.1. Introduction
4.2. Software Tools
4.3. Investigated Case Parameters
4.4. Results Discussion
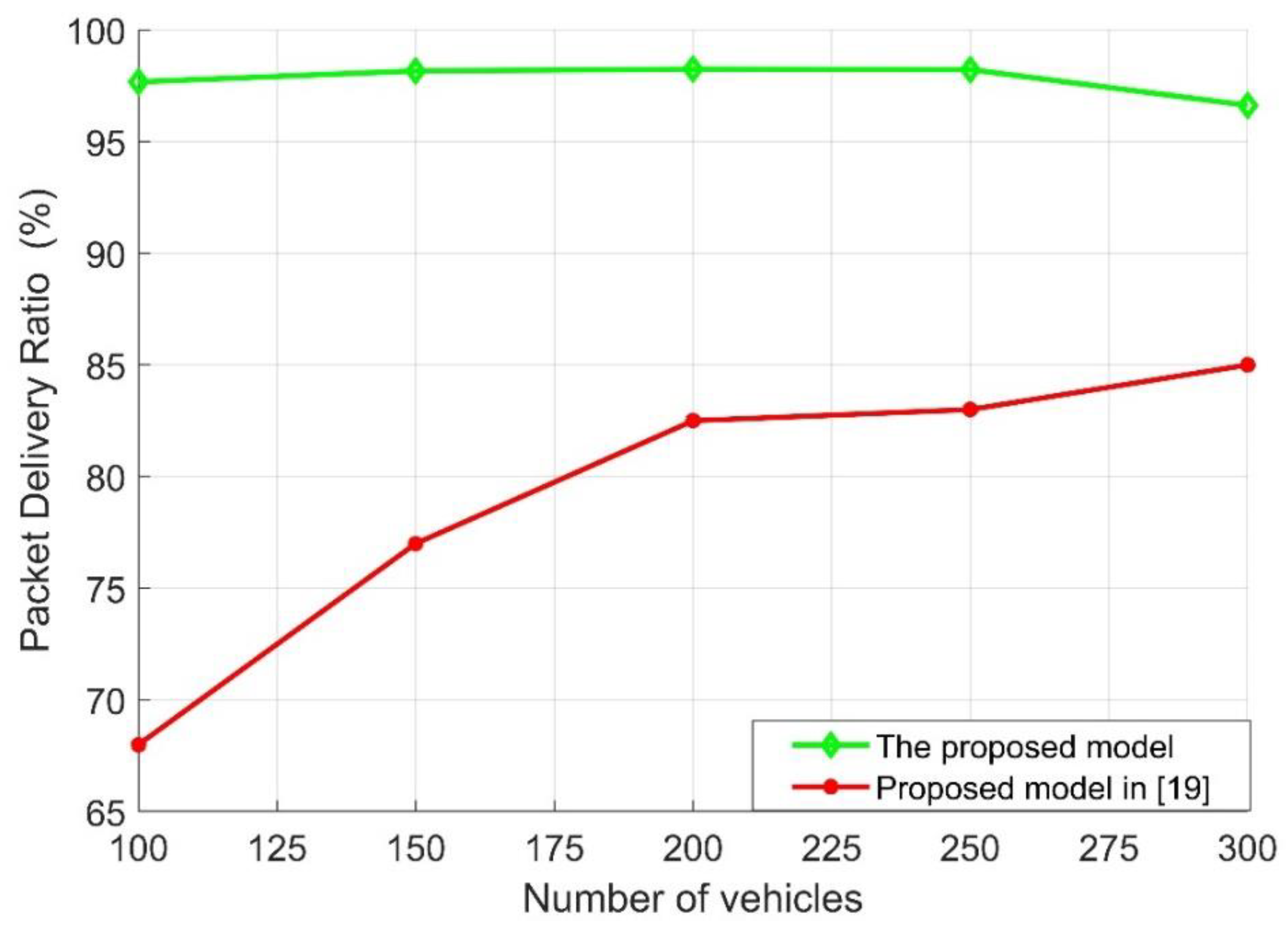
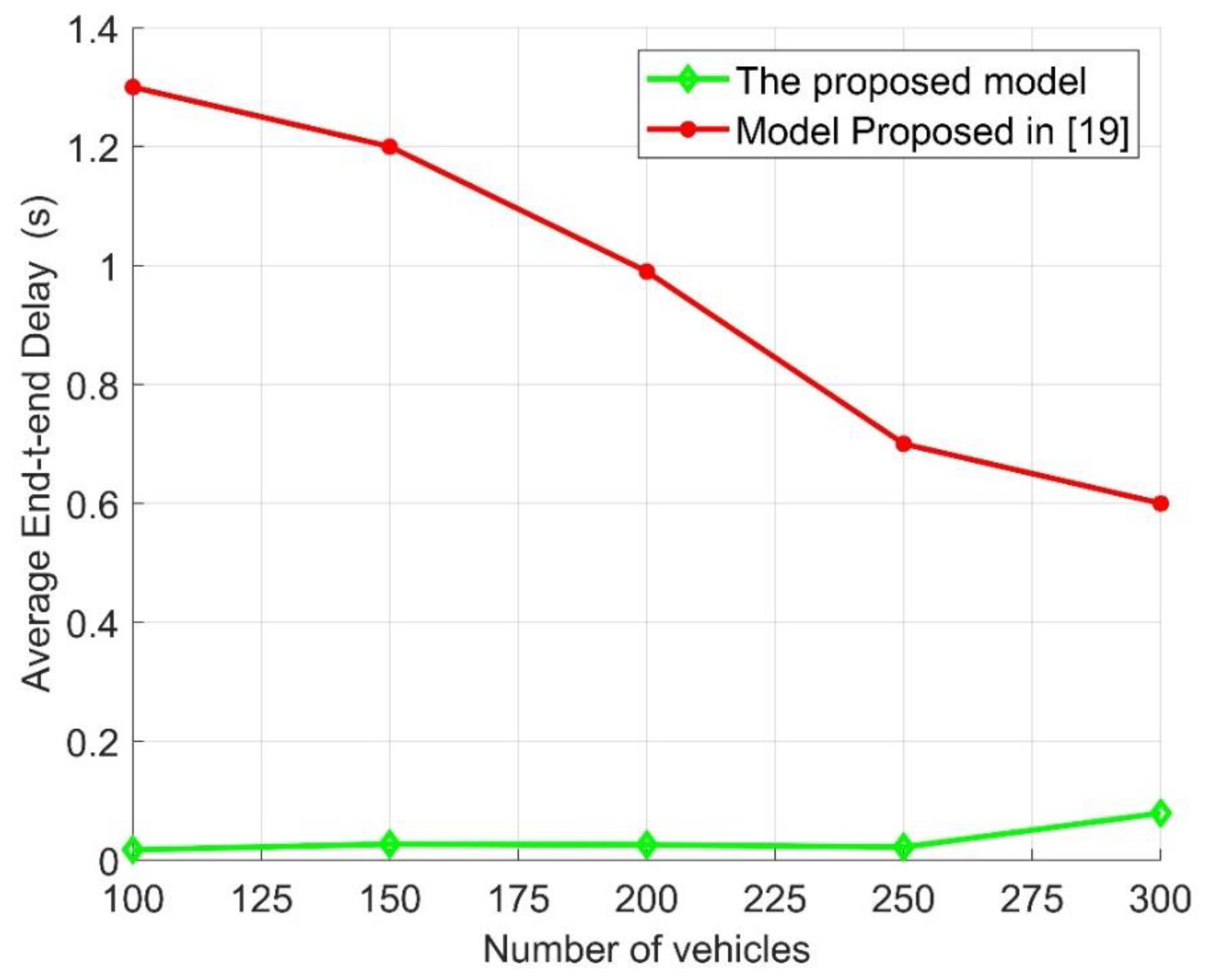
4.5. Comparative Analysis
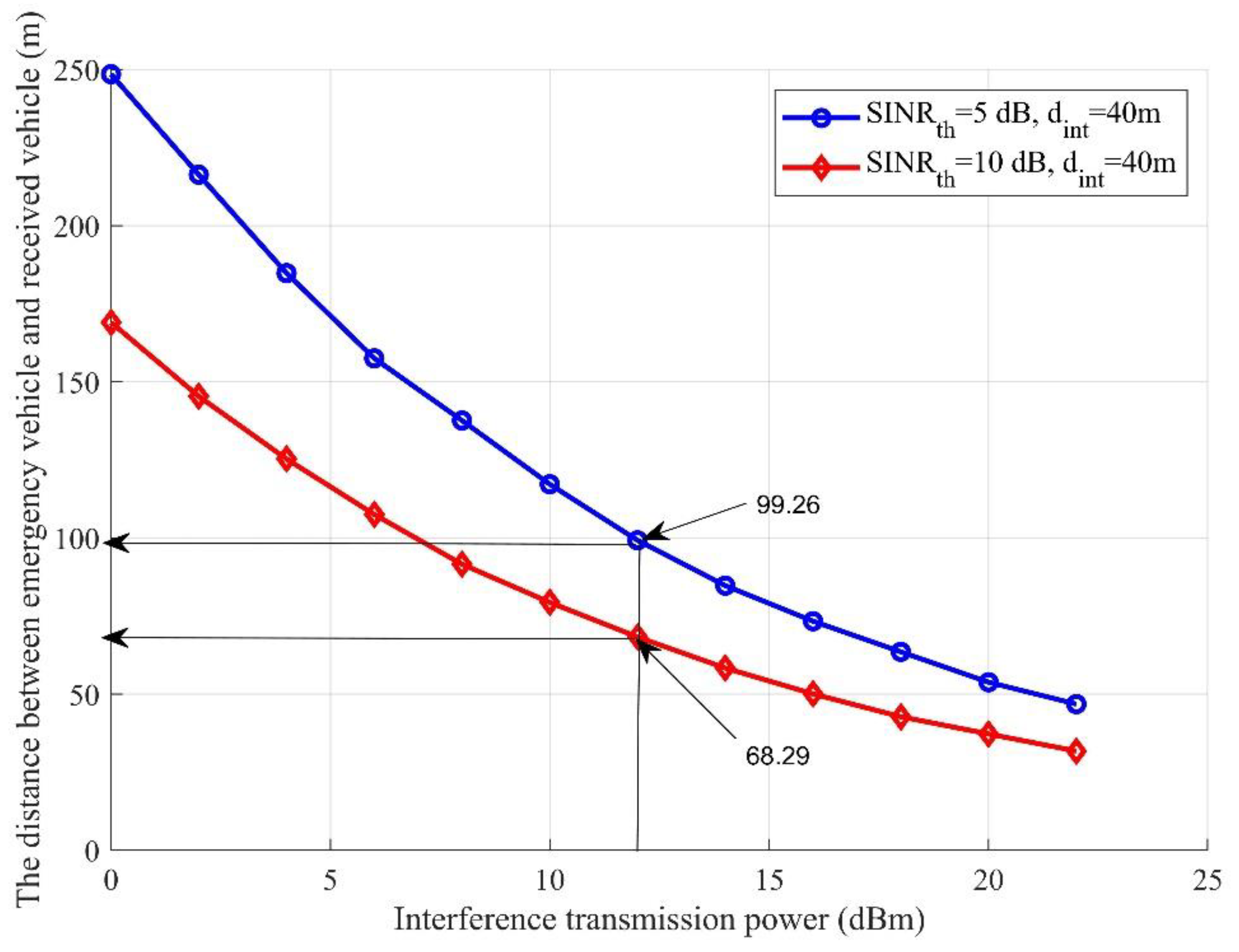
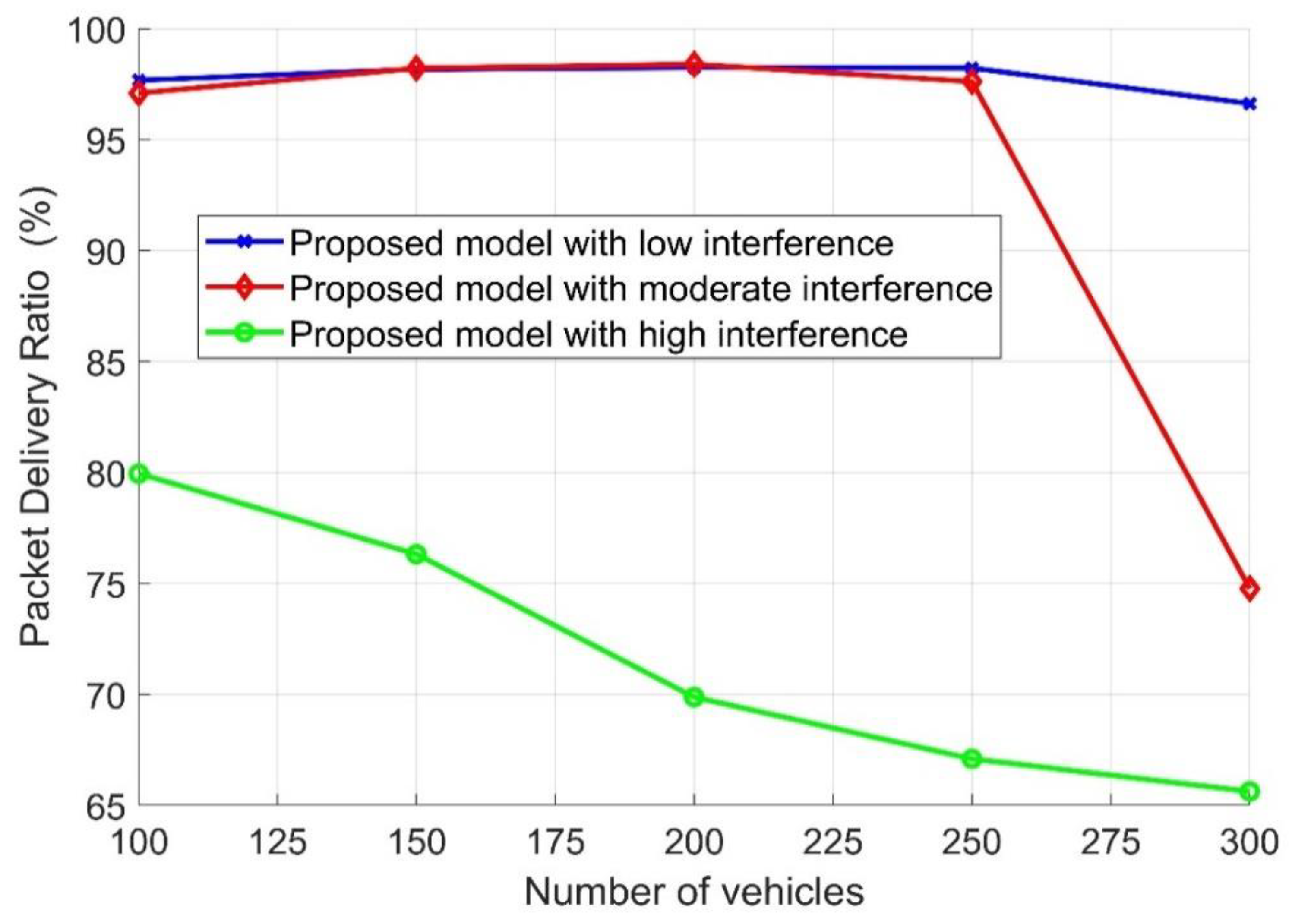
4.6. Interference Effect
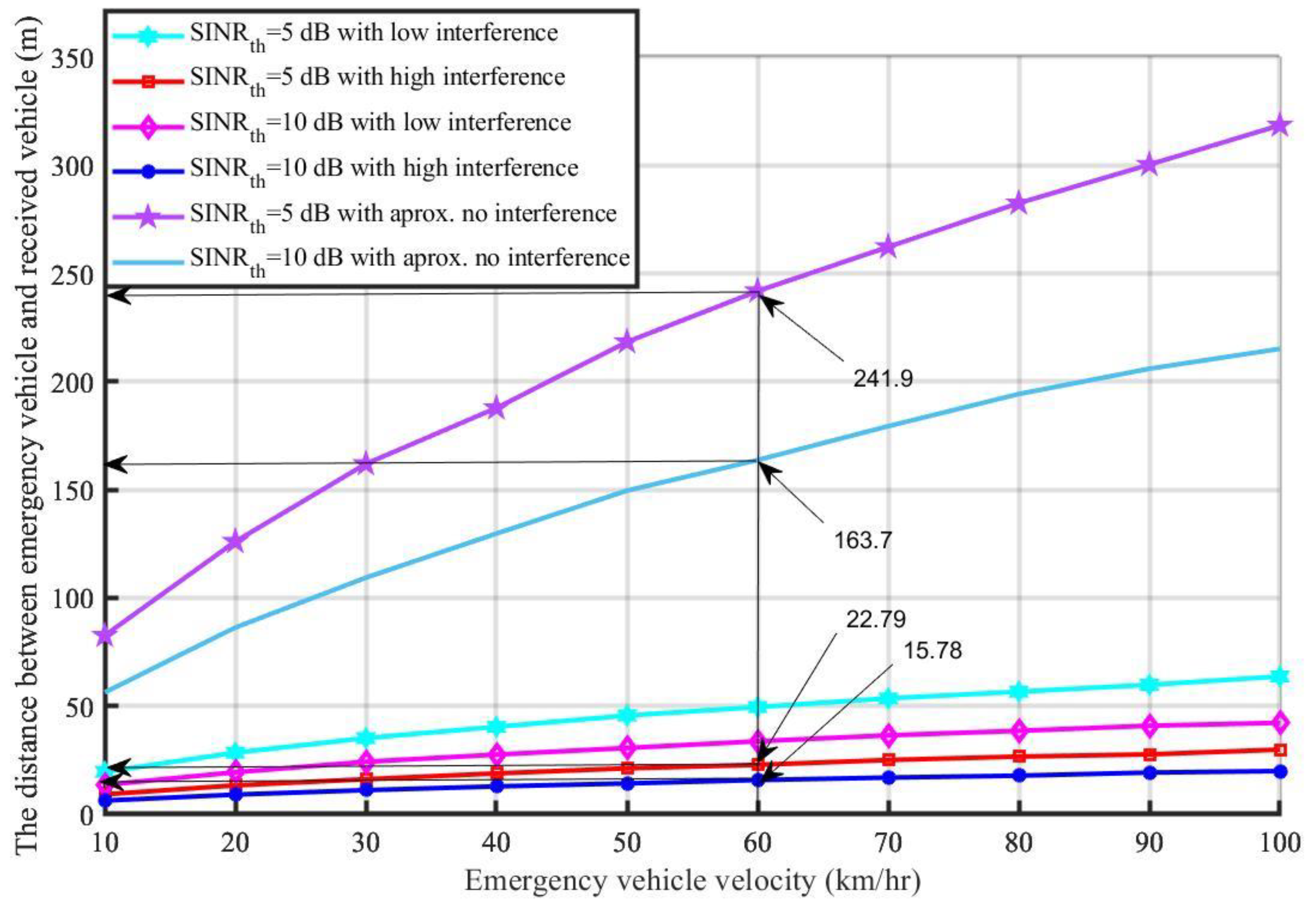
4.7. Emergency Vehicle Travel Time
4.8. Proposed Enhancement Adaptive Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Symbols
| Quality of service | |
| C1, C2 | Lagrangian optimization constraints |
| dVnVn+1 | Distance between two successive vehicles in the road |
| PD | The transmission power of any interference device |
| PDmax | The maximum transmission power of any transmission device |
| PC | The transmission power of any interference cellular user’s equipment |
| PCmax | The maximum transmission power of any cellular user’s equipment |
| Pv | The transmission power of any vehicle |
| Pvi | The transmission power of any interference vehicle |
| Pvmax | The maximum transmission power of any vehicle |
| Fading channel coefficient between any two successive vehicles | |
| Fading channel coefficient between the interfering device and the receiving vehicle | |
| Fading channel coefficient between the interfering CUE and the receiving vehicle | |
| Fading channel coefficient between the interfering vehicle and the receiving vehicle | |
| Path loss between any interfering device and the receiving vehicle | |
| Path loss between any interfering CUE and receiving vehicle | |
| Path loss between any interfering vehicle and receiving vehicle | |
| Path loss between any two V2V links | |
| PDR | Packet delivery ratio |
| E2E | Average end-to-end delay |
| pout | System outage probability |
| poutmax | Maximum system outage probability |
| Signal-to-interference-plus-noise ratio | |
| Signal-to-interference-plus-noise ratio threshold | |
| SINREVN | Signal-to-interference-plus-noise between the emergency vehicle and the nearest vehicle |
| poutEVN | Outage probability of the emergency vehicle and the nearest vehicle |
| dEVN | Distance between the emergency vehicle and the nearest vehicle |
| dEVmax | Maximum distance between the emergency vehicle and the nearest vehicle |
| Fading channel coefficient | |
| Noise power spectral density | |
| PS | Source transmission power |
| Path loss between the source and destination | |
| Emergency vehicle’s transmission power | |
| Fading channel coefficient between the emergency vehicle and the nearest vehicle | |
| Path loss between the emergency vehicle and the nearest vehicle | |
| Fading channel coefficient between the interfering device and the nearest vehicle | |
| Path loss between theinterfering device and the nearest vehicle | |
| Fading channel coefficient between theinterfering CUE and the nearest vehicle | |
| Path loss between the interfering CUE and the nearest vehicle | |
| Fading channel coefficient between the interfering vehicle and the nearest vehicle | |
| Path loss between the interfering vehicle and the nearest vehicle | |
| poutEVN | Outage probability of the emergency vehicle and the nearest vehicle |
| poutli | Outage probability of all the communication links in the lane i |
| Outage probability of the emergency vehicle and the nearest vehicle, and the nearest vehicle and the first vehicle in the traffic | |
| Outage probability of all communicating V2V links in the lane i | |
| Fading channel coefficient between the nearest vehicle and the first receiving vehicle on the road | |
| Path loss between the emergency vehicle and the nearest vehicle | |
| Fading channel coefficient between the nearest vehicle and the first receiving vehicle on the road | |
| Path loss between the interfering device and first receiving vehicle on the road | |
| Fading channel coefficient between the interfering CUE and the first receiving vehicle on the road | |
| Path loss between the interfering CUE and the first receiving vehicle on the road | |
| Fading channel coefficient between the interfering vehicle and the first receiving vehicle on the road | |
| Path loss between the interfering vehicle and the first receiving vehicle on the road | |
| Path loss constant | |
| Interference | |
| n | Number of vehicles on the road |
| Road length | |
| v | Vehicle velocity |
| VL | Vehicle length |
| λ, µ | Non-negative Lagrangian multipliers |
References
- Galarza, M.; Paradells, J. Improving road safety and user experience by employing dynamic in-vehicle information systems. IET Intell. Transp. Syst. 2019, 13, 738–744. [Google Scholar] [CrossRef]
- Zhenyu, L.; Lin, P.; Konglin, Z.; Lin, Z. Design and evaluation of V2X communication system for vehicle and pedestrian safety. J. China Univ. Posts Telecommun. 2015, 22, 18–26. [Google Scholar] [CrossRef]
- Karagiannis, G.; Altintas, O.; Ekici, E.; Heijenk, G.; Jarupan, B.; Lin, K.; Weil, T. Vehicular Networking: A Survey and Tutorial on Requirements, Architectures, Challenges, Standards and Solutions. IEEE Commun. Surv. Tutor. 2011, 13, 584–616. [Google Scholar] [CrossRef]
- Yang, L.; Li, H. Vehicle-to-vehicle communication based on a peer-to-peer network with graph theory and consensus algorithm. IET Intell. Transp. Syst. 2019, 13, 280–285. [Google Scholar] [CrossRef]
- Vinel, A.; Lyamin, N.; Isachenkov, P. Modeling of V2V Communications for C-ITS Safety Applications: A CPS Perspective. IEEE Commun. Lett. 2018, 22, 1600–1603. [Google Scholar] [CrossRef]
- Wang, R.; Xu, Z.; Zhao, X.; Hu, J. V2V-based method for detection of road traffic congestion. IET Intell. Transp. Syst. 2019, 13, 880–885. [Google Scholar] [CrossRef]
- Zheng, K.; Zheng, Q.; Chatzimisios, P.; Xiang, W.; Zhou, Y. Heterogeneous vehicular networking: A survey on architecture, challenges, and solutions. IEEE Commun. Surv. Tutor. 2015, 17, 377–2396. [Google Scholar] [CrossRef]
- Ligo, A.K.; Peha, J.M.; Ferreira, P.; Barros, A.J. Throughput and Economics of DSRC-Based Internet of Vehicles. IEEE Access 2018, 6, 7276–7290. [Google Scholar] [CrossRef]
- Wu, X.; Subramanian, S.; Guha, R.; White, R.G.; Li, J.; Lu, K.W.; Bucceri, A.; Zhang, T. Vehicular communications using DSRC: Challenges, enhancements, and evolution. IEEE J. Sel. Areas Commun. 2013, 31, 399–408. [Google Scholar]
- Yang, Y.; Fei, D.; Dang, S. Inter-Vehicle Cooperation Channel Estimation for IEEE 802.11p V2I Communications. J. Commun. Netw. 2017, 19, 227–238. [Google Scholar] [CrossRef]
- Tonguz, O.K.; Zhang, R. Harnessing Vehicular Broadcast Communications: DSRC-Actuated Traffic Control. IEEE Trans. Int. Trans. Syst. 2020, 21, 509–520. [Google Scholar] [CrossRef]
- Bae, J.-K.; Park, M.-C.; Yang, E.-J.; Seo, D.-W. Implementation and Performance Evaluation for DSRC-Based Vehicular Communication System. IEEE Access 2021, 9, 6878–6887. [Google Scholar] [CrossRef]
- Wu, N.; Li, D.; Xi, Y. Distributed Weighted Balanced Control of Traffic Signals for Urban Traffic Congestion. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3710–3720. [Google Scholar] [CrossRef]
- Ma, Q.; Zhang, S.; Qiao, Y.; Feng, M. Traffic Guidance Self-Organization Method for Neighbor Weaving Segments Based on Self-Organized Critical State. IEEE Access 2020, 8, 171784–171795. [Google Scholar] [CrossRef]
- Zhou, Z.; Lin, S.; Du, W.; Liang, H. Integration of Regional Demand Management and Signals Control for Urban Traffic Networks. IEEE Access 2019, 7, 20235–20248. [Google Scholar] [CrossRef]
- Wang, W.; Chen, J.-C.; Wu, Y.J.; Jim, Y. The Prediction of Freeway Traffic Conditions for Logistics Systems. IEEE Access 2019, 7, 138056–138061. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Su, R. Pedestrian-Safety-Aware Traffic Light Control Strategy for Urban Traffic Congestion Alleviation. IEEE Trans. Int. Trans. Syst. 2021, 22, 178–193. [Google Scholar] [CrossRef]
- León, J.P.A.; Rico-Novella, F.J.; Luis, J. Predictive Traffic Control and Differentiation on Smart Grid Neighborhood Area Networks. IEEE Access 2020, 8, 216805–216821. [Google Scholar] [CrossRef]
- Xu, C.; Xiong, Z.; Han, Z.; Zhao, G.; Yu, S. Link Reliability-Based Adaptive Routing for Multilevel Vehicular Networks. IEEE Trans. Veh. Technol. 2020, 69, 11771–11785. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, Y.; Chen, L.; Shi, J. A Stackelberg Game-Based Caching Incentive Scheme for Roadside Units in VANETs. Sensors 2020, 20, 6625. [Google Scholar] [CrossRef] [PubMed]
- Osman, R.A.; Peng, X.-H.; Omar, M. Adaptive cooperative communications for enhancing qos in vehicular networks. Phys. Commun. 2019, 34, 285–294. [Google Scholar] [CrossRef] [Green Version]
- Osman, R.A.; Peng, X.-H. QoS-Ensured Cooperative Vehicular Communications. Int. J. Adv. Syst. Measu. 2018, 11, 83–92. [Google Scholar]
- Zhou, J.; Tian, D.; Wang, Y.; Sheng, Z.; Duan, X.; Leung, V.C. Reliability-Optimal Cooperative Communication and Computing in Connected Vehicle Systems. IEEE Trans. Mob. Comput. 2019, 19, 1216–1232. [Google Scholar] [CrossRef]
- Zhao, D.; Qin, H.; Song, B.; Zhang, Y.; Du, X.; Guizani, M. A Reinforcement Learning Method for Joint Mode Selection and Power Adaptation in the V2V Communication Network in 5G. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 452–463. [Google Scholar] [CrossRef]
- Kim, T.; Park, Y.; Kim, H.; Hong, D. Cooperative Superposed Transmission in Cellular-Based V2V Systems. IEEE Trans. Veh. Technol. 2019, 68, 11888–11901. [Google Scholar] [CrossRef]
- Yang, F.; Han, J.-H.; Ding, X.; Wei, Z.; Bi, X. Spectral efficiency optimization and interference management for multi-hop D2D communications in VANETs. IEEE Trans. Veh. Technol. 2020, 69, 6422–6436. [Google Scholar] [CrossRef]
- Bonjorn, N.; Foukalas, F.; Cañellas, F.; Pop, P. Cooperative Resource Allocation and Scheduling for 5G eV2X Services. IEEE Access 2019, 7, 58212–58220. [Google Scholar] [CrossRef]
- Feteiha, M.F.; Ahmed, M.H. Multihop Best-Relay Selection for Vehicular Communication Over Highways Traffic. IEEE Trans. Veh. Technol. 2018, 67, 9845–9855. [Google Scholar] [CrossRef]
- Road Engineering Design Guidelines. In Lane Width Guideline; Transportation Services: Toronto, ON, Canada, 2017; pp. 1–11.
- CEDR. Safe Distance between Vehicles; CEDR: Santa Monica, CA, USA, 2010; pp. 1–9. [Google Scholar]
- Xu, Y. Quality of Service Provisions for Maritime Communications Based on Cellular Networks. IEEE Access 2017, 5, 23881–23890. [Google Scholar] [CrossRef]
- Ho, D.H.; Gulliver, A. Power Allocation in Cellular Networks Based on Outage Probability and Normalized SINR. IEEE Trans. Green Commun. Netw. 2020, 4, 783–793. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.; He, Q.; Bian, K.; Song, L. Joint Trajectory and Power Optimization for UAV Relay Networks. IEEE Commun. Lett. 2017, 22, 161–164. [Google Scholar] [CrossRef]
- Kim, M.; Lee, J. Impact of an Interfering Node on Unmanned Aerial Vehicle Communications. IEEE Trans. Veh. Technol. 2019, 68, 12150–12163. [Google Scholar] [CrossRef]
- Wang, S.; Wang, D.; Li, C.; Xu, W. Full Duplex AF and DF Relaying Under Channel Estimation Errors for V2V Communications. IEEE Access 2018, 6, 65321–65332. [Google Scholar] [CrossRef]
- Wang, Y.; Sheng, M.; Wang, X.; Wang, L.; Li, J. Mobile-Edge Computing: Partial Computation Offloading Using Dynamic Voltage Scaling. IEEE Trans. Commun. 2016, 64, 4268–4282. [Google Scholar] [CrossRef]
- Alkhalifa, I.S.; Almogren, A.S. NSSC: Novel Segment Based Safety Message Broadcasting in Cluster-Based Vehicular Sensor Network. IEEE Access 2020, 8, 34299–34312. [Google Scholar] [CrossRef]
- Liu, W.; He, X.; Huang, Z.; Ji, Y. Transmission Capacity Characterization in VANETs with Enhanced Distributed Channel Access. Electronics 2019, 8, 340. [Google Scholar] [CrossRef] [Green Version]
- Guo, C.; Liang, L.; Li, G.Y. Resource Allocation for Vehicular Communications With Low Latency and High Reliability. IEEE Trans. Wirel. Commun. 2019, 18, 3887–3902. [Google Scholar] [CrossRef]
- Khan, U.A.; Lee, S.S. Three-Dimensional Resource Allocation in D2D-Based V2V Communication. Electronics 2019, 8, 962. [Google Scholar] [CrossRef] [Green Version]
- Osman, R.A.; Peng, X.; Omar, M.A.; Gao, Q. Quality of service optimisation of device-to-device communications underlaying cellular networks. IET Commun. 2020, 15, 179–190. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| No | −144 dBm |
| B | 10 MHz |
| Pvmax | 33 dBm |
| PD | 17 or 23 dBm |
| PC | 17 or 23 dBm |
| Packet size | 512 bytes |
| fc | 5.9 GHz |
| Simulation time | 1000 s |
| Number of vehicles | 100~300 |
| Speed | 60 km/h |
| Traffic agent | CBR |
| Queue | PriQueue with a size of 50 packets |
| Propagation mode | Two-way model |
| Antenna | Omni-directional with a height of 1 m |
| Routing Protocol | DSRC |
| Number of seeds | 3 |
| Noise | AWGN |
| PLV2V | 127 + 30 log10(dVV) |
| PLCBS | 128.1 + 30 log10(dCBS) |
| PLD2D | 148 + 30 log10(dDD) |
| Vehicle Performance Before Receiving an Emergency Message | Vehicle Performance after Receiving an Emergency Message | ||||
|---|---|---|---|---|---|
| Vehicle Velocity (km/h) | Number of Vehicles per 1 km | Safe Distance between Vehicles (m) | Vehicle Velocity (km/h) | Number of Vehicles per 1 km | Safe Distance between Vehicles (m) |
| 30 | 46.1538 | 16.66667 | 10.9821 | 90.0807 | 6.1012 |
| 40 | 36.7347 | 22.22222 | 13.4790 | 80.0749 | 7.4883 |
| 50 | 30.5085 | 27.777778 | 15.6964 | 72.8851 | 8.7202 |
| 60 | 26.0870 | 33.333333 | 19.8838 | 65.7786 | 10.2025 |
| 70 | 22.7848 | 38.888889 | 22.3220 | 62.3188 | 11.0465 |
| 80 | 20.2247 | 44.444444 | 24.5729 | 57.4675 | 12.4011 |
| 90 | 18.1818 | 50 | 25.9517 | 53.6146 | 13.6516 |
| 100 | 16.5138 | 55.555556 | 28.4307 | 51.4997 | 14.4176 |
| 110 | 15.1261 | 61.111111 | 29.6037 | 48.0889 | 15.7948 |
| 120 | 13.9535 | 66.6666667 | 29.9143 | 46.6277 | 16.4465 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osman, R.A.; Zaki, A.I.; Abdelsalam, A.K. Novel Road Traffic Management Strategy for Rapid Clarification of the Emergency Vehicle Route Based on V2V Communications. Sensors 2021, 21, 5120. https://doi.org/10.3390/s21155120
Osman RA, Zaki AI, Abdelsalam AK. Novel Road Traffic Management Strategy for Rapid Clarification of the Emergency Vehicle Route Based on V2V Communications. Sensors. 2021; 21(15):5120. https://doi.org/10.3390/s21155120
Chicago/Turabian StyleOsman, Radwa Ahmed, Amira I. Zaki, and Ahmed Kadry Abdelsalam. 2021. "Novel Road Traffic Management Strategy for Rapid Clarification of the Emergency Vehicle Route Based on V2V Communications" Sensors 21, no. 15: 5120. https://doi.org/10.3390/s21155120
APA StyleOsman, R. A., Zaki, A. I., & Abdelsalam, A. K. (2021). Novel Road Traffic Management Strategy for Rapid Clarification of the Emergency Vehicle Route Based on V2V Communications. Sensors, 21(15), 5120. https://doi.org/10.3390/s21155120






