Damage Detection on a Beam with Multiple Cracks: A Simplified Method Based on Relative Frequency Shifts †
Abstract
:1. Introduction
2. Theoretical Background and Methodology
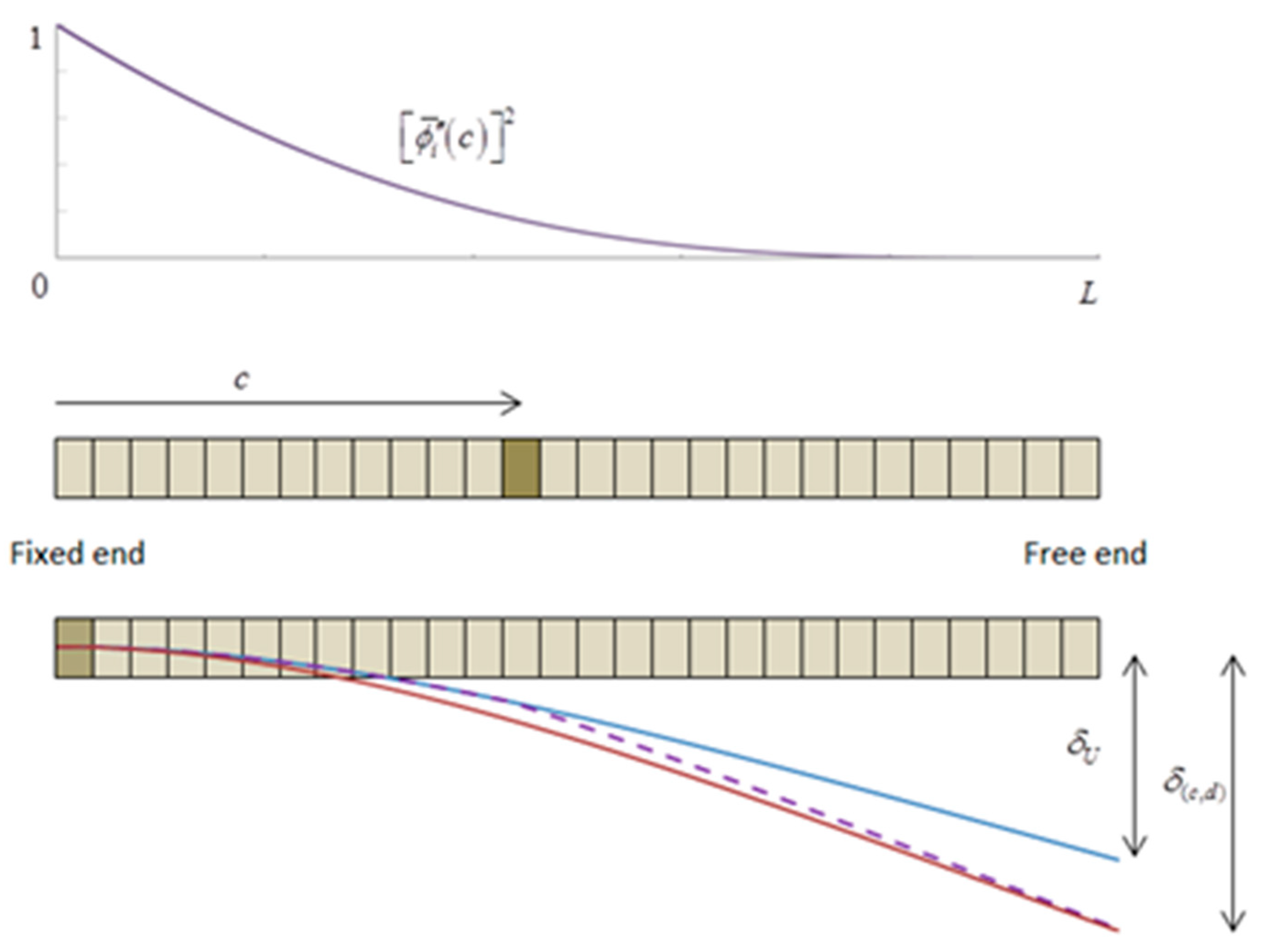
2.1. The Relative Frequency Shift (RFS) for Beams with One Crack
2.2. The RFS for the Case of Beams with Multiple Cracks
2.3. The Proposed Damage Detection Method
3. Numerical Study Regarding the Frequency Shifts Produced by Two Cracks
3.1. Simulation Methodology
- -
- Frequencies of the healthy beam from FE analysis;
- -
- Frequencies of the beam with the fixed crack from FE analysis;
- -
- Frequencies of the beam with the fixed crack with Equation (12);
- -
- Mass density for the ML-EHB considering the beam with the fixed crack involving Equation (15);
- -
- Frequencies of the beam with two cracks by superposition, using FE analysis for the ML-EHB, on which we generate the second crack;
- -
- Frequencies of the beam with two cracks by superposition, using Equation (16);
- -
- Frequencies of the beam with two cracks from FE analysis.
3.2. Simulations Made for Cracks Located Far from Each Other
3.3. Simulations Made for Closely Located Cracks
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef] [Green Version]
- Dimarogonas, A.D. Vibration of cracked structures: State of the art review. Eng. Fract. Mech. 1996, 55, 831–857. [Google Scholar] [CrossRef]
- Khiem, N.T.; Tran, H.T. A procedure for multiple crack identification in beam-like structures from natural vibration mode. J. Vib. Control 2014, 20, 1417–1427. [Google Scholar] [CrossRef]
- Gillich, G.R.; Mituletu, I.C.; Negru, I.; Tufoi, M.; Iancu, V.; Muntean, F. A Method to Enhance Frequency Readability for Early Damage Detection. J. Vib. Eng. Technol. 2015, 3, 637–652. [Google Scholar]
- Mituletu, I.C.; Gillich, G.R.; Maia, N.M.M. A method for an accurate estimation of natural frequencies using swept-sine acoustic excitation. Mech. Syst. Signal Process. 2019, 116, 693–709. [Google Scholar] [CrossRef]
- Friswell, M.I.; Penny, J.E.T.; Wilson, D.A.L. Using vibration data and statistical measures to locate damage in structures, modal analysis. Int. J. Anal. Exp. Modal Anal. 1994, 9, 239–254. [Google Scholar]
- Minda, P.F.; Praisach, Z.I.; Gillich, N.; Minda, A.A.; Gillich, G.R. On the efficiency of different dissimilarity estimators used in damage detection. Rom. J. Acoust. Vib. 2013, 10, 15–18. [Google Scholar]
- Mottershead, J.E.; Friswell, M.I. Model Updating In Structural Dynamics: A Survey. J. Sound Vib. 1993, 167, 347–375. [Google Scholar] [CrossRef]
- Adams, R.D.; Cawley, P.; Pye, C.J.; Stone, B.J. A vibration technique for non-destructively assessing the integrity of structures. J. Mech. Eng. Sci. 1978, 20, 93–100. [Google Scholar] [CrossRef]
- Gudmunson, P. Eigenfrequency changes of structures due to cracks, notches or other geometrical changes. J. Mech. Phys. Solids 1982, 30, 339–353. [Google Scholar] [CrossRef]
- Narkis, Y. Identification of crack location in vibrating simply supported beams. J. Sound Vib. 1994, 172, 549–558. [Google Scholar] [CrossRef]
- Liang, R.Y.; Choy, F.K.; Hu, J. Detection of cracks in beam structures using measurements of natural frequencies. J. Franklin Inst. 1991, 328, 505–518. [Google Scholar] [CrossRef]
- Gillich, G.R.; Wahab, M.A.; Praisach, Z.I.; Ntakpe, J.L. The influence of transversal crack geometry on the frequency changes of beams. In Proceedings of the International Conference on Noise and Vibration Engineering (ISMA2014) and International Conference on Uncertainty in Structural Dynamics (USD2014), Leuven, Belgium, 15–17 September 2014; Sas, P., Moens, D., Denayer, H., Eds.; Katholieke Universiteit: Leuven, Belgium, 2014; pp. 485–498. [Google Scholar]
- Rizos, P.F.; Aspragathos, N.; Dimarogonas, A.D. Identification of crack location and magnitude in a cantilever beam from the vibration modes. J. Sound Vib. 1990, 138, 381–388. [Google Scholar] [CrossRef]
- Owolabi, G.M.; Swamidas, A.S.J.; Seshadri, R. Crack detection in beams using changes in frequencies and amplitudes of frequency response functions. J. Sound Vib. 2003, 265, 1–22. [Google Scholar] [CrossRef]
- Mazanoglu, K. A Novel Methodology Using Simplified Approaches for Identification of Cracks in Beams. Lat. Am. J. Solids Struct. 2015, 12, 2460–2479. [Google Scholar] [CrossRef] [Green Version]
- Morassi, A.; Rollo, M. Identification of Two Cracks in a Simply Supported Beam from Minimal Frequency Measurements. J. Vib. Control 2001, 7, 729–739. [Google Scholar] [CrossRef]
- Khie, N.T.; Lien, T.V. A Simplified Method for Natural Frequency Analysis of A Multiple Cracked Beam. J. Sound Vib. 2001, 245, 737–751. [Google Scholar]
- Sha, G.; Radzieński, M.; Cao, M.; Ostachowicz, W. A novel method for single and multiple damage detection in beams using relative natural frequency changes. Mech. Syst. Signal Process. 2019, 132, 335–352. [Google Scholar] [CrossRef]
- Stubbs, N.; Broome, T.H.; Osegueda, R. Nondestructive construction error detection in large space structures. AIAA J. 1990, 28, 146–152. [Google Scholar] [CrossRef]
- Nahvi, H.; Jabbari, M. Crack detection in beams using experimental modal data and finite element model. Int. J. Mech. Sci. 2005, 47, 1477–1497. [Google Scholar] [CrossRef]
- Ruotolo, R.; Surace, C. Damage Assessment of Multiple Cracked Beams: Numerical Results and Experimental Validation. J. Sound Vib. 1997, 206, 567–588. [Google Scholar] [CrossRef]
- Moslem, K.; Nafaspour, R. Structural Damage Detection by Genetic Algorithms. AIAA J. 2002, 40, 1395–1401. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Bui, T.T.; De Roeck, G.; Wahab, M.A. Damage detection in Ca-Non Bridge using transmissibility and artificial neural networks. Struct. Eng. Mech. 2019, 71, 175–183. [Google Scholar]
- Khatir, S.; Dekemele, K.; Loccufier, M.; Khatir, T.; Wahab, M.A. Crack identification method in beam-like structures using changes in experimentally measured frequencies and Particle Swarm Optimization. C. R. Méc. 2018, 346, 110–120. [Google Scholar] [CrossRef]
- Gillich, G.R.; Furdui, H.; Wahab, M.A.; Korka, Z.I. A robust damage detection method based on multi-modal analysis in variable temperature conditions. Mech. Syst. Signal Process. 2019, 115, 361–379. [Google Scholar] [CrossRef]
- Sohn, H. Effects of environmental and operational variability on structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 539–560. [Google Scholar] [CrossRef]
- Wah, W.S.L.; Chen, Y.Y.; Owen, J.S. A regression-based damage detection method for structures subjected to changing environmental and operational conditions. Eng. Struct. 2021, 228, 111462. [Google Scholar]
- Wang, X.; Li, L.; Beck, J.L.; Xia, Y. Sparse Bayesian factor analysis for structural damage detection under unknown environmental conditions. Mech. Syst. Signal Process. 2021, 154, 107563. [Google Scholar] [CrossRef]
- Lakshmi, K. Detection and quantification of damage in bridges using a hybrid algorithm with spatial filters under environmental and operational variability. Structures 2021, 32, 617–631. [Google Scholar] [CrossRef]
- Yang, C.; Liu, Y. Detecting the damage of bridges under changing environmental conditions using the characteristics of the nonlinear narrow dimension of damage features. Mech. Syst. Signal Process. 2021, 159, 107842. [Google Scholar] [CrossRef]
- Kullaa, J. Robust damage detection in the time domain using Bayesian virtual sensing with noise reduction and environmental effect elimination capabilities. J. Sound Vib. 2020, 473, 115232. [Google Scholar] [CrossRef]
- Tufisi, C.; Gillich, G.R.; Hamat, C.O.; Manescu, T. Study regarding the effect of crack branching on the eigenfrequencies of beams. In Proceedings of the 13th International Conference on Damage Assessment of Structures, Porto, Portugal, 9–10 July 2019. [Google Scholar]
- Gillich, G.R.; Aman, A.T.; Wahab, M.A.; Tufisi, C. Detection of Multiple Cracks Using an Energy Method Applied to the Concept of Equivalent Healthy Beam. In Proceedings of the 13th International Conference on Damage Assessment of Structures, Porto, Portugal, 9–10 July 2019. [Google Scholar]
- Panteliou, S.D.; Chondros, T.G.; Argyrakis, V.C.; Dimarogonas, A.D. Damping Factor as an Indicator of Crack Severity. J. Sound Vib. 2001, 241, 235–245. [Google Scholar] [CrossRef]
- Ostachowicz, W.M.; Krawczuk, M. Analysis of the effect of cracks on the natural frequencies of a cantilever beam. J. Sound Vib. 1991, 150, 191–201. [Google Scholar] [CrossRef]
- Tufisi, C.; Gillich, G.R.; Hamat, C.O.; Biro, I.; Gillich, N.; Nedelcu, D. Exact solution for the severity of transverse cracks in prismatic beams. J. Phys. Conf. Ser. 2020, 1426, 012023. [Google Scholar] [CrossRef]
- Gillich, G.R.; Maia, N.M.M.; Mituletu, I.C.; Tufoi, M.; Iancu, V.; Korka, Z. A New Approach for Severity Estimation of Transversal Cracks in Multi-Layered Beams. Lat. Am. J. Solids Struct. 2016, 13, 1526–1544. [Google Scholar] [CrossRef] [Green Version]
- Gillich, N.; Tufisi, C.; Vasile, O.; Gillich, G.R. Statistical Method for Damage Severity and Frequency Drop Estimation for a Cracked Beam using Static Test Data. Rom. J. Acoust. Vib. 2019, 16, 47–51. [Google Scholar]
- Gillich, G.R.; Praisach, Z.I.; Wahab, M.A.; Vasile, O. Localization of transversal cracks in sandwich beams and evaluation of their severity. Shock Vib. 2014, 2014, 607125. [Google Scholar] [CrossRef]
- Gillich, G.R.; Praisach, Z.I. Modal identification and damage detection in beam-like structures using the power spectrum and time-frequency analysis. Signal Process. 2014, 96, 29–44. [Google Scholar] [CrossRef]
- Dahak, M.; Noureddine Touat, N.; Kharoubi, M. Damage detection in beam through change in measured frequency and undamaged curvature mode shape. Inverse Probl. Sci. Eng. 2019, 27, 1–26. [Google Scholar] [CrossRef]
- Tufisi, C.; Gillich, G.R.; Barbinta, C.I.; Nedelcu, D.; Hamat, C.O. A new predictive model to estimate the frequencies for beams with branched cracks. IOP Conf. Ser. Mater. Sci. Eng. 2020, 997, 012063. [Google Scholar] [CrossRef]
- Nedelcu, D.; Gillich, G.R. A structural health monitoring Python code to detect small changes in frequencies. Mech. Syst. Signal Process. 2021, 147, 107087. [Google Scholar] [CrossRef]





| Length L (mm) | Width b (mm) | Thickness h (mm) | Mass Density ρ (kg/m3) | Young Modulus E (N/m2) | Poisson Ratio ν (-) |
|---|---|---|---|---|---|
| 1000 | 50 | 5 | 7850 | 2 × 1011 | 0.3 |
| Mode No. | [Hz] | [Hz] | [Hz] | [Hz] | [Hz] |
|---|---|---|---|---|---|
| 1 | 0.002249 | 0.001516 | 0.000636 | 0.000147 | 0.000049 |
| 2 | 0.000819 | 0 | 0.001015 | 0.001366 | 0.000858 |
| 3 | 0.000167 | 0.000571 | 0.000683 | 0.000822 | 0.001742 |
| 4 | 0 | 0.001279 | 0.000284 | 0.000284 | 0.000569 |
| 5 | 0.000258 | 0.000946 | 0.001462 | 0.001462 | 0.000172 |
| 6 | 0.000662 | 0.000115 | 0.000029 | 0.000029 | 0.001353 |
| Mode No. | Freq. cF = 210 mm cM1F = 100 mm | Freq. cF = 210 mm cM2F = 400 mm | Freq. cF = 210 mm cM3F = 600 mm | Freq. cF = 210 mm cM4F = 700 mm | ||||
|---|---|---|---|---|---|---|---|---|
| FEM | Superp. | FEM | Superp. | FEM | Superp. | FEM | Superp. | |
| 1 | 4.0746 | 4.0746 | 4.0812 | 4.0812 | 4.0832 | 4.0832 | 4.0835 | 4.0836 |
| 2 | 25.606 | 25.606 | 25.601 | 25.601 | 25.591 | 25.592 | 25.606 | 25.605 |
| 3 | 71.704 | 71.704 | 71.668 | 71.667 | 71.657 | 71.657 | 71.593 | 71.591 |
| 4 | 140.45 | 140.45 | 140.41 | 140.41 | 140.41 | 140.41 | 140.37 | 140.37 |
| 5 | 232.25 | 232.25 | 231.97 | 231.97 | 231.98 | 231.97 | 232.28 | 232.27 |
| 6 | 347.18 | 347.19 | 347.40 | 347.41 | 347.41 | 347.41 | 346.95 | 346.95 |
| Crack Location cM [mm] | Squared Modal Curvature | Correction Coefficient | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mode Number | Mode Number | |||||||||
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| 200 | 0.526318 | 0.004905 | 0.155925 | 0.413497 | 0.360538 | 0.99840 | 0.99999 | 0.99953 | 0.99874 | 0.99891 |
| 202 | 0.522376 | 0.003779 | 0.163434 | 0.417974 | 0.350399 | 0.99841 | 0.99999 | 0.99950 | 0.99873 | 0.99894 |
| 204 | 0.51845 | 0.002803 | 0.170995 | 0.422 | 0.3398 | 0.99843 | 0.99999 | 0.99948 | 0.99872 | 0.99897 |
| 206 | 0.514541 | 0.001974 | 0.178598 | 0.425568 | 0.328777 | 0.99844 | 0.99999 | 0.99946 | 0.99871 | 0.99900 |
| 208 | 0.510647 | 0.001293 | 0.186233 | 0.428673 | 0.317371 | 0.99845 | 1.00000 | 0.99943 | 0.99870 | 0.99904 |
| 210 | 0.50677 | 0.000756 | 0.193892 | 0.431308 | 0.305621 | 0.99846 | 1.00000 | 0.99941 | 0.99869 | 0.99907 |
| 212 | 0.502909 | 0.000364 | 0.201564 | 0.43347 | 0.293569 | 0.99847 | 1.00000 | 0.99939 | 0.99868 | 0.99911 |
| 214 | 0.499064 | 0.000114 | 0.209241 | 0.435155 | 0.281257 | 0.99848 | 1.00000 | 0.99936 | 0.99868 | 0.99915 |
| 216 | 0.495235 | 0.00000537 | 0.216913 | 0.436362 | 0.268729 | 0.99850 | 1.00000 | 0.99934 | 0.99868 | 0.99918 |
| 218 | 0.491423 | 0.0000362 | 0.224571 | 0.437088 | 0.256029 | 0.99851 | 1.00000 | 0.99932 | 0.99867 | 0.99922 |
| 220 | 0.487626 | 0.000205 | 0.232205 | 0.437333 | 0.243201 | 0.99852 | 1.00000 | 0.99930 | 0.99867 | 0.99926 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gillich, G.-R.; Maia, N.M.M.; Wahab, M.A.; Tufisi, C.; Korka, Z.-I.; Gillich, N.; Pop, M.V. Damage Detection on a Beam with Multiple Cracks: A Simplified Method Based on Relative Frequency Shifts. Sensors 2021, 21, 5215. https://doi.org/10.3390/s21155215
Gillich G-R, Maia NMM, Wahab MA, Tufisi C, Korka Z-I, Gillich N, Pop MV. Damage Detection on a Beam with Multiple Cracks: A Simplified Method Based on Relative Frequency Shifts. Sensors. 2021; 21(15):5215. https://doi.org/10.3390/s21155215
Chicago/Turabian StyleGillich, Gilbert-Rainer, Nuno M. M. Maia, Magd Abdel Wahab, Cristian Tufisi, Zoltan-Iosif Korka, Nicoleta Gillich, and Marius Vasile Pop. 2021. "Damage Detection on a Beam with Multiple Cracks: A Simplified Method Based on Relative Frequency Shifts" Sensors 21, no. 15: 5215. https://doi.org/10.3390/s21155215
APA StyleGillich, G.-R., Maia, N. M. M., Wahab, M. A., Tufisi, C., Korka, Z.-I., Gillich, N., & Pop, M. V. (2021). Damage Detection on a Beam with Multiple Cracks: A Simplified Method Based on Relative Frequency Shifts. Sensors, 21(15), 5215. https://doi.org/10.3390/s21155215










