Coordinated Approach Fusing RCMDE and Sparrow Search Algorithm-Based SVM for Fault Diagnosis of Rolling Bearings
Abstract
:1. Introduction
2. Methodology
2.1. Variational Mode Decomposition
- (1)
- Initialization parameters , , , and n, n = 0;
- (2)
- n = n + 1, start the cycle;
- (3)
- Update the spectrum of each mode according to the following formula:
- (4)
- Update the center frequency:
- (5)
- Update the Lagrange multiplier as follows:where the parameter τ is used to update the Lagrange multiplier.
- (6)
- For the given discrimination accuracy, repeat steps (2)–(5) and e > 0 until the iterative condition is satisfied:
2.2. Refined Composite Multiscale Dispersion Entropy
2.3. Sparrow Search Algorithm
- (1)
- Initialize the sparrow population. Define the algorithm parameters and maximum number of iterations.
- (2)
- The fitness values of the initial population are calculated and sorted.
- (3)
- Use formulas (5)–(7) to update the locations of discoverers, participants, and watchmen.
- (4)
- Obtain the current optimal value, if the iteration effect is better, then update. Then repeat steps 2 to 6 until the maximum number of iterations is reached.
- (5)
- The global optimal value and optimal fitness value are outputted.
3. Proposed Approach
- (1)
- The k parameter of VMD is selected, and then the original vibration signal is decomposed into k intrinsic mode functions (IMFs) by VMD.
- (2)
- The best IMF component is selected.
- (3)
- The best IMF components are grouped and the RCMDE values of each group are calculated. The appropriate scale feature vectors are selected to represent the fault features.
- (4)
- The sparrow search algorithm is used to optimize the penalty factor c and kernel parameters σ of SVM.
- (5)
- The extracted fault feature vectors are inputted into the classifier for training.
- (6)
- The test set is inputted into the trained classifier for fault classification to verify the effectiveness of the proposed method.
4. Experiment and Discussion
4.1. Experimental Data
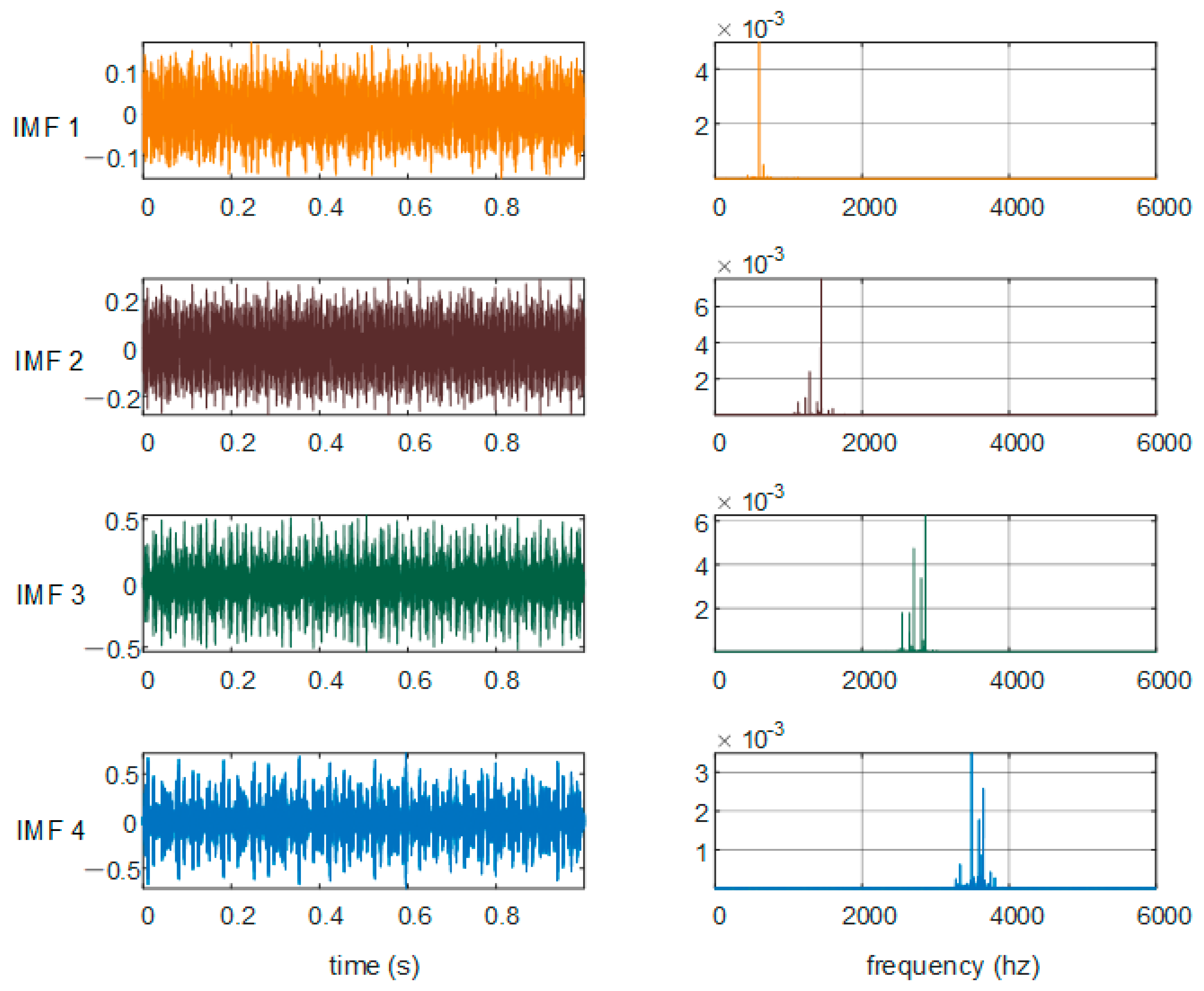
4.2. Signal Decomposition by VMD
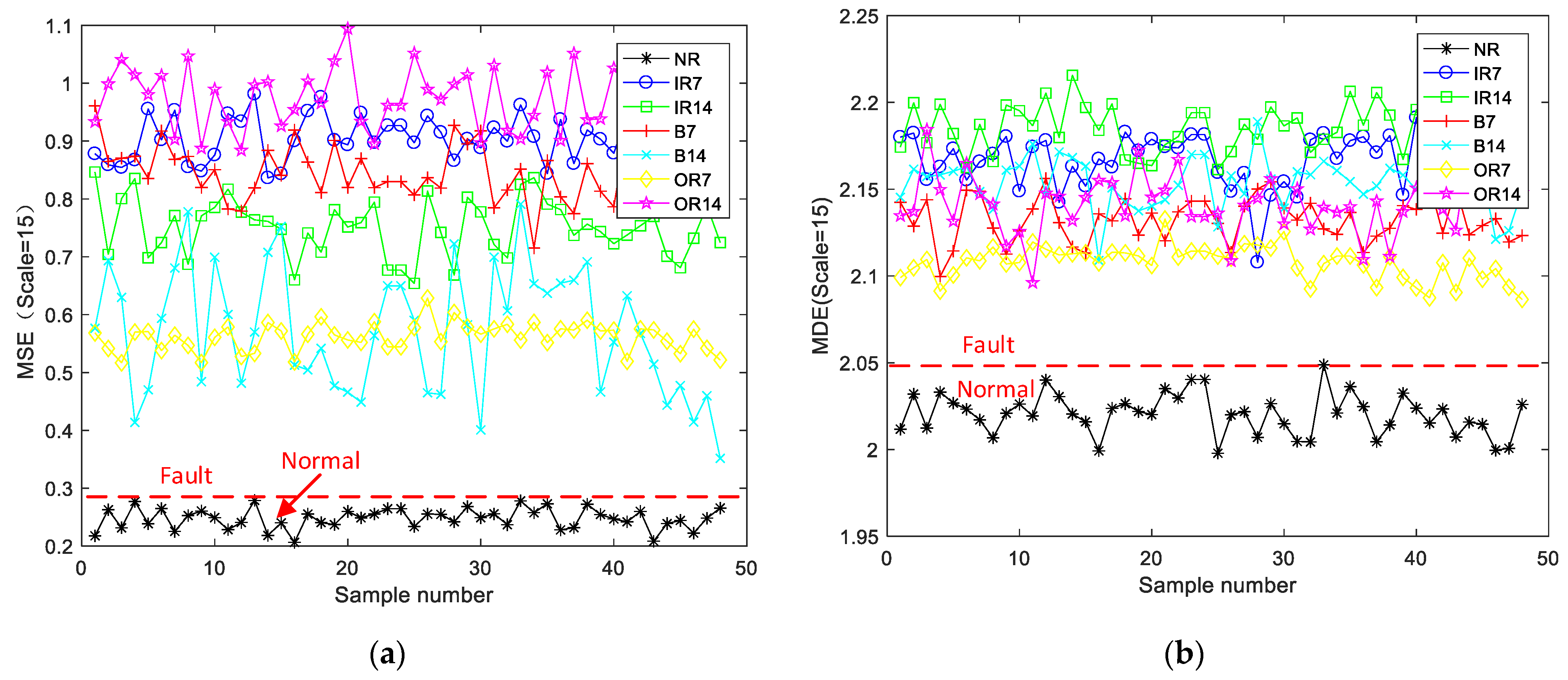
4.3. Feature Extraction by RCMDE
4.4. Parameter Setting of SSA
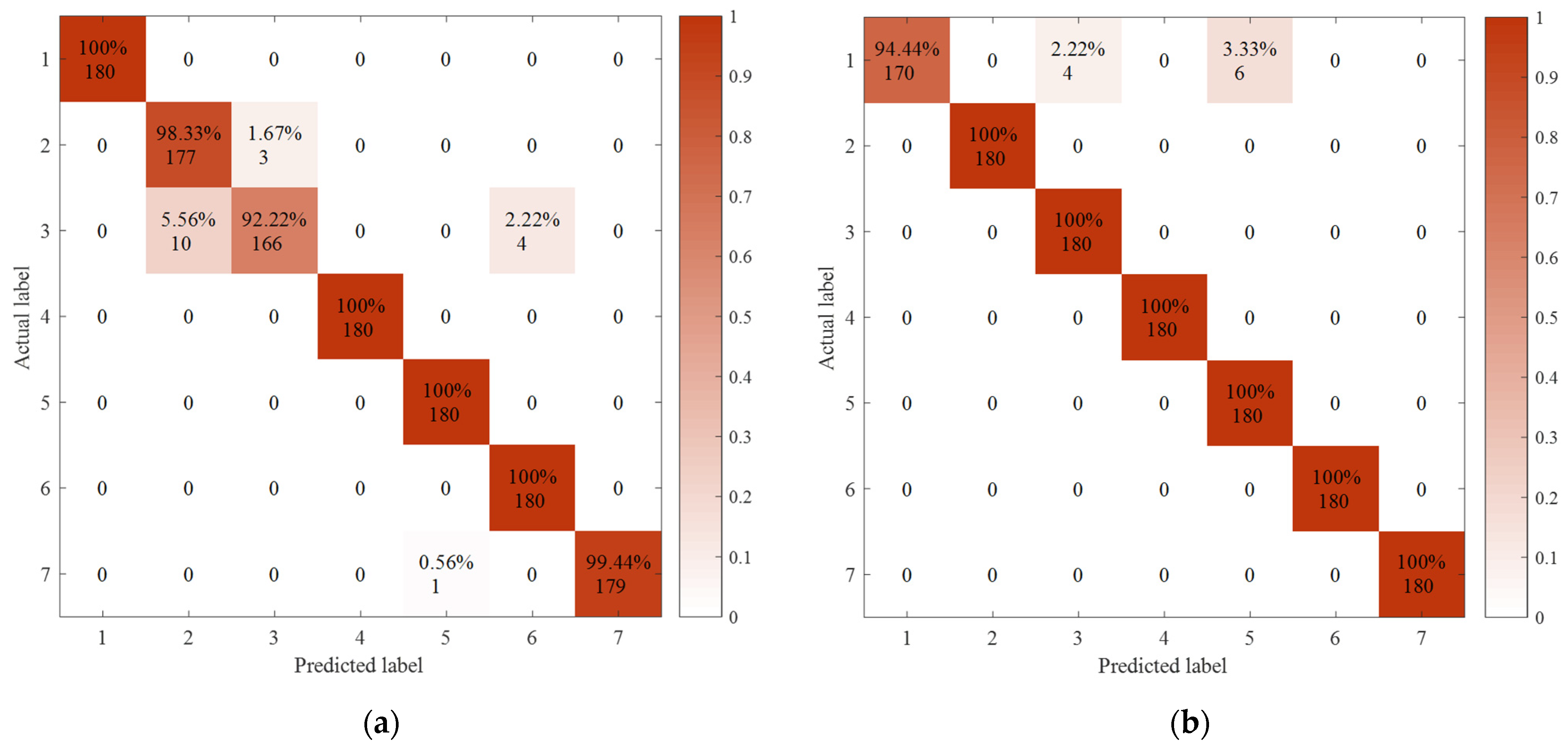
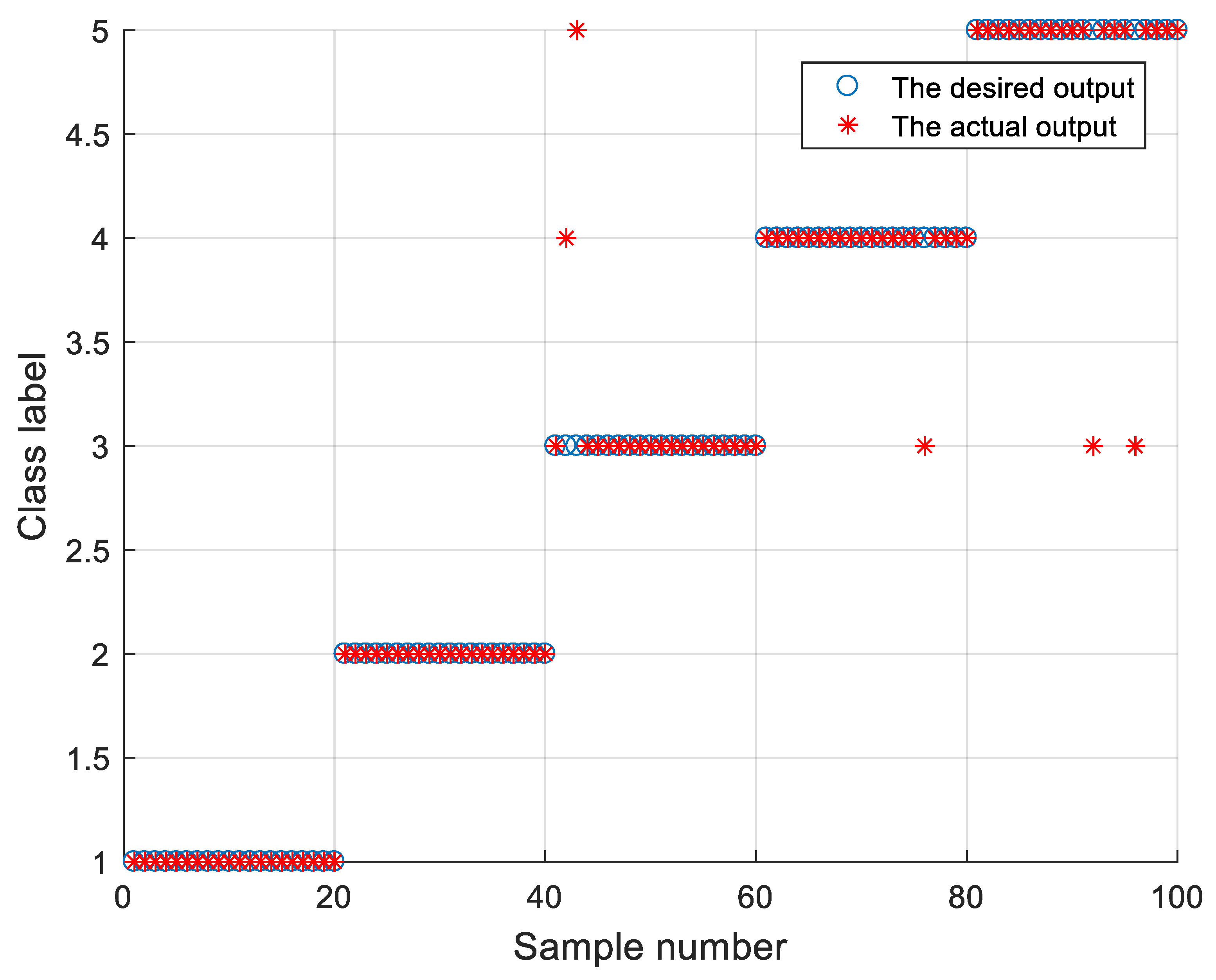
4.5. Results and Discussion in CWRU Bearing Dataset
5. Experimental Verification
5.1. Bearing Vibration Experiment of WTDS
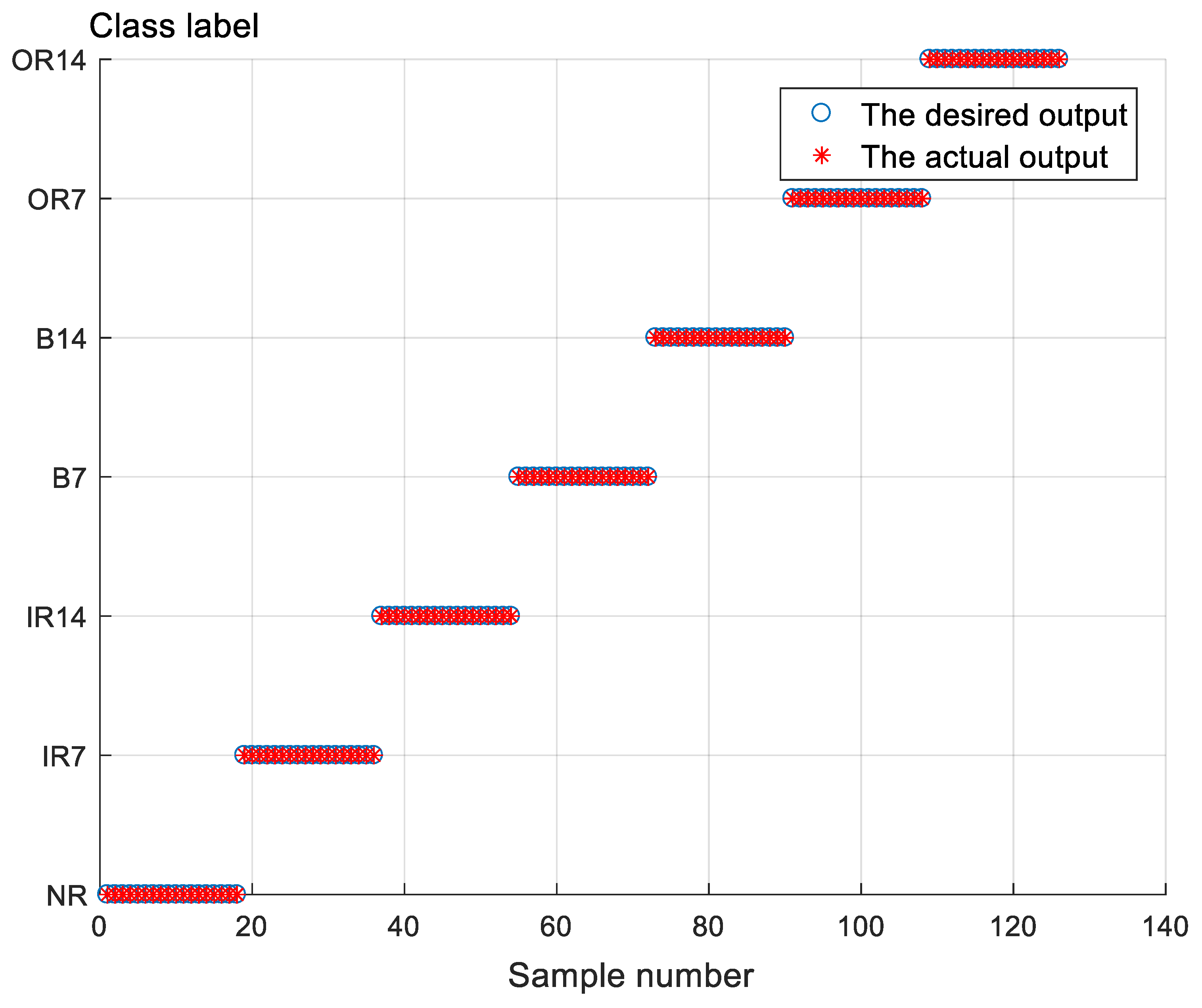
5.2. Results and Discussion in Bearing Vibration Experiment of WTDS
6. Conclusions
- (1)
- A new method of rolling-bearing-fault diagnosis was proposed. SSA was innovatively applied to optimize the parameters of SVM. Through experimental analysis and comparison, it was proven that this method not only identifies bearing-fault types quickly and effectively, but also has better performance than other similar methods.
- (2)
- Through experimental analysis, it is proved that the fault feature-extraction method based on VMD and RCMDE can fully mine the fault information.
- (3)
- The vibration experiment of rolling bearing is carried out using a WTDS to collect the acceleration signal, which further proves the effectiveness and universal of the proposed method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fu, W.; Shao, K.; Tan, J.; Wang, K. Fault Diagnosis for Rolling Bearings Based on Composite Multiscale Fine-Sorted Dispersion Entropy and SVM With Hybrid Mutation SCA-HHO Algorithm Optimization. IEEE Access 2020, 8, 13086–13104. [Google Scholar] [CrossRef]
- Tao, H.; Wang, P.; Chen, Y.; Stojanovic, V.; Yang, H. An unsupervised fault diagnosis method for rolling bearing using STFT and generative neural networks. J. Frankl. Inst. 2020, 357, 7286–7307. [Google Scholar] [CrossRef]
- Fu, W.; Tan, J.; Zhang, X.; Chen, T.; Wang, K. Blind Parameter Identification of MAR Model and Mutation Hybrid GWO-SCA Optimized SVM for Fault Diagnosis of Rotating Machinery. Complexity 2019, 2019, 3264969. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, Y.; Liao, Z.; Song, L.; Chen, P. A novel Fast Entrogram and its applications in rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2021, 154, 107582. [Google Scholar] [CrossRef]
- Chang, Y.; Bao, G.; Cheng, S.; He, T.; Yang, Q. Improved VMD-KFCM algorithm for the fault diagnosis of rolling bearing vibration signals. IET Signal Process. 2021, 15, 238–250. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, J.; Liu, J. Order bispectrum analysis based on fault characteristic frequency and its application to the fault diagno-sis of rolling bearings. Proc. CSEE 2013, 33, 123–129. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, W.; Zhang, S.; Sun, Y.; Zhang, S. A Hydraulic Pump Fault Diagnosis Method Based on the Modified Ensemble Empirical Mode Decomposition and Wavelet Kernel Extreme Learning Machine Methods. Sensors 2021, 21, 2599. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Zheng, J.; Yang, Y. A new method of nonstationary signal analysis local characteristic scale decomposition. J. Vib. Eng. 2012, 25, 215–220. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, S. Sample entropy-based roller bearing fault diagnosis method. J. Vib. Shock 2012, 31, 136–140. [Google Scholar] [CrossRef]
- Noman, K.; Wang, D.; Peng, Z.; He, Q. Oscillation based permutation entropy calculation as a dynamic nonlinear feature for health monitoring of rolling element bearing. Measurement 2021, 172, 108891. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wang, R.; Huang, W. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. J. Sound Vib. 2016, 360, 277–299. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Improved multiscale permutation entropy for biomedical signal analysis: Interpretation and application to electroencephalogram recordings. Biomed. Signal Process. Control. 2016, 23, 28–41. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Cheng, J.; Hu, S. Rotor fault diagnosis based on multiscale entropy. J. Vib. Meas. Diagn. 2013, 33, 294–297. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Abasolo, D.; Escudero, J. Refined Composite Multiscale Dispersion Entropy and its Application to Biomedical Signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Liu, X.; Luan, Z. Fault diagnosis of rotor based on VMD_IWT approximate entropy and PSO_SVM. Modul. Ma Chine Tool Autom. Manuf. Tech. 2019, 6, 106–108+118. [Google Scholar] [CrossRef]
- Ding, J.; Wang, Z.; Yao, L.; Cai, Y. Rolling bearing fault diagnosis based on GCMWPE and parameter optimization SVM. China Mech. Eng. 2021, 32, 147–155. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Cai, Y.; Zhang, J. Fault diagnosis method based on the entropy-manifold feature and SSO-SVM. J. Vib. Shock 2021, 40, 107–114. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Fu, W.; Tan, J.; Wang, K. Semi-supervised fault diagnosis of bearings based on the VMD dispersion entropy and improved SVDD with modified grey wolf optimizer. J. Vib. Shock. 2019, 38, 190–197. [Google Scholar] [CrossRef]
- Luo, S.; Yang, W.; Luo, Y. Fault Diagnosis of a Rolling Bearing Based on Adaptive Sparest Narrow-Band Decomposition and RefinedComposite Multiscale Dispersion Entropy. Entropy 2020, 22, 375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, C.; Lin, C. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Tech. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Bearing Data Center of the Case Western Reserve University. Available online: https://csegroups.case.edu/bearingdatacenter/home (accessed on 1 March 2021).
- Shao, K.; Fu, W.; Tan, J.; Wang, K. Coordinated approach fusing time-shift multiscale dispersion entropy and vibrational Harris hawks optimization-based SVM for fault diagnosis of rolling bearing. Measurement 2021, 173, 108580. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Coarse-Graining Approaches in Univariate Multiscale Sample and Dispersion Entropy. Entropy 2018, 20, 138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2018, 69, 401–412. [Google Scholar] [CrossRef]
- Han, T.; Li, Y.-F.; Qian, M. A Hybrid Generalization Network for Intelligent Fault Diagnosis of Rotating Machinery Under Unseen Working Conditions. IEEE Trans. Instrum. Meas. 2021, 70, 3520011. [Google Scholar] [CrossRef]







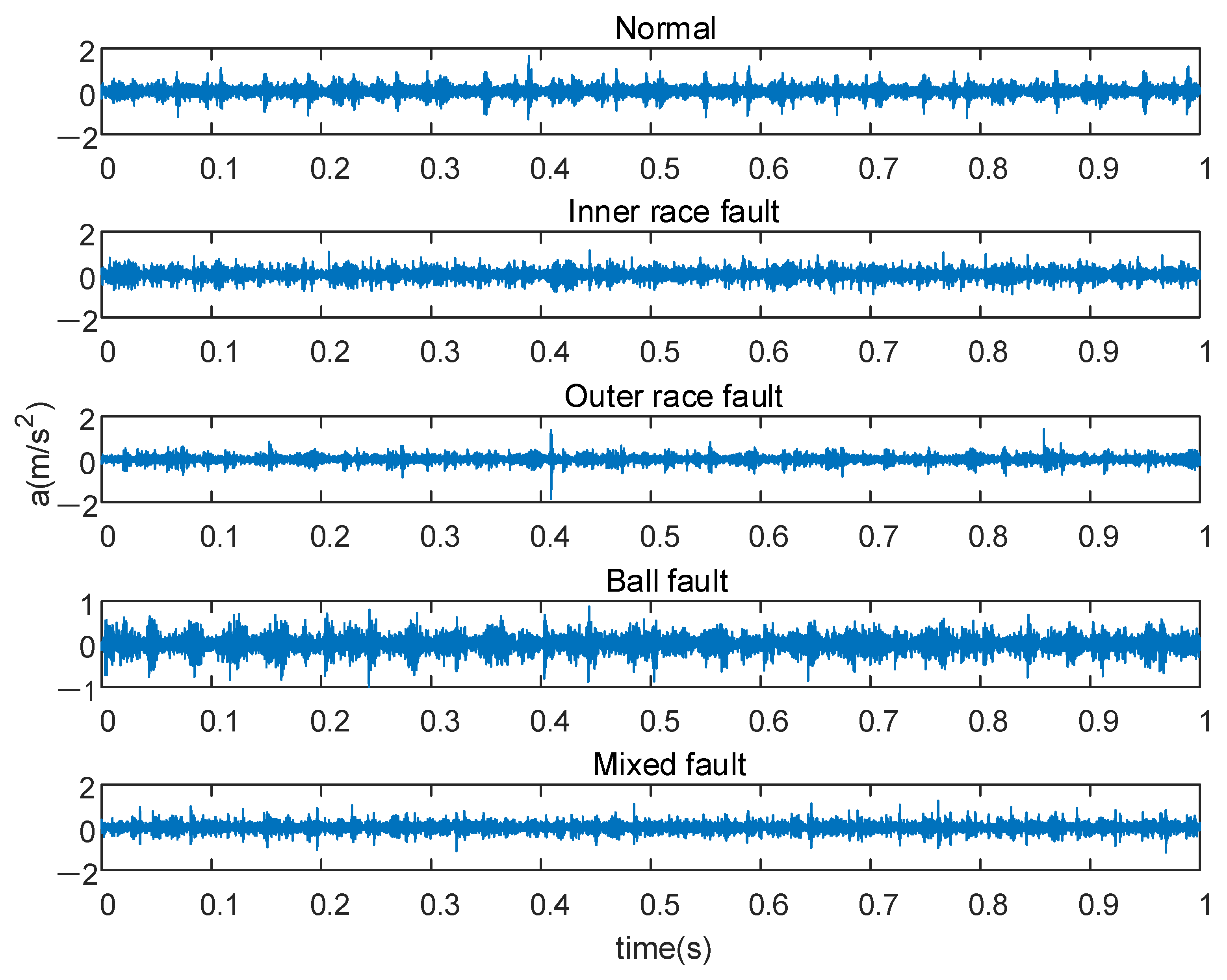
| Fault Type | Image | Classification Label | Fault Size (Inches) | Training Sample Number | Testing Sample Number |
|---|---|---|---|---|---|
| Normal |  | NR | 0 | 30 | 18 |
| Inner race fault |  | IR7 | 0.007 | 30 | 18 |
| IR14 | 0.014 | 30 | 18 | ||
| Ball fault |  | B7 | 0.007 | 30 | 18 |
| B14 | 0.014 | 30 | 18 | ||
| Outer race fault |  | OR7 | 0.007 | 30 | 18 |
| OR14 | 0.014 | 30 | 18 |
| Classification Label | IMF1 | IMF2 | IMF3 | IMF4 |
|---|---|---|---|---|
| NR | 3.9651 | 3.1130 | 2.0256 | 2.1682 |
| IR7 | 3.8240 | 2.7877 | 2.2784 | 2.1812 |
| IR14 | 4.3341 | 2.7363 | 2.2760 | 2.2113 |
| B7 | 4.2778 | 3.1388 | 2.2618 | 2.1427 |
| B14 | 4.2357 | 2.7653 | 2.2930 | 2.1689 |
| OR7 | 3.9152 | 2.1466 | 2.1199 | 2.1342 |
| OR14 | 4.1615 | 3.2886 | 2.1772 | 2.1546 |
| Entropy Method | Classification Algorithm | Accuracy (%) | CPU Time of Classification (s) |
|---|---|---|---|
| MSE | SVM | 98.57 | 74.51 |
| MDE | SVM | 99.05 | 74.11 |
| RCMDE | SVM | 99.92 | 75.27 |
| Population Size | Maximum Number of Iterations | Proportion of Discoverers | Proportion of Watchmen | Security Threshold | Search Range of Parameter c | Search Range of Parameter σ |
|---|---|---|---|---|---|---|
| 10 | 20 | 70% | 20% | 0.6 | [1100] | [1100] |
| Different Methods | Accuracy (%) | Standard Deviation | CPU Time of Classification (s) | ||
|---|---|---|---|---|---|
| Max | Min | Mean | |||
| VMD+MDE+SVM | 99.21 | 98.41 | 99.05 | 0.25 | 74.11 |
| VMD+RCMDE+SVM | 100 | 99.76 | 99.92 | 0.09 | 75.27 |
| VMD+RCMDE+ELM | 99.21 | 96.83 | 98.41 | 0.87 | 1.11 |
| The proposed method | 100 | 100 | 100 | 0 | 3.78 |
| Sensor Model | Sensitivity | Frequency Range | Temperature Range | Weight |
|---|---|---|---|---|
| PCB 333B40 | 500 mV/g | 0.5 Hz~3 kHz | −18~+66 °C | 7.5 g |
| Different Methods | Accuracy (%) | Standard Deviation | CPU Time (s) | ||
|---|---|---|---|---|---|
| Max | Min | Mean | |||
| VMD+MDE+SVM | 83.0 | 74.0 | 78.8 | 3.75 | 53.5 |
| VMD+RCMDE+SVM | 92.0 | 88.0 | 89.9 | 1.40 | 54.8 |
| VMD+RCMDE+ELM | 93.0 | 88.0 | 89.7 | 1.42 | 2.2 |
| The proposed method | 96.0 | 94.0 | 95.0 | 0.77 | 3.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, J.; Sun, W.; Wang, H.; Zhang, F. Coordinated Approach Fusing RCMDE and Sparrow Search Algorithm-Based SVM for Fault Diagnosis of Rolling Bearings. Sensors 2021, 21, 5297. https://doi.org/10.3390/s21165297
Lv J, Sun W, Wang H, Zhang F. Coordinated Approach Fusing RCMDE and Sparrow Search Algorithm-Based SVM for Fault Diagnosis of Rolling Bearings. Sensors. 2021; 21(16):5297. https://doi.org/10.3390/s21165297
Chicago/Turabian StyleLv, Jie, Wenlei Sun, Hongwei Wang, and Fan Zhang. 2021. "Coordinated Approach Fusing RCMDE and Sparrow Search Algorithm-Based SVM for Fault Diagnosis of Rolling Bearings" Sensors 21, no. 16: 5297. https://doi.org/10.3390/s21165297
APA StyleLv, J., Sun, W., Wang, H., & Zhang, F. (2021). Coordinated Approach Fusing RCMDE and Sparrow Search Algorithm-Based SVM for Fault Diagnosis of Rolling Bearings. Sensors, 21(16), 5297. https://doi.org/10.3390/s21165297




