IoT-Enabled Wireless Sensor Networks for Air Pollution Monitoring with Extended Fractional-Order Kalman Filtering
Abstract
:1. Introduction
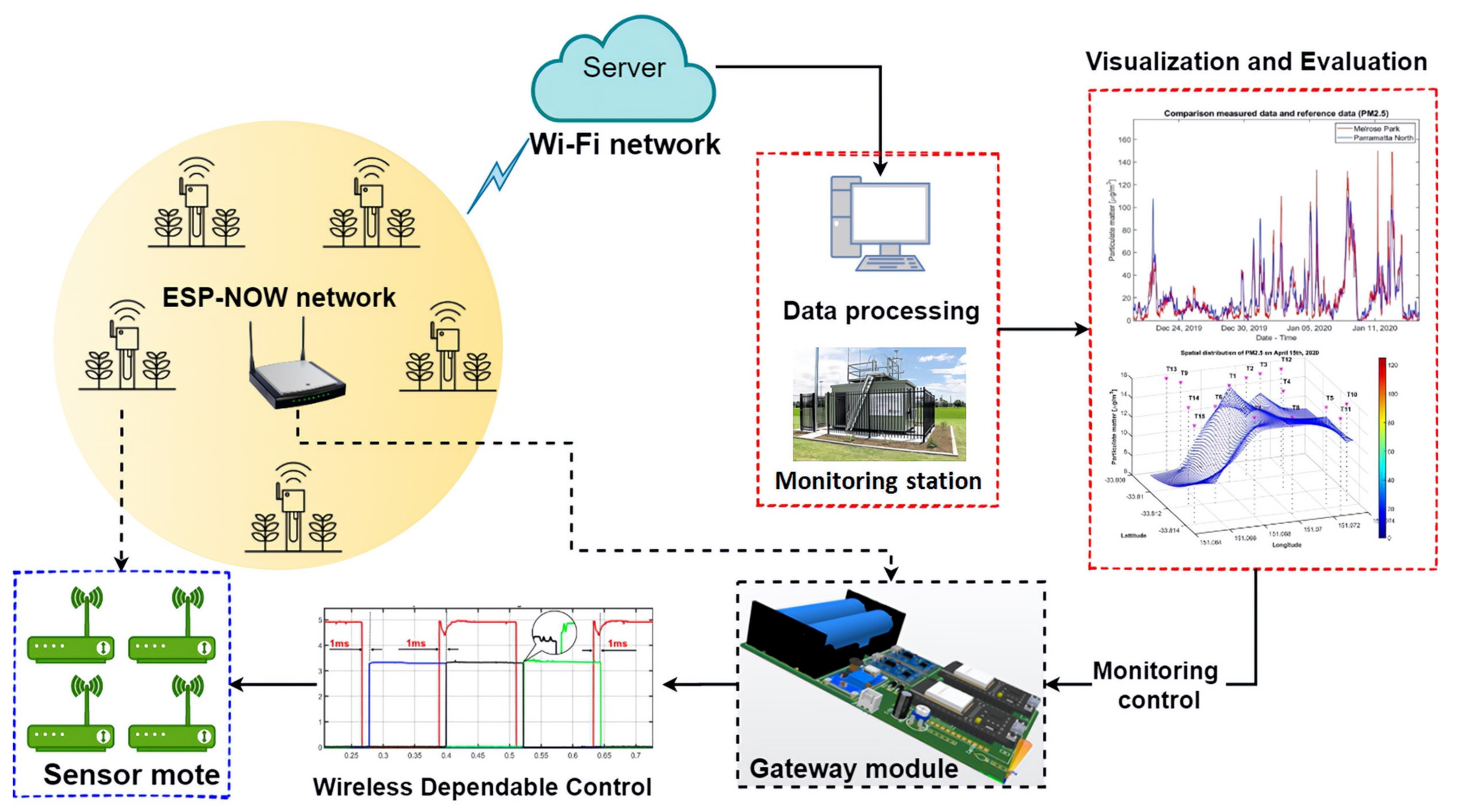
2. IoT-Enabled LWSN System Design
2.1. System Description
2.2. Dependable Monitoring Scheme
2.3. Test Validation
3. Extended Fractional-Order Kalman Filtering (EFKF) Algorithm
3.1. EFKF Derivation
3.2. EFKF Implementation
| Algorithm 1 Standard extended Kalman filtering algorithm |
|
4. Suburban Air Quality Monitoring System
4.1. Description of the Study Area and Experiment Period
4.2. Bushfire Period
4.3. Normal Session
4.4. COVID-19 Session
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organizationa. Ambient (Outdoor) Air Quality and Health. 2018. Available online: http://www.who.int/news-room/factsheets/detail/ambient-(outdoor)-air-quality-and-health (accessed on 5 March 2021).
- Grantz, D.; Garner, J.; Johnson, D. Ecological effects of particulate matter. Environ. Int. 2003, 29, 213–239. [Google Scholar] [CrossRef]
- Zhai, Y.; Liu, X.; Chen, H.; Xu, B.; Zhu, L.; Li, C.; Zeng, G. Source identification and potential ecological risk assessment of heavy metals in PM2.5 from Changsha. Sci. Total Environ. 2014, 493, 109–115. [Google Scholar] [CrossRef]
- Fuzzi, S.; Baltensperger, U.; Carslaw, K.; Decesari, S.; Denier van der Gon, H.; Facchini, M.C.; Fowler, D.; Koren, I.; Langford, B.; Lohmann, U.; et al. Particulate matter, air quality and climate: Lessons learned and future needs. Atmos. Chem. Phys. 2015, 15, 8217–8299. [Google Scholar] [CrossRef] [Green Version]
- Pienkosz, B.D.; Saari, R.K.; Monier, E.; Garcia-Menendez, F. Natural Variability in Projections of Climate Change Impacts on Fine Particulate Matter Pollution. Earth’s Future 2019, 7, 762–770. [Google Scholar] [CrossRef] [Green Version]
- Clements, A.L.; Griswold, W.G.; Rs, A.; Johnston, J.E.; Herting, M.M.; Thorson, J.; Collier-Oxandale, A.; Hannigan, M. Low-Cost Air Quality Monitoring Tools: From Research to Practice (A Workshop Summary). Sensors 2017, 17, 2478. [Google Scholar] [CrossRef] [Green Version]
- Samad, A.; Melchor Mimiaga, F.E.; Laquai, B.; Vogt, U. Investigating a Low-Cost Dryer Designed for Low-Cost PM Sensors Measuring Ambient Air Quality. Sensors 2021, 21, 804. [Google Scholar] [CrossRef]
- Maag, B.; Zhou, Z.; Thiele, L. A Survey on Sensor Calibration in Air Pollution Monitoring Deployments. IEEE Internet Things J. 2018, 5, 4857–4870. [Google Scholar] [CrossRef] [Green Version]
- Silva, I.; Guedes, L.A.; Portugal, P.; Vasques, F. Reliability and Availability Evaluation of Wireless Sensor Networks for Industrial Applications. Sensors 2012, 12, 806–838. [Google Scholar] [CrossRef] [Green Version]
- Bruneo, D.; Puliafito, A.; Scarpa, M. Dependability evaluation of Wireless Sensor Networks: Redundancy and topological aspects. Sensors 2010, 2010, 1827–1831. [Google Scholar] [CrossRef]
- Al-Sodairi, S.; Ouni, R. Reliable and energy-efficient multi-hop LEACH-based clustering protocol for wireless sensor networks. Sustain. Comput. Inform. Syst. 2018, 20, 1–13. [Google Scholar] [CrossRef]
- Nayak, P.; Devulapalli, A. A Fuzzy Logic-Based Clustering Algorithm for WSN to Extend the Network Lifetime. IEEE Sens. J. 2016, 16, 137–144. [Google Scholar] [CrossRef]
- Ha, Q.P.; Metia, S.; Phung, M.D. Sensing Data Fusion for Enhanced Indoor Air Quality Monitoring. IEEE Sens. J. 2020, 20, 4430–4441. [Google Scholar] [CrossRef] [Green Version]
- Xue, G.; Guo, J.; Xu, Y.; Zhao, W. The Fractional Kalman Filter Based Asynchronous Multi-Rate Sensors Information Fusion. In Proceedings of the 2018 10th International Conference on Modelling, Identification and Control (ICMIC), Guiyang, China, 2–4 July 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Hua, S.; Wang, S.; Jin, S.; Feng, S.; Wang, B. Wind speed optimisation method of numerical prediction for wind farm based on Kalman filter method. J. Eng. 2017, 2017, 1146–1149. [Google Scholar] [CrossRef]
- Lai, S.; Yang, T.; Wang, Z.; Chen, P. IoT implementation of Kalman Filter to improve accuracy of air quality monitoring and prediction. Appl. Sci. 2019, 9, 1831. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Chen, K.; Ding, C.; Wang, G.; Liu, Q.; Liu, X. An Adaptive Kalman Filtering Approach to Sensing and Predicting Air Quality Index Values. IEEE Access 2020, 8, 4265–4272. [Google Scholar] [CrossRef]
- Chen, K.; Yu, J. Short-term wind speed prediction using an unscented Kalman filter based state-space support vector regression approach. Appl. Energy 2014, 113, 690–705. [Google Scholar] [CrossRef]
- Metia, S.; Ha, Q.; Duc, H.N.; Scorgie, Y. Urban air pollution estimation using unscented Kalman filtered inverse modeling with scaled monitoring data. Sustain. Cities Soc. 2020, 54. [Google Scholar] [CrossRef]
- Tran, T.; Ha, Q. Dependable Control Systems with Internet of Things. ISA Trans. 2015, 59, 303–313. [Google Scholar] [CrossRef]
- Nguyen, H.A.D.; Nguyen, L.V.; Ha, Q.P. IoT-enabled Dependable Co-located Low-cost Sensing for Construction Site Monitoring. In Proceedings of the 37th International Symposium on Automation and Robotics in Construction (ISARC); International Association for Automation and Robotics in Construction (IAARC): Kitakyushu, Japan, 2020; pp. 616–624. [Google Scholar] [CrossRef]
- Ha, Q.; Phung, M.D. IoT-enabled dependable control for solar energy harvesting in smart buildings. IET Smart Cities 2019, 1, 61–70. [Google Scholar] [CrossRef] [Green Version]
- Espressif Systems. ESP32 Series the Datasheet, Version 3.4. 2020. Available online: https://www.espressif.com/sites/default/files/documentation/esp32_datasheet_en.pdf (accessed on 5 March 2021).
- Sierociuk, D.; Tejado, I.; Vinagre, B.M. Improved fractional Kalman filter and its application to estimation over lossy networks. Signal Process. 2011, 91, 542–552. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, W.; Yu, L. Distributed Fusion Estimation With Missing Measurements, Random Transmission Delays and Packet Dropouts. IEEE Trans. Autom. Control 2014, 59, 1961–1967. [Google Scholar] [CrossRef]
- Shen, H.; Xing, M.; Yan, H.; Park, J.H. Extended Dissipative Filtering for Persistent Dwell-Time Switched Systems With Packet Dropouts. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4796–4806. [Google Scholar] [CrossRef]
- Efe, M.Ö. Fractional Order Systems in Industrial Automation—A Survey. IEEE Trans. Ind. Inform. 2011, 7, 582–591. [Google Scholar] [CrossRef]
- Metia, S.; Oduro, S.D.; Duc, H.N.; Ha, Q. Inverse Air-Pollutant Emission and Prediction Using Extended Fractional Kalman Filtering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2051–2063. [Google Scholar] [CrossRef]
- Mukherjee, B.K.; Metia, S. Real-Time Air Quality Estimation from Station Data Using Extended Fractional Kalman Filter. In Modelling, Simulation and Intelligent Computing; Goel, N., Hasan, S., Kalaichelvi, V., Eds.; Springer: Singapore, 2020; pp. 375–383. [Google Scholar] [CrossRef]
- Oustaloup, A.; Melchior, P.; Lanusse, P.; Cois, O.; Dancla, F. The CRONE toolbox for Matlab. In Proceedings of the IEEE International Symposium on Computer-Aided Control System Design (Cat. No.00TH8537) (CACSD), Anchorage, AK, USA, 25–27 September 2000; pp. 190–195. [Google Scholar] [CrossRef]
- Tepljakov, A. FOMCON: Fractional-Order Modeling and Control Toolbox. In Fractional-Order Modeling and Control of Dynamic Systems; Springer International Publishing: Cham, Switzerland, 2017; pp. 107–129. [Google Scholar] [CrossRef]
- Hartley, T.T.; Lorenzo, C.F. Fractional-order system identification based on continuous order-distributions. Signal Process. 2003, 83, 2287–2300. [Google Scholar] [CrossRef]
- Valério, D.; Sá da Costa, J. Finding a fractional model from frequency and time responses. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 911–921. [Google Scholar] [CrossRef]
- New South Wale Government–Planning Industry and Environment. Search for and Download Air Quality Data. 2021. Available online: https://www.dpie.nsw.gov.au/air-quality/search-for-and-download-air-quality-data (accessed on 5 April 2021).
- Lee, C.H.; Wang, Y.B.; Yu, H.L. An efficient spatiotemporal data calibration approach for the low-cost PM2. 5 sensing network: A case study in Taiwan. Environ. Int. 2019, 130, 104838. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Li, Z.; Cheng, Z.; Ding, Y.; Lin, C.; Xu, Z. Air quality prediction at new stations using spatially transferred bi-directional long short-term memory network. Sci. Total Environ. 2020, 705, 135771. [Google Scholar] [CrossRef]
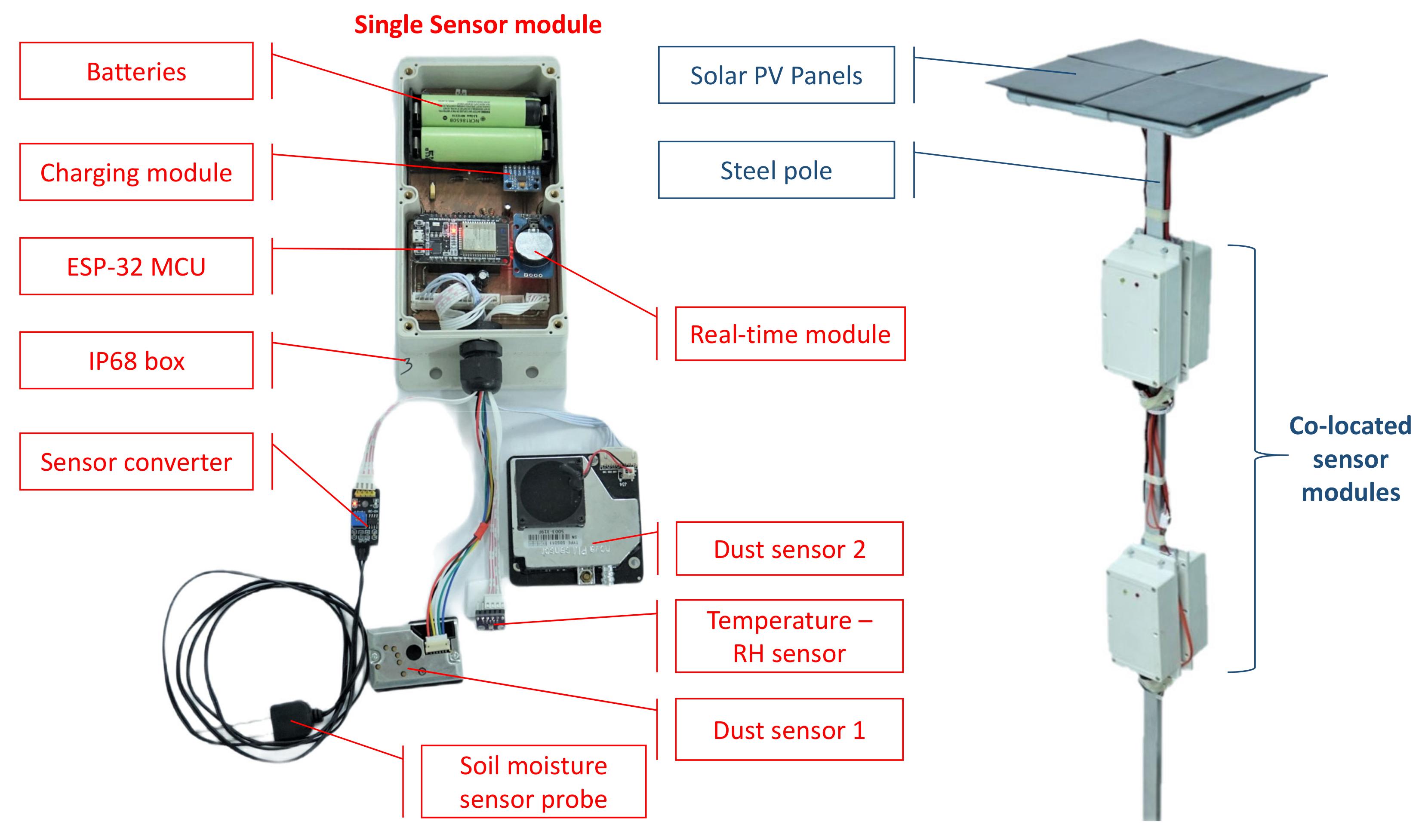









| Components | Features | Cost (USD) |
|---|---|---|
| Sensor SDS011 | PM2.5 and PM10 | 21 |
| BME280 | Air pressure, RH and temperature | 5 |
| Soil Moisture | Corrosion resistance type | 6 |
| Kit ESP32 Node MCU | IoT Microcontroller | 7 |
| TP4506 | Charging battery | 0.4 |
| HT016 | DC-to-DC converter | 0.4 |
| Solar panel | Harvesting solar energy | 7 |
| Battery 18650 | Supply voltage (2 cells) | 12 |
| Box (IP68) | Water and dust protection | 25 |
| Performance Indices→ | EFKF | EKF | ||||
|---|---|---|---|---|---|---|
| Nodes↓ | MAE | RMSE | PCC | MAE | RMSE | PCC |
| EMS1 | 1.4752 | 3.4059 | 0.9996 | 3.9403 | 11.9035 | 0.9749 |
| EMS2 | 1.4100 | 3.2470 | 0.9995 | 4.0939 | 11.6385 | 0.9731 |
| EMS3 | 1.5599 | 3.6213 | 0.9995 | 4.5112 | 12.9454 | 0.9738 |
| EMS4 | 1.5323 | 3.7088 | 0.9995 | 4.6182 | 13.5483 | 0.9730 |
| EMS5 | 1.1516 | 2.1521 | 0.9997 | 2.5089 | 5.0527 | 0.9862 |
| EMS6 | 1.1754 | 1.7911 | 0.9997 | 2.1400 | 3.7255 | 0.9865 |
| EMS7 | 1.5810 | 3.8564 | 0.9995 | 4.6820 | 13.7309 | 0.9742 |
| EMS8 | 1.5014 | 3.7478 | 0.9995 | 4.5629 | 13.2431 | 0.9752 |
| Performance Indices→ | EFKF | EKF | ||||
|---|---|---|---|---|---|---|
| Nodes↓ | MAE | RMSE | PCC | MAE | RMSE | PCC |
| EMS1 | 0.2069 | 0.2895 | 0.9995 | 0.6748 | 0.9410 | 0.9600 |
| EMS2 | 0.2216 | 0.3311 | 0.9992 | 1.0032 | 1.4237 | 0.9362 |
| EMS3 | 0.2009 | 0.3210 | 0.9995 | 0.8496 | 1.2745 | 0.9544 |
| EMS4 | 0.2072 | 0.3133 | 0.9994 | 0.9974 | 1.4191 | 0.9361 |
| EMS5 | 0.1766 | 0.2886 | 0.9994 | 0.9049 | 1.4601 | 0.9290 |
| EMS6 | 0.1679 | 0.2755 | 0.9992 | 0.8110 | 1.2135 | 0.9410 |
| EMS7 | 0.2185 | 0.3397 | 0.9994 | 0.9797 | 1.3946 | 0.9487 |
| EMS8 | 0.2360 | 0.3689 | 0.9995 | 1.0202 | 1.4850 | 0.9501 |
| Performance Indices→ | EFKF | EKF | ||||
|---|---|---|---|---|---|---|
| Nodes↓ | MAE | RMSE | PCC | MAE | RMSE | PCC |
| EMS1 | 0.2294 | 0.3920 | 0.9996 | 0.7945 | 1.3208 | 0.9698 |
| EMS2 | 0.1673 | 0.3012 | 0.9997 | 0.5719 | 0.9531 | 0.9747 |
| EMS3 | 0.1917 | 0.3415 | 0.9997 | 0.6505 | 1.0604 | 0.9753 |
| EMS4 | 0.1790 | 0.3388 | 0.9996 | 0.6847 | 1.3128 | 0.9633 |
| EMS5 | 0.1613 | 0.3064 | 0.9996 | 0.6221 | 1.1606 | 0.9653 |
| EMS6 | 0.1624 | 0.3061 | 0.9997 | 0.6158 | 1.0191 | 0.9732 |
| EMS7 | 0.1836 | 0.3502 | 0.9997 | 0.6178 | 1.0308 | 0.9790 |
| EMS8 | 0.1789 | 0.3395 | 0.9998 | 0.4979 | 0.8402 | 0.9849 |
| EMS9 | 0.2086 | 0.3600 | 0.9994 | 0.8928 | 1.7137 | 0.9408 |
| EMS10 | 0.1617 | 0.3007 | 0.9996 | 0.6130 | 1.1494 | 0.9641 |
| EMS11 | 0.2621 | 0.4801 | 0.9998 | 0.6013 | 1.0920 | 0.9868 |
| EMS12 | 0.1828 | 0.3281 | 0.9997 | 0.6513 | 1.0972 | 0.9717 |
| EMS13 | 0.2348 | 0.3962 | 0.9996 | 0.9219 | 1.5618 | 0.9586 |
| EMS14 | 0.1679 | 0.3094 | 0.9996 | 0.6249 | 1.1411 | 0.9662 |
| EMS15 | 0.2269 | 0.4122 | 0.9996 | 0.9183 | 1.7171 | 0.9563 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Metia, S.; Nguyen, H.A.D.; Ha, Q.P. IoT-Enabled Wireless Sensor Networks for Air Pollution Monitoring with Extended Fractional-Order Kalman Filtering. Sensors 2021, 21, 5313. https://doi.org/10.3390/s21165313
Metia S, Nguyen HAD, Ha QP. IoT-Enabled Wireless Sensor Networks for Air Pollution Monitoring with Extended Fractional-Order Kalman Filtering. Sensors. 2021; 21(16):5313. https://doi.org/10.3390/s21165313
Chicago/Turabian StyleMetia, Santanu, Huynh A. D. Nguyen, and Quang Phuc Ha. 2021. "IoT-Enabled Wireless Sensor Networks for Air Pollution Monitoring with Extended Fractional-Order Kalman Filtering" Sensors 21, no. 16: 5313. https://doi.org/10.3390/s21165313
APA StyleMetia, S., Nguyen, H. A. D., & Ha, Q. P. (2021). IoT-Enabled Wireless Sensor Networks for Air Pollution Monitoring with Extended Fractional-Order Kalman Filtering. Sensors, 21(16), 5313. https://doi.org/10.3390/s21165313






