Minimal Focal Spot Size Measured Based on Intensity and Power Flow
Abstract
:1. Introduction
2. Methods
2.1. Focusing of Light with Linear Polarization
2.2. Focusing of Light with Circular Polarization
2.3. Focusing of Light with Radial Polarization
2.4. Focusing of Optical Vortex with Radial Polarization
2.5. Focusing of Optical Vortex with Azimuthal Polarization
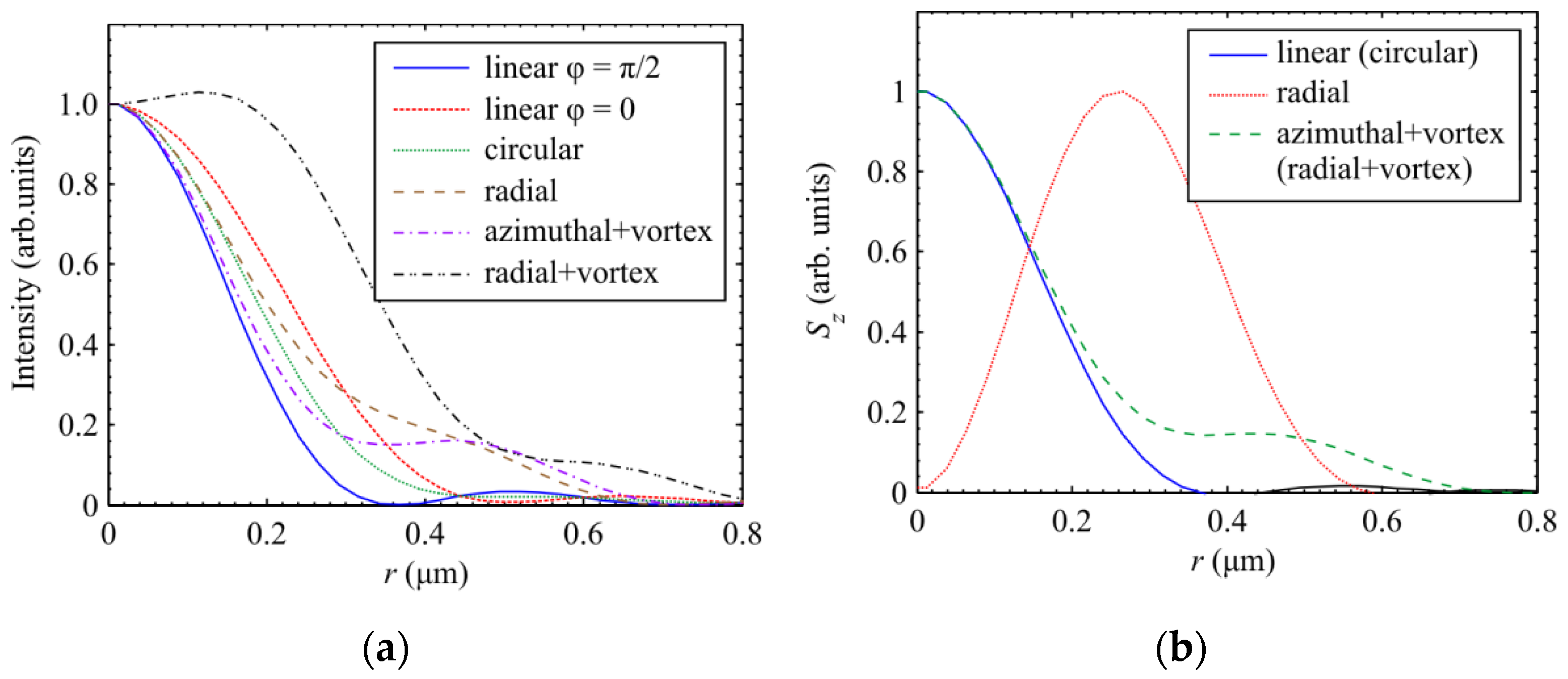
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gu, M.; Li, X.; Cao, Y. Optical storage arrays: A perspective for future big data storage. Light Sci. Appl. 2014, 3, e177. [Google Scholar] [CrossRef] [Green Version]
- Grosjean, T.; Courjon, D.; Bainier, C. Smallest lithographic marks generated by optical focusing systems. Opt. Lett. 2007, 32, 976–978. [Google Scholar] [CrossRef] [PubMed]
- De Angelis, F.; Patrini, M.; Das, G.; Maksymov, I.; Galli, M.; Businaro, L. A Hybrid Plasmonic—Photonic Nanodevice for Label-Free Detection of a Few Molecules. Nano Lett. 2008, 8, 2321–2327. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.W.; Kim, Y.G.; Choi, I.W.; Sung, J.H.; Lee, H.W.; Lee, S.K.; Nam, C.H. Realization of laser intensity over 1023 W/cm2. Optica 2021, 8, 630–635. [Google Scholar] [CrossRef]
- Wang, Q.; Tu, C.; Li, Y.; Wang, H. Polarization singularities: Progress, fundamental physics, and prospects. APL Photonics 2021, 6, 040901. [Google Scholar] [CrossRef]
- Dorn, R.; Quabis, S.; Leuchs, G. Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 2003, 91, 233901. [Google Scholar] [CrossRef] [PubMed]
- Hao, X.; Kuang, C.; Wang, T.; Liu, X. Phase encoding for sharper focus of the azimuthally polarized beam. Opt. Lett. 2010, 35, 3928–3930. [Google Scholar] [CrossRef]
- Nie, Z.; Shi, G.; Zhang, X.; Wang, Y.; Song, Y. Generation of super-resolution longitudinally polarized beam with ultra-long depth of focus using radially polarized hollow Gaussian beam. Opt. Commun. 2014, 331, 87–93. [Google Scholar] [CrossRef]
- Nie, Z.; Shi, G.; Li, D.; Zhang, X.; Wang, Y.; Song, Y. Tight focusing of a radially polarized Laguerre–Bessel–Gaussian beam and its application to manipulation of two types of particles. Phys. Lett. A 2015, 379, 857–863. [Google Scholar] [CrossRef]
- Ren, L.; Zhong, Z.; Zhang, B. Transversely polarized ultra-long optical needles generated by cylindrical polarized circular airy gaussian vortex beams. Opt. Commun. 2021, 483, 126618. [Google Scholar] [CrossRef]
- Lin, H.; Zhou, X.; Chen, Z.; Sasaki, O.; Li, Y.; Pu, J. Tight focusing properties of a circular partially coherent Gaussian beam. J. Opt. Soc. Am. A 2018, 35, 1974. [Google Scholar] [CrossRef]
- Yu, Y.; Huang, H.; Zhou, M.; Zhan, Q. Engineering of multi-segmented light tunnel and flattop focus with designed axial lengths and gaps. Opt. Commun. 2018, 407, 398–401. [Google Scholar] [CrossRef]
- Zhuang, J.; Zhang, L.; Deng, D. Tight-focusing properties of linearly polarized circular Airy Gaussian vortex beam. Opt. Lett. 2020, 45, 296. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, D. 4Pi focusing of spatially modulated radially polarized vortex beams. Opt. Lett. 2012, 37, 1286–1288. [Google Scholar] [CrossRef] [PubMed]
- Prabakaran, K.; Rajesh, K.B.; Sumathira, S.; Bharathi, M.D.; Hemamalini, R.; Musthafa, A.M.; Aroulmoji, V. Creation of Multiple Subwavelength Focal Spot Segments Using Phase Modulated Radially Polarized Multi Gaussian Beam. Chin. Phys. Lett. 2016, 33, 094203. [Google Scholar] [CrossRef]
- Lin, J.; Chen, R.; Jin, P.; Cada, M.; Ma, Y. Generation of longitudinally polarized optical chain by 4π focusing system. Opt. Commun. 2015, 340, 69–73. [Google Scholar] [CrossRef]
- Yu, Y.; Huang, H.; Lin, S.; Chen, M.; Zhan, Q. Generation of optical needles and bright spot arrays through reversing the radiation pattern of collinear antenna array. J. Opt. 2019, 21, 075602. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, B.; Dong, Y.; Wang, S.; Zhu, Z.; Bo, F.; Li, X. Generation of equilateral-polygon-like flat-top focus by tightly focusing radially polarized beams superposed with off-axis vortex arrays. Opt. Express 2017, 25, 26844–26852. [Google Scholar] [CrossRef]
- Chen, H.; Tripathi, S.; Toussaint, K.C. Demonstration of flat-top focusing under radial polarization illumination. Opt. Lett. 2014, 39, 834–837. [Google Scholar] [CrossRef]
- Ping, C.; Liang, C.; Wang, F.; Cai, Y. Radially polarized multi-Gaussian Schell-model beam and its tight focusing properties. Opt. Express 2017, 25, 32475–32490. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Peng, Z.; Wang, M.; Wang, H.; Wei, D.; Gao, H.; Li, F. Tailoring multi-singularity structure induced by a focused radially polarized beam. J. Opt. Soc. Am. A 2021, 38, 419–425. [Google Scholar] [CrossRef]
- Gong, L.; Wang, L.; Zhu, Z.; Wang, X.; Zhao, H.; Gu, B. Generation and manipulation of super-resolution spherical magnetization chains. Appl. Opt. 2016, 55, 5783. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Nie, Z.; Liu, X.; Lan, G.; Zhang, X.; Wang, Y.; Song, Y. Dynamic control of transverse magnetization spot arrays. Opt. Express 2018, 26, 16824. [Google Scholar] [CrossRef] [PubMed]
- Nie, Z.; Ding, W.; Shi, G.; Li, D.; Zhang, X.; Wang, Y.; Song, Y. Achievement and steering of light-induced sub-wavelength longitudinal magnetization chain. Opt. Express 2015, 23, 21296. [Google Scholar] [CrossRef]
- Udhayakumar, M.; Prabakaran, K.; Rajesh, K.B.; Jaroszewicz, Z.; Belafhal, A. Generating sub wavelength pure longitudinal magnetization probe and chain using complex phase plate. Opt. Commun. 2018, 407, 275–279. [Google Scholar] [CrossRef]
- Larocque, H.; Sugic, D.; Mortimer, D.; Taylor, A.J.; Fickler, R.; Boyd, R.W.; Dennis, M.R.; Karimi, E. Reconstructing the topology of optical polarization knots. Nat. Phys. 2018, 14, 1079–1082. [Google Scholar] [CrossRef] [Green Version]
- Bauer, T.; Banzer, P.; Karimi, E.; Orlov, S.; Rubano, A.; Marrucci, L.; Santamato, E.; Boyd, R.W.; Leuchs, G. Observation of optical polarization Möbius strips. Science 2015, 347, 964–966. [Google Scholar] [CrossRef]
- Wang, Y.; Gbur, G. Hilbert’s Hotel in polarization singularities. Opt. Lett. 2017, 42, 5154–5157. [Google Scholar] [CrossRef]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. A Math. Phys. Eng. Sci. 1959, 253, 358–379. [Google Scholar]
- Kotlyar, V.V.; Stafeev, S.S.; Kovalev, A.A. Sharp focusing of a light field with polarization and phase singularities of an arbitrary order. Comput. Opt. 2019, 43, 337–346. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Nalimov, A.G.; Stafeev, S.S. Exploiting the circular polarization of light to obtain a spiral energy flow at the subwavelength focus. J. Opt. Soc. Am. B 2019, 36, 2850–2855. [Google Scholar] [CrossRef]
- Youngworth, K.S.; Brown, T.G. Focusing of high numerical aperture cylindrical-vector beams. Opt. Express 2000, 7, 77–87. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Kovalev, A.A. Reverse and toroidal flux of light fields with both phase and polarization higher-order singularities in the sharp focus area. Opt. Express 2019, 27, 16689–16702. [Google Scholar] [CrossRef]
- Wei, P.; Li, N.; Feng, L. Two-photon polymerization system with diffractive superresolution element. IEEE Sens. J. 2011, 11, 194–198. [Google Scholar] [CrossRef]
- Bayat, N.; Mojabi, P. On the use of focused incident near-field beams in microwave imaging. Sensors 2018, 18, 3127. [Google Scholar] [CrossRef] [Green Version]
- Lindberg, J. Mathematical concept of optical superresolution. J. Opt. 2012, 14, 083001. [Google Scholar] [CrossRef]
- Urbach, H.P.; Pereira, S.F. Focused fields of given power with maximum electric field components. Phys. Rev. A 2009, 79, 013825. [Google Scholar] [CrossRef] [Green Version]
- Sergey-St/richwolf. Available online: https://github.com/Sergey-St/richwolf (accessed on 13 August 2021).

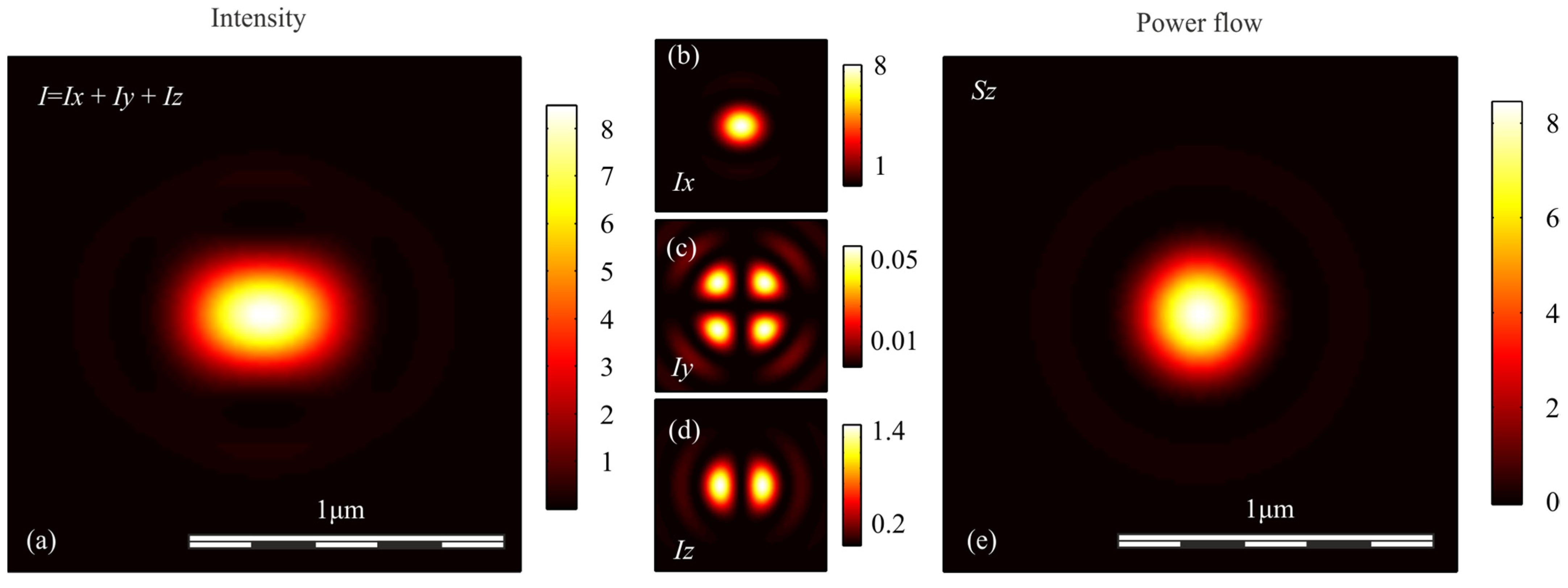
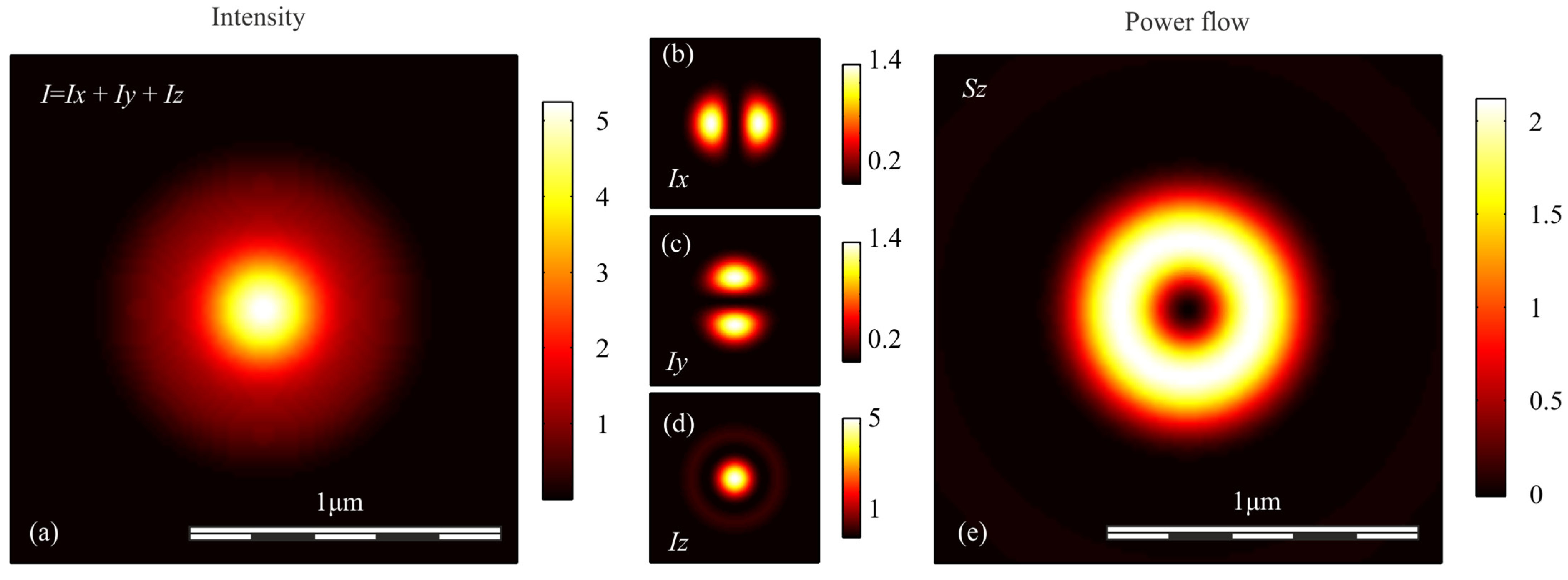
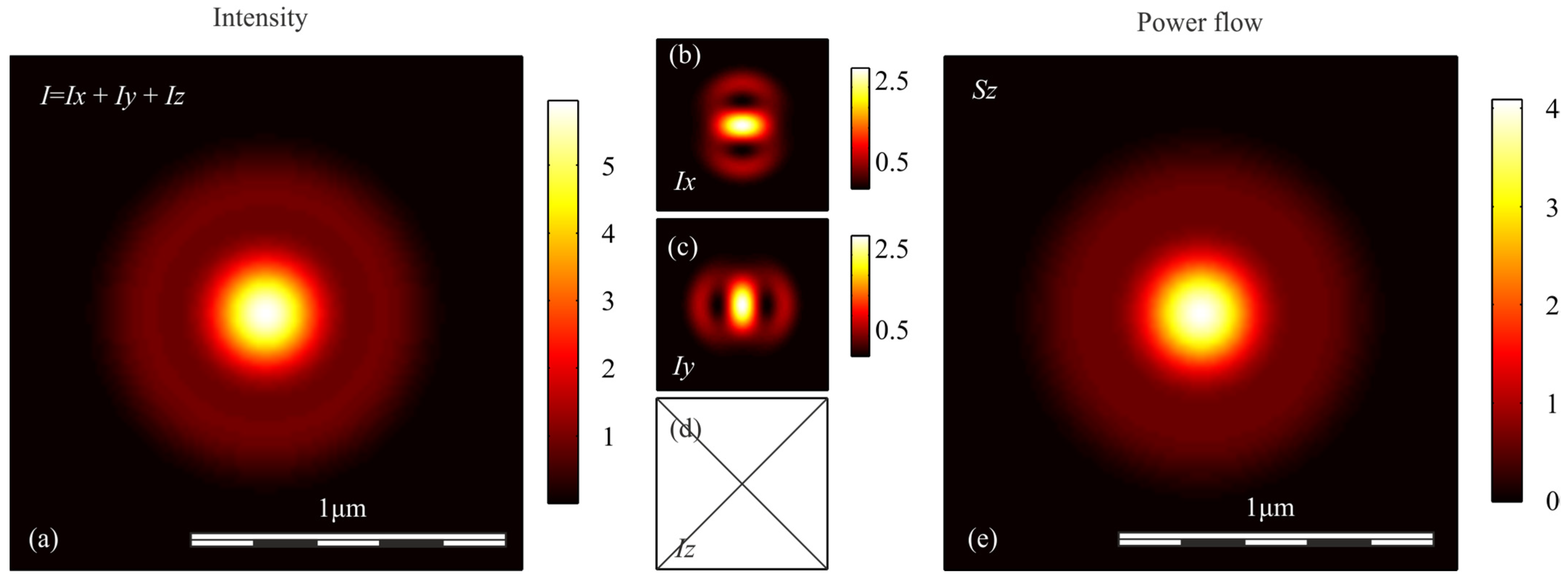
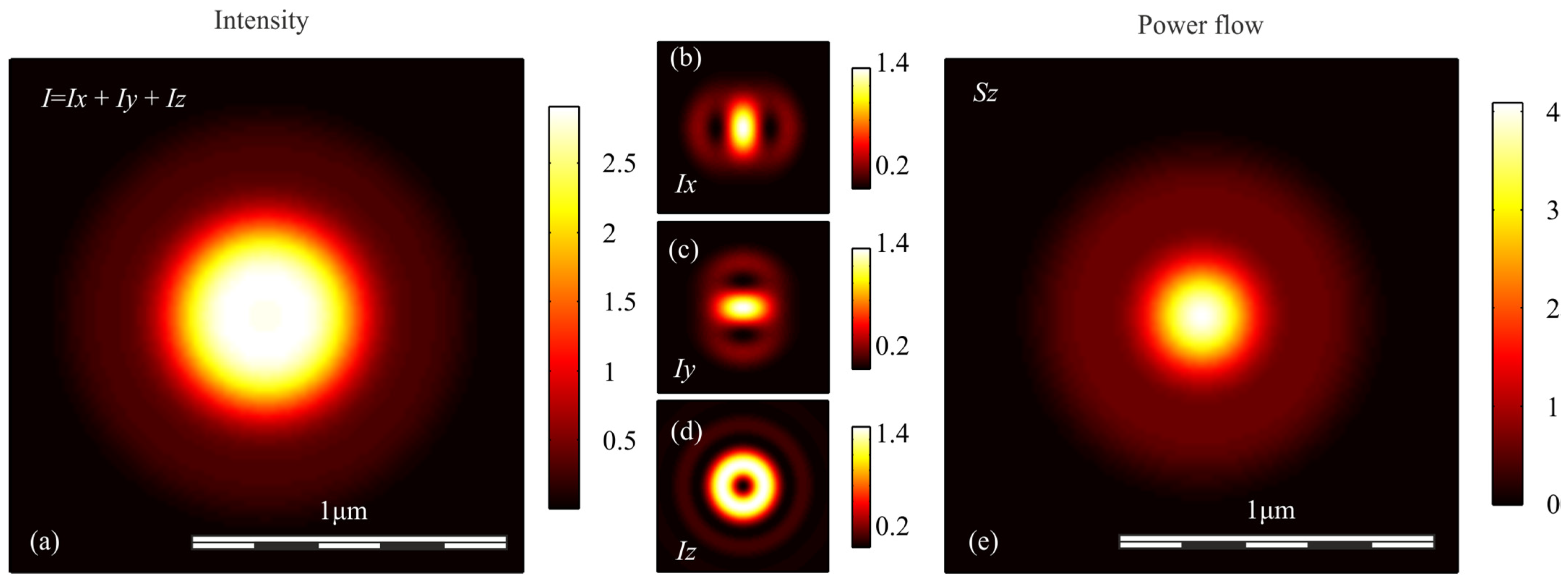
| Polarization | Intensity | Axial Energy Flow |
|---|---|---|
| Linear | ||
| Circular | ||
| Radial | ||
| Radial + vortex | ||
| Azimuthal + vortex |
| Polarization | Intensity | Longitudinal Component of the Poynting Vector Sz | ||
|---|---|---|---|---|
| FWHMx, Λ | FWHMy, Λ | FWHMx, Λ | FWHMy, Λ | |
| Circular | 0.600 | 0.600 | 0.536 | 0.536 |
| Linear | 0.731 | 0.503 | 0.536 | 0.536 |
| Radial | 0.633 | 0.633 | - | - |
| Radial + vortex | 1.075 | 1.075 | 0.557 | 0.557 |
| Azimuthal + vortex | 0.535 | 0.535 | 0.557 | 0.557 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotlyar, V.V.; Stafeev, S.S.; Zaitsev, V.D. Minimal Focal Spot Size Measured Based on Intensity and Power Flow. Sensors 2021, 21, 5505. https://doi.org/10.3390/s21165505
Kotlyar VV, Stafeev SS, Zaitsev VD. Minimal Focal Spot Size Measured Based on Intensity and Power Flow. Sensors. 2021; 21(16):5505. https://doi.org/10.3390/s21165505
Chicago/Turabian StyleKotlyar, Victor V., Sergey S. Stafeev, and Vladislav D. Zaitsev. 2021. "Minimal Focal Spot Size Measured Based on Intensity and Power Flow" Sensors 21, no. 16: 5505. https://doi.org/10.3390/s21165505
APA StyleKotlyar, V. V., Stafeev, S. S., & Zaitsev, V. D. (2021). Minimal Focal Spot Size Measured Based on Intensity and Power Flow. Sensors, 21(16), 5505. https://doi.org/10.3390/s21165505






