1. Introduction
The moon is the hub and bridge between mankind and the universe, while lunar exploration is the premise and basis of deep space exploration. Nowadays, the separated design of an immovable lander and rover is still the core method of zero-distance exploration on the moon. Many countries have made world-renowned achievements such as the Soviet/Russian Luna-9 [
1], the first lander to achieve lunar soft-landing, which absorbs impact energy using four airbags; American Surveyor-1 [
2], the first legged lander to reach the lunar surface, which uses three three-branch buffered legs filled with aluminum honeycomb material, providing technical support for Apollo program [
3]; Chinese Chang’e 4 [
4] reaches the far side of the moon first, which utilizes four similar buffer legs. Notably, all these landers are immovable and are designed to help the rover finish landing, so their exploration capacity is restricted to around the fixed landing site. Two kinds of rover are applied to expand the exploration range, one is a manned lunar rover, like LRV [
5], which can carry up to two astronauts, another is the unmanned wheeled rover, like Yutu 1 & 2 [
4,
6], which can maneuver quickly with scientific instruments. However, the separated design of the lander and rover creates a heavy and complex prober system. The rover only executes exploration in a circle district with the lander as the center and the safety distance as the radius.
Thanks to excellent traversing performance on irregular terrain [
7,
8], legged robots are promising to accomplish lunar exploration compared with a wheeled rover. On the one hand, the leg form is utilized in most existing landers, though they lack mobility on the lunar surface. On the other hand, legged robots are well designed in many fields such as running robots, Bigdog [
9], Cheetah-3 [
10] and Anymal [
11,
12]; underwater robots, Crabster [
13,
14]; heavy-duty robots, Octopus [
15]; and exploration robots, Athlete [
16], Spaceclimber [
17] and Spacebok [
18,
19]. Furthermore, to combine the excellent speed performance for wheeled robots on even terrain and a great adaptive capacity for legged robots on irregular terrain, the wheel-legged robot [
20] adopted a hierarchical framework to control wheel and leg motions; this has drawn a lot of researcher attention. Nevertheless, the current legged or wheel-legged robots are difficult to directly apply to lunar exploration. The hydraulic actuator is widely employed in HyQ2Max [
21] or Bigdog [
9] to obtain high explosive torque, which is infeasible for extraterrestrial exploration. The leg layout of a running robot cannot withstand the landing impact in all directions. The buffer capacity of the current robot is relatively weak, so the engine nozzle under the lander body will be easily damaged for colliding with the ground.
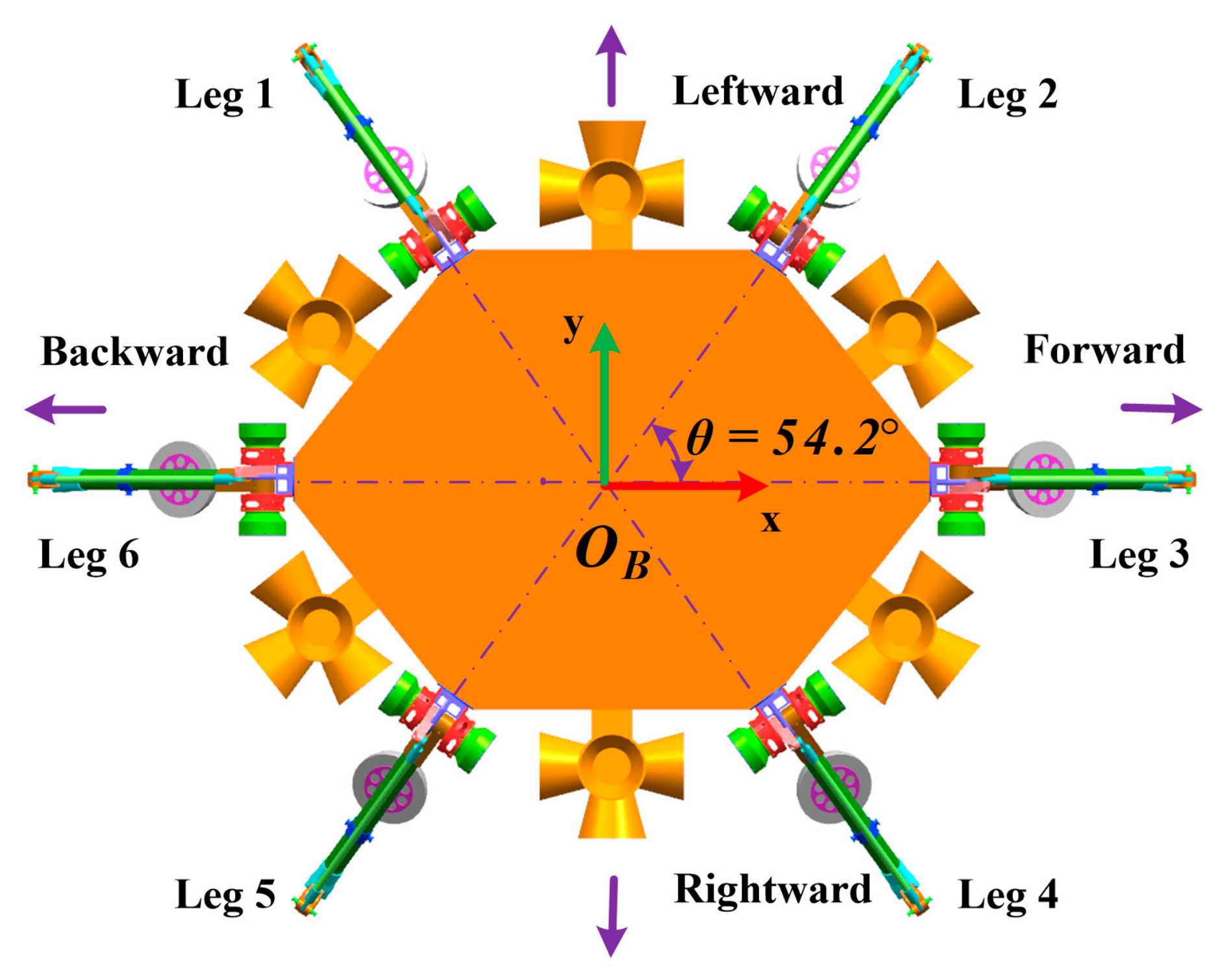
We have designed a six-legged movable repetitive lander “HexaMRL” in previous work to integrate the function of both lander and rover. IDUs are used to simulate the dynamic characters of an active dissipative system of spring and dampener by impedance control to achieve a buffered landing and protect the leg structure, different from the irreversible deformation of aluminum honeycomb material after landing [
22,
23,
24]. Hence, the lander can still execute locomotion as a rover. After exploration at a current landing site, it can fly to the next landing site using the engine and repetitively perform buffered landing tasks. This new exploration mode will significantly increase the utilization rate of an individual prober on the moon and greatly extend the exploration district. However, the repetitive work mode has higher requirements for the quality and fault-tolerant landing capacity of the lander.
In the harsh lunar environment (i.e., intense radiation, large temperature difference and ultravacuum), it is hard to repair with the remote operation if some failures occur on the IDUs. Fault-tolerant control (FTC) for the robot has attracted great attention all over the world and is pivotal for the prober to execute exploration tasks. Nowadays, FTC is generally achieved by the following three methods. Firstly, multiple drives are used in the active joints; for example, Zhang et al. [
25] employ dual-input/single-output (DISO) to drive the servo press machine. Secondly, the parallel robot could use a redundant drive [
26] to eliminate singularities in the workspace. The third one is to increase the DoF of robot end-effector, such as the Canadian space station’s remote manipulator system (SSRMS) [
27], which adopted seven series joints to improve the workspace. However, the above FTC relies on more drives or more complex mechanisms, which will increase the system mass and complexity that are difficult for the lander to accept. Furthermore, fault-tolerant landing is not generally considered in current landers because most of the existing landers are three-legged or four-legged, which constructively lack fault-tolerant landing capacity when one leg fails. For a three-legged lander like Surveyor-1, the remaining two legs cannot support the lander. As for four-legged landers like Apollo 11 [
3] or Chang’e 3, 4, & 5 [
4,
6,
28], the center of mass of the lander will move to the side of the supporting triangle constructed by the remaining three legs, leading to a failed buffer landing on the uneven lunar surface. Therefore, hard strict standards are required for the manufacture and control of such landers and would be abandoned if any failures occur.
The six-legged design in HexaMRL makes the fault-tolerant soft-landing feasible without any supplement of drivers or mechanisms. In this paper, we have systematically studied the fault-tolerant soft-landing performance on the moon for HexaMRL. Firstly, we analyze the classification and stability of the landing configuration and establish the relationship between fault number and landing configuration by the synthesis equation. Secondly, regarding stable configuration, the corresponding fault-tolerant landing algorithms are designed to achieve a buffered landing, and a quasi-incentre stability optimization method is further proposed to increase the stability margin during supported operations. Thirdly, to verify the fault-tolerant landing on the moon, a series of experiments including five-legged, four-legged and three-legged soft-landing with a vertical landing velocity of −1.9 m/s and a payload of 140 kg are successfully carried out on a 5-DoF lunar gravity ground testing platform.
The rest of the paper is organized as follows.
Section 2 introduces the lander system. The landing configuration is analyzed in
Section 3.
Section 4 and
Section 5 design the fault-tolerant algorithm and optimize the stability margin in supporting the operations, respectively.
Section 6 clarifies the fault-tolerant landing experiments, and
Section 7 discusses the experiment results. The last section is the conclusion and its expansion.
4. Fault-Tolerant Landing Algorithms
During the buffer landing period, the force and torque equations of the lander can be written as:
where
is the mass of the lander,
is the gravity acceleration on the moon,
is the number of normal supporting legs,
is the vertical supporting force of the i-th leg,
is the vector from the center of mass to the origin
of the body coordinate frame,
is the vector from
to the i-th foothold,
is the vector form of
,
and
are dividedly the resultant force and torque.
By adjusting the leg force
, we can control the stable body states. After landing, we desire a constant body height and a horizontal body plane. The
will be set to zero and the
will be employed to control the angle deviation of pitch and roll. The PID controller will generate the adjusted torque in real-time. Considering the desired stable values of angle and angular velocity are zero, the
will be calculated from the following equation:
where
,
,
,
,
and
are the proportional, integral and derivative gains in the x-axis and y-axis, respectively.
and
are the actual angles of roll and pitch.
and
are the corresponding velocities.
4.1. VI Configuration
In six-legged normal soft-landing, the force/torque balance equations can be written as follows in matrix form by substituting Equation (8) and
into Equation (7).
However, Equation (9) is an indeterminate equation group and has numerous solutions. It is time-consuming to solve the generalized inverse matrix in a real-time system. Here, a virtual three-legged supporting method (VTLSM) is proposed to allocate the adjusted force
quickly. As illustrated in
Figure 7, we divide the six supporting legs into two groups: leg 1-3-5 supporting (group A) and leg 2-4-6 supporting (group B). During buffer landing, the legs of each group provide half the adjusted force and torque. Then Equation (9) can be rewritten as follows:
where
,
and
are the number of supporting legs in each group. Particularly,
,
and
in group A while
,
and
in group B. Lastly, the indeterminate Equation (9) is transformed into a two determinate Equation (10) that will generate the adjusted foot force
easily in real-time by solving the inverse matrix of a 3 × 3 matrix.
The desired torque of the joint impedance controller in Equation (2) comes from the following equation:
where
is the vector form of adjusted leg force and
is the force Jacobian matrix.
4.2. V Configuration
As for five-legged landing, the 3 × 6 coefficient matrix in Equation (9) will be transformed into a 3 × 5 matrix that is still indeterminate. Here we chose configuration V-2 to illustrate the allocated process of leg forces. The force/torque balance equations are written as:
The VTLSM will be again used to quickly solve the foot force. There are ten virtual triangles (
) constructed by any three supporting legs. They are divided into two cases according to the ground projected position of the center of mass of the lander. If this point is inside the virtual supporting triangles, these triangles are valid, and the number of them is
. On the contrary, if the others are invalid and their number is
. The supporting legs of the valid triangle are leg 1-2-4, leg 1-2-5, leg 1-3-4, leg 1-4-5, leg 2-3-5 and leg 2-4-5, while the ones of the invalid triangle are leg 1-2-3, leg 2-3-4 and leg 3-4-5. Then the
is seven and
is three. Meanwhile, the Equation (10) is modified as follows:
Noticeably, the i-th supporting leg provides adjusted force in multiple valid triangles, so we will obtain the eventual foot force by the following sum operation:
In configuration V-1, we will just change the leg number to 2, 3, 4, 5 and 6. Then the adjusted force can be found by the similar Equations (13) and (14). The detailed classification of the virtual supporting triangle is listed in
Table 5.
4.3. IV and III Configurations
As for four-legged landing, the 3 × 6 coefficient matrix in Equation (9) will be transformed into a 3 × 4 matrix. For example, in IV-2 configuration, the force/torque balance equations are written as:
Similarly, we utilize the VTLSM to calculate the adjusted leg force in real-time. The classification of the virtual supporting triangle is listed in
Table 6.
As for three-legged landing, the 3 × 6 coefficient matrix in Equation (9) will be transformed into a 3 × 3 matrix. For configuration III-4, the equation is written as follows:
Then we can get the adjusted force directly by solving the inverse matrix without the usage of VTLSM.