State Estimation of Axisymmetric Target Based on Beacon Linear Features and View Relation
Abstract
:1. Introduction
- (1)
- Feature points extraction. For objects with obvious texture features, classic SIFT [7], SURF [8], ORB [9] methods, and so on can be used to complete the extraction of feature points. For the objects with unobvious texture features, it is often necessary to mark the feature points manually to achieve the purpose.
- (2)
- State solving method. The solving method can be divided into an iterative method and noniterative method [10]. The iterative method is to construct the objective function of minimizing the residuals of the image square, and then to obtain the optimal state solution through a Newton method [11] or Levenberg–Marquardt (LM) [12] algorithm. However, this algorithm involves many parameters and has low computational efficiency. Among the noniterative algorithms, P4P, P5P, and other algorithms establish the linear equations between the three-dimensional points and the pixel points, that is, the method for solving the homography matrix (C–H method) [13,14]. In addition, Toby Collins et al. [15] proposed a C–IPPE state estimation method, whose solution method is very fast and allows people to fully characterize the method in terms of degeneracies, number of returned solutions, and the geometric relationship of these solutions. In addition, the C–IPPE method is more accurate than the PnP methods in most cases. However, the C–H and C–IPPE state estimation methods based on feature points are extremely dependent on the accuracy of point detection and the accuracy of point pairs matching, and the error of corner detection will directly lead to the deviation of state calculation and the deterioration of robustness.
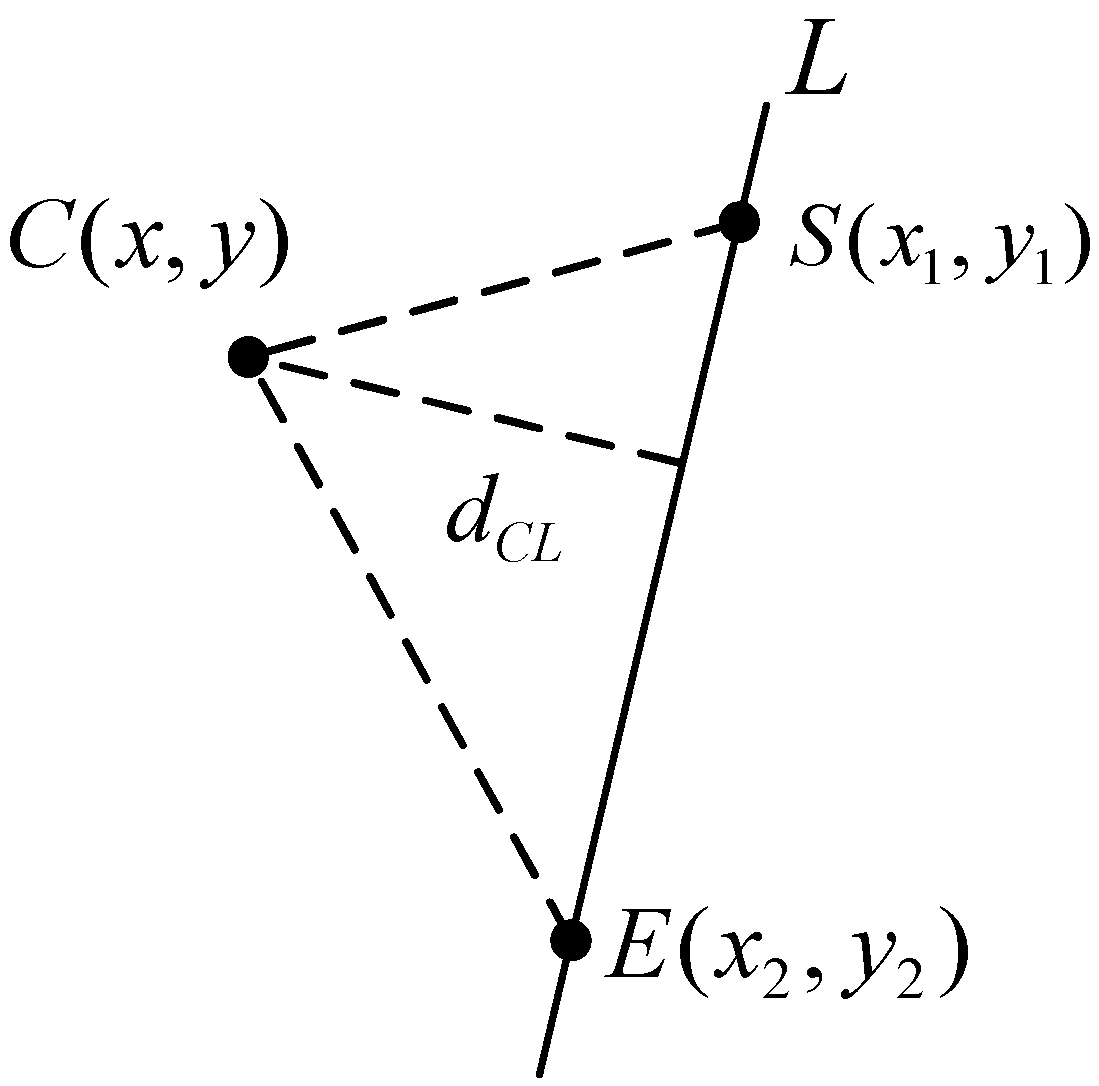
2. Extraction of Beacon Linear Features
- (1)
- Random acquisition of pixel points whose value is not 0 in the binary image, according to the polar co-ordinate system linear equation: , where represents the distance from the normal line to the origin, and is the angle between the normal line and the polar co-ordinate axis. A two-dimensional point corresponds to a straight line, mapped onto a homogeneous two-dimensional co-ordinate curve of , which represents all the straight lines of that pixel point.
- (2)
- PPHT method is applied, where each pixel on its curve for is used to vote. If the number of points in the polar co-ordinate system reaches the minimum number of votes, the corresponding line in the x–y co-ordinate system can be discovered.
- (3)
- The points on the line (and the distance between the points is less than the maximum distance set) are connected into line segments. Then, these points are all deleted and the parameters of the line segment are recorded (set starting point as and end point as ). The length of the line segment should meet the minimum length condition.
- (4)
- The above operations (1), (2), and (3) are repeated until all the pixels of the image have been traversed.
3. State Estimation Based on the Beacon Linear Features and View Relation
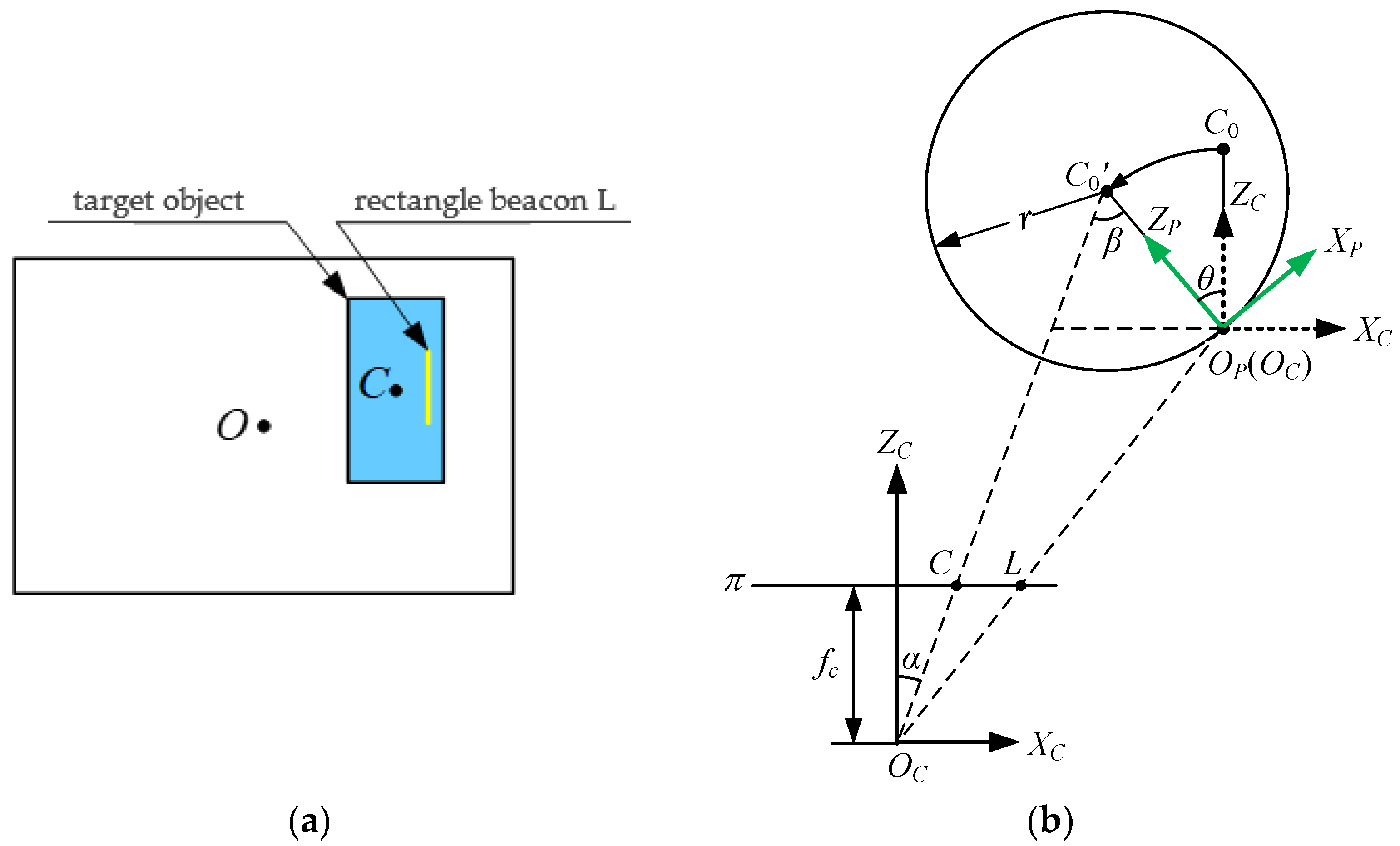
3.1. Target State Description
3.2. State–Solving Model Based on Rotation Matrix
3.2.1. The Target Only Rotates Ry( ) about The YC Axis
3.2.2. The Target Rotates about the ZC Axis and YC Axis
4. Experiment and Result Analysis
4.1. Line Feature Extraction Experiment
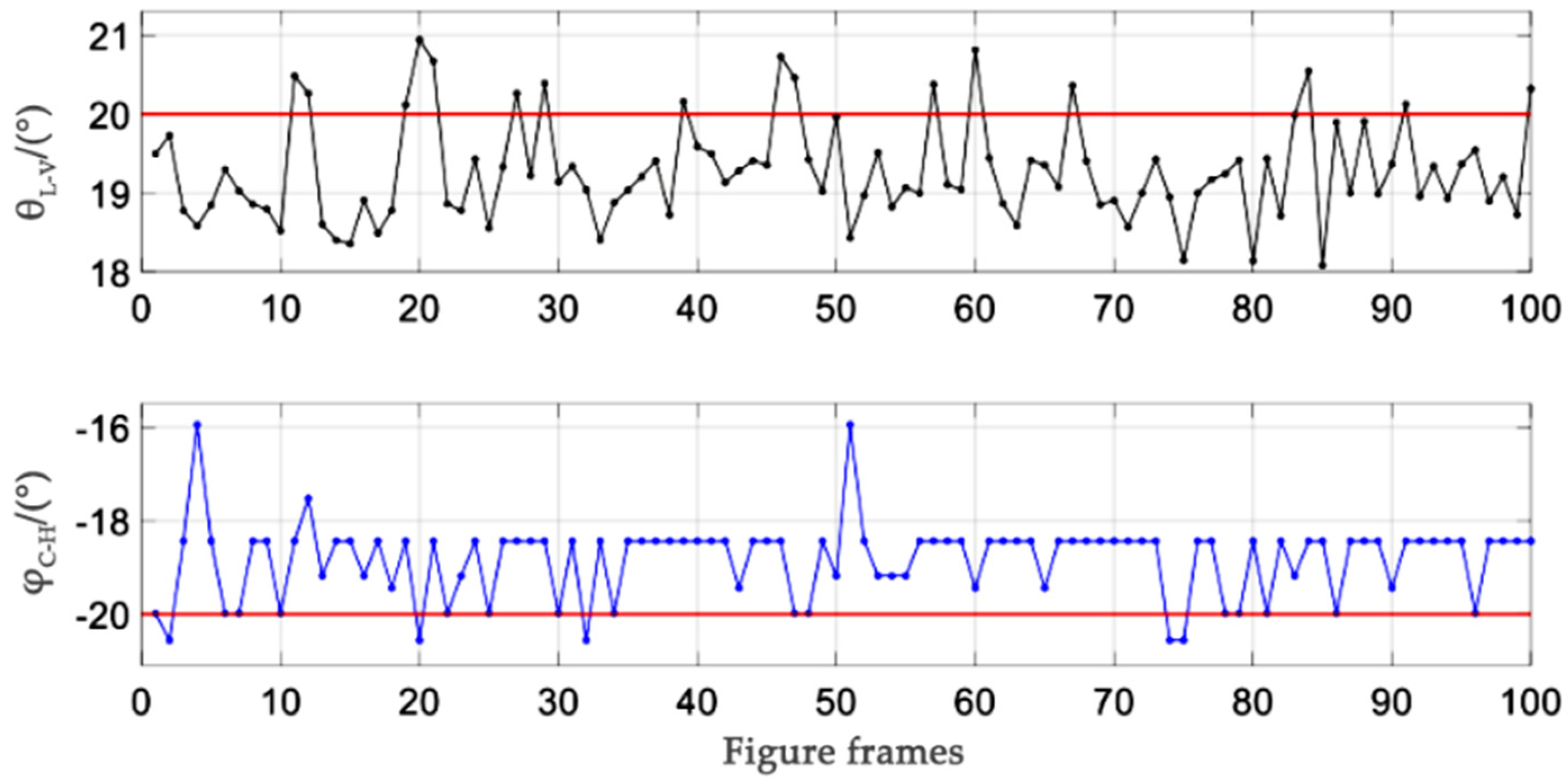
4.2. State Estimation Experiment and Analysis
- (a)
- Only rotate about axis
- (b)
- Only rotate about axis
- (c)
- Rotation angle about the axis and then about the axis
5. Conclusions
6. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, X.; Fan, X.; Yang, X.; Qiu, S. An image appearance based optimization scheme for monocular 6D pose estimation of SOR cabins. Optik 2019, 199, 163115. [Google Scholar] [CrossRef]
- Cheng, Q.; Sun, P.; Yang, C.; Yang, Y.; Liu, P.X. A morphing–Based 3D point cloud reconstruction framework for medical image processing. Comput. Methods Programs Biomed. 2020, 193, 105495. [Google Scholar] [CrossRef]
- Zhu, Q.; Wu, J.; Hu, H.; Xiao, C.; Chen, W. LIDAR Point Cloud Registration for Sensing and Reconstruction of Unstructured Terrain. Appl. Sci. 2018, 8, 2318. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Wang, M.; Zhao, X.; Zhang, D. Multi–View Pose Generator Based on Deep Learning for Monocular 3D Human Pose Estimation. Symmetry 2020, 12, 1116. [Google Scholar] [CrossRef]
- Kendall, A.; Grimes, M.; Cipolla, R. PoseNet: A Convolutional Network for Real–Time 6–DOF Camera Relocalization. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 13–16 December 2015. [Google Scholar]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: An Accurate O(n) Solution to the PnP Problem. Int. J. Comput. Vis. 2008, 81, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Lee, S. Information measure based tone mapping of outdoor LDR image for maximum scale-invariant feature transform extraction. Electron. Lett. 2020, 56, 544–546. [Google Scholar] [CrossRef]
- Zengxiu, S.; Xinhua, W.; Gang, L. Monocular Visual Odometry Based on Homogeneous SURF Feature Points. In Proceedings of the 2017 5th International Conference on Advanced Computer Science Applications and Technologies (ACSAT 2017), Beijing, China, 25 March 2017. [Google Scholar]
- Binbin, X.; Pengyuan, L.; Junning, Z. Research on Improved RGB–D SLAM Algorithm based on ORB Feature. In Proceedings of the 2018 3rd International Conference on Mechatronics and Information Technology (ICMIT 2018), Chengdu, China, 30 October 2018. [Google Scholar]
- Xia, J. Researches on Monocular Vision Based Pose Measurements for Space Targets. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2012. [Google Scholar]
- Pece, A.; Worrall, A. A statistically–based Newton method for pose refinement. Image Vis. Comput. 1998, 16, 541–544. [Google Scholar] [CrossRef]
- Ld, M.; Çetinkaya, K.; Ayyildiz, M. Predictive modeling of geometric shapes of different objects using image processing and an artificial neural network. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2016, 231, 1206–1216. [Google Scholar]
- Zhao, C.; Zhao, H. Accurate and robust feature–based homography estimation using HALF–SIFT and feature localization error weighting. J. Vis. Commun. Image Represent. 2016, 40, 288–299. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Diaz-Ramirez, V.H. Homography estimation by two PClines Hough transforms and a square–radial checkerboard pattern. Appl. Opt. 2018, 57, 3316–3322. [Google Scholar] [CrossRef] [PubMed]
- Collins, T.; Bartoli, A. Infinitesimal Plane–Based Pose Estimation. Int. J. Comput. Vis. 2014, 109, 252–286. [Google Scholar] [CrossRef]
- Wang, B.; He, X.; Wei, Z. A Method of Measuring Pose of Aircraft From Mono–view Based on Line Features. Comput. Meas. Control 2013, 21, 473–476. [Google Scholar]
- Xu, Y.; Jiang, Y.; Chen, F.; Liu, Y. Global Pose Estimation Iterative Algorithm for Multi–camera from Point and Line Correspondences. Acta Photonica Sin. 2010, 39, 1881–1888. [Google Scholar]
- Jl, B.; Shan, G.-L. Estimating Algorithm of 3D Attitude Angles of Flying Target Based on Fast Model Matching. J. Syst. Simul. 2012, 24, 656–659. [Google Scholar]
- Liu, L.; Zhao, G.; Bo, Y. Point Cloud Based Relative Pose Estimation of a Satellite in Close Range. Sensors 2016, 16, 824. [Google Scholar] [CrossRef] [Green Version]
- Vock, R.; Dieckmann, A.; Ochmann, S.; Klein, R. Fast template matching and pose estimation in 3D point clouds. Comput. Graph. 2019, 79, 36–45. [Google Scholar] [CrossRef]
- Yang, B.; Du, X.; Fang, Y.; Li, P.; Wang, Y. Review of rigid object pose estimation from a single image. J. Image Graph. 2021, 26, 334–354. [Google Scholar]
- Hong, M.-X.; Liang, S.-H. Image Segmentation based on Color Space. Comput. Knowl. Technol. 2020, 16, 225–227. [Google Scholar]
- Fakhrina, F.A.; Rahmadwati, R.; Wijono, W. Thinning Zhang-Suen dan Stentiford untuk Menentukan Ekstraksi Ciri (Minutiae) Sebagai Identifikasi Pola Sidik Jari. Maj. Ilm. Teknol. Elektro 2016, 15, 127–133. [Google Scholar]
- Zhao, K.; Han, Q.; Zhang, C.-B.; Xu, J.; Cheng, M.-M. Deep Hough Transform for Semantic Line Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2021. early access. [Google Scholar] [CrossRef]
- Matas, J.; Galambos, C.; Kittler, J. Robust Detection of Lines Using the Progressive Probabilistic Hough Transform. Comput. Vis. Image Underst. 2000, 78, 119–137. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv 3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Srithar, S.; Priyadharsini, M.; Margret Sharmila, F.; Rajan, R. Yolov3 Supervised Machine Learning Frame–work for Real–Time Object Detection and Localization. J. Phys. Conf. Ser. 2021, 1916, 012032. [Google Scholar] [CrossRef]
- Qiu, X.; Wang, G.; Zhao, Y.; Teng, Y.; Yu, L. Multi–pillbox Attitude Estimation Based on YOLOv3 and EPnP Algorithm. Comput. Meas. Control 2021, 29, 126–131. [Google Scholar]
- Gong, X.; Lv, Y.; Xu, X.; Wang, Y.; Li, M. Pose Estimation of Omnidirectional Camera with Improved EPnP Algorithm. Sensors 2021, 21, 4008. [Google Scholar] [CrossRef] [PubMed]
- Ozgoren, M.K. Comparative study of attitude control methods based on Euler angles, quaternions, angle–axis pairs and orientation matrices. Trans. Inst. Meas. Control 2019, 41, 1189–1206. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, J.; Jahangir, Z.; He, S.; Zhang, Q. Estimation of 6D Object Pose Using a 2D Bounding Box. Sensors 2021, 21, 2939. [Google Scholar] [CrossRef] [PubMed]
- Vass, G. Avoiding Gimbal Lock. 2009, Volume 32, pp. 10–11. Available online: https://web.b.ebscohost.com/ehost/detail/detail?vid=0&sid=fc8dc6c3–7405–4432–9c52–f94b8495b880%40pdc–v–sessmgr01&bdata=Jmxhbmc9emgtY24mc2l0ZT1laG9zdC1saXZl#AN=42208299&db=buh (accessed on 13 August 2021).






| Condition | Weak Light | Normal Light | Strong Light |
|---|---|---|---|
| 96.00% | 98.14% | 98.33% | |
| 77.33% | 91.38% | 74.67% | |
| 58.75% | 64.86% | 59.00% | |
| Average | 77.36% | 84.79% | 77.33% |
| True–Value | ||||
| 10 | 10.837 | 8.37 | 0 | 3.368 |
| −10 | −10.220 | 2.20 | −0.004 | −31.023 |
| 20 | 19.126 | −4.37 | 0.008 | 15.538 |
| −20 | −20.287 | 1.44 | 0 | −10.447 |
| 30 | 29.521 | −1.60 | −0.002 | 9.903 |
| −30 | −31.774 | 5.91 | 0 | −17.143 |
| 40 | 41.549 | 3.87 | 0 | 34.355 |
| −40 | −37.445 | −6.39 | 0 | −9.613 |
| 50 | 48.585 | −2.83 | 0 | 26.053 |
| −50 | −49.933 | −0.13 | 0 | 0 |
| 10 | 10.690 | 6.90 | 10.893 | 8.93 | 8.364 | −16.36 |
| −10 | −10.055 | 0.55 | −10.420 | 4.20 | −11.277 | 12.77 |
| 20 | 21.245 | 6.23 | 23.324 | 16.62 | 17.562 | −12.19 |
| −20 | −21.902 | 9.51 | −22.201 | 11.01 | −22.436 | 12.18 |
| 30 | 30.586 | 1.95 | 31.890 | 6.30 | 27.156 | −9.48 |
| −30 | −30.695 | 2.32 | −31.854 | 6.18 | −32.697 | 8.99 |
| Number | True–Value | L–V | C–H | C–IPPE |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 |
| Number | ||||
|---|---|---|---|---|
| 2 | −14.26 | 9.97 | 11.60 | −0.28 |
| 3 | −0.78 | 12.75 | 17.17 | 20.52 |
| 4 | −3.60 | −6.84 | −5.89 | −10.67 |
| 5 | 6.79 | 1.56 | 2.78 | 6.28 |
| 6 | −14.61 | −5.26 | −11.45 | −10.30 |
| 7 | −14.75 | −6.38 | −8.61 | −14.29 |
| 9.132 | 7.127 | 9.583 | 10.390 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Peng, S.; Liu, D. State Estimation of Axisymmetric Target Based on Beacon Linear Features and View Relation. Sensors 2021, 21, 5750. https://doi.org/10.3390/s21175750
Cao X, Peng S, Liu D. State Estimation of Axisymmetric Target Based on Beacon Linear Features and View Relation. Sensors. 2021; 21(17):5750. https://doi.org/10.3390/s21175750
Chicago/Turabian StyleCao, Xiaohua, Shuaiyu Peng, and Daofan Liu. 2021. "State Estimation of Axisymmetric Target Based on Beacon Linear Features and View Relation" Sensors 21, no. 17: 5750. https://doi.org/10.3390/s21175750
APA StyleCao, X., Peng, S., & Liu, D. (2021). State Estimation of Axisymmetric Target Based on Beacon Linear Features and View Relation. Sensors, 21(17), 5750. https://doi.org/10.3390/s21175750






