Homography Ranking Based on Multiple Groups of Point Correspondences
Abstract
:1. Introduction
- The proposed method ranks (sorts) multiple homographies corresponding to individual markers placed on the same plane to select the “best” homography for rectification. Our method handles the absence of position information between markers in the world and builds on top of many-to-one point correspondences. The algorithm is an extension of existing methods since it works with already estimated homography matrices and does not alter them. This easy-to-implement extension is efficient, with a quadratic algorithmic complexity in the number of markers, which is usually very low.
2. Related Work
2.1. Single Homography Estimation
2.2. Multiple Homography Estimation
2.3. Deep Learning-Based Approaches
3. Proposed Method
3.1. Preliminaries
3.2. Homography Ranking Algorithm
| Algorithm 1 Homography ranking. |
|
4. Experiments
4.1. Implementation Details
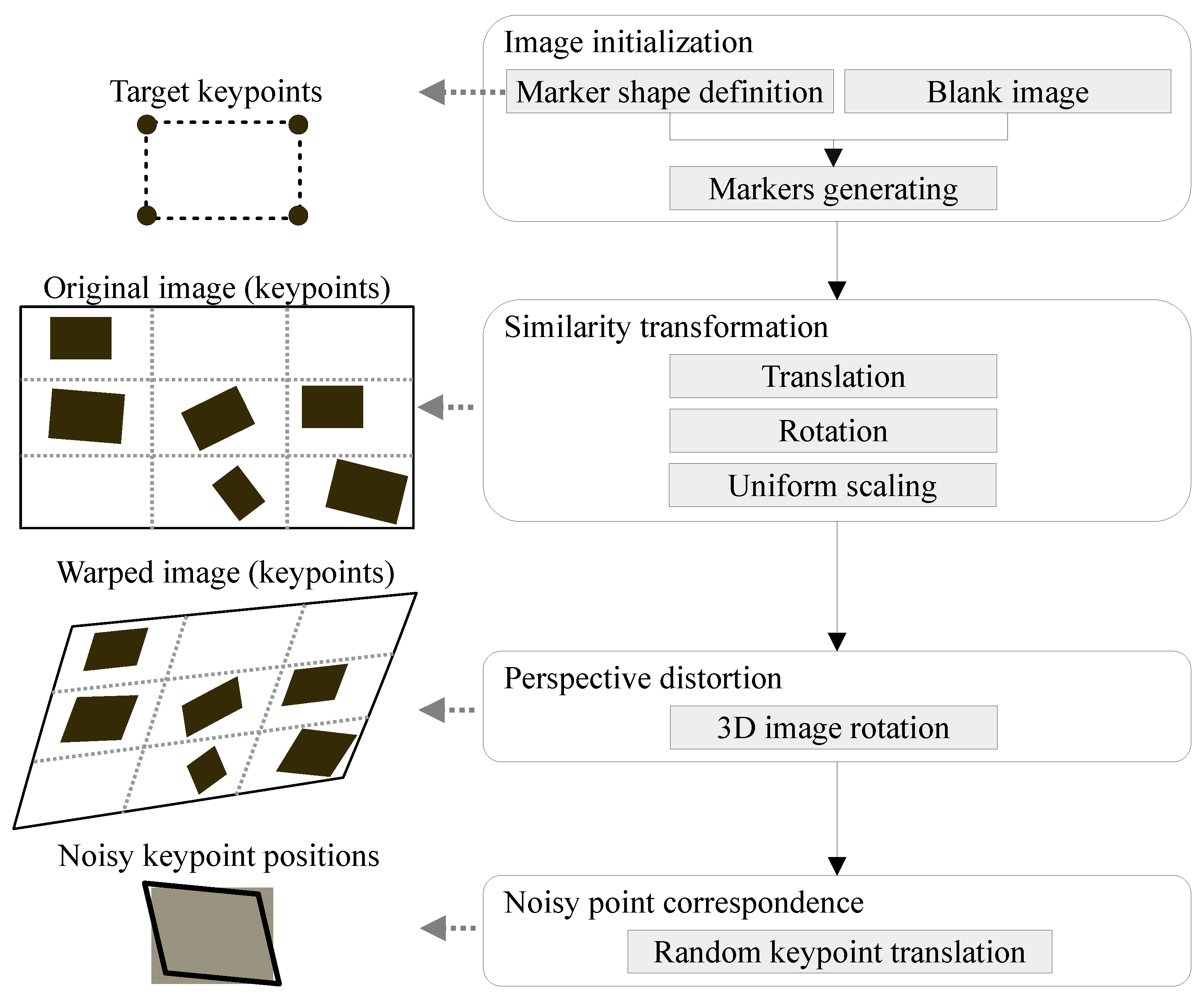
4.2. Dataset Creation
4.2.1. Image Initialization
4.2.2. Similarity Transformation
4.2.3. Perspective Distortion
4.2.4. Noisy Point Correspondence
4.3. Evaluation Methodology
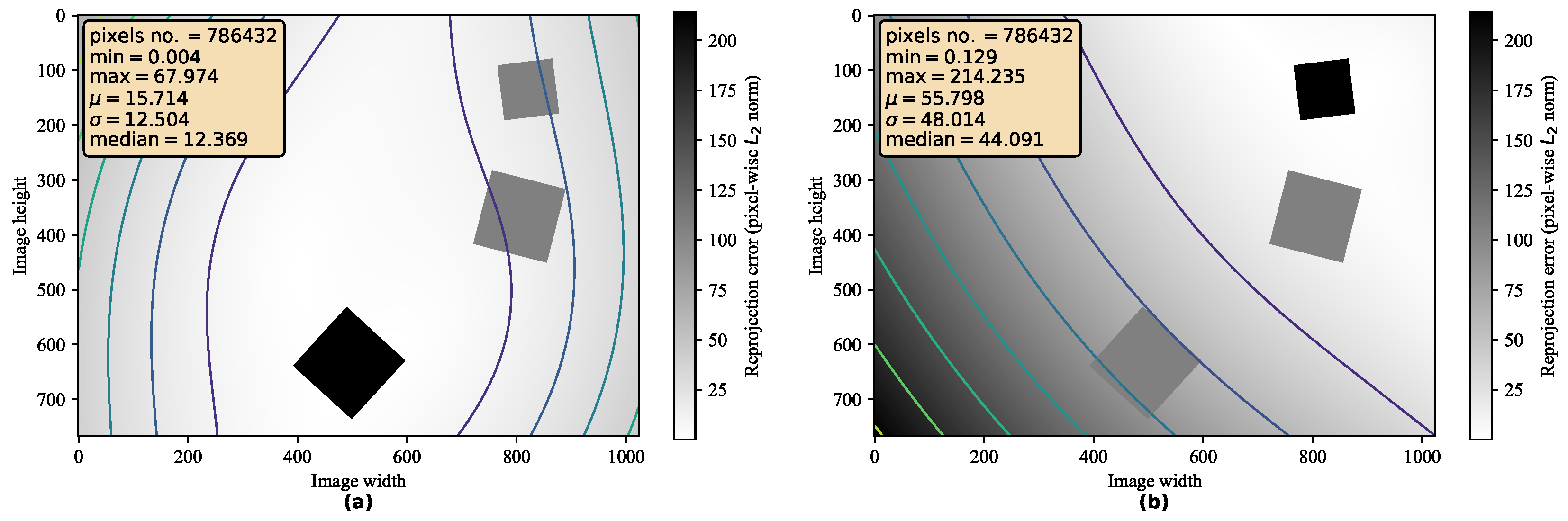
4.3.1. Error Computation
4.3.2. Evaluation Algorithm
| Algorithm 2 Evaluation algorithm. |
|
4.4. Results
4.4.1. Influence of Similarity Transformations
4.4.2. Influence of Noise
4.4.3. Influence of Variable Shapes
4.4.4. Influence of Number of Markers
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Method Details
Appendix A.2. Joint Optimization
References
- Geetha Kiran, A.; Murali, S. Automatic rectification of perspective distortion from a single image using plane homography. J. Comput. Sci. Appl. 2013, 3, 47–58. [Google Scholar]
- Bousaid, A.; Theodoridis, T.; Nefti-Meziani, S.; Davis, S. Perspective distortion modeling for image measurements. IEEE Access 2020, 8, 15322–15331. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Hartley, R.I. In defense of the eight-point algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 580–593. [Google Scholar] [CrossRef] [Green Version]
- Lu, S.; Chen, B.M.; Ko, C.C. Perspective rectification of document images using fuzzy set and morphological operations. Image Vis. Comput. 2005, 23, 541–553. [Google Scholar] [CrossRef]
- Miao, L.; Peng, S. Perspective rectification of document images based on morphology. In Proceedings of the 2006 International Conference on Computational Intelligence and Security, Guangzhou, China, 3–6 November 2006; Volume 2, pp. 1805–1808. [Google Scholar] [CrossRef]
- Adel, E.; Elmogy, M.; Elbakry, H. Image stitching based on feature extraction techniques: A survey. Int. J. Comput. Appl. 2014, 99, 1–8. [Google Scholar] [CrossRef]
- Gao, J.; Kim, S.J.; Brown, M.S. Constructing image panoramas using dual-homography warping. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 49–56. [Google Scholar] [CrossRef]
- Liu, W.X.; Chin, T. Smooth Globally Warp Locally: Video Stabilization Using Homography Fields. In Proceedings of the 2015 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Adelaide, SA, Australia, 23–25 November 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Mariyanayagam, D.; Gurdjos, P.; Chambon, S.; Brunet, F.; Charvillat, V. Pose estimation of a single circle using default intrinsic calibration. In Asian Conference on Computer Vision; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Arróspide, J.; Salgado, L.; Nieto, M.; Mohedano, R. Homography-based ground plane detection using a single on-board camera. IET Intell. Transp. Syst. 2010, 4, 149–160. [Google Scholar] [CrossRef] [Green Version]
- Luo, L.B.; Koh, I.S.; Min, K.Y.; Wang, J.; Chong, J.W. Low-cost implementation of bird’s-eye view system for camera-on-vehicle. In Proceedings of the 2010 Digest of Technical Papers International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 9–13 January 2010; pp. 311–312. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, M.; Jiang, G.; Pan, Z.; Lin, J. Image Registration Algorithm Based on Convolutional Neural Network and Local Homography Transformation. Appl. Sci. 2020, 10, 732. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhou, L.; Liu, H.; Shang, Y. A Flexible Online Camera Calibration Using Line Segments. J. Sens. 2016, 2016, 2802343. [Google Scholar] [CrossRef] [Green Version]
- Osuna-Enciso, V.; Cuevas, E.; Oliva, D.; Zúñiga, V.; Pérez-Cisneros, M.; Zaldívar, D. A Multiobjective Approach to Homography Estimation. Comput. Intell. Neurosci. 2015, 2016, 3629174. [Google Scholar] [CrossRef] [Green Version]
- Mou, W.; Wang, H.; Seet, G.; Zhou, L. Robust homography estimation based on non-linear least squares optimization. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013; pp. 372–377. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Bradski, G.; Kaehler, A. Learning OpenCV: Computer Vision with the OpenCV Library; O’Reilly Media, Inc.: Newton, MA, USA, 2008. [Google Scholar]
- Agarwal, A.; Jawahar, C.; Narayanan, P. A Survey of Planar Homography Estimation Techniques; Technical Report IIIT/TR/2005/12; Centre for Visual Information Technology: Telangana, India, 2005. [Google Scholar]
- Benligiray, B.; Topal, C.; Akinlar, C. STag: A stable fiducial marker system. Image Vis. Comput. 2019, 89, 158–169. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Wen, X.; Zhang, F.; Wang, X.; Wang, G. Homography estimation based on order-preserving constraint and similarity measurement. IEEE Access 2018, 6, 28680–28690. [Google Scholar] [CrossRef]
- Jawahar, C.; Jain, P. Homography estimation from planar contours. In Proceedings of the Third International Symposium on 3D Data Processing, Visualization, and Transmission (3DPVT’06), Chapel Hill, NC, USA, 14–16 June 2006; pp. 877–884. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, J.; Wang, G. Minimizing Geometric Distance by Iterative Linear Optimization. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Chum, O.; Pajdla, T.; Sturm, P. The geometric error for homographies. Comput. Vis. Image Underst. 2005, 97, 86–102. [Google Scholar] [CrossRef] [Green Version]
- Li, T.M.; Gharbi, M.; Adams, A.; Durand, F.; Ragan-Kelley, J. Differentiable programming for image processing and deep learning in Halide. ACM Trans. Graph. 2018, 37, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Song, W.H.; Jung, H.G.; Gwak, I.Y.; Lee, S.W. Oblique aerial image matching based on iterative simulation and homography evaluation. Pattern Recognit. 2019, 87, 317–331. [Google Scholar] [CrossRef]
- Vincent, E.; Laganiére, R. Detecting planar homographies in an image pair. In Proceedings of the ISPA 2001, the 2nd International Symposium on Image and Signal Processing and Analysis and 23rd International Conference on Information Technology Interfaces, Pula, Croatia, 19–21 July 2001; pp. 182–187. [Google Scholar] [CrossRef] [Green Version]
- Bose, B.; Grimson, E. Ground plane rectification by tracking moving objects. In Proceedings of the e Joint IEEE International Workshop on Visual Surveillance and Performance Evaluation of Tracking and Surveillance, Lausanne, Switzerland, 28 July 2003; Volume 7. [Google Scholar]
- Eriksson, A.; Van Den Hengel, A. Optimization on the manifold of multiple homographies. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 242–249. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, A.; López-de Teruel, P.E.; Fernández, L. Practical Planar Metric Rectification. In Proceedings of the BMVC, Edinburgh, UK, 4–7 September 2006; pp. 579–588. [Google Scholar]
- Pirchheim, C.; Reitmayr, G. Homography-based planar mapping and tracking for mobile phones. In Proceedings of the 2011 10th IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 26–29 October 2011; pp. 27–36. [Google Scholar] [CrossRef]
- Chojnacki, W.; Szpak, Z.L.; Brooks, M.J.; Van Den Hengel, A. Multiple homography estimation with full consistency constraints. In Proceedings of the 2010 International Conference on Digital Image Computing: Techniques and Applications, Sydney, NSW, Australia, 1–3 December 2010; pp. 480–485. [Google Scholar] [CrossRef] [Green Version]
- Park, K.w.; Shim, Y.J.; Lee, M.j.; Ahn, H. Multi-Frame Based Homography Estimation for Video Stitching in Static Camera Environments. Sensors 2020, 20, 92. [Google Scholar] [CrossRef] [Green Version]
- Cui, Z.; Jiang, K.; Wang, T. Unsupervised Moving Object Segmentation from Stationary or Moving Camera Based on Multi-frame Homography Constraints. Sensors 2019, 19, 4344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fraundorfer, F.; Schindler, K.; Bischof, H. Piecewise planar scene reconstruction from sparse correspondences. Image Vis. Comput. 2006, 24, 395–406. [Google Scholar] [CrossRef]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Deep Image Homography Estimation. arXiv 2016, arXiv:1606.03798. [Google Scholar]
- Zhang, J.; Wang, C.; Liu, S.; Jia, L.; Ye, N.; Wang, J.; Zhou, J.; Sun, J. Content-Aware Unsupervised Deep Homography Estimation. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 653–669. [Google Scholar]
- Le, H.; Liu, F.; Zhang, S.; Agarwala, A. Deep Homography Estimation for Dynamic Scenes. arXiv 2020, arXiv:2004.02132. [Google Scholar]
- Zhao, Q.; Ma, Y.; Zhu, C.; Yao, C.; Feng, B.; Dai, F. Image stitching via deep homography estimation. Neurocomputing 2021, 450, 219–229. [Google Scholar] [CrossRef]
- Tao, Y.; Ling, Z. Deep Features Homography Transformation Fusion Network—A Universal Foreground Segmentation Algorithm for PTZ Cameras and a Comparative Study. Sensors 2020, 20, 3420. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, X. STN-Homography: Direct Estimation of Homography Parameters for Image Pairs. Appl. Sci. 2019, 9, 5187. [Google Scholar] [CrossRef] [Green Version]
- Barath, D.; Hajder, L. Novel Ways to Estimate Homography from Local Affine Transformations. In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016), Rome, Italy, 27–29 February 2016; Magnenat-Thalmann, N., Richard, P., Linsen, L., Telea, A.C., Battiato, S., Imai, F.H., Braz, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 3, pp. 434–445. [Google Scholar] [CrossRef] [Green Version]
- Beck, G. Planar Homography Estimation from Traffic Streams via Energy Functional Minimization. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2016. [Google Scholar]
- Abdel-Aziz, Y.; Karara, H.; Hauck, M. Direct Linear Transformation from Comparator Coordinates into Object Space Coordinates in Close-Range Photogrammetry. Photogramm. Eng. Remote Sens. 2015, 81, 103–107. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Corfu, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the NIPS 2017 Workshop Autodiff, NIPS-W, Long Beach, CA, USA, 9 December 2017. [Google Scholar]
- Fletcher, R. Newton-Like Methods. In Practical Methods of Optimization; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2000; Chapter 3; pp. 44–79. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Science & Business Media: Hoboken, NJ, USA, 2006. [Google Scholar]







| Shape | Markers | Transl. | Rotation | Scale | Noise | Top Relative Improvement | Top Absolute Improvement | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Median | Mean | Stdev | Median | Mean | Stdev | ||||||
| square | 6 | no | no | no | no | 62.80% | 59.63% | 19.64% | 0.00029 | 0.00030 | 0.00014 |
| square | 6 | yes | no | no | no | 62.65% | 59.00% | 19.72% | 0.00028 | 0.00029 | 0.00013 |
| square | 6 | no | yes | no | no | 66.42% | 63.17% | 19.11% | 0.00041 | 0.00043 | 0.00020 |
| square | 6 | no | no | yes | no | 63.38% | 58.51% | 23.97% | 0.00024 | 0.00025 | 0.00015 |
| square | 6 | yes | yes | yes | no | 67.82% | 63.66% | 20.30% | 0.00035 | 0.00037 | 0.00019 |
| square | 6 | yes | yes | yes | yes | 64.11% | 59.26% | 22.12% | 22.07813 | 24.31773 | 15.00850 |
| 5-poly | 6 | yes | yes | yes | yes | 74.67% | 71.19% | 21.98% | 69.55532 | 336.26534 | 685.74274 |
| 7-poly | 6 | yes | yes | yes | yes | 71.02% | 65.63% | 22.99% | 46.79390 | 135.65737 | 395.75257 |
| 9-poly | 6 | yes | yes | yes | yes | 68.97% | 65.57% | 21.98% | 44.97627 | 115.12189 | 309.27201 |
| square | 3 | yes | yes | yes | yes | 46.91% | 41.36% | 31.58% | 14.77504 | 18.11548 | 20.67457 |
| square | 5 | yes | yes | yes | yes | 59.03% | 53.91% | 24.56% | 19.76285 | 22.53333 | 16.00804 |
| square | 7 | yes | yes | yes | yes | 66.19% | 62.41% | 19.98% | 23.87681 | 27.13637 | 32.28533 |
| square | 9 | yes | yes | yes | yes | 69.86% | 66.09% | 18.18% | 25.66452 | 26.68378 | 11.69754 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ondrašovič, M.; Tarábek, P. Homography Ranking Based on Multiple Groups of Point Correspondences. Sensors 2021, 21, 5752. https://doi.org/10.3390/s21175752
Ondrašovič M, Tarábek P. Homography Ranking Based on Multiple Groups of Point Correspondences. Sensors. 2021; 21(17):5752. https://doi.org/10.3390/s21175752
Chicago/Turabian StyleOndrašovič, Milan, and Peter Tarábek. 2021. "Homography Ranking Based on Multiple Groups of Point Correspondences" Sensors 21, no. 17: 5752. https://doi.org/10.3390/s21175752
APA StyleOndrašovič, M., & Tarábek, P. (2021). Homography Ranking Based on Multiple Groups of Point Correspondences. Sensors, 21(17), 5752. https://doi.org/10.3390/s21175752







