Multiplex Detection of Magnetic Beads Using Offset Field Dependent Frequency Mixing Magnetic Detection
Abstract
:1. Introduction
2. Materials and Methods
2.1. Magnetic Beads
2.2. Sample Preparation
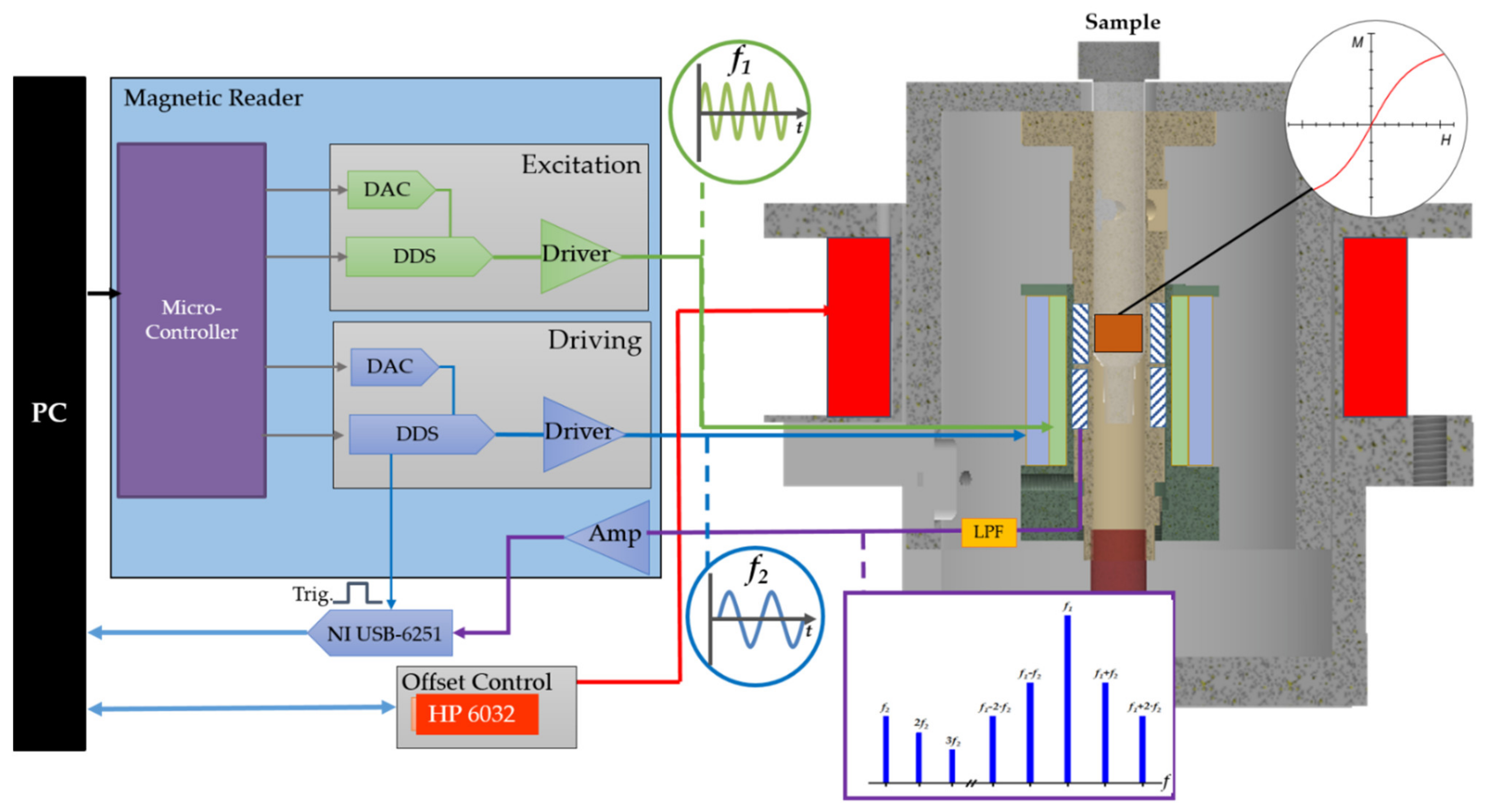
2.3. Frequency Mixing Magnetic Detection
2.4. Static Magnetic Offset Setup
2.5. Measurement Procedure
2.5.1. Measurement Protocol
2.5.2. Data Processing
2.6. Quadratic Programming Optimization
3. Results and Discussion
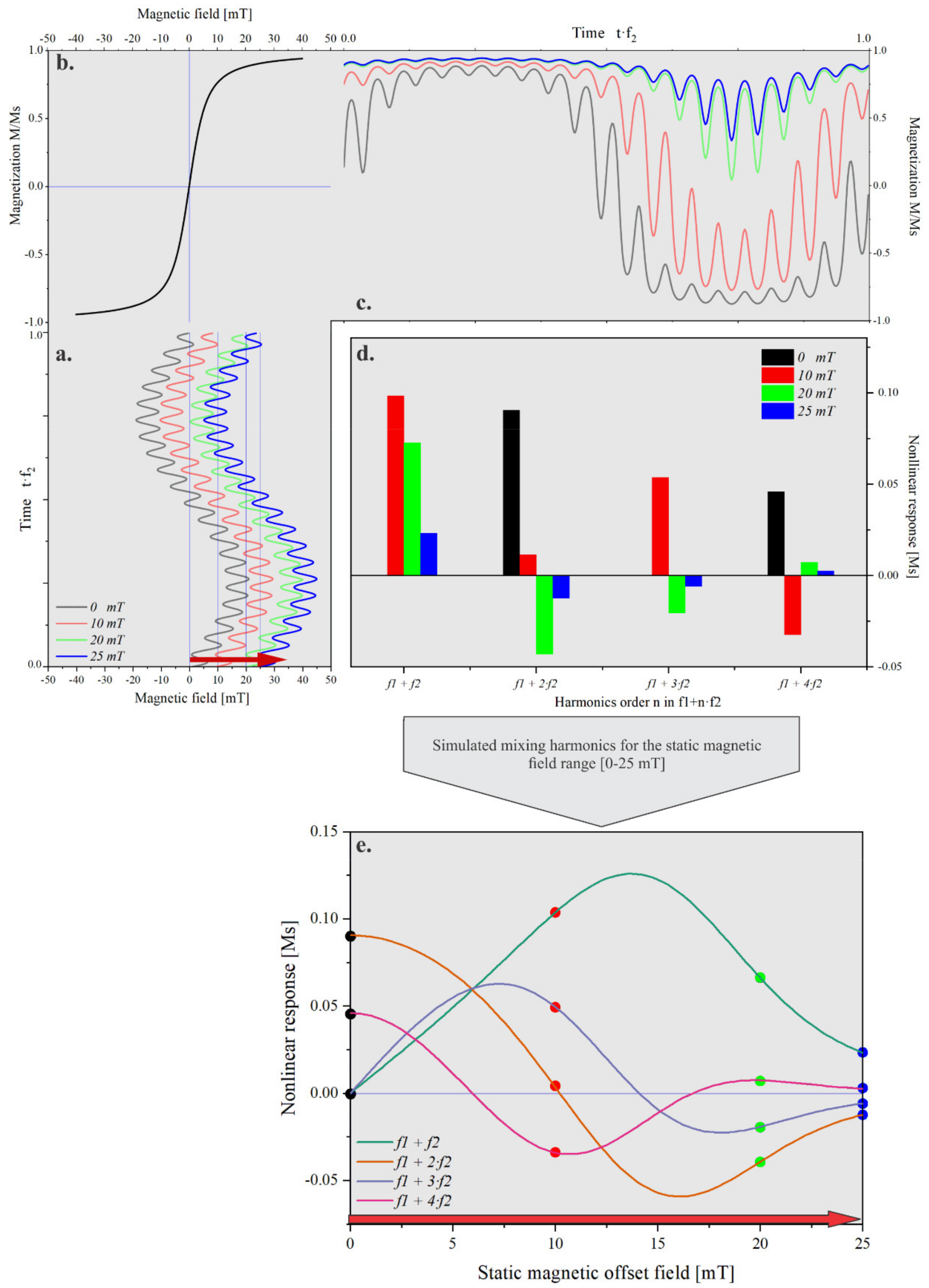
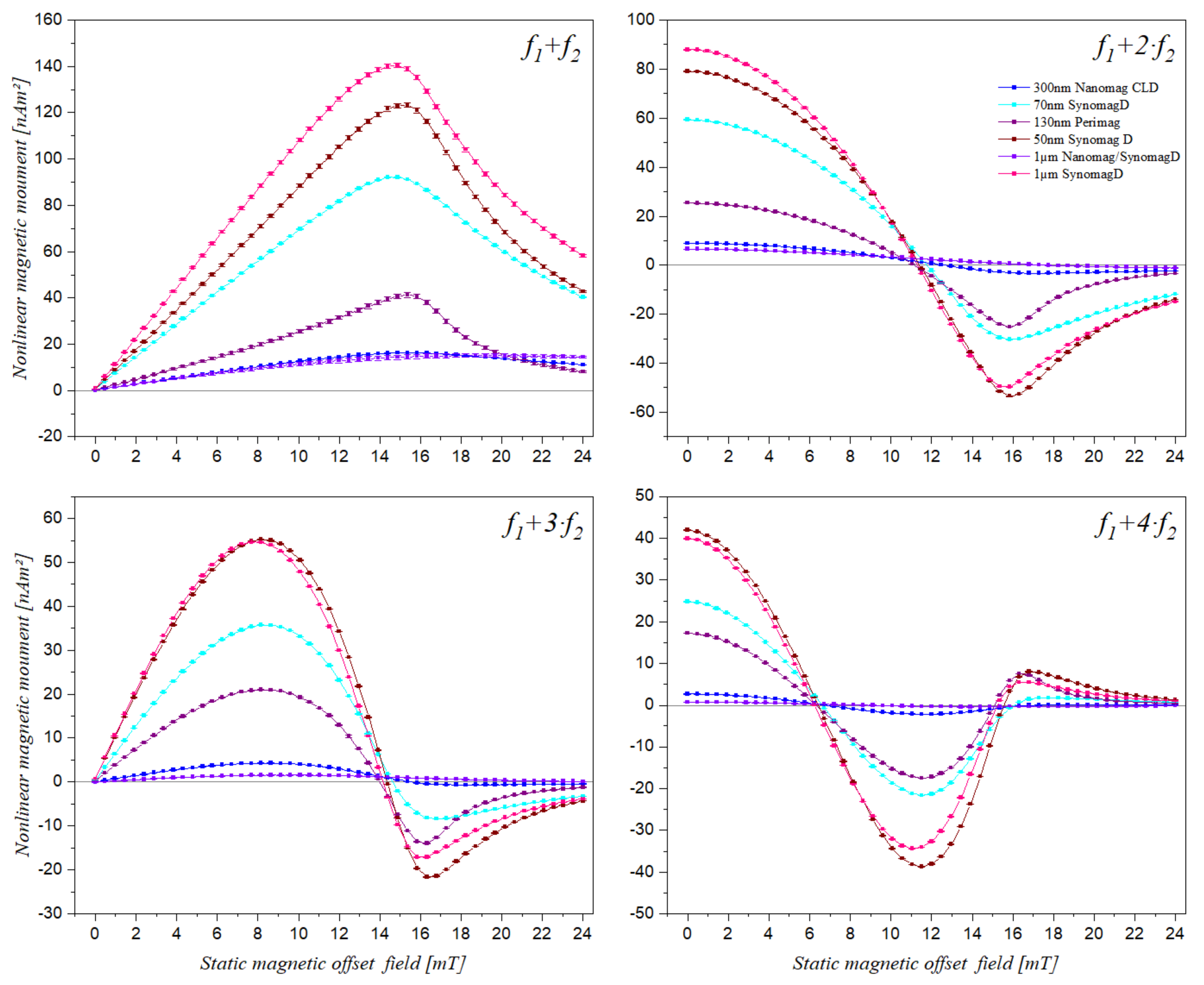
3.1. Static Magnetic Offset Field Scan of Different Superparamagnetic Beads
3.2. Effect of Amount of Beads on the Features of the Frequency Mixing Components
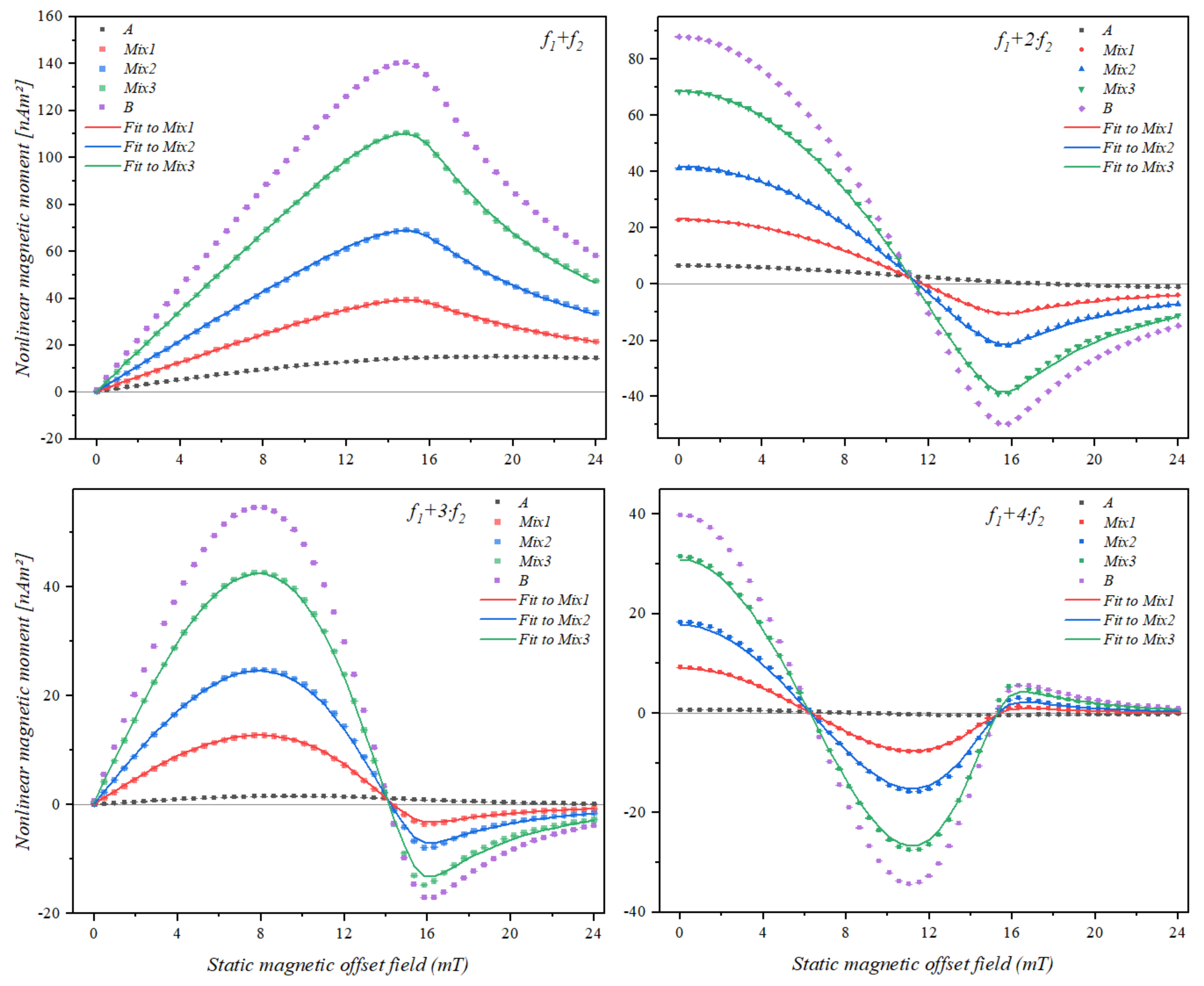
3.3. Static Magnetic Offset Field Scan of Samples Containing Two Different Types of Superparamagnetic Beads
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.-T.; Kolhatkar, A.G.; Zenasni, O.; Xu, S.; Lee, T.R. Biosensing Using Magnetic Particle Detection Techniques. Sensors 2017, 17, 2300. [Google Scholar] [CrossRef] [PubMed]
- Jalal, R.N.; Mehrbod, P.; Shojaei, S.; Labouta, H.I.; Mokarram, P.; Afkhami, A.; Madrakian, T.; Los, M.J.; Schaafsma, D.; Giersig, M.; et al. Magnetic Nanomaterials in Microfluidic Sensors for Virus Detection: A Review. ACS Appl. Nano Mater. 2021, 4, 4307–4328. [Google Scholar] [CrossRef]
- Sehl, O.C.; Gevaert, J.J.; Melo, K.P.; Knier, N.N.; Foster, P.J. A Perspective on Cell Tracking with Magnetic Particle Imaging. Tomography 2020, 6, 315–324. [Google Scholar] [CrossRef]
- Saritas, E.U.; Goodwill, P.W.; Croft, L.R.; Konkle, J.J.; Lu, K.; Zheng, B.; Conolly, S.M. Magnetic Particle Imaging (MPI) for NMR and MRI Researchers. J. Magn. Reson. 2013, 229, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Guigou, C.; Lalande, A.; Millot, N.; Belharet, K.; Grayeli, A.B. Use of Super Paramagnetic Iron Oxide Nanoparticles as Drug Carriers in Brain and Ear: State of the Art and Challenges. Brain Sci. 2021, 11, 24. [Google Scholar] [CrossRef] [PubMed]
- Jacob, A.; Chakravarthy, K. Engineering Magnetic Nanoparticles for Thermo-Ablation and Drug Delivery in Neurological Cancers. Cureus 2014. [Google Scholar] [CrossRef] [Green Version]
- Ha, Y.; Ko, S.; Kim, I.; Huang, Y.; Mohanty, K.; Huh, C.; Maynard, J.A. Recent Advances Incorporating Superparamagnetic Nanoparticles into Immunoassays. ACS Appl. Nano Mater. 2018, 1, 512–521. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.-H.; Juang, R.-S. Biochemical and Biomedical Applications of Multifunctional Magnetic Nanoparticles: A Review. J. Nanoparticle Res. 2011, 13, 4411–4430. [Google Scholar] [CrossRef]
- Guo, R.; Wang, S.; Huang, F.; Chen, Q.; Li, Y.; Liao, M.; Lin, J. Rapid Detection of Salmonella Typhimurium Using Magnetic Nanoparticle Immunoseparation, Nanocluster Signal Amplification and Smartphone Image Analysis. Sens. Actuators B Chem. 2019, 284, 134–139. [Google Scholar] [CrossRef]
- Liu, P.; Jonkheijm, P.; Terstappen, L.W.M.M.; Stevens, M. Magnetic Particles for CTC Enrichment. Cancers 2020, 12, 3525. [Google Scholar] [CrossRef]
- Astalan, A.P.; Ahrentorp, F.; Johansson, C.; Larsson, K.; Krozer, A. Biomolecular Reactions Studied Using Changes in Brownian Rotation Dynamics of Magnetic Particles. Biosens. Bioelectron. 2004, 19, 945–951. [Google Scholar] [CrossRef] [PubMed]
- Kotitz, R.; Matz, H.; Trahms, L.; Koch, H.; Weitschies, W.; Rheinlander, T.; Semmler, W.; Bunte, T. SQUID Based Remanence Measurements for Immunoassays. IEEE Trans. Appl. Supercond. 1997, 7, 3678–3681. [Google Scholar] [CrossRef]
- Krause, H.-J.; Wolters, N.; Zhang, Y.; Offenhäusser, A.; Miethe, P.; Meyer, M.H.F.; Hartmann, M.; Keusgen, M. Magnetic Particle Detection by Frequency Mixing for Immunoassay Applications. J. Magn. Magn. Mater. 2007, 311, 436–444. [Google Scholar] [CrossRef]
- Pietschmann, J.; Spiegel, H.; Krause, H.-J.; Schillberg, S.; Schröper, F. Sensitive Aflatoxin B1 Detection Using Nanoparticle-Based Competitive Magnetic Immunodetection. Toxins 2020, 12, 337. [Google Scholar] [CrossRef] [PubMed]
- Pietschmann, J.; Dittmann, D.; Spiegel, H.; Krause, H.-J.; Schröper, F. A Novel Method for Antibiotic Detection in Milk Based on Competitive Magnetic Immunodetection. Foods 2020, 9, 1773. [Google Scholar] [CrossRef]
- Achtsnicht, S.; Neuendorf, C.; Faßbender, T.; Nölke, G.; Offenhäusser, A.; Krause, H.-J.; Schröper, F. Sensitive and Rapid Detection of Cholera Toxin Subunit B Using Magnetic Frequency Mixing Detection. PLoS ONE 2019, 14, e0219356. [Google Scholar] [CrossRef]
- Meyer, M.H.F.; Krause, H.-J.; Hartmann, M.; Miethe, P.; Oster, J.; Keusgen, M. Francisella Tularensis Detection Using Magnetic Labels and a Magnetic Biosensor Based on Frequency Mixing. J. Magn. Magn. Mater. 2007, 311, 259–263. [Google Scholar] [CrossRef]
- Meyer, M.H.F.; Hartmann, M.; Krause, H.-J.; Blankenstein, G.; Mueller-Chorus, B.; Oster, J.; Miethe, P.; Keusgen, M. CRP Determination Based on a Novel Magnetic Biosensor. Biosens. Bioelectron. 2007, 22, 973–979. [Google Scholar] [CrossRef]
- Rettcher, S.; Jungk, F.; Kühn, C.; Krause, H.-J.; Nölke, G.; Commandeur, U.; Fischer, R.; Schillberg, S.; Schröper, F. Simple and Portable Magnetic Immunoassay for Rapid Detection and Sensitive Quantification of Plant Viruses. Appl. Environ. Microbiol. 2015, 81, 3039–3048. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Liu, J.; Saha, R.; Su, D.; Krishna, V.D.; Cheeran, M.C.-J.; Wang, J.-P. Magnetic Particle Spectroscopy for Detection of Influenza A Virus Subtype H1N1. ACS Appl. Mater. Interfaces 2020, 12, 13686–13697. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Y.; Wu, Y.; Xia, X.; Liao, Y.; Li, Q. Fluorescent Probe-Based Lateral Flow Assay for Multiplex Nucleic Acid Detection. Anal. Chem. 2014, 86, 5611–5614. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Sato, T.; Niwa, K.; Kawase, M.; Tanner, A.C.R.; Takahashi, N. Rapid and Sensitive PCR-Dipstick DNA Chromatography for Multiplex Analysis of the Oral Microbiota. BioMed Res. Int. 2014, 2014, e180323. [Google Scholar] [CrossRef] [PubMed]
- Panfilova, E.; Shirokov, A.; Khlebtsov, B.; Matora, L.; Khlebtsov, N. Multiplexed Dot Immunoassay Using Ag Nanocubes, Au/Ag Alloy Nanoparticles, and Au/Ag Nanocages. Nano Res. 2012, 5, 124–134. [Google Scholar] [CrossRef]
- Ling, Y.; Vassiliou, C.C.; Cima, M.J. Magnetic Relaxation-Based Platform for Multiplexed Assays. Analyst 2010, 135, 2360–2364. [Google Scholar] [CrossRef] [PubMed]
- Osterfeld, S.J.; Yu, H.; Gaster, R.S.; Caramuta, S.; Xu, L.; Han, S.-J.; Hall, D.A.; Wilson, R.J.; Sun, S.; White, R.L.; et al. Multiplex Protein Assays Based on Real-Time Magnetic Nanotag Sensing. Proc. Natl. Acad. Sci. USA 2008, 105, 20637–20640. [Google Scholar] [CrossRef] [Green Version]
- Rauwerdink, A.M.; Giustini, A.J.; Weaver, J.B. Simultaneous Quantification of Multiple Magnetic Nanoparticles. Nanotechnology 2010, 21, 455101. [Google Scholar] [CrossRef]
- Rauwerdink, A.M.; Weaver, J.B. Harmonic Phase Angle as a Concentration-Independent Measure of Nanoparticle Dynamics: Harmonic Phase Angle as Measure of Nanoparticle Dynamics. Med. Phys. 2010, 37, 2587–2592. [Google Scholar] [CrossRef] [Green Version]
- Rauwerdink, A.M.; Weaver, J.B. Concurrent Quantification of Multiple Nanoparticle Bound States. Med. Phys. 2011, 38, 1136–1140. [Google Scholar] [CrossRef] [Green Version]
- Achtsnicht, S.; Tödter, J.; Niehues, J.; Telöken, M.; Offenhäusser, A.; Krause, H.-J.; Schröper, F. 3D Printed Modular Immunofiltration Columns for Frequency Mixing-Based Multiplex Magnetic Immunodetection. Sensors 2019, 19, 148. [Google Scholar] [CrossRef] [Green Version]
- Achtsnicht, S.; Pourshahidi, A.M.; Offenhäusser, A.; Krause, H.-J. Multiplex Detection of Different Magnetic Beads Using Frequency Scanning in Magnetic Frequency Mixing Technique. Sensors 2019, 19, 2599. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Wang, Y.; Feng, Y.; Yu, L.; Wang, J.-P. Colorize Magnetic Nanoparticles Using a Search Coil Based Testing Method. J. Magn. Magn. Mater. 2015, 380, 251–254. [Google Scholar] [CrossRef]
- Tu, L.; Wu, K.; Klein, T.; Wang, J.-P. Magnetic Nanoparticles Colourization by a Mixing-Frequency Method. J. Phys. Appl. Phys. 2014, 47, 155001. [Google Scholar] [CrossRef]
- Wu, K.; Su, D.; Saha, R.; Liu, J.; Chugh, V.K.; Wang, J.-P. Magnetic Particle Spectroscopy: A Short Review of Applications Using Magnetic Nanoparticles. ACS Appl. Nano Mater. 2020, 3, 4972–4989. [Google Scholar] [CrossRef]
- Lenglet, L. Multiparametric Magnetic Immunoassays Utilizing Non-Linear Signatures of Magnetic Labels. J. Magn. Magn. Mater. 2009, 321, 1639–1643. [Google Scholar] [CrossRef]
- Alphandéry, E.; Lijeour, L.; Lalatonne, Y.; Motte, L. Different Signatures between Chemically and Biologically Synthesized Nanoparticles in a Magnetic Sensor: A New Technology for Multiparametric Detection. Sens. Actuators B Chem. 2010, 147, 786–790. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Liu, J.; Saha, R.; Peng, C.; Su, D.; Wang, Y.A.; Wang, J.-P. Investigation of Commercial Iron Oxide Nanoparticles: Structural and Magnetic Property Characterization. ACS Omega 2021, 6, 6274–6283. [Google Scholar] [CrossRef] [PubMed]
- Viereck, T.; Kuhlmann, C.; Draack, S.; Schiling, M.; Ludwig, F. Dual-frequency magnetic particle imaging of the Brownian particle contribution. J. Magn. Magn. Mater. 2017, 427, 156–161. [Google Scholar] [CrossRef]
- Möddel, M.; Meins, C.; Dieckhoff, J.; Knopp, T. Viscosity quantification using multi-contrast magnetic particle imaging. New J. Phys. 2018, 20, 083001. [Google Scholar] [CrossRef]
- Shasha, C.; Teeman, E.; Krishnan, K.M.; Szwargulski, P.; Knopp, T.; Möddel, M. Discriminating nanoparticle core size using multi-contrast MPI. Phys. Med. Biol. 2019, 64, 074001. [Google Scholar] [CrossRef]
- Krishnan, K.M. Fundamentals and Applications of Magnetic Materials; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Engelmann, U.M.; Shalaby, A.; Shasha, C.; Krishnan, K.M.; Krause, H.-J. Comparative Modeling of Frequency Mixing Measurements of Magnetic Nanoparticles Using Micromagnetic Simulations and Langevin Theory. Nanomaterials 2021, 11, 1257. [Google Scholar] [CrossRef] [PubMed]
- Engelmann, U.M.; Fitter, J.L.; Baumann, M. Assessing Magnetic Fluid Hyperthermia: Magnetic Relaxation Simulation, Modeling of Nanoparticle Uptake inside Pancreatic Tumor Cells and in Vitro Efficacy; Infinite Science Publishing: Lübeck, Germany, 2019. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer Series in Operations Research; Springer: New York, NY, USA, 1999. [Google Scholar]
- Murty, K.G. Linear Complementarity, Linear and Nonlinear Programming; Heldermann: Lemgo, Germany, 1988. [Google Scholar]
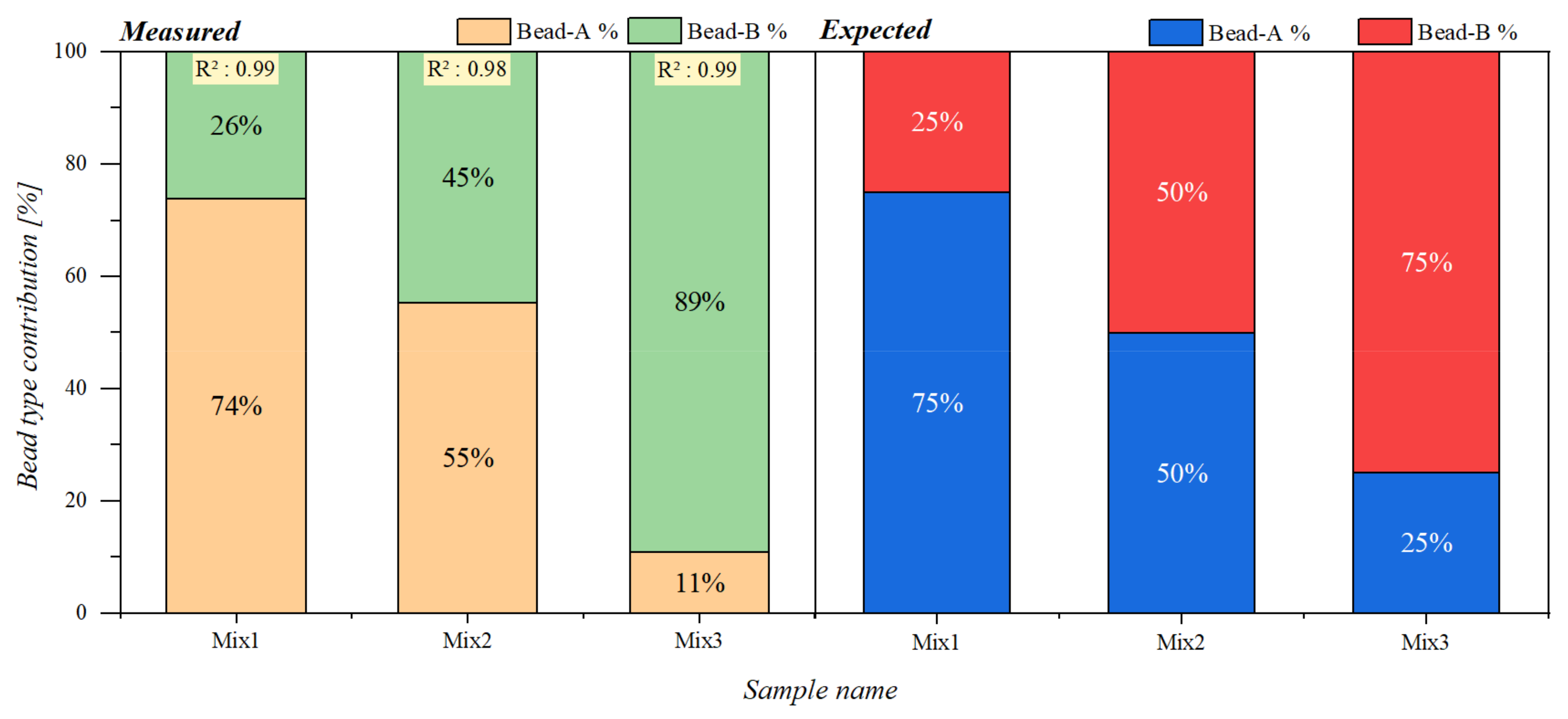

| Mixing Term | Bead Sample | 1µSynD-6 | 1µSynD-8 | 1µSynD-10 | Mean | Standard Deviation | Relative Std. Deviation |
|---|---|---|---|---|---|---|---|
| Amount | 6 µL | 8 µL | 10 µL | ||||
| f1 + f2 | Maximum (mT) | 14.48 | 14.65 | 14.66 | 14.60 | 0.10 | 0.7% |
| f1 + 2·f2 | Zero (mT) | 11.19 | 11.27 | 11.20 | 11.22 | 0.04 | 0.4% |
| Minimum (mT) | 15.49 | 15.57 | 15.63 | 15.57 | 0.07 | 0.4% | |
| f1 + 3·f2 | Maximum (mT) | 7.75 | 7.89 | 7.89 | 7.84 | 0.08 | 1.0% |
| Zero (mT) | 13.99 | 14.05 | 14.14 | 14.06 | 0.07 | 0.5% | |
| Minimum (mT) | 15.85 | 15.90 | 15.98 | 15.91 | 0.06 | 0.4% | |
| f1 + 4·f2 | 1st Zero (mT) | 6.19 | 6.24 | 6.30 | 6.24 | 0.06 | 0.9% |
| Maximum (mT) | 11.02 | 11.17 | 11.19 | 11.13 | 0.09 | 0.8% | |
| 2nd Zero (mT) | 15.02 | 15.06 | 15.03 | 15.04 | 0.02 | 0.1% | |
| Minimum (mT) | 16.25 | 16.25 | 16.34 | 16.28 | 0.05 | 0.3% |
| Mixture Samples | ||||||
|---|---|---|---|---|---|---|
| A (µL) | Mix1 (µL) | Mix2 (µL) | Mix3 (µL) | B (µL) | ||
| Bead Type | A | 10 | 7.5 | 5 | 2.5 | 0 |
| B | 0 | 2.5 | 5 | 7.5 | 10 | |
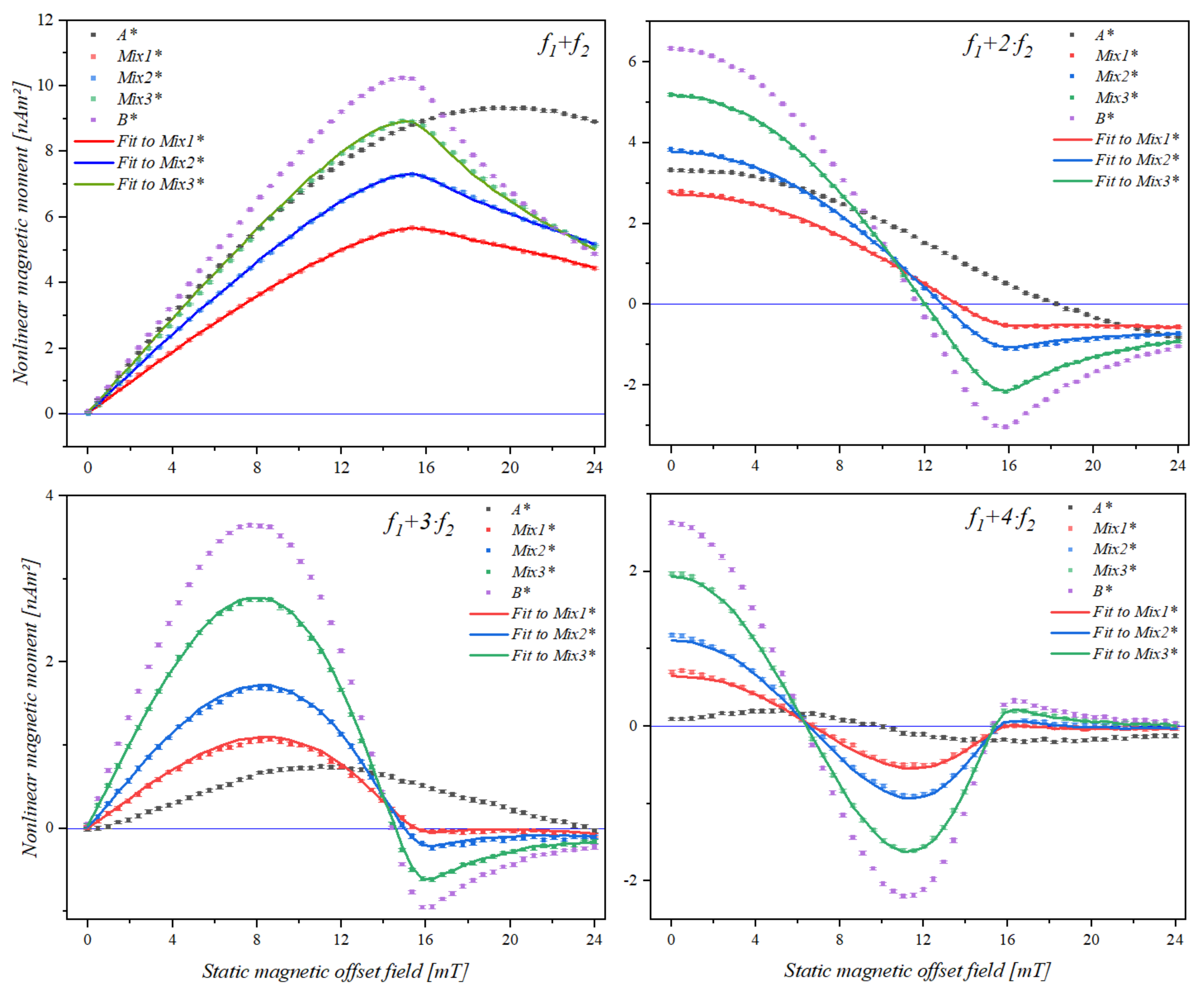
| Mixing Term | Bead Sample | A* | Mix1* | Mix2* | Mix3* | B* |
|---|---|---|---|---|---|---|
| f1 + f2 | Maximum (mT) | 19.87 | 15.60 | 15.22 | 14.92 | 14.68 |
| f1 + 2·f2 | Zero (mT) | 18.73 | 14.03 | 13.30 | 12.48 | 12.15 |
| Minimum (mT) | -- | 17.47 | 16.99 | 16.29 | 16.21 | |
| f1 + 3·f2 | Maximum (mT) | 11.02 | 8.27 | 8.10 | 7.79 | 7.78 |
| Zero (mT) | 23.65 | 15.59 | 15.10 | 14.49 | 14.40 | |
| Minimum (mT) | -- | -- | 16.55 | 16.18 | 16.17 | |
| f1 + 4·f2 | 1st Zero (mT) | 9.82 | 6.86 | 6.57 | 6.42 | 5.76 |
| Maximum (mT) | 17.39 | 11.47 | 11.43 | 11.20 | 11.18 | |
| 2nd Zero (mT) | -- | 15.78 | 15.69 | 15.40 | 16.38 | |
| Minimum (mT) | -- | -- | 17.05 | 16.38 | 16.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pourshahidi, A.M.; Achtsnicht, S.; Nambipareechee, M.M.; Offenhäusser, A.; Krause, H.-J. Multiplex Detection of Magnetic Beads Using Offset Field Dependent Frequency Mixing Magnetic Detection. Sensors 2021, 21, 5859. https://doi.org/10.3390/s21175859
Pourshahidi AM, Achtsnicht S, Nambipareechee MM, Offenhäusser A, Krause H-J. Multiplex Detection of Magnetic Beads Using Offset Field Dependent Frequency Mixing Magnetic Detection. Sensors. 2021; 21(17):5859. https://doi.org/10.3390/s21175859
Chicago/Turabian StylePourshahidi, Ali Mohammad, Stefan Achtsnicht, Mrinal Murali Nambipareechee, Andreas Offenhäusser, and Hans-Joachim Krause. 2021. "Multiplex Detection of Magnetic Beads Using Offset Field Dependent Frequency Mixing Magnetic Detection" Sensors 21, no. 17: 5859. https://doi.org/10.3390/s21175859
APA StylePourshahidi, A. M., Achtsnicht, S., Nambipareechee, M. M., Offenhäusser, A., & Krause, H.-J. (2021). Multiplex Detection of Magnetic Beads Using Offset Field Dependent Frequency Mixing Magnetic Detection. Sensors, 21(17), 5859. https://doi.org/10.3390/s21175859







