A GPU-Parallel Image Coregistration Algorithm for InSar Processing at the Edge
Abstract
:1. Introduction
2. Towards a GPU-Parallel Algorithm
- xcorr, a C program implementing incoherent spectral cross-correlation (Actually, xcorr implements also time correlation, but to the best of our knowledge, no available script uses this feature as main coregistration tool), which computes local sub-pixel offsets for each pair of corresponding patches within the SLC images;
- fitoffset.csh, a C shell script implementing least-square fitting of local offsets through trend2d tool from GMT [25], producing the transforming coefficients.
2.1. Decomposition
| Algorithm 1: GMTSAR xcorr algorithm. |
 |
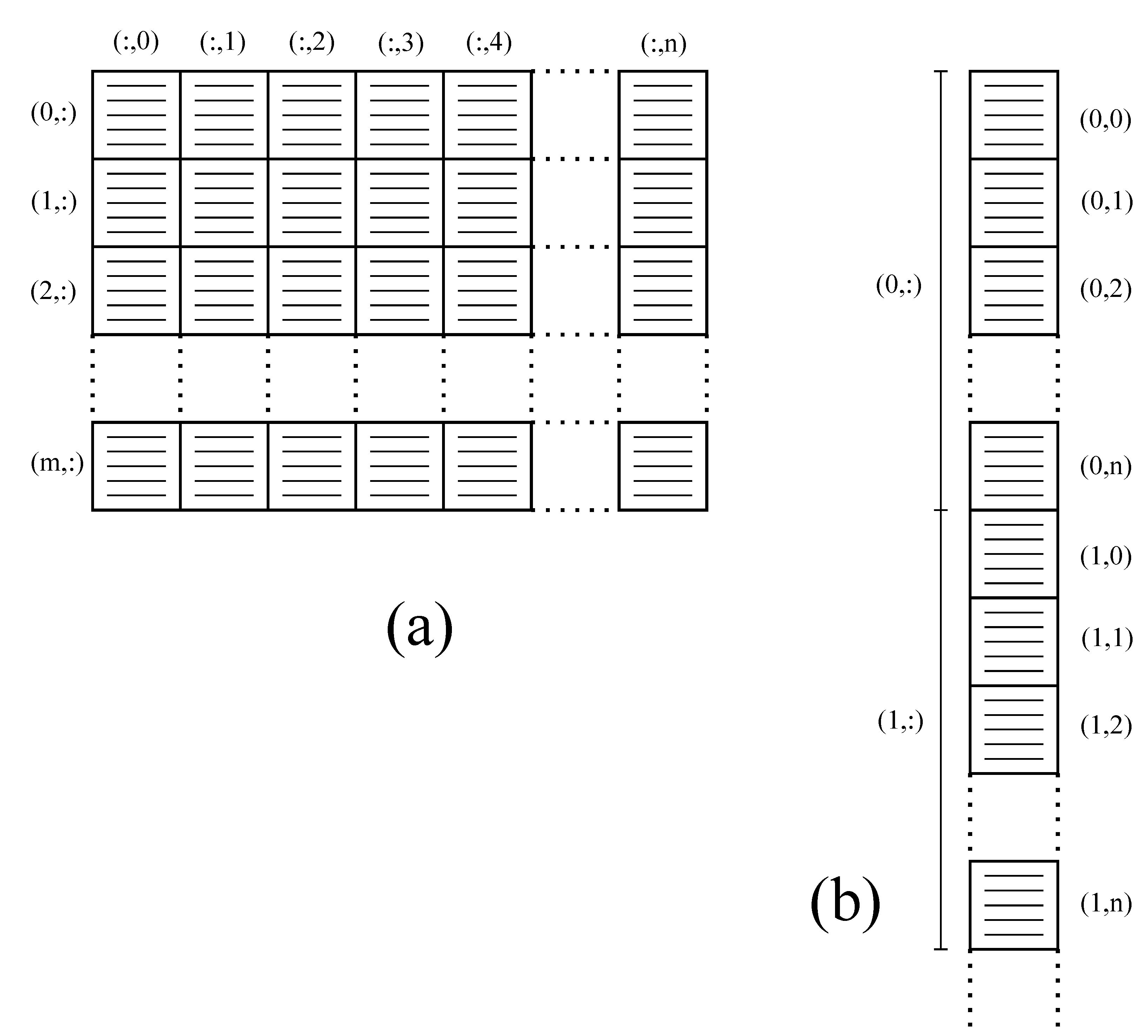
2.2. Data Structures
2.3. GPU Kernels
| Algorithm 2: GPU-parallel main algorithm. |
 |
- Line 6
- The first macro-operation on GPU is the FFT interpolation on range direction. It consists in:
- 6.1
- preliminary transformation in frequency domain along rows, exploiting CUFFT;
- 6.2
- zero-padding in the middle of each row to extend its length by (e.g., the original length);
- 6.3
- transformation back in time domain, also implemented with CUFFT;
- 6.4
- final point-wise scaling to compensate the amplitude loss induced by interpolation (see [28] for more details).
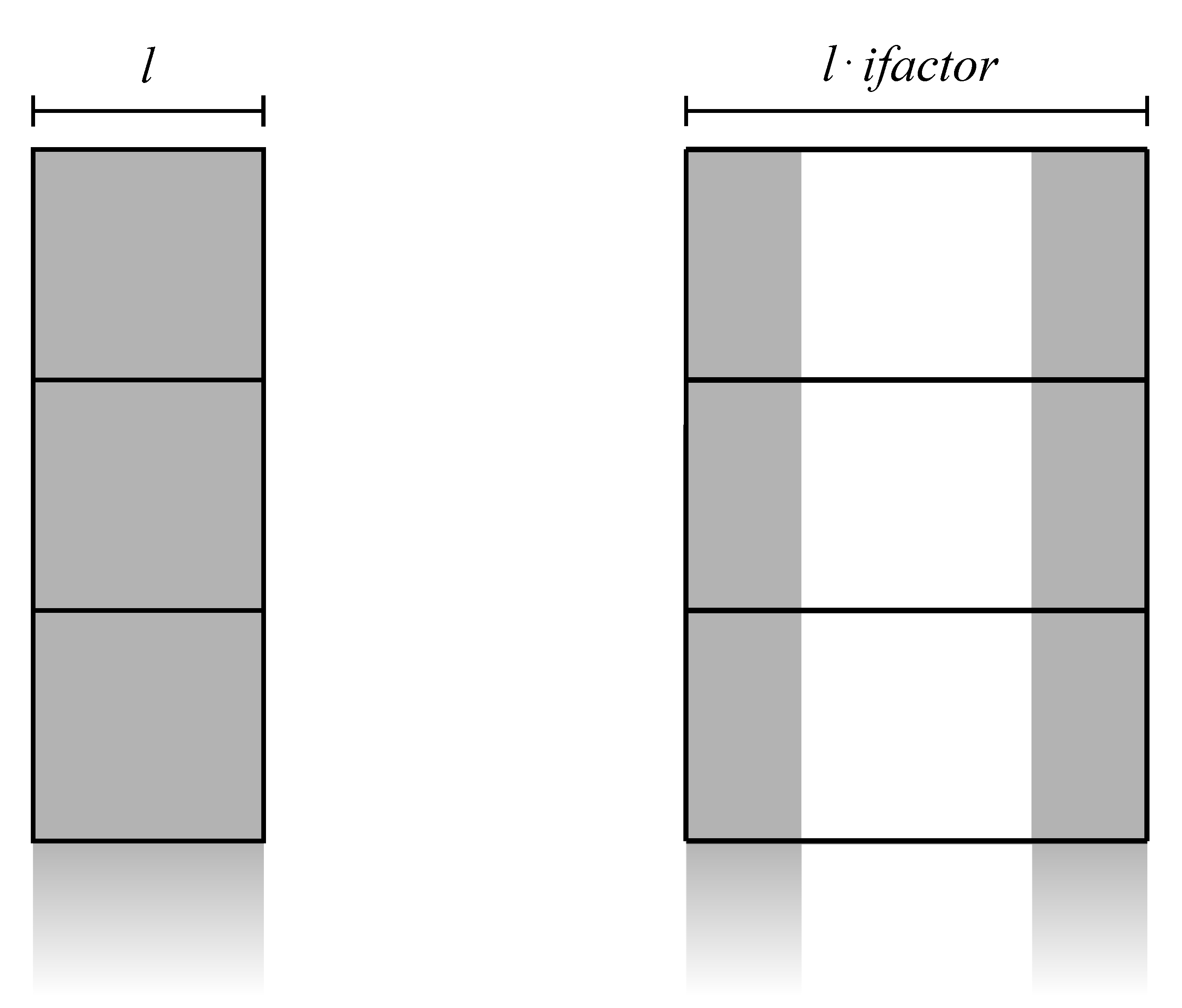
With the idea of taking advantage of both high bandwidth memory and its CUDA advanced copying tools, we can implement zero padding by splitting the input data into two vertical blocks copied on a zeroed larger workspace array (see Figure 3). Then, we can efficiently implement the final point-wise scaling using low-level decomposition on the entire strip length. The device memory footprint for completing the first step, supposing to execute FFT in place, is . - Line 7
- The following step consist in three sub-steps:
- 7.1
- point-wise conversion to amplitude, decomposed by ;
- 7.2
- computation of the mean value per patch, decomposed by ;
- 7.3
- point-wise subtraction per patch, decomposed by a modified .
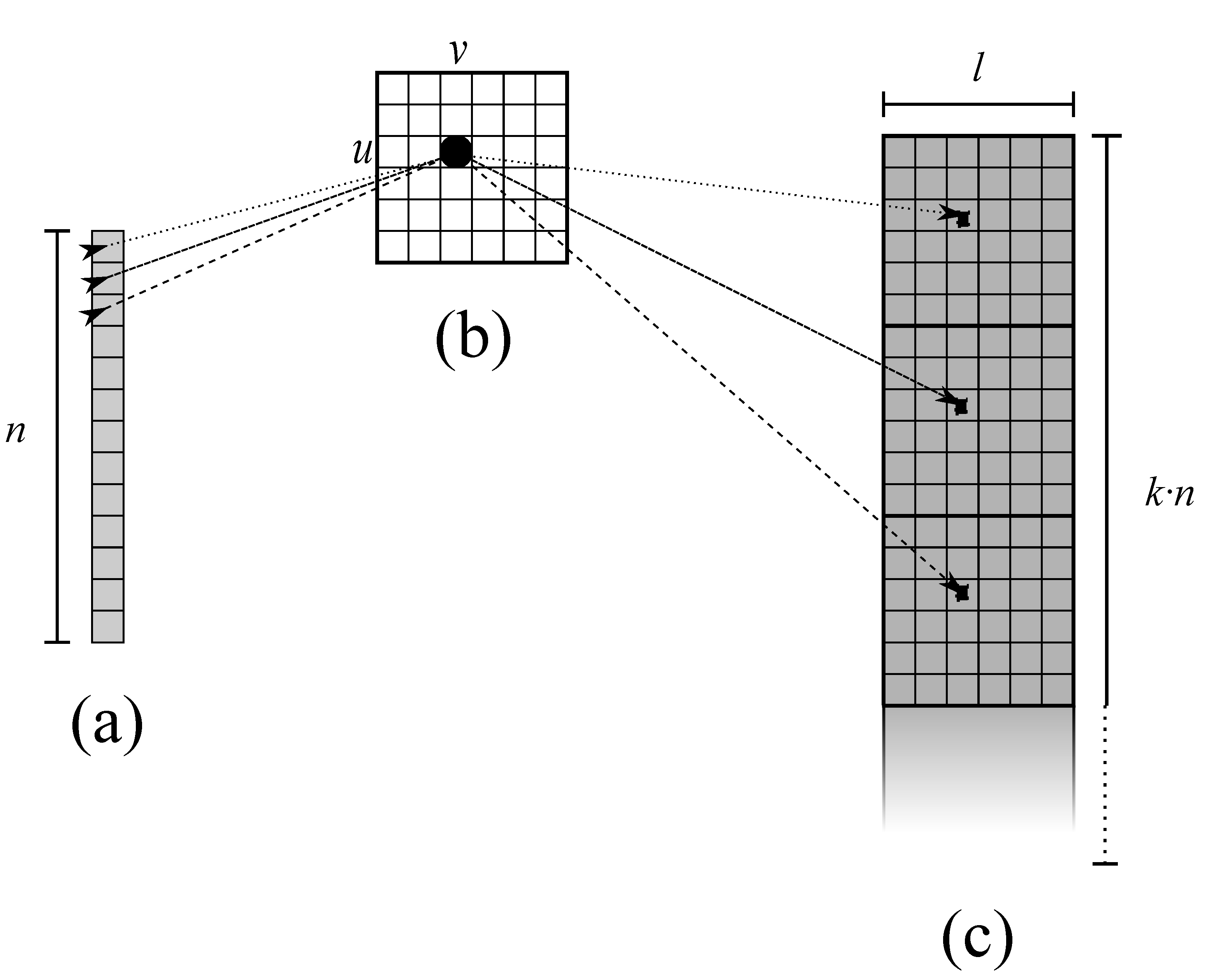
The first conversion can be designed as the previously described scaling kernel, copying result in a work area for the following sub-step. Then, by adopting a good strategy for GPU-parallel reduction available in the CUDA Samples, we can conveniently split the rows of the strip into a number of threads divisor of n, and compute each mean value per patch. For this operation, an additional array of n elements is necessary to store the results. Finally, a point-wise subtraction is necessary to implement patch centering, subtracting the same mean value from every point in the same patch. Thus, to optimize memory accesses, decomposition will be configured to assign every to the same . In other words, each will compute n subtractions accessing all n mean values stored in a fast shared memory (see Figure 4). The same will be applied to . The additional memory footprint for this step is n locations to store mean values.
| Algorithm 3: GPU-parallel algorithm for frequency cross-correlation. |
 |
- Line 2
- The calculation of Hadamard conjugate product in frequency domain consists in:
- 2.1
- preliminary transformation in frequency domain of both and , per patch, exploiting 2D CUFFT;
- 2.2
- point-wise conjugate product;
- 2.3
- transformation back in time domain of resulting , also implemented with 2D CUFFT.
We can configure the 2D FFTs straightforwardly using the data structure from Section 2.2 for strip-aligned patches. Then, we can decompose the point-wise product using , including computation of local complex conjugate. The additional memory footprint needed for this step, supposing to execute FFT in place, corresponds to the storage memory for which is . - Line 3
- We can implement the conversion as Line 7.1 in Algorithm 2.
- Line 4
- This reduction step can be decomposed and implemented as Line 7.2 in Algorithm 2.
- Line 5
- This step consists in computing the normalized cross-correlation in time domain:where is aligned to by , and are the correlation windows, and , with , .More in details:
- 5.1
- align and , per patch within strip, and store correlation windows in and ;
- 5.2
- point-wise products ofper strip;
- 5.3
- computation of the three sums, per patch within strip;
- 5.4
- computation of per patch within strip.
The alignment in sub-step 5.1 can be implemented through data copy from host to device with proper offset. Since products in 5.2 are similar to point-wise operators in Line 3, we can use the same decomposition . The sum is a reduction, and sub-step 5.3 can use the same decomposition as Line 4. Finally, sub-step 5.4 consists of products, and we can implement them sequentially. The additional memory footprint for this step corresponds to the two arrays for the strips of aligned patches, which consists of elements each, where is the size of the correlation window. - Line 6
- The normalization can follow the same strategy as Line 7.3 in Algorithm 2.
| Algorithm 4: GPU-parallel algorithm for high-resolution correlation. |
 |
- Line 2
- We can implement the copy of correlation values from to adopting , assigning the floating-point values to the real part of the complex array. This step is necessary to reorganize data for FFT interpolation in 2D. We choose data from in neighborhoods of pixel-level offsets from Algorithm 3 and then incorporate them in an array with the same patch strip structure as described in Section 2.2. Additional memory footprint for this step correspond to the size of a complex array with elements, where are the dimension of the neighbourhood around each per patch.
- Line 3
- This step can be implemented similarly to Line 6 of Algorithm 2, but with additional matrix transpose:
- 3.1
- preliminary transformation in frequency domain along row, exploiting CUFFT;
- 3.2
- zero-padding in the middle of each row to extend its length by (e.g., the original length);
- 3.3
- transformation back in time domain, also implemented with CUFFT;
- 3.4
- matrix transpose, to arrange data for the subsequent processing along columns of ;
- 3.5
- as 3.1;
- 3.6
- as 3.2;
- 3.7
- as 3.3;
- 3.8
- matrix transpose, to re-arrange data back to the original ordering.
The newly introduced matrix transpose follows a good GPU-parallel strategy available in the CUDA Samples involving shared memory tiles. We can imagine the strip of patches as a single matrix with rows. The additional memory footprint for this step consist in three temporary strips of patches: the first to interpolate along rows with elements; the second, with elements, to transpose the matrix; the third to interpolate along the other direction with elements. Final 2D interpolated data will need another array of complex elements. - Line 4
- This reduction step can be implemented as Line 4 of Algorithm 3, working on the real part of the array .
3. CUDA Implementation: Results
- Edge Computing near the sensor, with a System-on-Chip usable onboard a SAR platform;
- Edge Computing near the user, with two different workstation configurations;
- Component for a Cloud Computing application, with a typical GPU Computing configuration.
- Jetson Nano
- This is a small computing board ( mm) consisting of a stripped-down version of Tegra X1 (System-on-Chip). It integrates an NVIDIA Maxwell GPU with 128 CUDA cores on one Multiprocessor running at 921 MHz, sharing a 4 GB 64-bit LPDDR4 memory chip with a 4-core CPU ARM Cortex A57 running at 1.43 GHz. We used a development kit configuration for testing, which has a slot for an additional microSD card containing OS Ubuntu 18.04 LTS, software, and data;
- Q RTX 6000
- A workstation configuration: a graphic card NVIDIA Quadro RTX 6000 with 4608 CUDA cores on 72 Multiprocessors running at 1.77 GHz with a global memory of 22 GBytes, and 10-core CPU Intel Xeon Gold 5215 running at 2.5 GHz, OS CentOS Linux 7 (Core);
- GTX 1050 Ti
- Another workstation configuration: a graphic card NVIDIA GeForce GTX 1050 Ti with 768 CUDA cores on 6 Multiprocessors running at 1.42 GHz with a global memory of 4 GBytes, and 4-core CPU Intel Core i7-7700 running at 3.6 GHz, OS Linux Ubuntu 20.04.2 LTS;
- Tesla V100
- This is our data center configuration: the single node has an NVIDIA Tesla V100-SXM2-32GB with 5120 CUDA cores on 80 Multiprocessors running at 1.53 GHz with a global memory of 32GBytes, and a 16-core CPU Intel Xeon Gold 5218 running at 2.30GHz, OS CentOS Linux 7 (Core).
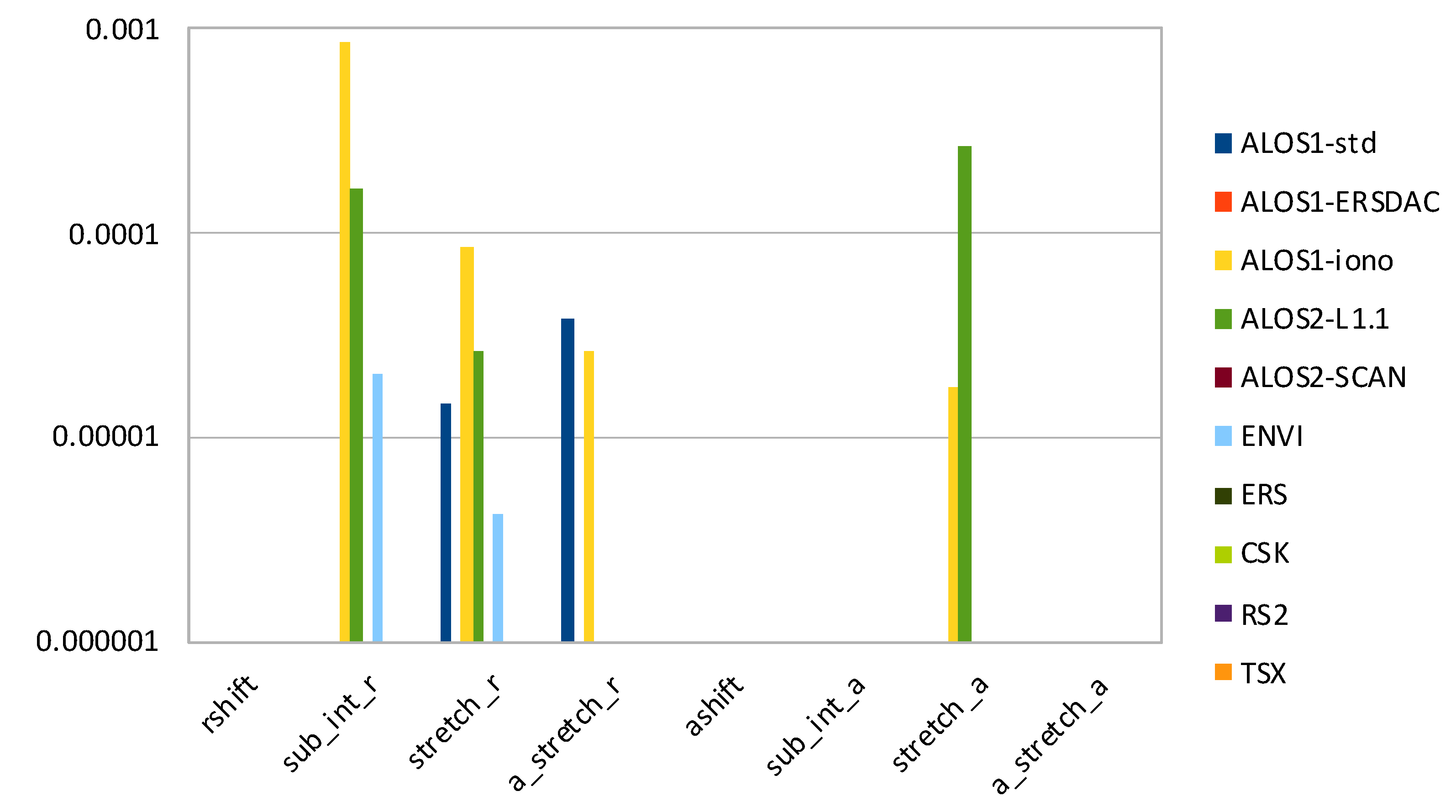
3.1. Accuracy
- rshift—range shift to align secondary image to primary image (in pixels);
- sub_int_r—decimal part of rshift;
- stretch_r—range stretch versus range;
- a_stretch_r—range stretch versus azimuth;
- ashift—azimuth shift to align secondary image to primary image (in pixels);
- sub_int_a—decimal part of ashift;
- stretch_a—azimuth stretch versus range;
- a_stretch_a—azimuth stretch versus azimuth.
3.2. Parallel Performance
- 5W
- with 2 online CPU cores with a maximal frequency of 918 MHz, and GPU maximal frequency set to 640 MHz;
- 10W
- with 4 online CPU cores with a maximal frequency of 1479 MHz and GPU maximal frequency set to 921.6 MHz.
3.3. Energy Efficiency
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, Q.; Vesecky, J.F.; Zebker, H.A. New approaches in interferometric SAR data processing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 560–567. [Google Scholar] [CrossRef]
- Scheiber, R.; Moreira, A. Coregistration of interferometric SAR images using spectral diversity. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2179–2191. [Google Scholar] [CrossRef]
- Li, F.; Goldstein, R. Studies of multibaseline spaceborne interferometric synthetic aperture radars. IEEE Trans. Geosci. Remote Sens. 1990, 28, 88–97. [Google Scholar] [CrossRef]
- Liao, M.; Lin, H.; Zhang, Z. Automatic Registration of INSAR Data Based on Least-Square Matching and Multi-Step Strategy. Photogramm. Eng. Remote Sens. 2004, 70, 1139–1144. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M. Crossed orbit interferometry: Theory and experimental results from SIR-B. Int. J. Remote Sens. 1988, 9, 857–872. [Google Scholar] [CrossRef]
- Anuta, P. Spatial Registration of Multispectral and Multitemporal Digital Imagery Using Fast Fourier Transform Techniques. IEEE Trans. Geosci. Electron. 1970, 8, 353–368. [Google Scholar] [CrossRef]
- Ferretti, A.; Monti-Guarnieri, A.; Prati, C.; Rocca, F.; Massonnet, D.; Lichtenegger, J. InSAR Principles: Guidelines for SAR Interferometry Processing and Interpretation (TM-19); ESA Publications: Noordwijk, The Netherlands, 2007. [Google Scholar]
- Jiang, H.; Feng, G.; Wang, T.; Bürgmann, R. Toward full exploitation of coherent and incoherent information in Sentinel-1 TOPS data for retrieving surface displacement: Application to the 2016 Kumamoto (Japan) earthquake. Geophys. Res. Lett. 2017, 44, 1758–1767. [Google Scholar] [CrossRef] [Green Version]
- Bamler, R.; Eineder, M. Accuracy of differential shift estimation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems. IEEE Geosci. Remote Sens. Lett. 2005, 2, 151–155. [Google Scholar] [CrossRef]
- Michel, R.; Avouac, J.P.; Taboury, J. Measuring ground displacements from SAR amplitude images: Application to the Landers Earthquake. Geophys. Res. Lett. 1999, 26, 875–878. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Bethel, J. Image coregistration in SAR interferometry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 433–438. [Google Scholar]
- Rufino, G.; Moccia, A.; Esposito, S. DEM generation by means of ERS tandem data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1905–1912. [Google Scholar] [CrossRef]
- Iorga, M.; Feldman, L.; Barton, R.; Martin, M.J.; Goren, N.; Mahmoudi, C. Fog Computing Conceptual Model; Number NIST SP 500-325; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge computing: Vision and challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Yousefpour, A.; Fung, C.; Nguyen, T.; Kadiyala, K.; Jalali, F.; Niakanlahiji, A.; Kong, J.; Jue, J.P. All one needs to know about fog computing and related edge computing paradigms: A complete survey. J. Syst. Archit. 2019, 98, 289–330. [Google Scholar] [CrossRef]
- Jo, J.; Jeong, S.; Kang, P. Benchmarking GPU-Accelerated Edge Devices. In Proceedings of the 2020 IEEE International Conference on Big Data and Smart Computing (BigComp), Busan, Korea, 19–22 February 2020; pp. 117–120. [Google Scholar]
- Romano, D.; Mele, V.; Lapegna, M. The Challenge of Onboard SAR Processing: A GPU Opportunity. In International Conference on Computational Science; Springer: Cham, Switzerland, 2020; pp. 46–59. [Google Scholar]
- Bhattacherjee, D.; Kassing, S.; Licciardello, M.; Singla, A. In-orbit Computing: An Outlandish thought Experiment? In Proceedings of the 19th ACM Workshop on Hot Topics in Networks, ACM, Virtual Event USA, 4–6 November 2020; pp. 197–204. [Google Scholar]
- Wang, H.; Chen, Q.; Chen, L.; Hiemstra, D.M.; Kirischian, V. Single Event Upset Characterization of the Tegra K1 Mobile Processor Using Proton Irradiation. In Proceedings of the 2017 IEEE Radiation Effects Data Workshop (REDW), New Orleans, LA, USA, 17–21 July 2017; pp. 1–4. [Google Scholar]
- Denby, B.; Lucia, B. Orbital Edge Computing: Machine Inference in Space. IEEE Comput. Archit. Lett. 2019, 18, 59–62. [Google Scholar] [CrossRef]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open radar interferometry software for mapping surface Deformation. Eos Trans. Am. Geophys. Union 2011, 92, 234. [Google Scholar] [CrossRef] [Green Version]
- Romano, D.; Lapegna, M.; Mele, V.; Laccetti, G. Designing a GPU-parallel algorithm for raw SAR data compression: A focus on parallel performance estimation. Future Gener. Comput. Syst. 2020, 112, 695–708. [Google Scholar] [CrossRef]
- Luebke, D. CUDA: Scalable parallel programming for high-performance scientific computing. In Proceedings of the 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Paris, France, 14–17 May 2008; pp. 836–838. [Google Scholar]
- Cui, H.; Zha, X. Parallel Image Registration Implementations for GMTSAR Package. Seismol. Res. Lett. 2018, 89, 1129–1136. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic Mapping Tools: Improved Version Released. Eos Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef] [Green Version]
- D’Amore, L.; Mele, V.; Romano, D.; Laccetti, G. Multilevel algebraic approach for performance analysis of parallel algorithms. Comput. Inform. 2019, 38, 817–850. [Google Scholar] [CrossRef]
- Laccetti, G.; Lapegna, M.; Mele, V.; Romano, D.; Szustak, L. Performance enhancement of a dynamic K-means algorithm through a parallel adaptive strategy on multicore CPUs. J. Parallel Distrib. Comput. 2020, 145, 34–41. [Google Scholar] [CrossRef]
- Lyons, R. Understanding Digital Signal Processing; Prentice Hall/PTR: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- GMTSAR Samples. Available online: https://topex.ucsd.edu/gmtsar/downloads/ (accessed on 31 August 2021).
- ArrayFire Documentation. Available online: https://arrayfire.org/docs/index.htm (accessed on 31 August 2021).
- The Generic Mapping Tools Documentation. Available online: https://docs.generic-mapping-tools.org/latest/ (accessed on 31 August 2021).
- Frigo, M.; Johnson, S. FFTW: An adaptive software architecture for the FFT. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP’98 (Cat. No.98CH36181), Seattle, WA, USA, 15 May 1998; Volume 3, pp. 1381–1384. [Google Scholar]
- Borgerding, M. Kiss FFT. 2021. Available online: https://github.com/mborgerding/kissfft (accessed on 31 August 2021).
- Brenner, N.M. Three FORTRAN Programs that Perform the Cooley-Tukey Fourier Transform. 1967. Available online: https://apps.dtic.mil/sti/citations/AD0657019 (accessed on 31 August 2021).
- CUDA for Tegra. Available online: http://docs.nvidia.com/cuda/cuda-for-tegra-appnote/index.html (accessed on 31 August 2021).
- Laccetti, G.; Lapegna, M.; Mele, V.; Montella, R. An adaptive algorithm for high-dimensional integrals on heterogeneous CPU-GPU systems. Concurr. Comput. Pract. Exp. 2019, 31, e4945. [Google Scholar] [CrossRef]
- Pilipović, R.; Risojević, V.; Božič, J.; Bulić, P.; Lotrič, U. An Approximate GEMM Unit for Energy-Efficient Object Detection. Sensors 2021, 21, 4195. [Google Scholar] [CrossRef] [PubMed]

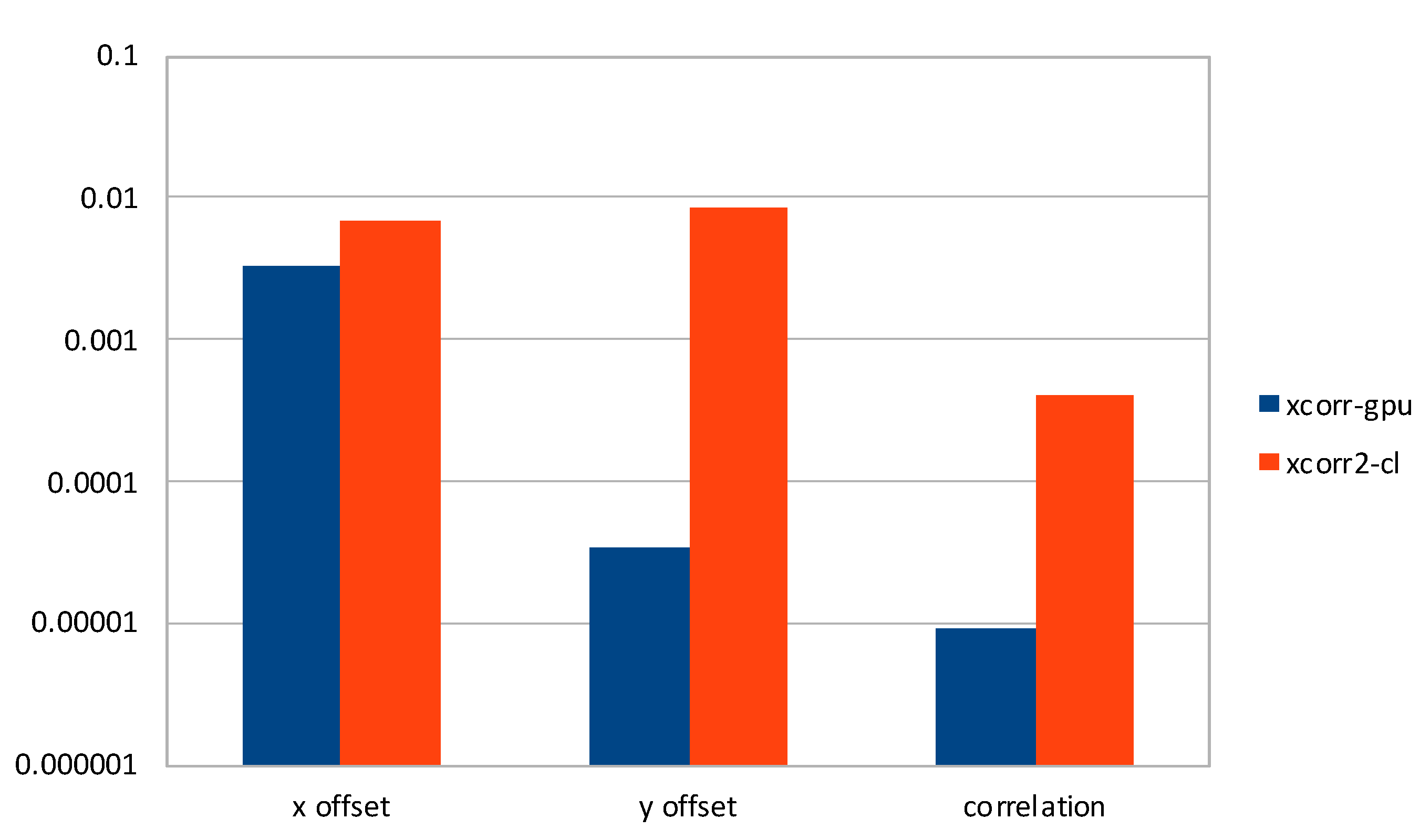


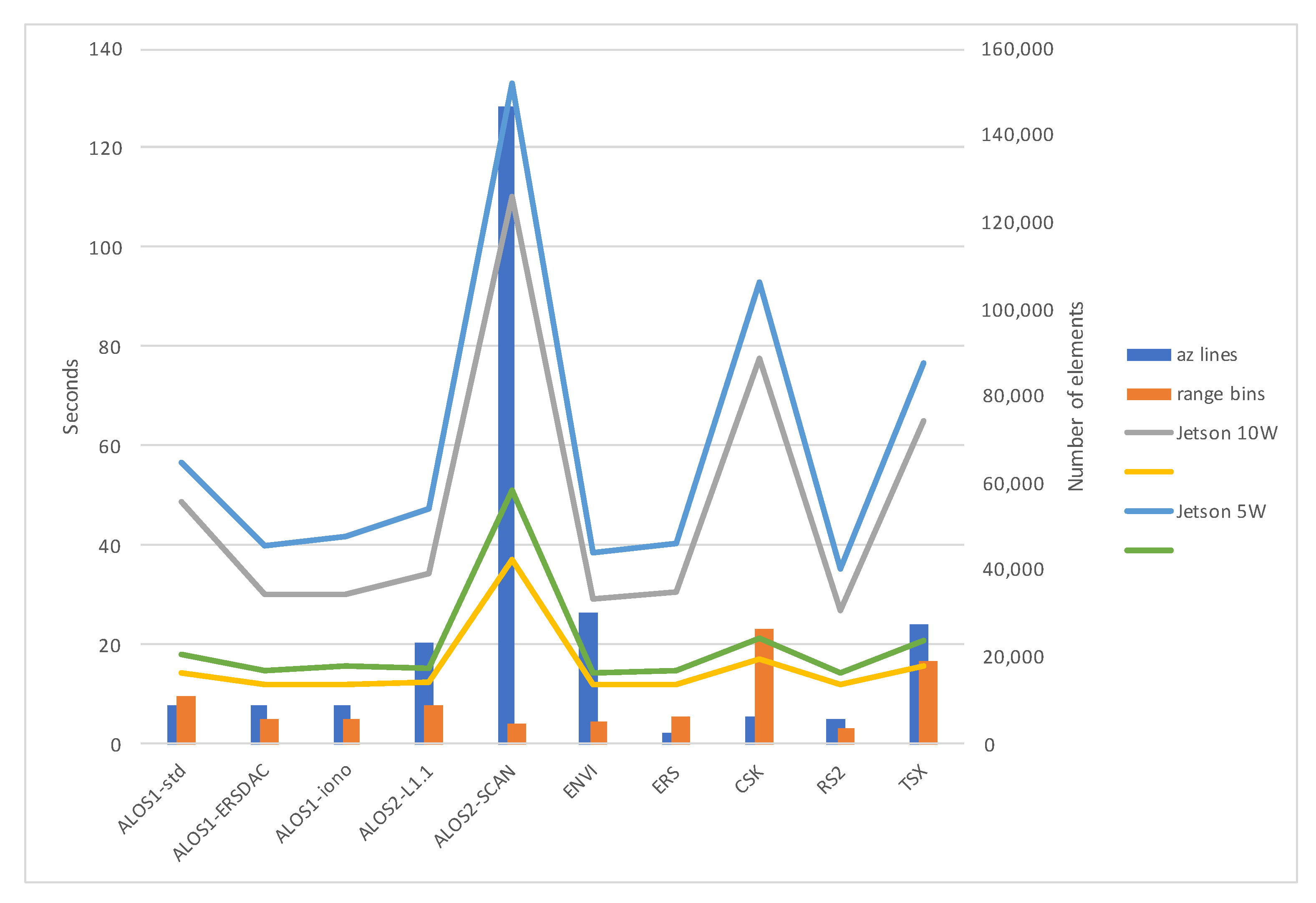

| Dataset | Rng Ptchs | Az Ptchs | Xsearch | Ysearch | Range Bins | Az Lines |
|---|---|---|---|---|---|---|
| ALOS-1 L1.0 (std format CEOS) | 20 | 50 | 128 | 128 | 11,304 | 9216 |
| ALOS-1 L1.0 (ERSDAC format) | 20 | 50 | 128 | 128 | 5652 | 9216 |
| ALOS-1 L1.0 (ionospheric correct.) | 20 | 50 | 128 | 128 | 5652 | 9216 |
| ALOS-2 L1.1 | 20 | 50 | 128 | 128 | 9072 | 23,264 |
| ALOS-2 L1.1 ScanSAR | 32 | 128 | 32 | 256 | 4668 | 146,512 |
| Envisat | 20 | 50 | 128 | 128 | 5191 | 30,316 |
| ERS | 20 | 50 | 128 | 128 | 6144 | 2800 |
| COSMOS-SkyMed | 20 | 50 | 128 | 128 | 26,400 | 6400 |
| RADARSAT-2 | 20 | 50 | 128 | 128 | 3416 | 5744 |
| TerraSAR-X | 20 | 50 | 128 | 128 | 18,880 | 27,748 |
| ALOS1-std | 3.6336 | 78.7273 | 0.0000 | 0.0000 | 0.1302 | 1.2789 |
| ALOS1-ERSDAC | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| ALOS1-iono | 1.7430 | 4.8203 | 0.1606 | 2.4173 | 0.0661 | 1.0841 |
| ALOS2-L1.1 | 0.2232 | 6.8359 | 0.0617 | 1.9505 | 0.1113 | 1.4019 |
| ALOS2-SCAN | 257.7355 | 1304.0729 | 0.4136 | 2.0613 | 0.0674 | 1.1977 |
| ENVI | 0.9211 | 6.3563 | 0.0000 | 0.0000 | 0.1456 | 1.1952 |
| ERS | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| CSK | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.1918 | 1.5716 |
| RS2 | 1.1243 | 5.6046 | 2.1927 | 4.8602 | 0.0721 | 1.3222 |
| TSX | 0.1877 | 2.7850 | 0.1501 | 2.4639 | 0.1526 | 1.1884 |
| ALOS1-std | 11.0006 | 95.7281 | 232.7862 | 2920.3151 | 6.0454 | 48.5996 |
| ALOS1-ERSDAC | 8.1439 | 55.1633 | 10.5945 | 20.0301 | 1.7251 | 8.8869 |
| ALOS1-iono | 12,130.5023 | 9285.8254 | 520.7860 | 4685.8129 | 382.4748 | 4410.2342 |
| ALOS2-L1.1 | 8952.9820 | 13,965.4362 | 2455.0701 | 4007.3684 | 8722.5570 | 9318.6598 |
| ALOS2-SCAN | 350.1252 | 1363.5214 | 92.0581 | 480.5890 | 2.6375 | 45.5144 |
| ENVI | 46.2160 | 310.2654 | 129.1276 | 488.1701 | 16.3460 | 56.1731 |
| ERS | 9.0660 | 35.9363 | 1.0588 | 9.2563 | 2.1657 | 6.9196 |
| CSK | 11.1924 | 145.2376 | 5.8288 | 78.5701 | 1.7991 | 1.5716 |
| RS2 | 20.7378 | 90.3963 | 29.0177 | 38.5728 | 0.7959 | 1.3222 |
| TSX | 8340.4977 | 10,780.5088 | 6546.1723 | 9227.6133 | 9145.9832 | 9347.5936 |
| V100 | xcorr (KISS) | xcorr-gpu | xcorr2-cl | ||
|---|---|---|---|---|---|
| Secs | Secs | Speed-Up | Secs | Speed-Up | |
| ALOS1-std | 135.069 | 3.511 | 38.470 | 4.149 | 32.555 |
| ALOS1-ERSDAC | 134.997 | 2.537 | 53.211 | 3.644 | 37.046 |
| ALOS1-iono | 157.726 | 2.874 | 54.880 | ||
| ALOS2-L1.1 | 134.679 | 3.083 | 43.684 | ||
| ALOS2-SCAN | 256.437 | 5.874 | 43.656 | 9.078 | 28.248 |
| ENVI | 134.073 | 2.469 | 54.303 | 3.361 | 39.891 |
| ERS | 135.272 | 2.668 | 50.702 | 3.786 | 35.730 |
| CSK | 138.973 | 5.601 | 24.812 | 6.394 | 21.735 |
| RS2 | 136.484 | 2.194 | 62.208 | 3.714 | 36.749 |
| TSX | 136.579 | 4.517 | 30.237 | ||
| Q RTX 6000 | xcorr (KISS) | xcorr-gpu | xcorr2-cl | ||
|---|---|---|---|---|---|
| Secs | Secs | Speed-Up | Secs | Speed-Up | |
| ALOS1-std | 154.501 | 3.701 | 41.746 | 4.394 | 35.162 |
| ALOS1-ERSDAC | 155.801 | 2.427 | 64.195 | 3.669 | 42.464 |
| ALOS1-iono | 161.377 | 3.007 | 53.667 | ||
| ALOS2-L1.1 | 154.458 | 3.076 | 50.214 | ||
| ALOS2-SCAN | 292.804 | 6.152 | 47.595 | 9.632 | 30.399 |
| ENVI | 155.429 | 2.349 | 66.168 | 3.651 | 42.572 |
| ERS | 155.089 | 2.414 | 64.246 | 3.849 | 40.293 |
| CSK | 157.835 | 5.676 | 27.807 | 6.366 | 24.793 |
| RS2 | 153.147 | 2.017 | 75.928 | 3.565 | 42.958 |
| TSX | 156.963 | 4.562 | 34.407 | ||
| GTX 1050 Ti | xcorr (FFTW) | xcorr (Brenner) | ||
|---|---|---|---|---|
| Total | sys | Total | sys | |
| ALOS1-std | 254.346 | 38.941 | 82.857 | 0.288 |
| ALOS1-ERSDAC | 253.54 | 38.969 | 83.219 | 0.145 |
| ALOS1-iono | 254.172 | 38.407 | 83.215 | 0.168 |
| ALOS2-L1.1 | 255.199 | 38.490 | 83.479 | 0.197 |
| ALOS2-SCAN | 1905.077 | 48.473 | 161.231 | 0.6 |
| ENVI | 254.147 | 38.349 | 83.184 | 0.168 |
| ERS | 254.104 | 39.050 | 83.555 | 0.216 |
| CSK | 254.59 | 39.368 | 86.213 | 0.528 |
| RS2 | 251.816 | 38.297 | 82.89 | 0.112 |
| TSX | 255.77 | 38.135 | 85.507 | 0.325 |
| GTX 1050 Ti | xcorr-gpu | xcorr2-cl | ||||||
|---|---|---|---|---|---|---|---|---|
| Total | sys | S-Up FFTW | S-Up Brenner | Total | sys | S-Up FFTW | S-Up Brenner | |
| ALOS1-std | 4.259 | 0.414 | 59.720 | 19.455 | 7.011 | 0.313 | 36.278 | 11.818 |
| ALOS1-ERSDAC | 3.308 | 0.334 | 76.644 | 25.157 | 5.133 | 0.225 | 49.394 | 16.213 |
| ALOS1-iono | 3.271 | 0.381 | 77.705 | 25.440 | ||||
| ALOS2-L1.1 | 3.854 | 0.352 | 66.217 | 21.660 | ||||
| ALOS2-SCAN | 9.367 | 0.901 | 203.382 | 17.213 | 16.326 | 0.673 | 116.690 | 9.876 |
| ENVI | 3.179 | 0.351 | 79.946 | 26.167 | 4.961 | 0.217 | 51.229 | 16.768 |
| ERS | 3.367 | 0.329 | 75.469 | 24.816 | 5.272 | 0.229 | 48.199 | 15.849 |
| CSK | 6.996 | 0.908 | 36.391 | 12.323 | 13.274 | 2.116 | 19.180 | 6.495 |
| RS2 | 2.936 | 0.26 | 85.768 | 28.232 | 4.375 | 0.213 | 57.558 | 18.946 |
| TSX | 5.681 | 0.709 | 45.022 | 15.051 | ||||
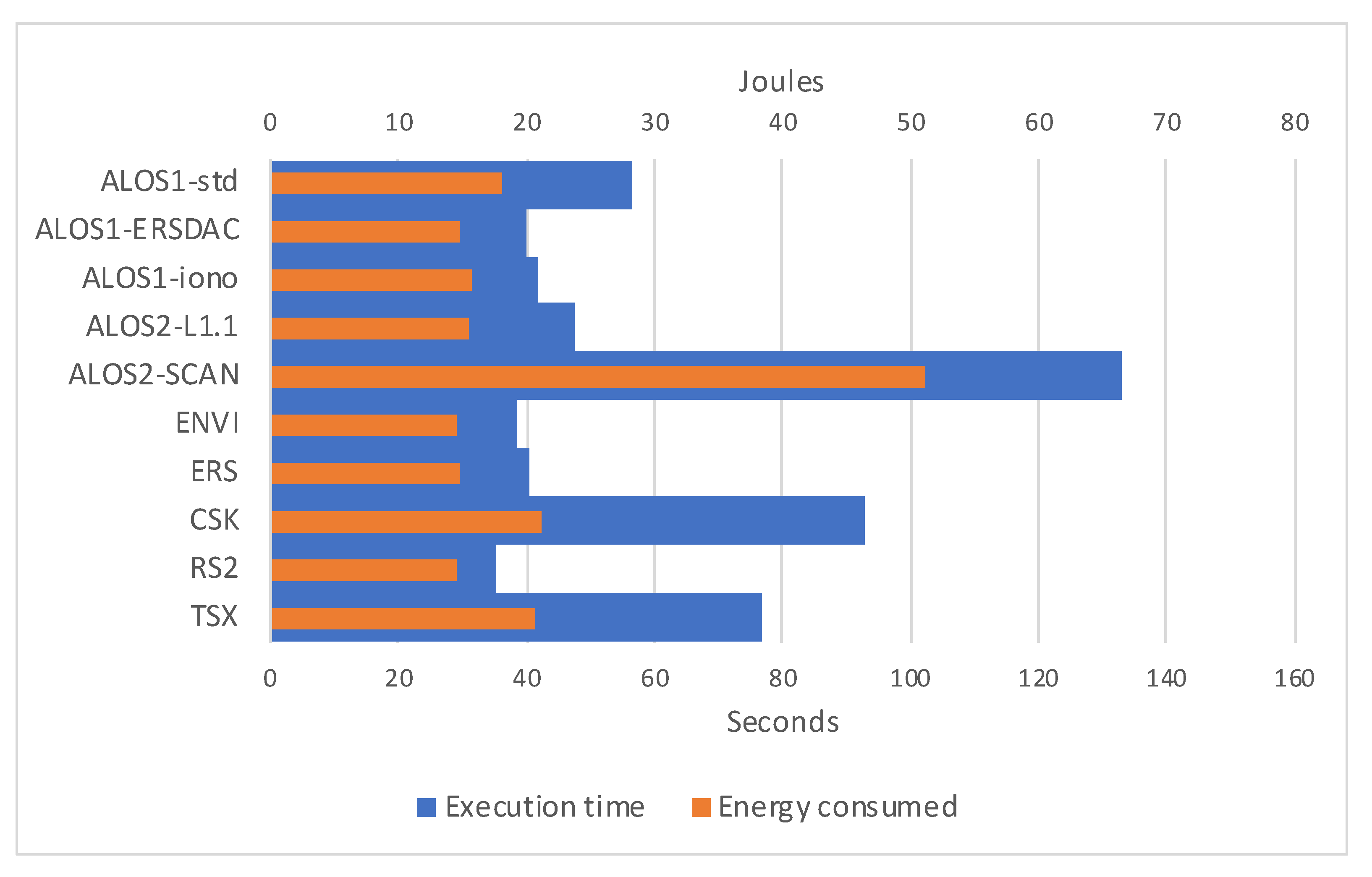
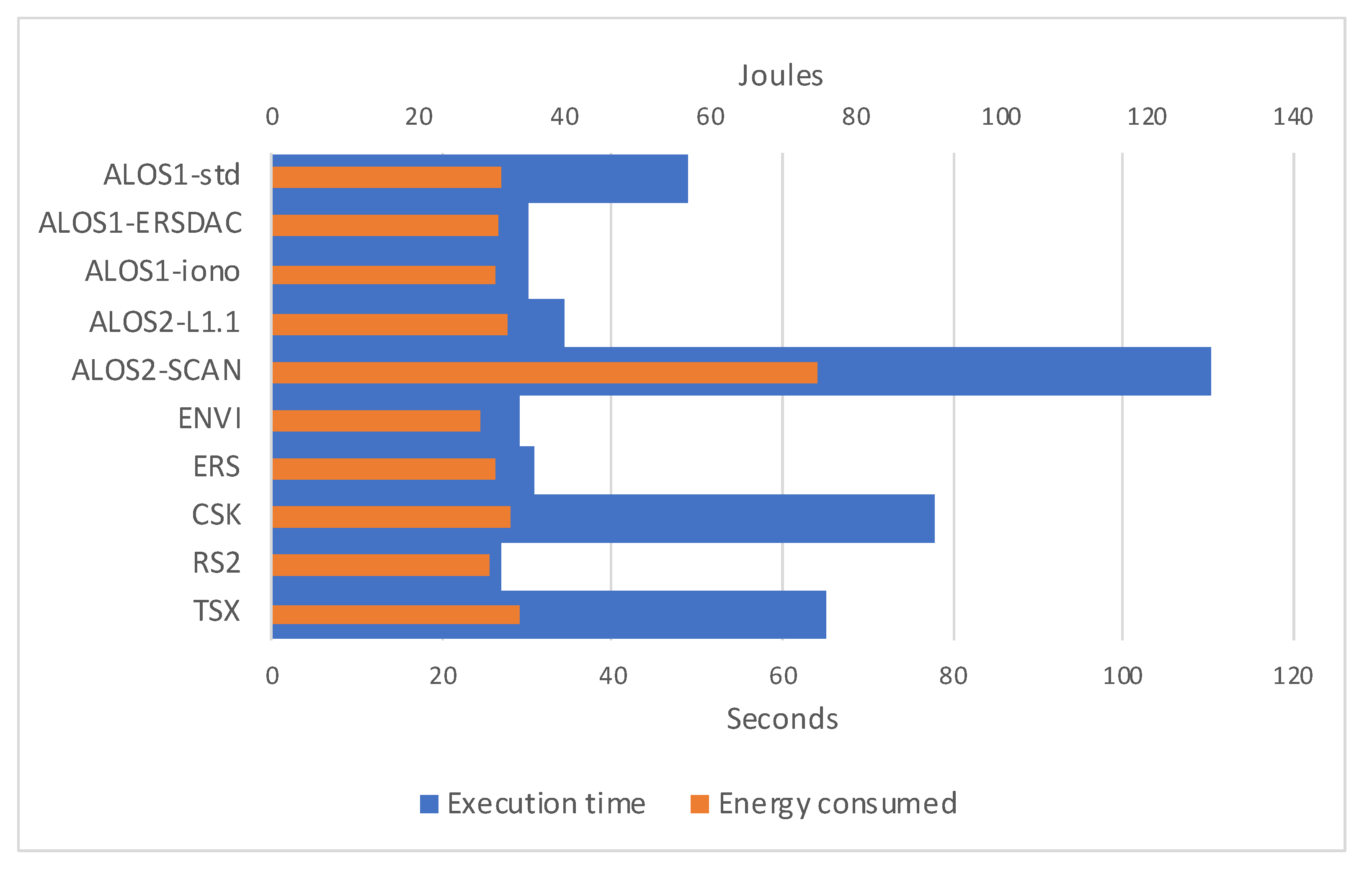
| Jetson Nano | xcorr-gpu 10 W | xcorr-gpu 5 W | ||
|---|---|---|---|---|
| Total | sys | Total | sys | |
| ALOS1-std | 48.912 | 14.332 | 56.569 | 18.18 |
| ALOS1-ERSDAC | 30.068 | 11.996 | 40.091 | 14.856 |
| ALOS1-iono | 30.206 | 12.176 | 41.937 | 15.756 |
| ALOS2-L1.1 | 34.412 | 12.316 | 47.454 | 15.492 |
| ALOS2-SCAN | 110.219 | 37.368 | 132.804 | 51.24 |
| ENVI | 29.159 | 11.828 | 38.612 | 14.568 |
| ERS | 30.671 | 12.236 | 40.372 | 14.728 |
| CSK | 77.725 | 17.076 | 92.772 | 21.176 |
| RS2 | 26.936 | 11.86 | 35.33 | 14.568 |
| TSX | 65.208 | 15.624 | 76.576 | 20.668 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romano, D.; Lapegna, M. A GPU-Parallel Image Coregistration Algorithm for InSar Processing at the Edge. Sensors 2021, 21, 5916. https://doi.org/10.3390/s21175916
Romano D, Lapegna M. A GPU-Parallel Image Coregistration Algorithm for InSar Processing at the Edge. Sensors. 2021; 21(17):5916. https://doi.org/10.3390/s21175916
Chicago/Turabian StyleRomano, Diego, and Marco Lapegna. 2021. "A GPU-Parallel Image Coregistration Algorithm for InSar Processing at the Edge" Sensors 21, no. 17: 5916. https://doi.org/10.3390/s21175916
APA StyleRomano, D., & Lapegna, M. (2021). A GPU-Parallel Image Coregistration Algorithm for InSar Processing at the Edge. Sensors, 21(17), 5916. https://doi.org/10.3390/s21175916







