1. Introduction
Estimating depth information is a crucial task in computer vision [
1]. Many challenging computer vision problems have proven to benefit from incorporating depth information, including 3D reconstruction, semantic segmentation, scene understanding, and object detection [
2]. Recently, depth from the light field has become one of the new hotspots, as light-field imaging captures much more information on the angular direction of light rays compared to monocular or binocular imaging [
1]. The plenoptic cameras such as Lytro and Raytrix facilitate the data acquirement of a light field. Refocusing images, sub–aperture images, and epipolar plane images (EPIs) can be generated from the light field data. Many new methods of depth estimation have emerged based on these derived images. Especially, EPI-based depth estimation is more popular.
EPIs exhibit a particular internal structure: every captured scene point corresponds to a linear trace in an EPI, where the slope of the trace reflects the scene point’s distance to the camera [
3]. Some methods have obtained depth maps by optimizing the slope metric of straight lines in EPIs, and standard feature metrics include color variance, 4D gradient, structure tensor, etc. It is challenging to model the occlusion, noise, and homogeneous region using feature metrics, so the accuracy of these methods is limited. Furthermore, the global optimization process is always computationally expensive, which hampers its practical usage.
With the rise of deep learning, some efforts have integrated feature extraction and optimization into a unified framework of convolutional neural networks, achieving good results. These advances are due to the feature extraction capability of deep neural networks. The research shows that convolutional neural networks are very good at feature extraction of texture images [
4]. However, the current depth estimation methods based on deep learning seldom directly use rich texture features in EPIs. Moreover, some methods use complex network structures with many parameters and less consideration of the computational cost. Taking EPINet [
5] as an example, it shows good performance against the HCI (Heidelberg Collaboratory for Image Processing) benchmark. However, the depth map resolution obtained by EPINet is lower than that of the central view image. It is not wholly pixel-wise prediction or lightweight.
In this paper, we focus on designing a novel neural network that directly utilizes textural features of EPIs based on epipolar geometry and balances depth estimation accuracy and computational time. Our main contribution is twofold:
EPI synthetic images: We stitch EPIs row by row or column by column to generate horizontal or vertical EPI synthetic images with more obvious texture. The two EPI synthetic images, as well as the central view image, are used as the multi-stream inputs of our network. In this way, a convolutional neural network (CNN) can play an essential role in texture feature extraction and depth-estimation accuracy. As far as we know, our work is the first to use EPI synthetic image as the input of a depth estimation network. In terms of multi-stream inputs, our network is significantly different from EPINet [
5], which takes the sub-aperture image stack as the input of each stream, whereas we use EPI synthetic images.
New CNN architecture for end-to-end lightweight computing: We employ skip-connections to fuse structural information in shallow layers and semantic information in deep layers to reduce our network parameters and computational time. Furthermore, transposed convolution modules are used to improve the resolution of the output disparity map in order to be consistent with the central view image, thus forming an end-to-end training model and cutting down training complexity.
As an extended version of our conference paper [
6], this paper enriches the principle description and experimental verification. The remainder of the paper is organized as follows.
Section 2 reports related studies on depth estimation using EPIs from the light field.
Section 3 describes the geometric principle and synthetic texture used in our method.
Section 4 details our network architecture, including the general framework, multi-stream inputs, skip-connections, and the loss function used in training.
Section 5 presents the experiments performed and discusses the results. Finally,
Section 6 concludes this paper.
2. Related Work
In the following, we briefly introduce existing approaches, focusing our description on the light-field depth estimation methods using EPIs. According to different technical principles, EPI-based depth estimation methods can be divided into two types: EPI analysis and deep learning.
EPI analysis-based methods extract depth information from the light field by evaluating the directions of the lines in EPIs. The idea is to try out all the different directions: the one with the least color variance along the line is most likely to give the correct depth value. Based on this point, several methods use different ways to measure color variance. Kim et al. employed a modified Parzen window estimation with an Epanechenikov kernel [
3]. Tao et al. [
7] used the standard deviation to measure correspondence cues, then combined this with the defocus cue to calculate depth. Since all EPI data has a similar gradient pattern, it is unnecessary to try out all hypothetical depth values to find the optimal. Accordingly, Mun et al. [
8] efficiently reduced the number of angular candidates for cost computation.
Similarly, Han et al. [
9] select only eight sub-aperture images with different directions to compute stereo disparity and fuse stereo disparity and defocus response, based on guided filtering, to produce high-quality depth maps. Other EPI-analysis-based methods employ gradient or a structural tensor. For example, Wanner and Goldluecke [
10] applied the 2D structure tensor to measure the direction of each position in the EPIs. Li et al. [
11] used the depth estimation from the structure tensor as a starting point, followed by a refinement step based on examining the color correspondence along the detected line from the structure tensor. To reduce the computational complexity associated with match cost functions, Neri et al. [
12] make a local estimation based on the maximization of the total loglikelihood spatial density aggregated along the epipolar lines. Using epipolar geometry, Lourenco et al. [
13] first detect enlarged silhouettes, then devise a structural inpainting method to reconstruct the disparity map. Li and Jin [
14] propose a novel tensor, Kullback-Leibler Divergence (KLD), to analyze the histogram distributions of the EPI’s window. Then, depths calculated from vertical and horizontal EPIs’ tensors are fused according to the tensors’ variation scale for a high-quality depth map. Through EPI analysis, Schilling et al. [
15] integrate occlusion processing into a depth estimation model to maximize the use of the available data and obtain general accuracy and quality of object borders. Jean et al. [
16] and Lin et al. [
17] use frequency domain information and focus stacks on estimating depth, respectively. Some studies extend gradient and tensor analysis to 4D space. Berent et al. [
18] apply a segmentation technique to identify the 4D plenoptic structures and consequently the depths. Lüke et al. [
19] encoded depth information in the “slopes” of the planes in 4D ray space that correspond to a point in the 3D world, so an eigenvalue analysis on the 4D local structure tensor is performed to distinguish types of structure.
Recently, deep learning-based methods continue to emerge. Heber et al. [
20] explored a convolutional neural network to predict the 2D hyperplane orientation in the light-field domain, corresponding to the depth of the 3D scene point. Heber also formulated a convex optimization problem with high-order regularization. From this point of view, Heber’s CNN is not an end-to-end network for depth estimation. Guo et al. [
21] also disentangled a complex task into multiple simple sub-tasks, and a tailored subnetwork realized each subtask. Finally, an occlusion-aware network was proposed for predicting occlusion regions accurately. In 2017, Herber et al. [
22] presented a U-shaped regression network involving two symmetric parts, an encoding and a decoding part. This network unifies ideas from 2D EPI analysis with spatial matching-based approaches by learning 3D filters for disparity estimation based on EPI volumes. To enhance the reliability of depth predictions, Shin et al. [
5] design a multi-steam network that encodes each epipolar plane image separately. Since each epipolar plane image has its unique geometric characteristics, the multi-stream network fed with different images can take advantage of these characteristics. However, the output resolution of this network is smaller than that of sub-aperture images, which inconveniences subsequent applications such as 3D reconstruction. Liang [
23] proposed EPI-refocus-net, a convolutional neural network that combines EPI cue and refocusing cue for depth estimation. Zhou et al. [
24] introduced a hybrid learning architecture to combine multimodal cues from multiple light-field representations. Ma et al. [
25] proposed a novel end-to-end network (VommaNet) to retrieve multi-scale features from reflective and texture-less regions for accurate disparity estimation
3. Geometric Principle and Texture Synthesis
Different from the traditional camera, the light-field camera adds a microlens array (MLA) between the sensor and the main lens. Through the main lens and MLA, the ray recorded by the light-field camera includes not only the position but the direction. Light-field imaging geometry and data lay the foundation for light-field depth estimation.
There are many ways to represent the light field, among which the two-plane parametrization (2PP) is very intuitive and commonly used. 2PP representation considers the light field as a collection of pinhole views from several viewpoints parallel to a common image plane. In this way, a 4D light field is defined as the set of rays on a ray space
, passing through two planes Π and
in 3D space; as shown in
Figure 1, the 2D plane
contains the viewpoints given by (
s,
t), and
denotes the image plane parameterized by the coordinates (
u,
v). Therefore, each ray can be uniquely identified by intersections (
u,
v) and (
s,
t) with two planes. A 4D light field can be formulated as a map:
An EPI can be regarded as a 2D slice of a 4D light field. If the coordinate
v in the image plane
is a constant
v*, and the coordinate
t in the image plane
keeps the value of
t*, we will get a horizontal slice
Sv*,
t* of 4D light field, parameterized by coordinates
u and
s, that is
In a 4D light field, an image under fixed viewpoint coordinates (
s*,
t*) is called a sub-aperture image
, as shown in Formula (3). If (
s*,
t*) is the center of all viewpoints, the image is also called the central view image. The sub-aperture image from the light field is similar to the scene image captured by a monocular camera.
Figure 2 shows an example of a central view image and an EPI, where (a) is the central view image of the scene and (b) is the EPI in the horizontal direction. When we generate the EPI of
Figure 2b from the light field data, the coordinate
v is fixed at the position of the red dotted line in
Figure 2a. In other words, the EPI of
Figure 2b corresponds to the row of the red dotted line in
Figure 2a. In
Figure 2, the width of the EPI is the same as that of the central view image, and its height depends on the angular resolution of the light field (i.e., the range of the coordinate s).
The EPI shown in
Figure 2 presents a distinct linear texture. It has been proved that the slopes of straight lines in an EPI contain depth information [
10]. Let us consider the geometry of the map expression (2). In the set of rays emitted from a point
P(
X,
Y,
Z), the rays whose coordinates are (
u,
v*,
s,
t*) satisfy the geometric relationship shown in
Figure 1, where
v*,
t* are constants and
u,
s are variables. According to the triangle similarity principle, the relationship between the image-point coordinates and the viewpoint coordinates conforms to Equation (4).
In Equation (4), and signify the coordinate changes of viewpoint and image point respectively, where , ; Z represents the depth of the point P, and l denotes the distance between two planes and .
Under the assumption of Lambert’s surface, the pixels corresponding to the same object point have the same gray level. These pixels with approximate gray values are arranged in a straight line when the 4D light field is transformed into 2D EPI. Equation (4) shows that the slope of the straight line is proportional to the depth of its corresponding object point. Therefore, the linear texture can be used as the geometric basis for depth estimation.
Figure 2 only shows an EPI corresponding to one row in the central view image. In fact, each row position of the central view corresponds to its own EPI. Suppose we generate EPI for each row of the central view image, and stitch these EPIs one by one from top to bottom according to their corresponding row numbers in the central view image. In that case, we will get a horizontal EPI synthetic image abbreviated as EPIh for the whole scene.
Figure 3 shows an example in which (a) is a central view image and (b) is part of a horizontal EPI synthetic image.
EPIi and
EPIj selected in
Figure 3b represent EPI images corresponding to rows
i and
j in the central view image, respectively. These EPIs similar to
EPIi are stitched from top to bottom to form a horizontal EPI synthetic image. It should be emphasized that
Figure 3b is only a part of the vertical clipping of the whole EPIh so that the texture structure of the EPIh can be presented at a large display scale.
Similarly, in formula (2), if the coordinates
u and
s remain unchanged, but the coordinates
v and
t change, we will obtain an EPI corresponding to a column of pixels in the central view image. Then EPIs of each column in the central view image can be stitched into a vertical EPI synthetic image (EPIv).
Figure 3c is part of a vertical EPI synthetic image, where the frames of
EPIk and
EPIl represent EPI images corresponding to columns
k and
l in the central view image, respectively.
It can be seen from the above synthesis process that the EPI synthetic images not only have local linear texture contained depth information but also integrate the spatial association information of the row or column in the central view image. Therefore, we use EPIh and EPIv as inputs of the deep neural network to improve feature extraction.
Figure 3 illustrates some examples of these input images.
4. Network Architecture
Our deep neural network designed for depth estimation is described in this section. We first state the overall design ideas and outline the network architecture, followed by two structural details of our network, namely multi-stream inputs and skipconnections. Finally, we introduce the loss function used in training the network.
4.1. General Framework
We formulate depth estimation from the light field as a spatially dense prediction task, and design a deep convolution neural network (ESTNet) to predict the depth of each pixel in the central view image.
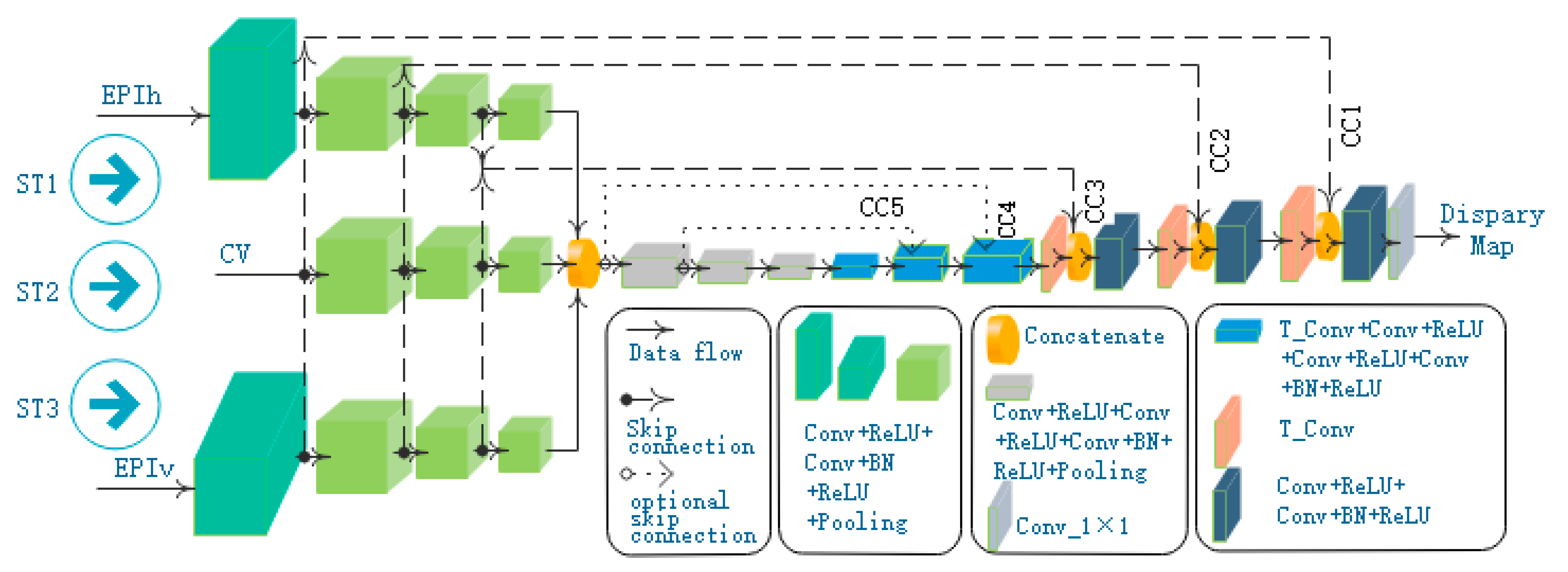
In general, the proposed model is a convolutional network with multi-stream inputs and some skip-connections shown in
Figure 4. In essence, our network is a two-stage network. The first stage conducts a downsampling task, and the second stage performs an upsampling job. The downsampling part encodes input images in a lower dimensionality, while the upsampling part is designed to decode feature maps and produce dense predictions of each pixel.
In the downsampling stage, a multi-stream architecture is utilized to learn the geometry information of the light field. The main idea behind the multi-stream architecture is to receive different inputs from light-field data and extract and fuse their features. Three streams are designed with the respective input of the horizontal EPI synthetic image (EPIh), the central view image (CV), and the vertical EPI synthetic image (EPIv). Different from EPInet [
5], EPIh and EPIv are fed with EPI synthetic images rather than the stack of the sub-aperture images in one direction. CNN is used to encode features in each stream. Then the outputs of these streams are concatenated for further encoding of features.
In the upsampling stage, the transposed convolution layer is used as the core of the decoding module to improve the resolution of the feature map. Besides, the connections between modules with the same resolution in the downsampling stage, and the upsampling stage are established to fuse the lower texture information and the upper semantic information. For the sake of the single-channel disparity map computation, a convolution layer is added at the end of the network.
4.2. Multi-Stream Architecture
As shown in
Figure 4, our model has three feature extraction streams: ST1, ST2, and ST3, which are fed with EPIh, CV, and EPIv, respectively.
The stream of ST1 is composed of four blocks with similar structures. Each block is a stack of convolutional layers: the first convolutional layer is followed by activation of ReLU, a batch normalization (BN) operation is executed after the second convolutional layer and provides input for a ReLU activation, and the end of each block is a max-pooling layer. The block structures in ST2 and ST3 are the same as those in ST1. In addition, ST3 contains the same number of blocks as ST1, and ST2 has only three blocks.
Now we discuss the size of input images for the three streams. Suppose the dimensions of the light field are
, where
are angular resolution in a row and a column direction, respectively;
indicate space resolution in a row and a column direction, respectively;
represents the number of channels in a light-field image. EPIh generated from light-field data has the dimension of
, the dimension of EPIv is
, and the size of CV is
. For example, the images in
Figure 3 were generated from the (9,9,381,381,3) dimensional light-field data collected by the Lytro camera. The resolution of the central view image (
Figure 3a) is 381 × 381, and the resolution of EPIh should be 3429 × 381. However,
Figure 3b is only a part of EPIh, and its resolution is 1450 × 381.
As mentioned above, the input images in the three streams have different dimensions. However, the output of each stream should reach the same resolution for concatenation processing. Therefore, the parameters, such as the size and the stride for convolutional kernel or max pooling, should be set reasonably.
In the first block of the ST1 stream, as shown in
Table 1, the first convolutional layer filters the
-dimensional EPIh with 10 kernels of size (3,3) and a stride of 1 pixel. The second convolutional layer also has 10 kernels of size (3,3) and 1-pixel stride, followed by batch normalization (BN) layer and ReLU activation. The end of the first block is spatial pooling carried out by the max-pooling layer. Max-pooling is performed over a (9,1) pixel window, with stride (9,1). The first block of the ST3 stream is of similar structure as ST1′s first block, but ST3′s max-pooling stride is (1,9).
After the first block processing of the ST1 stream, its output resolution is consistent with that of the CV image. The same is true for the first block of the ST3 stream. Therefore, the identical layer structure is designed for the remaining three blocks in ST1 and ST3 streams and the blocks in ST2 stream. In these blocks, all the convolutional layers have kernel size of (3,3) and stride of 1 pixel, and a Max pooling layer use (2,2) window to slide with stride 2. The convolutional layers in one block have the same number of filters and the exact size of feature maps. However, from one block to the next, the feature map size is halved; the number of filters is doubled to preserve the time complexity per layer.
After the feature extraction of the three streams, we cascade their output results and then employ three blocks to extract features further. These blocks are shown in the gray box in
Figure 4, where each block is composed of two Conv + ReLU layers, one Conv + BN + ReLU layer, and one max pooling layer.
After the above encoding stage of feature extraction, the network enters an expansive path that decodes the feature maps. This stage of the network consists of six blocks which are divided into two types. The first type block includes one transposed convolution layer, two Conv + ReLU layers, and one Conv + BN + ReLU layer.
Table 2 lists the parameters of the first type block. Compared with the first type block, the second type block adds a cascade layer to realize skip-connections and reduce a Conv + ReLU layer. Finally, we use a 1 × 1 convolutional layer to get the disparity map.
4.3. Skip Connections
Compared with high-level feature maps, shallow features have smaller receptive fields and therefore contain less semantic information, but the image details are preserved better [
26]. Since depth estimation requires both accurate location information and precise category prediction, fusing shallow and high-level feature maps is a good way to improve depth estimation accuracy. Therefore, the proposed model utilizes skip-connections to retain shallow detailed information from the encoder directly.
Skip-connections connect neurons in non-adjacent layers in a neural network. As shown in
Figure 4, dotted lines indicate skip-connections. With those skip-connections in a concatenation fashion, local features can be transferred directly from a block of the encoder to the corresponding block of the decoder.
In
Figure 4, CC1, CC2, and CC3 are the three skip-connections proposed in this paper. In order to analyze the impact of the number of skip-connections on our network performance, we compared the experimental results when adding CC4 and CC5 in the experimental section. The shallow feature map is directly connected to the deep feature map, which is essentially a cascade operation, so it is necessary to ensure that the resolution of the two connected feature maps is equal. In theory, skip-connections can be established for blocks with the same resolution in the two stages, but the experiment shows that three skip-connections can achieve better results.
4.4. Loss Function
The intuitive meaning of the loss function is obvious: the worse the performance of the model, the greater the loss, so the value of the corresponding loss function should be larger. When training a network model, the gradient of the loss function is the basis of updating network parameters. Ideally, the large value of the loss function indicates that the model does not perform well, and the gradient of the loss function should be large to update the model parameters quickly. Therefore, the selection of loss function affects the training and performance of the model.
We try to train the proposed network (ESTNet) with the loss function of log-cosh. Log-cosh is calculated by the logarithm of hyperbolic cosine of prediction error, as shown in Formula (5), where
and
refer to the ground-truth value and the prediction value respectively, and the subscript
represents the pixel index.
The loss function of log-cosh is usually applied to regression problems, and its central part has the following characteristics: if the value of is small, it is approximately equal to , and while is large, it is close to . This means that log-cosh works much like mean square error (MSE), but is not easily affected by outliers.
6. Conclusions
In this paper, ESTNet is designed for light-field depth estimation. The idea behind our design is the principle of epipolar geometry and the texture extraction ability of a convolutional neural network (CNN). We first analyze the proportional relationship between the depth information and the slope of the straight line in an EPI, and then combine EPIs by row or column to generate EPI synthetic images with more linear texture. The proposed ESTNet network uses multi-stream inputs to receive three kinds of image with different texture characteristics: horizontal EPI synthetic image (EPIh), central view image (CV), and vertical EPI synthetic image (EPIv). EPIh and EPIv have more abundant textures suitable for feature extraction by CNN. ESTNet is an encoding-decoding network. Convolution and pooling blocks encode features, and then the transposed convolution blocks decode features to recover depth information. Skip-connections are added between encoding blocks and decoding blocks to fuse the shallow location information and deep semantic information. The experimental results show that EPI synthetic images as the input of CNN are conducive to improving depth estimation performance, and our ESTNet can better balance the accuracy of depth estimation and computational time.
Since the strides of the first max-pooling layers of ST1 and ST3 in ESTNet are (9,1) and (1,9), respectively, the limitation of our method is that the number of views used in EPI synthetic images is fixed to nine. At present, the number of horizontal and vertical views of most light field cameras is nine or more. If there are more than nine views in the horizontal or vertical direction, we can select only nine. Therefore, although this method cannot be adaptive to the number of views, it can estimate depth from light-field data captured by most plenoptic cameras available.