Optical Fibre Sensor for Capillary Refill Time and Contact Pressure Measurements under the Foot
Abstract
:1. Introduction
2. Methodology
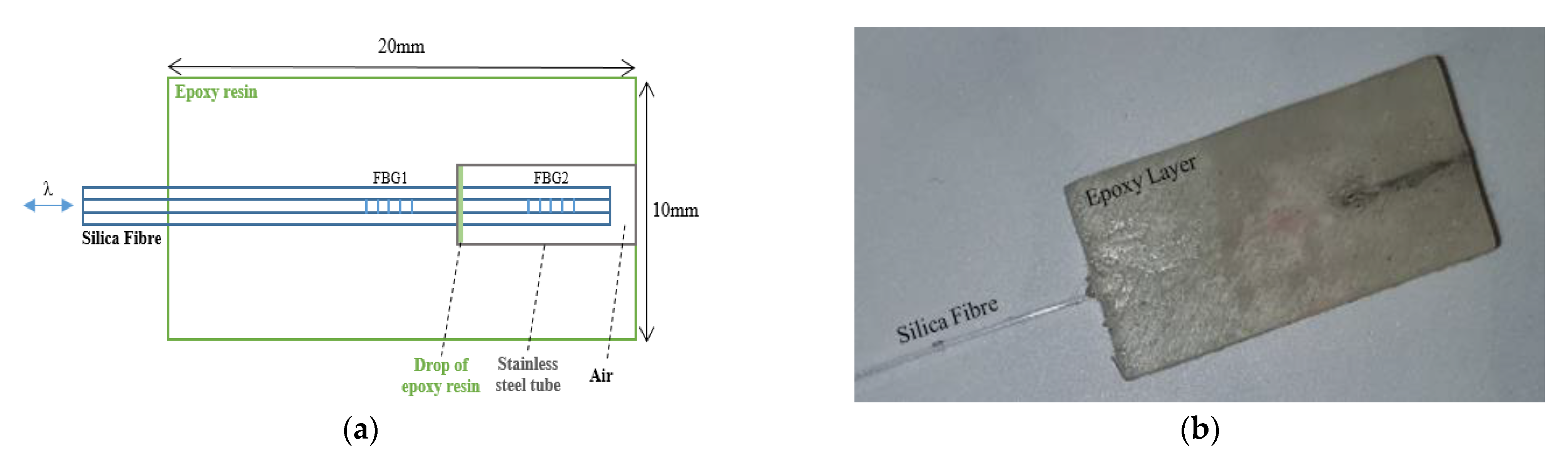
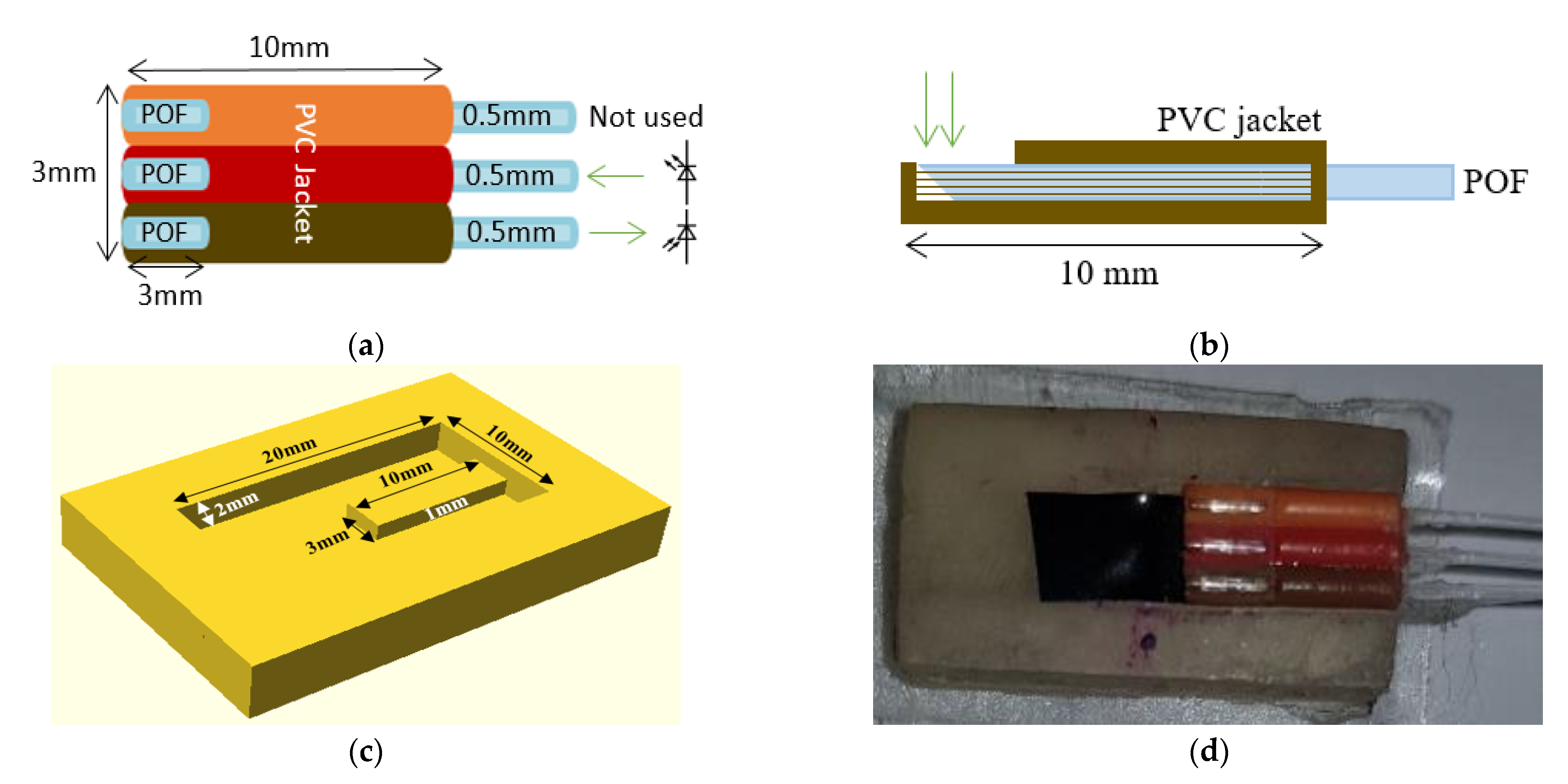
2.1. Sensor Design
2.1.1. Contact Pressure
2.1.2. PPG Sensor
2.1.3. Combined Sensor for Contact Pressure and CRT
2.2. Experiments
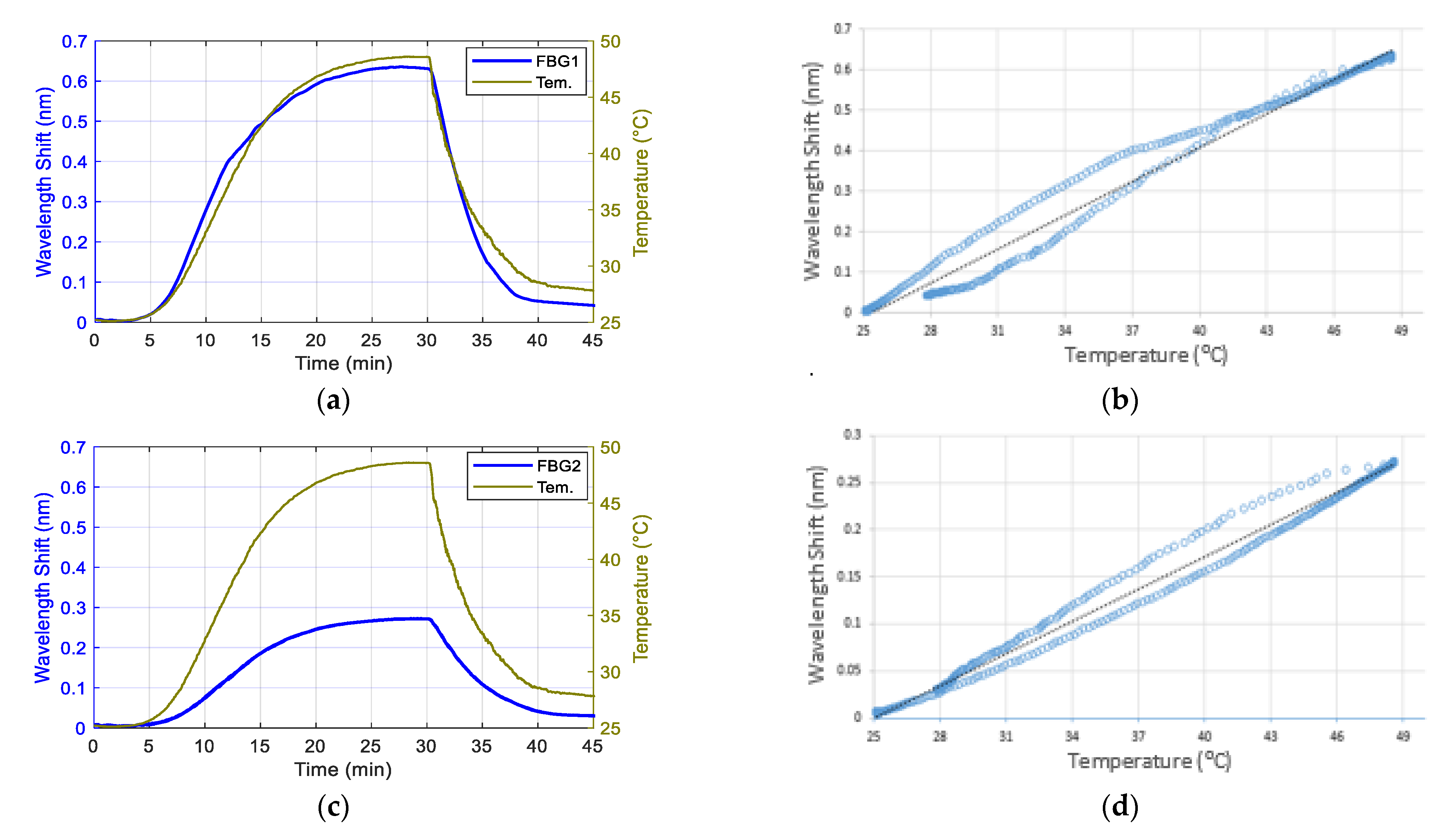
2.2.1. Temperature Calibration of the FBG Sensors
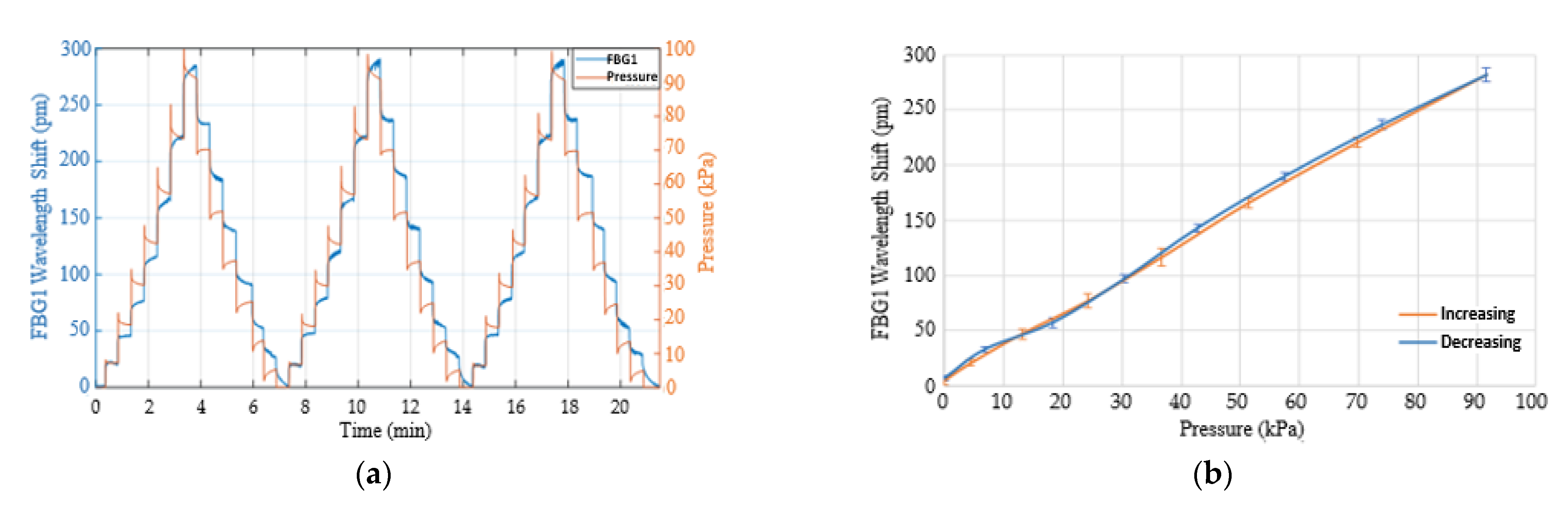
2.2.2. Contact Pressure Calibration
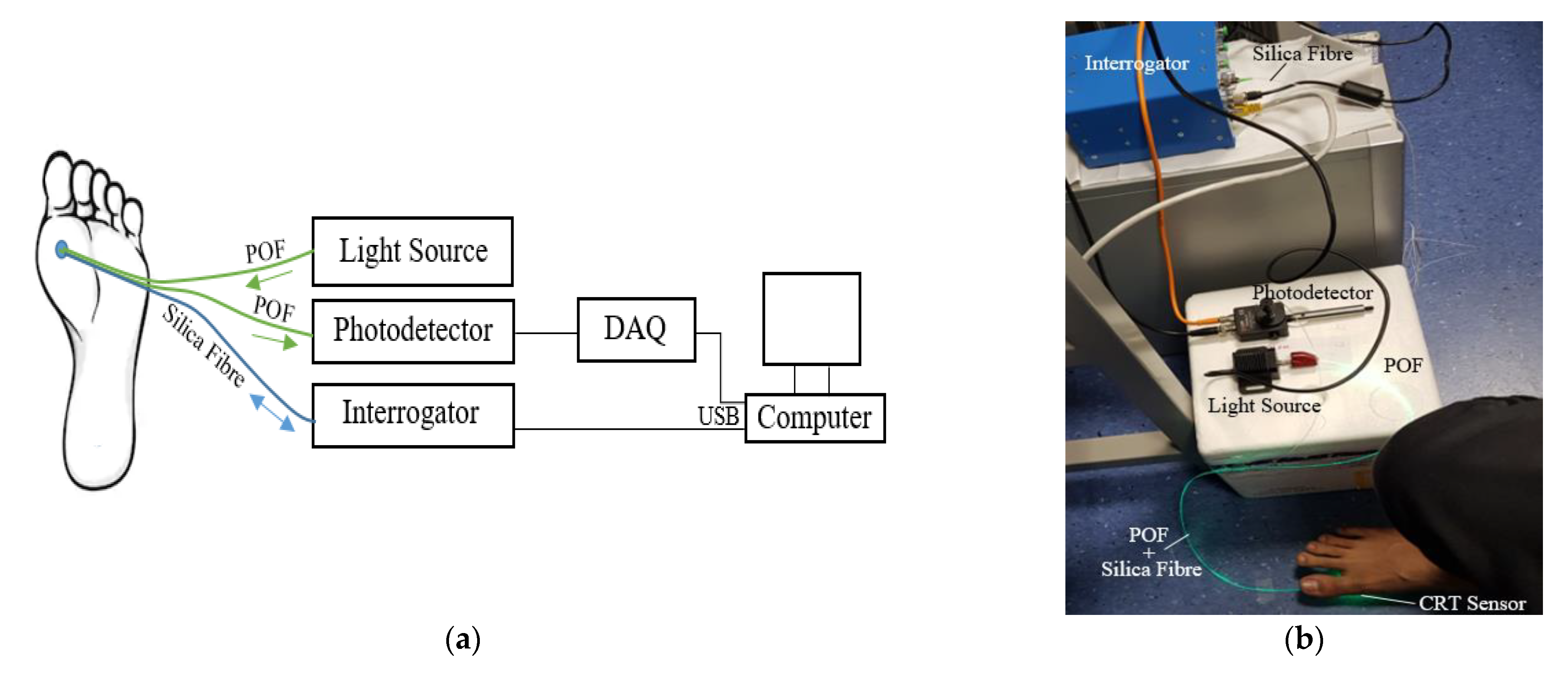
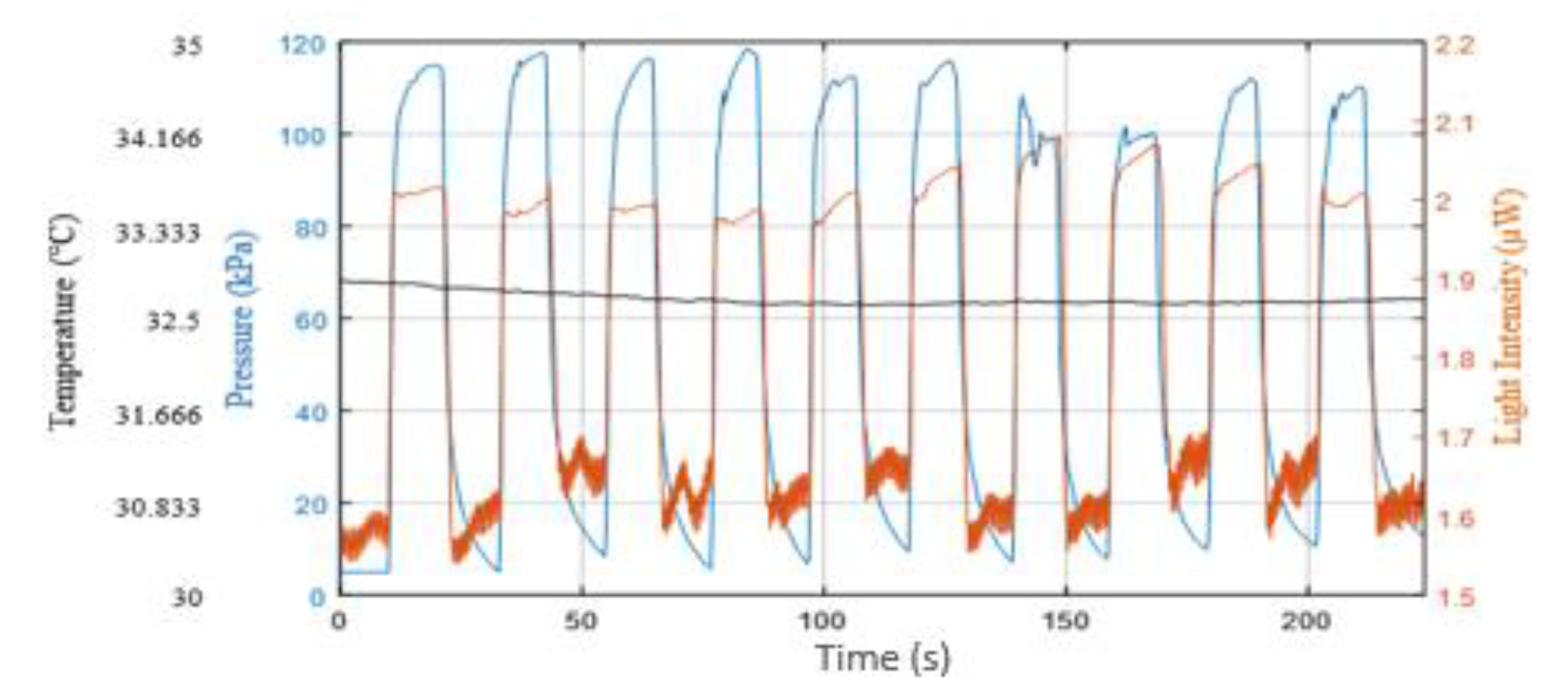
2.2.3. CRT and Contact Pressure Measurements
2.3. Signal Processing
3. Results and Discussion
3.1. Temperature Response of the Contact Pressure Sensor
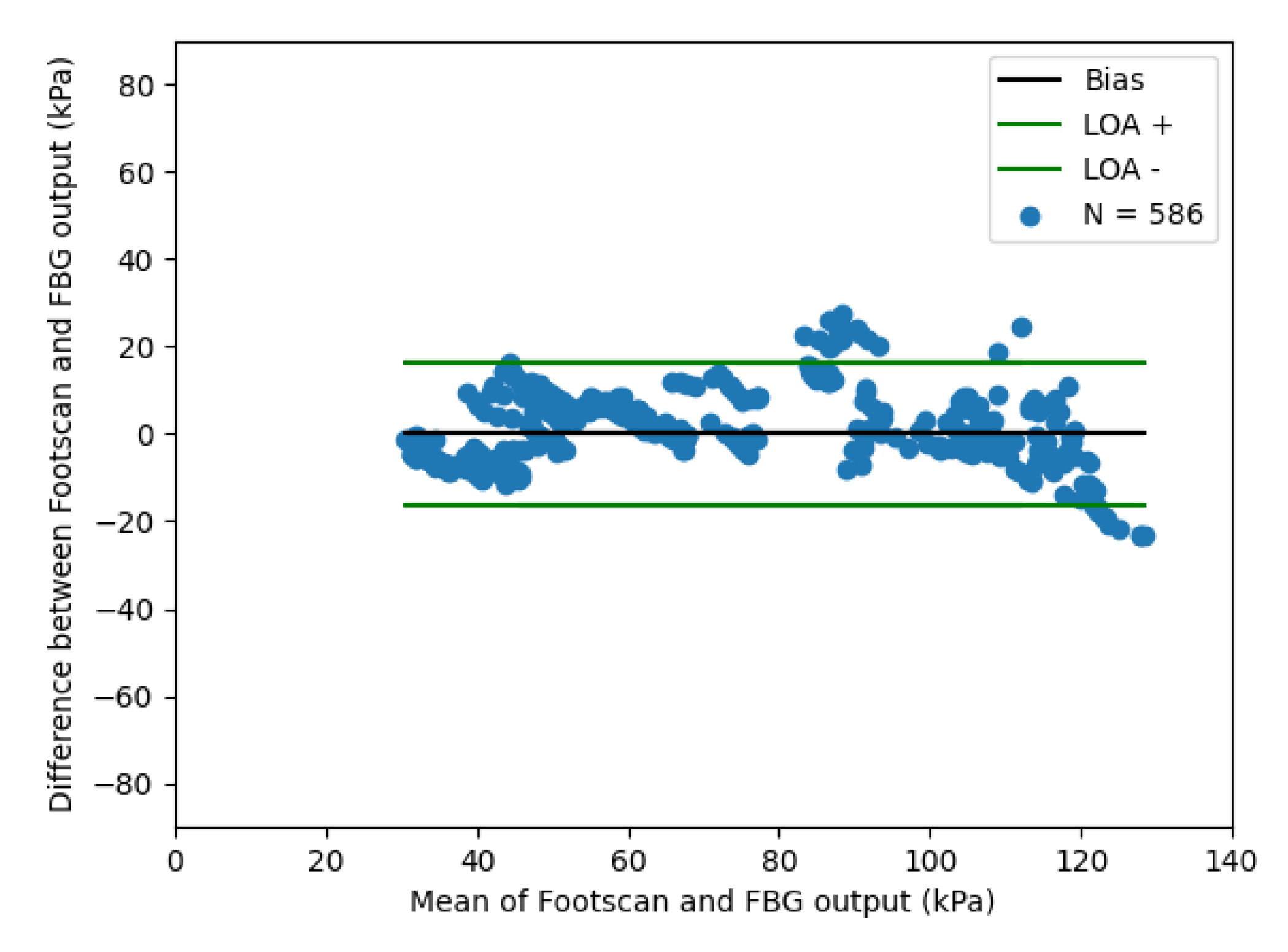
3.2. Response of the Contact Pressure Sensor to Applied Loads
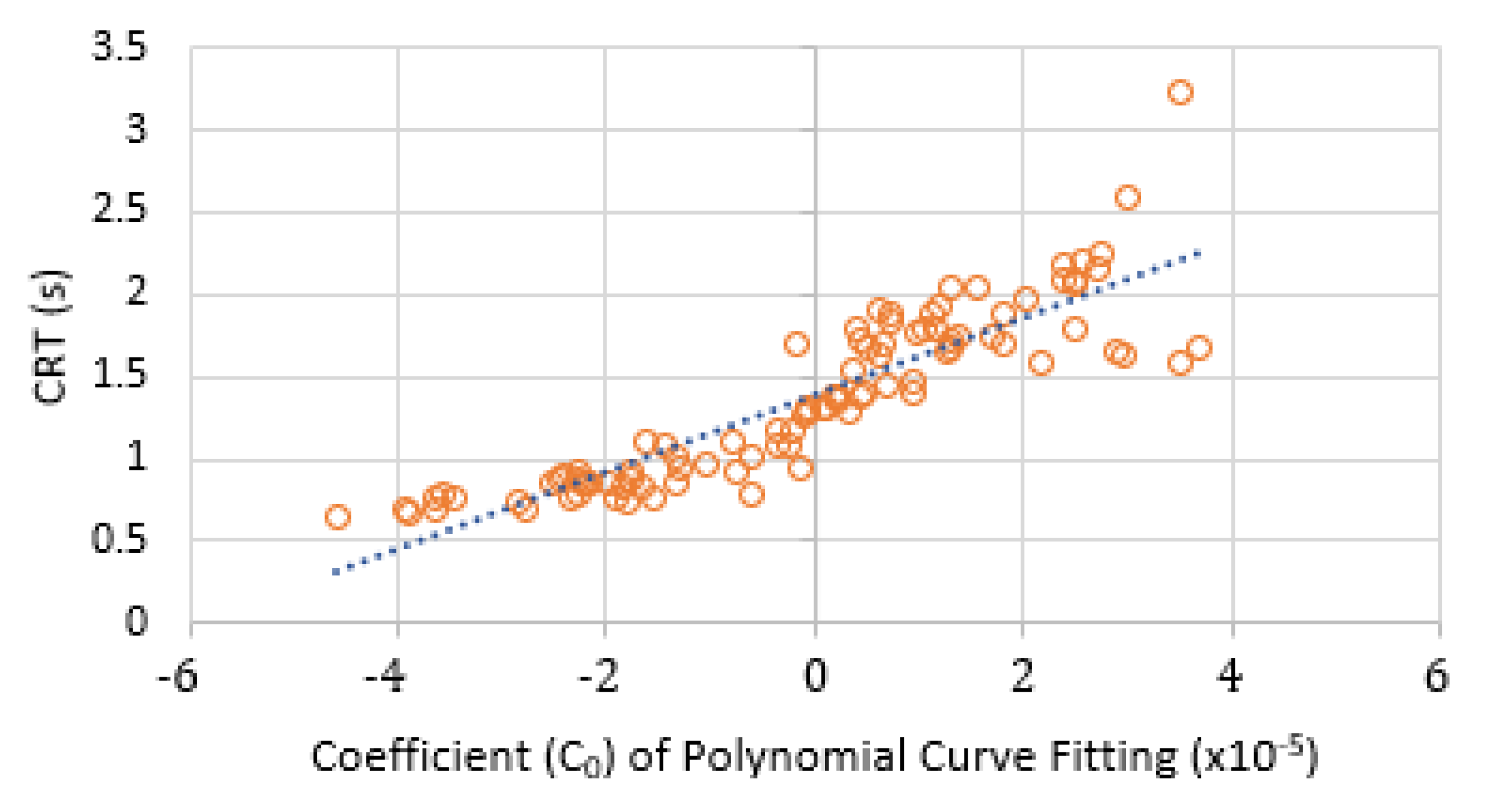
3.3. Capillary Refill Time Measurement on the Sole of the Foot
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Ethical Statements
Appendix A
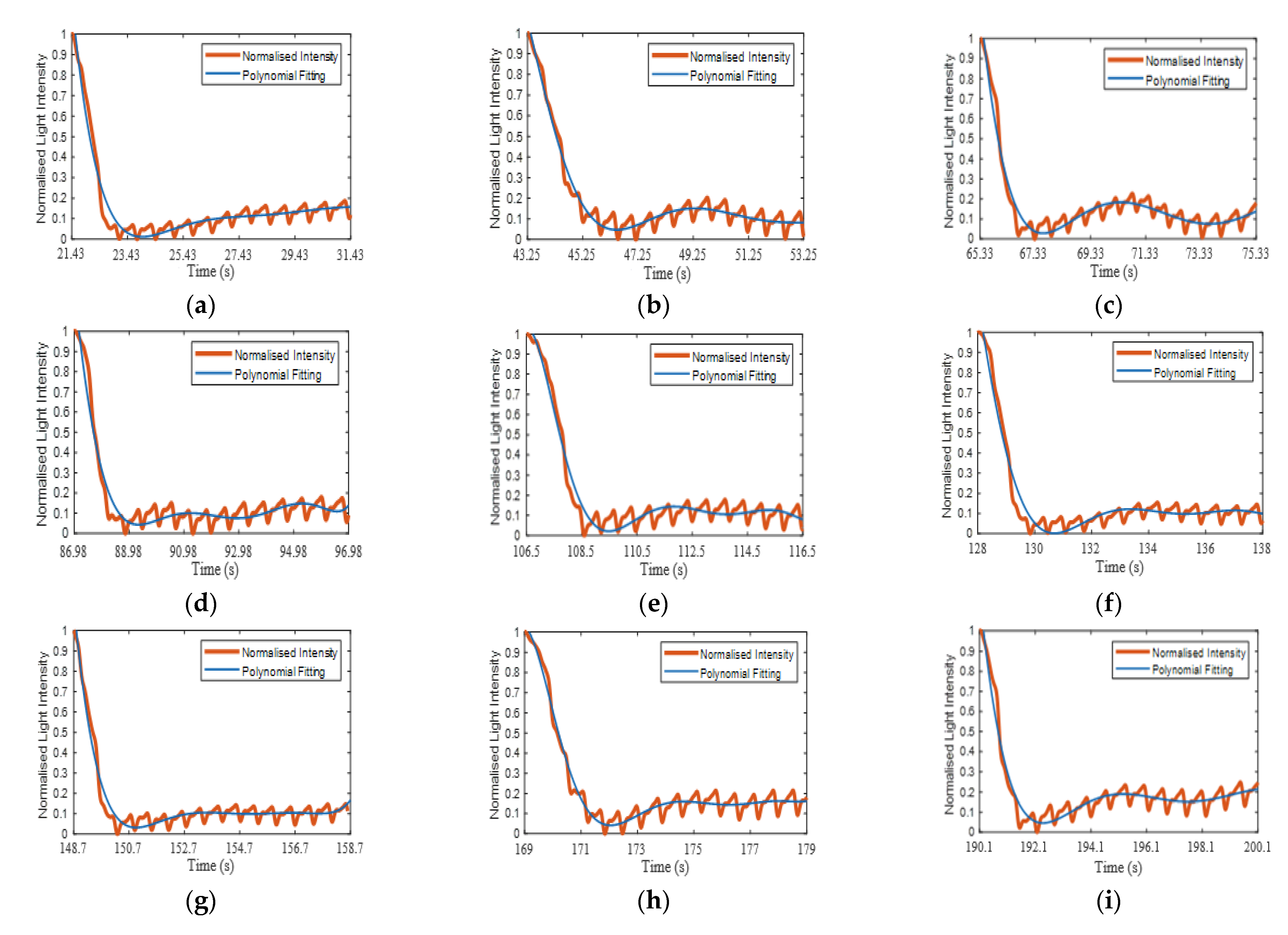
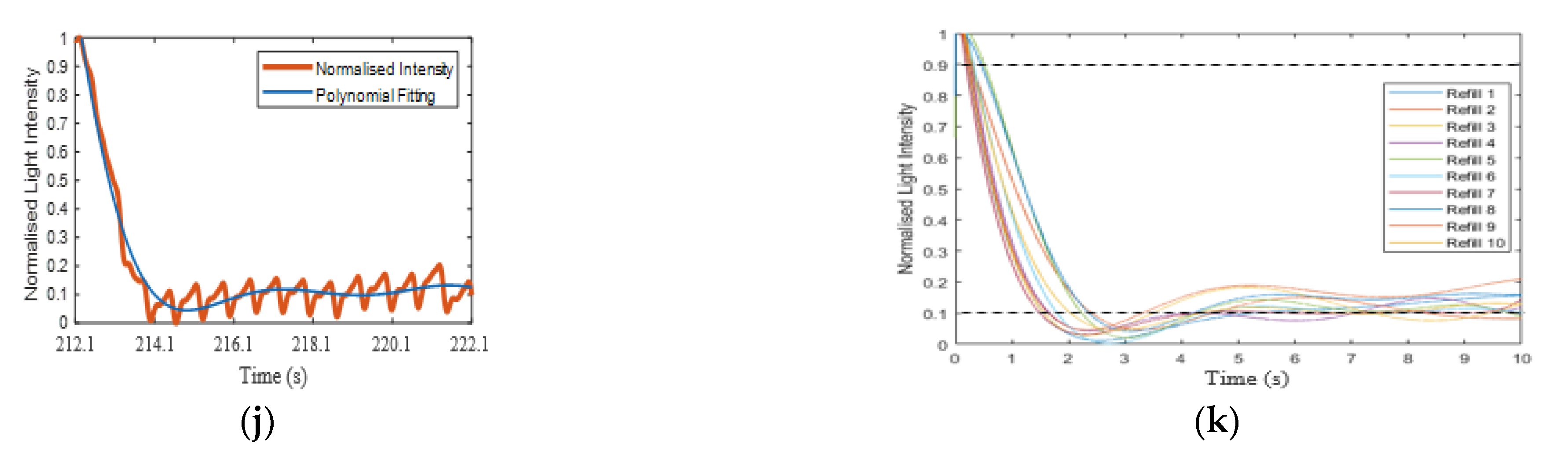
Appendix A.1. Results of CRT Measurements
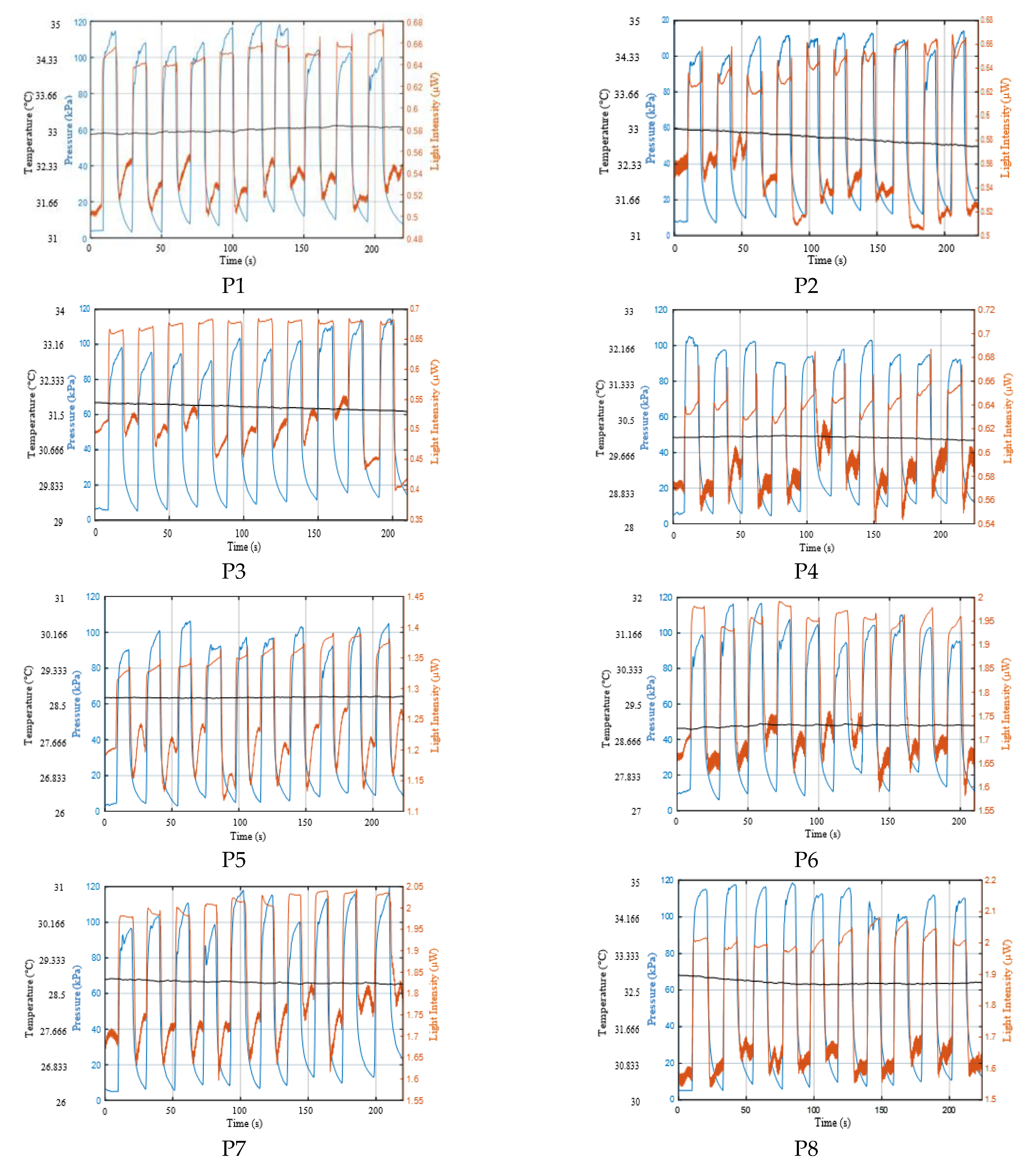

Appendix A.2. Curve Fitting of Refilling Signal


References
- King, D.; Morton, R.; Bevan, C. How to use capillary refill time. Arch. Dis. Child. Educ. Pract. Ed. 2014, 99, 111–116. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Correia, R.; Ballaji, H.; Korposh, S.; Hayes-Gill, B.; Morgan, S. Optical Fibre Sensor for Simultaneous Measurement of Capillary Refill Time and Contact Pressure. Sensors 2020, 20, 1388. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, B.; Kelly, A.-M.; Kerr, D.; Clooney, M.; Jolley, D. Impact of patient and environmental factors on capillary refill time in adults. Am. J. Emerg. Med. 2008, 26, 62–65. [Google Scholar] [CrossRef]
- Gorelick, M.H.; Shaw, K.N.; Baker, M.D. Effect of ambient temperature on capillary refill in healthy children. Pediatrics 1993, 92, 699–702. [Google Scholar]
- Schriger, D.L.; Baraff, L. Defining normal capillary refill: Variation with age, sex, and temperature. Ann. Emerg. Med. 1988, 17, 932–935. [Google Scholar] [CrossRef]
- Morley, R.; Webb, F. Setting up a diabetic foot clinic. Diabet. Foot J. 2019, 22, 18–32. [Google Scholar]
- Armstrong, D.G.; Boulton, A.J.; Bus, S.A. Diabetic foot ulcers and their recurrence. N. Engl. J. Med. 2017, 376, 2367–2375. [Google Scholar] [CrossRef]
- Espensen, E.H.; Armstrong, D.G. The Diabetic Foot: A cancer by any other name. Pod. Now 2017, 20, 19. [Google Scholar]
- Kruse, I.; Edelman, S. Evaluation and treatment of diabetic foot ulcers. Clin. Diabetes 2006, 24, 91–93. [Google Scholar] [CrossRef] [Green Version]
- Klupp, N.L.; Keenan, A.M. An evaluation of the reliability and validity of capillary refill time test. Foot 2007, 17, 15–20. [Google Scholar] [CrossRef]
- Kviesis-Kipge, E.; Curkste, E.; Spigulis, J.; Gardovska, D. Optical Studies of the Capillary Refill Kinetics in Fingertips. In World Congress on Medical Physics and Biomedical Engineering; Springer: Berlin/Heidelberg, Germany, 2009; pp. 377–379. [Google Scholar]
- Shavit, I.; Brant, R.; Nijssen-Jordan, C.; Galbraith, R.; Johnson, D.W. A novel imaging technique to measure capillary-refill time: Improving diagnostic accuracy for dehydration in young children with gastroenteritis. Pediatrics 2006, 118, 2402–2408. [Google Scholar] [CrossRef]
- Shinozaki, K.; Capilupi, M.J.; Saeki, K.; Hirahara, H.; Horie, K.; Kobayashi, N.; Weisner, S.; Kim, J.; Lampe, J.W.; Becker, L.B. Blood refill time: Clinical bedside monitoring of peripheral blood perfusion using pulse oximetry sensor and mechanical compression. Am. J. Emerg. Med. 2018, 36, 2310–2312. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blaxter, L.L.; Morris, D.E.; Crowe, J.A.; Henry, C.; Hill, S.; Sharkey, D.; Vyas, H.; Hayes-Gill, B.R. An automated quasi-continuous capillary refill timing device. Physiol. Meas. 2015, 37, 83. [Google Scholar] [CrossRef] [Green Version]
- Pickard, A.; Karlen, W.; Ansermino, J.M. Capillary refill time: Is it still a useful clinical sign? Anesth. Analg. 2011, 113, 120–123. [Google Scholar] [CrossRef] [PubMed]
- Shinozaki, K.; Jacobson, L.S.; Saeki, K.; Kobayashi, N.; Weisner, S.; Falotico, J.M.; Li, T.; Kim, J.; Lampe, J.W.; Becker, L.B. The standardized method and clinical experience may improve the reliability of visually assessed capillary refill time. Am. J. Emerg. Med. 2020, 44, 284–290. [Google Scholar] [CrossRef] [PubMed]
- Correia, R.; James, S.; Lee, S.W.; Morgan, S.P.; Korposh, S. Biomedical application of optical fibre sensors. J. Opt. 2018, 20, 073003. [Google Scholar] [CrossRef]
- Massaroni, C.; Saccomandi, P.; Schena, E. Medical Smart Textiles Based on Fiber Optic Technology: An Overview. J. Funct. Biomater. 2015, 6, 204–221. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.; Li, Y.; Yang, S.; Liu, C. FBG sensing temperature characteristic and application in oil/gas down-hole measurement. Front. Optoelectron. China 2009, 2, 233–238. [Google Scholar] [CrossRef]
- Massaroni, C.; Caponero, M.A.; D’Amato, R.; Lo Presti, D.; Schena, E. Fiber bragg grating measuring system for simultaneous monitoring of temperature and humidity in mechanical ventilation. Sensors 2017, 17, 749. [Google Scholar] [CrossRef]
- Correia, R.; Li, J.; Staines, S.; Chehura, E.; James, S.W.; Kutner, J.; Dewhurst, P.; Ferreira, P.; Tatam, R.P. Fibre Bragg grating based effective soil pressure sensor for geotechnical applications. In Proceedings of the 20th International Conference on Optical Fibre Sensors, Edinburgh, UK, 5–9 October 2009; Volume 7503, p. 75030F. [Google Scholar]
- Weng, X.; Chen, J.; Wang, J. Fiber Bragg Grating-Based Performance Monitoring of Piles Fiber in a Geotechnical Centrifugal Model Test. Adv. Mater. Sci. Eng. 2014, 2014, 659276. [Google Scholar] [CrossRef] [Green Version]
- Correia, R.; Chehura, E.; Li, J.; James, S.W.; Tatam, R.P. Enhanced sensitivity fibre Bragg grating (FBG) load sensor. Meas. Sci. Technol. 2010, 21, 094006. [Google Scholar] [CrossRef]
- Correia, R.; Blackman, O.R.; Hernandez, F.U.; Korposh, S.; Morgan, S.P.; Hayes-Gill, B.R.; James, S.W.; Evans, D.; Norris, A. Highly sensitive contact pressure measurements using FBG patch in endotracheal tube cuff. In Proceedings of the Sixth European Workshop on Optical Fibre Sensors, Limerick, Ireland, 31 May–3 June 2016; Volume 9916, p. 99161F. [Google Scholar]
- Liang, M.F.; Fang, X.Q.; Wu, G.; Xue, G.Z.; Li, H.W. A fiber bragg grating pressure sensor with temperature compensation based on diaphragm-cantilever structure. Optik (Stuttg) 2017, 145, 503–512. [Google Scholar] [CrossRef]
- Ballaji, H.K.; Correia, R.; Korposh, S.; Hayes-Gill, B.R.; Hernandez, F.U.; Salisbury, B.; Morgan, S.P. A Textile Sleeve for Monitoring Oxygen Saturation Using Multichannel Optical Fibre Photoplethysmography. Sensors 2020, 20, 6568. [Google Scholar] [CrossRef]
- Davenport, J.J.; Hickey, M.; Phillips, J.P.; Kyriacou, P.A. Method for producing angled optical fiber tips in the laboratory. Opt. Eng. 2016, 55, 026120. [Google Scholar] [CrossRef]
- Galante, N. Photoplethysmographic Waveform Analysis During Lower Body Negative Pressure Simulated Hypovolemia as a Tool to Distinguish Regional Differenes in Microvascular Blood Flow Reguation. Ph.D. Thesis, Yale University, New Haven, CT, USA, 2009. [Google Scholar]
- NS, G.R.S.; Vijayakumar, M.V.; Samraj, A. Performance Evaluation of PPG based multimodal biometric system using modified Min-Max Normalization. Int. J. Appl. Eng. Res. 2018, 13, 11279–11284. [Google Scholar]
- Kviesis-Kipge, E.; Curkste, E.; Spigulis, J.; Eihvalde, L. Real-time analysis of skin capillary-refill processes using blue LED. In Proceedings of the Biophotonics: Photonic Solutions for Better Health Care II, Brussels, Belgium, 12–16 April 2010; Volume 7715, p. 771523. [Google Scholar]
- Lanting, S.M.; Barwick, A.L.; Twigg, S.M.; Johnson, N.A.; Baker, M.K.; Chiu, S.K.; Caterson, I.D.; Chuter, V.H. Post-occlusive reactive hyperaemia of skin microvasculature and foot complications in type 2 diabetes. J. Diabetes Complicat. 2017, 31, 1305–1310. [Google Scholar] [CrossRef] [PubMed]
- Vassilios, B.; Neuman, M.I. Capillary refill time diagnostic apparatus and methods. U.S. Patent 9,603,559, 2017. [Google Scholar]
- Evans, J.A.; May, J.; Ansong, D.; Antwi, S.; Asafo-Adjei, E.; Nguah, S.B.; Osei-Kwakye, K.; Akoto, A.O.Y.; Ofori, A.O.; Sambian, D.; et al. Capillary refill time as an independent prognostic indicator in severe and complicated malaria. J. Pediatr. 2006, 149, 676–681. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. On the Analysis of Fingertip Photoplethysmogram Signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Fu, T.-H.; Shing-Hong, L.; Tang, K.-T. Heart rate extraction from photoplethysmogram waveform using wavelet multi-resolution analysis. J. Med. Biol. Eng. 2008, 28, 229–232. [Google Scholar]
- Butler, M.J.; Crowe, J.A.; Hayes-Gill, B.R.; Rodmell, P.I. Motion limitations of non-contact photoplethysmography due to the optical and topological properties of skin. Physiol. Meas. 2016, 37, N27–N37. [Google Scholar] [CrossRef] [PubMed]
- Mihailov, S.J. Fiber bragg grating sensors for harsh environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef] [PubMed]
- Panacol-Elosol GmbH. Vitralit®1655-Datasheet; Panacol-Elosol GmbH: Steinbach, Germany, 2019. [Google Scholar]
- Esposito, M.; Buontempo, S.; Petriccione, A.; Zarrelli, M.; Breglio, G.; Saccomanno, A.; Szillasi, Z.; Makovec, A.; Cusano, A.; Chiuchiolo, A.; et al. Fiber Bragg Grating sensors to measure the coefficient of thermal expansion of polymers at cryogenic temperatures. Sens. Actuators A Phys. 2013, 189, 195–203. [Google Scholar] [CrossRef]






| Refill | RMSE | R2 | C0 | CRT (s) | Stable Blood Volume (s) | Ratio of A2/A1 (%) | Average PI (%) | (P-P)ave Interval (s) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.038 | 0.95 | −6.57 × 10−7 | 1.29 | 4.77 | 9 | 2.08 | 0.68 |
| 2 | 0.036 | 0.97 | 2.37 × 10−5 | 1.86 | 5.96 | 15 | 2.65 | 0.67 |
| 3 | 0.040 | 0.95 | 7.95 × 10−7 | 1.22 | 5.07 | 18 | 2.33 | 0.61 |
| 4 | 0.049 | 0.94 | 2.29 × 10−6 | 1.22 | 4.26 | 10 | 2.49 | 0.66 |
| 5 | 0.046 | 0.96 | 1.80 × 10−5 | 1.65 | 5.15 | 14 | 2.51 | 0.66 |
| 6 | 0.042 | 0.96 | 9.58 × 10−6 | 1.47 | 5.19 | 12 | 2.43 | 0.68 |
| 7 | 0.035 | 0.96 | 3.23 × 10−6 | 1.18 | 4.43 | 10 | 2.53 | 0.65 |
| 8 | 0.037 | 0.97 | 1.83 × 10−5 | 1.73 | 5.52 | 16 | 3.14 | 0.68 |
| 9 | 0.042 | 0.94 | 1.89 × 10−6 | 1.21 | 4.94 | 19 | 2.99 | 0.68 |
| 10 | 0.043 | 0.95 | 1.32 × 10−5 | 1.53 | 5.13 | 12 | 2.89 | 0.68 |
| Ave. | 0.041 | 0.96 | 9.03 × 10−6 | 1.44 ± 0.25 | 5.04 ± 0.49 | 13.5 ± 3.47 | 2.60 ± 0.32 | 0.67 ± 0.02 |
| No. | Average Values | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | C0 | CRT (s) | Stable Blood Volume (s) | Ratio A2/A1 | PI (%) | (P-P)ave Interval (s) | Temp. (°C) | Pressure (kPa) | ||
| ON | OFF | ||||||||||
| P1 | 0.028 | 0.97 | −1.66 × 10−5 | 0.91 | 3.91 ± 1.19 | 9.70 ± 4.24 | 1.21 ± 0.29 | 0.66 ± 0.01 | 33.0 | 105.22 | 9.71 |
| P2 | 0.035 | 0.94 | −2.42 × 10−5 | 0.82 | 3.09 ± 0.36 | 7.90 ± 3.45 | 1.00 ± 0.33 | 0.66 ± 0.02 | 32.8 | 104.94 | 12.50 |
| P3 | 0.033 | 0.96 | −2.11 × 10−5 | 0.84 | 3.33 ± 0.32 | 9.40 ± 3.57 | 1.47 ± 0.52 | 0.70 ± 0.03 | 31.7 | 97.34 | 10.32 |
| P4 | 0.043 | 0.91 | −2.08 × 10−5 | 0.93 | 3.57 ± 1.14 | 20.11 ± 5.06 | 2.45 ± 0.21 | 0.69 ± 0.04 | 30.0 | 94.56 | 10.33 |
| P5 | 0.021 | 0.99 | 2.38 × 10−6 | 1.41 | 8.35 ± 0.49 | 38.50 ± 9.63 | 0.61 ± 0.11 | 0.76 ± 0.04 | 28.7 | 97.03 | 7.44 |
| P6 | 0.035 | 0.98 | 1.22 × 10−5 | 1.82 | 5.58 ± 0.94 | 17.63 ± 7.73 | 2.02 ± 0.16 | 0.77 ± 0.04 | 29.0 | 101.25 | 9.51 |
| P7 | 0.028 | 0.97 | 1.25 × 10−5 | 1.65 | 6.27 ± 2.45 | 24.00 ± 5.34 | 1.21 ± 0.12 | 0.74 ± 0.04 | 28.8 | 102.67 | 8.56 |
| P8 | 0.041 | 0.96 | 9.03 × 10−6 | 1.44 | 5.04 ± 0.49 | 13.50 ± 3.47 | 2.60 ± 0.32 | 0.67 ± 0.02 | 32.7 | 109.62 | 7.93 |
| P9 | 0.034 | 0.98 | 1.58 × 10−5 | 1.89 | 5.95 ± 0.49 | 12.70 ± 1.77 | 1.59 ± 0.20 | 0.70 ± 0.04 | 34.1 | 96.94 | 8.23 |
| P10 | 0.039 | 0.97 | 1.59 × 10−5 | 1.94 | 6.17 ± 0.88 | 14.20 ± 4.80 | 1.89 ± 0.17 | 0.69 ± 0.03 | 34.5 | 102.21 | 7.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballaji, H.K.; Correia, R.; Liu, C.; Korposh, S.; Hayes-Gill, B.R.; Musgrove, A.; Morgan, S.P. Optical Fibre Sensor for Capillary Refill Time and Contact Pressure Measurements under the Foot. Sensors 2021, 21, 6072. https://doi.org/10.3390/s21186072
Ballaji HK, Correia R, Liu C, Korposh S, Hayes-Gill BR, Musgrove A, Morgan SP. Optical Fibre Sensor for Capillary Refill Time and Contact Pressure Measurements under the Foot. Sensors. 2021; 21(18):6072. https://doi.org/10.3390/s21186072
Chicago/Turabian StyleBallaji, Hattan K., Ricardo Correia, Chong Liu, Serhiy Korposh, Barrie R. Hayes-Gill, Alison Musgrove, and Stephen P. Morgan. 2021. "Optical Fibre Sensor for Capillary Refill Time and Contact Pressure Measurements under the Foot" Sensors 21, no. 18: 6072. https://doi.org/10.3390/s21186072
APA StyleBallaji, H. K., Correia, R., Liu, C., Korposh, S., Hayes-Gill, B. R., Musgrove, A., & Morgan, S. P. (2021). Optical Fibre Sensor for Capillary Refill Time and Contact Pressure Measurements under the Foot. Sensors, 21(18), 6072. https://doi.org/10.3390/s21186072







