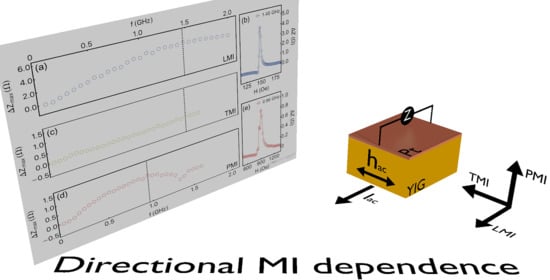
Directional Field-Dependence of Magnetoimpedance Effect on Integrated YIG/Pt-Stripline System
Abstract
:1. Introduction
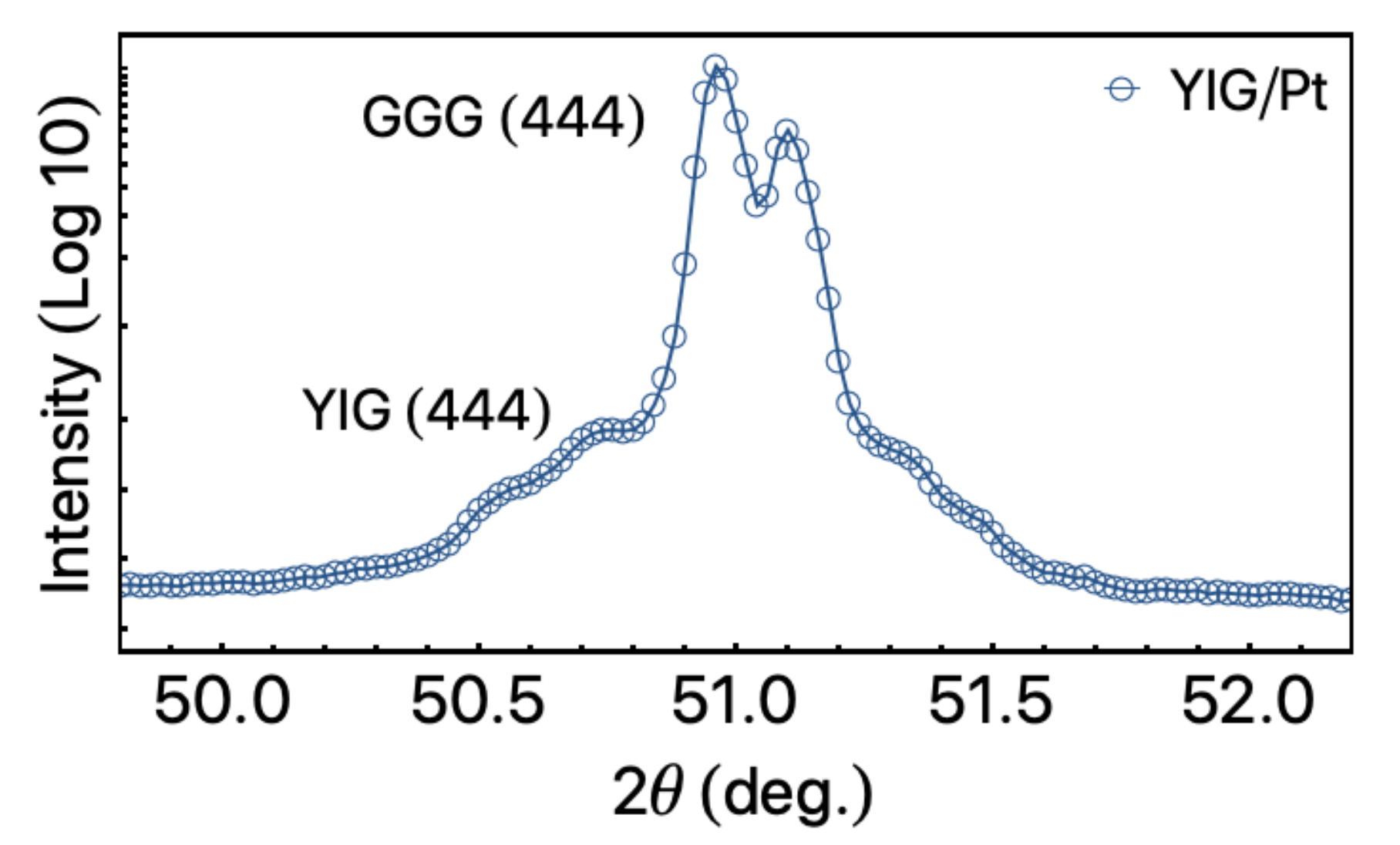
2. Experiment
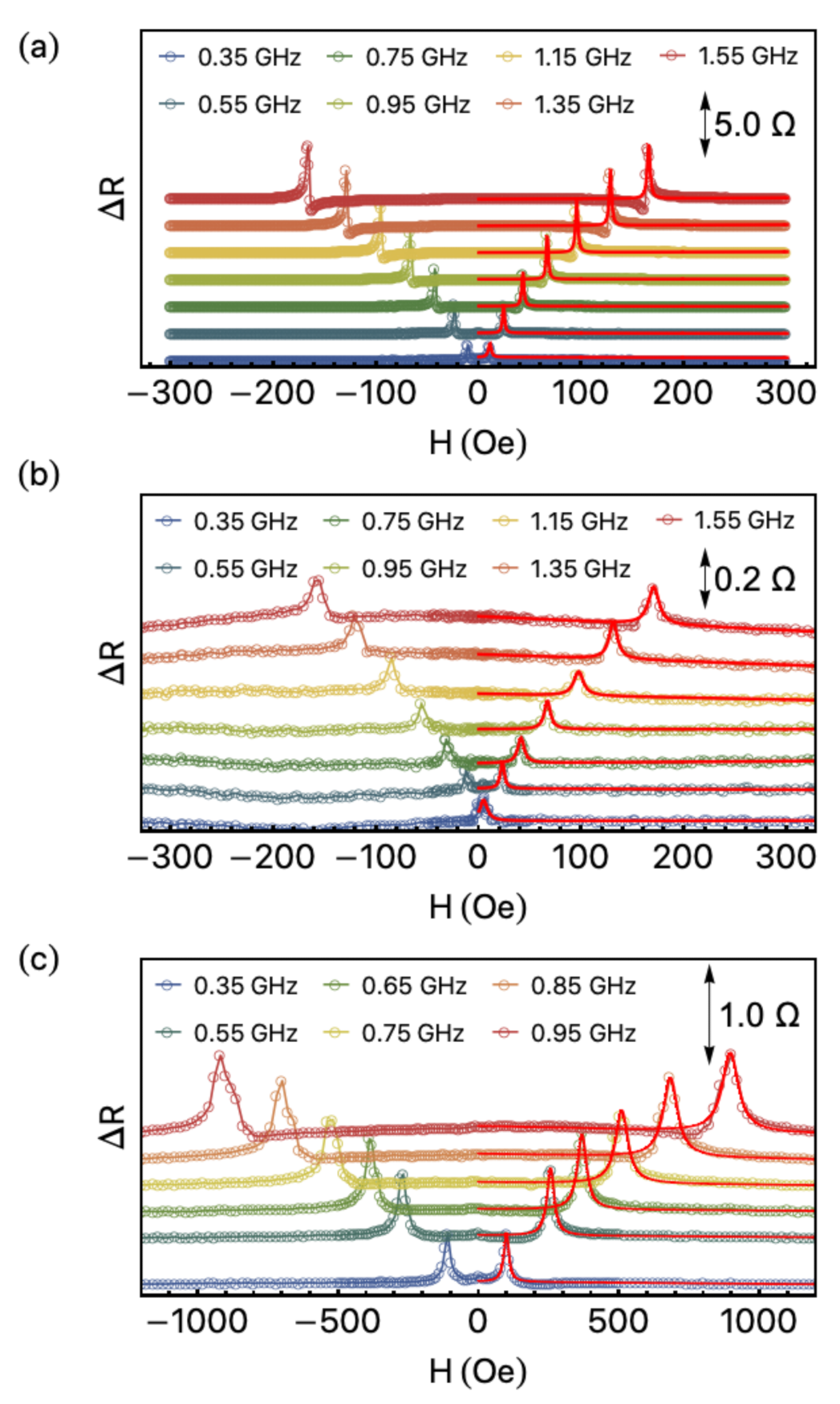
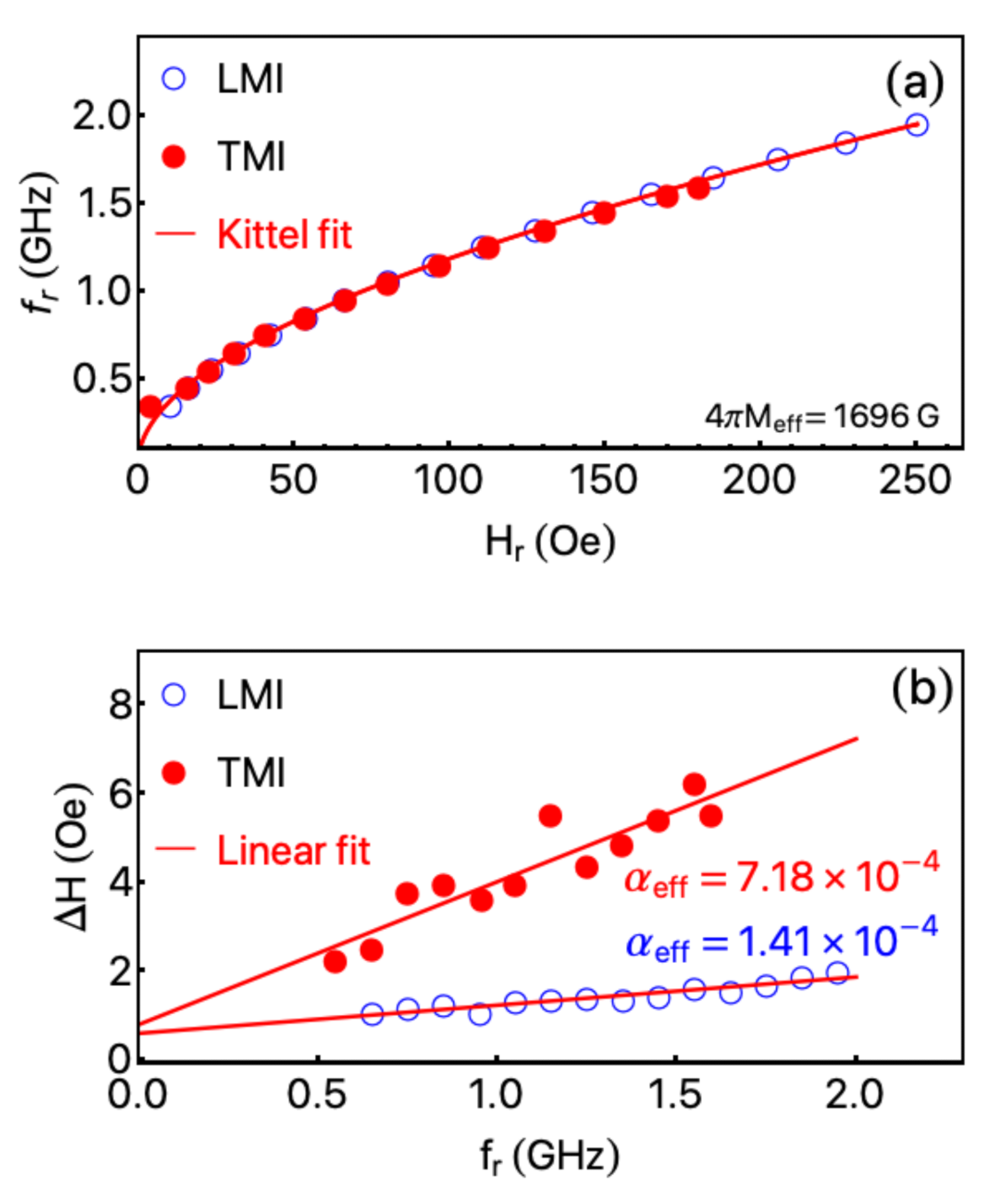
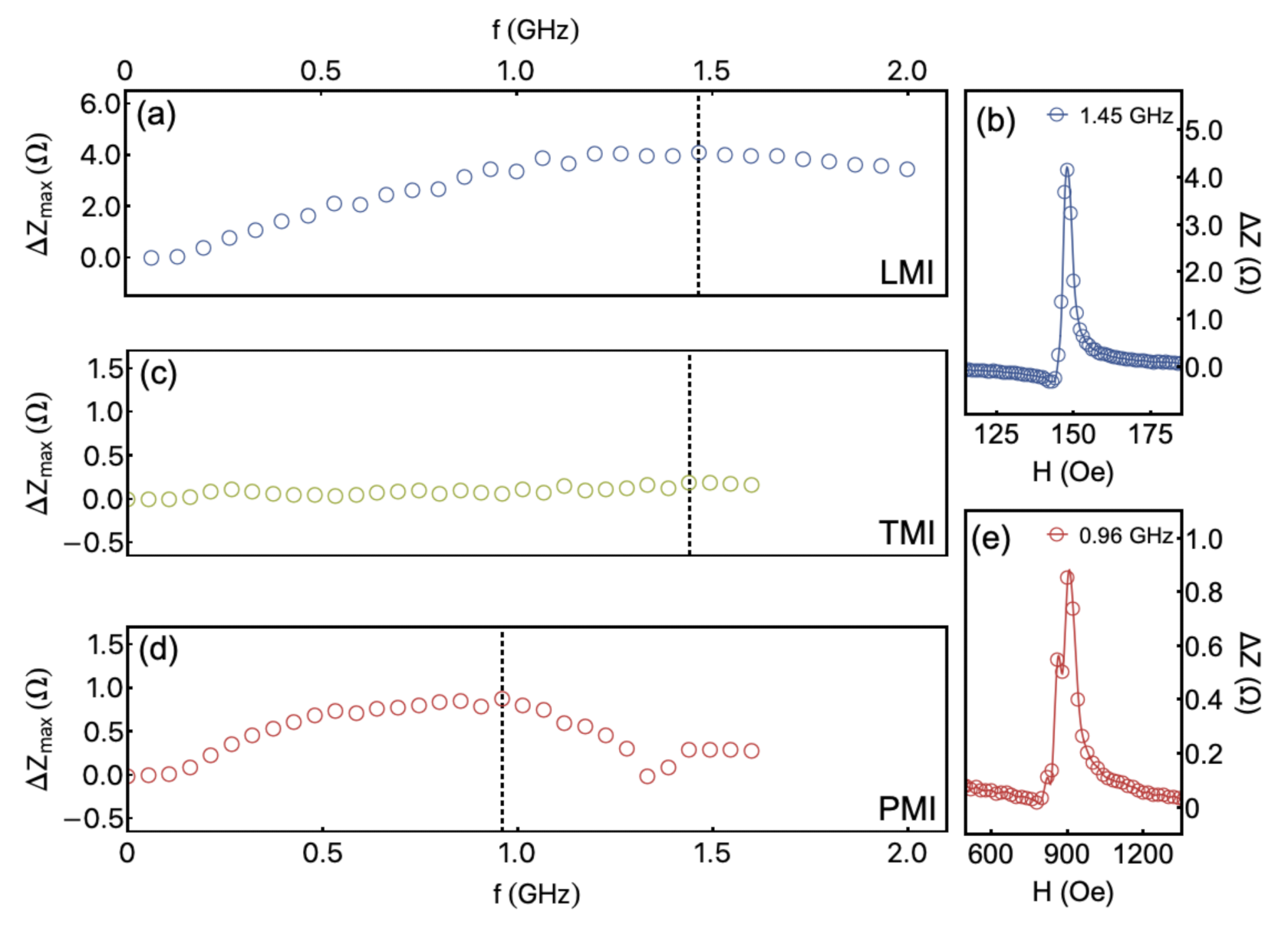
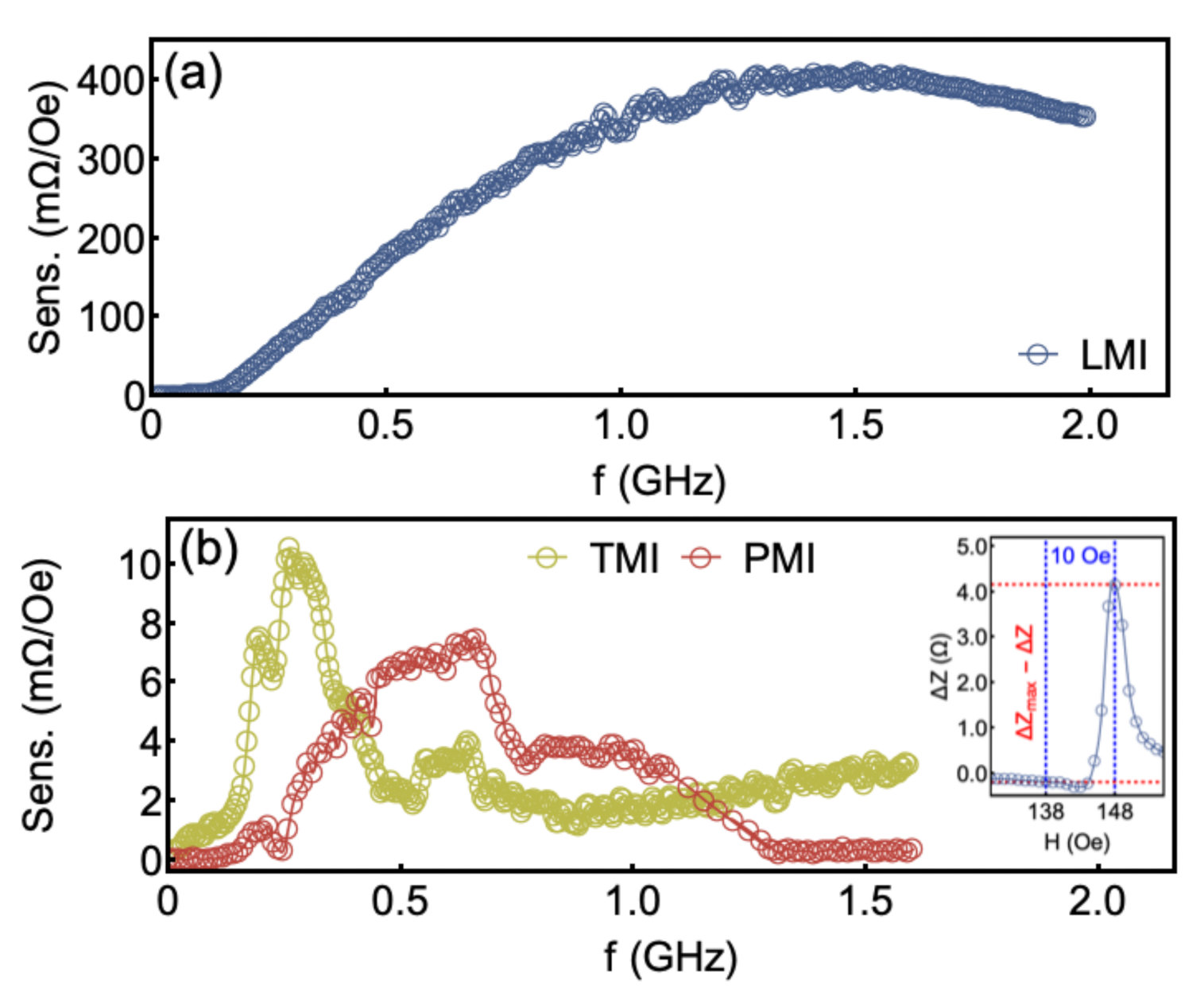
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Kraus, L. GMI modeling and material optimization. Sens. Actuators A Phys. 2003, 106, 187–194. [Google Scholar] [CrossRef]
- Kraus, L. Theory of giant magneto-impedance in the planar conductor with uniaxial magnetic anisotropy. J. Magn. Magn. Mater. 1999, 195, 764–778. [Google Scholar] [CrossRef]
- Hika, K.; Panina, L.V.; Mohri, K. Magneto-impedance in sandwich film for magnetic sensor heads. IEEE Trans. Magn. 1996, 32, 4594–4596. [Google Scholar] [CrossRef]
- Panina, L.V.; Makhnovskiy, D.P.; Mapps, D.J.; Zarechnyuk, D.S. Two-dimensional analysis of magnetoimpedance in magnetic/metallic multilayers. J. Appl. Phys. 2001, 89, 7221–7223. [Google Scholar] [CrossRef]
- Panina, L.V.; Mohri, K. Magneto-impedance effect in amorphous wires. Appl. Phys. Lett. 1994, 65, 1189–1191. [Google Scholar] [CrossRef]
- Sommer, R.L.; Chien, C.L. Role of magnetic anisotropy in the magnetoimpedance effect in amorphous alloys. Appl. Phys. Lett. 1995, 67, 857. [Google Scholar] [CrossRef]
- Sommer, R.L.; Chien, C.L. Longitudinal, transverse, and perpendicular magnetoimpedance in nearly zero magnetostrictive amorphous alloys. Phys. Rev. B 1996, 53, R5982–R5985. [Google Scholar] [CrossRef] [PubMed]
- Sommer, R.L.; Chien, C.L. Longitudinal and transverse magneto-impedance in amorphous Fe73.5Cu1Nb3Si13.5B9 films. Appl. Phys. Lett. 1995, 67, 3346. [Google Scholar] [CrossRef]
- Morikawa, T.; Nishibe, Y.; Yamadera, H.; Nonomura, Y.; Takeuchi, M.; Sakata, J.; Taga, Y. Enhancement of giant magneto-impedance in layered film by insulator separation. IEEE Trans. Magn. 1996, 32, 4965–4967. [Google Scholar] [CrossRef]
- Yelon, A.; Menard, D.; Britel, M.; Ciureanu, P.; Menard, D.; Britel, M.; Ciureanu, P. Calculations of giant magnetoimpedance and of ferromagnetic resonance response are rigorously equivalent. Appl. Phys. Lett. 1996, 69, 3084. [Google Scholar] [CrossRef]
- Menard, D.; Yelon, A. Theory of longitudinal magnetoimpedance in wires. J. Appl. Phys. 2000, 88, 379–393. [Google Scholar] [CrossRef]
- Melnikov, G.Y.; Lepalovskij, V.N.; Svalov, A.V.; Safronov, A.P.; Kurlyandskaya, G.V. Magnetoimpedance Thin Film Sensor for Detecting of Stray Fields of Magnetic Particles in Blood Vessel. Sensors 2021, 21, 3621. [Google Scholar] [CrossRef] [PubMed]
- Rouhani, A.A.; Matin, L.F.; Mohseni, S.M.; Zoriasatain, S. A Domain Dynamic Model Study of Magneto-impedance Sensor in the Presence of Inhomogeneous Magnetic Fields. J. Supercond. Nov. Magn. 2021, 34, 571–580. [Google Scholar] [CrossRef]
- Nakai, T. Nondestructive Detection of Magnetic Contaminant in Aluminum Casting Using Thin Film Magnetic Sensor. Sensors 2021, 21, 4063. [Google Scholar] [CrossRef]
- Li, B.; Kavaldzhiev, M.N.; Kosel, J. Flexible magnetoimpedance sensor. J. Magn. Magn. Mater. 2015, 378, 499–505. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Takezawa, M.; Ohdaira, H.; Arai, K.I.; Haga, A. Directivity and sensitivity of high-frequency carrier type thin-film magnetic field sensor. Sens. Actuators A Phys. 2000, 81, 102–105. [Google Scholar] [CrossRef] [Green Version]
- Kurlyandskaya, G.V.; Sánchez, M.L.; Hernando, B.; Prida, V.M.; Gorria, P.; Tejedor, M. Giant-magnetoimpedance-based sensitive element as a model for biosensors. Appl. Phys. Lett. 2003, 82, 3053–3055. [Google Scholar] [CrossRef]
- Wang, T.; Yang, Z.; Lei, C.; Lei, J.; Zhou, Y. An integrated giant magnetoimpedance biosensor for detection of biomarker. Biosens. Bioelectron. 2014, 58, 338–344. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Q.; Li, X.; Pan, H.; Wang, J.; Zhao, Z. Detection of AFP with an ultra-sensitive giant magnetoimpedance biosensor. Sens. Actuators B Chem. 2019, 293, 53–58. [Google Scholar] [CrossRef]
- Kurlyandskaya, G.; Levit, V. Magnetic Dynabeads® detection by sensitive element based on giant magnetoimpedance. Biosens. Bioelectron. 2005, 20, 1611–1616. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Y.; Lei, C.; Sun, X.c.; Zhou, Y. A flexible giant magnetoimpedance-based biosensor for the determination of the biomarker C-reactive protein. Microchim. Acta 2015, 182, 2411–2417. [Google Scholar] [CrossRef]
- Kang, Y.M.; Wee, S.H.; Baik, S.I.; Min, S.G.; Yu, S.C.; Moon, S.H.; Kim, Y.W.; Yoo, S.I. Magnetic properties of YIG (Y3Fe5O12) thin films prepared by the post annealing of amorphous films deposited by rf-magnetron sputtering. J. Appl. Phys. 2005, 97, 10A319. [Google Scholar] [CrossRef]
- Evelt, M.; Safranski, C.; Aldosary, M.; Demidov, V.E.; Barsukov, I.; Nosov, A.P.; Rinkevich, A.B.; Sobotkiewich, K.; Li, X.; Shi, J.; et al. Spin Hall-induced auto-oscillations in ultrathin YIG grown on Pt. Sci. Rep. 2018, 8, 1269. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Serga, A.A.; Chumak, A.V.; Hillebrands, B. YIG magnonics. J. Phys. D. Appl. Phys. 2010, 43, 264002. [Google Scholar] [CrossRef]
- Čermák, J.; Abrahám, A.; Fabián, T.; Kaboš, P.; Hyben, P. YIG based LPE films for microwave devices. J. Magn. Magn. Mater. 1990, 83, 427–429. [Google Scholar] [CrossRef]
- Lotze, J.; Huebl, H.; Gross, R.; Goennenwein, S.T. Spin Hall magnetoimpedance. Phys. Rev. B-Condens. Matter Mater. Phys. 2014, 90, 174419. [Google Scholar] [CrossRef] [Green Version]
- Hahn, C.; De Loubens, G.; Klein, O.; Viret, M.; Naletov, V.V.; Ben Youssef, J. Comparative measurements of inverse spin Hall effects and magnetoresistance in YIG/Pt and YIG/Ta. Phys. Rev. B 2013, 87, 174417. [Google Scholar] [CrossRef] [Green Version]
- Kang, C.; Wang, T.; Jiang, C.; Chen, K.; Chai, G. Investigation of the giant magneto-impedance effect of single crystalline YIG based on the ferromagnetic resonance effect. J. Alloys Compd. 2021, 865, 158903. [Google Scholar] [CrossRef]
- Medwal, R.; Chaudhuri, U.; Vas, J.V.; Deka, A.; Gupta, S.; Duchamp, M.; Asada, H.; Fukuma, Y.; Mahendiran, R.; Rawat, R.S. Magnetoimpedance of Epitaxial Y3Fe5 O12 (001) Thin Film in Low-Frequency Regime. ACS Appl. Mater. Interfaces 2020, 12, 41802–41809. [Google Scholar] [CrossRef]
- Santos, J.; Silva, E.; Rosa, W.; Bohn, F.; Correa, M. Role of the spin-orbit coupling on the effective damping parameter in Y3Fe5O12/(Ag,W) bilayers explored through magnetoimpedance effect. Mater. Lett. 2019, 256, 126662. [Google Scholar] [CrossRef]
- Correa, M.; Rosa, W.; Melo, A.; Silva, E.; Della Pace, R.; Oliveira, A.; Chesman, C.; Bohn, F.; Sommer, R. Magnetoimpedance effect in ferrimagnetic insulator yttrium iron garnet films capped by copper. J. Magn. Magn. Mater. 2019, 480, 6–10. [Google Scholar] [CrossRef]
- Cao Van, P.; Surabhi, S.; Dongquoc, V.; Kuchi, R.; Yoon, S.G.; Jeong, J.R. Effect of annealing temperature on surface morphology and ultralow ferromagnetic resonance linewidth of yttrium iron garnet thin film grown by rf sputtering. Appl. Surf. Sci. 2018, 435, 377–383. [Google Scholar] [CrossRef]
- Shang, T.; Zhan, Q.F.; Ma, L.; Yang, H.L.; Zuo, Z.H.; Xie, Y.L.; Li, H.H.; Liu, L.P.; Wang, B.M.; Wu, Y.H.; et al. Pure spin-Hall magnetoresistance in Rh/Y3Fe5O12 hybrid. Sci. Rep. 2015, 5, 17734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, L.; Jia, K.; He, Y.; Wang, G.; Zhong, Z.; Zhang, H. Pulsed laser deposition grown yttrium-iron-garnet thin films: Effect of composition and iron ion valences on microstructure and magnetic properties. Appl. Surf. Sci. 2019, 483, 947–952. [Google Scholar] [CrossRef]
- Gamino, M.; Silva, E.; Alves Santos, O.; Mendes, J.; Rodríguez-Suárez, R.; Machado, F.; Azevedo, A.; Rezende, S. The role of metallic nanoparticles in the enhancement of the spin Hall magnetoresistance in YIG/Pt thin films. J. Magn. Magn. Mater. 2018, 466, 267–272. [Google Scholar] [CrossRef]
- Castel, V.; Vlietstra, N.; van Wees, B.J.; Youssef, J.B. Frequency and power dependence of spin-current emission by spin pumping in a thin-film YIG/Pt system. Phys. Rev. B 2012, 86, 134419. [Google Scholar] [CrossRef] [Green Version]
- Correa, M.; Santos, J.; Silva, B.; Raza, S.; Della Pace, R.; Chesman, C.; Sommer, R.; Bohn, F. Exploring the magnetization dynamics, damping and anisotropy in engineered CoFeB/(Ag, Pt) multilayer films grown onto amorphous substrate. J. Magn. Magn. Mater. 2019, 485, 75–81. [Google Scholar] [CrossRef]
- Wu, M. Nonlinear Spin Waves in Magnetic Film Feedback Rings. In Solid State Physics; Academic Press: Cambridge, MA, USA, 2010; Volume 62, pp. 163–224. [Google Scholar] [CrossRef]
- Rezende, S.M.; Rodríguez-Suárez, R.L.; Azevedo, A. Magnetic relaxation due to spin pumping in thick ferromagnetic films in contact with normal metals. Phys. Rev. B 2013, 88, 014404. [Google Scholar] [CrossRef]
- Maier-Flaig, H.; Harder, M.; Gross, R.; Huebl, H.; Goennenwein, S.T.B. Spin pumping in strongly coupled magnon-photon systems. Phys. Rev. B 2016, 94, 054433. [Google Scholar] [CrossRef] [Green Version]
- Schoen, M.A.W.; Lucassen, J.; Nembach, H.T.; Koopmans, B.; Silva, T.J.; Back, C.H.; Shaw, J.M. Magnetic properties in ultrathin 3d transition-metal binary alloys. II. Experimental verification of quantitative theories of damping and spin pumping. Phys. Rev. B 2017, 95, 134411. [Google Scholar] [CrossRef] [Green Version]
- Noack, T.B.; Vasyuchka, V.I.; Bozhko, D.A.; Heinz, B.; Frey, P.; Slobodianiuk, D.V.; Prokopenko, O.V.; Melkov, G.A.; Kopietz, P.; Hillebrands, B.; et al. Enhancement of the Spin Pumping Effect by Magnon Confluence Process in YIG/Pt Bilayers. Phys. Status Solidi 2019, 256, 1900121. [Google Scholar] [CrossRef]
- Chang, H.; Praveen Janantha, P.A.; Ding, J.; Liu, T.; Cline, K.; Gelfand, J.N.; Li, W.; Marconi, M.C.; Wu, M. Role of damping in spin Seebeck effect in yttrium iron garnet thin films. Sci. Adv. 2017, 3, e1601614. [Google Scholar] [CrossRef] [Green Version]
- Jungfleisch, M.B.; Chumak, A.V.; Kehlberger, A.; Lauer, V.; Kim, D.H.; Onbasli, M.C.; Ross, C.A.; Kläui, M.; Hillebrands, B. Thickness and power dependence of the spin-pumping effect in Y3Fe5O12/Pt heterostructures measured by the inverse spin Hall effect. Phys. Rev. B 2015, 91, 134407. [Google Scholar] [CrossRef] [Green Version]
- Hait, S.; Husain, S.; Barwal, V.; Gupta, N.K.; Pandey, L.; Svedlindh, P.; Chaudhary, S. Comparison of high temperature growth versus post-deposition in situ annealing in attaining very low Gilbert damping in sputtered Co2FeAl Heusler alloy films. J. Magn. Magn. Mater. 2021, 519, 167509. [Google Scholar] [CrossRef]
- Husain, S.; Akansel, S.; Kumar, A.; Svedlindh, P.; Chaudhary, S. Growth of Co2FeAl Heusler alloy thin films on Si(100) having very small Gilbert damping by Ion beam sputtering. Sci. Rep. 2016, 6, 28692. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souza, A.L.R.; Gamino, M.; Ferreira, A.; de Oliveira, A.B.; Vaz, F.; Bohn, F.; Correa, M.A. Directional Field-Dependence of Magnetoimpedance Effect on Integrated YIG/Pt-Stripline System. Sensors 2021, 21, 6145. https://doi.org/10.3390/s21186145
Souza ALR, Gamino M, Ferreira A, de Oliveira AB, Vaz F, Bohn F, Correa MA. Directional Field-Dependence of Magnetoimpedance Effect on Integrated YIG/Pt-Stripline System. Sensors. 2021; 21(18):6145. https://doi.org/10.3390/s21186145
Chicago/Turabian StyleSouza, Arthur L. R., Matheus Gamino, Armando Ferreira, Alexandre B. de Oliveira, Filipe Vaz, Felipe Bohn, and Marcio A. Correa. 2021. "Directional Field-Dependence of Magnetoimpedance Effect on Integrated YIG/Pt-Stripline System" Sensors 21, no. 18: 6145. https://doi.org/10.3390/s21186145
APA StyleSouza, A. L. R., Gamino, M., Ferreira, A., de Oliveira, A. B., Vaz, F., Bohn, F., & Correa, M. A. (2021). Directional Field-Dependence of Magnetoimpedance Effect on Integrated YIG/Pt-Stripline System. Sensors, 21(18), 6145. https://doi.org/10.3390/s21186145