Locking Multi-Laser Frequencies to a Precision Wavelength Meter: Application to Cold Atoms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Feedback Bandwidth
3. Results
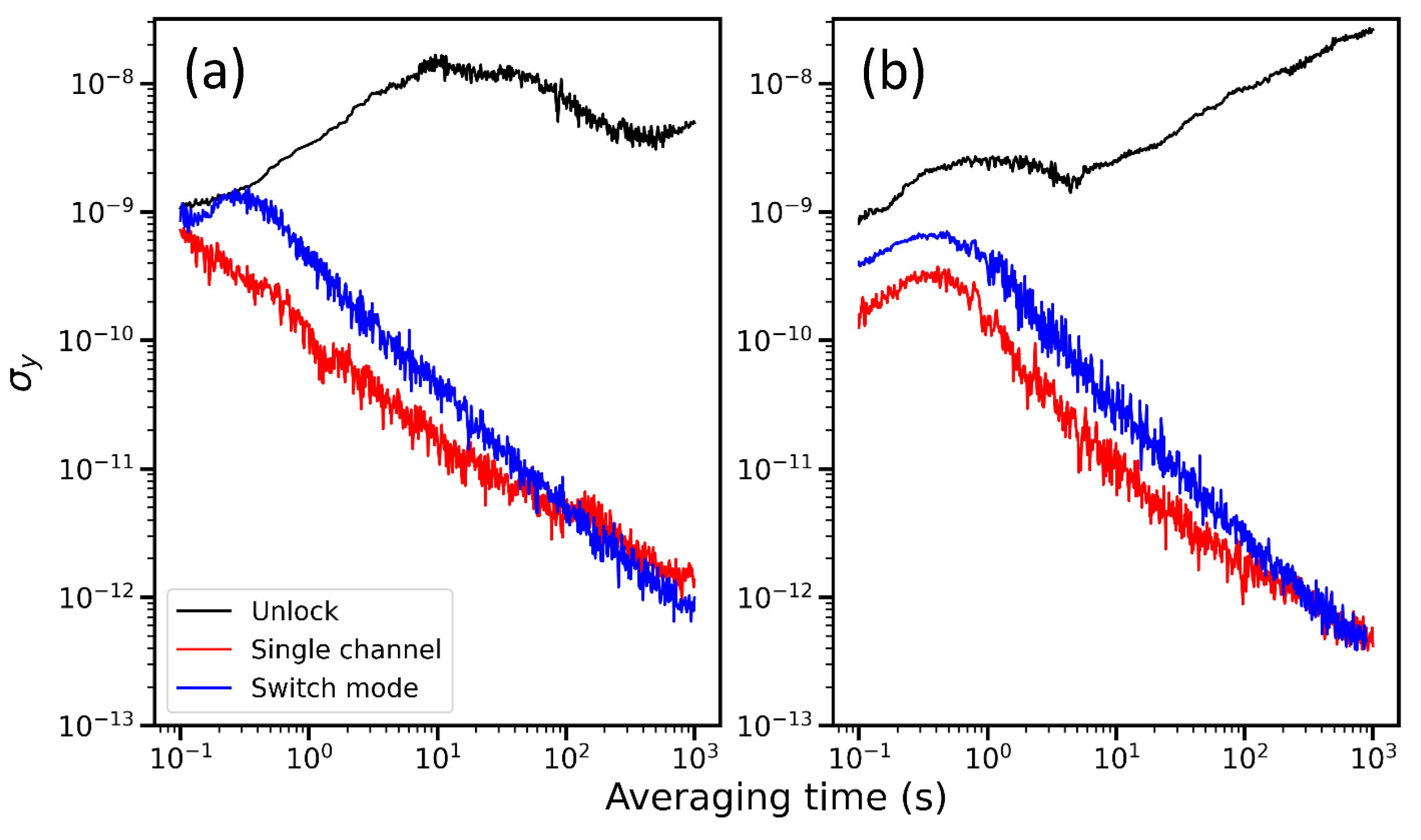
3.1. Allan Deviation Measurement
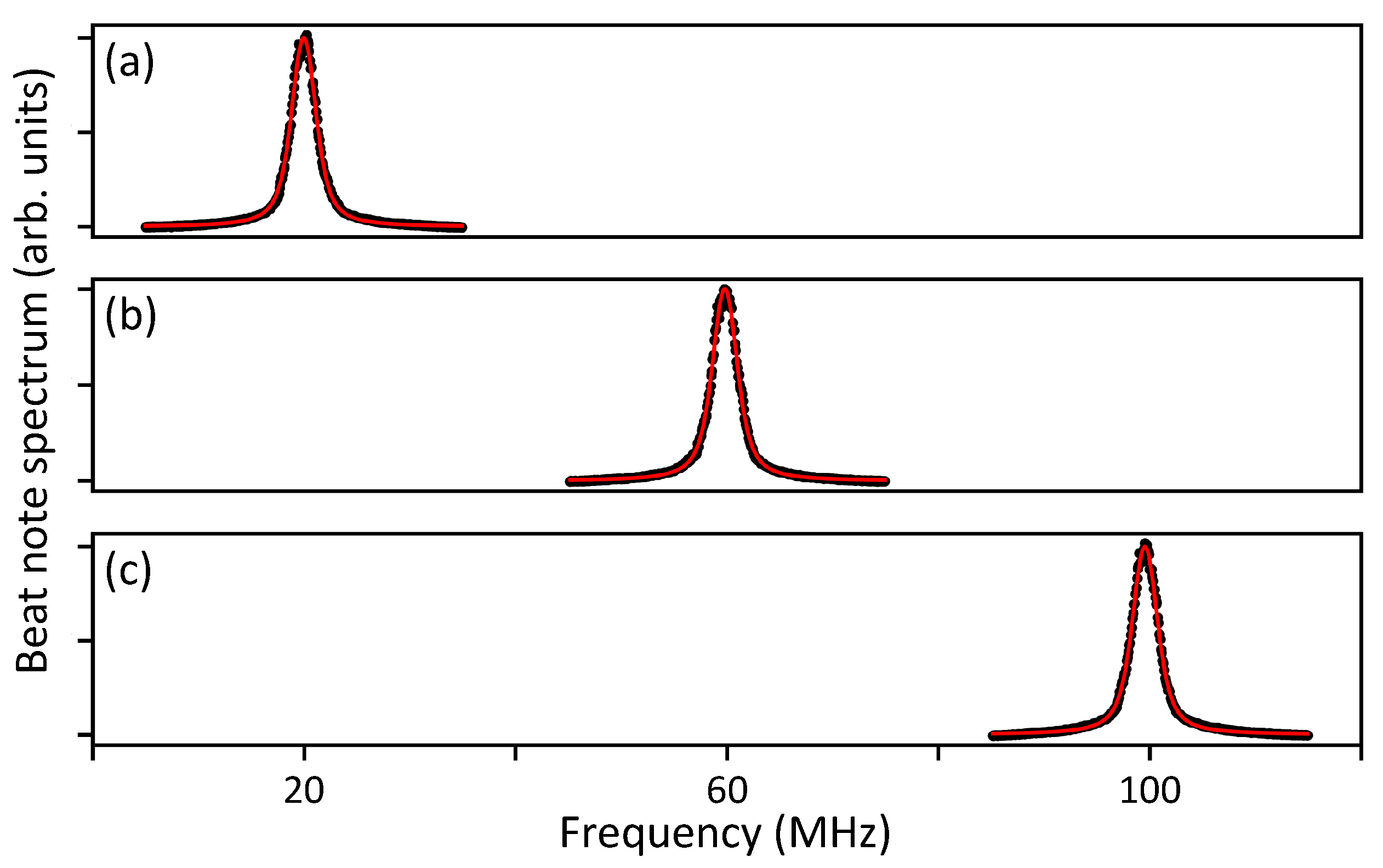
3.2. Heterodyne Measurement
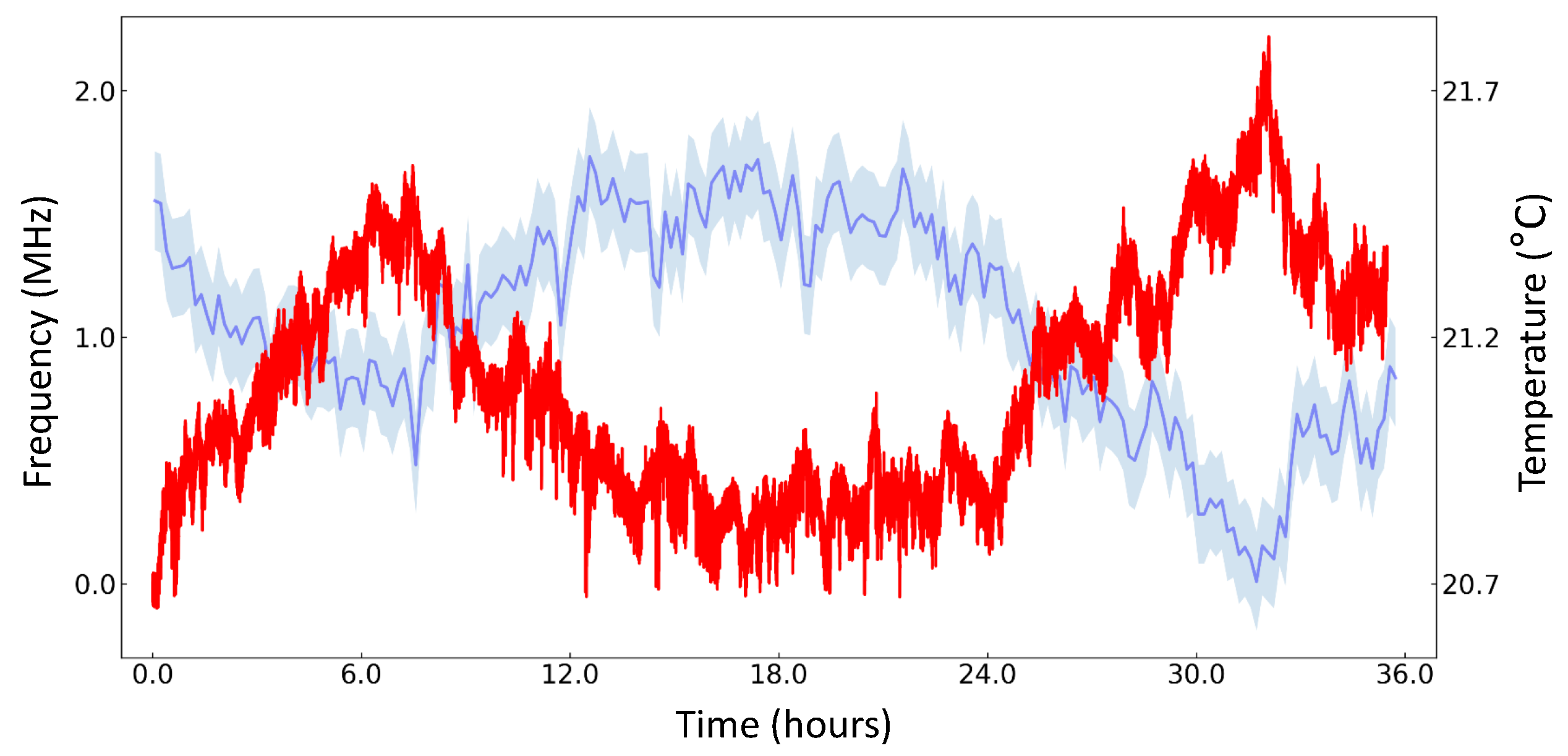
3.3. WLM Drift Measurement
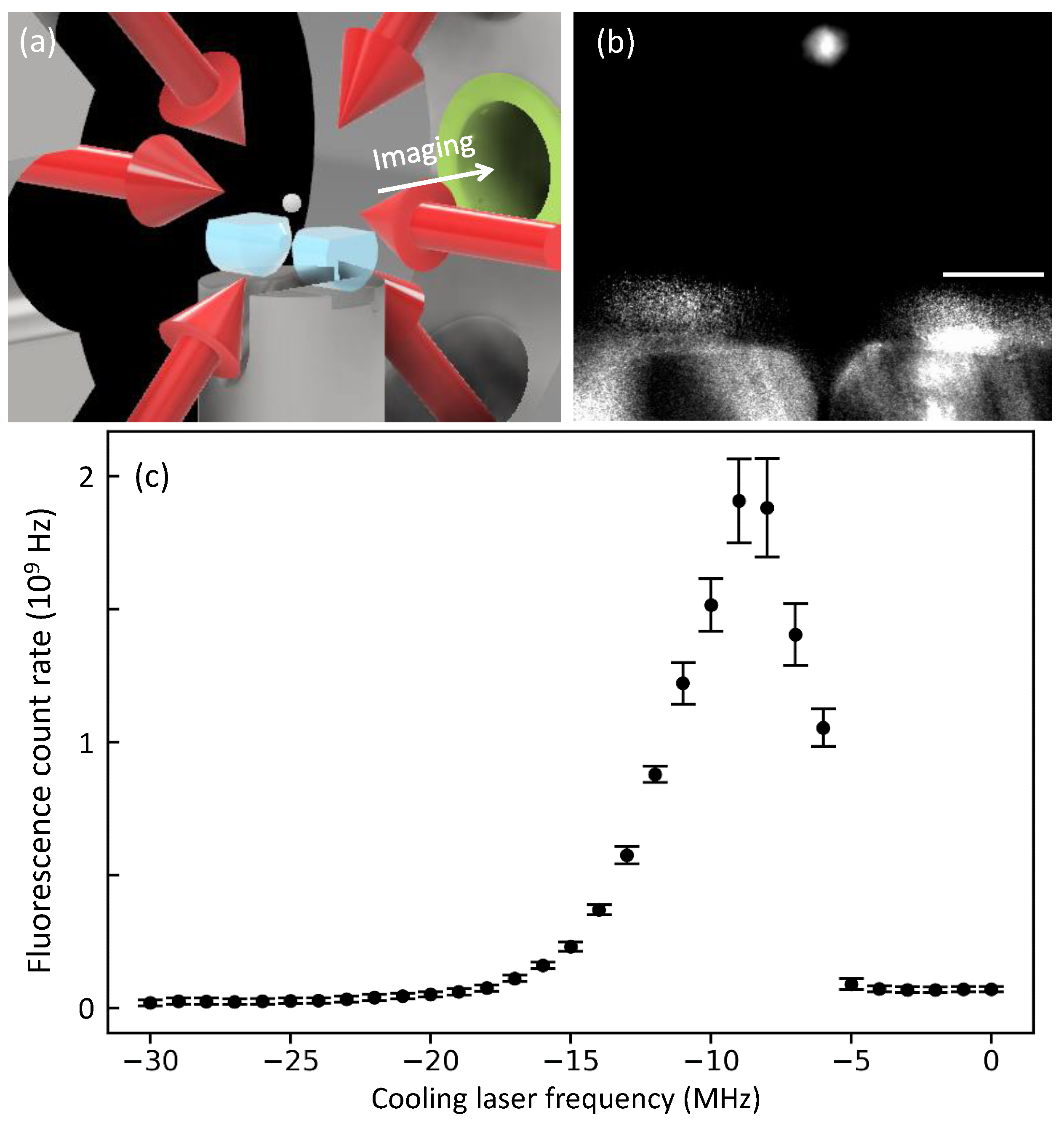
3.4. Application to Cold Atom Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hall, J.L. Nobel Lecture: Defining and measuring optical frequencies. Rev. Mod. Phys. 2006, 78, 1279–1295. [Google Scholar] [CrossRef] [Green Version]
- Hänsch, T.W. Nobel Lecture: Passion for precision. Rev. Mod. Phys. 2006, 78, 1297–1309. [Google Scholar] [CrossRef] [Green Version]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical atomic clocks. Rev. Mod. Phys. 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Kim, W.; Park, C.; Kim, J.R.; Choi, Y.; Kang, S.; Lim, S.; Lee, Y.L.; Ihm, J.; An, K. Tunneling-Induced Spectral Broadening of a Single Atom in a Three-Dimensional Optical Lattice. Nano Lett. 2011, 11, 729–733. [Google Scholar] [CrossRef]
- Léonard, J.; Lee, M.; Morales, A.; Karg, T.M.; Esslinger, T.; Donner, T. Optical transport and manipulation of an ultracold atomic cloud using focus-tunable lenses. New J. Phys. 2014, 16, 093028. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.R.; Chong, K.O.; Kim, J.; An, K. Observation of efficient sub-Doppler cooling under a nonzero magnetic field in a moving optical lattice. Phys. Rev. A 2018, 97, 063420. [Google Scholar] [CrossRef]
- Leibfried, D.; Blatt, R.; Monroe, C.; Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 2003, 75, 281–324. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.; Friebe, K.; Fioretto, D.A.; Schüppert, K.; Ong, F.R.; Plankensteiner, D.; Torggler, V.; Ritsch, H.; Blatt, R.; Northup, T.E. Ion-Based Quantum Sensor for Optical Cavity Photon Numbers. Phys. Rev. Lett. 2019, 122, 153603. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Oh, S.H.; Han, J.; Son, G.; Kim, J.; Kim, J.; Lee, M.; An, K. Realization of superabsorption by time reversal of superradiance. Nat. Photonics 2021, 15, 272–276. [Google Scholar] [CrossRef]
- Drever, R.W.P.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Demtröder, W. Laser Spectroscopy: Basic Concepts and Instrumentation; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Black, E.D. An introduction to Pound-Drever-Hall laser frequency stabilization. Am. J. Phys. 2000, 69, 79–87. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Martin, M.J.; Benko, C.; Hall, J.L.; Ye, J.; Hagemann, C.; Legero, T.; Sterr, U.; Riehle, F.; Cole, G.D.; et al. Reduction of residual amplitude modulation to 1 × 10−6 for frequency modulation and laser stabilization. Opt. Lett. 2014, 39, 1980–1983. [Google Scholar] [CrossRef]
- Kobtsev, S.; Kandrushin, S.; Potekhin, A. Long-term frequency stabilization of a continuous-wave tunable laser with the help of a precision wavelengthmeter. Appl. Opt. 2007, 46, 5840–5843. [Google Scholar] [CrossRef]
- Barwood, G.P.; Gill, P.; Huang, G.; Klein, H.A. Automatic laser control for a 88Sr+ optical frequency standard. Meas. Sci. Technol. 2012, 23, 055201. [Google Scholar] [CrossRef]
- Couturier, L.; Nosske, I.; Hu, F.; Tan, C.; Qiao, C.; Jiang, Y.H.; Chen, P.; Weidemüller, M. Laser frequency stabilization using a commercial wavelength meter. Rev. Sci. Instrum. 2018, 89, 043103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qian, Y.; Liang, S.; Huang, Y.; Hua, Y.; Kelin, G.; Gao, K. Long-Term Frequency Stabilization of Multi-Lasers Based on Wavemeter. Chin. J. Lasers 2019, 46, 0211004. [Google Scholar] [CrossRef]
- Hannig, S.; Pelzer, L.; Scharnhorst, N.; Kramer, J.; Stepanova, M.; Xu, Z.T.; Spethmann, N.; Leroux, I.D.; Mehlstäubler, T.E.; Schmidt, P.O. Towards a transportable aluminium ion quantum logic optical clock. Rev. Sci. Instrum. 2019, 90, 053204. [Google Scholar] [CrossRef]
- Ghadimi, M.; Bridge, E.M.; Scarabel, J.; Connell, S.; Shimizu, K.; Streed, E.; Lobino, M. Multichannel optomechanical switch and locking system for wavemeters. Appl. Opt. 2020, 59, 5136–5141. [Google Scholar] [CrossRef]
- Bause, R.; Li, M.; Schindewolf, A.; Chen, X.Y.; Duda, M.; Kotochigova, S.; Bloch, I.; Luo, X.Y. Tune-Out and Magic Wavelengths for Ground-State 23Na40K Molecules. Phys. Rev. Lett. 2020, 125, 023201. [Google Scholar] [CrossRef] [PubMed]
- McNally, R.L.; Kozyryev, I.; Vazquez-Carson, S.; Wenz, K.; Wang, T.; Zelevinsky, T. Optical cycling, radiative deflection and laser cooling of barium monohydride (138Ba1H). New J. Phys. 2020, 22, 083047. [Google Scholar] [CrossRef]
- Kajava, T.T.; Lauranto, H.M.; Salomaa, R.R.E. Fizeau interferometer in spectral measurements. J. Opt. Soc. Am. B 1993, 10, 1980–1989. [Google Scholar] [CrossRef]
- Lawson, P. Principles of Long Baseline Stellar Interferometry; JPL Publication: Pasadena, CA, USA, 2000. [Google Scholar]
- Stoykova, E.; Nenchev, M. Gaussian beam interaction with an air-gap Fizeau interferential wedge. J. Opt. Soc. Am. A 2010, 27, 58–68. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.highfinesse.com/en/technology/fizeau-principle.html (accessed on 17 September 2021).
- Allan, D. Statistics of atomic frequency standards. Proc. IEEE 1966, 54, 221–230. [Google Scholar] [CrossRef] [Green Version]
- Riley, W.; Howe, D. Handbook of Frequency Stability Analysis; Special Publication (NIST SP); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2008. [Google Scholar]
- Osinski, M.; Buus, J. Linewidth broadening factor in semiconductor lasers—An overview. IEEE J. Quantum Electron. 1987, 23, 9–29. [Google Scholar] [CrossRef]
- Stéphan, G.M.; Tam, T.T.; Blin, S.; Besnard, P.; Têtu, M. Laser line shape and spectral density of frequency noise. Phys. Rev. A 2005, 71, 043809. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Meng, Z.; Wang, J.; Chen, W. Ultra-narrow linewidth measurement based on Voigt profile fitting. Opt. Express 2015, 23, 6803–6808. [Google Scholar] [CrossRef] [PubMed]
- Saleh, K.; Millo, J.; Didier, A.; Kersalé, Y.; Lacroûte, C. Frequency stability of a wavelength meter and applications to laser frequency stabilization. Appl. Opt. 2015, 54, 9446–9449. [Google Scholar] [CrossRef] [Green Version]
- Saakyan, S.A.; Sautenkov, V.A.; Vilshanskaya, E.V.; Vasiliev, V.V.; Zelener, B.B.; Zelener, B.V. Frequency control of tunable lasers using a frequency-calibrated λ-meter in an experiment on preparation of Rydberg atoms in a magneto-optical trap. Quantum Electron. 2015, 45, 828–832. [Google Scholar] [CrossRef]
- Lee, W.K.; Park, C.Y.; Heo, M.S.; Yu, D.H.; Kim, H. Robust frequency stabilization and linewidth narrowing of a laser with large intermittent frequency jumps using an optical cavity and an atomic beam. Appl. Opt. 2020, 59, 8918–8924. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Huang, X.; Notcutt, M.; Zanon-Willette, T.; Foreman, S.M.; Boyd, M.M.; Blatt, S.; Ye, J. Compact, thermal-noise-limited optical cavity for diode laser stabilization at 1 × 10−15. Opt. Lett. 2007, 32, 641–643. [Google Scholar] [CrossRef] [Green Version]
- Choi, Y.; Kang, S.; Lim, S.; Kim, W.; Kim, J.R.; Lee, J.H.; An, K. Quasieigenstate Coalescence in an Atom-Cavity Quantum Composite. Phys. Rev. Lett. 2010, 104, 153601. [Google Scholar] [CrossRef]
- Kang, S.; Lim, S.; Hwang, M.; Kim, W.; Kim, J.R.; An, K. Controlled generation of single photons in a coupled atom-cavity system at a fast repetition-rate. Opt. Express 2011, 19, 2440–2447. [Google Scholar] [CrossRef]
- Lee, D.; Kim, M.; Hong, J.; Kim, J.; Kang, S.; Choi, Y.; An, K.; Lee, M. Novel characterization of an optical cavity with small mode volume. arXiv 2021, arXiv:2102.05853. [Google Scholar]
- Sagna, N.; Dudle, G.; Thomann, P. The capture process in spherical magneto-optical traps: Experiment and 1D magnetic field models. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 3213–3224. [Google Scholar] [CrossRef] [Green Version]
- Yoon, S.; Choi, Y.; Park, S.; Ji, W.; Lee, J.H.; An, K. Characteristics of single-atom trapping in a magneto-optical trap with a high magnetic-field gradient. J. Phys. Conf. Ser. 2007, 80, 012046. [Google Scholar] [CrossRef]
- Zhang, P.; Guo, Y.; Li, Z.; Chi Zhang, Y.; Zhang, Y.; Du, J.; Li, G.; Wang, J.; Zhang, T. Temperature determination of cold atoms based on single-atom countings. J. Opt. Soc. Am. B 2011, 28, 667–670. [Google Scholar] [CrossRef] [Green Version]
- Hood, C.J.; Chapman, M.S.; Lynn, T.W.; Kimble, H.J. Real-Time Cavity QED with Single Atoms. Phys. Rev. Lett. 1998, 80, 4157–4160. [Google Scholar] [CrossRef]
- Kuhn, A.; Hennrich, M.; Rempe, G. Deterministic Single-Photon Source for Distributed Quantum Networking. Phys. Rev. Lett. 2002, 89, 067901. [Google Scholar] [CrossRef] [Green Version]
- Du, J.J.; Li, W.F.; Wen, R.J.; Li, G.; Zhang, T.C. Experimental investigation of the statistical distribution of single atoms in cavity quantum electrodynamics. Laser Phys. Lett. 2015, 12, 065501. [Google Scholar] [CrossRef] [Green Version]
- Domokos, P.; Ritsch, H. Mechanical effects of light in optical resonators. J. Opt. Soc. Am. B 2003, 20, 1098–1130. [Google Scholar] [CrossRef]
- Chough, Y.T.; An, K. Quantum-trajectory analysis of an optical Stern-Gerlach experiment. Phys. Rev. A 2004, 69, 063817. [Google Scholar] [CrossRef]
- Graham, R.; Schlautmann, M.; Zoller, P. Dynamical localization of atomic-beam deflection by a modulated standing light wave. Phys. Rev. A 1992, 45, R19–R22. [Google Scholar] [CrossRef]
- Gangloff, D.; Shi, M.; Wu, T.; Bylinskii, A.; Braverman, B.; Gutierrez, M.; Nichols, R.; Li, J.; Aichholz, K.; Cetina, M.; et al. Preventing and reversing vacuum-induced optical losses in high-finesse tantalum (V) oxide mirror coatings. Opt. Express 2015, 23, 18014–18028. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Kuo, G.S. Optical switching technology comparison: Optical MEMS vs. other technologies. IEEE Commun. Mag. 2003, 41, S16–S23. [Google Scholar] [CrossRef]
- Cao, T.; Hu, T.; Zhao, Y. Research Status and Development Trend of MEMS Switches: A Review. Micromachines 2020, 11, 694. [Google Scholar] [CrossRef]
- Song, Y.; Panas, R.M.; Hopkins, J.B. A review of micromirror arrays. Precis. Eng. 2018, 51, 729–761. [Google Scholar] [CrossRef]
- Mahameed, R.; Sinha, N.; Pisani, M.B.; Piazza, G. Dual-beam actuation of piezoelectric AlN RF MEMS switches monolithically integrated with AlN contour-mode resonators. J. Micromech. Microeng. 2008, 18, 105011. [Google Scholar] [CrossRef] [Green Version]
- Knoernschild, C.; Kim, C.; Lu, F.P.; Kim, J. Multiplexed broadband beam steering system utilizing high speed MEMS mirrors. Opt. Express 2009, 17, 7233–7244. [Google Scholar] [CrossRef] [Green Version]
- Seok, T.J.; Kwon, K.; Henriksson, J.; Luo, J.; Wu, M.C. Wafer-scale silicon photonic switches beyond die size limit. Optica 2019, 6, 490–494. [Google Scholar] [CrossRef]
- Khalid, M.; Omatu, S. A neural network controller for a temperature control system. IEEE Contr. Syst. Mag. 1992, 12, 58–64. [Google Scholar] [CrossRef]
- Zhang, K.; Guliani, A.; Ogrenci-Memik, S.; Memik, G.; Yoshii, K.; Sankaran, R.; Beckman, P. Machine Learning-Based Temperature Prediction for Runtime Thermal Management Across System Components. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 405–419. [Google Scholar] [CrossRef]
- Brandi, S.; Piscitelli, M.S.; Martellacci, M.; Capozzoli, A. Deep reinforcement learning to optimise indoor temperature control and heating energy consumption in buildings. Energy Build. 2020, 224, 110225. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Kim, K.; Lee, D.; Shin, Y.; Kang, S.; Kim, J.-R.; Choi, Y.; An, K.; Lee, M. Locking Multi-Laser Frequencies to a Precision Wavelength Meter: Application to Cold Atoms. Sensors 2021, 21, 6255. https://doi.org/10.3390/s21186255
Kim J, Kim K, Lee D, Shin Y, Kang S, Kim J-R, Choi Y, An K, Lee M. Locking Multi-Laser Frequencies to a Precision Wavelength Meter: Application to Cold Atoms. Sensors. 2021; 21(18):6255. https://doi.org/10.3390/s21186255
Chicago/Turabian StyleKim, Junwoo, Keumhyun Kim, Dowon Lee, Yongha Shin, Sungsam Kang, Jung-Ryul Kim, Youngwoon Choi, Kyungwon An, and Moonjoo Lee. 2021. "Locking Multi-Laser Frequencies to a Precision Wavelength Meter: Application to Cold Atoms" Sensors 21, no. 18: 6255. https://doi.org/10.3390/s21186255
APA StyleKim, J., Kim, K., Lee, D., Shin, Y., Kang, S., Kim, J.-R., Choi, Y., An, K., & Lee, M. (2021). Locking Multi-Laser Frequencies to a Precision Wavelength Meter: Application to Cold Atoms. Sensors, 21(18), 6255. https://doi.org/10.3390/s21186255





