Optimal Localization of Smart Aggregate Sensor for Concrete Damage Monitoring in PSC Anchorage Zone
Abstract
:1. Introduction
2. Concrete Anchorage Zone under Prestress Force
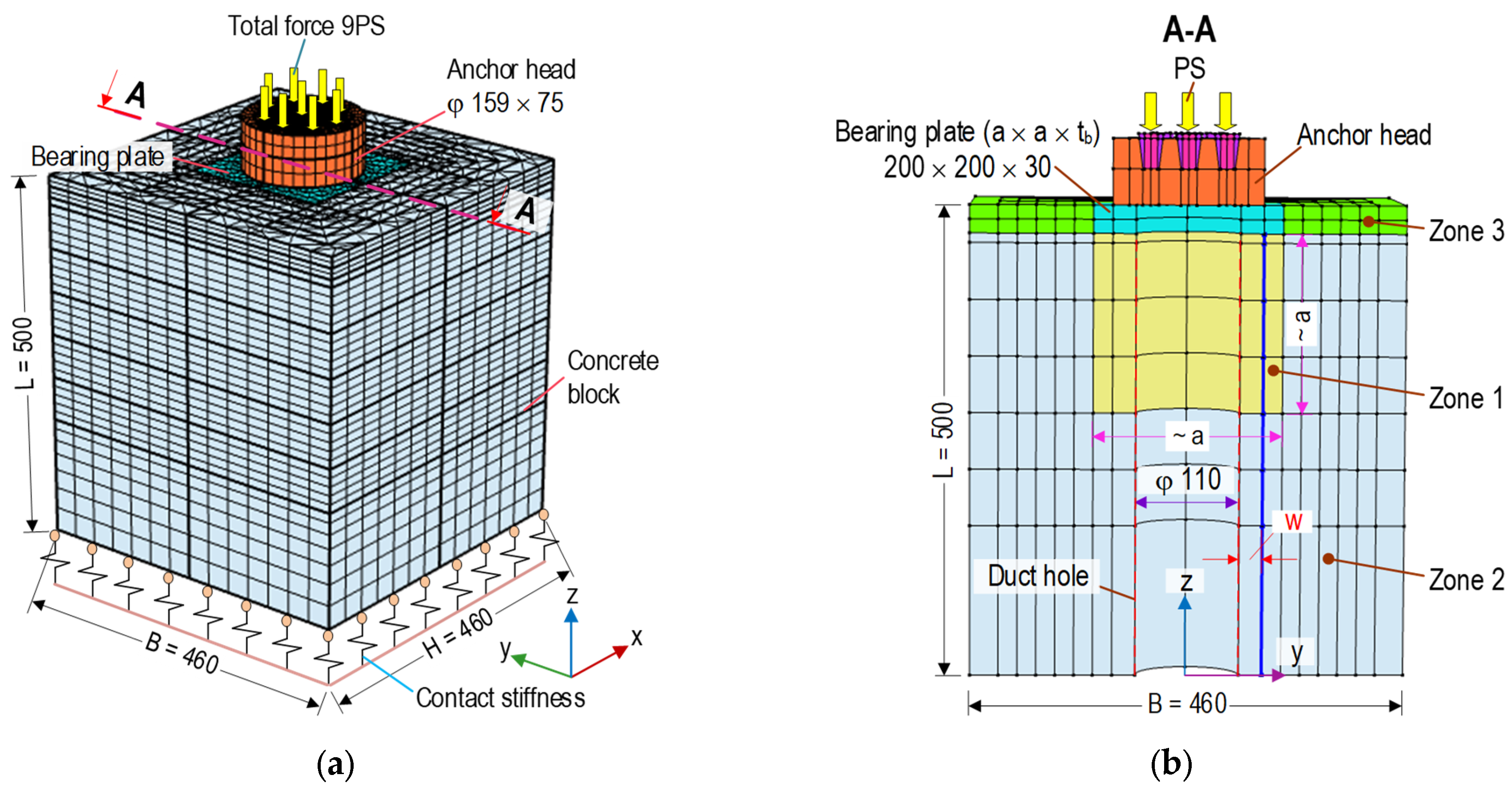
2.1. FE Model of Concrete Anchorage Zone
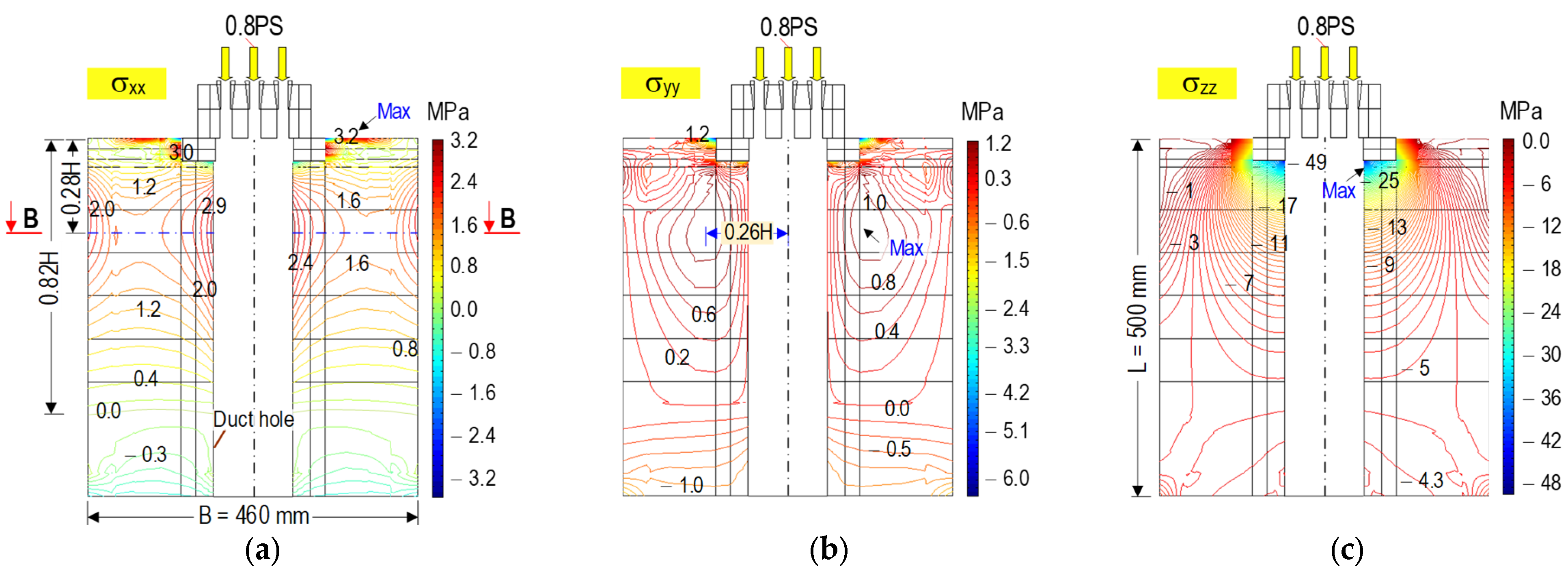
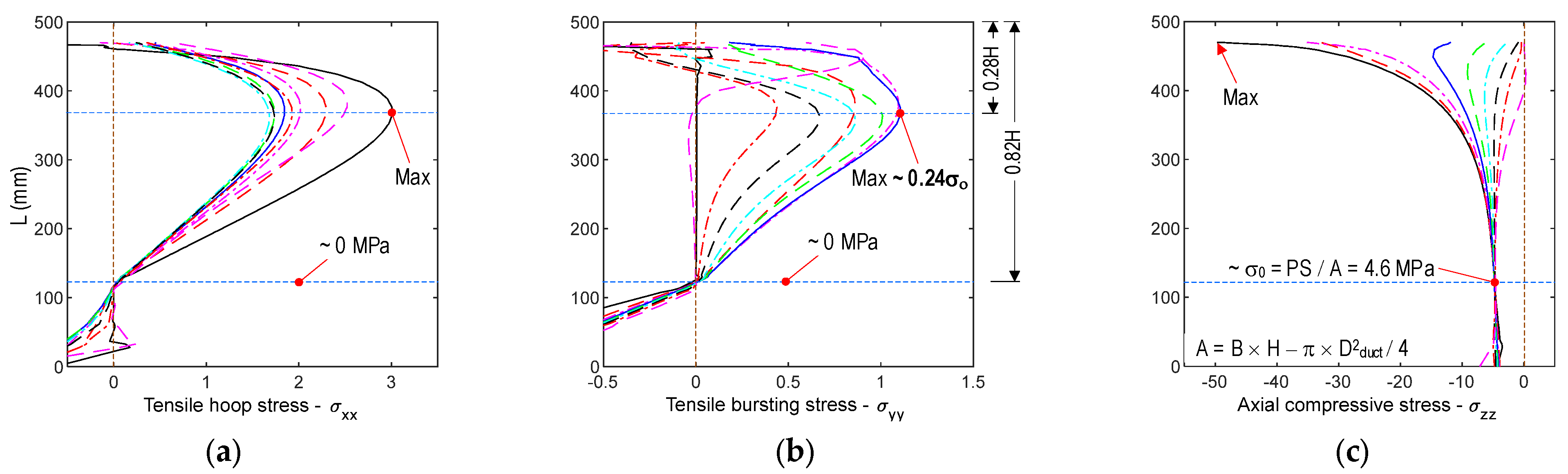
2.2. Stress Distribution Induced by Prestress Force
3. Smart Aggregate for Impedance Monitoring in Anchorage Zone
3.1. Impedance Model for PZT-Embedded SA Sensor
3.2. FE Model of SA-Embedded Concrete Anchorage Zone
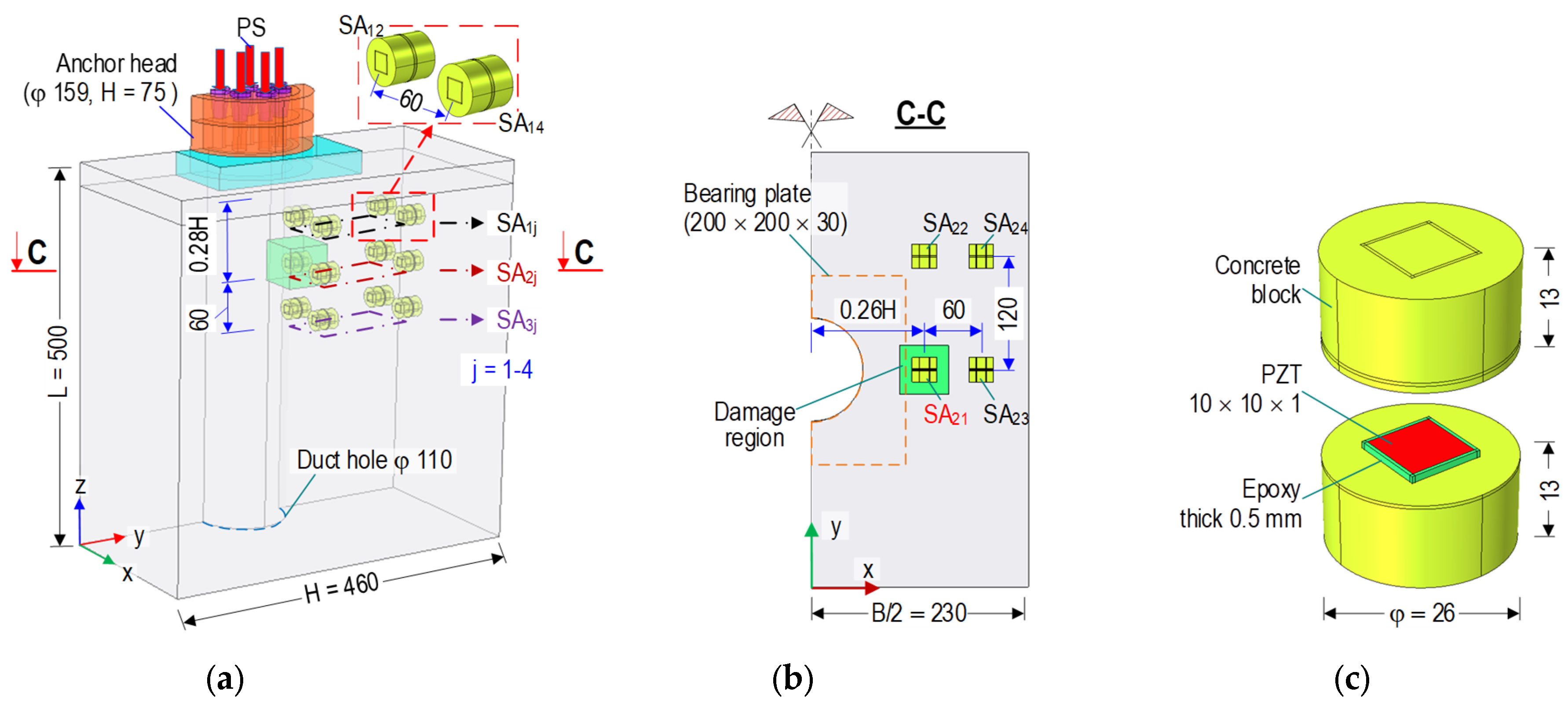
3.2.1. Anchorage Zone with SA Sensor
3.2.2. Simulation Scenarios for SA Sensor Localization
3.3. Optimal Location of SA Sensors for Damage Monitoring
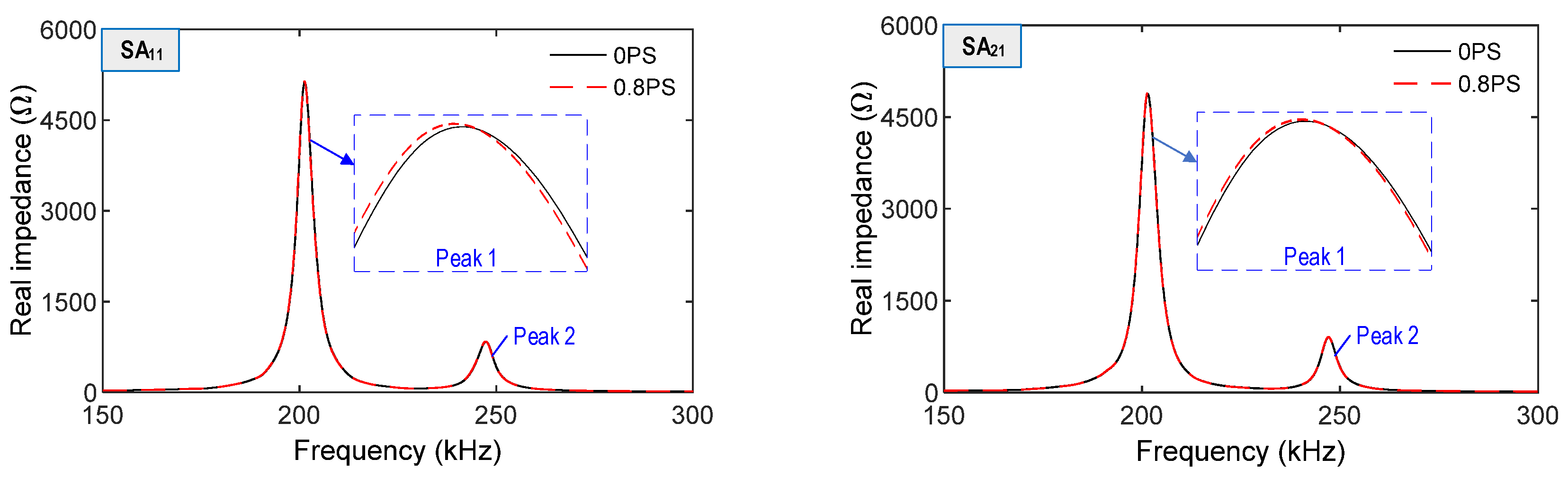
3.3.1. Impedance Responses of SA Sensors under Prestress Forces
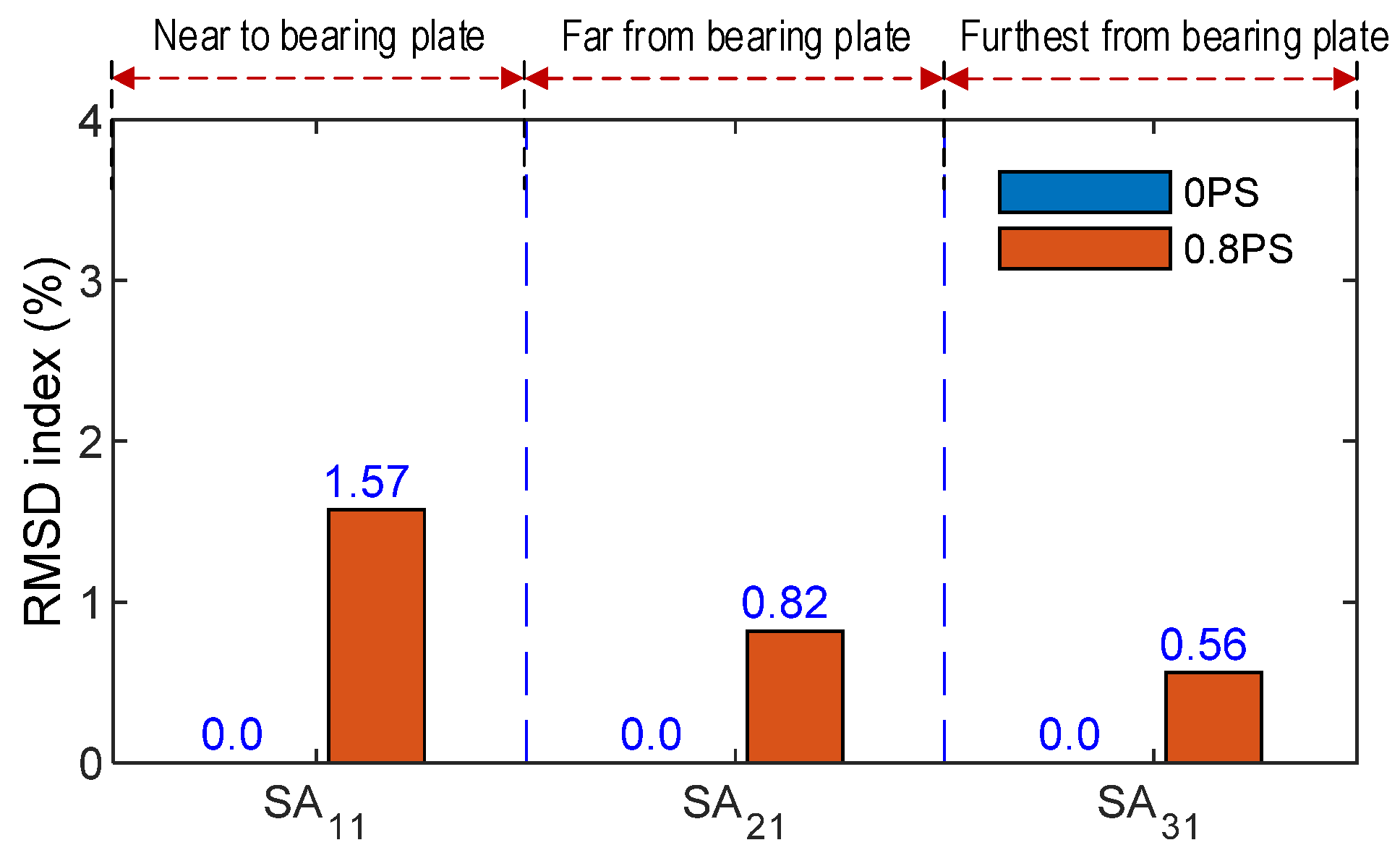
3.3.2. Optimal Location of SA Sensors in Anchorage Zone
4. Experimental Evaluation of SA Sensor for Damage Monitoring in PSC Anchorage Zone
4.1. Prototype Design of SA Sensor
4.2. Analysis of Optimal SA Sensor Location in PSC Anchorage Zone
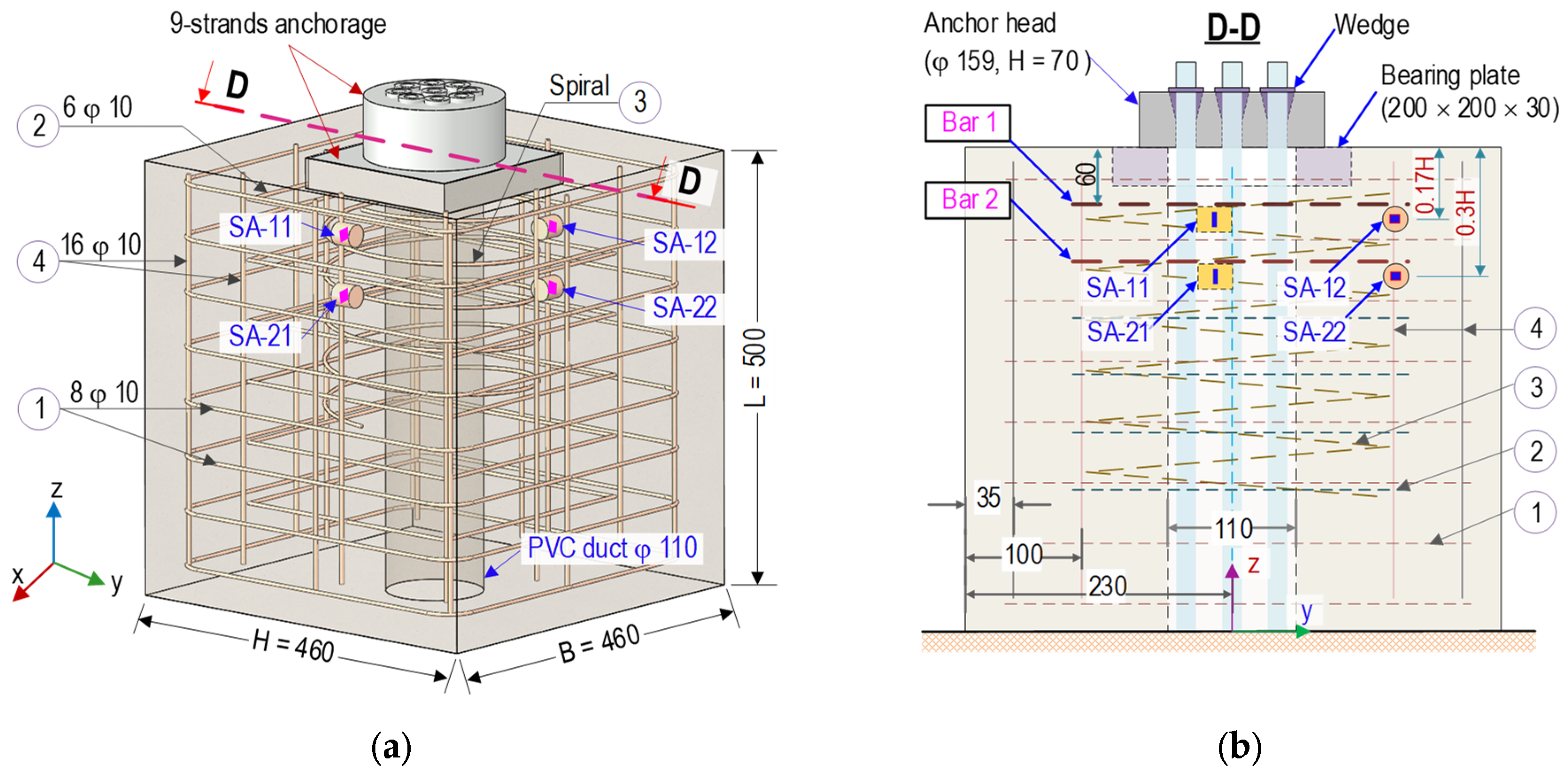
4.2.1. Design of SA-Embedded PSC Anchorage Zone
4.2.2. Deployment of SA Sensors
4.2.3. Test Scenarios for Impedance Monitoring
4.3. Impedance Signatures of SA Sensors under Prestress-Force Variation
4.3.1. Impedance Responses of SA Sensors in Intact Case
4.3.2. Impedance Responses of SA Sensors under Loading Cases
4.4. Damage Monitoring Using Impedance Features of SA Sensors
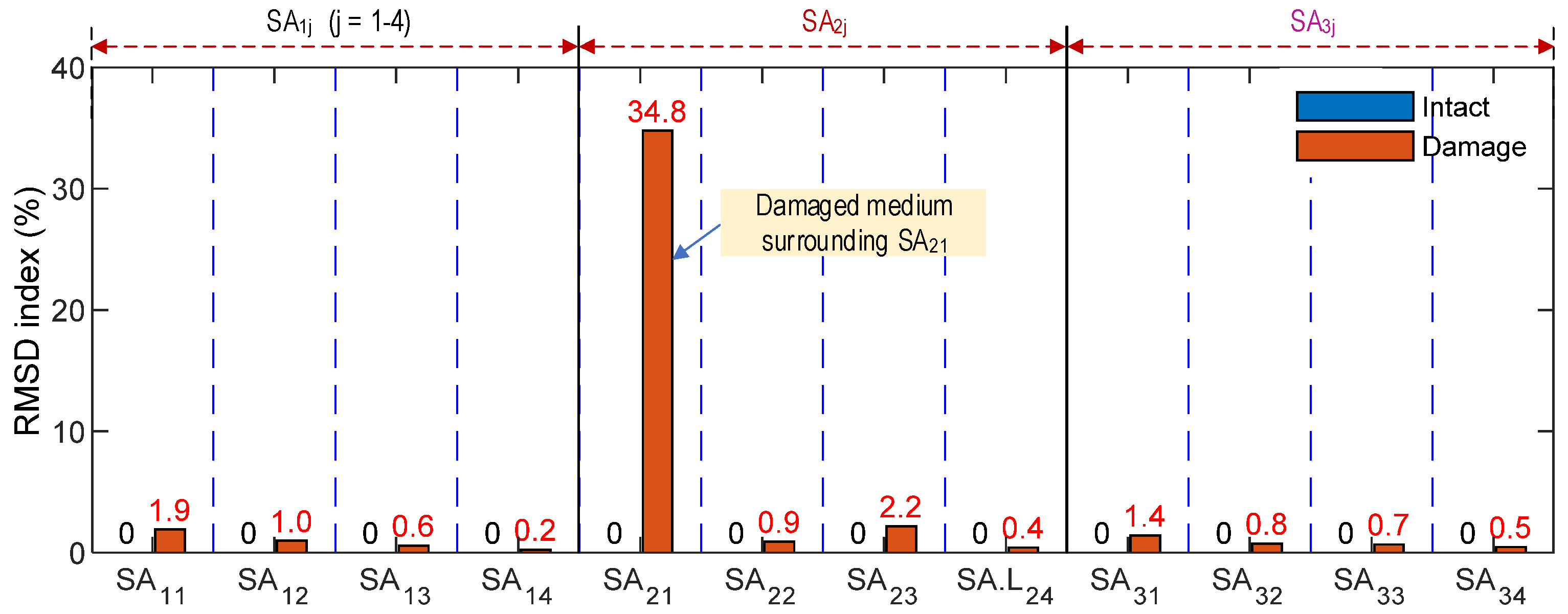
4.4.1. Sensitivity of SA Sensors under Prestress-Force Variation
4.4.2. Discussion on SA Sensor’s Performance in PSC Anchorage Zone
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nawy, E.G. Prestressed Concrete: A Fundamental Approach, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Breen, J.E.; Burdet, O.; Roberts, C.; Sanders, D.; Wollmann, G. Anchorage zone reinforcement for post-tensioned concrete girders. In NCHRP Report 356; Transportation Research Board: Washington, DC, USA, 1994. [Google Scholar]
- Burdet, O.L. Analysis and Design of Anchorage Zones in Post-Tensioned Concrete Bridges. Ph.D. Thesis, The University of Texas, Austin, TX, USA, 1990. [Google Scholar]
- Li, Z.N.; Tang, J.; Li, Q.S. Optimal sensor locations for structural vibration measurements. Appl. Acoust. 2004, 65, 807–818. [Google Scholar] [CrossRef]
- Meo, M.; Zumpano, G. On the optimal sensor placement techniques for a bridge structure. Eng. Struct. 2005, 27, 1488–1497. [Google Scholar] [CrossRef]
- Chang, M.; Pakzad, S.N. Optimal sensor placement for modal identification of bridge systems considering number of sensing nodes. J. Bridge. Eng. 2014, 19, 04014019. [Google Scholar] [CrossRef] [Green Version]
- Hiba, A.J.; Glisic, B. Monitoring of prestressing forces in prestressed concrete structures—An overview. Struct. Control. Health Monit. 2019, 26, e2374. [Google Scholar]
- Meng, Q.; Zhu, J.; Wang, T. Numerical prediction of long-term deformation for prestressed concrete bridges under random heavy traffic loads. J. Bridge. Eng. 2019, 24, 04019107. [Google Scholar] [CrossRef]
- Worley, R.; Dewoolkar, M.M.; Xia, T.; Farrell, R.; Orfeo, D.; Burns, D. Acoustic emission sensing for crack monitoring in prefabricated and prestressed reinforced concrete bridge girders. J. Bridge. Eng. 2019, 24, 04019018. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, A.B.M.; Rice, J.A.; Hamilton, H.R. Wire breakage detection using relative strain variation in unbonded posttensioning anchors. J. Bridge. Eng. 2015, 20, 04014056. [Google Scholar] [CrossRef]
- Chen, S.Z.; Wu, G.; Xing, T.; Feng, D.C. Prestressing force monitoring method for a box girder through distributed long-gauge FBG sensors. Smart Mater. Struct. 2017, 27, 015015. [Google Scholar] [CrossRef]
- Kim, T.M.; Kim, D.H.; Kim, M.K.; Lim, Y.M. Fiber Bragg grating-based long-gauge fiber optic sensor for monitoring of a 60m full-scale prestressed concrete girder during lifting and loading. Sens. Actuator A Phys. 2016, 252, 134–145. [Google Scholar] [CrossRef]
- Na, W.S.; Baek, J. A review of the piezoelectric electromechanical impedance-based structural health monitoring technique for engineering structures. Sensors 2018, 18, 1307. [Google Scholar] [CrossRef] [Green Version]
- Jiao, P.; Egbe, K.I.; Xie, Y.; Matin Nazar, A.; Alavi, A.H. Piezoelectric sensing techniques in structural health monitoring: A state-of-the-art review. Sensors 2020, 20, 3730. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, Y.; Lu, Y. Sensitivity of PZT impedance sensors for damage detection of concrete structures. Sensors 2008, 8, 327. [Google Scholar] [CrossRef] [Green Version]
- Ai, D.; Luo, H.; Zhu, H. Numerical and experimental investigation of flexural performance on prestressed concrete structures using electromechanical admittance. Mech. Syst. Signal. Process. 2019, 128, 244–265. [Google Scholar] [CrossRef]
- Nguyen, K.D.; Kim, J.T. Smart PZT-interface for wireless impedance-based prestress-loss monitoring in tendon-anchorage connection. Smart Struct. Syst. 2012, 9, 489–504. [Google Scholar] [CrossRef]
- Huynh, T.C.; Lee, K.S.; Kim, J.T. Local dynamic characteristics of PZT impedance interface on tendon anchorage under prestress force variation. Smart Struct. Syst. 2015, 15, 375–393. [Google Scholar] [CrossRef]
- Talakokula, V.; Bhalla, S.; Gupta, A. Corrosion assessment of reinforced concrete structures based on equivalent structural parameters using electro-mechanical impedance technique. J. Intell. Mater. Syst. Struct. 2013, 25, 484–500. [Google Scholar] [CrossRef]
- Shin, S.W.; Qureshi, A.R.; Lee, J.Y.; Yun, C.B. Piezoelectric sensor-based nondestructive active monitoring of strength gain in concrete. Smart Mater. Struct. 2008, 17, 055002. [Google Scholar] [CrossRef]
- Kocherla, A.; Subramaniam, K.V.L. Embedded electrical impedance-based PZT sensor for monitoring hydrating concrete: Development and evaluation. Smart Mater. Struct. 2020, 29, 055038. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled electro-mechanical analysis of adaptive material systems-determination of the actuator power consumption and system energy transfer. J. Intell. Mater. Syst. Struct. 1994, 5, 335–343. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.; Rogers, C.A. Electro-mechanical impedance modeling of active material systems. Smart Mater. Struct. 1996, 5, 171–186. [Google Scholar] [CrossRef]
- Soh, C.K.; Tseng, K.K.H.; Bhalla, S.; Gupta, A. Performance of smart piezoceramic patches in health monitoring of a RC bridge. Smart Mater. Struct. 2000, 9, 533–542. [Google Scholar] [CrossRef]
- Narayanan, A.; Subramaniam, K.V.L. Sensing of damage and substrate stress in concrete using electro-mechanical impedance measurements of bonded PZT patches. Smart Mater. Struct. 2016, 25, 095011. [Google Scholar] [CrossRef]
- Huynh, T.C.; Kim, J.T. Quantitative damage identification in tendon anchorage via PZT interface-based impedance monitoring technique. Smart Struct. Syst. 2017, 20, 181–195. [Google Scholar]
- Dang, N.L.; Huynh, T.C.; Pham, Q.Q.; Lee, S.Y.; Kim, J.T. Damage-sensitive impedance sensor placement on multi-strand anchorage based on local stress variation analysis. Struct. Control. Health Monit. 2020, 27, e2547. [Google Scholar] [CrossRef]
- Ai, D.; Lin, C.; Luo, H.; Zhu, H. Temperature effect on electromechanical admittance–based concrete structural health monitoring. Struct. Health Monit. 2020, 19, 661–692. [Google Scholar] [CrossRef]
- Huynh, T.C.; Kim, J.T. RBFN-based temperature compensation method for impedance monitoring in prestressed tendon anchorage. Struct. Control Health Monit. 2018, 25, e2173. [Google Scholar] [CrossRef]
- Zhang, C.; Panda, G.P.; Yan, Q.; Zhang, W.; Vipulanandan, C.; Song, G. Monitoring early-age hydration and setting of portland cement paste by piezoelectric transducers via electromechanical impedance method. Constr. Build. Mater. 2020, 258, 120348. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Y.; Hu, X. Early-age strength monitoring of the recycled aggregate concrete using the EMI method. Smart Mater. Struct. 2021, 30, 055017. [Google Scholar] [CrossRef]
- Gu, H.; Song, G.; Dhonde, H.; Mo, Y.L.; Yan, S. Concrete early-age strength monitoring using embedded piezoelectric transducers. Smart Mater. Struct. 2006, 15, 1837–1845. [Google Scholar] [CrossRef]
- Du, G.; Zhang, J.; Zhang, J.; Song, G. Experimental Study on Stress Monitoring of Sand-Filled Steel Tube during Impact Using Piezoceramic Smart Aggregates. Sensors 2017, 17, 1930. [Google Scholar] [CrossRef] [Green Version]
- Dixit, A.; Bhalla, S. Prognosis of fatigue and impact induced damage in concrete using embedded piezo-transducers. Sens. Actuator A Phys. 2018, 274, 116–131. [Google Scholar] [CrossRef]
- Negi, P.; Chhabra, R.; Kaur, N.; Bhalla, S. Health monitoring of reinforced concrete structures under impact using multiple piezo-based configurations. Constr. Build. Mater. 2019, 222, 371–389. [Google Scholar] [CrossRef]
- Ai, D.; Luo, H.; Zhu, H. Diagnosis and validation of damaged piezoelectric sensor in electromechanical impedance technique. J. Intell. Mater. Syst. Struct. 2016, 28, 837–850. [Google Scholar] [CrossRef]
- Campeiro, L.M.; Da Silveira, R.Z.M.; Baptista, F.G. Impedance-based damage detection under noise and vibration effects. Struct. Health Monit. 2018, 17, 654–667. [Google Scholar] [CrossRef]
- Koo, K.Y.; Park, S.; Lee, J.J.; Yun, C.B. Automated impedance-based structural health monitoring incorporating effective frequency shift for compensating temperature effects. J. Intell. Mater. Syst. Struct. 2009, 20, 367–377. [Google Scholar] [CrossRef]
- Vsl 2018. VSL Strand Post-Tensioning Systems. Available online: https://vsl.com/home/technologies/post-tensioning-systems/ (accessed on 6 May 2019).
- Dang, N.L.; Huynh, T.C.; Kim, J.T. Local strand-breakage detection in multi-strand anchorage system using an impedance-based stress monitoring method-feasibility study. Sensors 2019, 19, 1054. [Google Scholar] [CrossRef] [Green Version]
- AASHTO LRFD Bridge. Design Specifications, SI Units; American Association of State Highway and Transportation: Washington, DC, USA, 2007. [Google Scholar]
- Song, G.; Gu, H.; Mo, Y.L. Smart aggregates: Multi-functional sensors for concrete structures—a tutorial and a review. Smart Mater. Struct. 2008, 17, 033001. [Google Scholar] [CrossRef]
- Pham, Q.Q.; Dang, N.L.; Kim, J.T. Piezoelectric sensor-embedded smart rock for damage monitoring in a prestressed anchorage zone. Sensors 2021, 21, 353. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Fan, S.; Yang, J.; Kitipornchai, S. Numerical and experimental investigation of electro-mechanical impedance based concrete quantitative damage assessment. Smart Mat. and Struct. 2020, 29, 055025. [Google Scholar] [CrossRef]
- Zhao, S.; Fan, S.; Chen, J. Quantitative assessment of the concrete gravity dam damage under earthquake excitation using electro-mechanical impedance measurements. Eng. Struct. 2019, 191, 162–178. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Rogers, C.A. Recent advancements in the electro-mechanical (e/m) impedance method for structural health monitoring and NDE, Smart Structures and Materials 1998: Smart Structures and Integrated Systems. Int. Soc. Opt. Photonics 1998, 3329, 536–547. [Google Scholar]
- Ai, D.; Luo, H.; Wang, C.; Zhu, H. Monitoring of the load-induced RC beam structural tension/compression stress and damage using piezoelectric transducers. Eng. Struct. 2018, 154, 38–51. [Google Scholar] [CrossRef]
- Feng, Q.; Liang, Y.; Song, G. Real-time monitoring of early-age concrete strength using piezoceramic-based smart aggregates. Int. J. Aerosp. Eng. 2019, 32, 04018115. [Google Scholar] [CrossRef]
- Kocherla, A.; Subramaniam, K.V.L. Embedded smart PZT-based sensor for internal damage detection in concrete under applied compression. Measurement 2020, 163, 108018. [Google Scholar] [CrossRef]





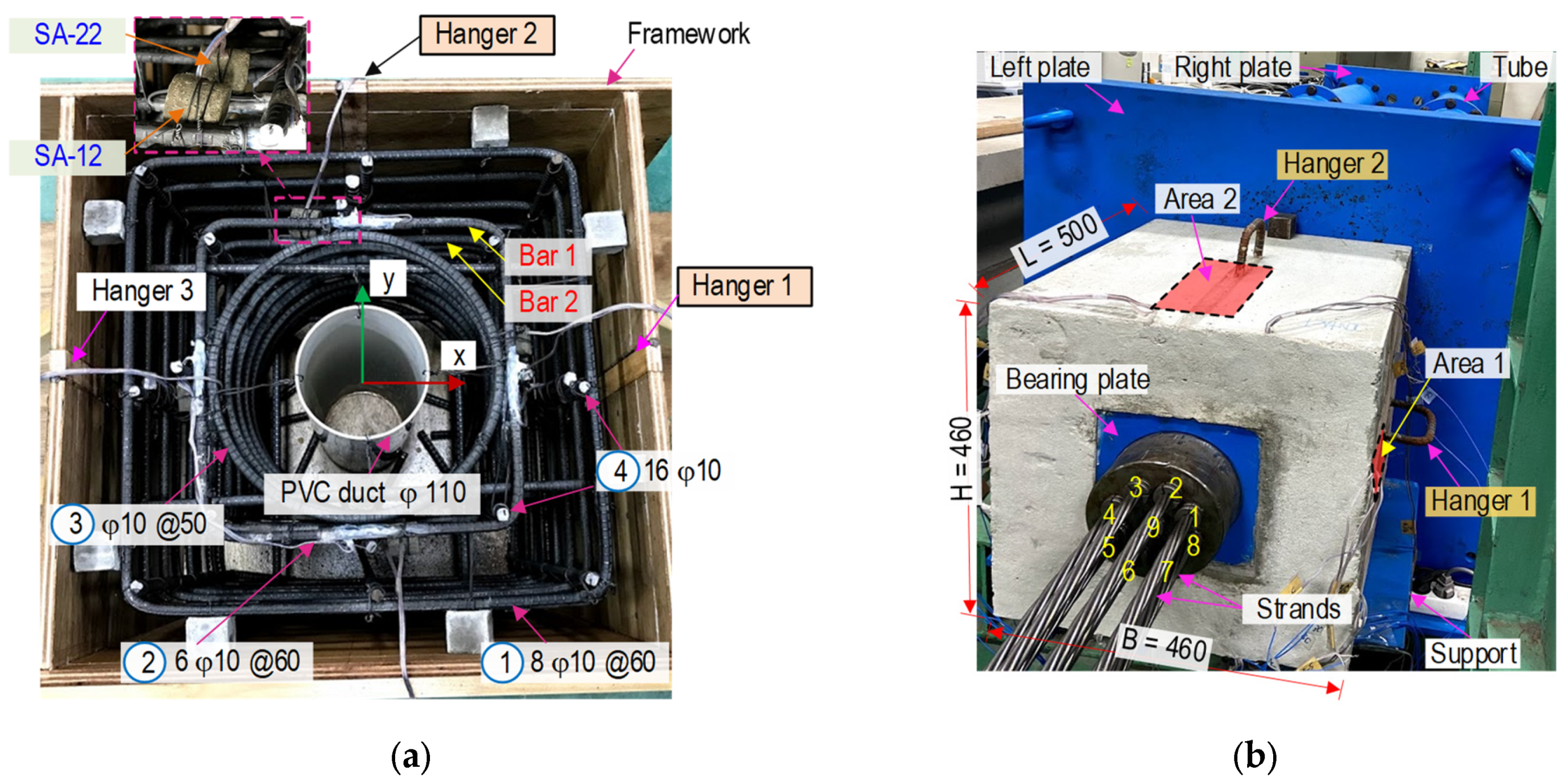
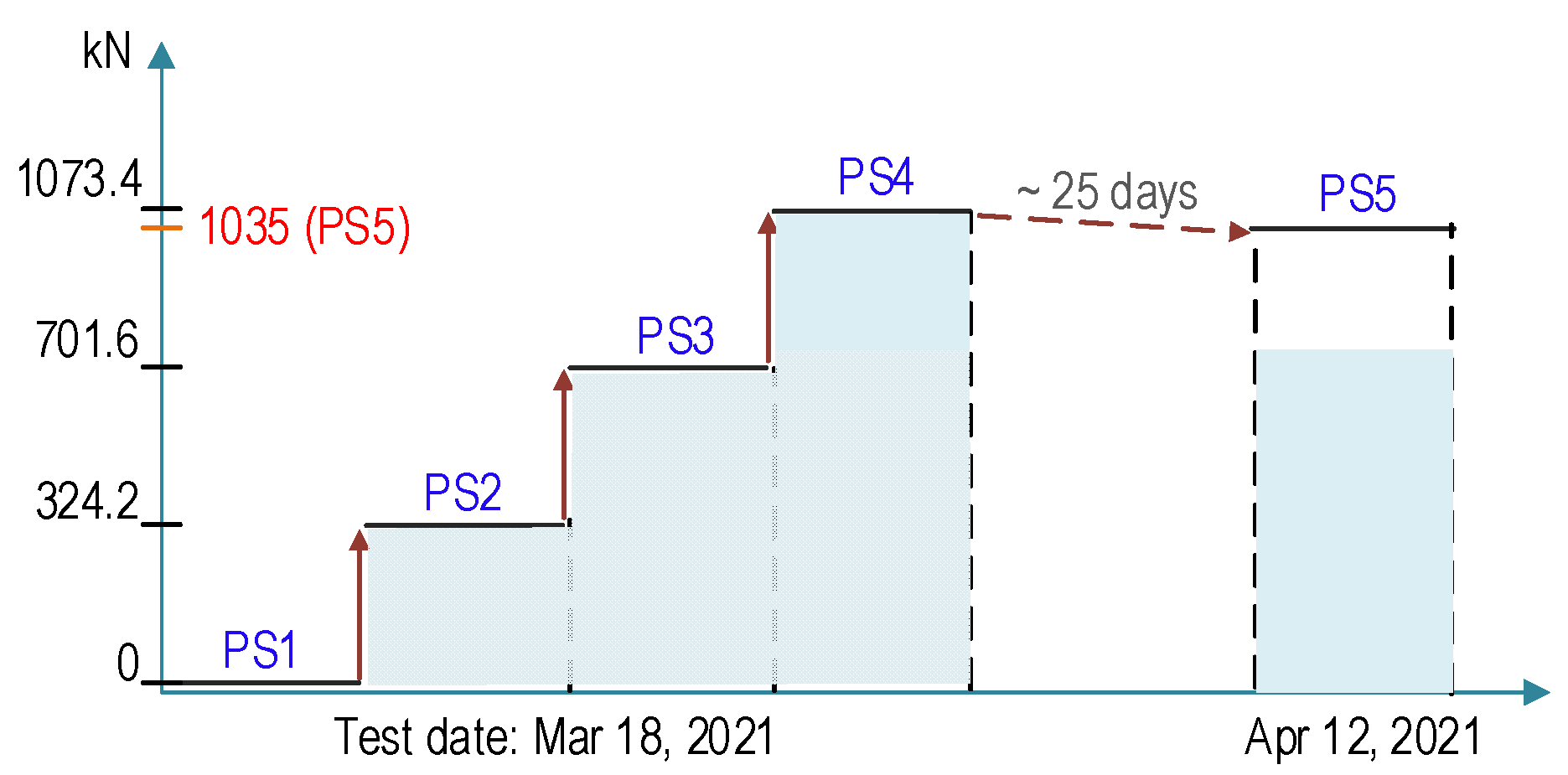


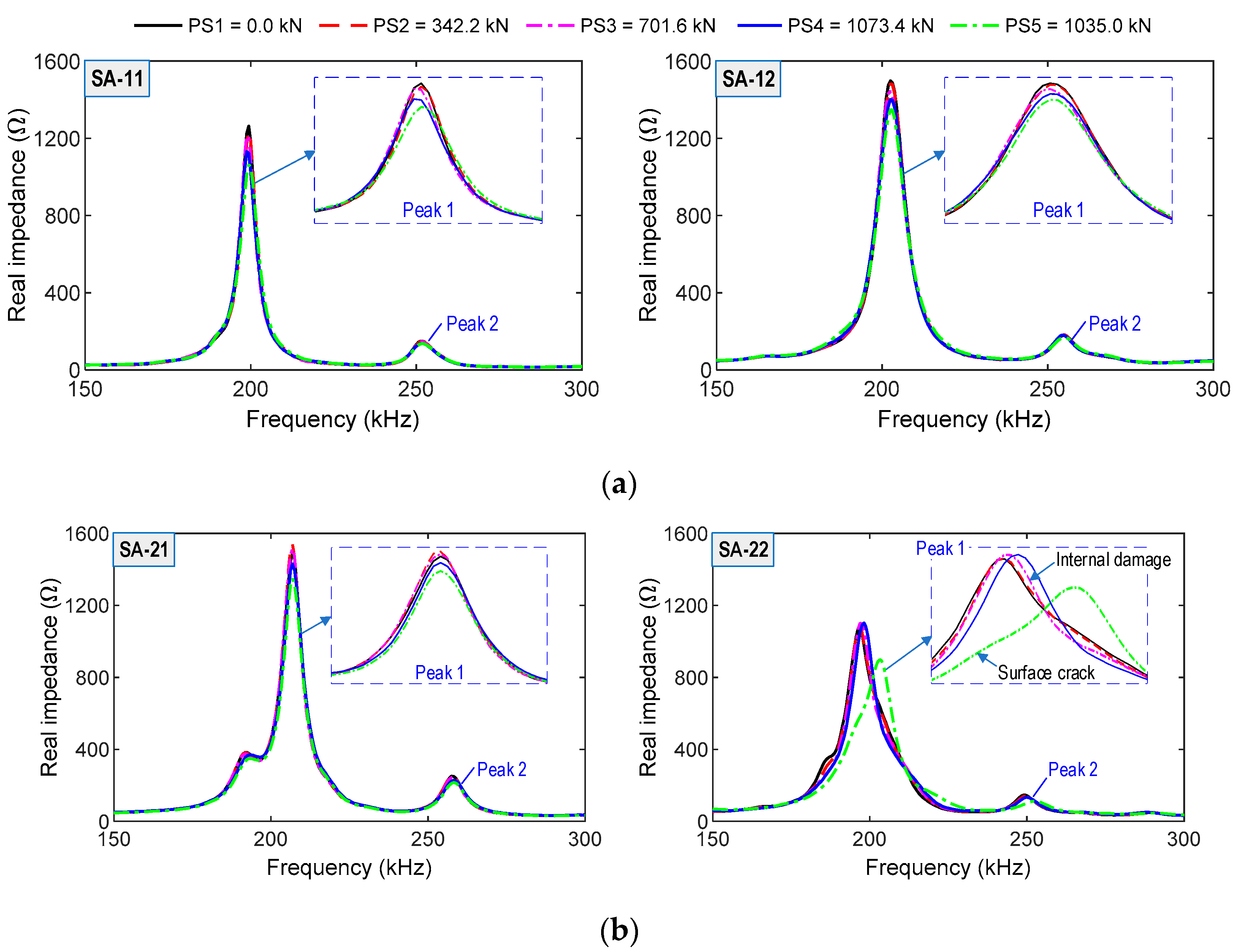

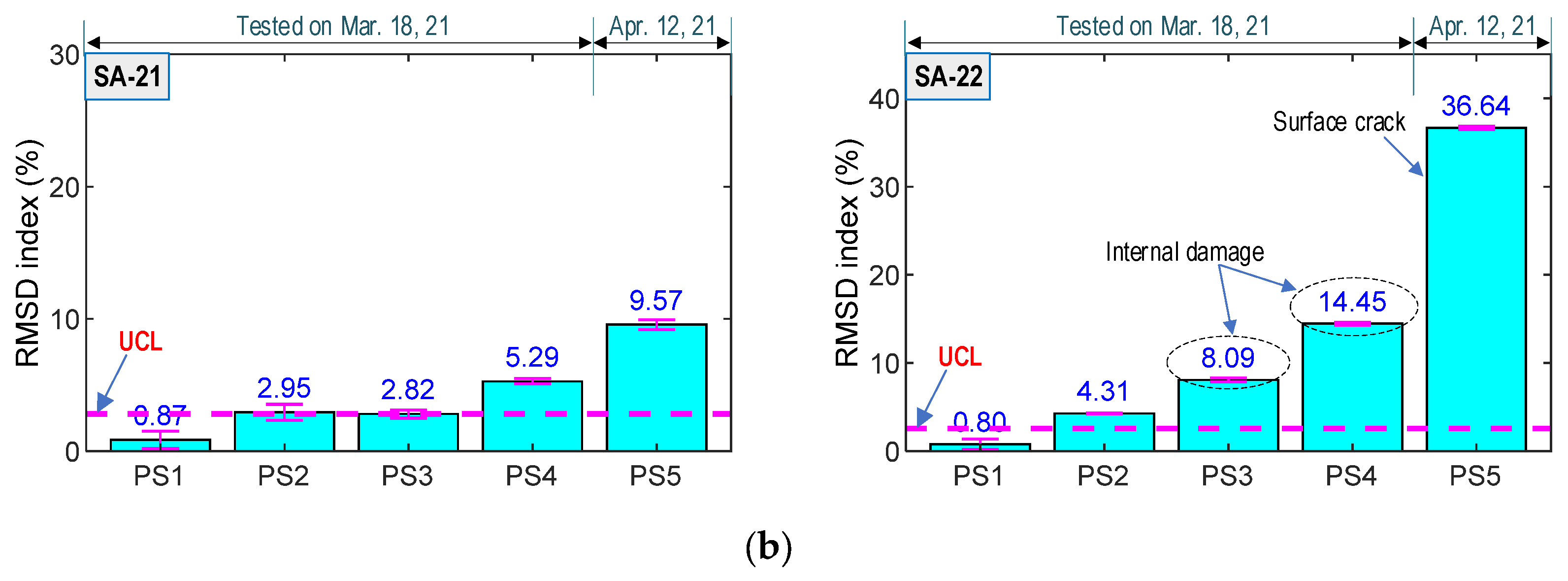
| Parameters | Anchor Head & Wedge | Pure Concrete |
|---|---|---|
| Mass density, ρ (kg/m3) | 7850 | 2400 |
| Poisson’s ratio, ν | 0.3 | 0.2 |
| Young’s modulus, E (GPa) | 200 | 27.7 |
| Compressive strength, σc (MPa) | 460 | 30 |
| Tensile strength, σt (MPa) | 460 | 3.0 |
| Young’s Modulus, E (GPa) | Poisson’s Ratio, ν | Mass Density,ρ (kg/m3) | Dielectric Constant, εT33 (F/m) | Coupling Constant, d31 (m/V) | Damping Loss Factor, η | Dielectric Loss Factor, δ |
|---|---|---|---|---|---|---|
| 62.1 | 0.35 | 7750 | 1.53 × 10−8 | −1.71 × 10−10 | 0.0125 | 0.015 |
| Case | Intact | Applied Force | SA Sensor | Simulation |
|---|---|---|---|---|
| 1 | 0PS | 0.8PS | SA11, SA21, SA31 | SA’s impedance responses based on internal stress distribution |
| 2 | 0PS | 1.2PS (*) | SA1j, SA2j, SA3j | SA’s impedance responses based on tensile concrete damage |
| Concrete Properties | Mixture 1 (*) | Mixture 2 (**) |
|---|---|---|
| Sand (kg) | 80.1 | 81.8 |
| Aggregate (Dmax 25) (kg) | 99.8 | 98.7 |
| Cement (kg) | 34.6 | 33.2 |
| Water (liter) | 15.6 | 16.1 |
| Tested concrete slump (cm) | 11.0 | 18.5 |
| Tested compressive strength, σc (MPa) | 23.3 | 16.7 |
| Properties | Concrete | Rebar | Steel Strand | Epoxy | PZT 5A |
|---|---|---|---|---|---|
| Young’s modulus (GPa) | 20.7 | 200 | 197 | 0.74 | 62.1 |
| Poisson’s ratio | 0.20 | 0.33 | 0.33 | 0.38 | 0.35 |
| Mass density (kg/m3) | 2400 | 7850 | 7850 | 1090 | 7750 |
| Compressive strength (MPa) | 16.7 | - | - | 32.3 | - |
| Yield strength (MPa) | - | 400 | 1860 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, Q.-Q.; Dang, N.-L.; Ta, Q.-B.; Kim, J.-T. Optimal Localization of Smart Aggregate Sensor for Concrete Damage Monitoring in PSC Anchorage Zone. Sensors 2021, 21, 6337. https://doi.org/10.3390/s21196337
Pham Q-Q, Dang N-L, Ta Q-B, Kim J-T. Optimal Localization of Smart Aggregate Sensor for Concrete Damage Monitoring in PSC Anchorage Zone. Sensors. 2021; 21(19):6337. https://doi.org/10.3390/s21196337
Chicago/Turabian StylePham, Quang-Quang, Ngoc-Loi Dang, Quoc-Bao Ta, and Jeong-Tae Kim. 2021. "Optimal Localization of Smart Aggregate Sensor for Concrete Damage Monitoring in PSC Anchorage Zone" Sensors 21, no. 19: 6337. https://doi.org/10.3390/s21196337
APA StylePham, Q.-Q., Dang, N.-L., Ta, Q.-B., & Kim, J.-T. (2021). Optimal Localization of Smart Aggregate Sensor for Concrete Damage Monitoring in PSC Anchorage Zone. Sensors, 21(19), 6337. https://doi.org/10.3390/s21196337








