1. Introduction
The crankshaft is a critical component of the automobile engine, and its machining quality directly affects engine performance and reliability. Therefore, crankshaft manufacturing plays a very significant role in the automotive industry. In the mass production of engine crankshafts, the pin chasing grinding technology based on the oscillating grinding machines has been widely implemented to meet machining accuracy and efficiency requirements [
1,
2]. During the oscillating grinding, the workpiece rotation-axis (C axis) and the transverse feed of grinding carriage-axis (X axis) are executed to keep the grinding wheel tangent with the crankshaft pin journals [
3,
4,
5,
6]. The oscillating grinding method is capable of providing higher machining efficiency, more flexibility, and better precision than the traditional grinding method that needs an appropriative fixture to adjust the rotation center repeatedly [
1]. Recently, the application of the oscillating grinding machines in the automotive and shipping industry has progressed, and thus the reliability and stability of the oscillating grinding machines continues to grow. According to the characteristics of the oscillating grinding process, the contour error components of the crankshaft pin journal apparently contain error information of the C axis and X axis. The contour errors of the crankshaft pin journal are the most intuitive data in production field selective inspection. If the mapping relation between the contour error components of the crankshaft pin journal and the axis position control error of the oscillating grinding machine can be built, it would be great significance for the reliability maintenance of the oscillating grinding machine.
Engineering surface texture is considered as the “fingerprint” of the manufacturing process [
7], where the performance information of the machine tool, the condition information of the cutting tool, and the characteristic information of materials are involved [
8]. The oscillating grinding contour error of the crankshaft pin journal, which contains the performance information of the grinder, the condition information of the grinding wheel, and the performance of the crankshaft material, is the fingerprint of the pin chasing grinding process. According to the special characteristics of the pin chasing grinding process, the C axis and X axis have an obvious effect on the contour error of the crankshaft pin journal. Conversely, the crankshaft contour error based on this kind of grinding process apparently covers the performance information of the oscillating grinding machines, especially the performance information of C axis and X axis. There are some traditional contour error analysis methods, such as the Fourier transform and the wavelet transform [
8,
9,
10,
11], which are based on the integral transform and required to design or choose the proper basis function according to the signal characteristics of the contour error. These analysis methods strongly depend on the prior knowledge and lack of flexibility and adaptivity in analyzing and processing real and complicated signals. Empirical mode decomposition (EMD), proposed by Huang et al. in 1998 [
12], can be used to decompose a complicated signal into a series of intrinsic mode functions (IMFs) and they verified that, even in the worst conditions, the instantaneous frequency of IMFs obtained by Hilbert transform can map into the required physical factors. To solve the mode mixing problem in EMD, an ensemble empirical mode decomposition (EEMD) was presented by Wu and Huang [
13]. The EEMD method does not need to design a basis function based on prior knowledge. The decomposition is posterior and completely driven by the data. The EEMD method is an adaptive mode decomposition method and has been widely used in machinery fault diagnosis [
14,
15]. However, there are no references to contour error analysis using EEMD.
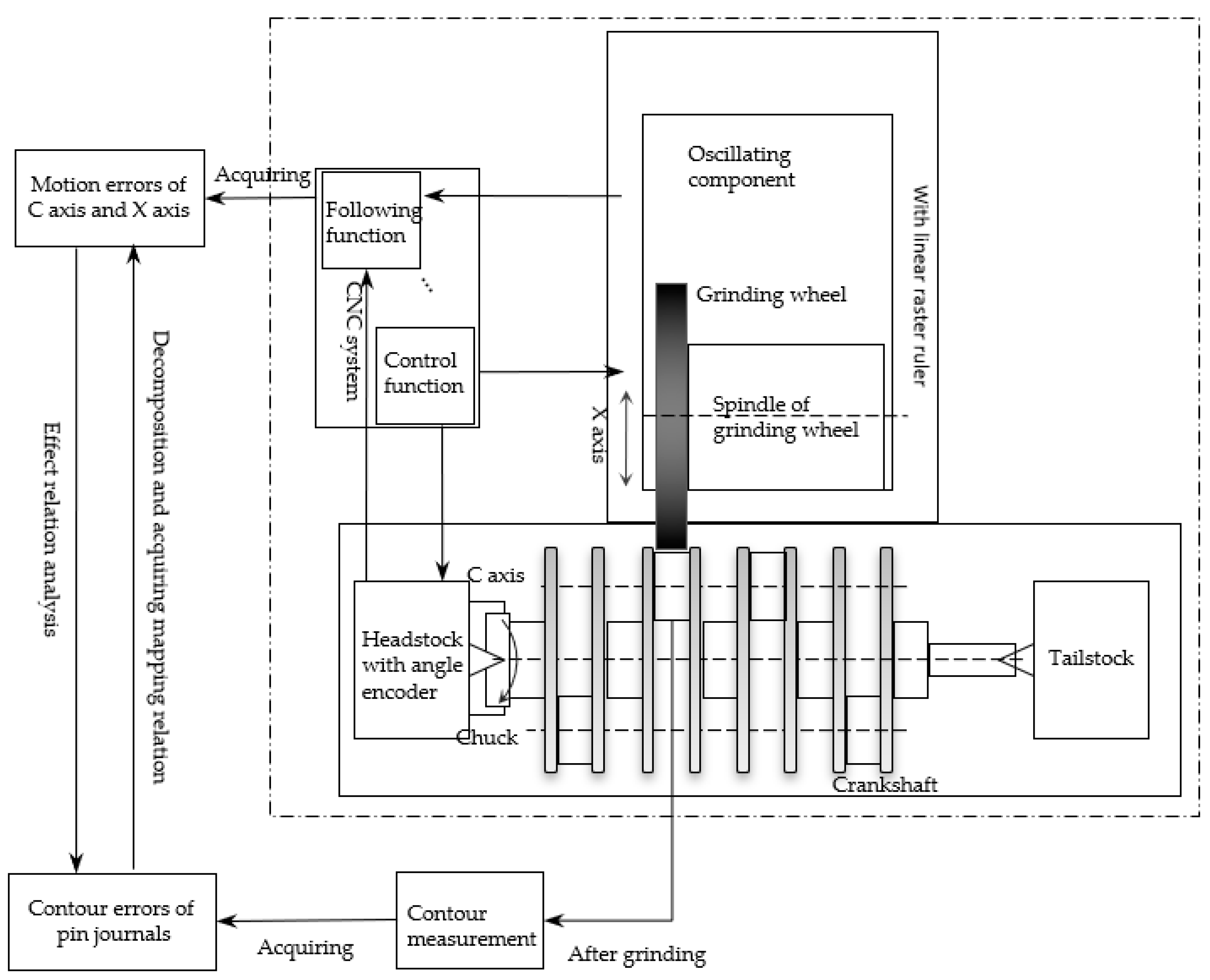
The schematic of an oscillating grinder and the error sources are illustrated in
Figure 1. The contour error of the crankshaft pin journal is measured after oscillating grinding. Computerized numerical control (CNC) system of the crankshaft oscillating grinder can acquire the real-time position information of the axes, which contains position control errors of the C axis and X axis. In this paper, a contour error decomposition method of the crankshaft pin journal based on EEMD is firstly proposed. As the contour error is closed data, periodic extension is applied in both ends for avoiding the boundary effect. According to the contour generating principle of the crankshaft pin journal by oscillating grinding, a calculation method to identify the effect of the axis position control error on the contour error of the crankshaft pin journal is then proposed. Finally, through the grinding experiments, the error data are acquired and measured to calculate and decompose the contour error by using the proposed methods for obtaining the mapping relation between the crankshaft pin journal contour error and the axis position control error. The mapping relation can be applied in predicting the key functional component performance of machine tools from the oscillating grinding workpiece contour error, which is of great significance for the automatic crankshaft production line, to improve efficiency and accuracy by selective inspection and monitoring.
2. Contour Error Decomposition Based on EEMD
The EMD, proposed by Huang et al. in 1998 [
12], can decompose a complicated signal into a series of intrinsic mode functions (IMFs) based on the local characteristic time scale of the signal. An IMF satisfies the following two conditions: (1) The number of extrema and zero-crossings must be either equal or different at most by one; (2) At any point, the mean of the upper and lower envelopes from the signal is zero. If the
jth IMF component is indicated as
Cj, then the original signal
X(
t) can be described as,
where
r is the residue of the signal and it is a monotonic function. In essence, EMD is an adaptive dyadic filter bank [
16] which can decompose white noise into a series of IMF components with different center frequency [
17]. In terms of practical application, as the measured data are not white noise, the mode mixing problem may appear. The result of mode mixing is that the IMF components lose physical significance of decomposition.
To overcome the mode mixing problem in EMD, EEMD was proposed by Wu and Huang [
13]. The decomposition of the crankshaft pin journal contour error based on EEMD is illustrated in
Figure 2. The contour error represents closed data with the same head and tail. In order to avoid boundary effect, each end of contour error data is periodically extended with the same original contour error data. After EEMD decomposition, on third of the middle data from each component is selected as the decomposition result, then ranked from high frequency to low frequency. In theory, the contour error data does not include the 0 UPR (undulation per revolution) information which represents the dimension error information and 1 UPR information, which represents center deviation information of the crankshaft pin journal. Therefore, the lowest order component
C1 of the pin journal contour error is composed of the previous order component, the components with frequency less than 2 UPR, and the residual component. If the contour error is decomposed into
M components,
corresponds to EEMD decomposition component in reverse order for the
component
(
). For the remaining high frequency components of EEMD decomposition, these components are combined into
as the highest component of crankshaft contour error decomposition.
3. Effect of Axis Position Control Error on the Crankshaft Pin Journal Contour Error
In the oscillating grinding process, the grinding wheel is always tangent with a crankshaft pin journal. The contour of crankshaft pin journal is produced by reciprocating motion of grinding wheel following rotational motion of crankshaft. Under ideal conditions, the contour of the crankshaft pin journal is a standard circle. The principle diagram of the crankshaft oscillating grinding motion is illustrated in
Figure 3. The grinding point (tangent point)
G is in the connecting line between the center of the pin journal
and the center of grinding wheel
. The crankshaft is driven under the workpiece driven by axis
C and the pin journals rotate around the center
O of the main journal. The grinding wheel implements reciprocating chasing motion along the X axis and realizes the grinding of crankshaft pin journals.
The contour control point (,) represents the motion control position information which determines the contour of the pin journal. This point maps the contour point (,) of the pin journal.
The contour control equation is,
Equation (2) can be transformed as,
According to the geometric relationship, Equation (4) can be achieved as,
From Equations (3) and (4), Equation (5) can be obtained as follows,
where
is the distance from the center of the grinding wheel
to the rotation center of the crankshaft
, with reciprocating motion of grinding wheel along X axis.
is the eccentric distance of the pin journal, which is the distance from center of the pin journal
to the rotation center of the crankshaft
.
is the radius of the pin journal, which is the distance from the grinding point
to the center of the pin journal
.
is the radius of the grinding wheel.
is the angle between
and
, which is the rotation angle of the crankshaft controlled by C axis.
is the angle between the extended line of
and
, which is the angle corresponding to the grinding point passing through the arc.
When a workpiece is ground, the theoretical grinding motion control equations can be derived from Equation (2),
where
and
are the motion control parameters and they are constants. When a super hard grinding wheel is chosen, like the CBN grinding wheel,
may be considered as a constant because of the negligible wear.
According to Equations (6) and (7), the CNC system of the machine tool controls the motion of C axis and X axis to machine the pin journals. Only if the practical motion positions of C axis and X axis accurately meet the requirements of the equations, the grinding result is an ideal circle. However, in the practical machining, the motion control of the C axis and X axis both have errors. Therefore, the contour of the ground pin journal is not a standard circle.
To accurately obtain the grinding contour generation mechanism of the crankshaft pin journal and the relation between the machine tool position control information and the crankshaft pin journal contour information, the coordinate system is created in the pin journal, where the grinding process can be considered as the grinding wheel rotation around the pin journal. If the elastic deformation of the grinding wheel and the workpiece is neglected, the inner envelope of the grinding wheel trajectory is the grinding contour of the pin journal, as illustrated in
Figure 4.
According to the above principle and neglecting elastic deformation of the mechanical system, the grinding wheel and workpiece utilize the practical contour control point (
,
), which is the practical coordinate position of grinder C axis and X axis, to interact for achieving crankshaft pin journal contour (
,
). The principle diagram of the pin chasing grinding motion is illustrated in
Figure 5.
In the xOy
1 coordinate system, the trajectory point of the grinding wheel center corresponds to the polar coordinate (
,
) and the rectangular coordinate (
,
). In the xO
py coordinate system, the grinding wheel center corresponds to the polar coordinate (
,
) and the rectangular coordinate (
,
). Then, the following equations can be obtained,
According to Equations (8) and (9), Equations (10) and (11) can be obtained,
Let
denote the trajectory function of the grinding wheel center. According to the geometric relationship, the following equations can be obtained,
From Equations (12) and (13), the contour information (,) of the crankshaft pin journal with the crankshaft rotation center O, the practical pin journal center Op and the phase reference positive x axis direction can be inferred.
The base circle can be obtained from the crankshaft pin journal contour by least square fit. The difference of the practical contour and the base circle is the contour error [
18]. In the position control, the deviation between the actual value and the theoretical value is inevitable. Therefore, the main factors that cause the contour error of the crankshaft pin journal root in the position control error of X axis and C axis. The basic geometric relationship is shown in
Figure 5, and the principle of the pin chasing grinding motion relationship is illustrated by Equations (10)–(13). The calculation process of the crankshaft contour error caused by the axis position control error is described in
Figure 6.
The axis position control error is the difference of the theoretical and the actual control value. If the basic machining parameters are known, the axis position control error is the equivalent information with the theoretical control value and the actual control value. To simplify the process, the theoretical control value and the actual control value of the axis can be directly acquired from the CNC system. The calculation of the effect of the C axis position control error on the crankshaft contour error is firstly conducted by the actual control value of the C axis and the theoretical control value of the X axis. Then, crankshaft contour information can be applied to calculate the contour error. Similarly, the effect of the X axis position control error on the crankshaft contour error can be obtained.