Design of Insulation Tape Tension Control System of Transformer Winding Machine Based on Fuzzy PID
Abstract
:1. Introduction
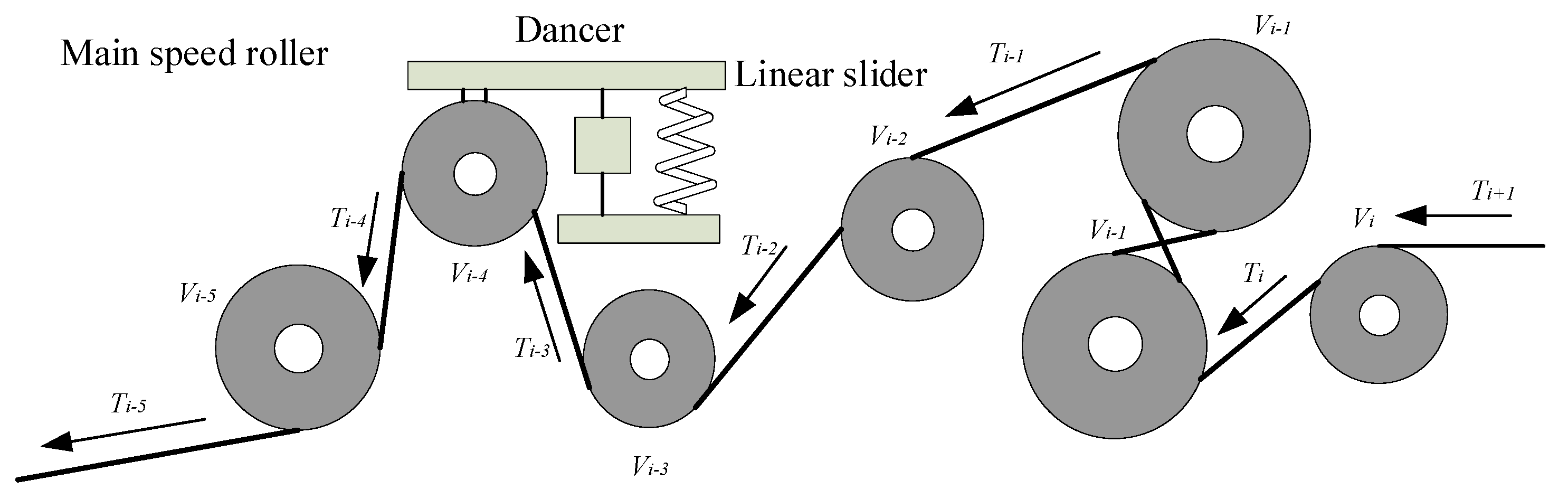
2. Mechanical Structure and Dynamics Model
2.1. Dynamic Model of Roller
2.2. Dynamic Model of Electromagnetic Brake Roller
2.3. Dynamic Model of Main Speed Roller
2.4. Dynamic Model of Guide Roller
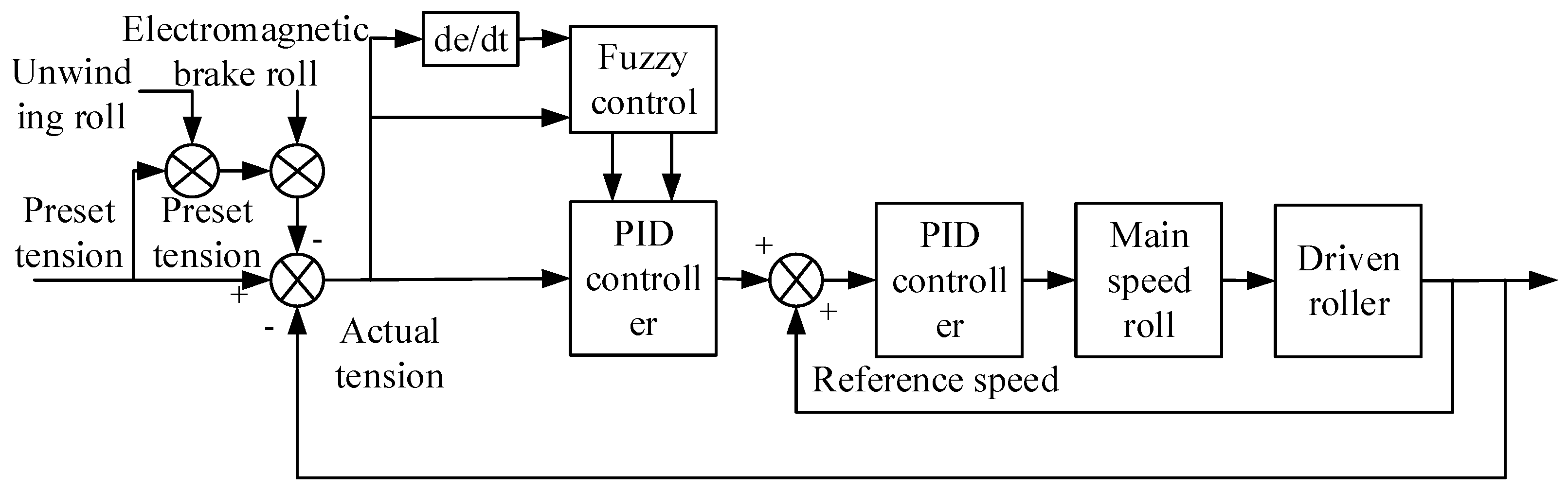
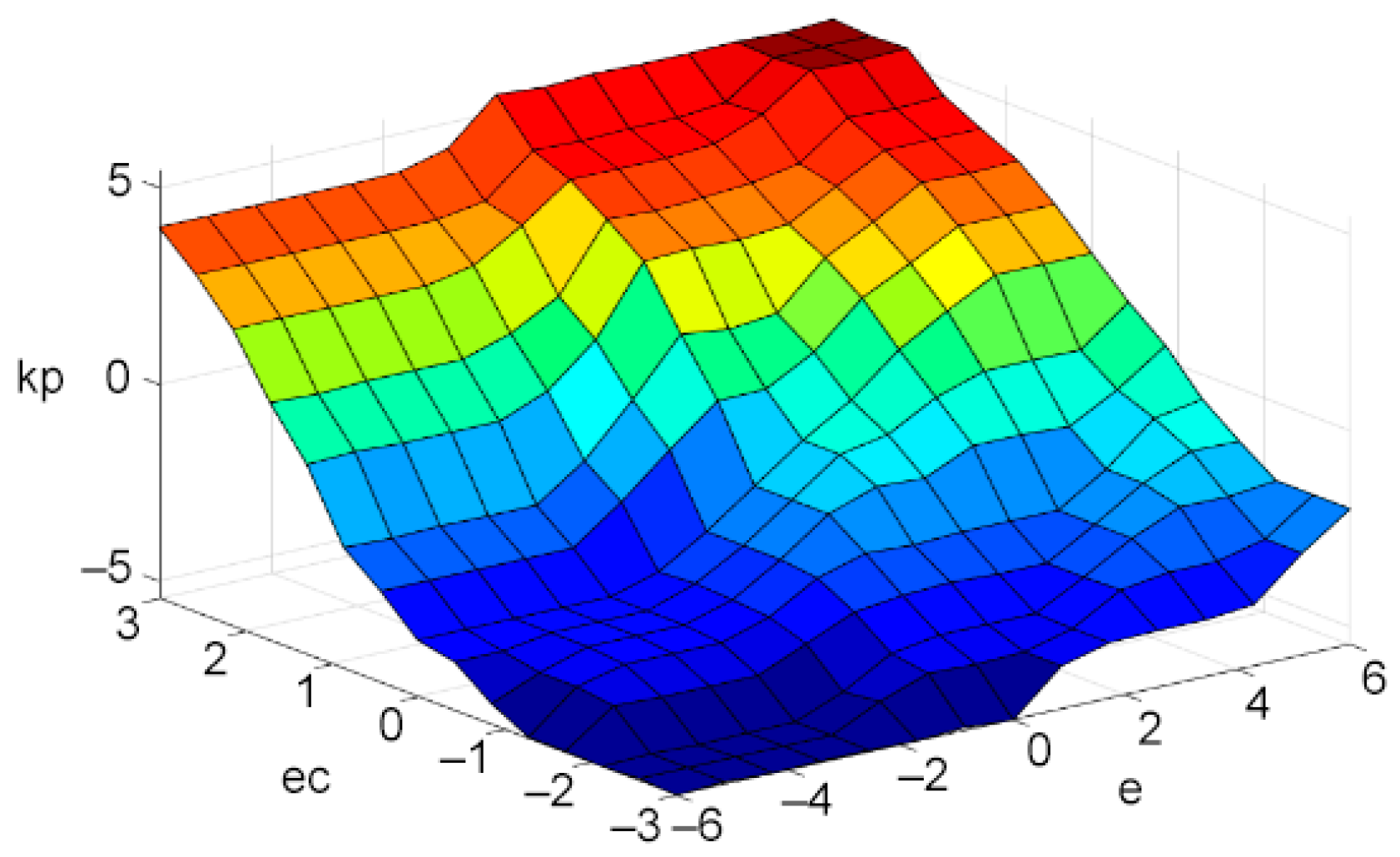
3. Design of Fuzzy Control System for Winding Machine
3.1. Fuzzy PID Control
3.2. Fuzzification
3.3. Fuzzy Rule
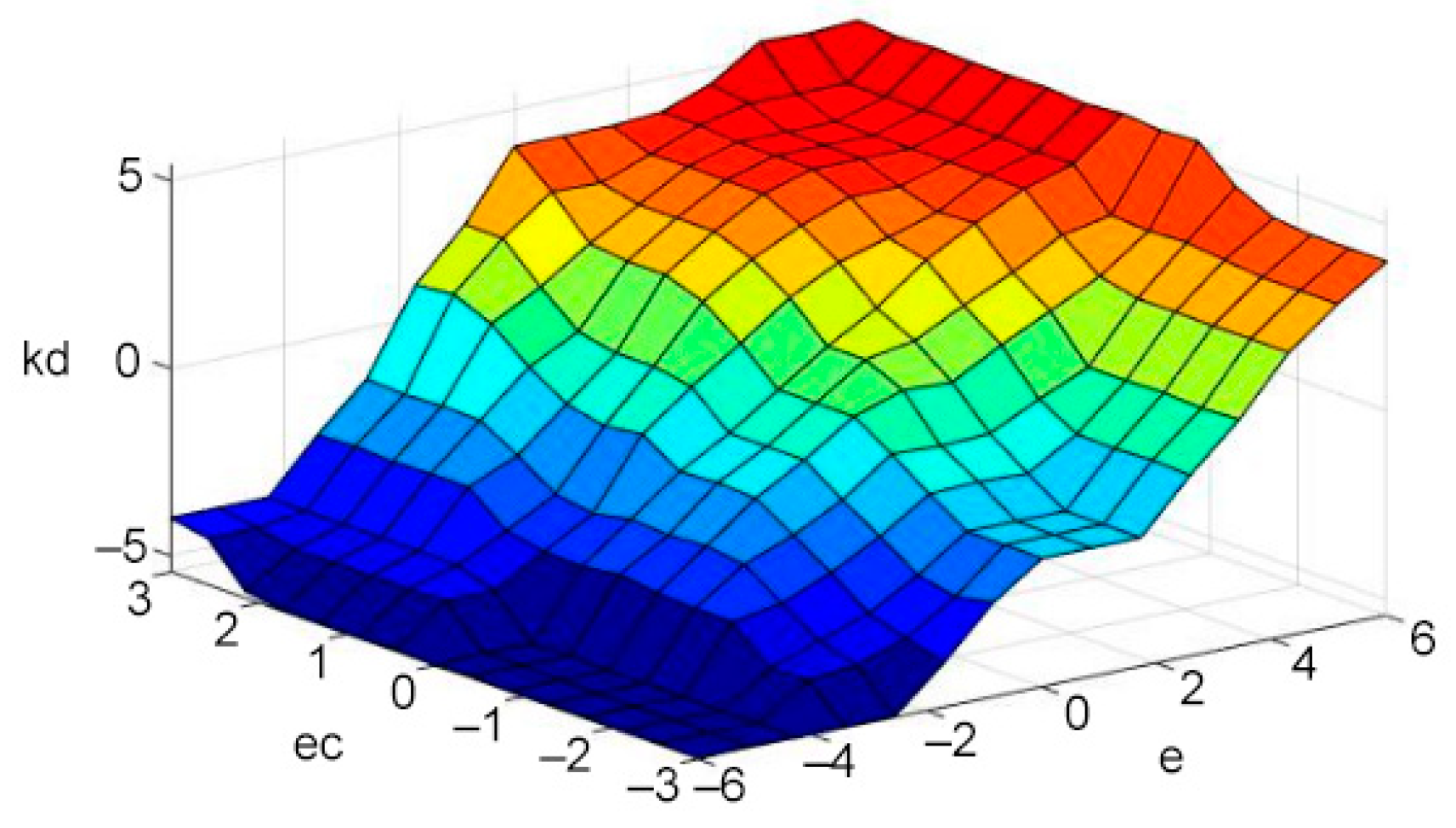
3.4. Defuzzification
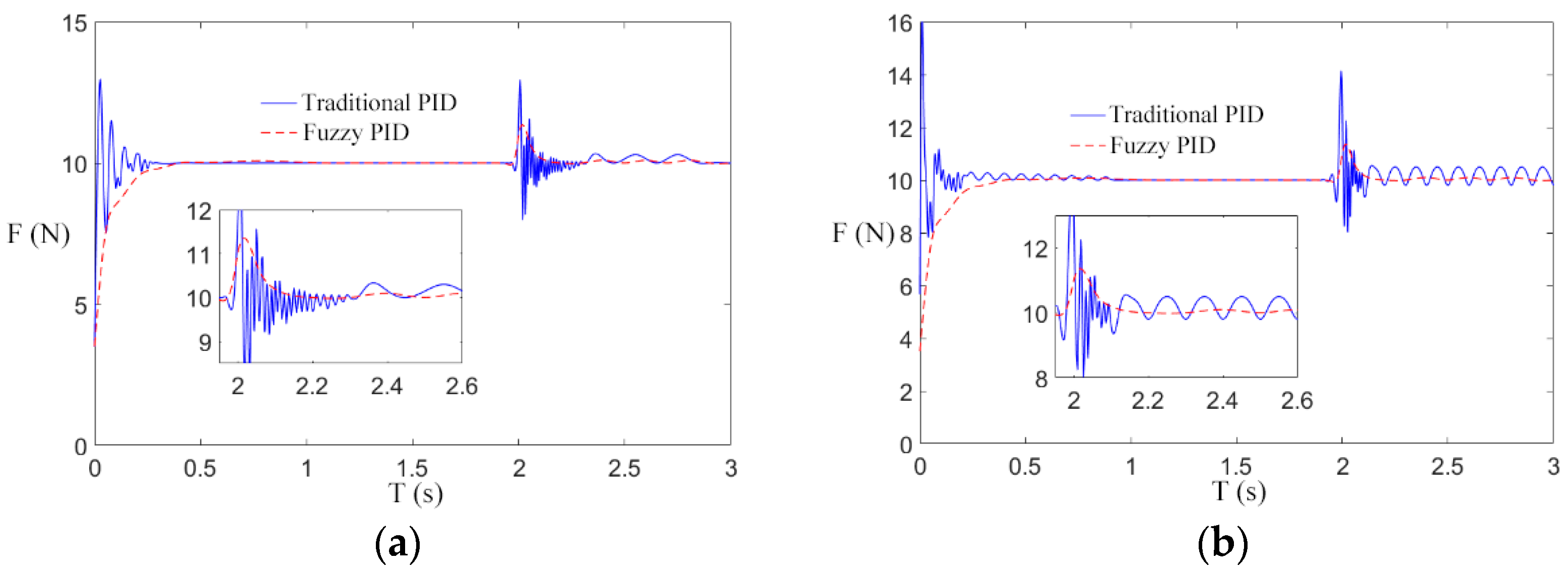
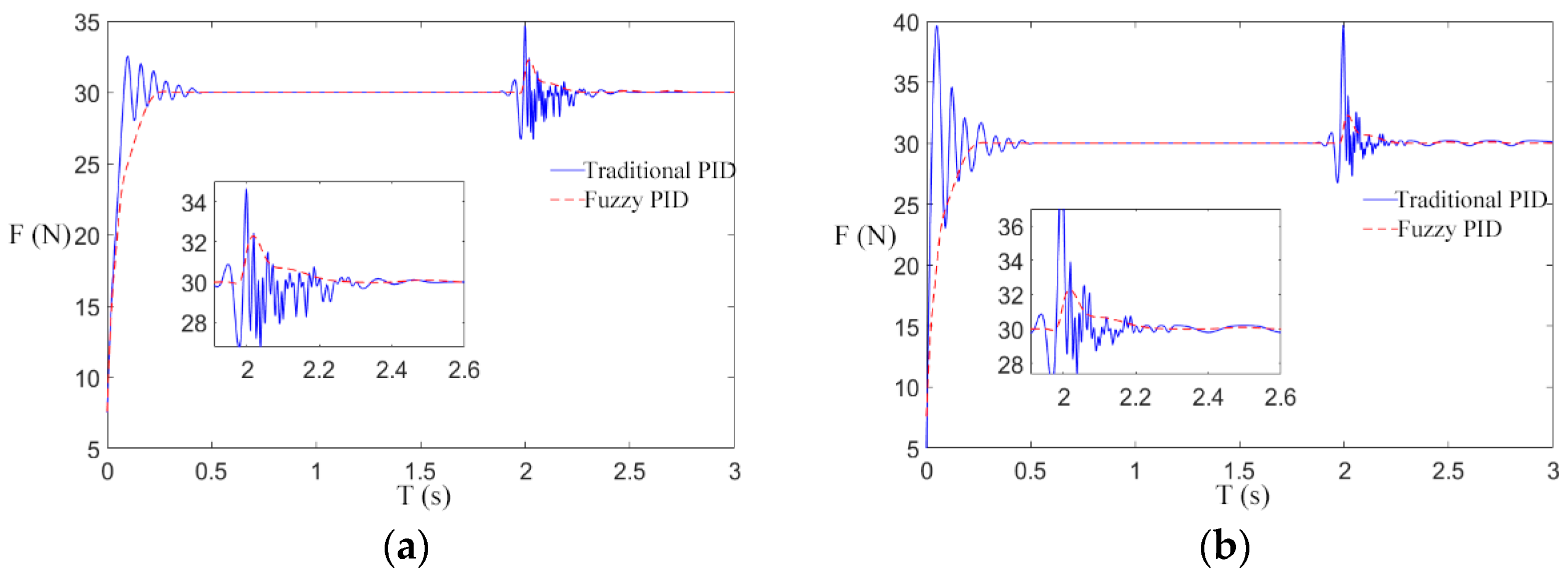
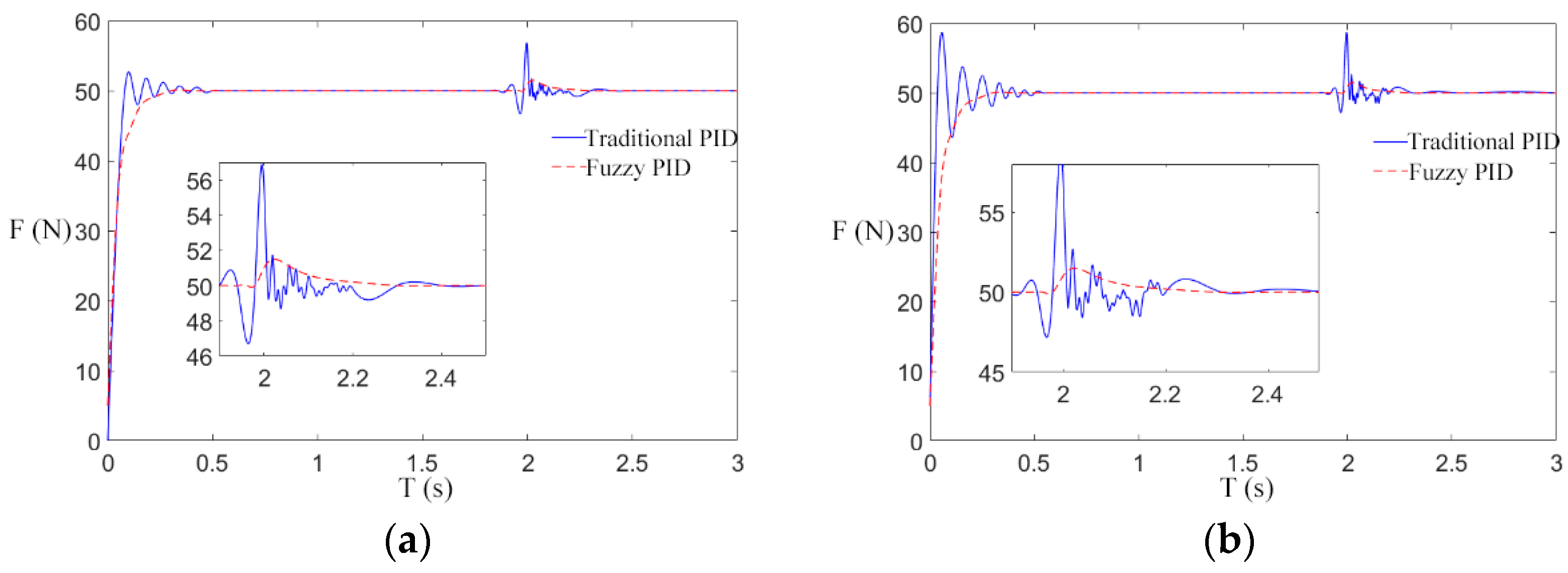
4. Simulation and Result Analysis
4.1. System Mechanical Parameters
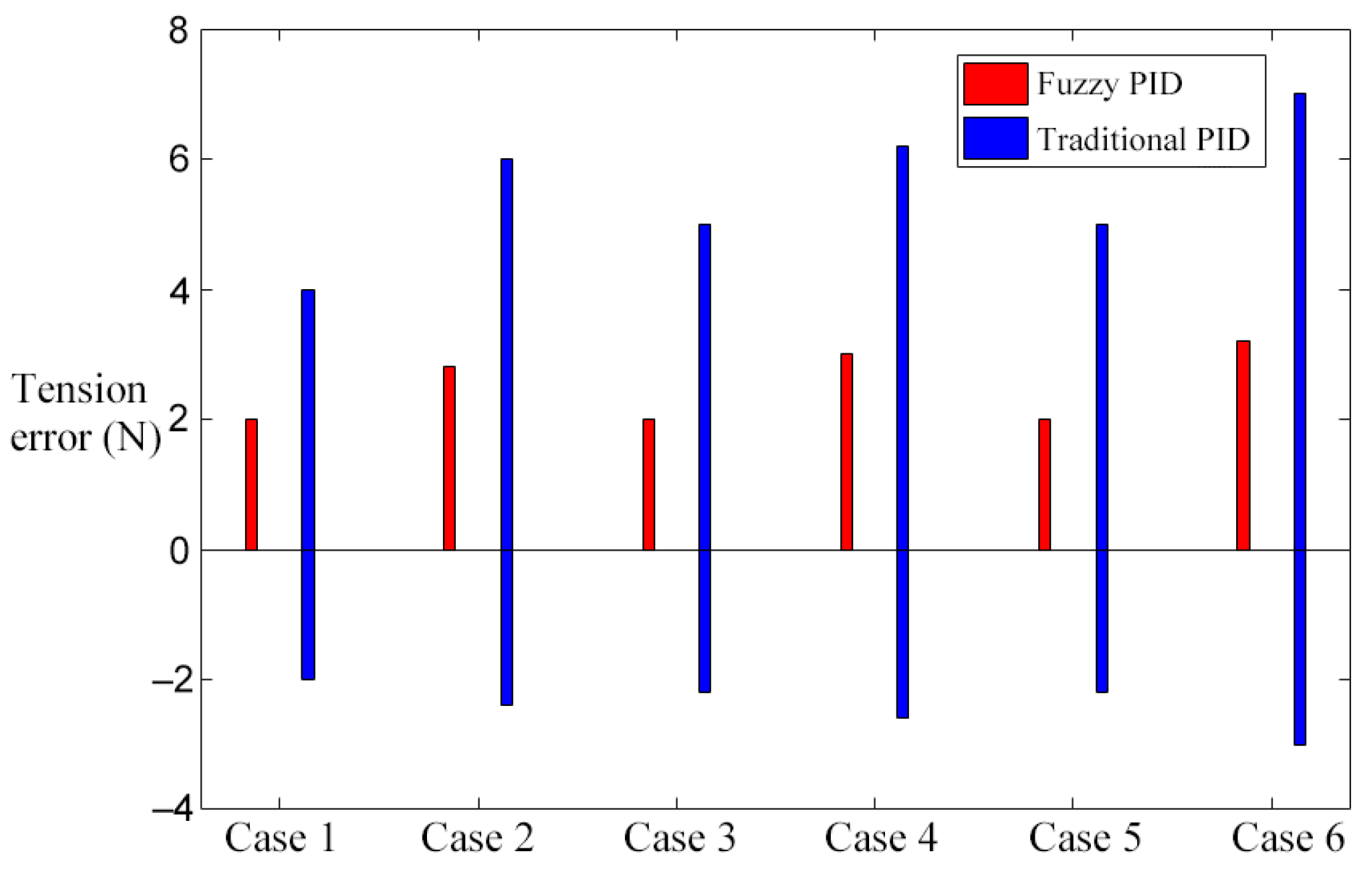
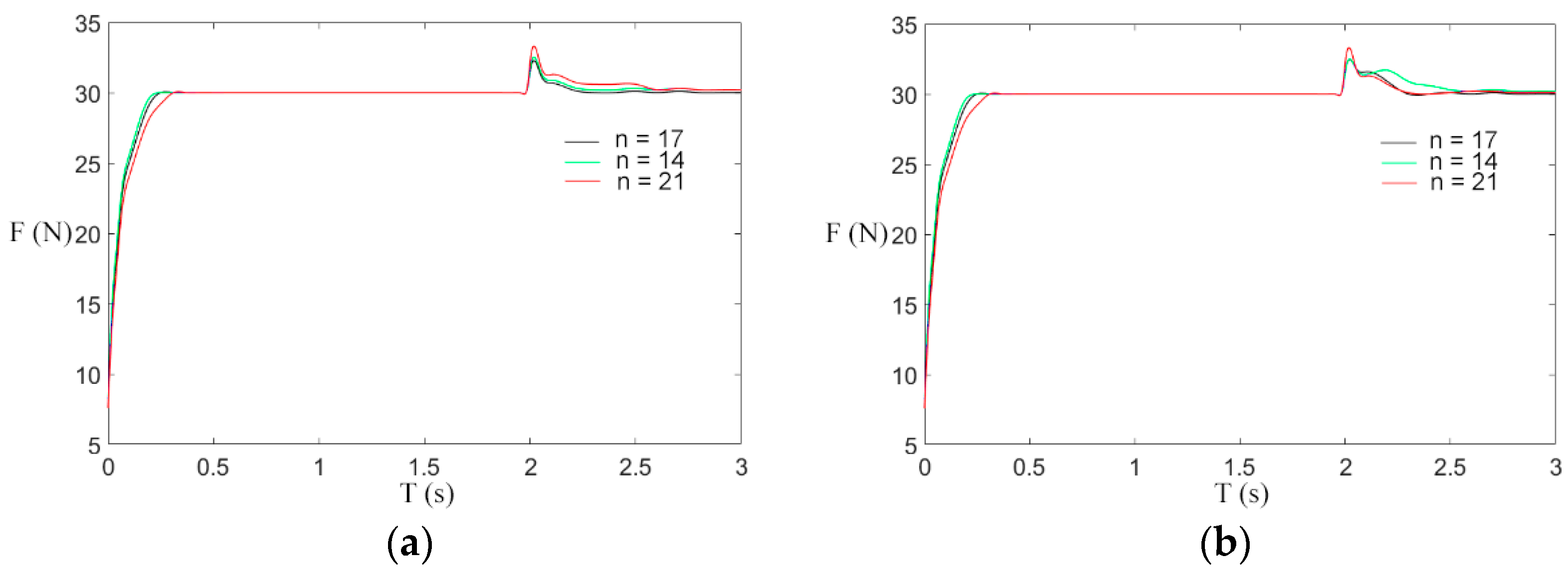
4.2. Analysis of Simulation Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X. Research on Quasi-Automatic Control System of Power Transformer Vertical Winding Machine; Shandong University: Jinan, China, 2016. [Google Scholar]
- Zhao, X.; Dong, Z.; Wang, J. Development of Automatic Winding Machine. Equip. Electron. Prod. Manuf. 2010, 39, 41–45. [Google Scholar]
- Feldmann, K.; Wenger, U. Optimization for wire tensioners. In Proceedings of the Electrical Insulation Conference and Electrical Manufacturing and Coil Winding Conference, Cincinnati, OH, USA, 18 October 2001. [Google Scholar]
- Sauter, D.; Jamouli, H.; Keller, J.Y.; Ponsart, J.C. Actuator fault compensation for a winding machine. Control Eng. Pract. 2005, 13, 1307–1314. [Google Scholar] [CrossRef]
- Mahawan, B.; Luo, Z.H. High-speed high-precision tracking control for electronically controlled winding machines. Control Eng. Pract. 2001, 9, 563–571. [Google Scholar] [CrossRef]
- Wen, P.; Stapleton, C.; Li, Y. Tension Control of a Winding Machine for Rectangular Coils. In Proceedings of the ICARCV 2008: 10th International Conference on Control Automation, Robotics and Vision, Hanoi, Vietnam, 2–5 December 2008; pp. 2031–2037. [Google Scholar]
- Ponsart, J.C.; Theilliol, D.; Aubrun, C. Virtual sensors design for active fault tolerant control system applied to a winding machine. Control Eng. Pract. 2010, 18, 1037–1044. [Google Scholar] [CrossRef]
- Rodrigues, M.; Sahnoun, M.; Theilliol, D.; Ponsart, J.C. Sensor fault detection and isolation filter for polytopic LPV systems: A winding machine application. J. Process. Control 2013, 23, 805–816. [Google Scholar] [CrossRef] [Green Version]
- Join, C.; Ponsart, J.C.; Sauter, D.; Theilliol, D. Nonlinear filter design for fault diagnosis: Application to the three-tank system. IEE Proc. Control Theory Appl. 2005, 152, 55–64. [Google Scholar] [CrossRef]
- Li, L.B.; Sun, L.L.; Zhang, S.Z.; Yang, Q.Q. Speed tracking and synchronization of multiple motors using ring coupling control and adaptive sliding mode control. Isa Trans. 2015, 58, 635–649. [Google Scholar] [CrossRef]
- Quanjin, M.; Rejab, M.R.M.; Idris, M.S.; Zhang, B.; Merzuki, M.N.M.; Kumar, N.M. Wireless technology applied in 3-axis filament winding machine control system using MIT app inventor. Iop Conf. 2019, 22, 46–54. [Google Scholar] [CrossRef]
- Shi, Y.; Yan, L.; Yang, K. Advanced Composite Strip Winding Strip Laying Molding Technology. Aeronaut. Manuf. Technol. 2010, 46, 32–36. [Google Scholar]
- Xue, B. Development and Application of Automatic Winding Machine Control System; Harbin Institute of Technology: Harbin, China, 2011. [Google Scholar]
- Hu, H.; Gao, Q.; Liu, J.; Hou, M.; Wang, C. Design of a Kind of Automatic Winding Machine. Shanghai Textile Sci. Technol. 2017, 45, 56–59. [Google Scholar]
- Wang, Z.; Tang, T.; Xu, Z.; Ni, H. Design and experiment of automatic tension control system for trawl winch on fishing boat. Trans. Chin. Soc. Agric. Eng. 2017, 33, 90–94. [Google Scholar]
- Zhao, P. Design and Development of Control System of Transformer Combined Winding Machine; Shandong University: Shangdong, China, 2014. [Google Scholar]
- Yuan, S.; Zhao, C.; Guo, L. Uncoupled PID Control of Coupled Multi-Agent Nonlinear Uncertain systems. J. Syst. Sci. Complex. 2018, 31, 4–21. [Google Scholar] [CrossRef]
- Chen, Y.J.; Jiang, X.M.; Yang, G.Y. Design of Tension Control of a Winding Machine for Rectangular Component. J. Tianjin Polytech. Univ. 2012, 8, 34–45. [Google Scholar]
- Lu, J.S.; Cheng, M.Y.; Su, K.H.; Tsai, M.C. Wire Tension Control of an Automatic Motor Winding Machine-niterative Learning Sliding Mode Control Approach. Robot. Comput.-Integr. Manuf. 2018, 50, 50–62. [Google Scholar] [CrossRef]
- Kwon, J.-W.; Byung-Il, K. Design of Novel High Performance Dual Rotor Flux-Switching Drum Winding Machine. J. Electr. Eng. Technol. 2019, 14, 2019–2025. [Google Scholar] [CrossRef]
- Song, C. Research on Full Digital Tension Control System for Winding Machine; Zhejiang University: Hangzhou, China, 2019. [Google Scholar]
- Xu, J.; Zhang, J.; Liu, M.; Yang, H. Research on Automatic Layout Control Technology of Automatic Transformer Winder. Comput. Meas. Control 2019, 27, 96–104. [Google Scholar]
- Li, X. Improvement of Synchronization Control Accuracy of Automatic Winding Machine. Electron. Technol. Softw. Eng. 2017, 116, 7. [Google Scholar]
- Peng, F.; Yang, X.; Peng, Z. Optimization of Winding Parameters of Accelerometer Coil Based on Uniform Design. J. New Ind. 2019, 9, 106–111. [Google Scholar]
- Wang, L. Research on the Control Method of High Follow-up Winder; Changchun University of Science and Technology: Changchun, China, 2018. [Google Scholar]
- Tang, S.; Zhang, Y.; Duan, H. Application of Frequency Conversion Technology in Winding Machine. Times Agricult. Mach. 2018, 45, 175–177. [Google Scholar]
- Gao, Y.; Zhu, Q. Design and Research of Precision Winding System. Autom. Instrum. 2017, 32, 69–72. [Google Scholar]
- Xie, Y. Study on Trajectory Planning and Winding Tension of Small Motor Stator Winding Robot; Harbin University of Science and Technology: Harbin, China, 2019. [Google Scholar]
- Liu, H.; Guo, J.; Sun, Y.; Ren, J. Two-axis Servo-controlled Winding Machine System. Electr. Drive. 2010, 40, 9–12. [Google Scholar]
- Wu, Q.; Liu, Z.; Zhang, B.; Qiu, M.; Zhou, W. Experimental Research on Tension Balance Control of Reciprocating Winding Diamond Wire Saw. Int. J. Adv. Manuf. Technol. 2017, 91, 423–431. [Google Scholar] [CrossRef]
- Wen, L.; Chen, Z.; Guo, R.; Shao, L. The Application of Variable Domain Fuzzy PID Control in AC Power Generation System. Electr. Mach. Control. Appl. 2020, 47, 34–41. [Google Scholar]
- Zhang, X.; Xu, M.; Zheng, D.; Li, Z. Simulation Analysis of BLDCM Based on Variable Domain Fuzzy PID Control. Small Spec. Electr. Mach. 2020, 48, 54–57. [Google Scholar]
- Cheng, L. Modeling of Magnetorheological Damper and Fuzzy Control of Automotive Semi-Active Suspension; Jiangsu University: Zhenjiang, China, 2020. [Google Scholar]
- Chen, J.; Cheng, S.; Xu, M. Motion Control Method of Agent Based on Fuzzy Control Theory. Aeronaut. Sci. Technol. 2019, 30, 74–78. [Google Scholar]
- Liu, J. Research on Three Intuitionistic Fuzzy Decision-Making Methods and Its Application in Man-Machine Task Assignment; Nanjing University: Nanjing, China, 2019. [Google Scholar]
- Nie, W.; Liu, W.; Chen, B. Application of Fuzzy Matrix Correlation Degree and Risk Preference in FMEA Decision Making. Stat. Decis. 2019, 5, 34–50. [Google Scholar]
- Guo, N.; Li, C.; Wang, D.; Zhang, N.; Song, L. Local Path Planning of Mobile Robot Based on Fuzzy Control. J. Shandong Univ. Technol. (Nat. Sci. Ed.) 2020, 34, 24–29. [Google Scholar]
- Diao, Q. Research and Application of Adaptive Motion Control System for Intelligent Vehicle; Chongqing University of Technology: Chongqing, China, 2019. [Google Scholar]

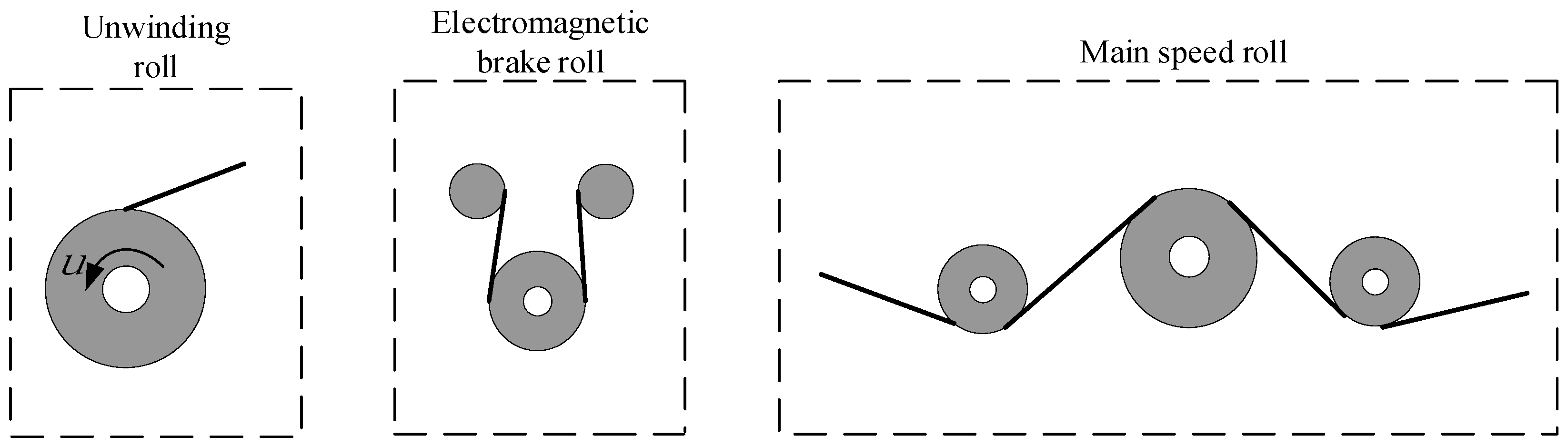








| Device | Characteristic |
|---|---|
| Unwinding roller | Apply small tension; Minimize tension deviations due to changes in velocity acceleration, radius, and inertia. |
| Electromagnetic brake roller | Apply high tension; Prevent the introduction of greater tension interference. |
| Main speed roller | Adjust the tension to get the target tension; |
| Adjust the speed and track the coil speed. |
| ∆e\e | NB | NM | NS | ZO | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| NB | NB | NB | NB | NB | NM | NM | NS |
| NM | NB | NB | NM | NM | NM | NS | NS |
| NS | NB | NM | NM | NS | NS | NS | ZO |
| ZO | NM | NM | NS | NS | ZO | PS | PS |
| PS | NS | NS | ZO | PS | PS | PM | PM |
| PM | PS | PS | PM | PM | PM | PB | PB |
| PB | PM | PM | PM | PB | PB | PB | PB |
| ∆e\e | NB | NM | NS | ZO | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| NB | NB | NB | NB | NB | NB | NB | NM |
| NM | NB | NB | NB | NB | NM | NM | NM |
| NS | NB | NM | NM | NS | NS | ZO | ZO |
| ZO | NS | NS | ZO | ZO | PS | PS | PM |
| PS | NS | NS | ZO | PS | PM | PM | PM |
| PM | PS | PS | PS | PM | PM | PM | PB |
| PB | PM | PM | PB | PB | PB | PB | PB |
| Parameter | Device | Numerical Value |
|---|---|---|
| The moment of inertia of the unwinding roller | ||
| The radius of the unwinding roller | ||
| The moment of inertia of the electromagnetic brake | ||
| The radius of the electromagnetic brake | ||
| The moment of inertia of the guide roller | ||
| The radius of the guide roller | ||
| Span | ||
| b | Friction coefficient | 0.0015 |
| L | Unwinding length |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, L.; Suo, H.; Ren, H. Design of Insulation Tape Tension Control System of Transformer Winding Machine Based on Fuzzy PID. Sensors 2021, 21, 6512. https://doi.org/10.3390/s21196512
Deng L, Suo H, Ren H. Design of Insulation Tape Tension Control System of Transformer Winding Machine Based on Fuzzy PID. Sensors. 2021; 21(19):6512. https://doi.org/10.3390/s21196512
Chicago/Turabian StyleDeng, Liwei, Hongfei Suo, and Haonan Ren. 2021. "Design of Insulation Tape Tension Control System of Transformer Winding Machine Based on Fuzzy PID" Sensors 21, no. 19: 6512. https://doi.org/10.3390/s21196512
APA StyleDeng, L., Suo, H., & Ren, H. (2021). Design of Insulation Tape Tension Control System of Transformer Winding Machine Based on Fuzzy PID. Sensors, 21(19), 6512. https://doi.org/10.3390/s21196512







