Efficient Optical Sensing Based on Phase Shift of Waves Supported by a One-Dimensional Photonic Crystal
Abstract
:1. Introduction
2. Theoretical Model
2.1. Material Characterization
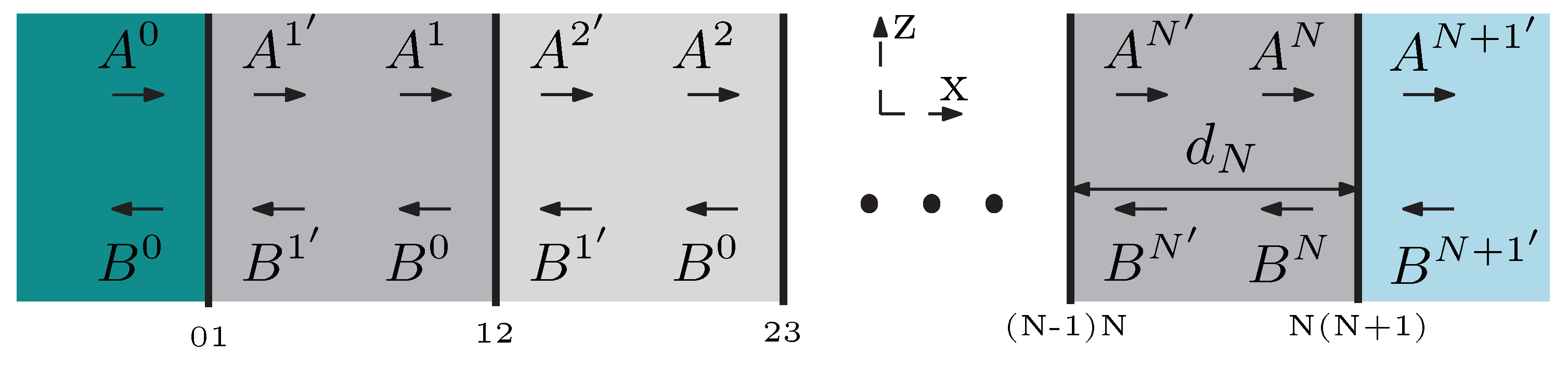
2.2. Matrix Formalism
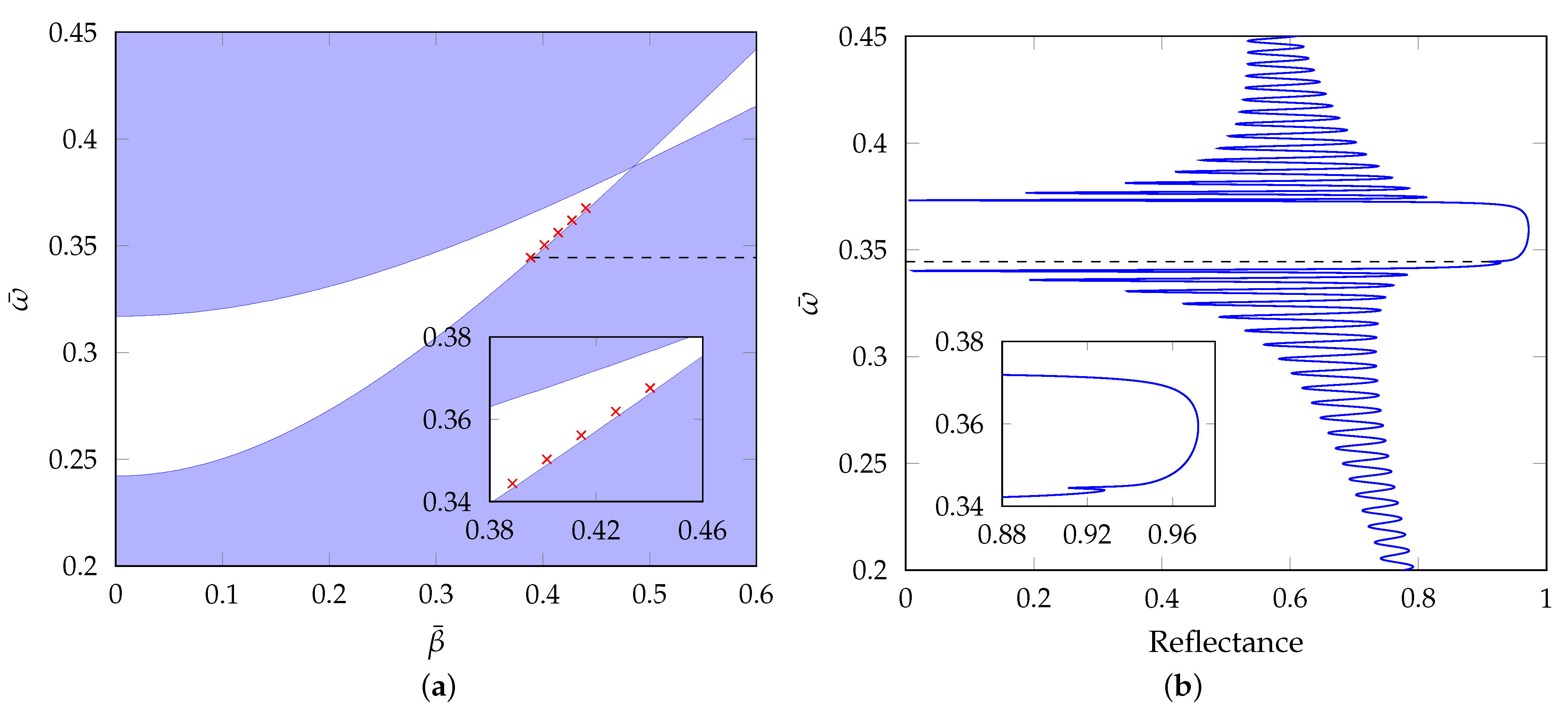
2.3. Band Structure
3. Theoretical Results
4. Experimental Set-Up
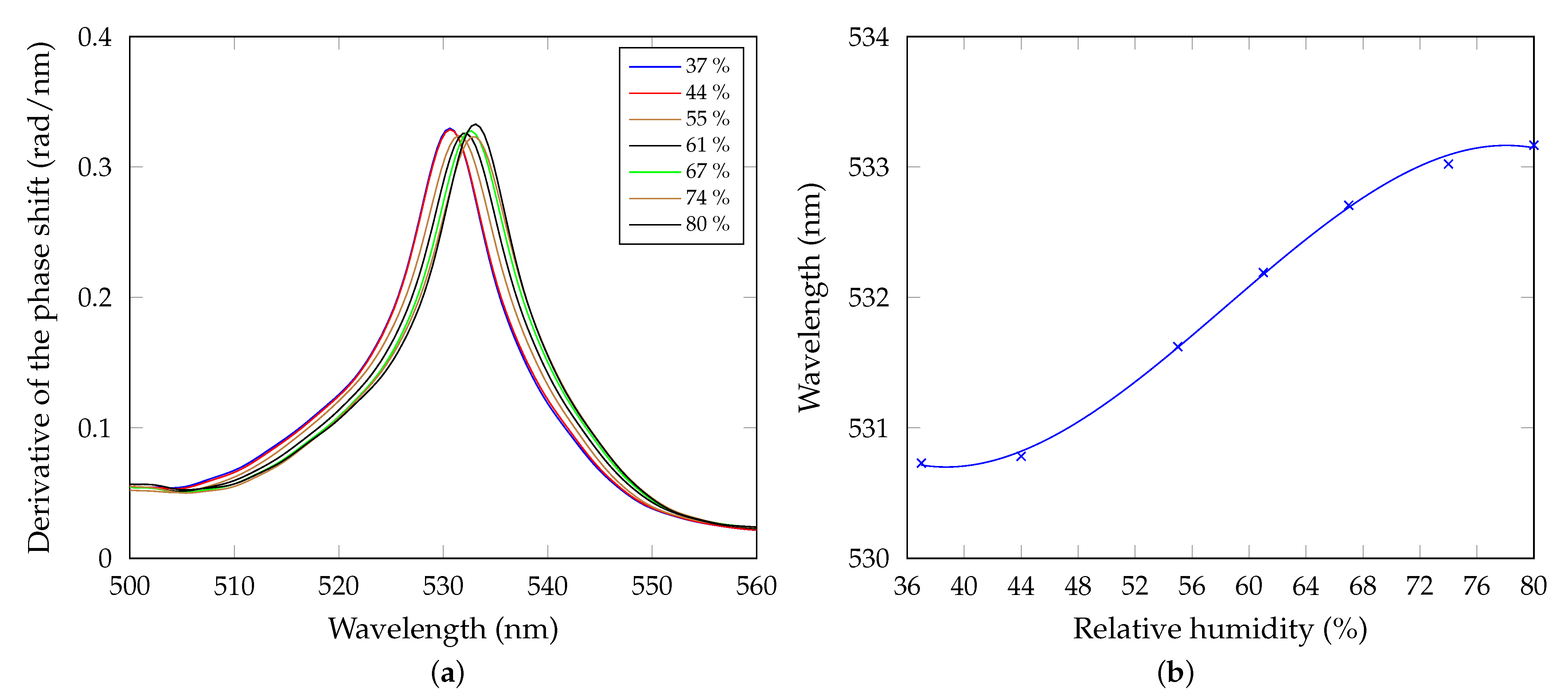
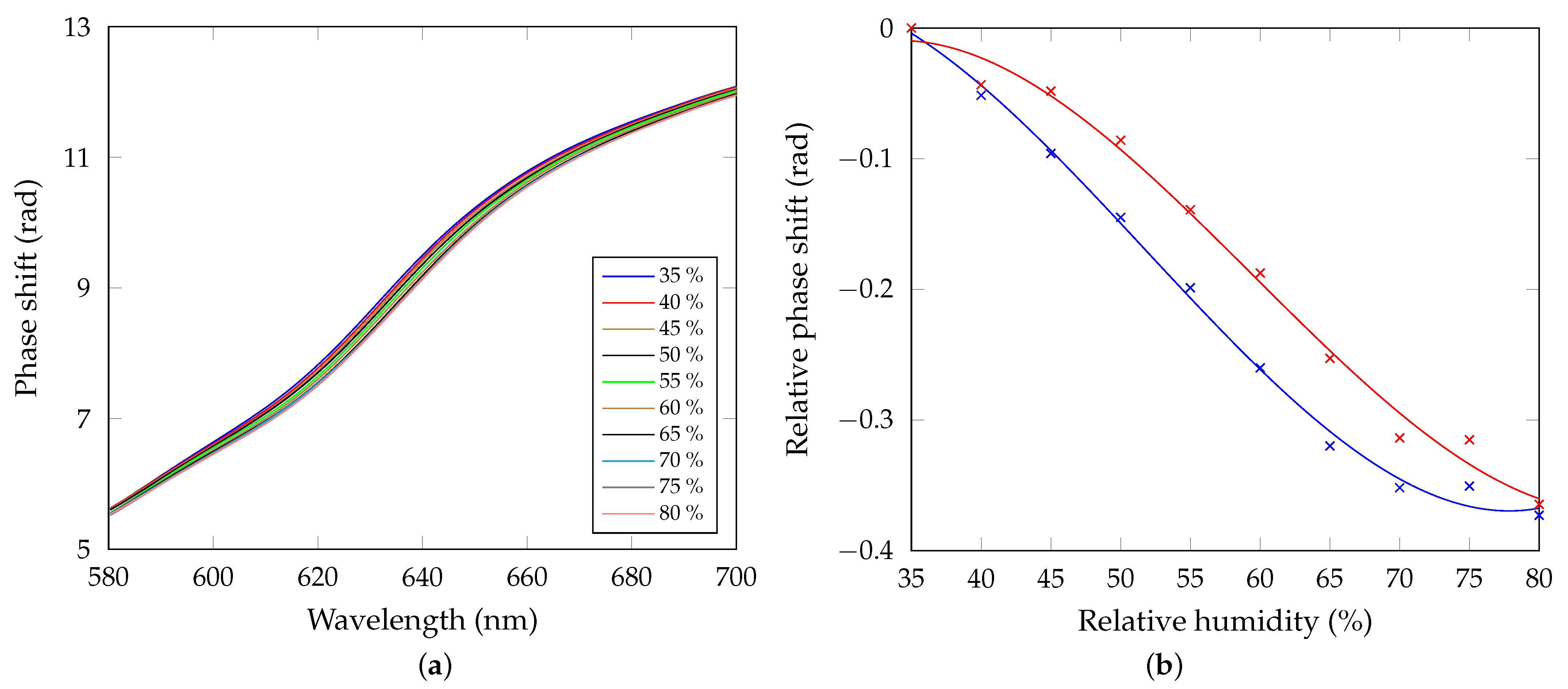
5. Experimental Results
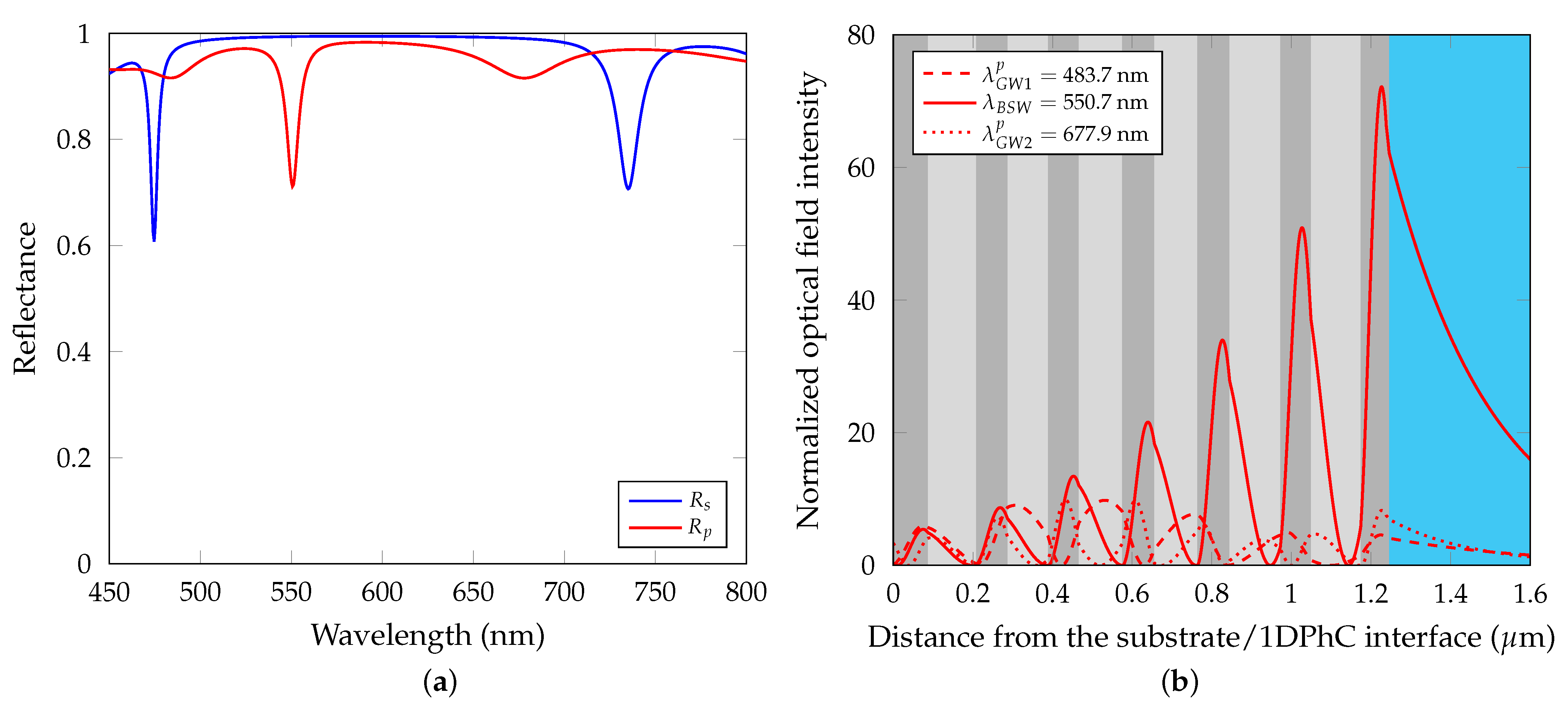
5.1. The BSW-Based Response
5.2. The GW-Based Response
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Meade, R.D.; Brommer, K.D.; Rappe, A.M.; Joannopoulos, J.D. Electromagnetic Bloch waves at the surface of a photonic crystal. Phys. Rev. B 1991, 44, 10961–10964. [Google Scholar] [CrossRef] [PubMed]
- Robertson, W.M.; Arjavalingam, G.; Meade, R.D.; Brommer, K.D.; Rappe, A.M.; Joannopoulos, J.D. Observation of surface photons on periodic dielectric arrays. Opt. Lett. 1993, 18, 528–530. [Google Scholar] [CrossRef] [Green Version]
- MacLeod, H. Thin-Film Optical Filters; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Lee, K.J.; Wawro, D.; Priambodo, P.S.; Magnusson, R. Agarose-gel based guided-mode resonance humidity sensor. IEEE Sens. J. 2007, 7, 409–414. [Google Scholar] [CrossRef]
- We, Z.; Huang, J.; Li, J.; Li, J.; Liu, X.; Ni, X. A compact double-folded substrate integrated waveguide re-entrant cavity for highly sensitive humidity sensing. Sensors 2019, 19, 3308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di Palma, P.; Sansone, L.; Taddei, C.; Campopiano, S.; Iadiciccoi, A. Fiber optic probe based on self-assembled photonic crystal for relative humidity sensing. J. Light. Technol. 2019, 37, 4610–4618. [Google Scholar] [CrossRef]
- Gryga, M.; Ciprian, D.; Hlubina, P. Guided-mode resonance based humidity sensing using a multilayer dielectric structure. Opt. Express 2020, 28, 28954–28960. [Google Scholar] [CrossRef] [PubMed]
- Guillermain, E.; Lysenko, V.; Orobtchouk, R.; Benyattou, T.; Roux, S.; Pillonnet, A.; Perriat, P. Bragg surface wave device based on porous silicon and its application for sensing. Appl. Phys. Lett. 2007, 90, 241116. [Google Scholar] [CrossRef]
- Farmer, A.; Friedli, A.C.; Wright, S.M.; Robertson, W.M. Biosensing using surface electromagnetic waves in photonic band gap multilayers. Sens. Actuators B Chem. 2012, 173, 79–84. [Google Scholar] [CrossRef]
- Kang, X.B.; Wen, L.; Wang, Z.G. Design of guided Bloch surface wave resonance bio-sensors with high sensitivity. Opt. Commun. 2017, 383, 531–536. [Google Scholar] [CrossRef]
- Kovalevich, T.; Belharet, D.; Robert, L.; Ulliac, G.; Kim, M.S.; Herzig, H.P.; Grosjean, T.; Bernal, M.P. Bloch surface waves at the telecommunicationwavelength with Lithium Niobate as top layer for integrated optics. Appl. Opt. 2019, 58, 1757–1762. [Google Scholar] [CrossRef] [Green Version]
- Kong, W.; Zheng, Z.; Wan, Y.; Li, S.; Liu, J. High-sensitivity sensing based on intensity-interrogated Bloch surface wave sensors. Sens. Actuators B Chem. 2014, 193, 467–471. [Google Scholar] [CrossRef]
- Deng, C.Z.; Ho, Y.L.; Lee, Y.C.; Wang, Z.; Tai, Y.H.; Zyskowski, M.; Daiguji, H.; Delaunay, J.J. Two-pair multilayer Bloch surface wave platform in the near- and mid-infrared regions. Appl. Phys. Lett. 2019, 115, 091102. [Google Scholar] [CrossRef]
- Gan, S.; Wang, H.; Liang, J.; Dai, X.; Xiang, Y. Ultra-Sensitive Refractive Index Sensors Based on Bloch Surface Waves With Transition Metal Dichalcogenides. IEEE Sens. J. 2019, 19, 8675–8680. [Google Scholar] [CrossRef]
- Gryga, M.; Vala, D.; Kolejak, P.; Gembalova, L.; Ciprian, D.; Hlubina, P. One-dimensional photonic crystal for Bloch surface waves and radiation modes based sensing. Opt. Mater. Express 2019, 9, 4009–4022. [Google Scholar] [CrossRef]
- Gryga, M.; Ciprian, D.; Hlubina, P. Bloch surface wave resonance based sensors as an alternative to surface plasmon resonance sensors. Sensors 2020, 20, 5119. [Google Scholar] [CrossRef] [PubMed]
- Gryga, M.; Ciprian, D.; Gembalova, L.; Hlubina, P. Sensing based on Bloch surface wave and self-referenced guided mode resonances employing a one-dimensional photonic crystal. Opt. Express 2021, 29, 12996–13010. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.K.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 1801433. [Google Scholar] [CrossRef]
- Arafat, M.M.; Dinan, B.; Akba, S.A.; Haseeb, A.S.M.A. Gas Sensors Based on One Dimensional Nanostructured Metal-Oxides: A Review. Sensors 2012, 12, 7207–7258. [Google Scholar] [CrossRef]
- Sharma, A.; Tomar, M.; Gupta, V. Room temperature trace level detection of NO2 gas using SnO2 modified carbon nanotubes based sensor. J. Mater. Chem. 2012, 22, 23608–23616. [Google Scholar] [CrossRef]
- Tyagi, P.; Sharma, A.; Tomar, M.; Gupta, V. Metal oxide catalyst assisted SnO2 thin film based SO2 gas sensor. Sens. Actuators B Chem. 2016, 224, 282–289. [Google Scholar] [CrossRef]
- Sinibaldi, A.; Rizzo, R.; Figliozzi, G.; Descrovi, E.; Danz, N.; Munzert, P.; Anopchenko, A.; Michelotti, F. A full ellipsometric approach to optical sensing with Bloch surface waves on photonic crystals. Opt. Express 2013, 21, 23331–23344. [Google Scholar] [CrossRef]
- Li, Y.; Yang, T.; Song, S.; Pang, Z.; Du, G. Phase properties of Bloch surface waves and their sensing applications. Appl. Phys. Lett. 2013, 103, 041116. [Google Scholar] [CrossRef]
- Li, Y.; Yang, T.; Pang, Z.; Du, G.; Song, S. Phase-sensitive Bloch surface wave sensor based on variable angle spectroscopic ellipsometry. Opt. Express 2014, 22, 21403–21410. [Google Scholar] [CrossRef]
- Watad, I.; Jabalee, M.A.; Aizen, A.; Abdulhalim, I. Critical angle based sensor with improved figure of merit using dip detection. Opt. Lett. 2015, 40, 4388–4391. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Zheng, Z.; Cheng, M.; Kong, W.; Liu, K. Polarimetric-Phase-Enhanced Intensity Interrogation Scheme for Surface Wave Optical Sensors with Low Optical Loss. Sensors 2018, 18, 3262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hlubina, P.; Gryga, M.; Ciprian, D.; Pokorny, P.; Gembalova, L.; Sobota, J. High performance liquid analyte sensing based on Bloch surface wave resonances in the spectral domain. Opt. Laser Technol. 2022, 145, 107492. [Google Scholar] [CrossRef]
- Mehrabani, S.; Kwong, P.; Gupta, M.; Arman, A. Hybrid microcavity humidity sensor. Appl. Phys. Lett. 2013, 102, 241101. [Google Scholar] [CrossRef]
- Urbancova, P.; Chylek, J.; Hlubina, P.; Pudis, D. Guided-Mode Resonance-Based Relative Humidity Sensing Employing a Planar Waveguide Structure. Sensors 2020, 20, 6788. [Google Scholar] [CrossRef]
- Peng, J.; Wang, W.; Qu, Y.; Sun, T.; Lv, D.; Dai, J.; Yang, M. Thin films based one-dimensional photonic crystal for humidity detection. Sens. Actuators A Phys. 2017, 263, 209–215. [Google Scholar] [CrossRef]
- Fuentes, O.; Corres, J.M.; Matias, I.R.; Villar, I. Generation of Lossy Mode Resonances in Planar Waveguides Toward Development of Humidity Sensors. J. Light. Technol. 2019, 37, 2300–2306. [Google Scholar] [CrossRef]
- Bohorquez, D.L.; Villar, I.; Corres, J.M.; Matias, I.R. Generation of lossy mode resonances in a broadband range with multilayer coated coverslips optimized for humidity sensing. Sens. Actuators B Chem. 2020, 325, 128795. [Google Scholar] [CrossRef]
- Deng, S.; Wang, P.; Yu, X. Phase-sensitive surface plasmon resonance sensors: Recent progress and future prospects. Sensors 2017, 17, 2819. [Google Scholar] [CrossRef] [Green Version]
- Watad, I.; Abdulhalim, I. Spectropolarimetric surface plasmon resonance sensor and the selection of the best polarimetric function. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 4600609. [Google Scholar] [CrossRef]
- Yesilkoy, F.; Terborg, R.A.; Pello, J.; Belushkin, A.A.; Jahani, Y.; Pruneri, V.; Altug, H. Phase-sensitive plasmonic biosensor using a portable and large field-of-view interferometric microarray imager. Light Sci. Appl. 2018, 7, 17152. [Google Scholar] [CrossRef]
- Wang, D.; Loo, J.F.C.; Chen, J.; Yam, Y.; Chen, S.C.; He, H.; Kong, S.K.; Ho, H.P. Recent advances in surface plasmon resonance imaging sensors. Sensors 2019, 19, 1266. [Google Scholar] [CrossRef] [Green Version]
- Watad, I.; Abdulhalim, I. Phase-shifted polarimetric surface plasmon resonance sensor using a liquid crystal retarder and a diverging beam. Opt. Lett. 2019, 44, 1607–1610. [Google Scholar] [CrossRef]
- Barth, I.; Conteduca, D.; Reardon, C.; Johnson, S.; Krauss, T.F. Common-path interferometric label-free protein sensing with resonant dielectric nanostructures. Light Sci. Appl. 2020, 9, 96. [Google Scholar] [CrossRef] [PubMed]
- Abutoama, M.; Abuleil, M.; Abdulhalim, I. Resonant Subwavelength and Nano-Scale Grating Structures for Biosensing Application: A Comparative Study. Sensors 2021, 21, 4523. [Google Scholar] [CrossRef] [PubMed]
- Polyanskiy, M.N. Refractive Index Database. Available online: http://refractiveindex.info (accessed on 27 September 2021).
- Ciddor, P. Refractive index of air: New equations for the visible and near infrared. Appl. Opt. 1996, 35, 1566–1573. [Google Scholar] [CrossRef] [PubMed]
- Mouchet, S.; Deparis, O.; Vigneron, J.P. Unexplained high sensitivity of the reectance of porous natural photonic structures to the presence of gases and vapours in the atmosphere. Proc. SPIE 2012, 8424, 842425. [Google Scholar]
- Du, B.; Yang, D.; Ruan, Y.; Jia, P.; Ebendorff-Heidepriem, H. Compact plasmonic fiber tip for sensitive and fast humidity and human breath monitoring. Opt. Lett. 2020, 45, 985–988. [Google Scholar] [CrossRef] [PubMed]
- Daimon, M.; Masumura, A. Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region. Appl. Opt. 2007, 46, 3811–3820. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P. Optical Waves in Layered Media; John Wiley and Sons, Inc.: Somerset, NJ, USA, 2005. [Google Scholar]
- Pettersson, L.A.A.; Roman, L.S.; Inganäs, O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys. 1999, 86, 487–496. [Google Scholar] [CrossRef]
- Kaňok, R.; Ciprian, D.; Hlubina, P. Surface plasmon resonance-based sensing utilizing spatial phase modulation in an imaging interferometer. Sensors 2020, 20, 1616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hlubina, P.; Duliakova, M.; Kadulova, M.; Ciprian, D. Spectral interferometry-based surface plasmon resonance sensor. Opt. Commun. 2015, 354, 240–245. [Google Scholar] [CrossRef]
- D’Amico, A.; Natale, C.D. A contribution on some basic definitions of sensors properties. IEEE Sens. J. 2001, 1, 183–190. [Google Scholar] [CrossRef]

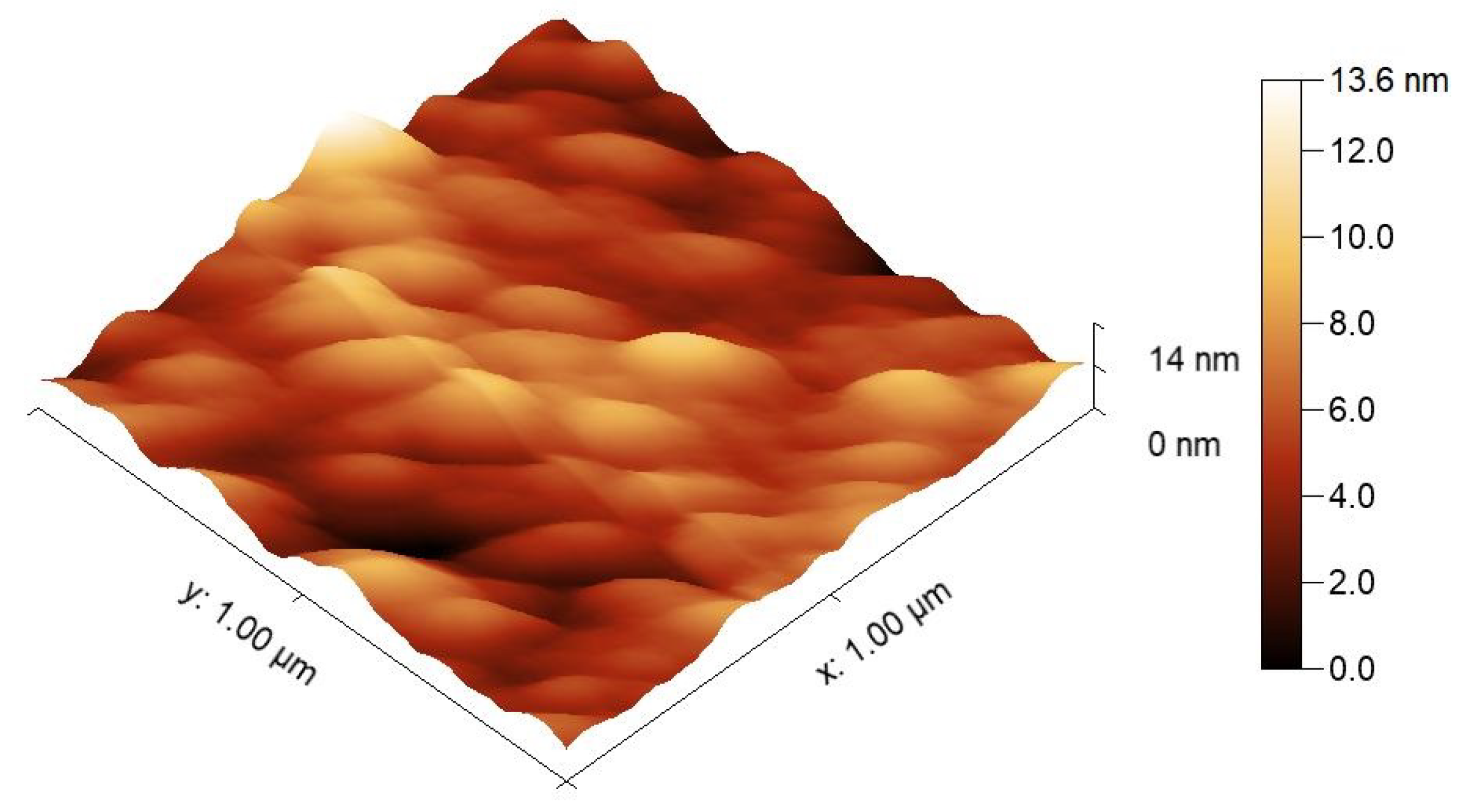






| Layer | Thickness (nm) | Layer | Thickness (nm) |
|---|---|---|---|
| 87.65 | 120.21 | ||
| 79.09 | 101.75 | ||
| 77.28 | 109.24 | ||
| 80.74 | 108 | ||
| 80.89 | 127.3 | ||
| 76.85 | 125.02 | ||
| 64.41 | 6.96 |
| Material | Method | RH Range | Sensitivity (nm/%RH) | Ref. |
|---|---|---|---|---|
| plasmonic multilayer | surface plasmon wave resonance | 20–80% | 0.072 | [16] |
| dielectric multilayer | surface Bloch wave resonance | 22–80% | 0.065 | [16] |
| polymer coating | whispering gallery mode resonance | 0–60% | 0.013 | [28] |
| agarose gel | guided mode resonance | 20–80% | 0.150 | [4] |
| porous thin film | photonic crystal mode resonance | 11–84% | 0.296 | [30] |
| indium tin oxide | lossy mode resonance | 65–90% | 0.212 | [31] |
| copper oxide | lossy mode resonance | 30–90% | 0.636 | [32] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaňok, R.; Hlubina, P.; Gembalová, L.; Ciprian, D. Efficient Optical Sensing Based on Phase Shift of Waves Supported by a One-Dimensional Photonic Crystal. Sensors 2021, 21, 6535. https://doi.org/10.3390/s21196535
Kaňok R, Hlubina P, Gembalová L, Ciprian D. Efficient Optical Sensing Based on Phase Shift of Waves Supported by a One-Dimensional Photonic Crystal. Sensors. 2021; 21(19):6535. https://doi.org/10.3390/s21196535
Chicago/Turabian StyleKaňok, Roman, Petr Hlubina, Lucie Gembalová, and Dalibor Ciprian. 2021. "Efficient Optical Sensing Based on Phase Shift of Waves Supported by a One-Dimensional Photonic Crystal" Sensors 21, no. 19: 6535. https://doi.org/10.3390/s21196535
APA StyleKaňok, R., Hlubina, P., Gembalová, L., & Ciprian, D. (2021). Efficient Optical Sensing Based on Phase Shift of Waves Supported by a One-Dimensional Photonic Crystal. Sensors, 21(19), 6535. https://doi.org/10.3390/s21196535






