Motion-Encoded Electric Charged Particles Optimization for Moving Target Search Using Unmanned Aerial Vehicles
Abstract
:1. Introduction
- -
- The formulation of the optimization problem with a suitable objective function and the required constraints represents the targeted problem accurately.
- -
- The use of motion-encoding mechanism with ECPO to increase the efficacy of the algorithm. This duo has neither been tried before in the literature nor in solving any optimization problems.
- -
- Comparing the proposed mechanism with 10 commonly used metaheuristic optimization algorithms strengthens the logic of using it in moving target search applications. It is also compared with MPSO, used in a recently published research paper to solve a similar optimization problem.
- -
- The presentation of the convergence curves for all the used optimization methods in a single plot to ease the comparison of their performance.
2. Problem Formulation
2.1. Target Model
2.2. Sensor Model
2.3. Belief Map Update
2.4. Objective Function
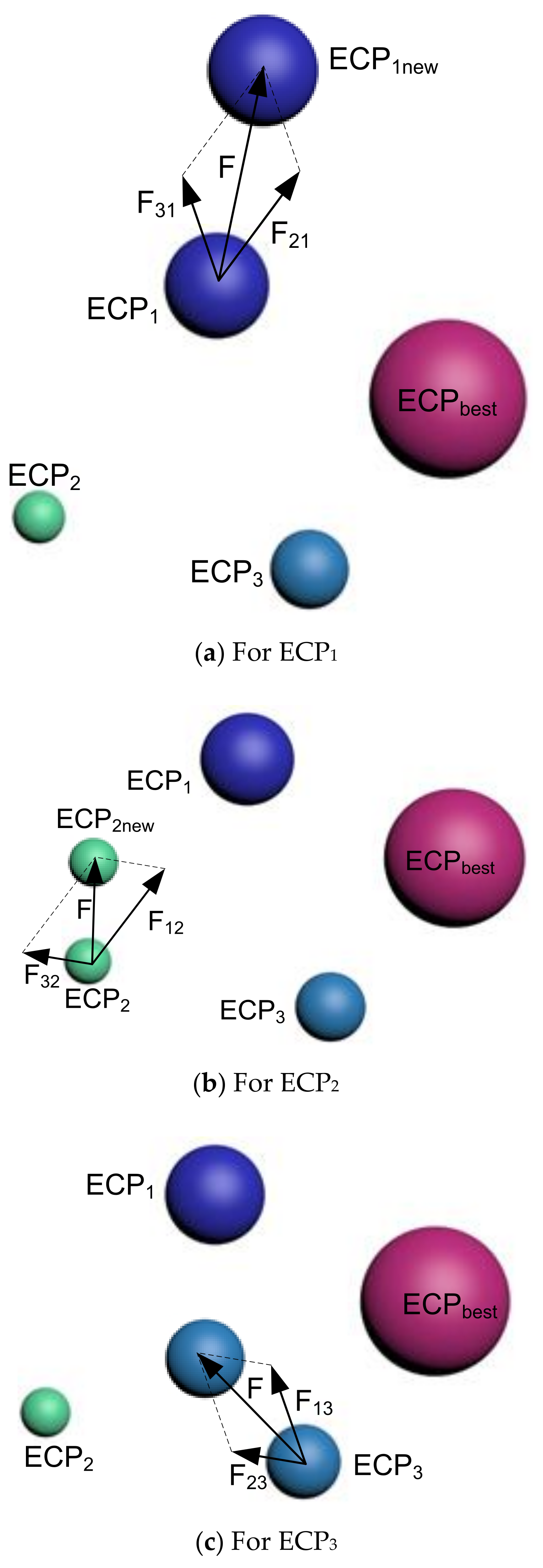
3. Motion-Encoded Electric Charged Particles Optimization (ECPO-ME) Algorithm
3.1. Description
- nECP: the total number of ECPs,
- MaxITER: the maximum number of iterations,
- nECPI: the number of ECPs which are interacting with themselves in one of the three strategies,
- naECP: the archive pool size.
3.2. Pseudocode
| Algorithm 1 ECPO pseudocode |
|
3.3. Algorithm
3.3.1. Initialization
3.3.2. Archive Pool
3.3.3. Selection
3.3.4. Interaction
Strategy 1
Strategy 2
Strategy 3
3.3.5. Checking the Bounds
3.3.6. Diversification
3.3.7. Diversification
| Algorithm 2 Pseudocode for the diversification phase |
| 1 For 2 For 3 4 select a random ECP from the archive pool (k) 5 6 End If 7 End For |
3.3.8. Population Update
3.3.9. Criteria for Termination
3.3.10. Constraint Handling
3.3.11. Motion Encoding (ME)
4. Application, Results, and Discussion
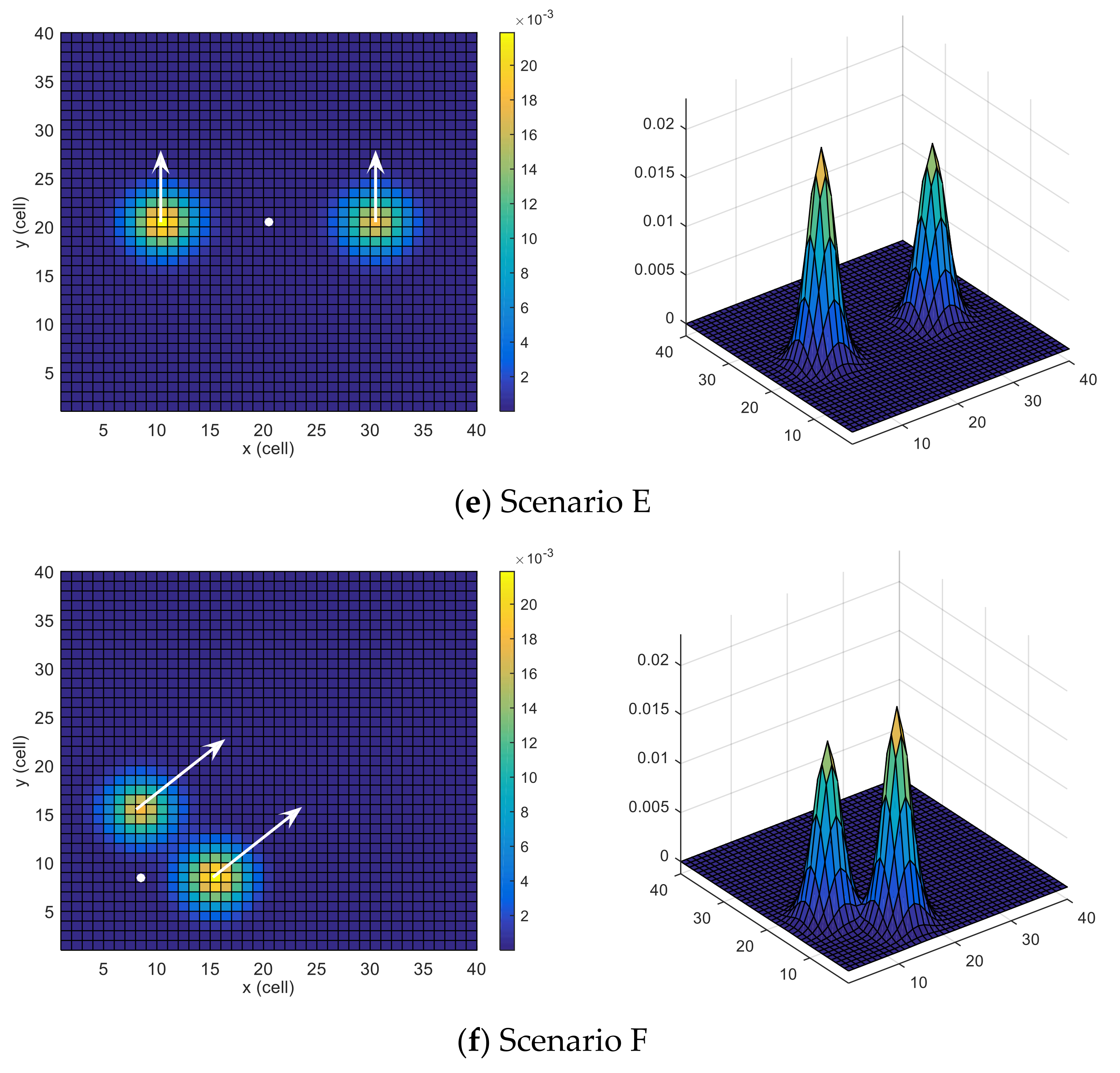
4.1. Scenarios
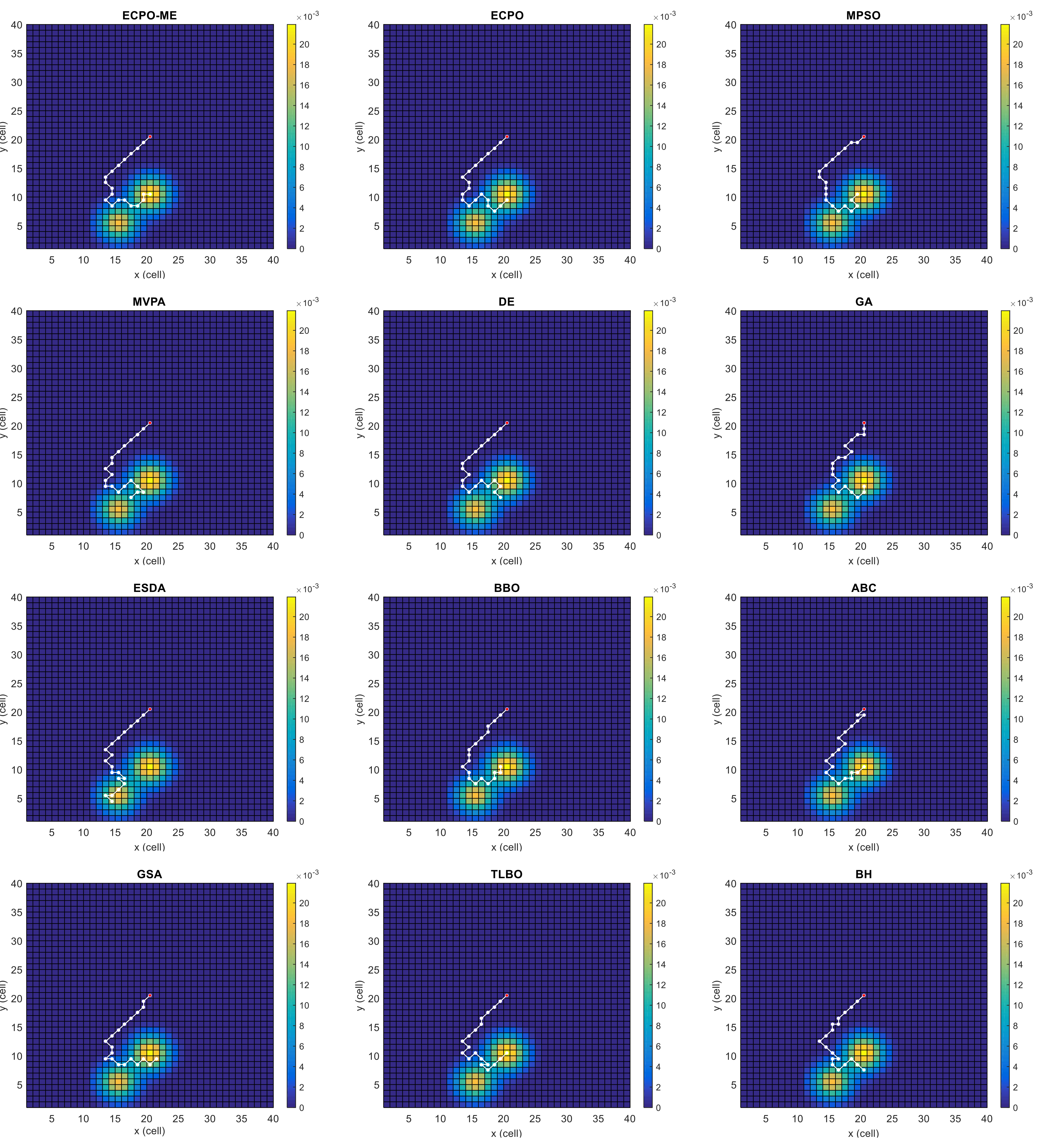
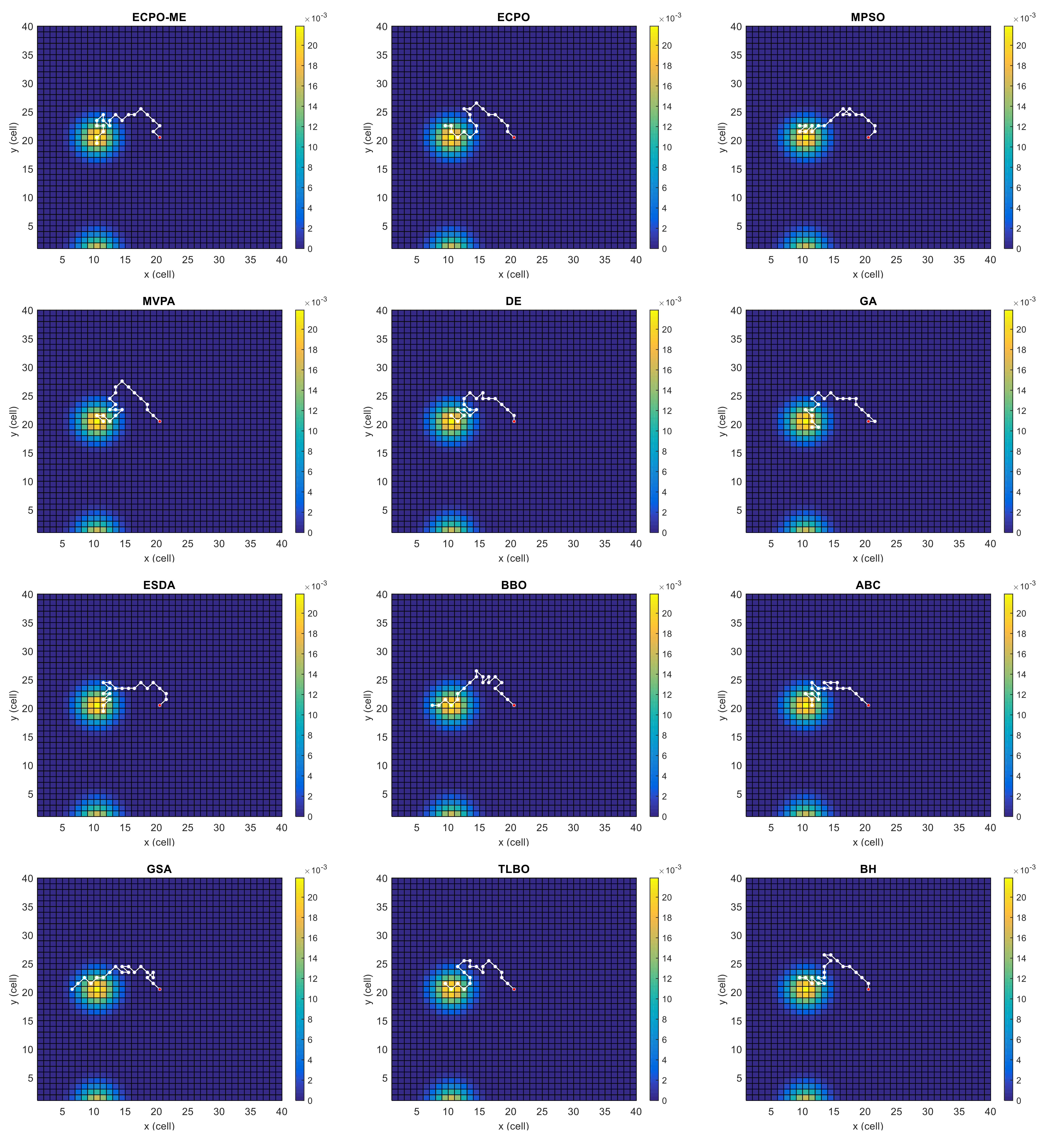
4.2. Comparing Algorithms
4.3. Results
- -
- For Scenario A, the proposed ECPO-ME algorithm obtained the best results for the ‘BEST’, the ‘MEAN’ and, the ‘MEDIAN values. The TLBO algorithm obtained the highest ‘WORST’ and ‘SD’ Values.
- -
- For Scenario B, the TLBO obtained a slightly better value than the ECPO-ME in terms of the ‘BEST’ values. However, the ECPO-ME obtained the best results of the ‘MEAN’, the ‘MEDIAN, the ‘WORST’ and the ‘SD’ values compared to the remaining algorithms.
- -
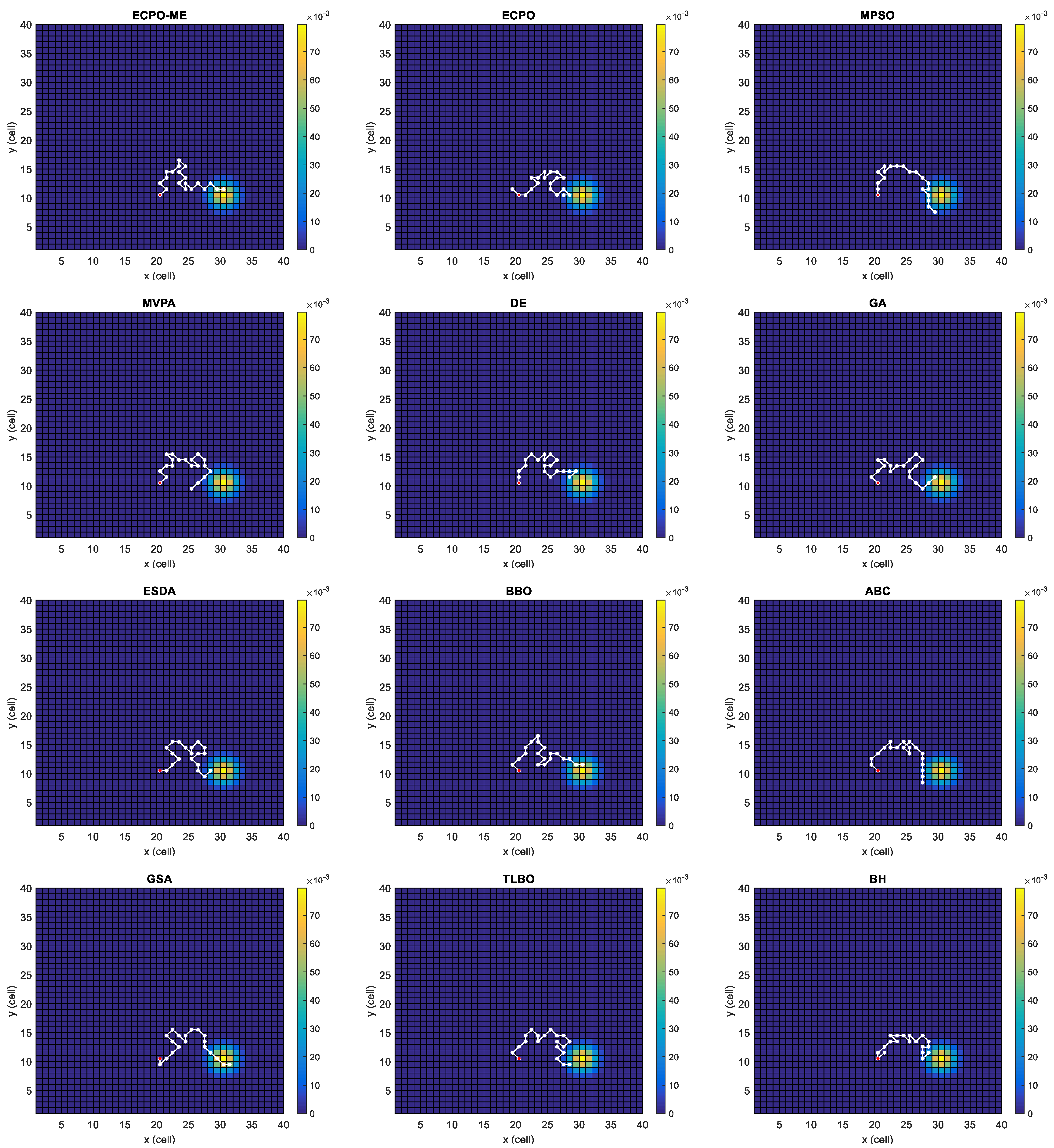
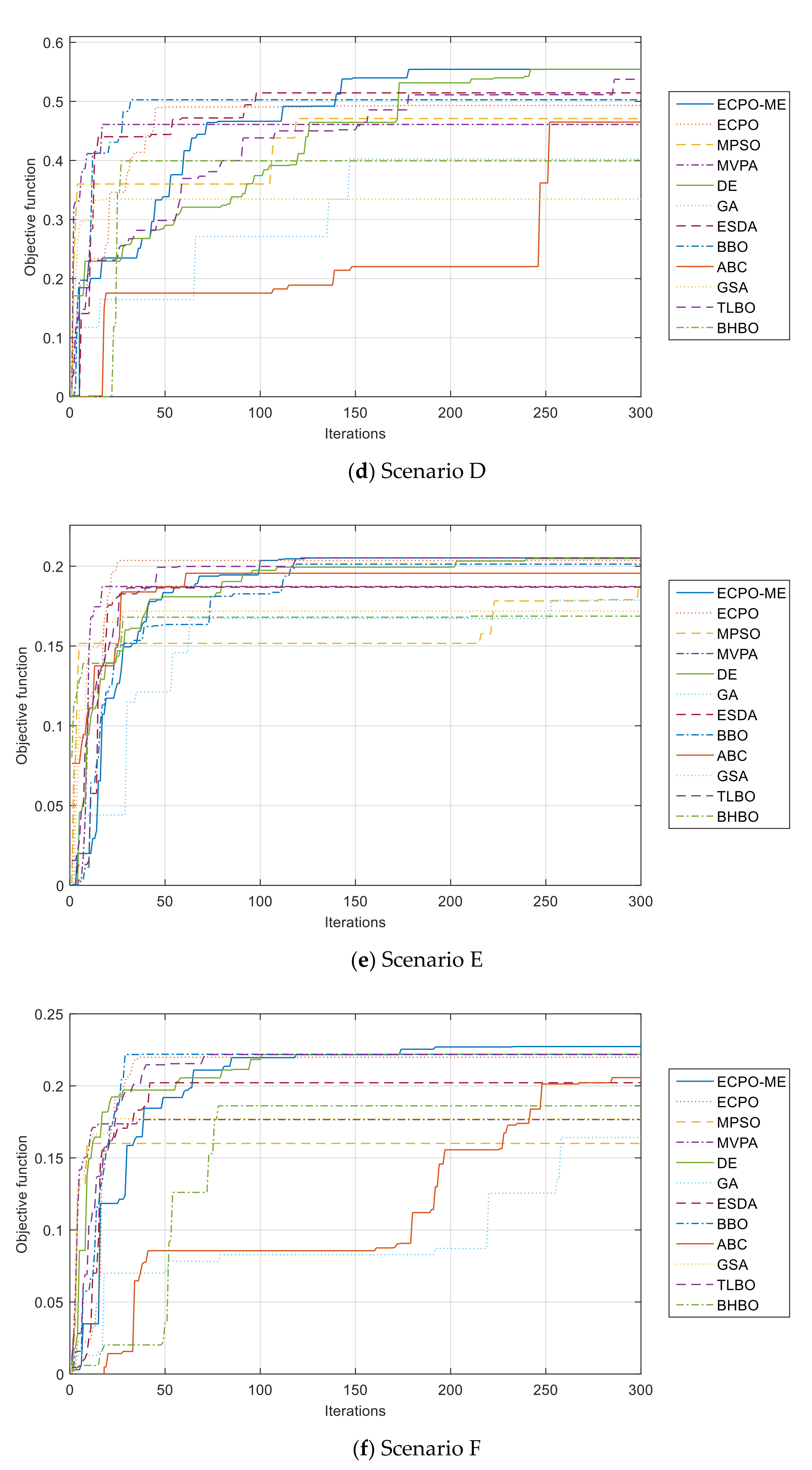
- For Scenario C and Scenario D, the proposed ECPO-ME outperformed the other algorithms in terms of the statistical performance indicators used in this study. It is worth mentioning that the DE achieved equally good results to ECPO-ME in terms of the ‘BEST’ values.
- -
- For Scenario E, the proposed ECPO-ME showed better performance than all the remaining algorithms in terms of the ‘BEST’, the ‘MEAN’ and the ‘MEDIAN values while the DE achieved better results in terms of the ‘WORST’ and the ‘SD’ values.
- -
- For Scenario F, the proposed ECPO-ME achieved a better result than all the remaining algorithms in terms of the ‘BEST’, the ‘MEDIAN’ and the ‘WORST’ values, while the TLBO was better in terms of the ‘MEAN’ and ‘SD’ values.
- -
- All algorithms gave an FR equal to 100, which reflects that all of them could find a solution (i.e., a path) in all the runs and for all the investigated scenarios except for the ABC algorithm for Scenario D (FR = 93.33%).
- -
- For scenarios with high probability regions, like Scenario C and Scenario D, the likelihood of finding the target is higher because there is no need to divide or spread the chances of finding the target in other areas.
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Huo, L.; Zhu, J.; Li, Z.; Ma, M. A Hybrid Differential Symbiotic Organisms Search Algorithm for UAV Path Planning. Sensors 2021, 21, 3037. [Google Scholar] [CrossRef] [PubMed]
- Jayaweera, H.M.P.C.; Hanoun, S. UAV Path Planning for Reconnaissance and Look-Ahead Coverage Support for Mobile Ground Vehicles. Sensors 2021, 21, 4595. [Google Scholar] [CrossRef]
- Behjati, M.; Mohd Noh, A.B.; Alobaidy, H.A.H.; Zulkifley, M.A.; Nordin, R.; Abdullah, N.F. LoRa Communications as an Enabler for Internet of Drones towards Large-Scale Livestock Monitoring in Rural Farms. Sensors 2021, 21, 5044. [Google Scholar] [CrossRef]
- Liu, Y.; Qiu, M.; Hu, J.; Yu, H. Incentive UAV-Enabled Mobile Edge Computing Based on Microwave Power Transmission. IEEE Access 2020, 8, 28584–28593. [Google Scholar] [CrossRef]
- Ochoa, S.F.; Santos, R. Human-centric wireless sensor networks to improve information availability during urban search and rescue activities. Inf. Fusion 2015, 22, 71–84. [Google Scholar] [CrossRef]
- Bourgault, F.; Furukawa, T.; Durrant-Whyte, H.F. Optimal search for a lost target in a Bayesian world. Springer Tracts Adv. Robot. 2006, 24, 209–222. [Google Scholar] [CrossRef]
- Raap, M.; Meyer-Nieberg, S.; Pickl, S.; Zsifkovits, M. Aerial Vehicle Search-Path Optimization: A Novel Method for Emergency Operations. J. Optim. Theory Appl. 2017, 172, 965–983. [Google Scholar] [CrossRef]
- Lanillos, P.; Yañez-Zuluaga, J.; Ruz, J.J.; Besada-Portas, E. A Bayesian approach for constrained multi-agent minimum time search in uncertain dynamic domains. In Proceedings of the GECCO 2013 Genetic and Evolutionary Computation Conference, Amsterdam, The Netherlands, 6–10 July 2013; pp. 391–398. [Google Scholar]
- Chen, S.; Xiong, G.; Chen, H.; Negrut, D. MPC-based path tracking with PID speed control for high-speed autonomous vehicles considering time-optimal travel. J. Cent. South Univ. 2020, 27, 3702–3720. [Google Scholar] [CrossRef]
- Jiang, K.; Yang, D.; Liu, C.; Zhang, T.; Xiao, Z. A Flexible Multi-Layer Map Model Designed for Lane-Level Route Planning in Autonomous Vehicles. Engineering 2019, 5, 305–318. [Google Scholar] [CrossRef]
- Sujit, P.B.; Ghose, D. Self assessment-based decision making for multiagent cooperative search. IEEE Trans. Autom. Sci. Eng. 2011, 8, 705–719. [Google Scholar] [CrossRef]
- Hu, J.; Xie, L.; Lum, K.Y.; Xu, J. Multiagent information fusion and cooperative control in target search. IEEE Trans. Control Syst. Technol. 2013, 21, 1223–1235. [Google Scholar] [CrossRef]
- Furukawa, T.; Bourgault, F.; Lavis, B.; Durrant-Whyte, H.F. Recursive Bayesian search-and-tracking using coordinated UAVs for lost targets. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; Volume 2006, pp. 2521–2526. [Google Scholar]
- Perez-Carabaza, S.; Besada-Portas, E.; Lopez-Orozco, J.A.; de la Cruz, J.M. Ant colony optimization for multi-UAV minimum time search in uncertain domains. Appl. Soft Comput. J. 2018, 62, 789–806. [Google Scholar] [CrossRef]
- Trummel, K.E.; Weisinger, J.R. Complexity of the optimal searcher path problem. Oper. Res. 1986, 34, 324–327. [Google Scholar] [CrossRef] [Green Version]
- Bernstein, D.S.; Givan, R.; Immerman, N.; Zilberstein, S. The complexity of decentralized control of Markov decision processes. Math. Oper. Res. 2002, 27, 819–840. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Eagle, J.N.; Yee, J.R. Optimal branch-and-bound procedure for the constrained path, moving target search problem. Oper. Res. 1990, 38, 110–114. [Google Scholar] [CrossRef] [Green Version]
- Lanillos, P.; Besada-Portas, E.; Pajares, G.; Ruz, J.J. Minimum time search for lost targets using cross entropy optimization. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, Portugal, 7–12 October 2012; pp. 602–609. [Google Scholar]
- Gan, S.K.; Sukkarieh, S. Multi-UAV target search using explicit decentralized gradient-based negotiation. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 751–756. [Google Scholar]
- Mathews, G.; Durrant-Whyte, H.; Prokopenko, M. Asynchronous gradient-based optimisation for team decision making. In Proceedings of the IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3145–3150. [Google Scholar]
- Sarmiento, A.; Murrieta-Cid, R.; Hutchinson, S. An efficient motion strategy to compute expected-time locally optimal continuous search paths in known environments. Adv. Robot. 2009, 23, 1533–1560. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.; Tang, G.; Xie, D.; Han, L. Three-dimensional neural network tracking control of autonomous underwater vehicles with input saturation. J. Cent. South Univ. 2020, 27, 1754–1769. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Motion-encoded particle swarm optimization for moving target search using UAVs. Appl. Soft Comput. 2020, 97, 106705. [Google Scholar] [CrossRef]
- Qiming, Z.; Husheng, W.; Zhaowang, F. A review of intelligent optimization algorithm applied to unmanned aerial vehicle swarm search task. In Proceedings of the 2021 11th International Conference on Information Science and Technology (ICIST), Chengdu, China, 21–23 May 2021; pp. 383–393. [Google Scholar]
- Bouchekara, H.R.E.H. Electric Charged Particles Optimization and Its Application to the Optimal Design of a Circular Antenna Array; Springer: Dordrecht, The Netherlands, 2020; ISBN 0123456789. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 Novembre–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H. Most Valuable Player Algorithm: A novel optimization algorithm inspired from sport. Oper. Res. 2017, 20, 139–195. [Google Scholar] [CrossRef]
- Georgioudakis, M.; Plevris, V. A Comparative Study of Differential Evolution Variants in Constrained Structural Optimization. Front. Built Environ. 2020, 6, 102. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Massachusetts, MA, USA, 1975. [Google Scholar]
- Bouchekara, H.R.E.H. Electrostatic Discharge Algorithm (ESDA): A Novel Nature-Inspired Optimization Algorithm and its Application to Worst-Case Tolerance Analysis of An EMC Filter. IET Sci. Meas. Technol. 2019, 13, 491–499. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef] [Green Version]
- Karaboga, D. Artificial bee colony algorithm. Scholarpedia 2010, 5, 6915. [Google Scholar] [CrossRef]
- Mittal, H.; Tripathi, A.; Pandey, A.C.; Pal, R. Gravitational search algorithm: A comprehensive analysis of recent variants. Multimed. Tools Appl. 2020, 80, 7581–7608. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H. Optimal power flow using black-hole-based optimization approach. Appl. Soft Comput. J. 2014, 24, 879–888. [Google Scholar] [CrossRef]






| ECPO-ME | ECPO | MPSO | MVPA | DE | GA | ESDA | BBO | ABC | GSA | TLBO | BH | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario A | BEST | 0.20551 | 0.20116 | 0.18138 | 0.19810 | 0.20197 | 0.16030 | 0.18885 | 0.19948 | 0.18511 | 0.19572 | 0.20485 | 0.18101 |
| MEAN | 0.19239 | 0.16555 | 0.06021 | 0.11085 | 0.18960 | 0.13368 | 0.14730 | 0.17851 | 0.14966 | 0.04258 | 0.19207 | 0.13570 | |
| MEDIAN | 0.19118 | 0.18091 | 0.03225 | 0.12225 | 0.18942 | 0.13315 | 0.15159 | 0.18132 | 0.16003 | 0.00095 | 0.19115 | 0.13742 | |
| WORST | 0.18209 | 0.03135 | 0.00000 | 0.00002 | 0.17250 | 0.10551 | 0.09942 | 0.11788 | 0.00131 | 0.00000 | 0.18303 | 0.06931 | |
| SD | 0.00593 | 0.04174 | 0.06305 | 0.06100 | 0.00630 | 0.01466 | 0.02609 | 0.01696 | 0.03707 | 0.06203 | 0.00587 | 0.02547 | |
| FR | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| Scenario B | BEST | 0.27634 | 0.26252 | 0.22652 | 0.26014 | 0.27466 | 0.22486 | 0.23978 | 0.26156 | 0.24424 | 0.18925 | 0.27689 | 0.23919 |
| MEAN | 0.25724 | 0.23126 | 0.10670 | 0.17272 | 0.24516 | 0.18563 | 0.18328 | 0.21522 | 0.19452 | 0.05717 | 0.25216 | 0.19299 | |
| MEDIAN | 0.25820 | 0.24153 | 0.11274 | 0.19613 | 0.24909 | 0.18932 | 0.18379 | 0.23196 | 0.20196 | 0.04139 | 0.25462 | 0.19735 | |
| WORST | 0.23530 | 0.14698 | 0.01105 | 0.03688 | 0.14928 | 0.15175 | 0.11802 | 0.11055 | 0.01471 | 0.00009 | 0.22876 | 0.13430 | |
| SD | 0.00964 | 0.02539 | 0.05659 | 0.06069 | 0.02339 | 0.01860 | 0.03786 | 0.04466 | 0.04892 | 0.05281 | 0.01293 | 0.02803 | |
| FR | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| Scenario C | BEST | 0.68662 | 0.64070 | 0.58442 | 0.64361 | 0.68662 | 0.54835 | 0.64221 | 0.66811 | 0.61142 | 0.51114 | 0.67221 | 0.60402 |
| MEAN | 0.64158 | 0.52614 | 0.30143 | 0.37015 | 0.62170 | 0.46797 | 0.47561 | 0.55109 | 0.49444 | 0.22860 | 0.63269 | 0.49182 | |
| MEDIAN | 0.64997 | 0.55979 | 0.31420 | 0.39419 | 0.63538 | 0.47210 | 0.48670 | 0.59358 | 0.52423 | 0.23693 | 0.63631 | 0.50913 | |
| WORST | 0.57162 | 0.26147 | 0.00240 | 0.01434 | 0.35432 | 0.36236 | 0.27549 | 0.23189 | 0.26933 | 0.00000 | 0.55967 | 0.36322 | |
| SD | 0.02876 | 0.10643 | 0.17289 | 0.15426 | 0.06193 | 0.05306 | 0.08845 | 0.10633 | 0.09406 | 0.13620 | 0.03111 | 0.07498 | |
| FR | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| Scenario D | BEST | 0.55431 | 0.49309 | 0.47090 | 0.46095 | 0.55431 | 0.40220 | 0.51444 | 0.50274 | 0.46497 | 0.33458 | 0.53742 | 0.39930 |
| MEAN | 0.48849 | 0.38766 | 0.24390 | 0.31673 | 0.45452 | 0.29675 | 0.31233 | 0.35144 | - | 0.20418 | 0.46575 | 0.28810 | |
| MEDIAN | 0.49887 | 0.38931 | 0.23998 | 0.32675 | 0.44347 | 0.29698 | 0.30451 | 0.33692 | - | 0.20486 | 0.46263 | 0.27994 | |
| WORST | 0.40148 | 0.26634 | 0.04982 | 0.09241 | 0.32458 | 0.21807 | 0.18826 | 0.22614 | - | 0.00002 | 0.37301 | 0.18647 | |
| SD | 0.03120 | 0.05620 | 0.08177 | 0.09298 | 0.06339 | 0.04411 | 0.07879 | 0.07564 | - | 0.08891 | 0.04044 | 0.05650 | |
| FR | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 93.33 | 100 | 100 | 100 | |
| Scenario E | BEST | 0.20518 | 0.20358 | 0.18901 | 0.18726 | 0.20477 | 0.17868 | 0.18686 | 0.20130 | 0.19559 | 0.17188 | 0.20518 | 0.16870 |
| MEAN | 0.19008 | 0.17367 | 0.11979 | 0.13986 | 0.18615 | 0.13753 | 0.14400 | 0.17809 | 0.16200 | 0.07077 | 0.18893 | 0.13598 | |
| MEDIAN | 0.18870 | 0.18154 | 0.12904 | 0.14625 | 0.18395 | 0.14029 | 0.14865 | 0.17725 | 0.16468 | 0.07634 | 0.18830 | 0.13544 | |
| WORST | 0.17187 | 0.11000 | 0.00021 | 0.02299 | 0.17277 | 0.09305 | 0.04521 | 0.15401 | 0.04478 | 0.00012 | 0.16969 | 0.07844 | |
| SD | 0.00801 | 0.02362 | 0.05092 | 0.03505 | 0.00787 | 0.01839 | 0.03434 | 0.01107 | 0.02810 | 0.05553 | 0.00867 | 0.02228 | |
| FR | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| Scenario F | BEST | 0.22728 | 0.21985 | 0.16005 | 0.17661 | 0.22195 | 0.16416 | 0.20217 | 0.22195 | 0.20572 | 0.17721 | 0.22175 | 0.18615 |
| MEAN | 0.20007 | 0.18020 | 0.07334 | 0.10851 | 0.19650 | 0.10638 | 0.13038 | 0.19142 | 0.15022 | 0.06385 | 0.20008 | 0.13070 | |
| MEDIAN | 0.21024 | 0.18573 | 0.07296 | 0.13480 | 0.20160 | 0.11310 | 0.14440 | 0.20465 | 0.15892 | 0.03687 | 0.20930 | 0.13941 | |
| WORST | 0.16650 | 0.08188 | 0.00129 | 0.00564 | 0.13640 | 0.04128 | 0.03171 | 0.08111 | 0.00041 | 0.00070 | 0.16648 | 0.02830 | |
| SD | 0.01978 | 0.03226 | 0.05025 | 0.05427 | 0.02234 | 0.03378 | 0.04813 | 0.03334 | 0.05207 | 0.06128 | 0.01820 | 0.04135 | |
| FR | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alanezi, M.A.; Bouchekara, H.R.E.H.; Shahriar, M.S.; Sha’aban, Y.A.; Javaid, M.S.; Khodja, M. Motion-Encoded Electric Charged Particles Optimization for Moving Target Search Using Unmanned Aerial Vehicles. Sensors 2021, 21, 6568. https://doi.org/10.3390/s21196568
Alanezi MA, Bouchekara HREH, Shahriar MS, Sha’aban YA, Javaid MS, Khodja M. Motion-Encoded Electric Charged Particles Optimization for Moving Target Search Using Unmanned Aerial Vehicles. Sensors. 2021; 21(19):6568. https://doi.org/10.3390/s21196568
Chicago/Turabian StyleAlanezi, Mohammed A., Houssem R. E. H. Bouchekara, Mohammad S. Shahriar, Yusuf A. Sha’aban, Muhammad S. Javaid, and Mohammed Khodja. 2021. "Motion-Encoded Electric Charged Particles Optimization for Moving Target Search Using Unmanned Aerial Vehicles" Sensors 21, no. 19: 6568. https://doi.org/10.3390/s21196568








