A Setup for Measuring the Centering Error of a Dual-Element Pyroelectric Infrared Sensor Module
Abstract
:1. Introduction
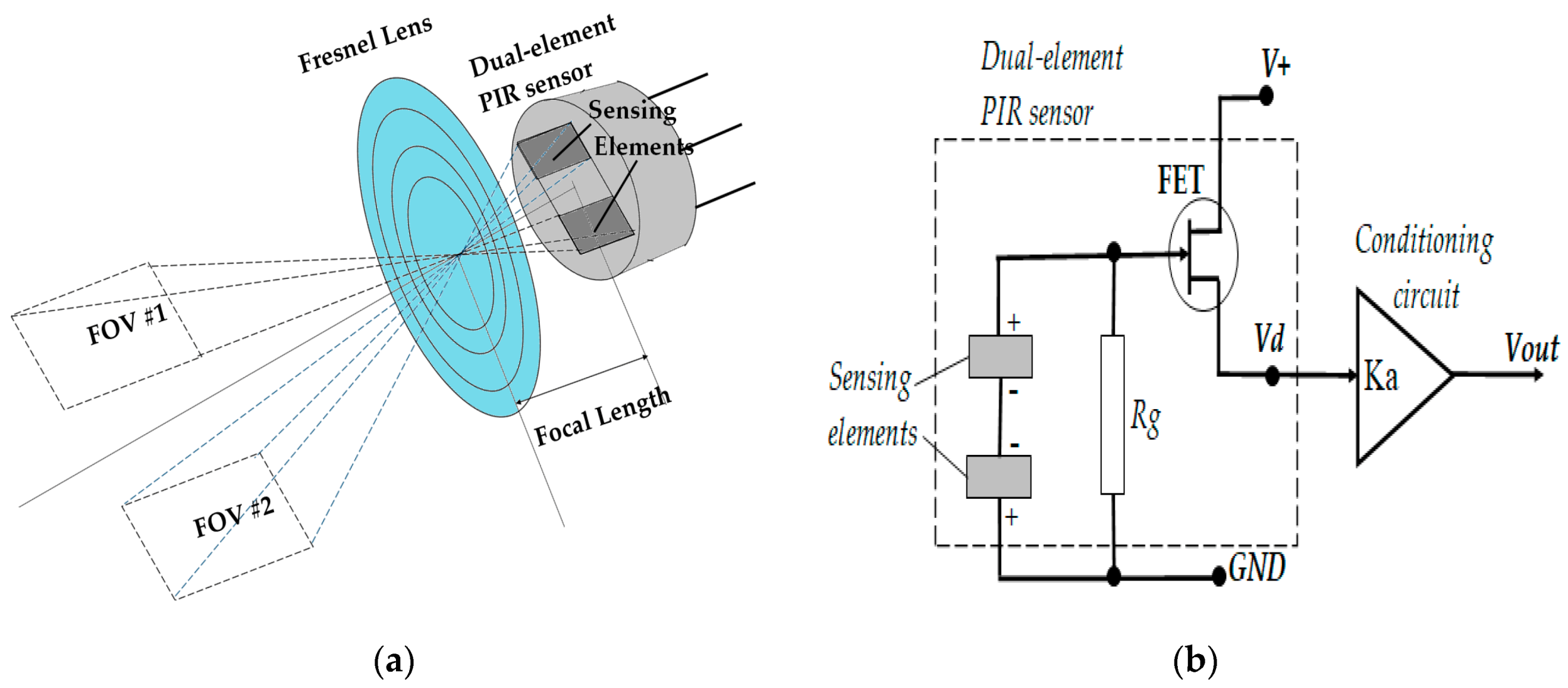
2. Dual-Element PIR Sensor Module
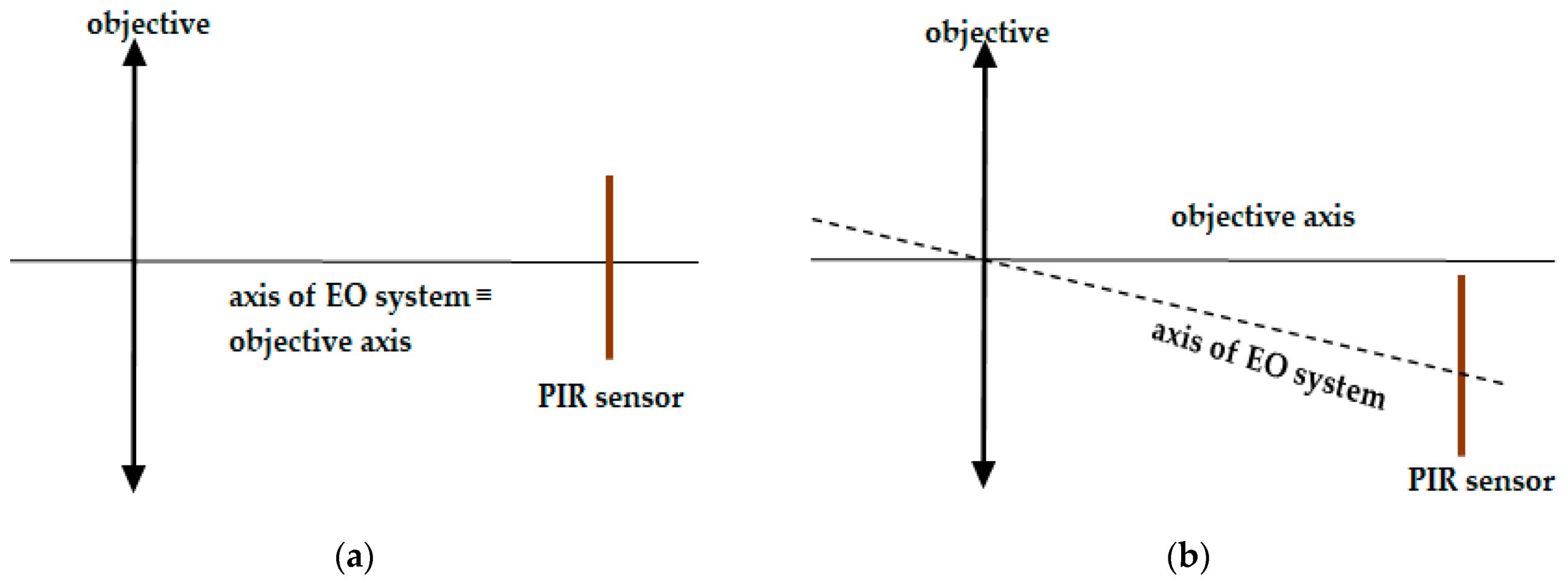
- If the IR radiation power emitted from sources within the two FOVs of PIR sensing elements is equal all the time, the output voltage amplitude of the sensor module will be zero in an ideal condition (without any noises), or insignificant in reality (with the presence of noises);
- Even in the case that the IR radiation powers emitted from sources within two FOVs are unequal due to their differential component in the transfer function, if the difference in quality between those powers is settled, then the output voltage amplitude will settle to zero in ideal conditions (without noises), or insignificant in real conditions (with noises).
3. Measurement Setup Based on Modulated Infrared Radiation
3.1. The Proposed Idea
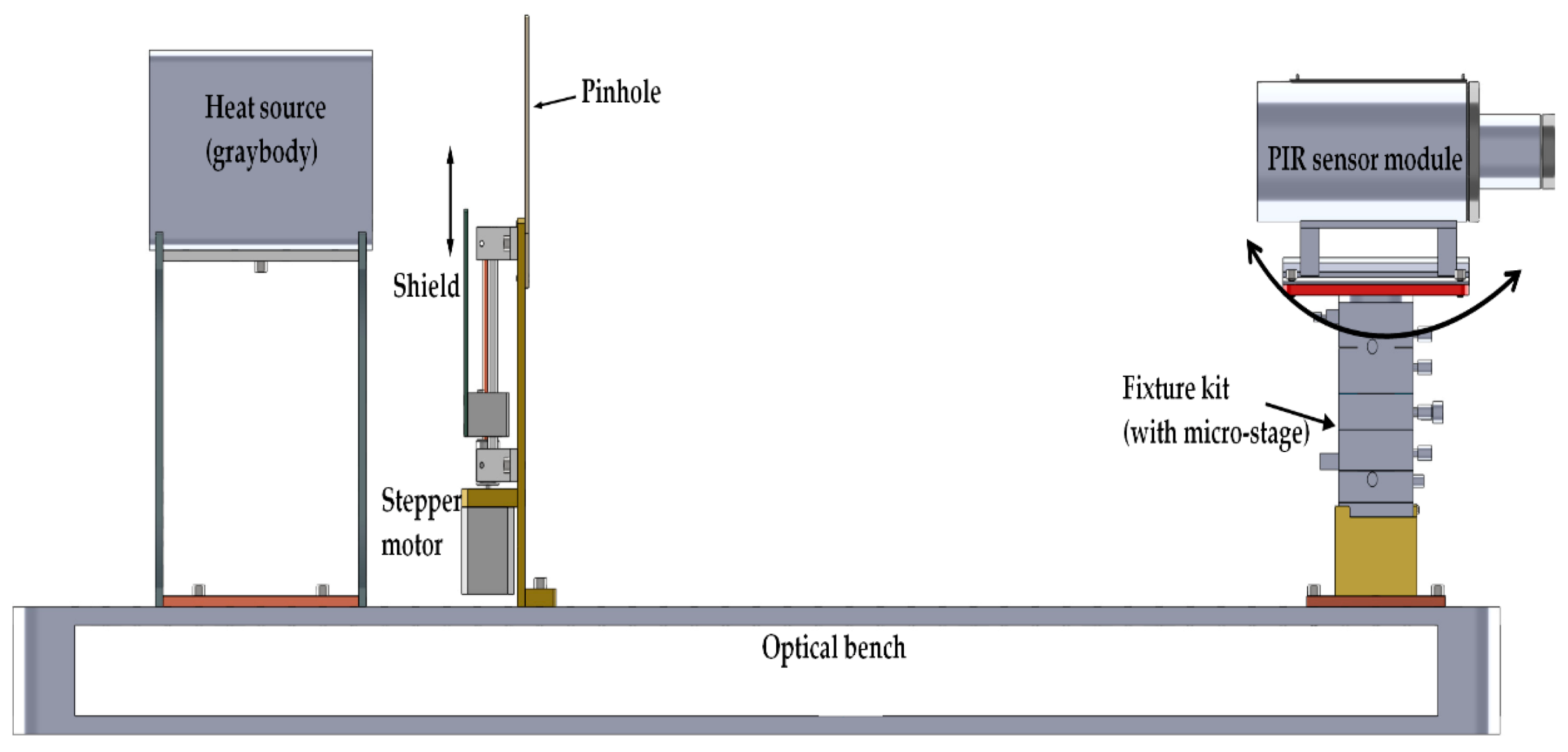
- A graybody heat source with a rectangular heating surface, which was intended to be a Lambertian surface;
- An optical shutter that was designed and made by our research team, with a rectangular pinhole and moving shield which was motorized by a stepper motor controlled by an embedded microsystem;
- A fixture kit that is based on a manual optical micro-stage, specifically for mounting the sensor module. The micro-stage was able to turn the sensor module around the vertical axis with a resolution of 0.02 degrees.
3.2. Analysis for Measurement Sensitivity

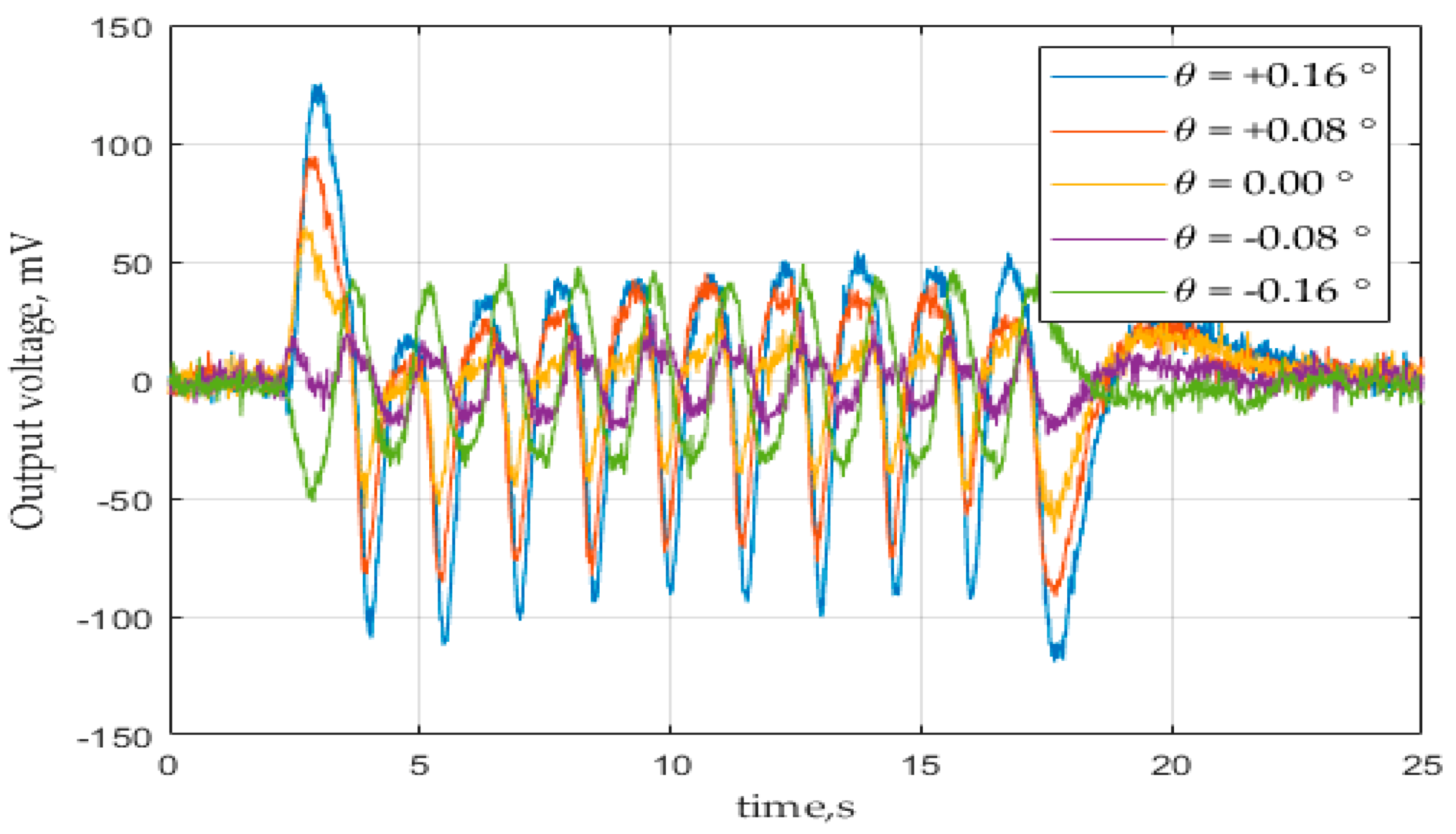
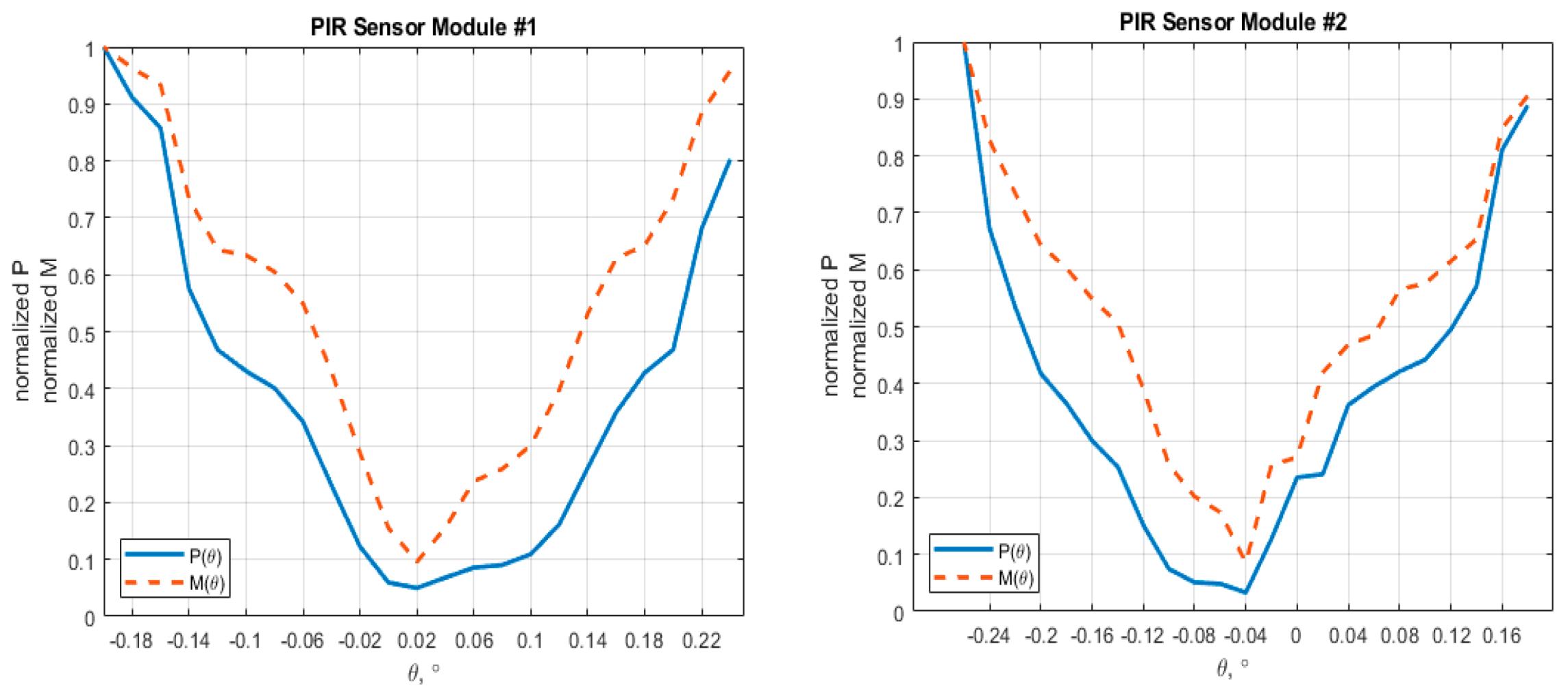
4. Experimental Result
- Method #1: The angular position of the optical axis is the position where the power spectral density (PSD) of the output signal reaches minimum;
- Method #2: The angular position of the optical axis is the position where the magnitude of the output signal at the modulation frequency reaches minimum.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Whatmore, R.W. Pyroelectric devices and materials. Rep. Prog. Phys. 1986, 49, 1335–1386. [Google Scholar] [CrossRef]
- Hossain, A.; Rashid, M.H. Pyroelectric Detectors and Their Applications. IEEE Trans. Ind. Appl. 1991, 27, 824–829. [Google Scholar] [CrossRef]
- Grulois, T.; Druart, G.; Sauer, H.; Chambon, M.; Guérineau, N.; Magli, S.; Lasfargues, G.; Chavel, P. Reduction of material mass of optical component in cryogenic camera by using high-order Fresnel lens on a thin germanium substrate. Appl. Opt. 2015, 54, 6313–6320. [Google Scholar] [CrossRef] [PubMed]
- Shankar, M.; Burchett, J.B.; Hao, Q.; Guenther, B.D.; Brady, D.J. Human-tracking systems using pyroelectric infrared detectors. Opt. Eng. 2006, 45, 106401. [Google Scholar] [CrossRef] [Green Version]
- Zappi, P.; Farella, E.; Benini, L. Tracking Motion Direction and Direction with Pyroelectric IR Sensors. IEEE Sens. J. 2010, 10, 1486–1494. [Google Scholar] [CrossRef]
- Yun, J.; Song, M.-H. Detecting Direction of Movement Using Pyroelectric Infrared Sensors. IEEE Sens. J. 2014, 14, 1482–1489. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Yan, B. Distributed Multi-Human Location Algorithm Using Naive Bayes Classifier for a Binary Pyroelectric Infrared Sensor Tracking System. IEEE Sens. J. 2016, 16, 216–223. [Google Scholar] [CrossRef]
- Hussain, T.M.; Baig, A.M.; Saadawi, T.N.; Ahmed, S.A. Infrared Pyroelectric Sensor for Detection of Vehicular Traffic Using Digital Signal Processing Techniques. IEEE Trans. Veh. Technol. 1995, 44, 683–689. [Google Scholar] [CrossRef]
- Erden, F.; Toreyin, B.U.; Soyer, E.B.; Inac, I.; Gunay, O.; Kose, K.; Cetin, A.E. Wavelet based flickering flame detector using differential PIR sensors. Fire Saf. J. 2012, 53, 13–18. [Google Scholar] [CrossRef] [Green Version]
- Quang, V.V.; Thang, V.T. A novel system for measuring vehicle speed via analog signals of pyroelectric infrared sensors. Int. J. Mod. Phys. B 2021, 35, 2140028. [Google Scholar] [CrossRef]
- Kastek, M.; Madura, H.; Morawski, M.; Piatkowski, T.; Powiada, E.; Polakowski, H. Test bed for measurement of angular parameters of passive infrared sensors. Infrared Phys. Technol. 2007, 49, 198–201. [Google Scholar] [CrossRef]
- Zaltz, A.; Christo, D. Methods for the control of centering error in the fabrication and assembly of optical elements. In Proceedings of the Los Angeles Technical Symposium, Los Angeles, CA, USA, 27–29 January 1982; Volume 0330. [Google Scholar]
- Chrzanowski, K. Report B01/19 Introduction to Boresight of Electro-Optical Surveillance Systems; INFRAMET: Stare Babice, Poland, 2019; Available online: https://www.inframet.com/Literature/Boresigh_Intro.pdf (accessed on 5 August 2021).
- KUBE Electronics AG. KUBE PIR SingleZone Fresnel Lenses. Available online: https://kube.ch/wp-content/uploads/documents/kube_single_fresnel_lenses.pdf (accessed on 5 August 2021).
- Murata Manufacturing Co., Ltd. Datasheet of IRA-S230ST01. Available online: https://www.murata.com/en-us/api/pdfdownloadapi?cate=&partno=IRA-S230ST01 (accessed on 5 August 2021).
- Ronald, G.D.; Melvin, H.F.; Nichols, J. Introduction to Infrared and Electro-Optical Systems, 2nd ed.; Artech House: Norwood, MA, USA, 2012; pp. 126–128. [Google Scholar]
- Odon, A. Modelling and Simulation of the Pyroelectric Detector Using MATLAB/Simulink. Meas. Sci. Rev. 2010, 10, 195–199. [Google Scholar] [CrossRef] [Green Version]
- FAS Military Analysis Network. Infrared Propagation and Detection. Available online: http://fas.org/man/dod-101/navy/docs/es310/IRprop/IRprop.htm (accessed on 5 August 2021).



| Parameter | Value | Unit |
|---|---|---|
| Sensing element dimension, he × we | 2 × 1 | mm × mm |
| Gap between sensing elements, wg | 1 | mm |
| Thermal time constant, τTh | 0.5 | s |
| Electrical time constant, τe | 0.08 | s |
| Sensor amplifier gain, Kd | 2200 | V∙s/W |
| Circuit amplifier gain, Ka | 20 | (none) |
| Lens diameter, D | 50 | mm |
| Objective focal length, f | 50.9 | mm |
| Dimensions of pinhole, HP × WP | 45 × 45 | mm × mm |
| Distance, R | 850 | mm |
| Working wavelength range, λ1 ÷ λ2 | 5 ÷ 12 | µm |
| Heat source emissivity, ε | 0.95 | (none) |
| Atmosphere attenuation, η | 1 | (none) |
| Transmittance of the lens, τ 1 | 0.75 | (none) |
| Background temperature, Tb | 298 | K |
| Tested Module | Turned Angle, ° | P, mV2 | M, mV |
|---|---|---|---|
| Sensor Module #1 | +0.24 | 977.71 | 41.66 |
| +0.22 | 829.40 | 38.48 | |
| … | … | … | |
| +0.06 | 208.74 | 10.32 | |
| +0.04 | 166.02 | 6.78 | |
| +0.02 | 60.53 | 4.16 | |
| 0.00 | 144.98 | 6.75 | |
| −0.02 | 189.53 | 12.49 | |
| … | … | … | |
| −0.20 | 1218.17 | 43.49 | |
| −0.22 | 1449.07 | 48.41 | |
| Sensor module #2 | +0.18 | 2252.51 | 60.74 |
| +0.16 | 2054.72 | 56.90 | |
| … | … | … | |
| 0.00 | 610.54 | 18.13 | |
| −0.02 | 322.23 | 17.26 | |
| −0.04 | 84.01 | 5.74 | |
| −0.06 | 122.90 | 11.68 | |
| −0.08 | 189.24 | 13.52 | |
| … | … | … | |
| −0.24 | 1704.31 | 55.47 | |
| −0.26 | 2535.29 | 67.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thang, V.T.; Quang, V.V.; Bui, N.-T. A Setup for Measuring the Centering Error of a Dual-Element Pyroelectric Infrared Sensor Module. Sensors 2021, 21, 6684. https://doi.org/10.3390/s21196684
Thang VT, Quang VV, Bui N-T. A Setup for Measuring the Centering Error of a Dual-Element Pyroelectric Infrared Sensor Module. Sensors. 2021; 21(19):6684. https://doi.org/10.3390/s21196684
Chicago/Turabian StyleThang, Vu Toan, Vu Van Quang, and Ngoc-Tam Bui. 2021. "A Setup for Measuring the Centering Error of a Dual-Element Pyroelectric Infrared Sensor Module" Sensors 21, no. 19: 6684. https://doi.org/10.3390/s21196684
APA StyleThang, V. T., Quang, V. V., & Bui, N.-T. (2021). A Setup for Measuring the Centering Error of a Dual-Element Pyroelectric Infrared Sensor Module. Sensors, 21(19), 6684. https://doi.org/10.3390/s21196684








