Piezoelectric Sensor-Embedded Smart Rock for Damage Monitoring in a Prestressed Anchorage Zone
Abstract
:1. Introduction
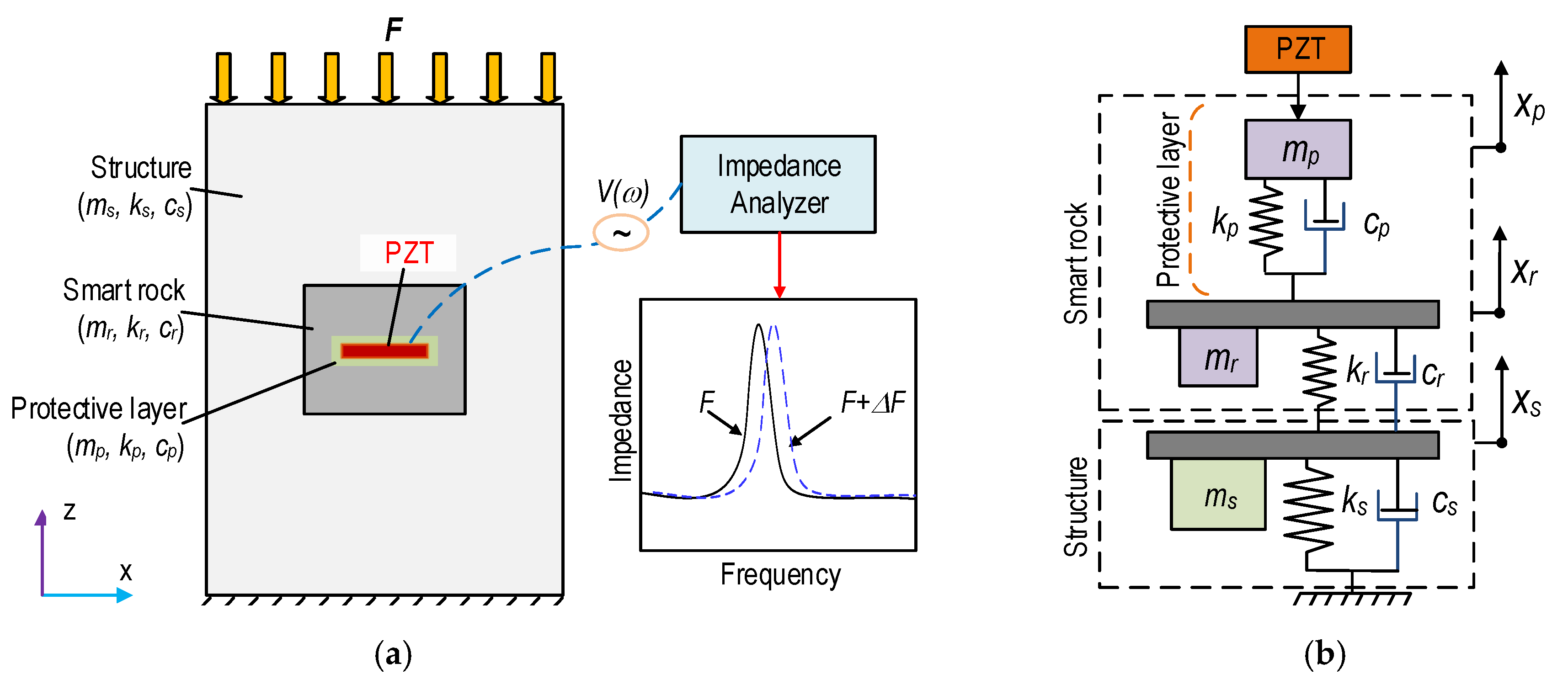
2. Theoretical Model of the Piezoelectric Sensor-Embedded Smart Rock
2.1. Impedance Measurement Model of the PZT-Embedded Smart Rock
2.2. Mechanism of the PZT-Embedded Smart Rock under Compression
2.3. Statistical Quantification of the Impedance Responses
3. PZT-Embedded Smart Rock for Impedance-Based Concrete Damage Detection
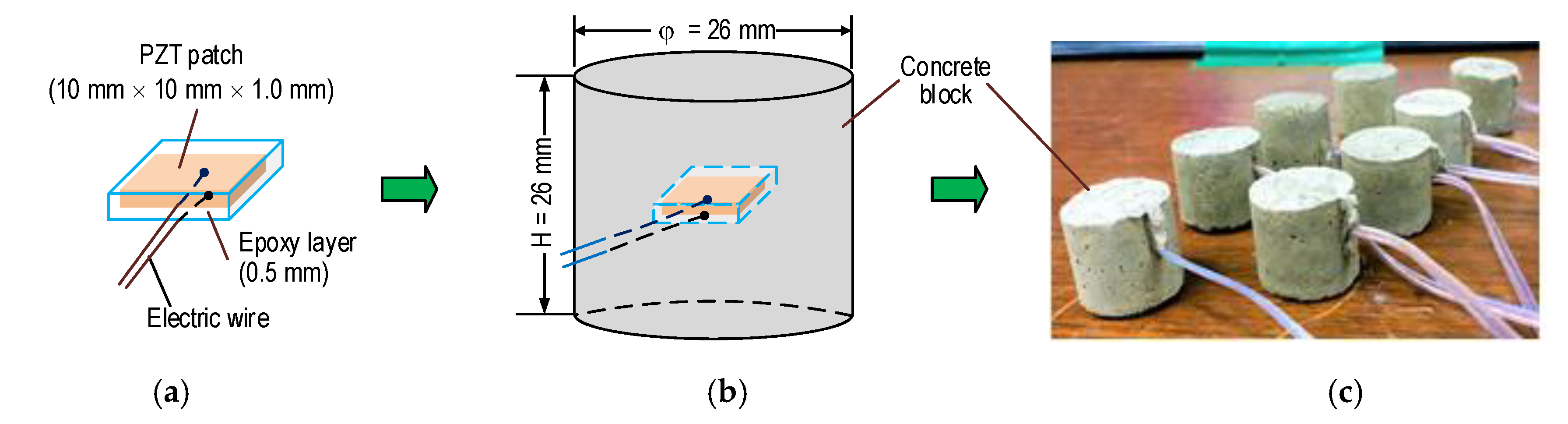
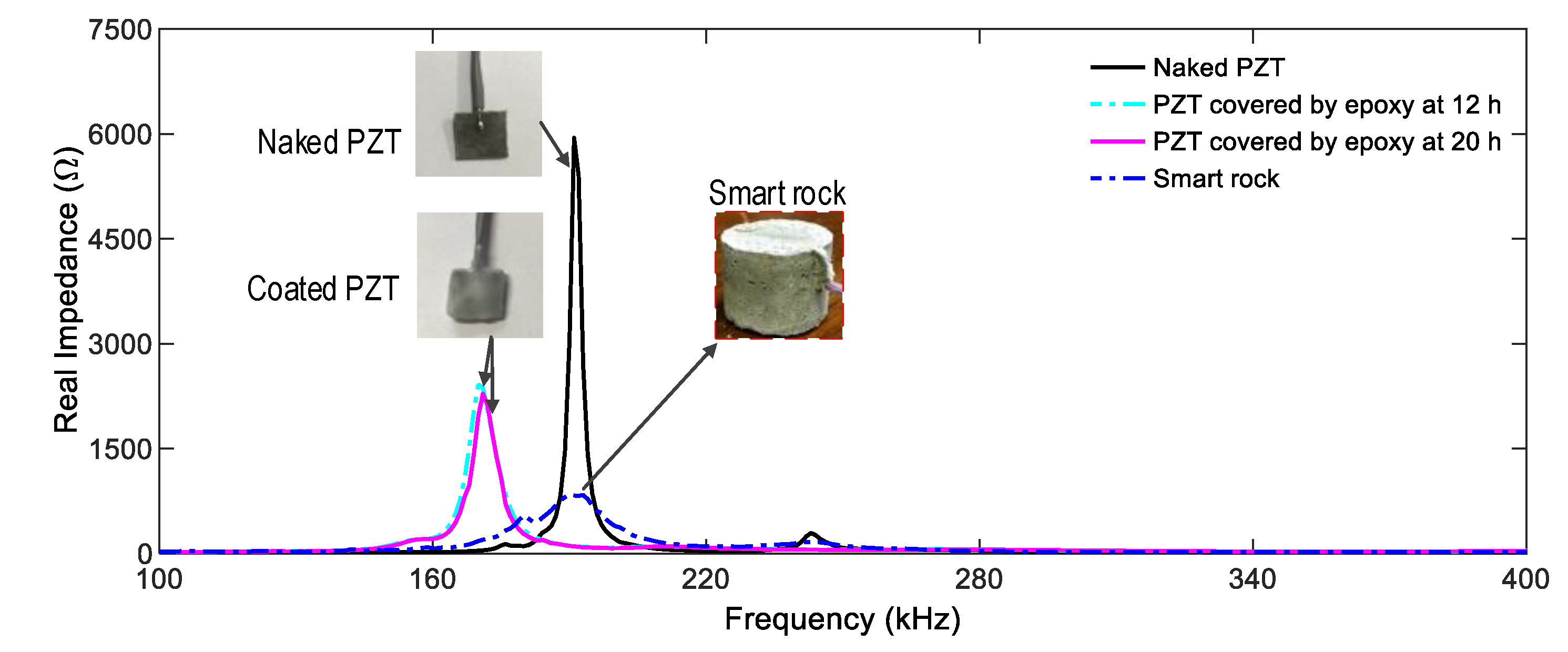
3.1. Prototype Design of the PZT-Embedded Smart Rock
3.2. Numerical Analysis of Smart Rock-Based Impedance Monitoring
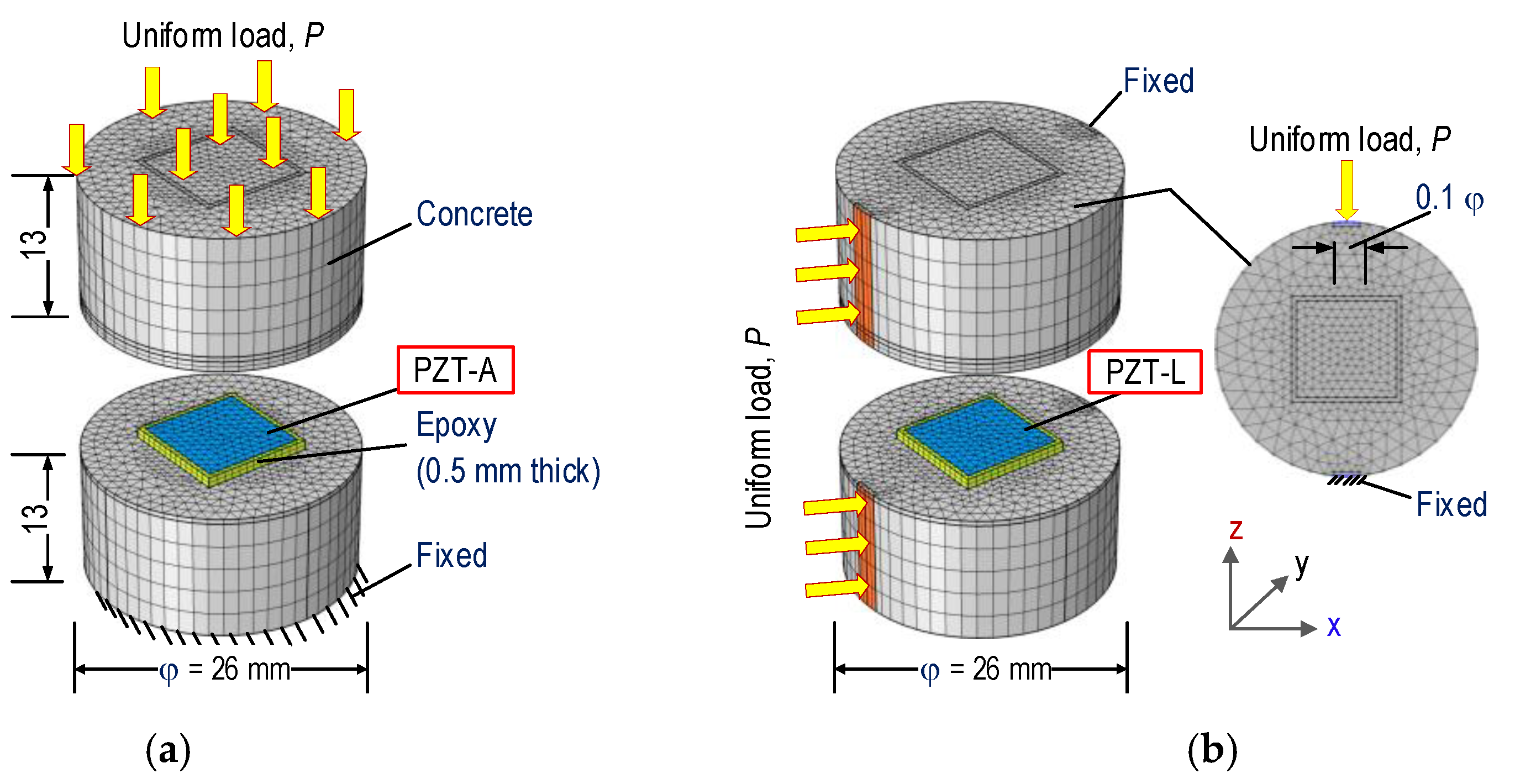
3.2.1. Finite Element Model of PZT-Embedded Smart Rock
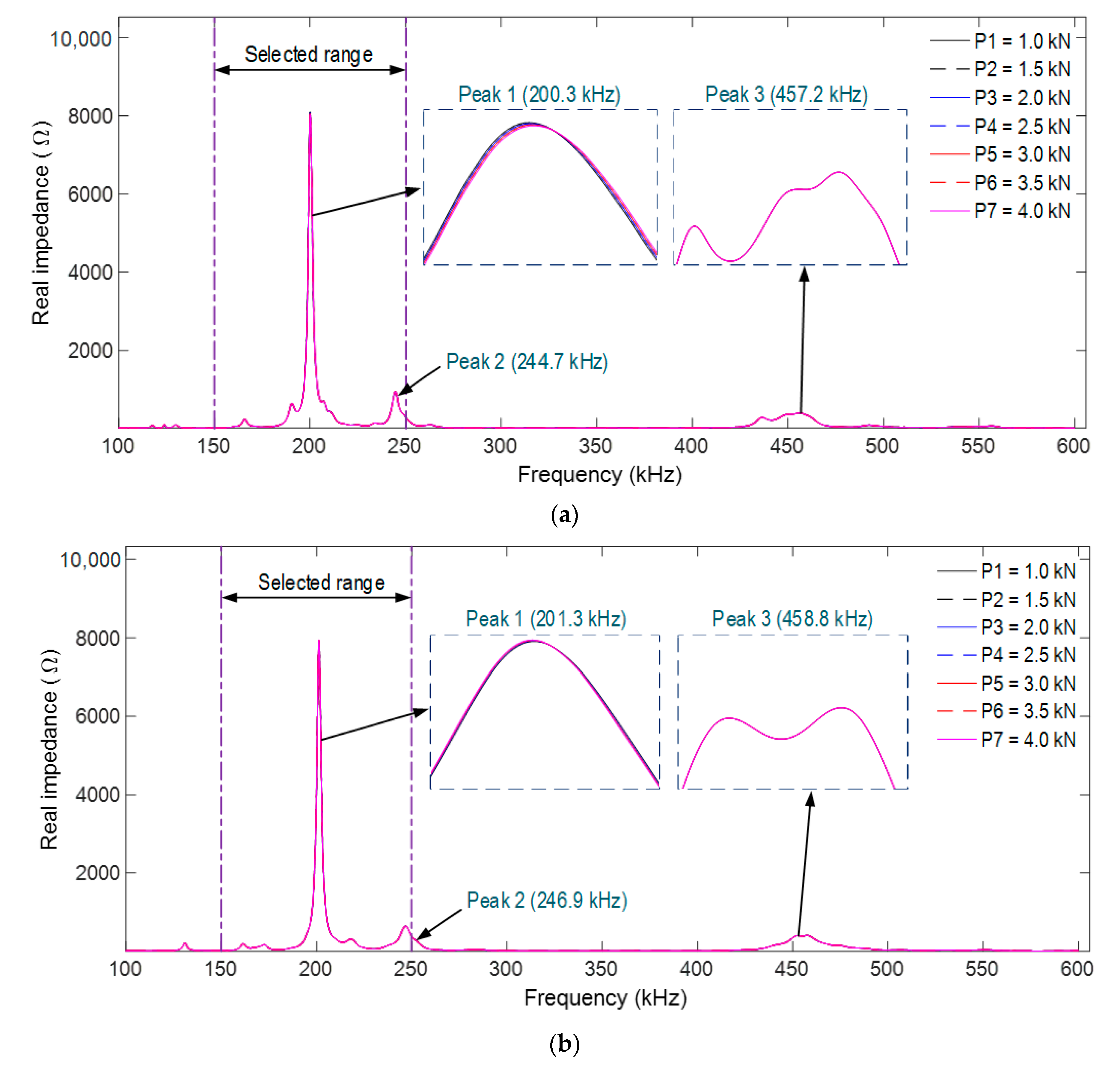
3.2.2. Numerical Impedance Responses of the PZT-Embedded Smart Rock
3.3. Experimental Analysis of Smart Rock-Based Impedance Monitoring
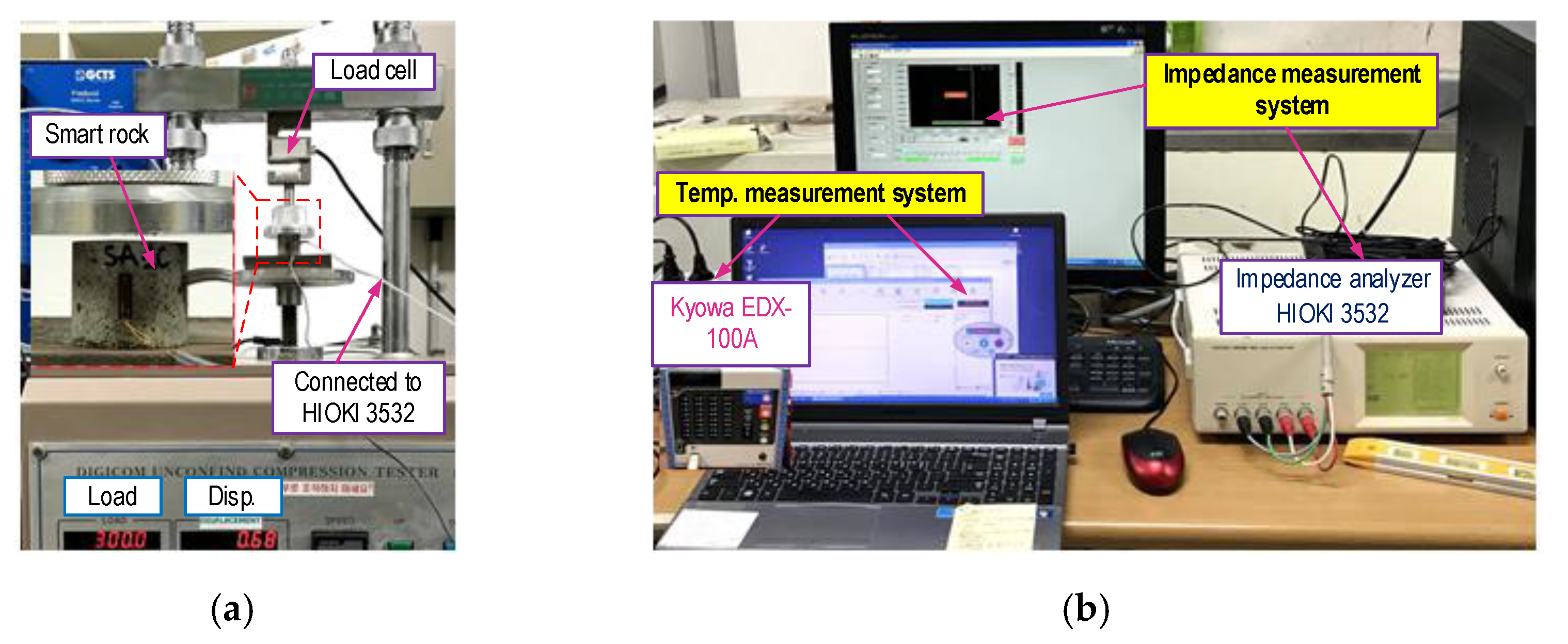
3.3.1. Experimental Set-Up on the Compressive Tester
3.3.2. Experimental Impedance Responses of the PZT-Embedded Smart Rock under Compression
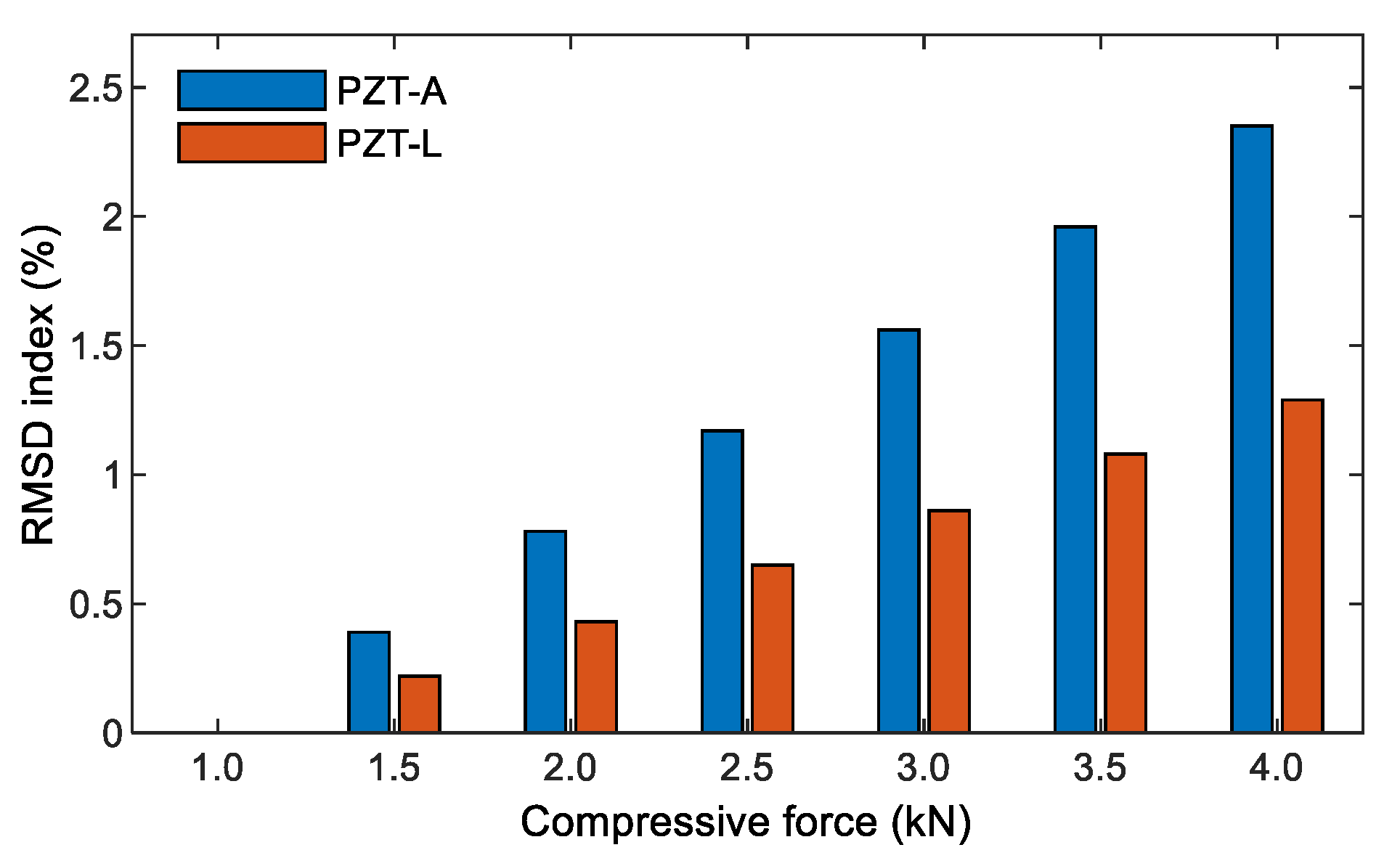
3.4. Sensitivity of the Impedance Responses via PZT-Embedded Smart Rock to Stress Variation
4. Feasibility Evaluation of PZT-Embedded Smart Rock for Concrete Damage Detection in Prestressed Anchorage Zone
4.1. Test Set-Up and Test Scenarios
4.1.1. Experimental Set-Up on the Anchorage Zone
4.1.2. Test Scenarios for Impedance Measurement in the Anchorage Zone
4.2. Damage Monitoring Results on the Anchorage Zone using the Smart Rock
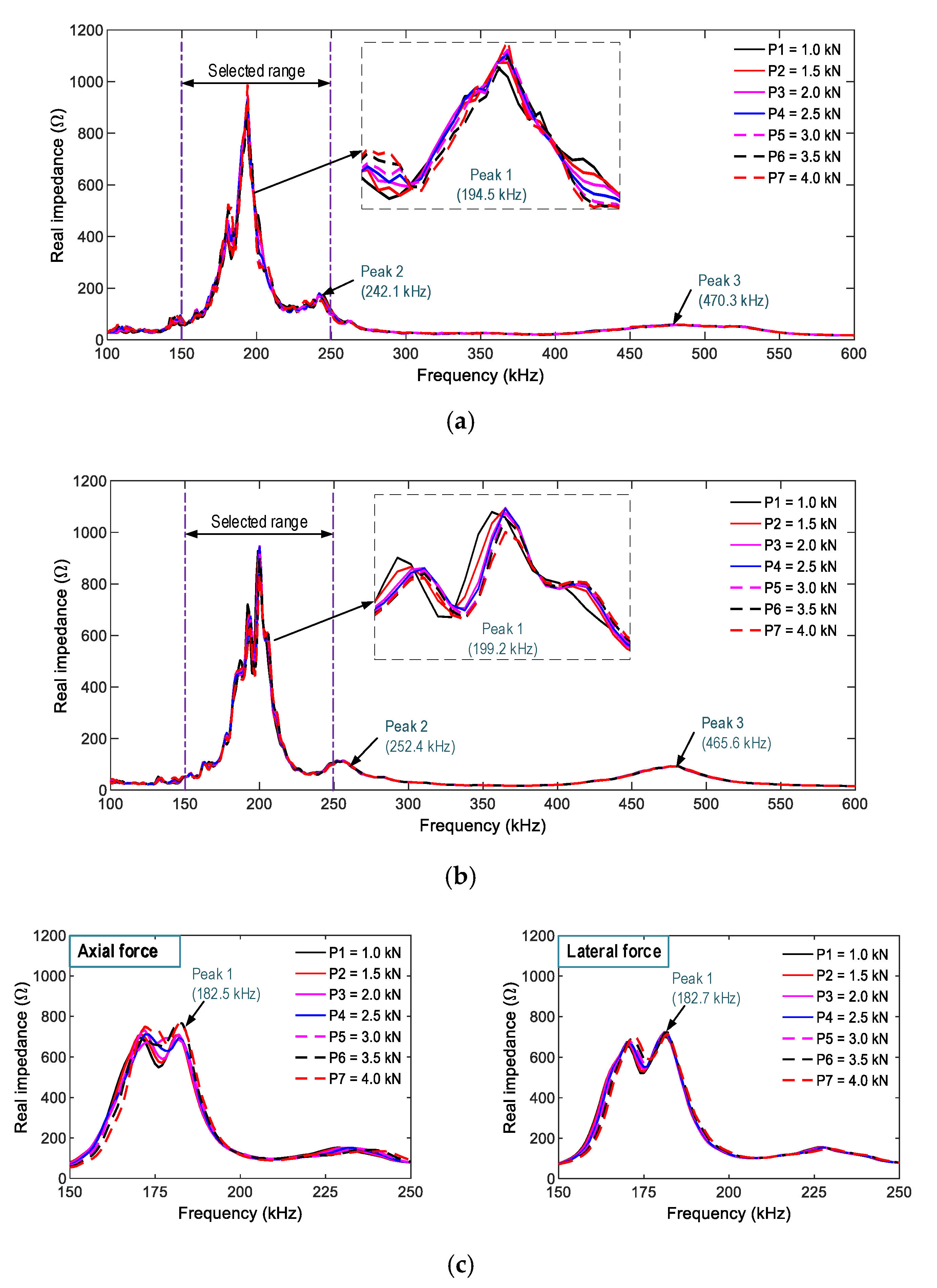
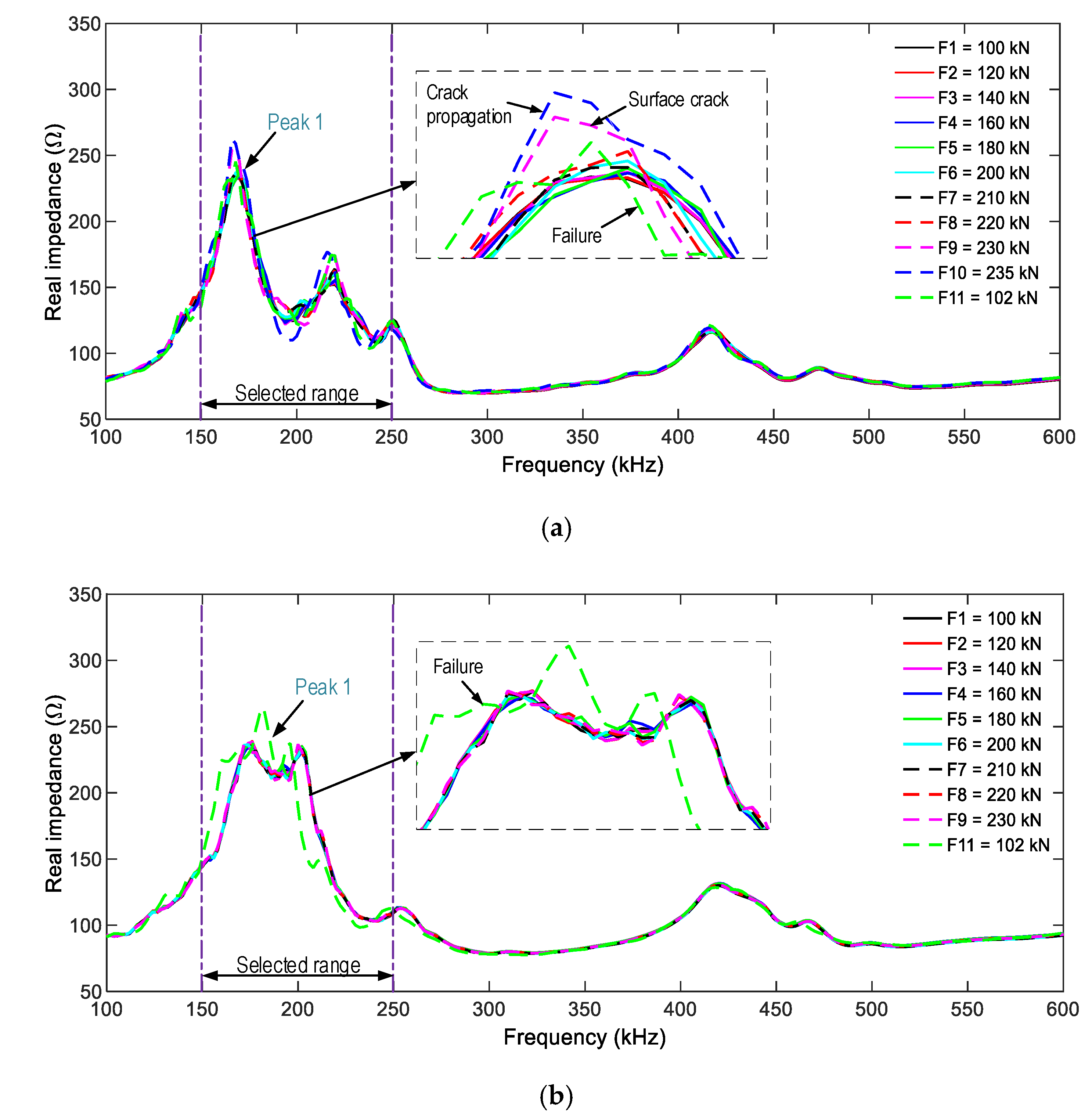
4.2.1. Impedance Responses of PZT-Embedded Smart Rocks and Surface-Mounted PZTs
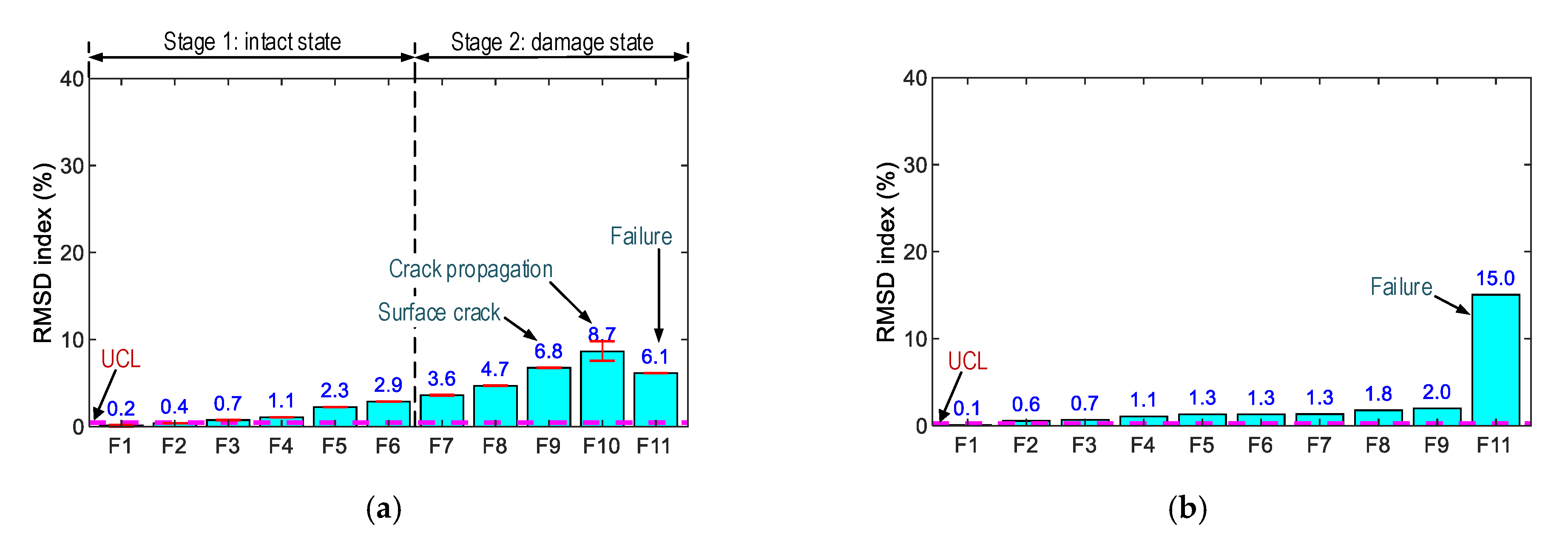
4.2.2. Damage Monitoring in the Anchorage Zone Using PZT’s Impedance Features
4.2.3. Discussion of the Damage Monitoring on the Anchorage Zone using Smart Rock
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mehrabi, A.B.; Ligozio, C.A.; Ciolko, A.T.; Wyatt, S.T. Evaluation, rehabilitation planning, and stay-cable replacement design for the hale boggs bridge in Luling, Louisiana. J. Bridge Eng. 2010, 15, 364–372. [Google Scholar] [CrossRef]
- Hou, D.W.; Zhao, J.L.; Shen, J.S.L.; Chen, J. Investigation and improvement of strut-and-tie model for design of end anchorage zone in post-tensioned concrete structure. Constr. Build. Mater. 2017, 136, 482–494. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Cho, S.; Spencer, B.F., Jr.; Fan, J. Automated assessment of cracks on concrete surfaces using adaptive digital image processing. Smart Struct. Syst. 2014, 14, 719–741. [Google Scholar] [CrossRef]
- Kim, J.T.; Park, J.H.; Lee, B.J. Vibration-based damage monitoring in model plate-girder bridges under uncertain temperature conditions. Eng. Struct. 2007, 29, 1354–1365. [Google Scholar] [CrossRef]
- Ho, D.D.; Kim, J.T.; Stubbs, N.; Park, W.S. Prestress-force estimation in PSC girder using modal parameters and system identification. Adv. Struct. Eng. 2012, 15, 997–1012. [Google Scholar] [CrossRef]
- Lee, S.; Kalos, N. Non-destructive testing methods in the US for bridge inspection and maintenance. Ksce J. Civ. Eng. 2014, 18, 1322–1331. [Google Scholar] [CrossRef]
- Grosse, C.U. Acoustic emission localization methods for large structures based on beam forming and array techniques. In Proceedings of the 7th International Symposium on Nondestructive Testing in Civil Engineering (NDTCE), Nantes, France, 30 June–3 July 2009; Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.216.3234&rep=rep1&type=pdf (accessed on 6 January 2021).
- Aryan, P.; Sampath, S.; Sohn, H. An Overview of Non-Destructive Testing Methods for Integrated Circuit Packaging Inspection. Sensors 2018, 18, 1981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henault, J.M.; Quiertant, M.; Delepine-Lesoille, S.; Salin, J.; Moreau, G.; Taillade, F. Benzarti, K. Quantitative strain measurement and crack detection in RC structures using a truly distributed fiber optic sensing system. Constr. Build. Mater. 2012, 37, 916–923. [Google Scholar] [CrossRef]
- Du, C.; Dutta, S.; Kurup, P.; Yu, T.; Wang, X. A review of railway infrastructure monitoring using fiber optic sensors. Sens. Actuators A Phys. 2020, 303, 111728. [Google Scholar] [CrossRef]
- Lacidogna, G.; Piana, G.; Accornero, F.; Carpinteri, A. Multi-technique damage monitoring of concrete beams: Acoustic Emission, Digital Image Correlation, Dynamic Identification. Constr. Build. Mater. 2020, 242, 118114. [Google Scholar] [CrossRef]
- Lacidogna, G.; Piana, G.; Carpinteri, A. Acoustic Emission and Modal Frequency Variation in Concrete Specimens under Four-Point Bending. Appl. Sci. 2017, 7, 339. [Google Scholar] [CrossRef]
- Kim, J.T.; Park, J.H.; Hong, D.S.; Park, W.S. Hybrid health monitoring of prestressed concrete girder bridges by sequential vibration-impedance approaches. Eng. Struct. 2010, 32, 115–128. [Google Scholar] [CrossRef]
- Dang, N.L.; Huynh, T.C.; Kim, J.T. Local Strand-Breakage Detection in Multi-Strand Anchorage System Using an Impedance-Based Stress Monitoring Method-Feasibility Study. Sensors 2019, 19, 1054. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Hu, Y.; Lu, Y. Sensitivity of PZT impedance sensors for damage detection of concrete structures. Sensors 2008, 8, 327–346. [Google Scholar] [CrossRef] [Green Version]
- Negi, P.; Chhabra, R.; Kaur, N.; Bhalla, S. Health monitoring of reinforced concrete structures under impact using multiple piezo-based configurations. Constr. Build. Mater. 2019, 222, 371–389. [Google Scholar] [CrossRef]
- Ai, D.; Luo, H.; Wang, C.; Zhu, H. Monitoring of the load-induced RC beam structural tension/compression stress and damage using piezoelectric transducers. Eng. Struct. 2018, 154, 38–51. [Google Scholar] [CrossRef]
- Narayanan, A.; Subramaniam, K.V.L. Experimental evaluation of load-induced damage in concrete from distributed microcracks to localized cracking on electro-mechanical impedance response of bonded PZT. Constr. Build. Mater. 2016, 105, 536–544. [Google Scholar] [CrossRef]
- Baptista, F.G.; Budoya, D.E.; De Almeida, V.A.; Ulson, J.A. An experimental study on the effect of temperature on piezoelectric sensors for impedance-based structural health monitoring. Sensors 2014, 14, 1208–1227. [Google Scholar] [CrossRef]
- Huynh, T.C.; Kim, J.T. RBFN-based temperature compensation method for impedance monitoring in prestressed tendon anchorage. Struct. Control Health Monit. 2018, 25, e2173. [Google Scholar] [CrossRef]
- Gianesini, B.M.; Cortez, N.E.; Antunes, R.A.; Vieira Filho, J. Method for removing temperature effect in impedance-based structural health monitoring systems using polynomial regression. Struct. Health Monit. 2020. [Google Scholar] [CrossRef]
- Gu, H.; Song, G.; Dhonde, H.; Mo, Y.L.; Yan, S. Concrete early-age strength monitoring using embedded piezoelectric transducers. Smart Mater. Struct. 2006, 15, 1837–1845. [Google Scholar] [CrossRef]
- Feng, Q.; Liang, Y.; Song, G. Real-Time Monitoring of Early-Age Concrete Strength Using Piezoceramic-Based Smart Aggregates. J. Aerosp. Eng. 2019, 32, 04018115. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Balamonica, K.; Priya, C.B.; Reddy, A.L.; Gopalakrishnan, N. Comparative performance of various smart aggregates during strength gain and damage states of concrete. Smart Mater. Struct. 2015, 24, 085016. [Google Scholar] [CrossRef]
- Breen, J.E. Anchorage Zone Reinforcement for Post-Tensioned Concrete Girders; Transportation Research Board: Washington, DC, USA, 1994. [Google Scholar]
- Theryo, T.S. Anchorage zone design and detailing from practical perspective. In Proceedings of the FDOT Transportation Symposium, Orlando, FL, USA, 29–30 May 2019. [Google Scholar]
- Mao, W.; Gou, H.; He, Y.; Pu, Q. Local Stress Behavior of Post-Tensioned Prestressed Anchorage Zones in Continuous Rigid Frame Arch Railway Bridge. Appl. Sci. 2018, 8, 1833. [Google Scholar] [CrossRef] [Green Version]
- Hanoon, A.N.; Jaafar, M.S.; Hejazi, F.; Aziz, F.N.A. Strut-and-tie model for externally bonded CFRP-strengthened reinforced concrete deep beams based on particle swarm optimization algorithm: CFRP debonding and rupture. Constr. Build. Mater. 2017, 147, 428–447. [Google Scholar] [CrossRef]
- He, Z.Q.; Liu, Z. Optimal three-dimensional strut-and-tie models for anchorage diaphragms in externally prestressed bridges. Eng. Struct. 2010, 32, 2057–2064. [Google Scholar] [CrossRef]
- Wu, J.; Xian, G.; Li, H. A novel anchorage system for CFRP cable: Experimental and numerical investigation. Compos. Struct. 2018, 194, 555–563. [Google Scholar] [CrossRef]
- Dang, N.L.; Pham, Q.Q.; Kim, J.T. Piezoelectric-based Hoop-Type Interface for Impedance Monitoring of Local Strand Breakage in Prestressed Multi-Strands Anchorage. Struct. Control Health Monit. 2021, 28, 1–20. [Google Scholar]
- Min, J.; Yun, C.B.; Hong, J.W. An electromechanical impedance-based method for tensile force estimation and damage diagnosis of post-tensioning systems. Smart Struct. Syst. 2016, 17, 107–122. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Soh, C.K. Effect of varying axial load under fixed boundary condition on admittance signatures of electromechanical impedance technique. J. Intell. Mater. Syst. Struct. 2012, 23, 815–826. [Google Scholar] [CrossRef]
- Kim, J.T.; Nguyen, K.D.; Huynh, T.C. Wireless health monitoring of stay cable using piezoelectric strain response and smart skin technique. Smart Struct. Syst. 2013, 12, 381–397. [Google Scholar] [CrossRef]
- Park, S.; Shin, H.H.; Yun, C.B. Wireless impedance sensor nodes for functions of structural damage identification and sensor self-diagnosis. Smart Mater. Struct. 2009, 18, 055001. [Google Scholar] [CrossRef]
- Huynh, T.C.; Nguyen, T.D.; Ho, D.D.; Dang, N.L.; Kim, J.T. Sensor Fault Diagnosis for Impedance Monitoring Using a Piezoelectric-Based Smart Interface Technique. Sensors 2020, 20, 510. [Google Scholar] [CrossRef] [Green Version]
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled Electro-Mechanical Analysis of Adaptive Material Systems-Determination of the Actuator Power Consumption and System Energy Transfer. J. Intell. Mater. Syst. Struct. 1994, 5, 12–20. [Google Scholar] [CrossRef]
- Kundu, T.; Narayanan, A.; Subramaniam, K.V.L. Early age monitoring of cement mortar using embedded piezoelectric sensors. In Proceedings of the Health Monitoring of Structural and Biological Systems 2016, Las Vegas, NV, USA, 21–24 March 2016. [Google Scholar]
- Wang, D.; Zhu, H. Monitoring of the strength gain of concrete using embedded PZT impedance transducer. Constr. Build. Mater. 2011, 25, 3703–3708. [Google Scholar] [CrossRef]
- Kocherla, A.; Subramaniam, K.V.L. Embedded smart PZT-based sensor for internal damage detection in concrete under applied compression. Measurement 2020, 163, 108018. [Google Scholar] [CrossRef]
- Nawy, E.G. Prestressed Concrete: A Fundamental Approach; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Giurgiutiu, V.; Rogers, C.A. Recent advancements in the electromechanical (E/M) impedance method for structural health monitoring and NDE, Smart Structures and Materials 1998: Smart Structures and Integrated Systems. Int. Soc. Opt. Photonics 1998, 3329, 536–547. [Google Scholar]
- Huynh, T.C.; Lee, K.S.; Kim, J.T. Local dynamic characteristics of PZT impedance interface on tendon anchorage under prestress force variation. Smart Struct. Syst. 2015, 15, 375–393. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.L. Smart aggregates: Multi-functional sensors for concrete structures—A tutorial and a review. Smart Mater. Struct. 2008, 17, 1–17. [Google Scholar]
- Negi, P.; Chakraborty, T.; Kaur, N.; Bhalla, S. Investigations on effectiveness of embedded PZT patches at varying orientations for monitoring concrete hydration using EMI technique. Constr. Build. Mater. 2018, 169, 489–498. [Google Scholar] [CrossRef]
- Huynh, T.C.; Dang, N.L.; Kim, J.T. Advances and challenges in impedance-based structural health monitoring. Struct. Monit. Maint. 2017, 4, 301–329. [Google Scholar]
- Yang, Y.; Lim, Y.Y.; Soh, C.K. Practical issues related to the application of the electromechanical impedance technique in the structural health monitoring of civil structures: I. Experiment. Smart Mater. Struct. 2008, 17, 035008. [Google Scholar] [CrossRef]
- Ai, D.; Lin, C.; Zhu, H. Embedded piezoelectric transducers based early-age hydration monitoring of cement concrete added with accelerator/retarder admixtures. J. Intell. Mater. Syst. Struct. 2020. [Google Scholar] [CrossRef]
- Bagherzadeh, R.; Sadeghi, A.H.; Latifi, M. Utilizing polypropylene fibers to improve physical and mechanical properties of concrete. Text. Res. J. 2011, 82, 88–96. [Google Scholar] [CrossRef]
- Epoxy, Fix Your Things with PC-Products. Available online: https://www.pcepoxy.com/wp-content/uploads/2017/07/superepoxydatabackcolor.pdf (accessed on 9 December 2019).
- Zhao, S.; Fan, S.; Yang, J.; Kitipornchai, S. Numerical and experimental investigation of electro-mechanical impedance based concrete quantitative damage assessment. Smart Mater. Struct. 2020, 29, 055025. [Google Scholar] [CrossRef]
- Bhalla, S.; Soh, C.K. Electromechanical Impedance Modeling for Adhesively Bonded Piezo-Transducers. J. Intell. Mater. Syst. Struct. 2004, 15, 955–972. [Google Scholar] [CrossRef]
- Vsl 2018. VSL Strand Post-Tensioning Systems. Available online: https://vsl.com/home/technologies/post-tensioning-systems/ (accessed on 6 January 2021).
- Huynh, T.C.; Dang, N.L.; Kim, J.T. Preload Monitoring in Bolted Connection Using Piezoelectric-Based Smart Interface. Sensors 2018, 18, 2766. [Google Scholar] [CrossRef] [Green Version]
- Aashto, L. AASHTO LRFD Bridge Design Specifications, SI Units; American Association of State Highway and Transportation: Washington, DC, USA, 2007. [Google Scholar]
- Roberts, C. Behavior and Design of the Local Anchorage Zone in Post-Tensioned Concrete. Master’s Thesis, The University of Texas, Austin, TX, USA, 1990. [Google Scholar]
- Dang, N.L.; Huynh, T.C.; Pham, Q.Q.; Lee, S.Y.; Kim, J.T. Damage-sensitive impedance sensor placement on multi-strand anchorage based on local stress variation analysis. Struct. Control Health Monit. 2020, 27, e2547. [Google Scholar]
- Zhang, C.; Yan, Q.; Panda, G.P.; Wu, W.; Song, G.; Vipulanandan, C. Real-time monitoring stiffness degradation of hardened cement paste under uniaxial compression loading through piezoceramic-based electromechanical impedance method. Constr. Build. Mater. 2020, 256, 119395. [Google Scholar] [CrossRef]


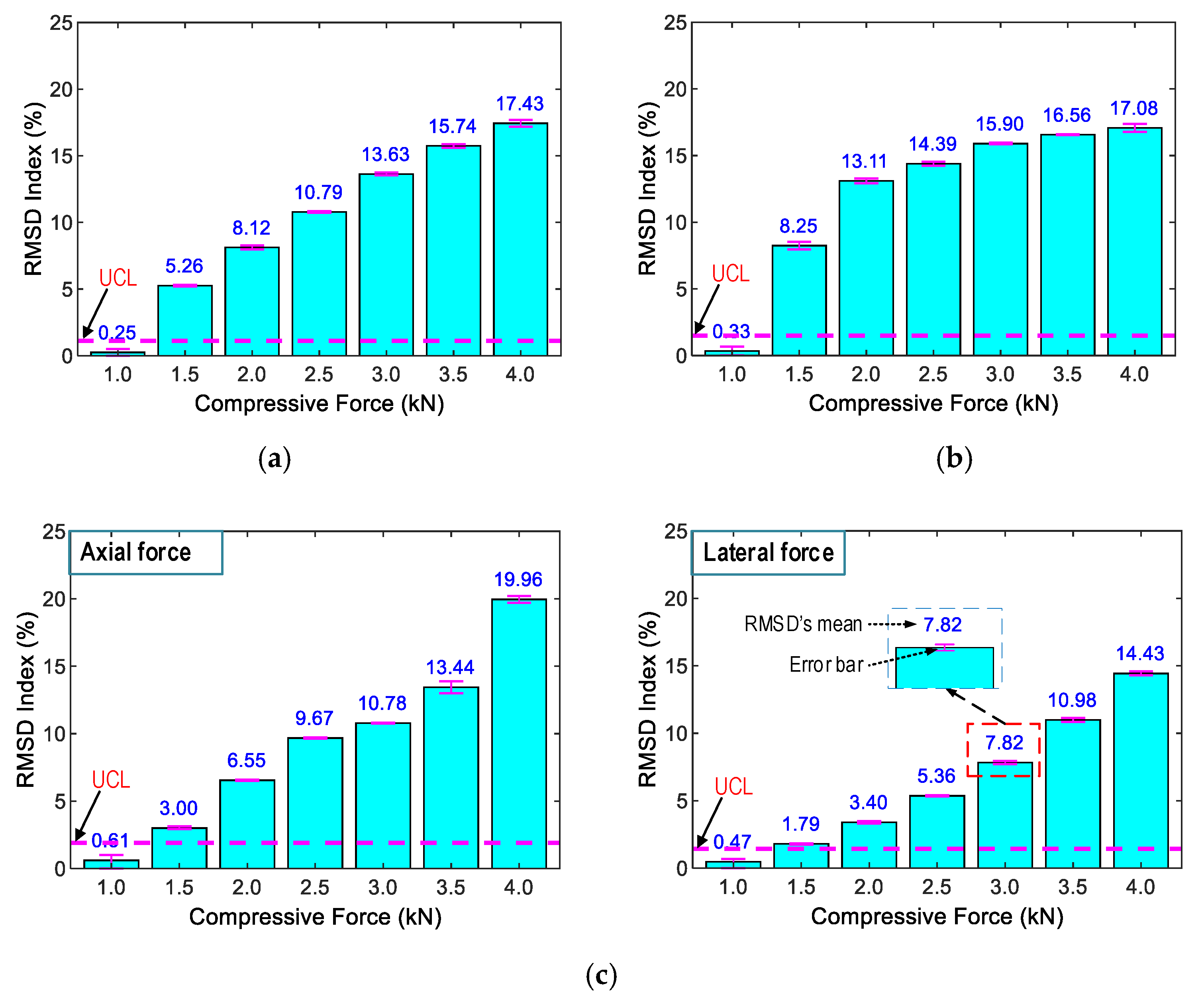
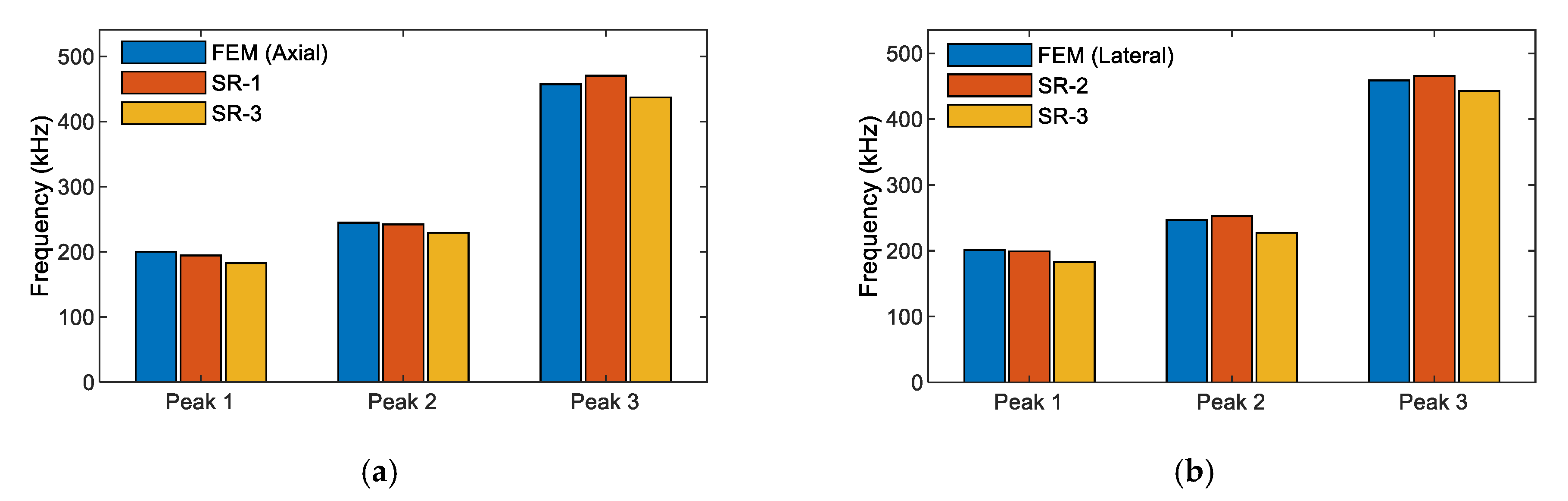
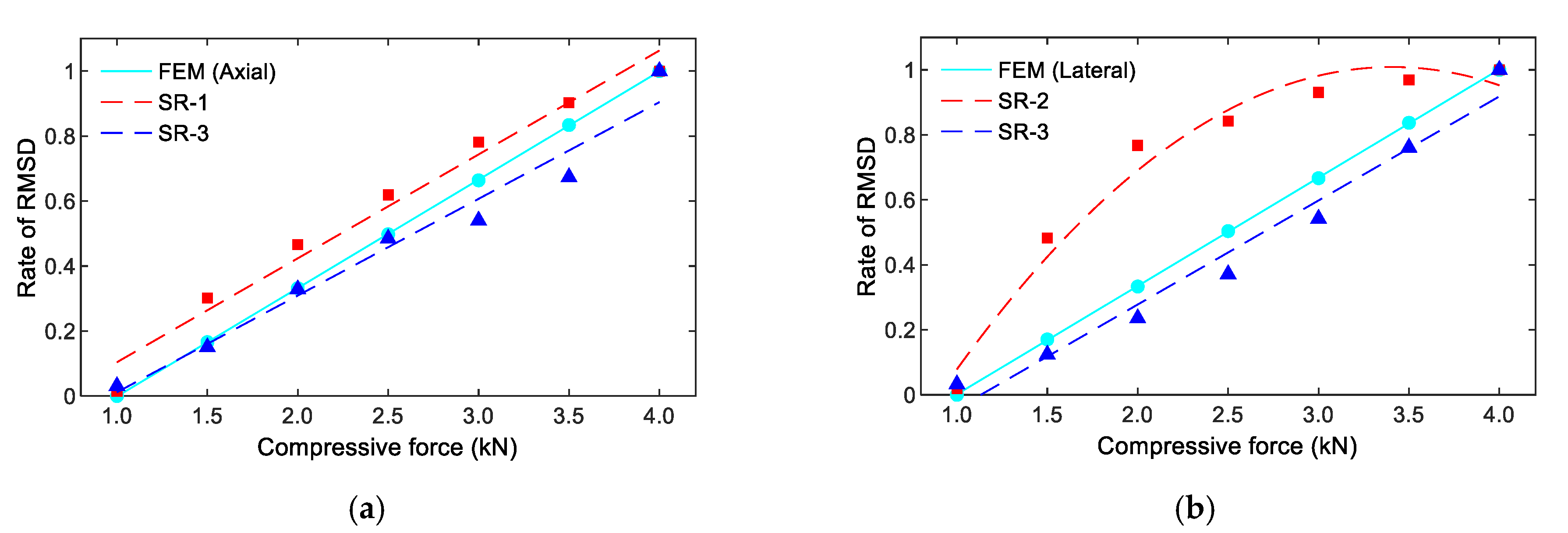


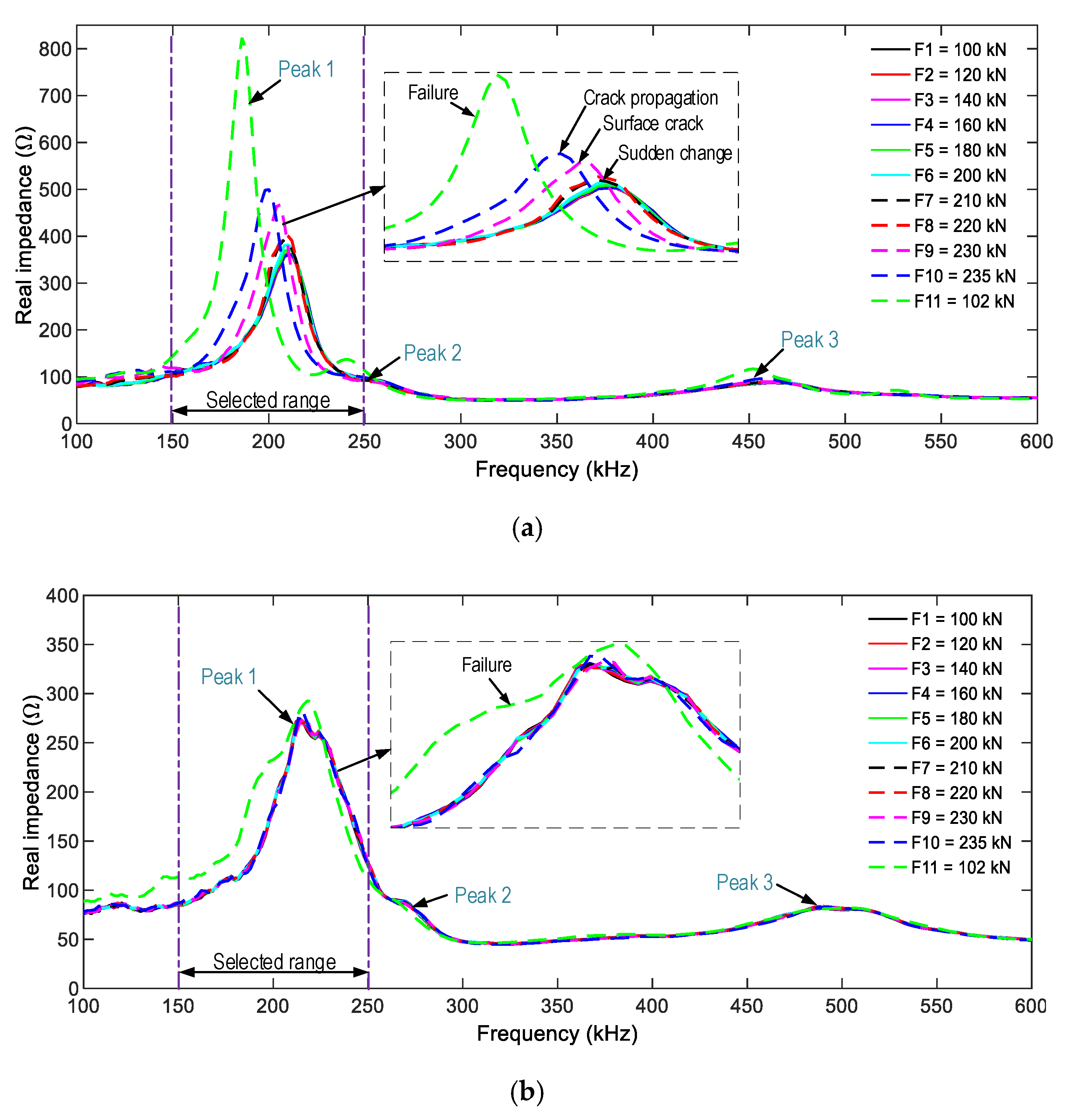

| Material | Mass (kg) |
|---|---|
| Cement | 346 |
| Sand | 800 |
| Aggregate (Dmax 25) | 997 |
| Water | 165 |
| Mass Density, ρ (kg/m3) | Dielectric Constant | Coupling Constant d31 (m/V) | Young’s Modulus E (GPa) | Damping Loss Factor η | Dielectric Loss Factor δ |
|---|---|---|---|---|---|
| 7750 | 1.53 × 10−8 | −1.71 × 10−10 | 62.1 | 0.0125 | 0.015 |
| Properties | Concrete | Epoxy |
|---|---|---|
| Young’s modulus (GPa) | 23.6 | 0.74 |
| Poisson’s ratio | 0.2 | 0.3 |
| Mass density (kg/m3) | 2300 | 1090 |
| Tensile strength (MPa) | 2.3 | 20.1 |
| Compressive strength (MPa) | 23.3 | 32.3 |
| Test | Name | Force Direction | Applied Load | |
|---|---|---|---|---|
| Axial | Lateral | |||
| 1 | SR-1 | o | - | P1 (1.0 kN) → P7 (4.0 kN) 0.5 kN incrementin a row |
| 2 | SR-2 | - | o | |
| 3 | SR-3 | o | - | |
| 4 | - | o | ||
| Case | Applied Force | Concrete Surface’s Crack Development | |
|---|---|---|---|
| F (kN) | Bearing Stress σb (MPa) ** | ||
| F1 → F6 | 100 → 200 | 17.3 → 34.6 | |
| F7 | 210 | 36.4 | |
| F8 | 220 | 38.1 | |
| F9 | 230 | 39.8 | |
| F10 | 235 * | 40.7 | |
| F11 | 102 | 17.7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, Q.-Q.; Dang, N.-L.; Kim, J.-T. Piezoelectric Sensor-Embedded Smart Rock for Damage Monitoring in a Prestressed Anchorage Zone. Sensors 2021, 21, 353. https://doi.org/10.3390/s21020353
Pham Q-Q, Dang N-L, Kim J-T. Piezoelectric Sensor-Embedded Smart Rock for Damage Monitoring in a Prestressed Anchorage Zone. Sensors. 2021; 21(2):353. https://doi.org/10.3390/s21020353
Chicago/Turabian StylePham, Quang-Quang, Ngoc-Loi Dang, and Jeong-Tae Kim. 2021. "Piezoelectric Sensor-Embedded Smart Rock for Damage Monitoring in a Prestressed Anchorage Zone" Sensors 21, no. 2: 353. https://doi.org/10.3390/s21020353






