The Effect of Miss and Tuck Stitches on a Weft Knit Strain Sensor
Abstract
:1. Introduction
2. Related Work
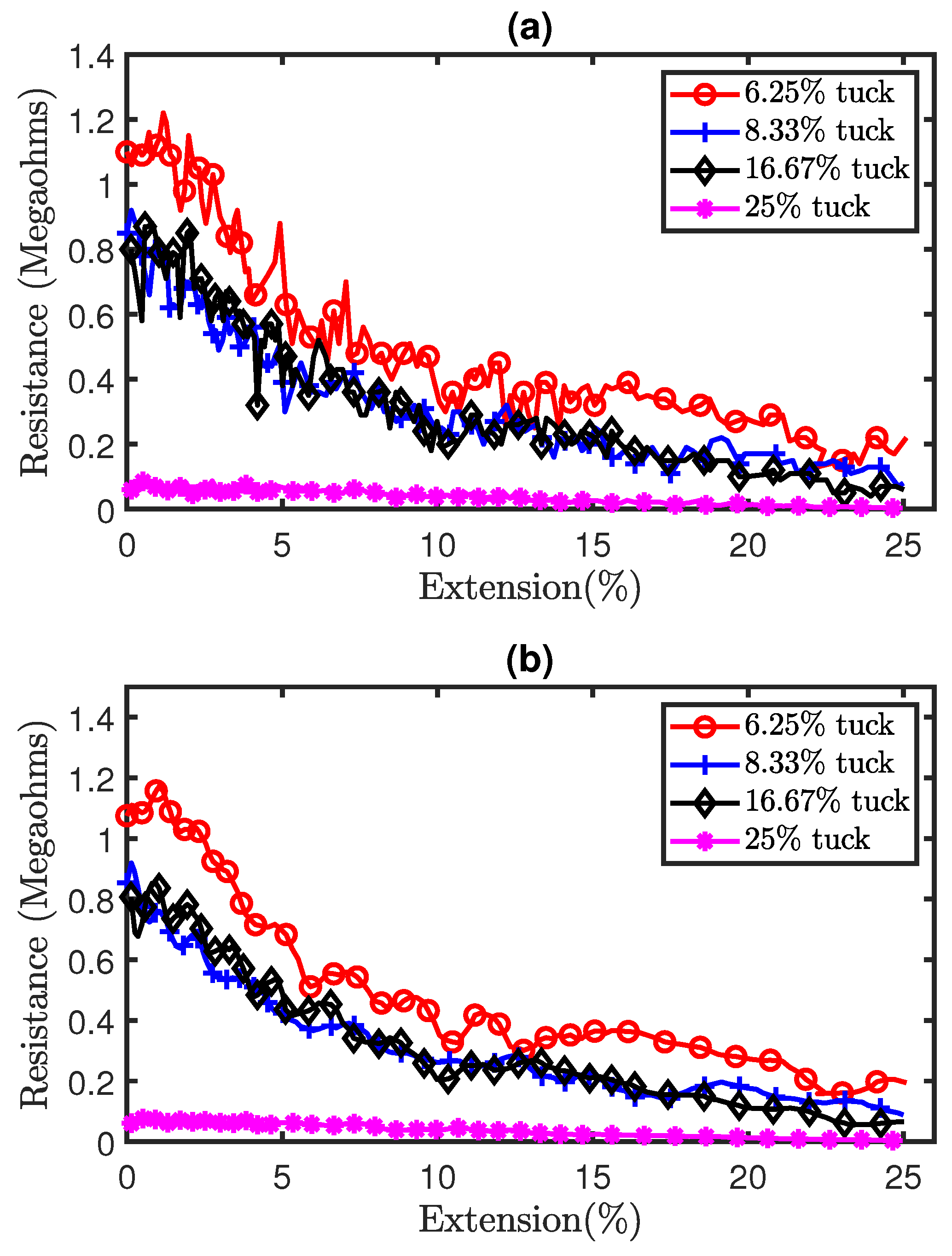
- The samples with M2T of (40:10) and (10:40) showed the largest dynamic range. This is excellent for strain applications, because the sensor can absorb the strain due to its flexibility.
- The variation of resistance values was more stable in the four samples than in the control sample. This allows for more accurate measurements in strain sensing applications. The samples with the most stable resistance values were samples with M2T of (10:40) and (45:5).
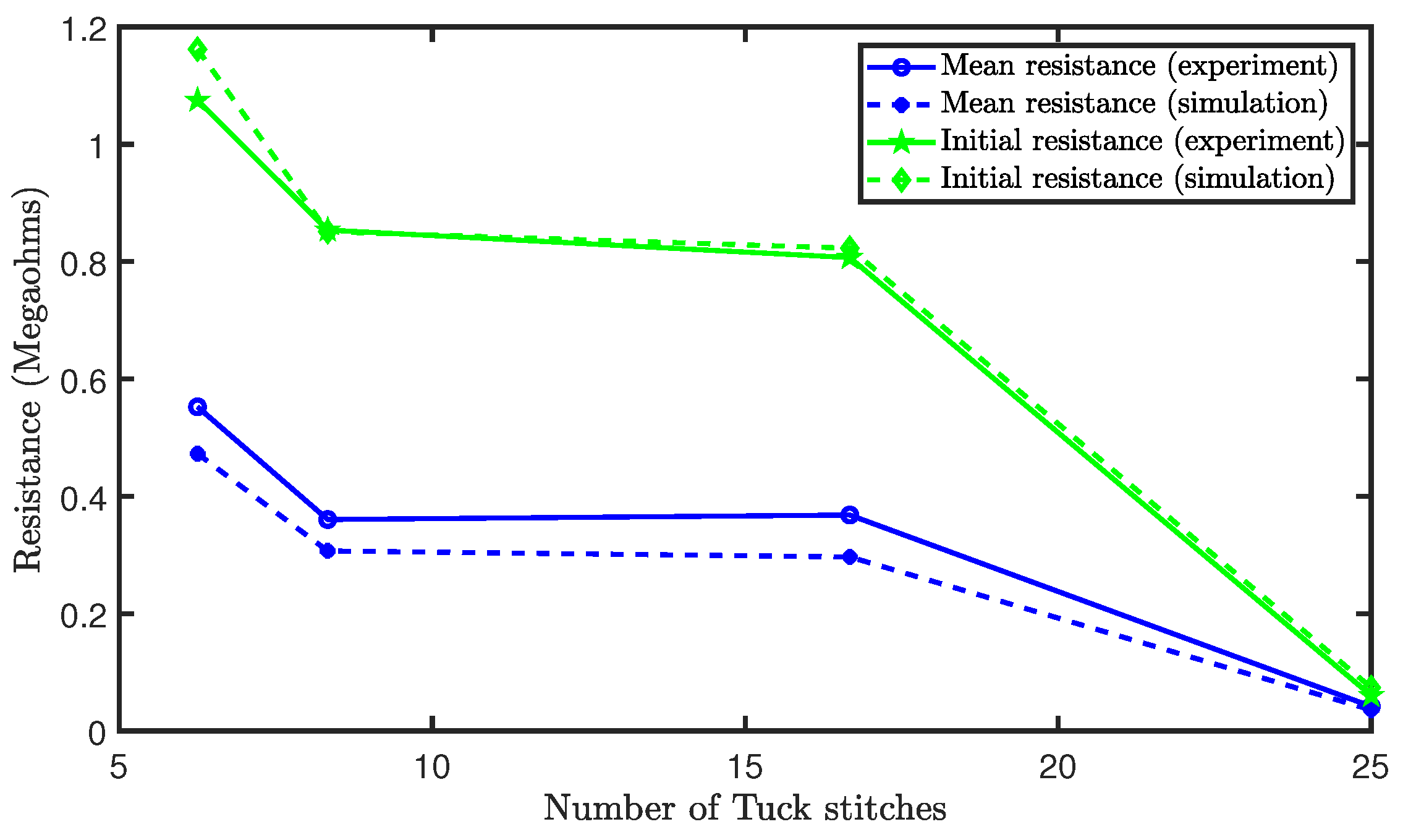
- Samples with a higher fabric thickness had a lower MER, while samples with a lower optical porosity had a lower MER. A lower MER is needed for an optimal regulation of the contact resistance, and this is achieved because a higher fabric thickness and lower optical porosity increase the contact area between the yarns. It was observed that all four samples had a lower MER when compared to the control sample with samples with M2T of (10:40) and (45:5) being the lowest.
3. Materials and Methods
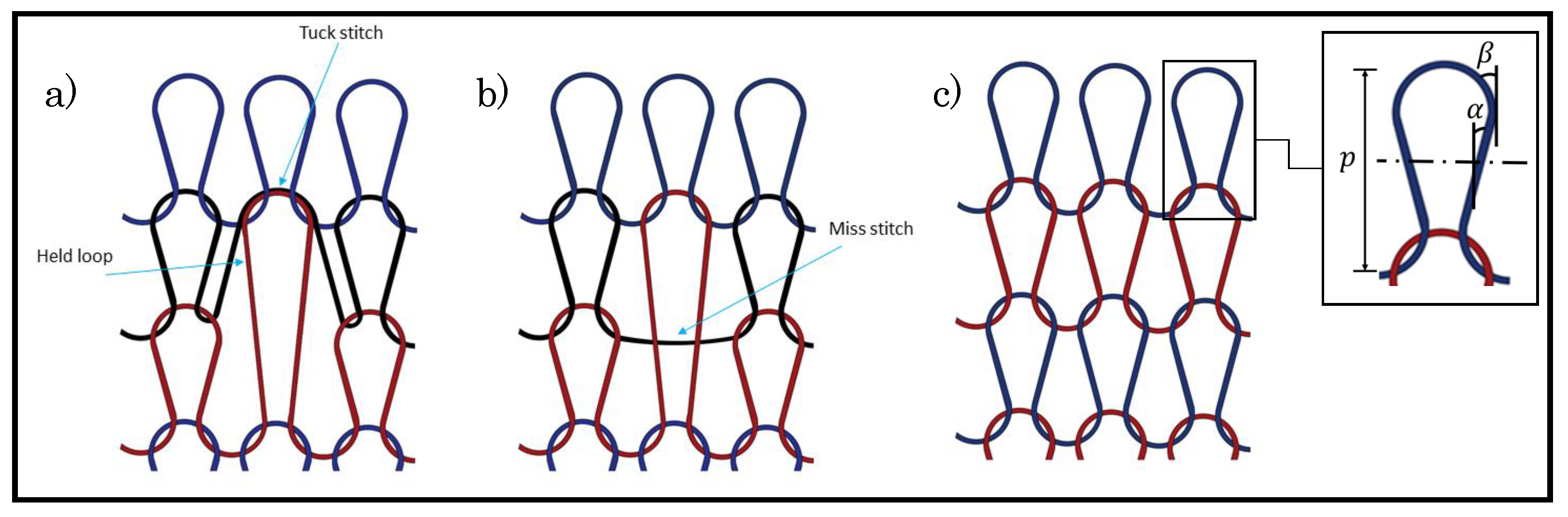
3.1. Electromechanical Model of a Tuck Stitch
- The conductive yarn used is a perfect intrinsic conductor.
- The lengths of the head of a tuck stitch and the head of its held knitted loop stitch are equal.
- The head and sinker of a knitted loop stitch are of equal lengths.
3.2. Electromechanical Model of a Miss Stitch
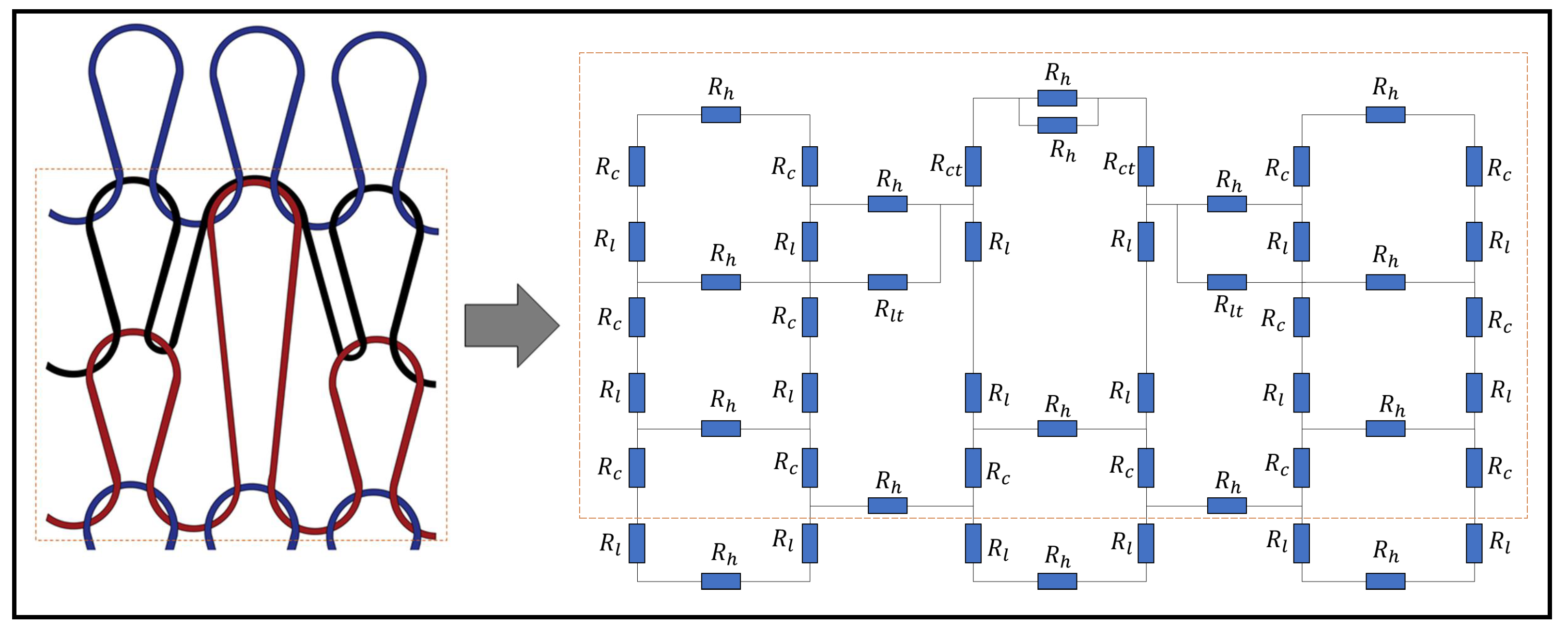
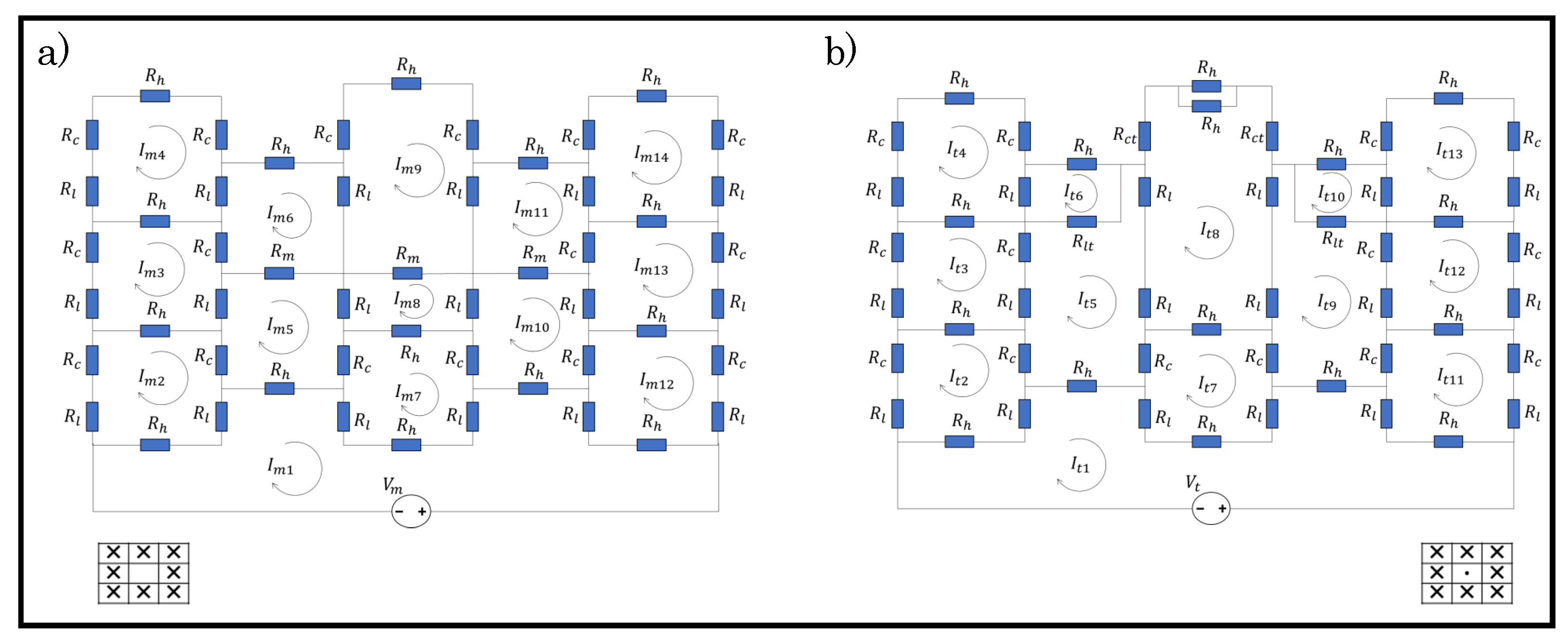
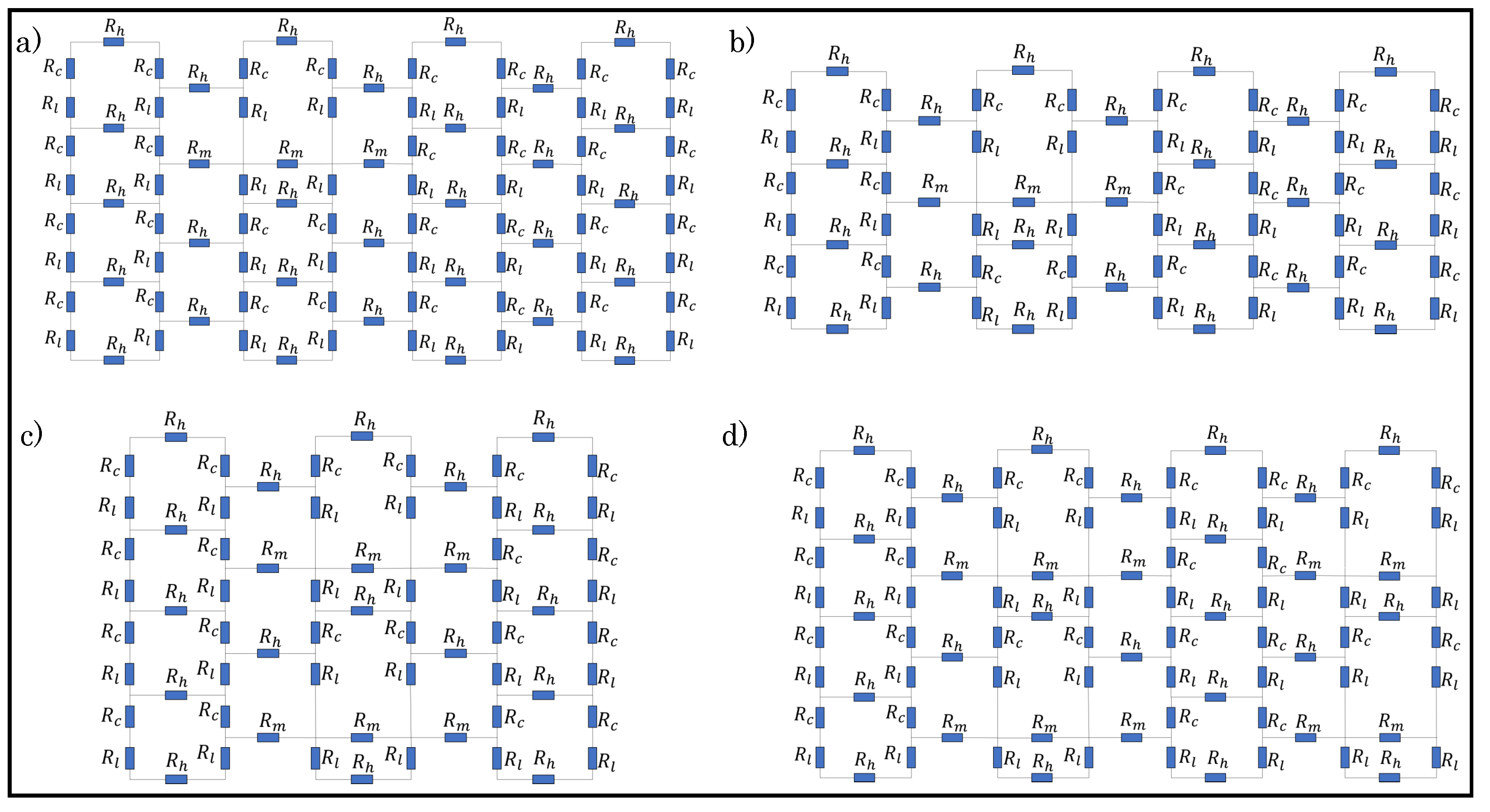
3.3. Circuit Analysis
3.4. Determination of Contact Resistance
| Algorithm 1 Contact Resistance Solution |
|
3.5. Simulation Parameters
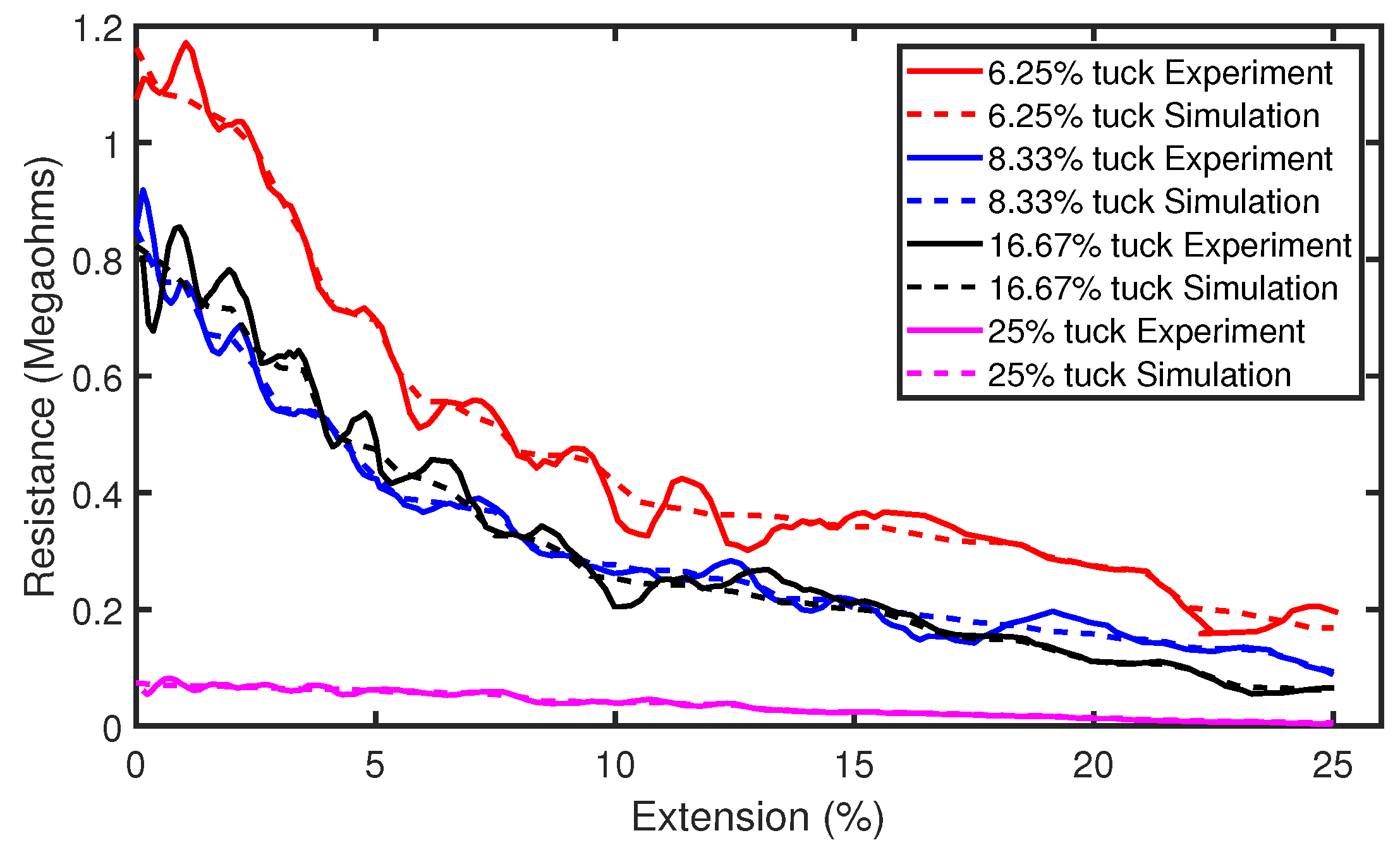
3.6. Experimental Validation
3.6.1. Sample Preparation
3.6.2. Experimental Procedure
4. Results and Discussion
4.1. Effect of Tuck Stitches on a Weft Knit Sensor
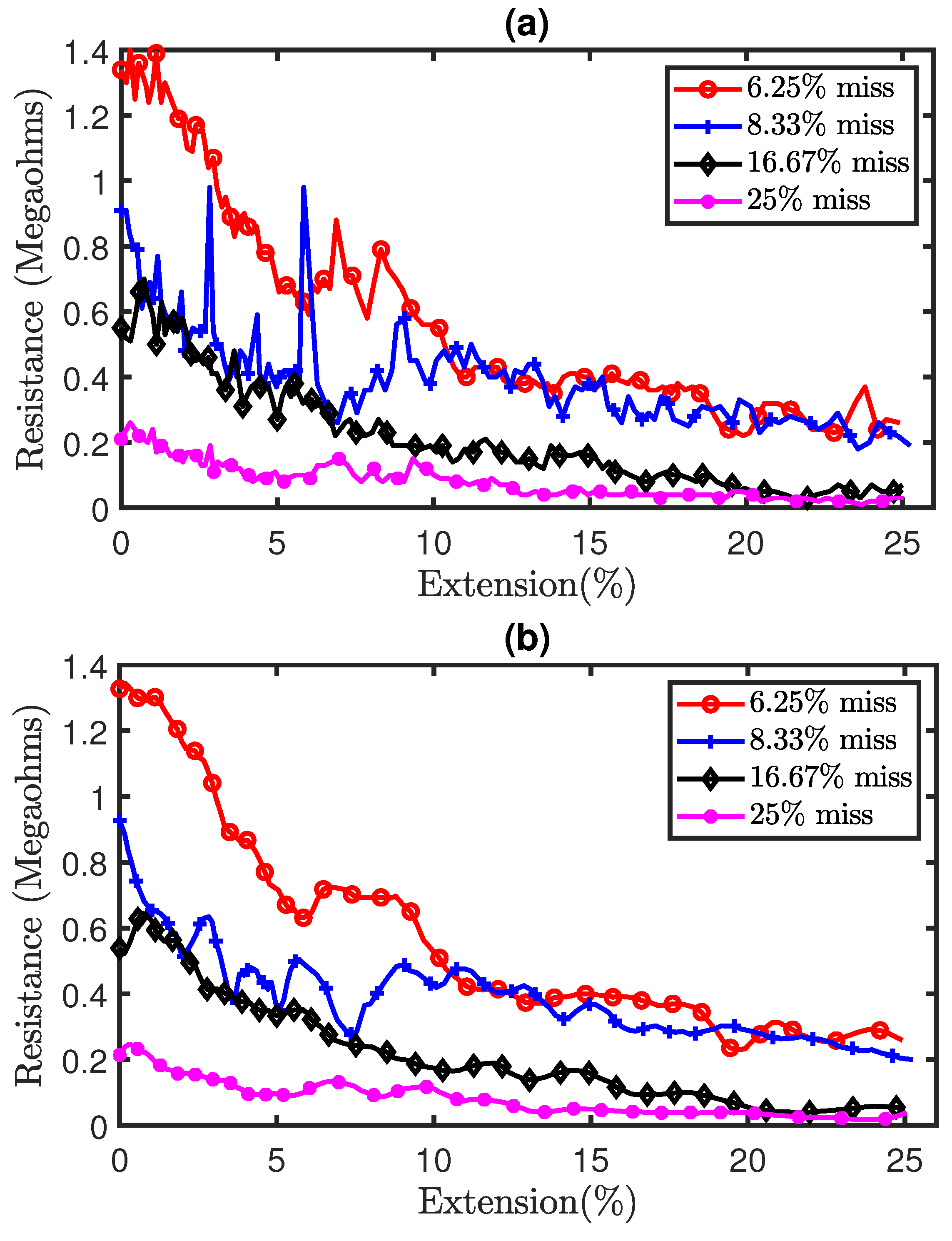
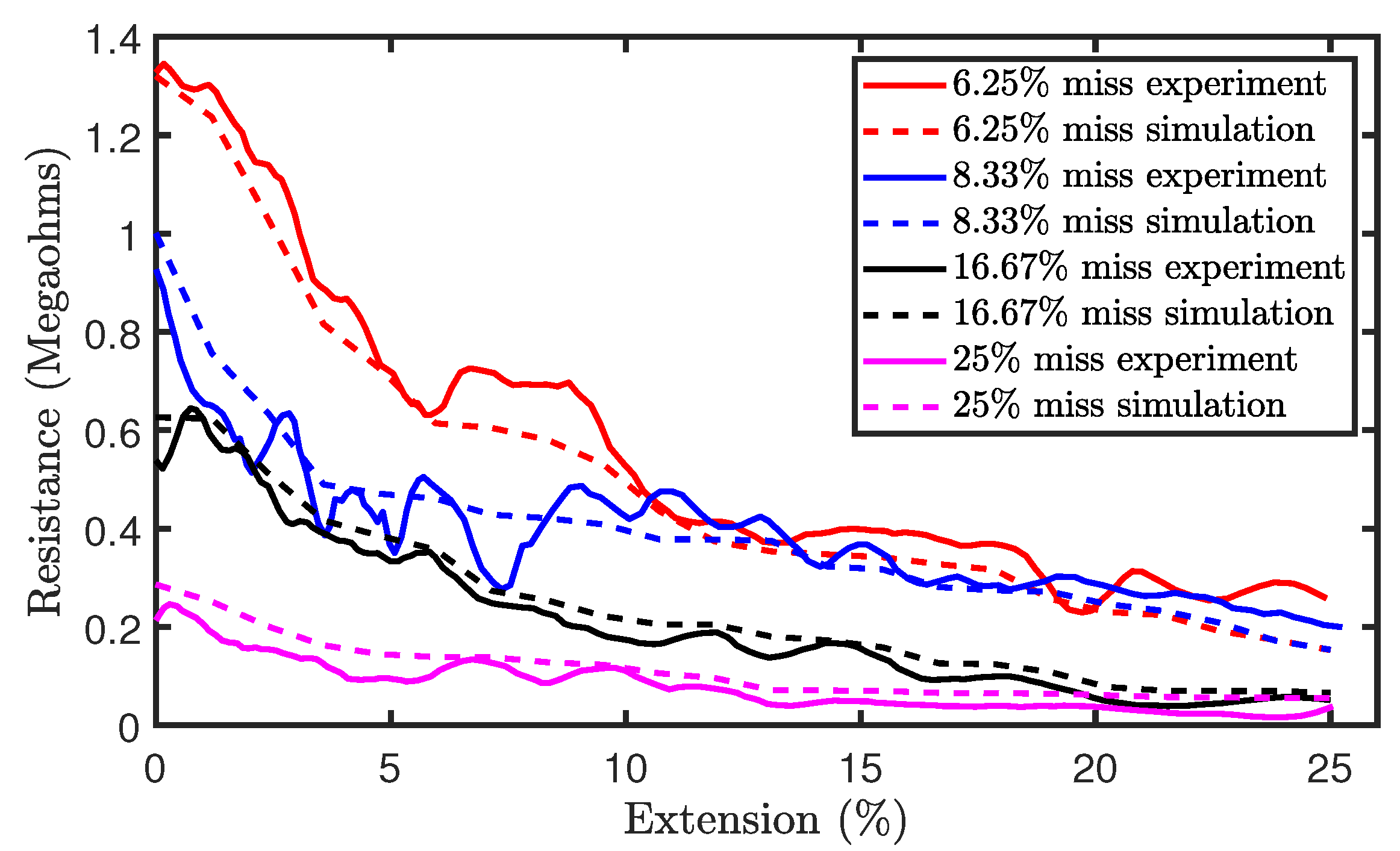
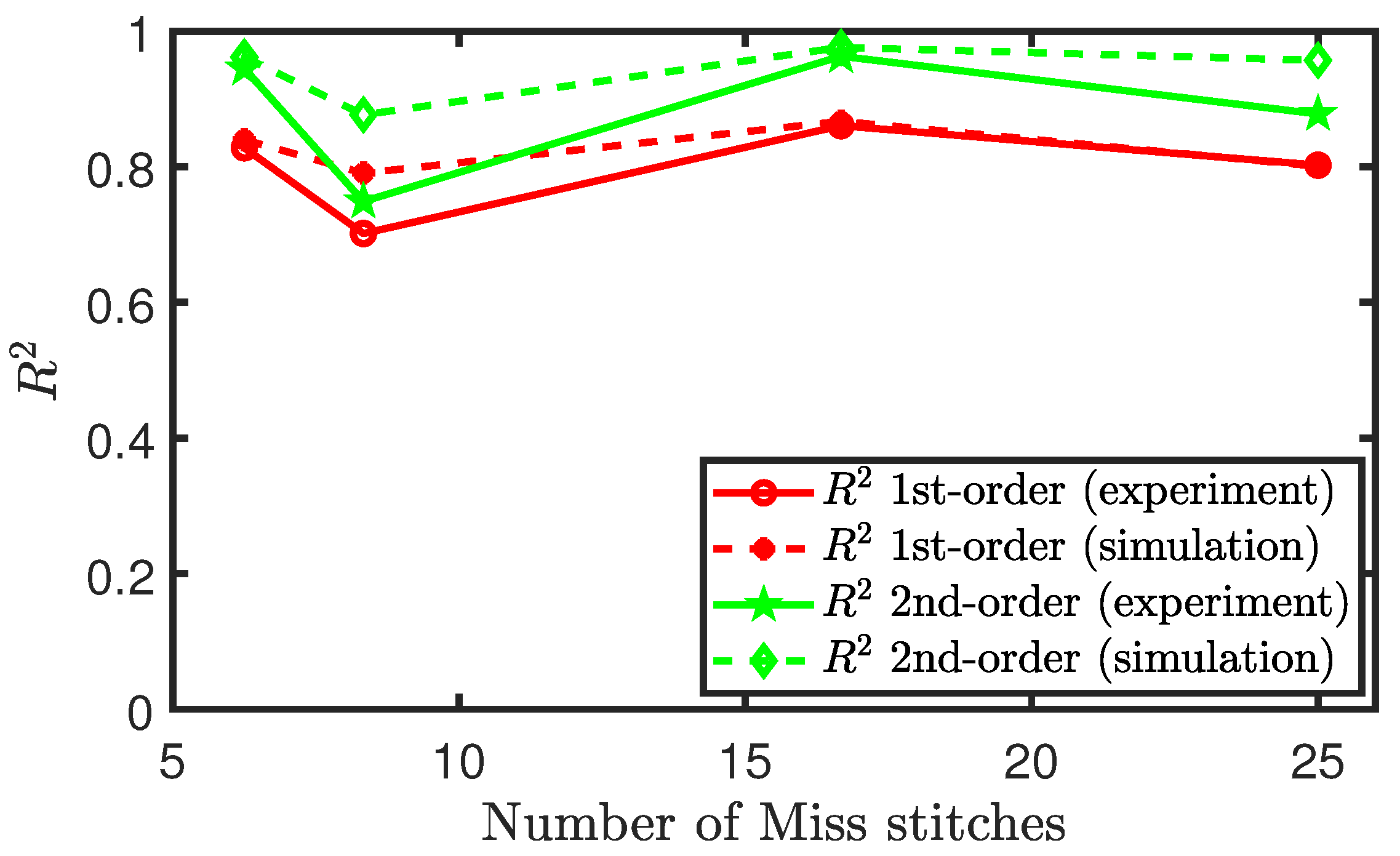
4.2. Effect of Miss Stitches on a Weft Knit Sensor
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiang, C.; Guo, J.; Sun, R.; Hinitt, A.; Helps, T.; Taghavi, M.; Rossiter, J. Electroactive textile actuators for breathability control and thermal regulation devices. Polymers 2019, 11, 1199. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Almohammed, B.; Ismail, A.; Sali, A. Electro-textile wearable antennas in wireless body area networks: Materials, antenna design, manufacturing techniques, and human body consideration—A review. Text. Res. J. 2020. [Google Scholar] [CrossRef]
- Ferri, J.; Llinares Llopis, R.; Martinez, G.; Lidon Roger, J.V.; Garcia-Breijo, E. Comparison of E-Textile Techniques and Materials for 3D Gesture Sensor with Boosted Electrode Design. Sensors 2020, 20, 2369. [Google Scholar] [CrossRef] [PubMed]
- Atalay, O.; Kennon, W.R.; Demirok, E. Weft-knitted strain sensor for monitoring respiratory rate and its electro-mechanical modeling. IEEE Sens. J. 2015, 15, 110–122. [Google Scholar] [CrossRef]
- Patron, D.; Mongan, W.; Kurzweg, T.P.; Fontecchio, A.; Dion, G.; Anday, E.K.; Dandekar, K.R. On the use of knitted antennas and inductively coupled RFID tags for wearable applications. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 1047–1057. [Google Scholar] [CrossRef]
- Isaia, C.; McMaster, S.A.; McNally, D. Study of Performance of Knitted Conductive Sleeves as Wearable Textile Strain Sensors for Joint Motion Tracking. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 4555–4558. [Google Scholar]
- Wang, J.; Soltanian, S.; Servati, P.; Ko, F.; Weng, M. A knitted wearable flexible sensor for monitoring breathing condition. J. Eng. Fibers Fabr. 2020, 15, 1558925020930354. [Google Scholar] [CrossRef]
- Li, Y.; Miao, X.; Raji, R.K. Flexible knitted sensing device for identifying knee joint motion patterns. Smart Mater. Struct. 2019, 28, 115042. [Google Scholar] [CrossRef]
- Zhang, H.; Tao, X.; Wang, S.; Yu, T. Electro-mechanical properties of knitted fabric made from conductive multi-filament yarn under unidirectional extension. Text. Res. J. 2005, 75, 598–606. [Google Scholar] [CrossRef]
- Fan, W.; He, Q.; Meng, K.; Tan, X.; Zhou, Z.; Zhang, G.; Yang, J.; Wang, Z.L. Machine-knitted washable sensor array textile for precise epidermal physiological signal monitoring. Sci. Adv. 2020, 6, eaay2840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ou, J.; Oran, D.; Haddad, D.D.; Paradiso, J.; Ishii, H. SensorKnit: Architecting textile sensors with machine knitting. 3D Print. Addit. Manuf. 2019, 6, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Atalay, O.; Kennon, W.R.; Husain, M.D. Textile-based weft knitted strain sensors: Effect of fabric parameters on sensor properties. Sensors 2013, 13, 11114–11127. [Google Scholar] [CrossRef] [PubMed]
- Atalay, O.; Kennon, W. Knitted strain sensors: Impact of design parameters on sensing properties. Sensors 2014, 14, 4712–4730. [Google Scholar] [CrossRef]
- Holm, R. Electric Contacts: Theory and Application; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Atalay, O.; Tuncay, A.; Husain, M.D.; Kennon, W.R. Comparative study of the weft-knitted strain sensors. J. Ind. Text. 2017, 46, 1212–1240. [Google Scholar] [CrossRef]
- Spencer, D.J. Knitting Technology: A Comprehensive Handbook and Practical Guide; Woodward Publishing: Cambridge, UK, 2001; Volume 16. [Google Scholar]
- McMaster, S.A. Method for Making Electrically Conductive Textiles and Textile Sensor. U.S. Patent 10,119,208, 6 November 2018. [Google Scholar]
- Liu, S.; Liu, Y.; Li, L. The impact of different proportions of knitting elements on the resistive properties of conductive fabrics. Text. Res. J. 2019, 89, 881–890. [Google Scholar] [CrossRef]
- Liu, S.; Yang, C.; Zhao, Y.; Tao, X.M.; Tong, J.; Li, L. The impact of float stitches on the resistance of conductive knitted structures. Text. Res. J. 2016, 86, 1455–1473. [Google Scholar] [CrossRef]
- Postle, R.; Munden, D. Analysis of the Dry-Relaxed Knitted-Loop Configuration: Part I: Two-Dimensional Analysis. J. Text. Inst. 1967, 58, 329–351. [Google Scholar] [CrossRef]
- Kurbak, A.; Kayacan, O. Basic studies for modeling complex weft knitted fabric structures part V: Geometrical modeling of tuck stitches. Text. Res. J. 2008, 78, 577–582. [Google Scholar] [CrossRef]
- Munden, D. The geometry and dimensional properties of plain-knit fabrics. J. Text. Inst. Trans. 1959, 50, T448–T471. [Google Scholar] [CrossRef]
- Zhang, H.; Tao, X. From wearable to aware: Intrinsically conductive electrotextiles for human strain/stress sensing. In Proceedings of the 2012 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), Hong Kong, China, 5–7 January 2012; pp. 468–471. [Google Scholar]
- Li, L.; Au, W.M.; Wan, K.M.; Wan, S.H.; Chung, W.Y.; Wong, K.S. A resistive network model for conductive knitting stitches. Text. Res. J. 2010, 80, 935–947. [Google Scholar] [CrossRef]






| % of Miss/Tuck Stitches | Loop Configuration (Miss) | Loop Configuration (Tuck) |
|---|---|---|
| 6.25% |  |  |
| 8.33% | 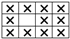 | 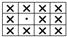 |
| 16.67% | 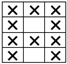 |  |
| 25% | 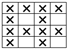 | 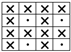 |
| Parameters | Values |
|---|---|
| Number of courses | 72 |
| Number of wales | 72 |
| 24.75 | |
| 10.85 | |
| Course spacing (mm) | 3 |
| Wale spacing (mm) | 2 |
| 300 | |
| Yarn’s Diameter (mm) | 0.4 |
| Configuration | Wales/cm | Courses/cm | Stitch Density |
|---|---|---|---|
| 6.25% Miss | 5.00 | 5.39 | 26.95 |
| 8.33% Miss | 4.56 | 5.43 | 24.76 |
| 16.67% Miss | 4.97 | 5.50 | 27.34 |
| 25% Miss | 5.04 | 6.05 | 30.49 |
| 6.25% Tuck | 4.11 | 5.48 | 22.52 |
| 8.33% Tuck | 4.07 | 5.63 | 22.91 |
| 16.67% Tuck | 3.60 | 6.49 | 23.64 |
| 25% Tuck | 3.16 | 7.24 | 22.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayodele, E.; Zaidi, S.A.R.; Scott, J.; Zhang, Z.; Hafeez, M.; McLernon, D. The Effect of Miss and Tuck Stitches on a Weft Knit Strain Sensor. Sensors 2021, 21, 358. https://doi.org/10.3390/s21020358
Ayodele E, Zaidi SAR, Scott J, Zhang Z, Hafeez M, McLernon D. The Effect of Miss and Tuck Stitches on a Weft Knit Strain Sensor. Sensors. 2021; 21(2):358. https://doi.org/10.3390/s21020358
Chicago/Turabian StyleAyodele, Emmanuel, Syed Ali Raza Zaidi, Jane Scott, Zhiqiang Zhang, Maryam Hafeez, and Des McLernon. 2021. "The Effect of Miss and Tuck Stitches on a Weft Knit Strain Sensor" Sensors 21, no. 2: 358. https://doi.org/10.3390/s21020358
APA StyleAyodele, E., Zaidi, S. A. R., Scott, J., Zhang, Z., Hafeez, M., & McLernon, D. (2021). The Effect of Miss and Tuck Stitches on a Weft Knit Strain Sensor. Sensors, 21(2), 358. https://doi.org/10.3390/s21020358






